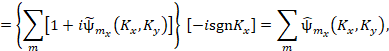1. Introduction

Optical diagnostics methods largely determine the level of experimental research in modern hydro and gas dynamics. The choice of convective flows as an object of optical diagnostics is explained by the special importance of convection in geodynamics, atmospheric and ocean physics, in hydrodynamic and thermophysical processes with phase transitions [1, 2]. Interest in these problems has escalated recently due to the intensification of cyclic processes of melting and ice formation in the Arctic and Antarctic regions, which have a huge impact on the world's oceans and climate. Experimental and theoretical studies of convective processes and of the dynamics of the water - ice phase transition, which take into account the anomaly of water density in the region of 0 ÷ 4 ° C, are necessary for numerous technical and technological applications [3]. The study of the dynamics of phase transitions in a supercooled liquid and the evolution of convective structures in a water-ice system requires the use of non-perturbing diagnostic methods based on modern advances in optics, laser technology and information technology. The present work is motivated by the need for such research.

2. Method and experimental setup

A simplified diagram of a research complex containing an optical diagnostics system and an experimental stand is shown in Figure 1.

 

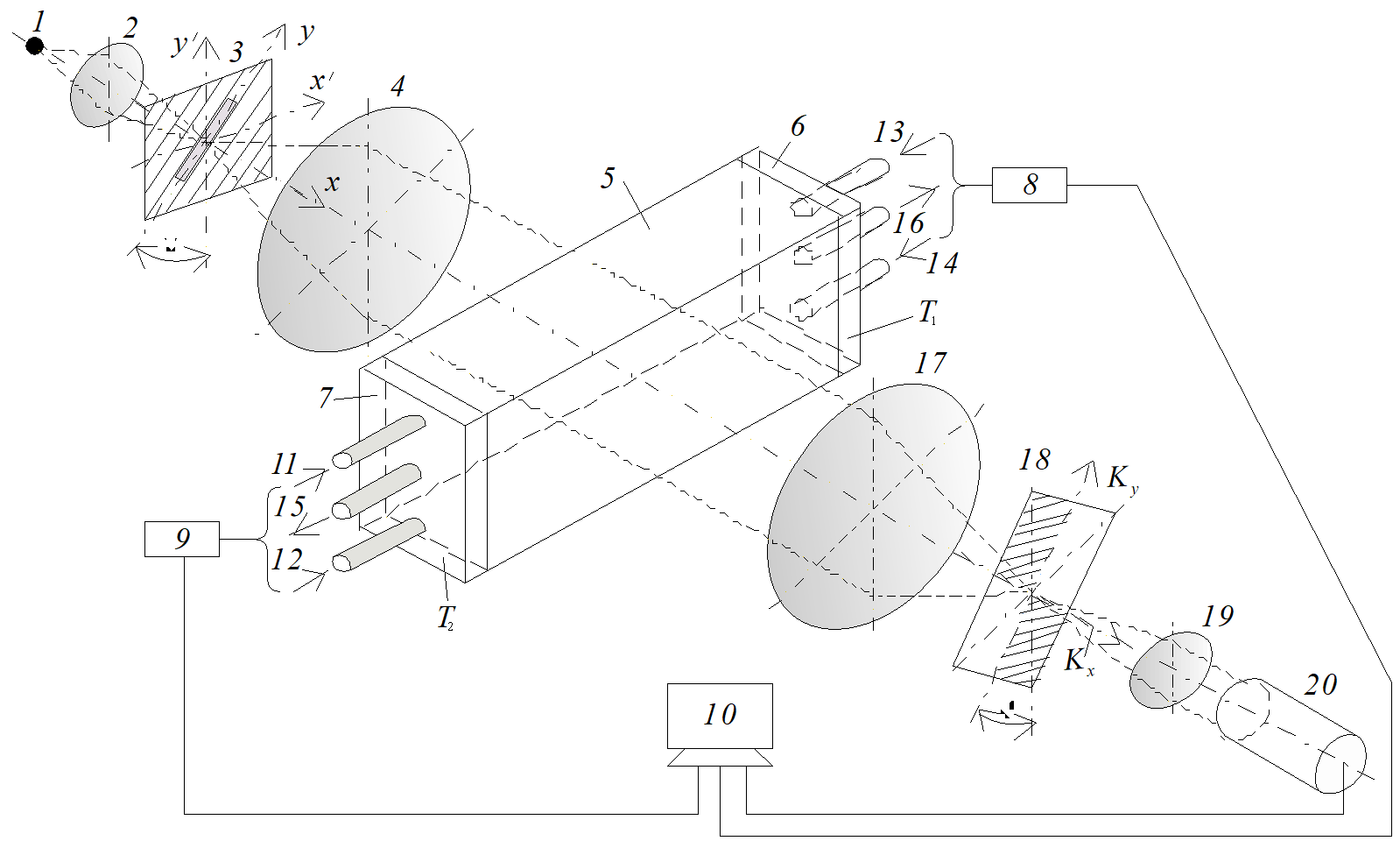
Fig. 1. Scheme of the experimental setup.

 

Fig. 2. The rectangular cavity with water. Optical tubes that feed the refrigerant to the heat transfer side plates are visible.

 

The diagram contains a lighting module consisting of a light source 1 (DRSh - 250 mercury lamp), a condenser lens 2 and a slit diaphragm 3 placed in the front focal plane of the lens 4, which forms a probing field in the test medium. Here water is used as the medium and it fills up the rectangular cavity 5 with transparent glasses of optical quality (Fig. 2). The internal dimensions of the cavity are 136 × 86 × 30 mm, the side walls are formed by high-quality cooled flat parallel copper plates 6 and 7. The temperature of one of the plates (T₁) is controlled and maintained by a thermostat within up to -28°C. The temperature of the other plate (T₂) is in the range from room temperature to ~ 8.0°C. Inside the plates there are cavities into which coolant is supplied from thermostats 8 and 9. Thermostats are controlled by computer 10 according to a given program. The tubes supplying the refrigerant to the heat exchange side plates are designated as 11-14, the outflow tubes are 15, 16. The arrangement of the feed tubes and outflow tubes may vary according to the conditions of the experiment. The distance between the tubes is 80 mm. The lens 17 forms in the frequency plane the Fourier spectrum of the probing light field perturbed by the medium under study. The quadrant Hilbert filter 18 is placed in the Fourier plane of the lens 17. The frequency axis K_х of the Hilbert filter is orthogonal to the direction of the image of the slit diaphragm of the light source (ψ=45°). The lens 19 performs the inverse Fourier transform of the Hilbert spectrum of the optical signal. The visualized phase structure of the light field, perturbed by the medium under study, is recorded by the digital video camera 20 connected to the computer 16. The optical diagnostics system was implemented on the basis of the serial IAB-463M shadow device [3], in which the following modules were modified: the light source module, the Fourier filtering module of the optical signal and the image recording module of the phase perturbations of the light field induced by the medium under study. The probing field, formed by the lens 4, passes through the test medium (water), in which the boundary conditions for temperature (T₁ and T₂, T₁ <T₂) are set according to a given program by lateral thermostatted surfaces 6 and 7. In the space between the thermostatted surfaces, convective structures arise, which appear as perturbations of the fields of optical phase density. These structures are induced by Rayleigh-Benard convection and complicated by the presence of a phase transition and an anomaly in the density of water in the temperature range of 0÷4°C.

 

Near the lateral temperature-controlled surface, as the temperature gradient grows, water turns into a supercooled liquid, passing into a state of unstable equilibrium. In such a medium, the transition from liquid phase to solid-crystalline state occurs. This is a phase transition of the first kind. It becomes apparent through the appearance of a crystallization wave and is accompanied by an energy release. In its turn the release affects the dynamic distribution of the optical phase density gradient in supercooled water and induces phase perturbations in the probing light field, the Fourier spectrum of which forms in the frequency plane of the lens 17.

 

The coherent transfer function of the spatial-frequency filter 18 that performs the one-dimensional Hilbert transform is described by the following expression:

 

+

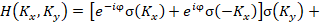
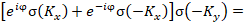
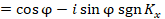
(1)

 

where 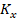and 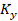are spatial frequencies; 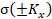and 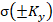are Heaviside functions; 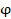is the phase shift defined by the corresponding quadrant of the spatial-frequency filter. A filter with a coherent transfer function (1) performs a one-dimensional Foucault-Hilbert transform.

 

In the Fourier plane the spatial frequency axis 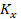is orthogonal to the image of the slot light source. Fourier spectrum of the light field directly after the filter:

 

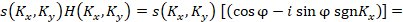
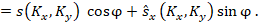
(2)

 

Here 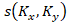is the spatial-frequency Fourier spectrum of the light field perturbed by the medium under study; 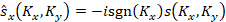is the Fourier spectrum of the light field subjected to a one-dimensional Hilbert transform along the axis 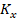. The phase shift 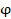is a function of the wave length 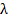of the probing light field: 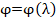. When the wavelength 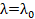, satisfies the condition 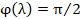, the Fourier filter 18 performs a one-dimensional Hilbert transform:

 

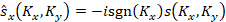
(3)

 

If the medium under study induces only phase perturbations of the probe field, the Fourier spectrum of the disturbed field is described by the expression

 

 

 

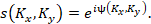
Filtered Fourier-spectrum of phase perturbations:

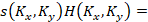
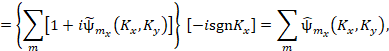
(4)

 

where 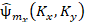is the Fourier-spectrum of phase perturbations corresponding to the mth-order Hilbert-fringe. Here it is taken into account that the Hilbert-transform has quasi-differentiating properties. Therefore, the Hilbert image reflects the structure of the phase perturbation field gradients.

The camcorder lens 19 performs the Fourier-transform of the filtered Fourier- spectrum of phase perturbations

 

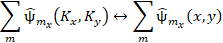
(5)

 

The phase structures (4) visualized by one-dimensional Hilbert transform are recorded by a camcorder photomatrix. Image of a one-dimensional Hilbert image of phase perturbations

 

 

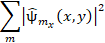
is analyzed in the coordinate system (хХ, уХ), rotated relative to the coordinate system (х, у) by a=45°:

 

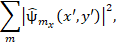
(6)

 

Where .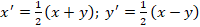

In case of a broadband source, a one-dimensional Foucault-Hilbert transform is performed with a coherent transfer function of the filter (1). The result of filtering is the transformation of the phase perturbations field into an analytical signal, which is a superposition of the filtered signal and its Hilbert-image. Hence, the signal detected by the photomatrix is a superposition of phase perturbation images and its Hilbert-forms. The recorded image is a structure consisting of Hilbert-fringes, displaying the gradients of perturbations of the optical phase density in the medium under study.

3. Results

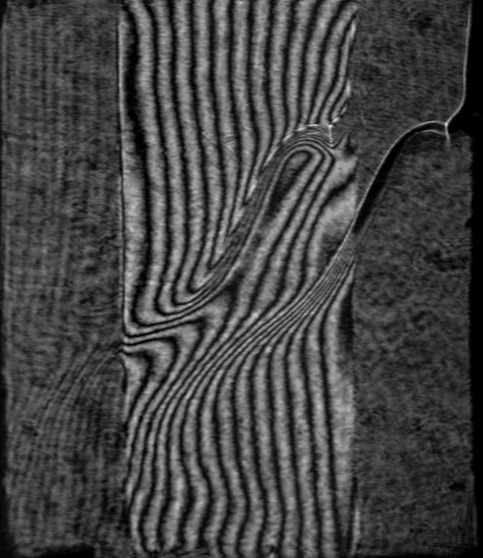
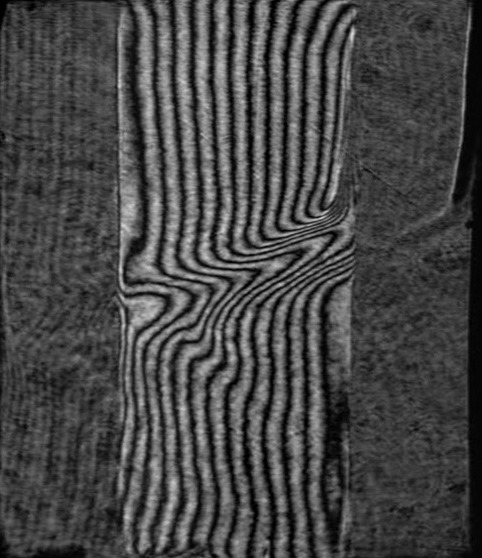
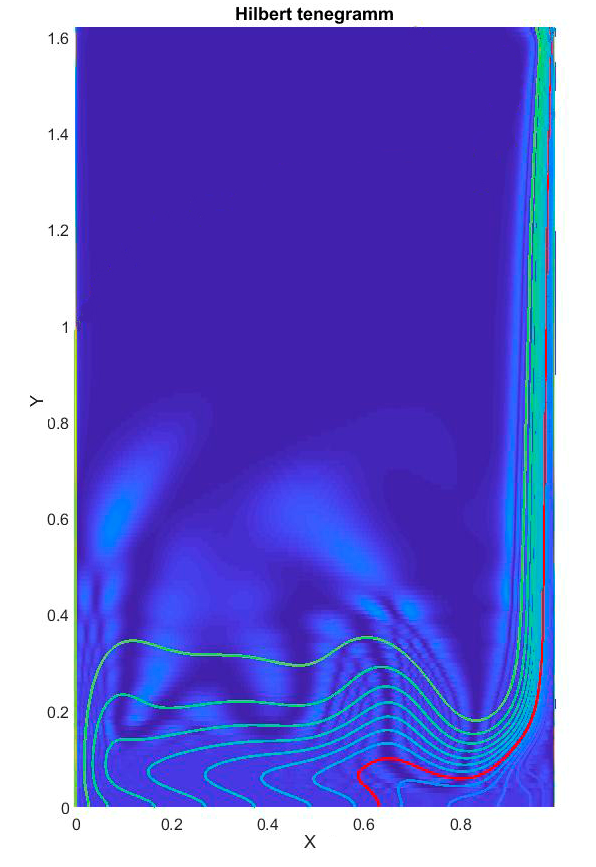
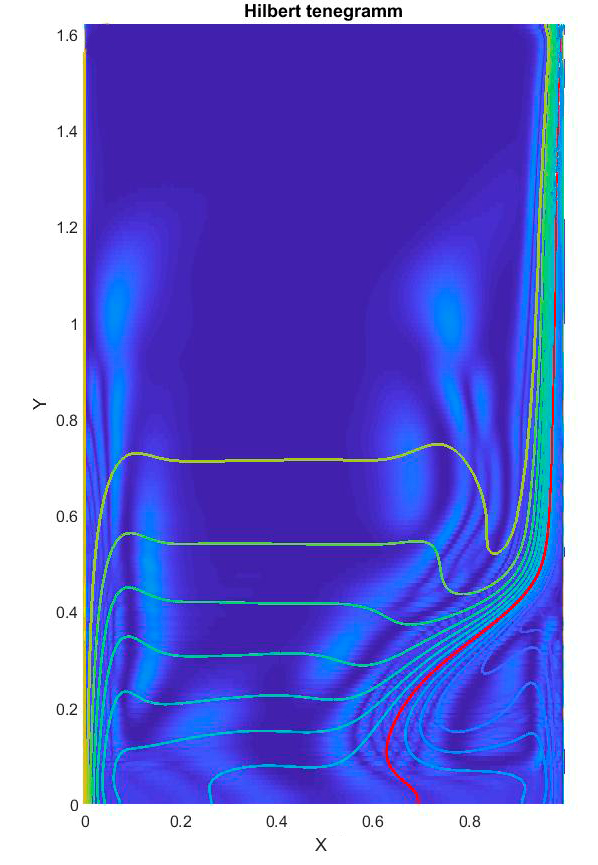
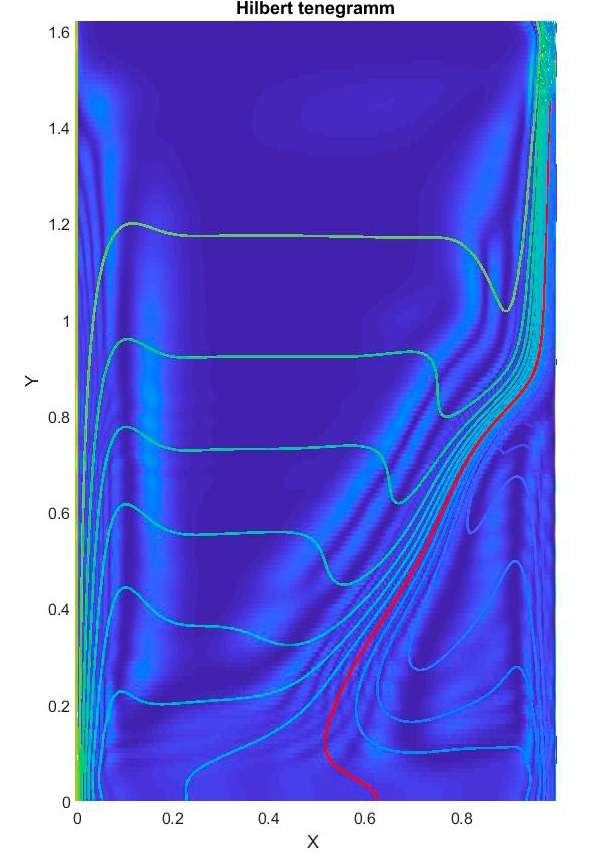
Figure 3 shows a selection of frames from a video film which illustrates the Hilbert-visualization of convective structures in a layer of fresh water bounded by vertical flat heat-transfer surfaces.

 

 

Fig. 3. Video frames illustrating Hilbert-visualization of convective structures and phase transition in water.

 

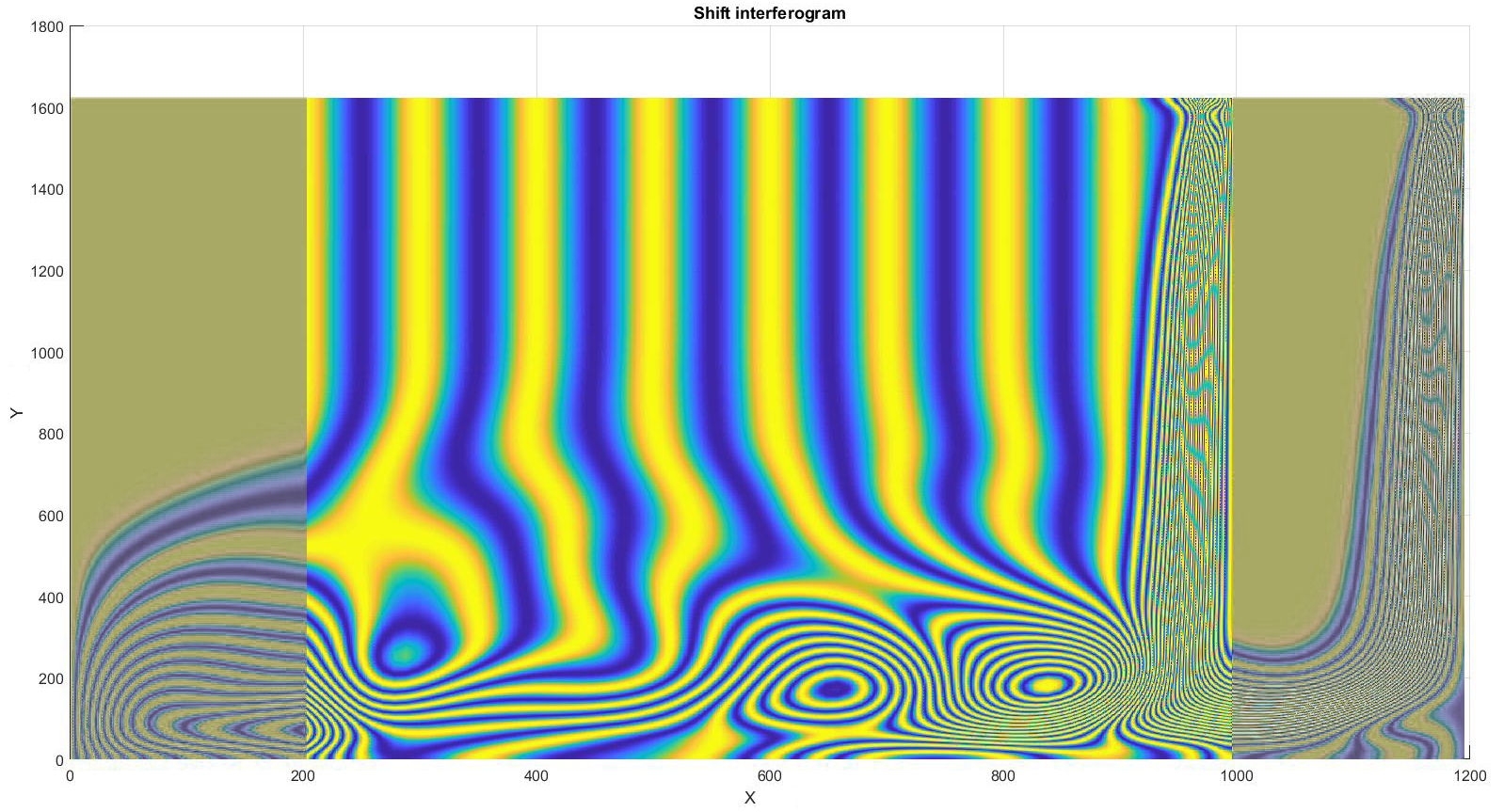
Figure 4 presents an example of convective structures and a phase transition in the same layer, visualized by shear interferometry. Hilbertrograms and shear interferograms display extremes of the phase gradients and correspond to isotherms.

The usage for the approximation of Bernstein polynomials allows you to build a grid that adapts to the deformations of the interference lines. Figure 5 illustrates the approximation of interference fringes by Bezier curves.

 

Fig. 4. Shear interferograms visualizing convective structures and phase transitions in a vertical layer of fresh water.

 

 

Fig. 5. Approximation by Bezier curves of interference fringes on the shear interferogram.

 

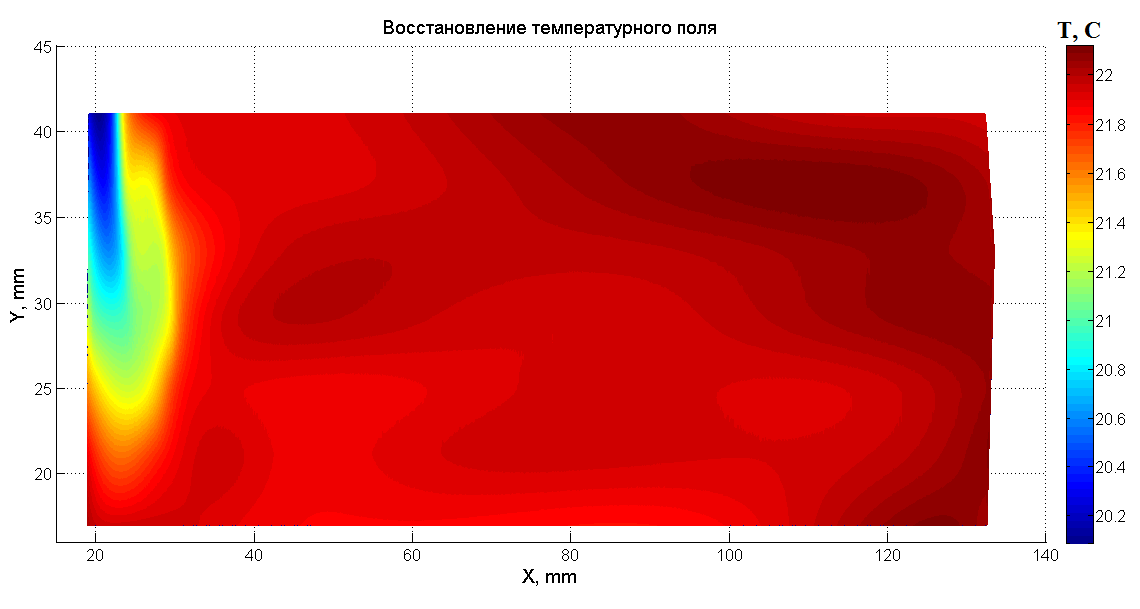
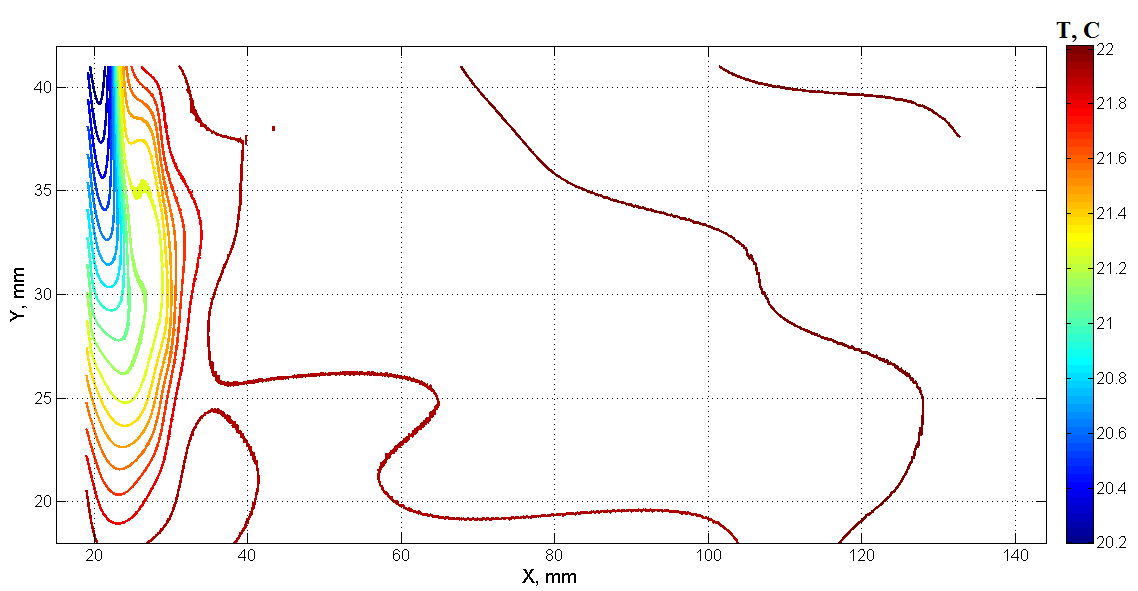
By approximating the interference and Hilbert fringes by Bernshtein's polynomials, it is possible to build a uniform grid over which two-dimensional spline interpolation is performed and the temperature field is restored (Fig. 6, 7).

 

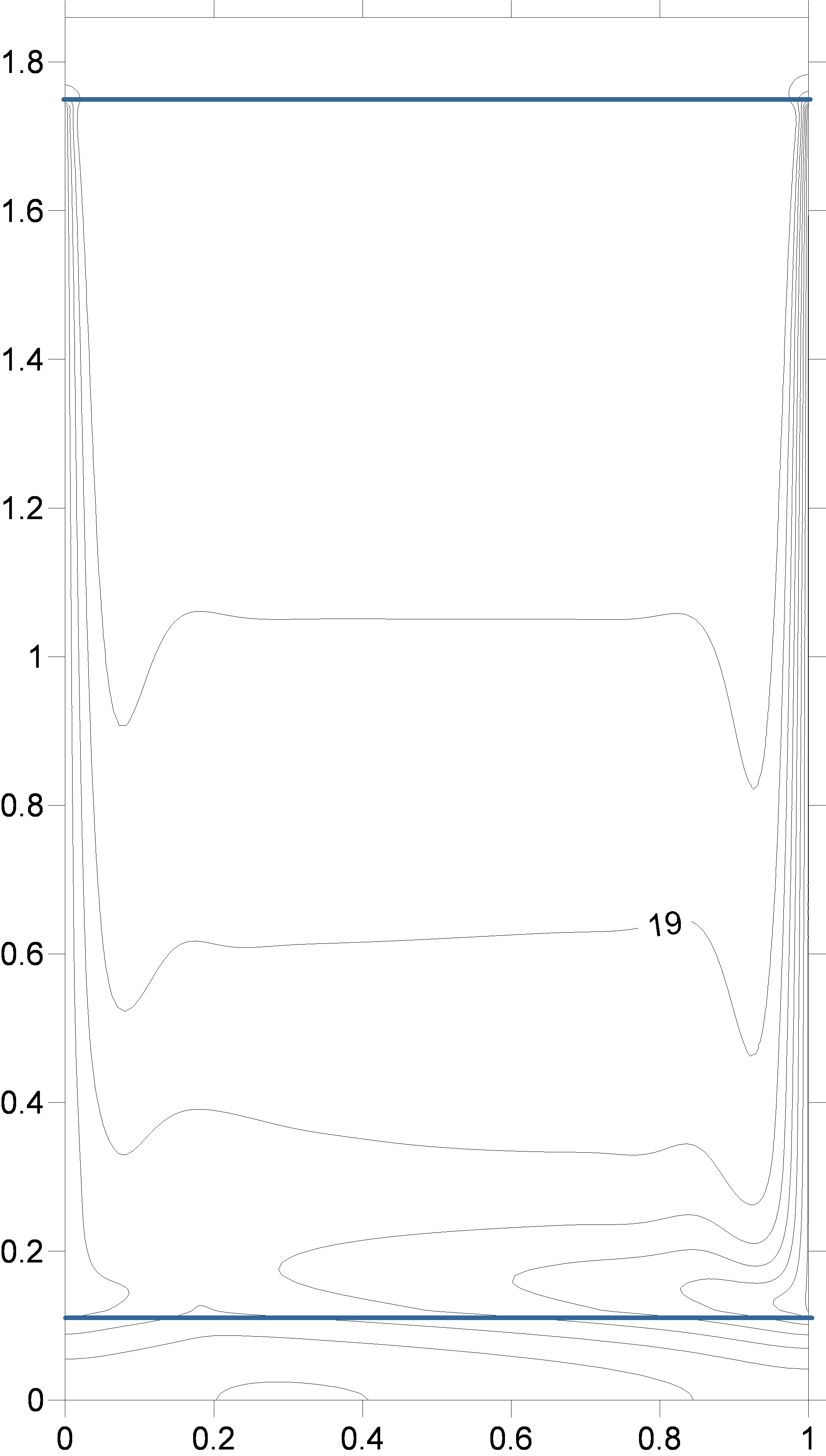
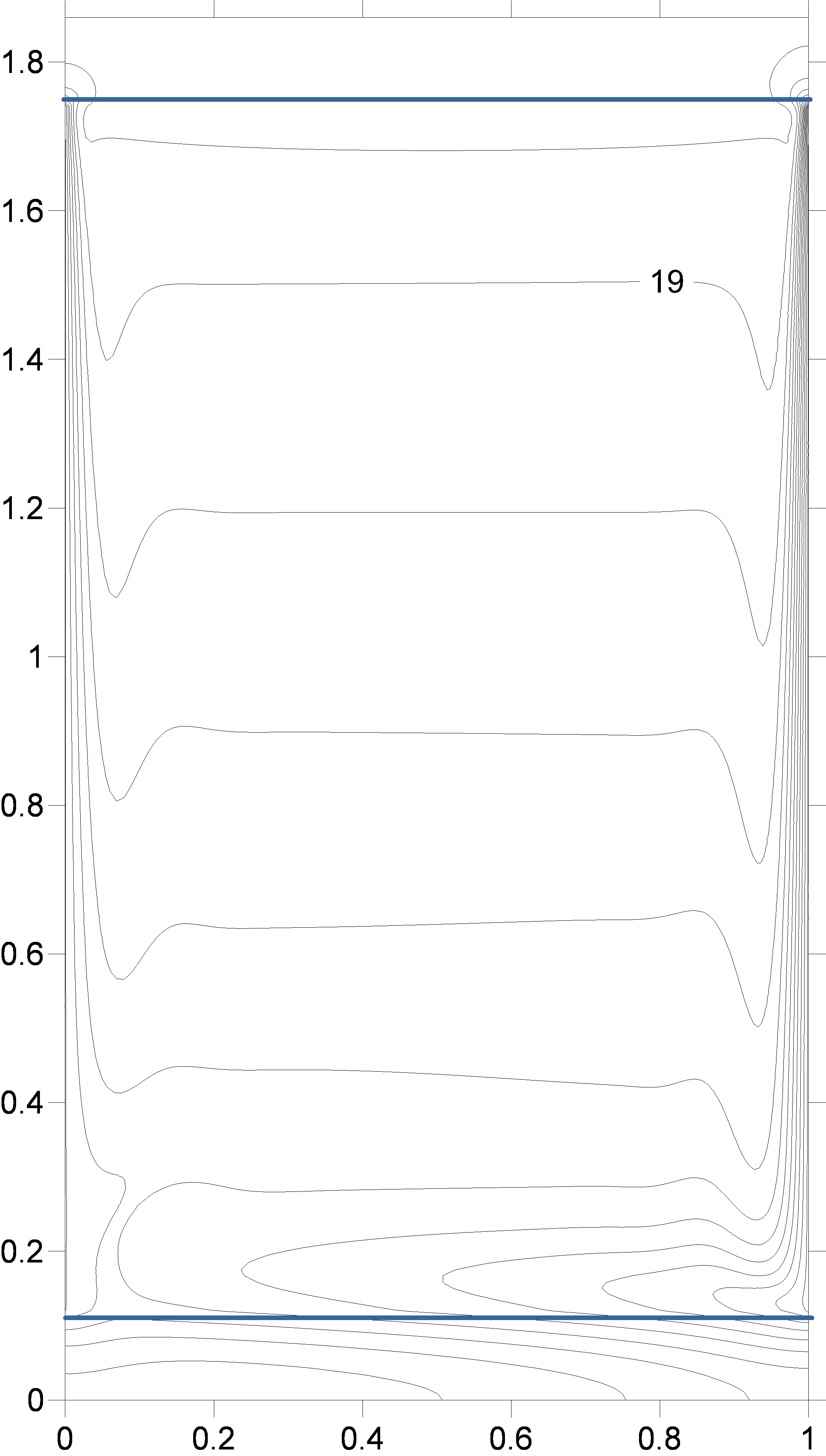
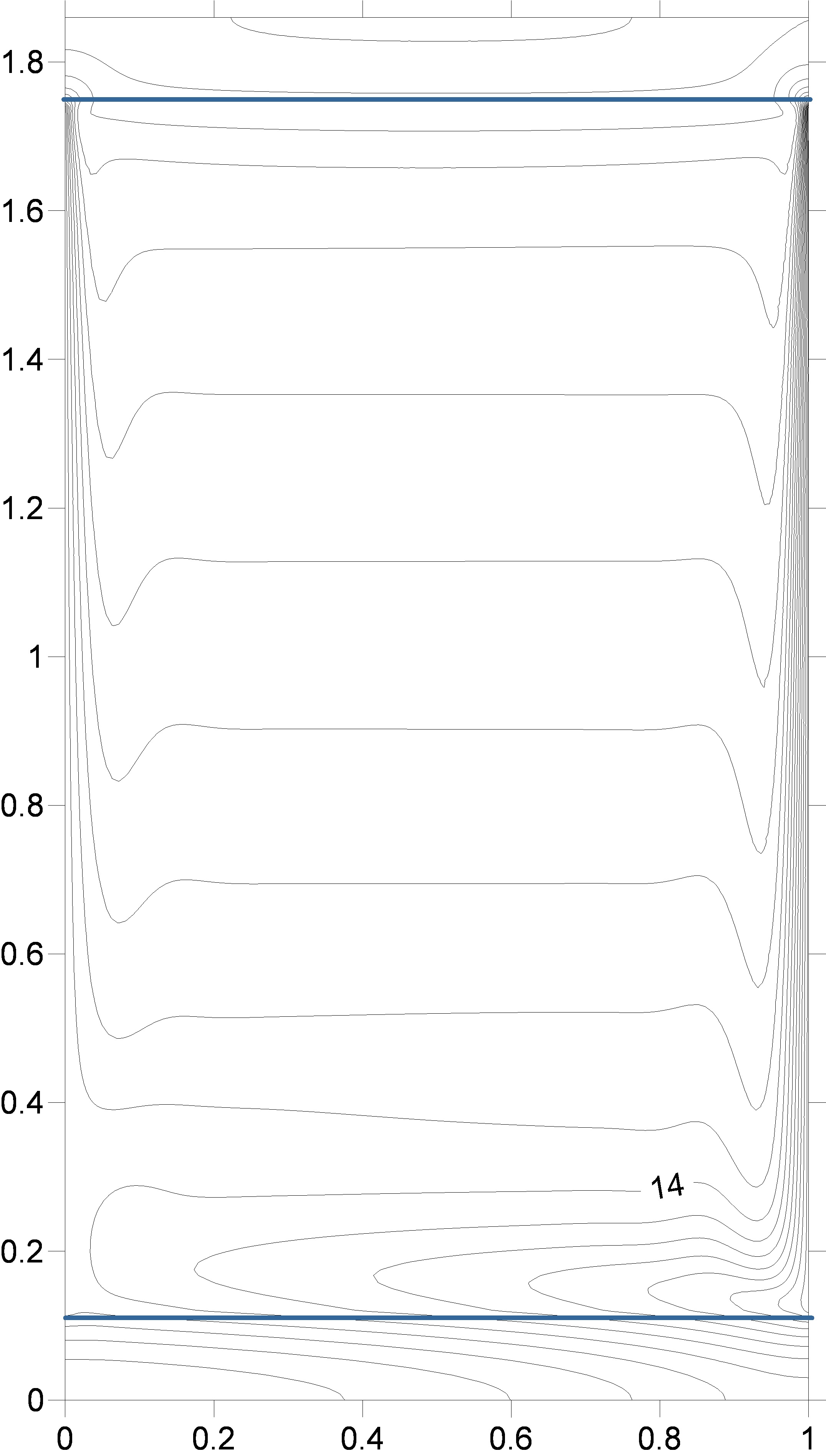
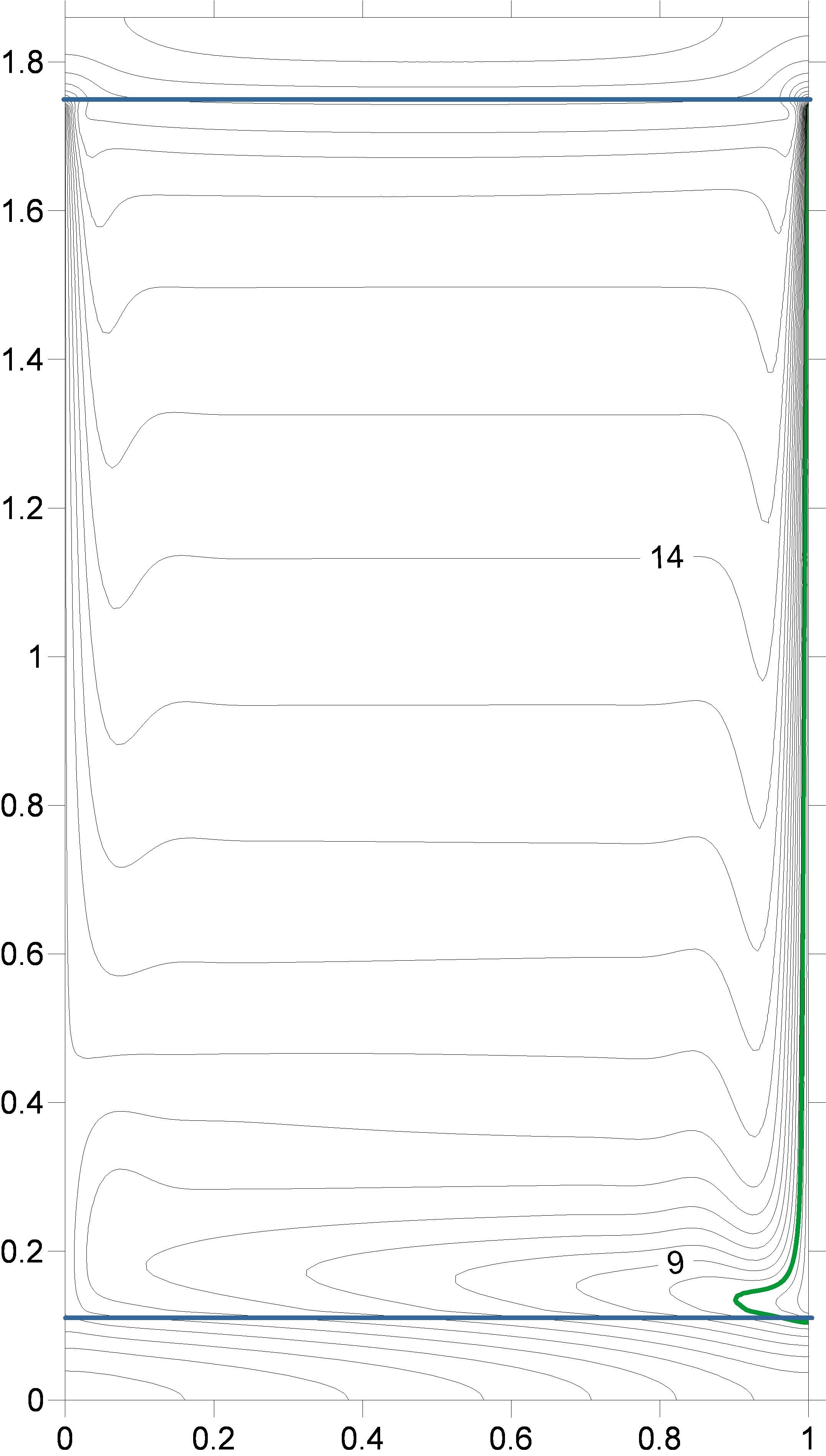
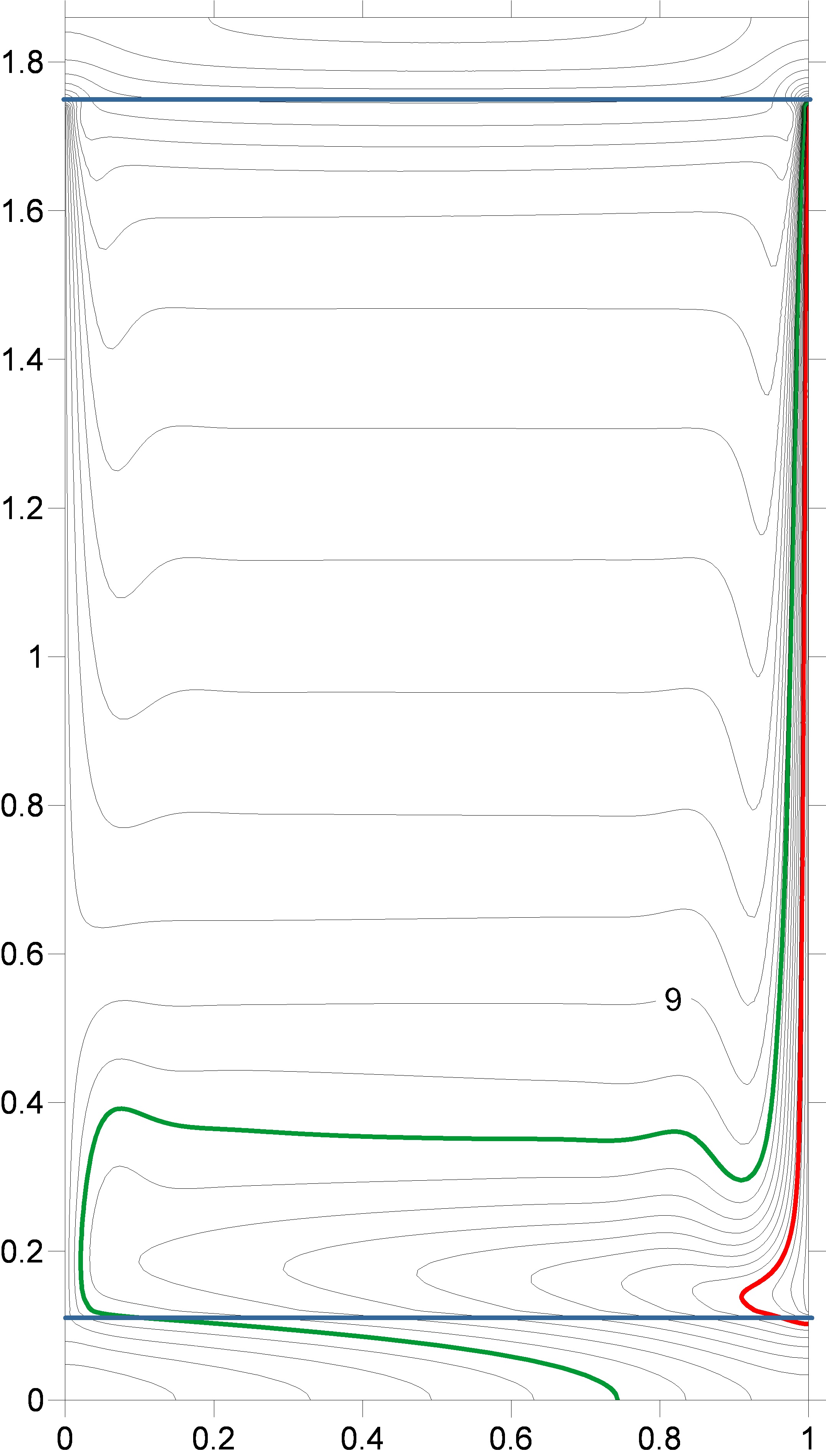
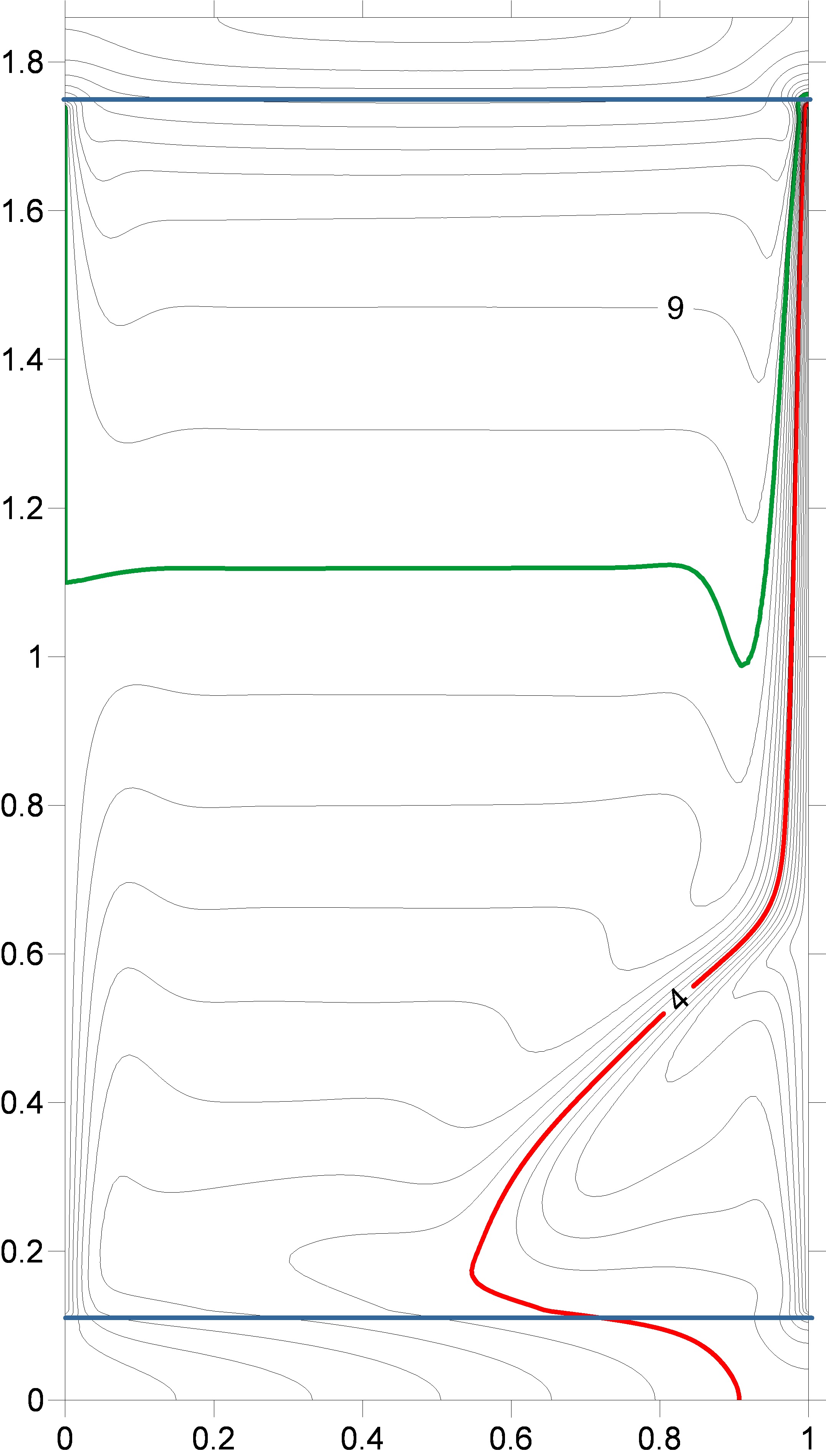
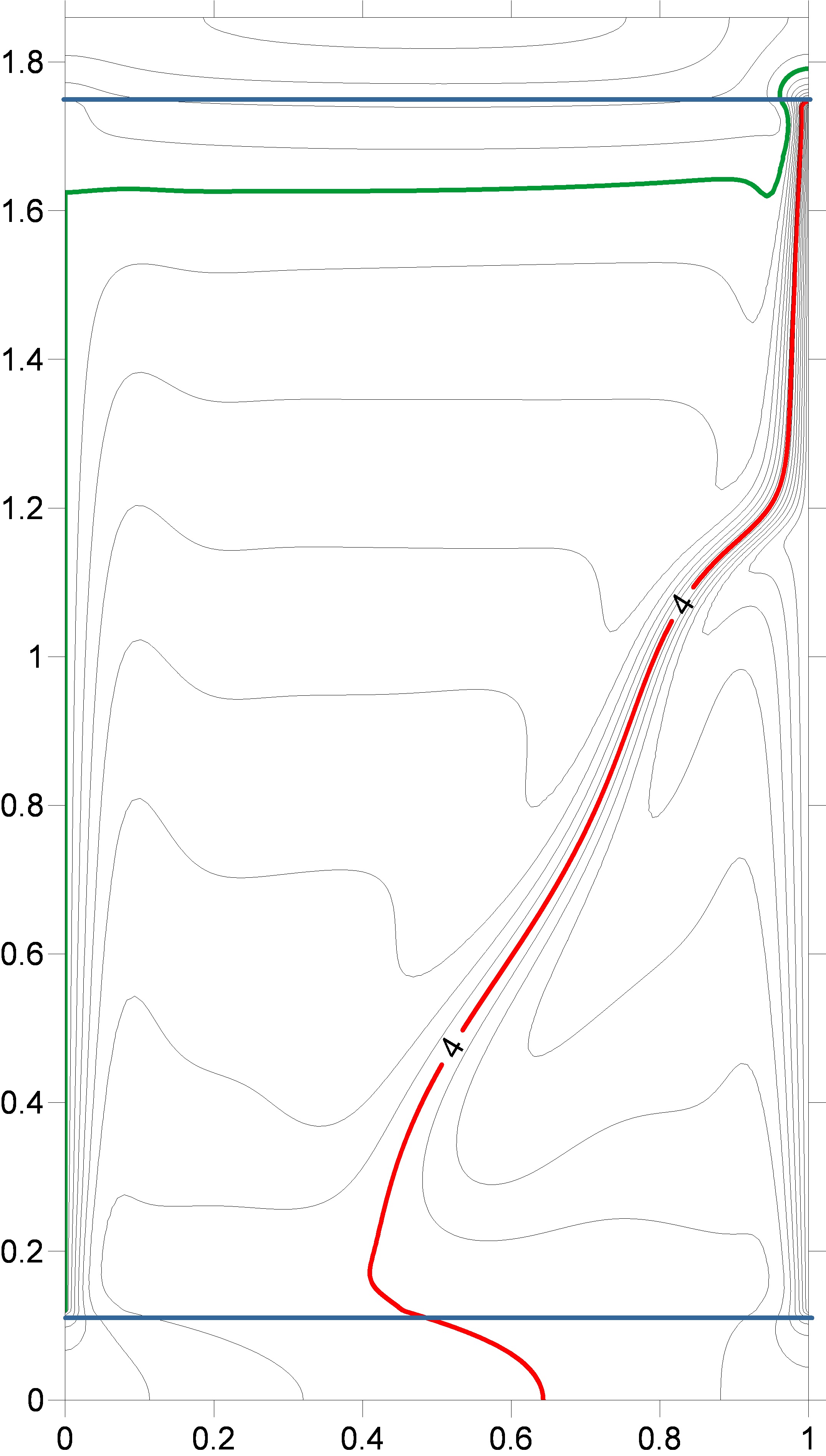
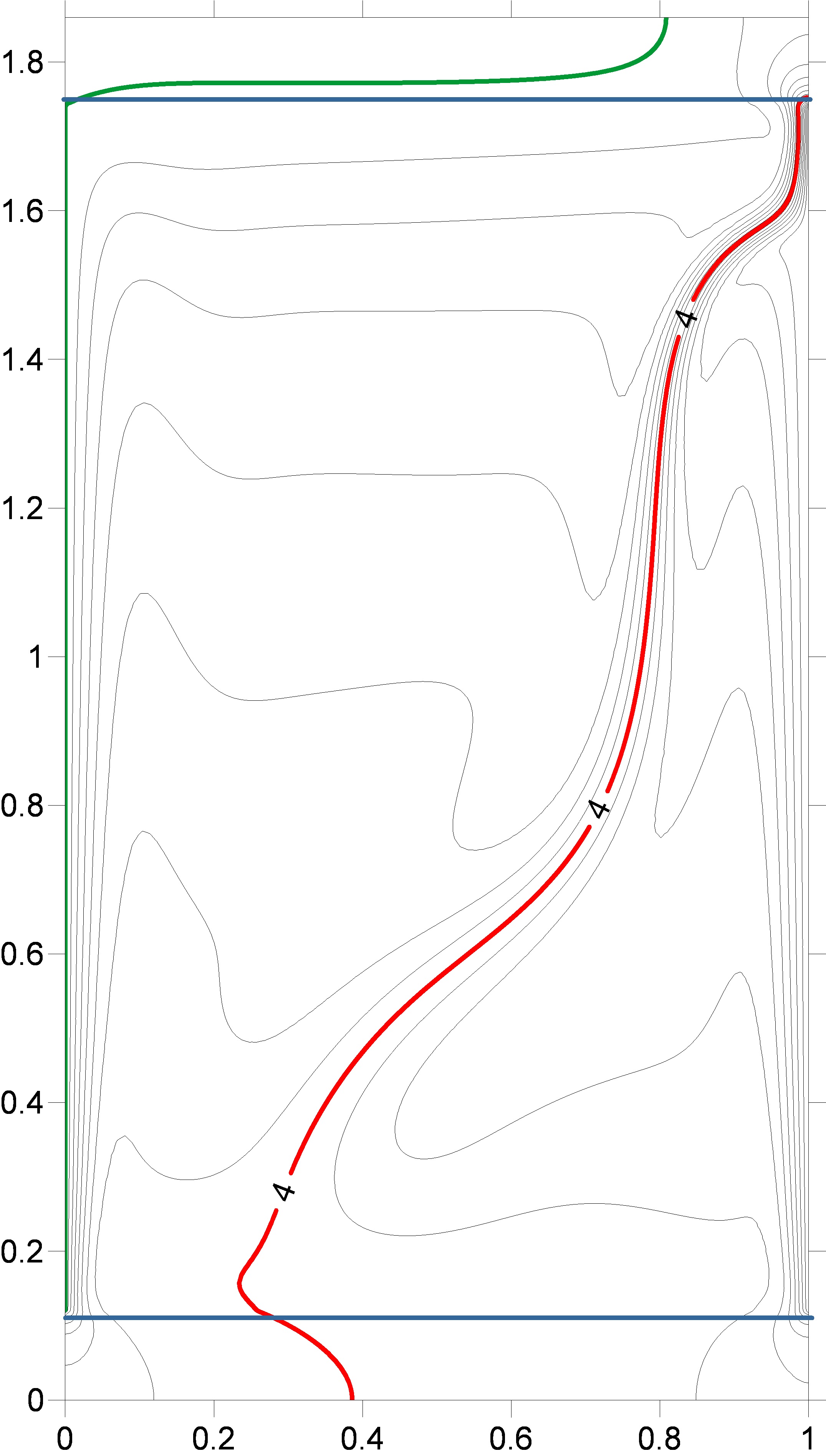
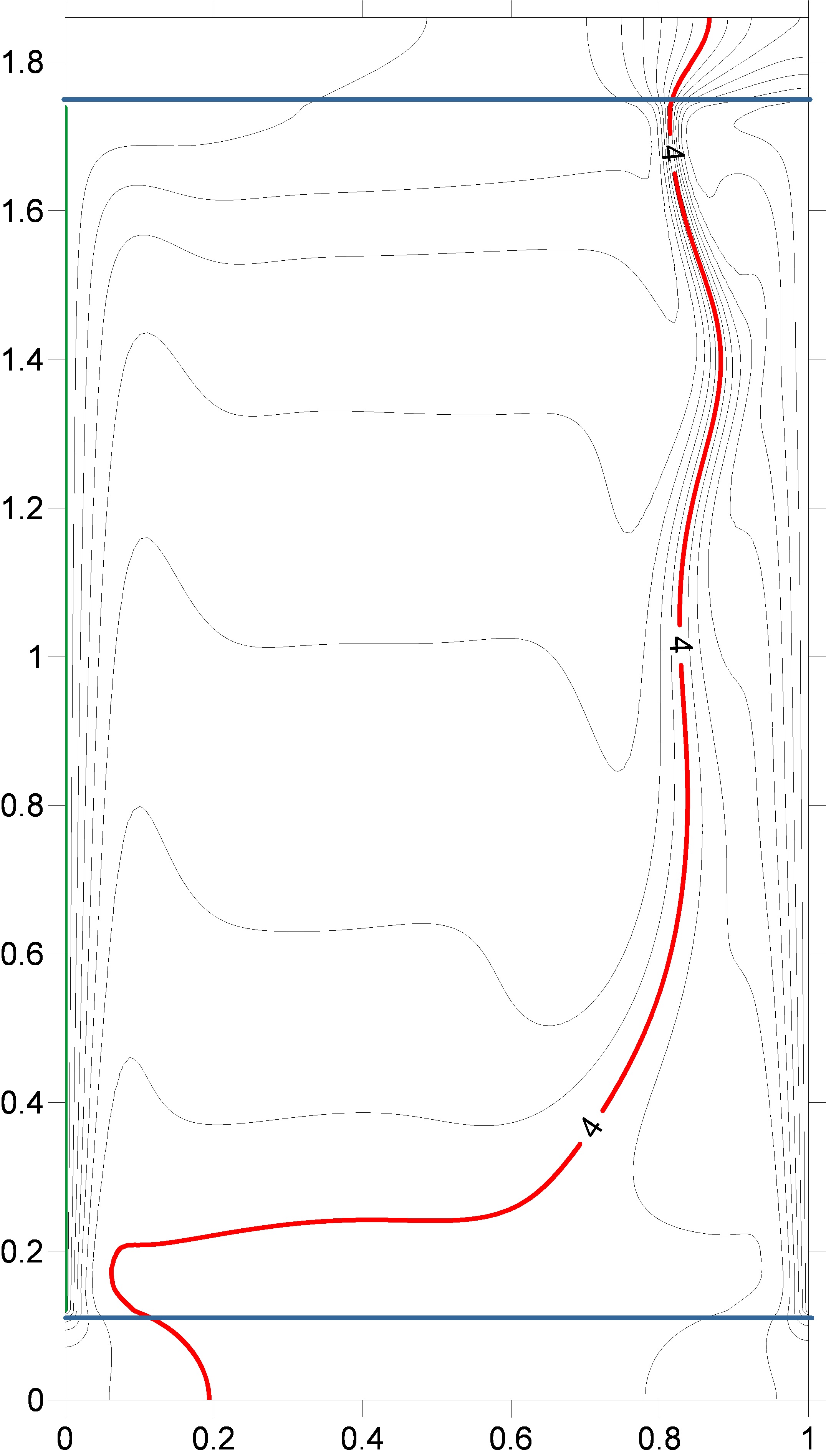
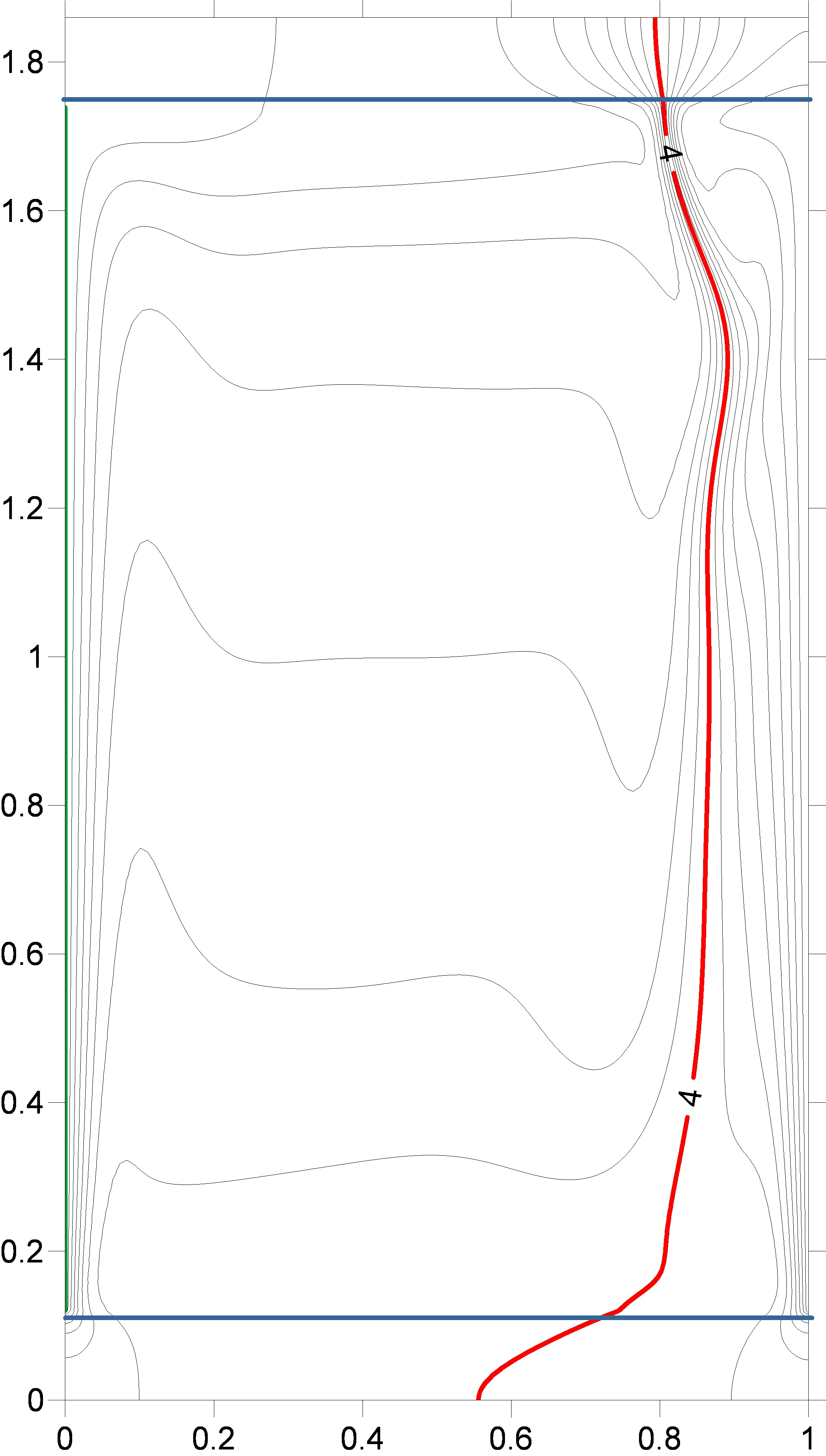
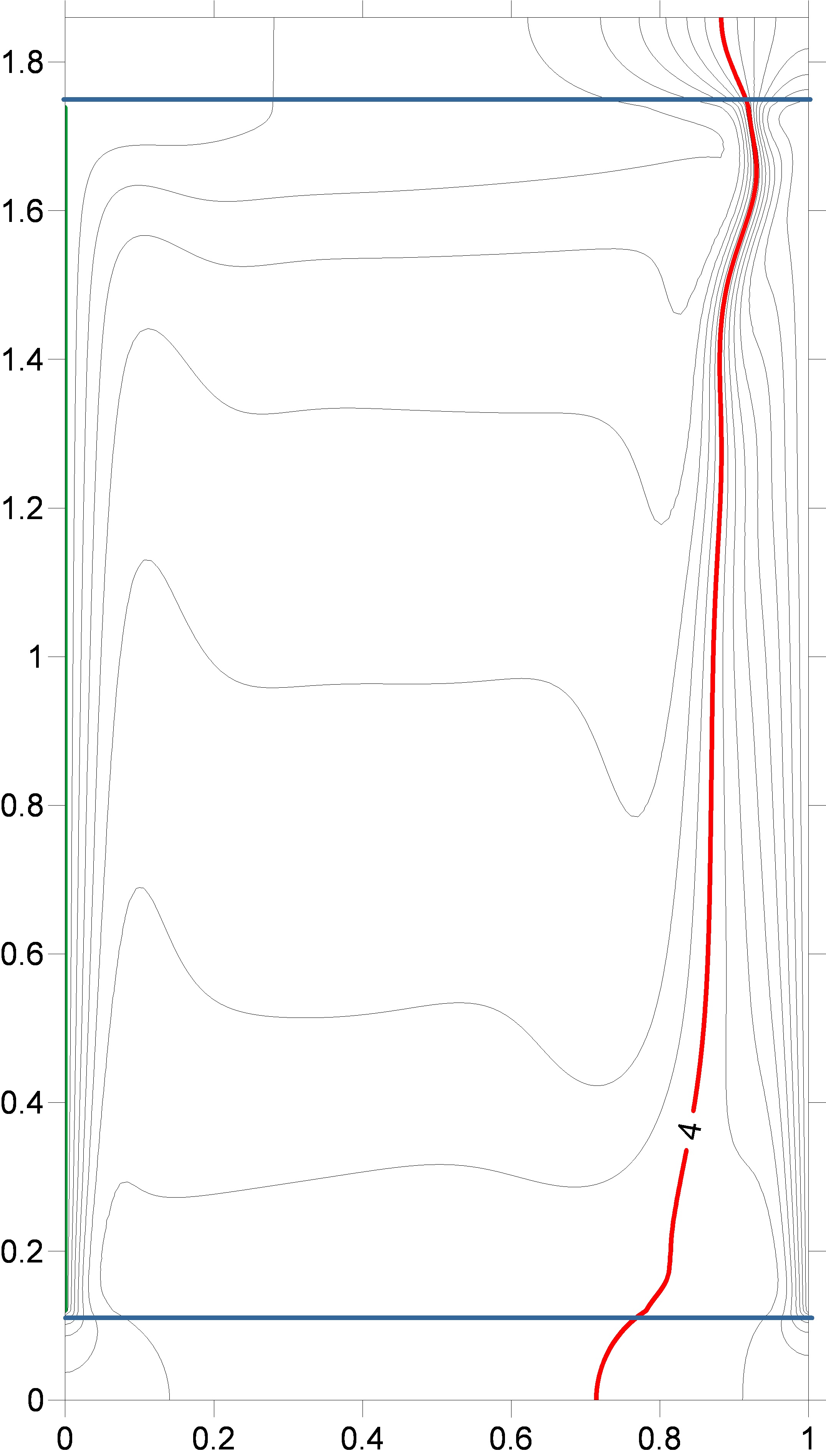
Figure 8 presents the results of numerical modeling of the temperature-field isotherms induced by non-stationary heat-exchange boundary conditions in the monotonic cooling mode of vertical walls. As verification, reconstruction of shear interferograms and Hilbert images from a numerical model of isotherms was performed.

 

Dimensions of the computational domain: liquid layer thickness 84 mm., layer height 136 mm. The initial system temperature is 20 degrees Celsius. The left wall cools linearly in time to 8°C within 2500 s, the right one to 0°C within the same time period. The upper and lower horizontal borders of the cavity are 10 mm thick. Outer surfaces (Plexiglas) of the horizontal walls are adiabatic. In Figure 8, the isotherm with T=4°C is highlighted in red and with T=8°C in green.

 

Fig. 8. Numerical simulation of the evolution of isotherms induced by unsteady boundary conditions in a vertical layer of water.

 

Convective heat transfer in fluid in a two-dimensional formulation is described by a dimensionless system of Navier-Stokes equations, energy and continuity in the Boussinesq approximation, written in terms of temperature T , vorticity ω and stream function ψ:

 

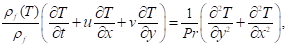
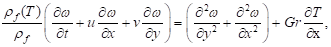
(7)

 

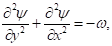
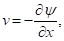
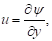
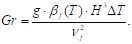
Conductive heat transfer in massive (Plexiglas) horizontal walls is described by the heat equation:

 

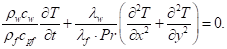
(8)

 

Designations in equations (7) and (8): ν_f - kinematic viscosity of fluid, m²/s; λ_f - thermal conductivity of fluid, W/m•K; λ_w - thermal conductivity of horizontal walls material, W/m•K; ρ_f - density of fluid, kg/m³; ρ_w - density of horizontal walls, kg/m³; с_pf - specific heat of fluid, J/kg•K; с_w - specific heat of horizontal walls material, J/kg•K; g - gravitational acceleration, m/s²; β_f - thermal expansion coefficient of fluid, K^-1; H - height of fluid layer, m; Pr - Prandtl number; Gr - Grashof number; x, y - dimensionless Cartesian coordinates; T - dimensionless temperature; ω - dimensionless vorticity; ψ - dimensionless stream function; u, v - dimensionless velocity components: horizontal and vertical.

 

The problems are solved numerically by the finite element method in conjugate formulation. In solving the motion equation, the dependences of the density and coefficient of volume thermal expansion on temperature are considered. To calculate the constant parameters, we used fixed values of the thermophysical properties of water at 0°C and of Plexiglas. Water properties: density ρ_f = 999.839 kg/m³; coefficient of kinematic viscosity ν_f = 1.793∙10^-6 m²/s; coefficient of thermal conductivity λ_f = 0.554 W/(m•K); specific heat с_pf = 4218 J/(kg•K); crystallization heat R = 333.7 kJ/kg. Properties of Plexiglas wall: ρ_f = 1180 kg/m3; λ_w = 0,195 W/(m•K); с_w = 1270 J/(kg•K).

 

At the solid boundaries in the system, the no-slip condition is set for the velocity (and, as a consequence, for the stream function). The boundary condition for the vortex is obtained from the field of the stream function using the method of conjugate resultants [4]. At the boundaries of the liquid with solid walls, the condition of continuity of temperature and heat flux is set. A non-uniform triangular grid, condensed to varying degrees to all borders of the computational domain, with the number of nodes ≈4*104, was used. Linear basis functions have been defined on elements. To build a triangulation, a cellular step-by-step algorithm using the maximum angle was used [5].

 

The program implements an iterative process, in which, if necessary, the desired values of variables from the previous steps and the calculated values of the coefficients from the parameters were substituted. The temperature field was calculated first, and then the vortex and stream function fields. In an iterative process inside the time step, the relaxation method was used. The finite-element system of linear algebraic equations was solved by the iterative method of the local-optimal scheme (LOS) with incomplete decomposition into lower and upper triangular matrices (LU) [4].

Hilbertograms and shear interferograms synthesized from numerical models of isotherms related to time points: a) - 122 s; b) - 305 s; c) - 710 s after turning on the thermostats that control the temperature of the heat exchange surfaces, are presented in Figure 9.

 

Fig. 9. Examples of numerically modeled fields of isotherms (a, b, c), reconstructed from these fields of gilbertograms and shear interferograms (red line-isotherm + 4 ° ‘).

 

 

The isotherm corresponding to the inversion of water density (+4°‘) is highlighted in red. It divides the space into two areas. Above the isotherm (+4°C), a vortex motion of convective structures occurs and is directed clockwise. Under this isotherm, the vortex motion of convective structures occurs counterclockwise. The conjugate vortices formed above and below the isotherm (+4°C) transfer the warm water downwards, and the cooled water upwards.

 

Figure 10 shows the interferogram corresponding to this convective structure: a) - experimentally obtained; b) - numerical model.

 

Fig. 10. Shift interferograms: a - experimental; b - numerical model.

 

 

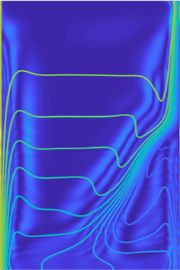
Fig. 11. Hilbertograms: a - experimental; b - numerical model.

 

Figure 11 shows: a - the experimentally obtained gilbertograms; b - the gilbertograms synthesized from the structure of numerically simulated isotherms. The Hilbert bands corresponding to extremums of isotherm gradients are clearly visible. Figures 9-11 illustrate the qualitative adequacy of the results of numerical simulation and experiment.

Conclusion

The study of convective currents induced by non-stationary boundary conditions and their influence on the structure and dynamics of the phase transition are relevant for the development of crystal growing technologies [6], understanding the anomalies of formation and melting ice in the Arctic and in the Antarctic regions. Studies to date have been performed only with a narrow range of parameters and so far have no systemic nature. Solutions of gallium, cadmium-mercury-tellurium and some other substances and materials have similar dependences between the density and temperature. Therefore, water can be used as a melt simulator fluid for testing single-crystal production technologies. The scope of application of the results obtained by methods of optical diagnostics and numerical modeling adapted to this problem is not limited to currents of a convective nature. It can be extended to solving fundamental and applied problems in experimental hydro and gas dynamics, thermal physics, biology, and medicine.

This work was carried out with the partial support of the Russian Foundation for Basic Research (18-38-00790 mol. a).

Bibliography

1. A. J. Smits, N. N. Lim. Flow Visualization. Imperial College Press. 2010.

2. Lappa M. Thermal Collection: Patterns, Evolution and Stability. Chichester: John Willey Sons. 2010.

3. V. A. Arbuzov, E. V. Arbuzov, Yu. N. Dubnishchev, V. S. Berdnikov, O. S. Melekhina. Dynamics of the crystallization front induced by the temperature gradient at the upper boundary of a horizontal layer of a a fluid. Optoelectronics, Instrumentation and Data Processing. 2017, Volume 53, Issue 2, pp 131-135.

4. Yu. G. Soloveychik, M. E. Royak, M. G. Persova. The finite element method for solving scalar and vector problems. Novosibirsk: NSTU, 2007. 896 p.[in Russian].

5. A. V. Skvortsov. Delaunay triangulation and its application. Tomsk: TSU, 2002. 128 p. [in Russian].

6. V. S. Berdnikov, V. A. Vinokurov, V. V. Vinokurov. Effect of nonstationary regimes of the natural and mixed convection of melts on heat transfer and the forms of crystallization fronts in the Czochralski method. Bulletin of the Russian Academy of Sciences: Physics 2017, Volume 81, Issue 10, pp 1257-1264.