Introduction

The use of physically correct methods for the calculation of illumination, simulating the propagation of light and its interaction with the scene objects, is becoming increasingly used in various fields of science and industry. In the classical usage of these methods for realistic images generation [1] or for designing of various optical and lighting devices [2], the results of optical simulation are usually presented in the form of graphs, tables or images of the distribution of such light characteristics as luminance, illuminance or intensity registered on virtual radiation receivers. This form of results representation is sufficient when we are interested in the simulation result only. However, in some cases, we also need to know how it was obtained, or what had the greatest impact on the result. For example, during simulation the luminance distribution on the surface of the phone keyboard backlight system, the developer needs to understand how the light from the light sources passes through the entire illumination system and goes through the upper edge of the key (Fig. 1). Another relevant example is the analysis of stray light in a lens objective. The developer needs to understand which surface of the lens and which lens creates a highlight on the image. To obtain comprehensive information on the light propagation in the optical system, it is convenient to visualize the trajectories of the simulated rays. A visual representation of the trajectories of light rays in the optical system is also useful for a software developer, as a means of debugging and optimizing algorithms [3].

 

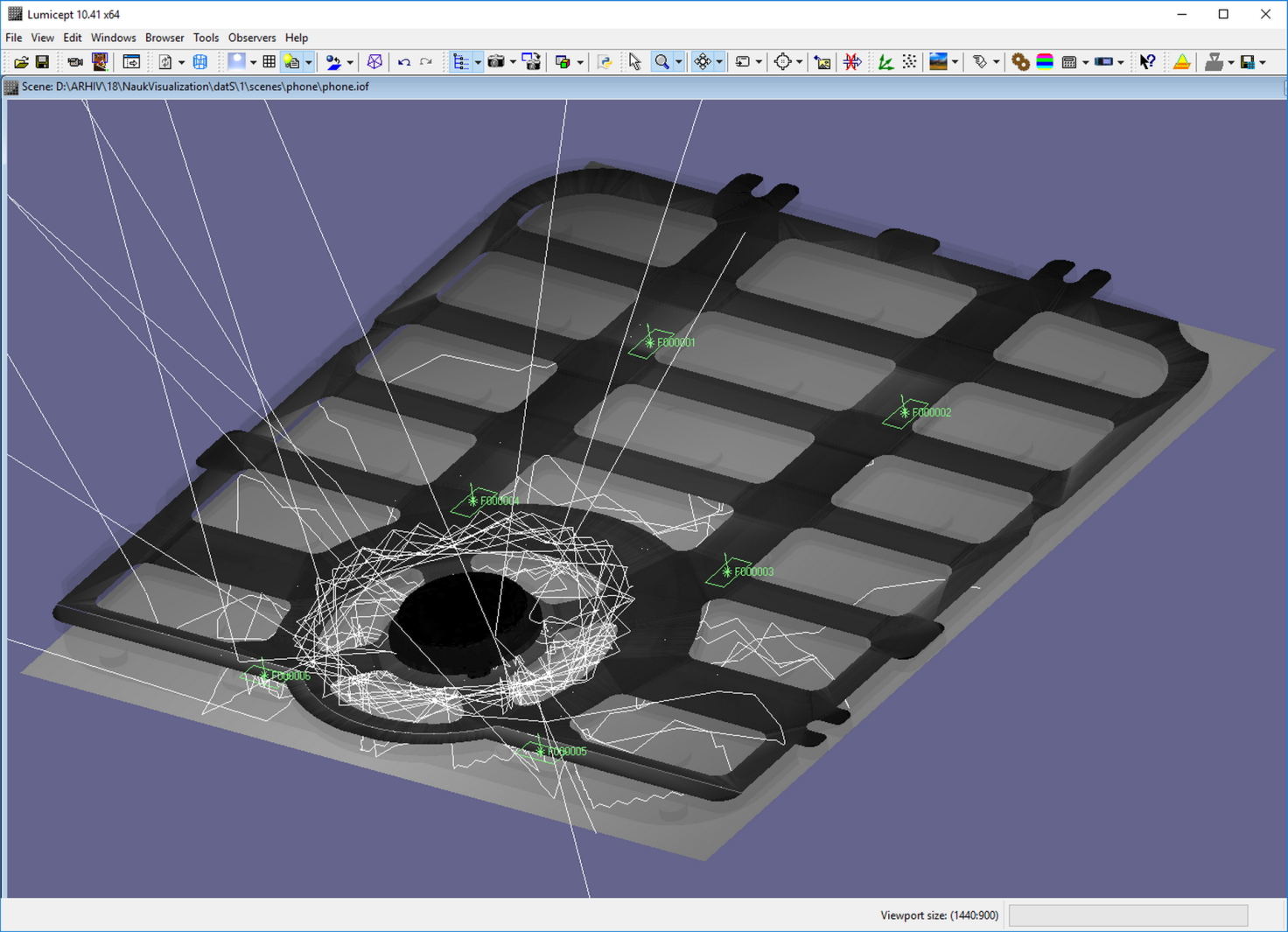
Fig. 1. Rays hit the center button

 

Currently, the generation of realistic images based on physically correct lighting simulation is used in all new areas. For example, the use of physically correct synthesized images and video sequences in the training systems of artificial intelligence [4] [5] [6] is promising. The correctness of the resulting images is crucial in all these applications. Otherwise, the goal will not be achieved, and the intelligent system will be trained incorrectly. However, this physical correctness may be impaired due to errors in the simulation program or user errors when describing scenes, the geometry of objects, optical properties of objects. Visualization of the propagation of light rays is one of the most effective means for detecting and analyzing such errors [3], [7].

For all these reasons, the visualization of the trajectories of light rays has actually become the basic functionality of modern optical simulation systems. Initially, a visual representation of the ray trajectories was implemented in systems for the synthesis of realistic images and optical simulation, developed at Keldysh Institute of Applied Mathematics RAS (KIAM) [7-9], in the late 90s. However, the use of these systems for solving complex problems of designing modern optical devices revealed certain disadvantages of the implemented ray visualization algorithms, such as:

•        Slow raytracing;

•        The impossibility of storing the rays obtained by tracing for subsequent detailed analysis;

•        Absence of possibility to visualize rays paths only for a part of the scene – for selected light sources, geometrical objects and virtual measuring devices;

•        Absence of integration with computer-aided design (CAD) systems.

The slowing down of the ray tracing process was caused by the visualization technology used, since one of the requirements for the previous implementation was the sequential visualization of the ray traced segments one by one. In this technology, the algorithm could use only one thread for calculations. Using OpenGL to render segments in this mode is also inefficient. As a result, when simulating on a typical modern computer (Intel Core i7-4770 3.4GHz 32GB RAM), the speed of direct Monte Carlo ray tracing for a typical scene is ~ 1.2 million rays per second, while the visualization of traced rays occurs at a speed of only ~ 1300 rays per second. It was senseless to add ray storing to the existing algorithm at such a speed of tracing. Removing these limitations actually required redesigning the entire ray visualization module. The main requirements for the development of a new system were the effective use of multi-core computers both for ray tracing and for analyzing the simulation results, as well as the integration with CATIA CAD.

To meet the new requirements, we have developed new algorithms that efficiently use multi-core processors. A new module for visualization of light propagation was implemented in the basic standalone system Lumicept and in the corresponding system integrated into CATIA. The first results were reported at conferences [10] and [11].

Selecting objects for simulation

Optical simulation in CATIA CAD system has certain specifics related to the representation of geometric objects in the scene. The scene in the CATIA system document contains a large number of geometrical objects and light sources, not all of which are of interest to the user in this simulation and visualization of the rays. This may be caused by the user's desire to exclude auxiliary objects from modeling or, on the contrary, to include in this simulation only a part of the scene objects forming a certain light beam, or to use only that part of the scene where the user assumes certain problems. For these reasons, appropriate simulation in CATIA begins with the selection of objects for the simulation.

The selection of objects for simulation is in fact the creation of a new scene from objects that already exist. The corresponding dialogues for the subsystem integrated in CATIA are shown in Fig. 2. In the left part of Fig. 2 shows a dialog in which the objects selected for simulation are displayed. The objects themselves can be selected either directly in the scene rendering window, or in the scene tree view as it is shown in the right-hand side of Fig. 2.

 

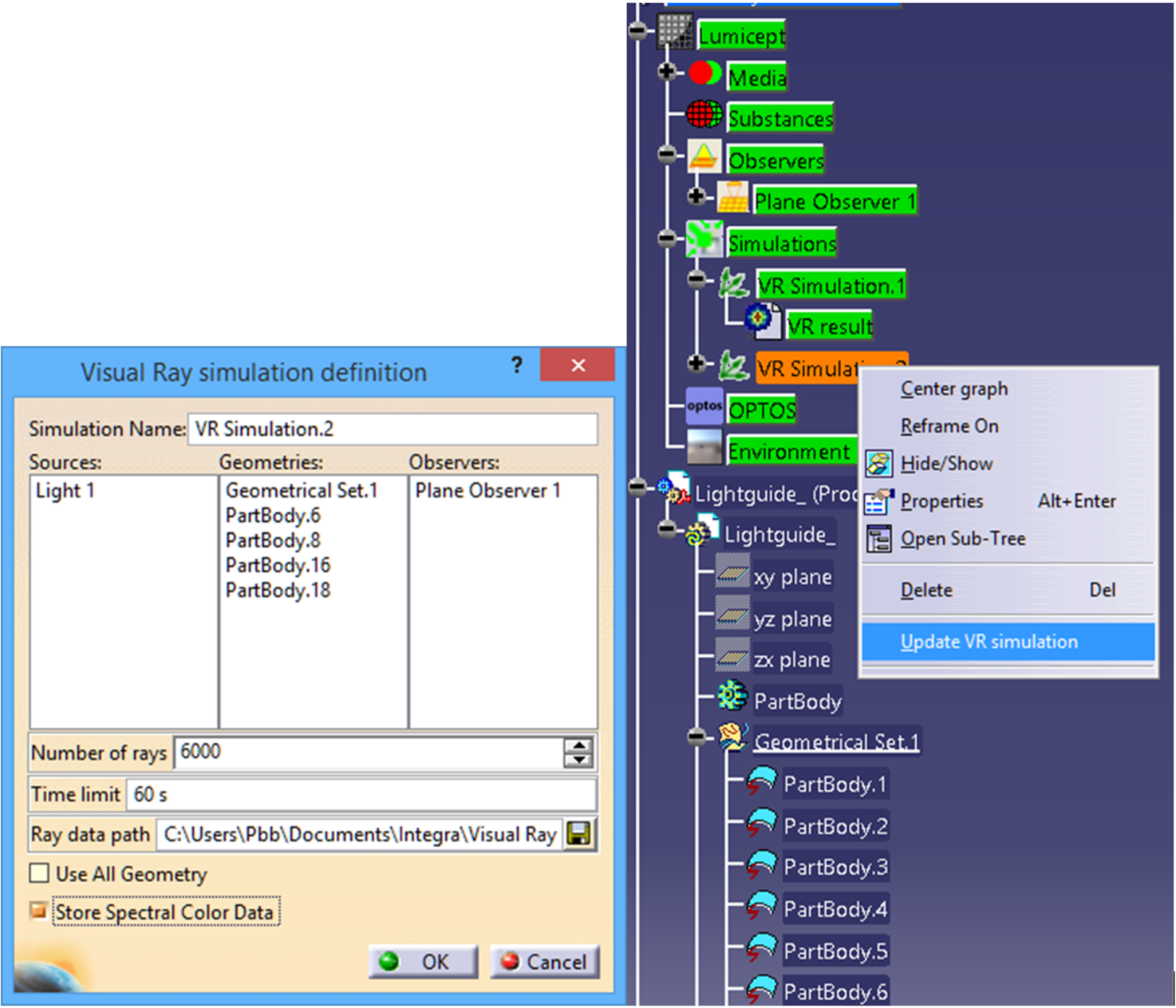
Fig. 2. Objects used for light propagation visualization, scene objects tree and start of the simulation

 

In the dialog, it is also possible to specify the saving of data in a spectral form. Also the user can set the path for saving the simulation results, the number of rays saved and the time limit for the simulation. After closing the dialog, the ordered simulation is displayed in the scene tree and can be started as shown on the right side of Fig. 2, using the drop-down dialog. The user can create an unlimited number of such simulations for different purposes. The dialogue shown in Fig. 2 was implemented, of course, using the appropriate CATIA tools for user interface creation.

The simulation itself is performed in the special module named I2 Server which is built basing on the Lumicept system developed in KIAM. Interrogation scheme of CATIA system and I2 Server module is represented in the upper part of Fig. 3.

 

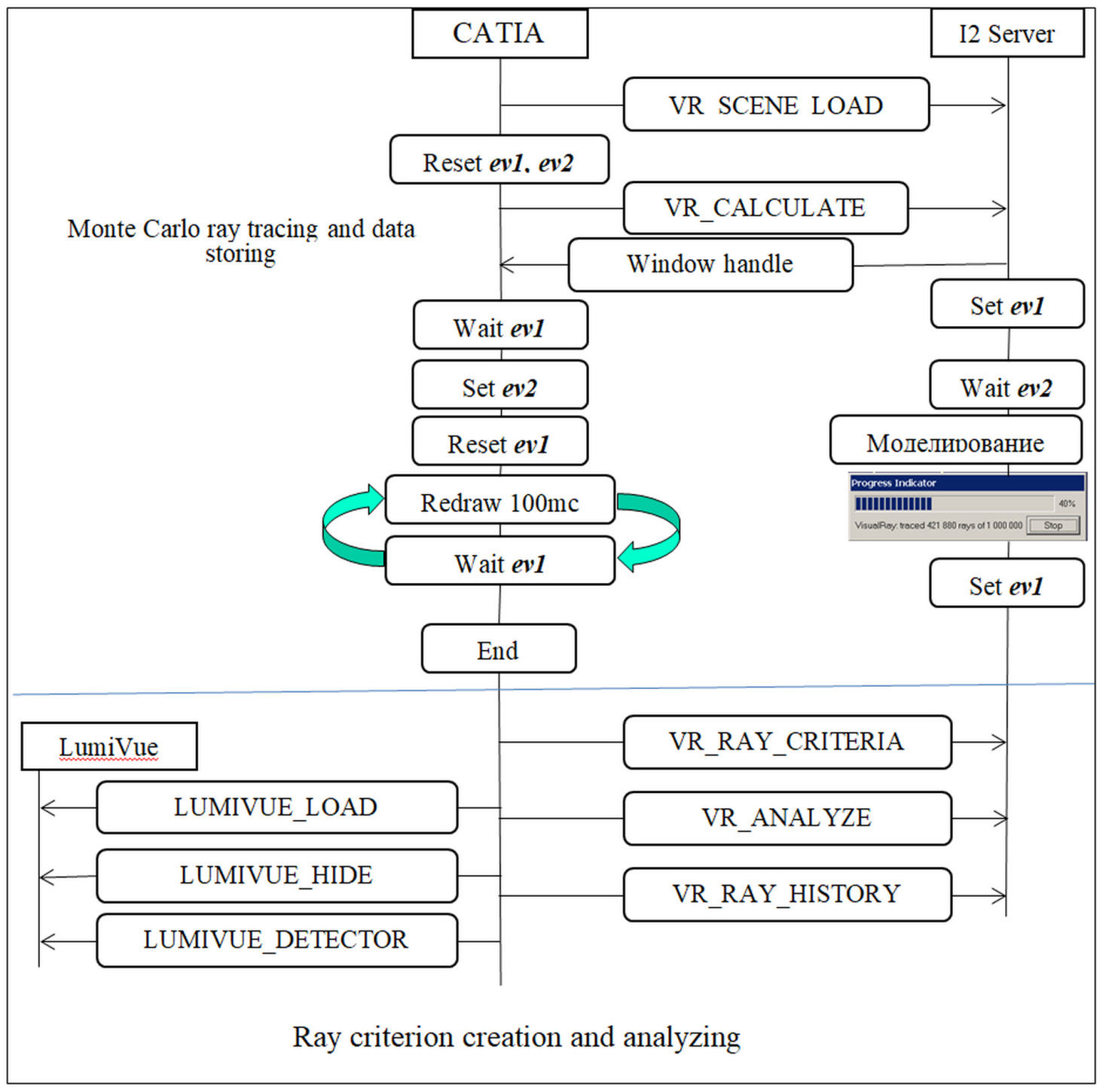
Fig. 3. Scheme of interrogation of CATIA with I2 Server and LumiVue in the light propagation visualization subsystem

 

CATIA creates the scene description in the binary format of Lumicept system, stores it to disk and sends the VR_SCENE_LOAD (scene loading) command to I2 Server, and then VR_CALCULATE command (Monte Carlo raytracing with storing rays to a file for visualization). Additional parameters (path to the saved scene data, path to the file for rays storing, time limit, number of rays, etc.) are sent using the shared memory. Schemes of execution of different commands in I2 Server are similar to each other. Here there is a detailed description for VR_CALCULATE command execution because it is the most complicated command.

 

1.     CATIA resets the ev1 and ev2 events, sends the VR_CALCULATE message (using Windows messages system) and waits for setting of ev1 event.

2.     I2_Server after receiving VR_CALCULATE message takes from shared memory path to the file, loads the scene from it, puts its own window descriptor to shared memory, sets the ev1 event and waits for ev2 event setting.

3.     CATIA takes from shared memory the window descriptor, resets the ev1 event and sets the ev2 event.

4.     After ev2 event is set I2 Server executes the simulation command and after its completion sets the ev1 event. During simulation the progress bar shows the progress of the command execution: ratio of number of simulated rays to number of totally required rays in percent. The simulation results are stored to disk by I2 Server.

5.     CATIA, while waiting for setting ev1 event, does redraw of its own window each 100 milliseconds, and simultaneously makes I2 Server window active and topmost. After ev1 event is set CATIA updates data and scene tree in its own document corresponding to the scene which was stored to disk by I2 Server.

Simulation and rays storing

The algorithm for storing the rays obtained by tracing for one portion of the rays is shown in Fig. 4. In fact, this is the same Monte Carlo ray tracing, which is used for the global illumination calculation. Rays built with a Monte Carlo tracing will be saved if the corresponding simulation parameter is set. In fact, the calculation kernel provides simultaneous computation of global illumination, storing the results in the form of irradiance maps or illuminance values on virtual measuring instruments, and the ray storing. The illumination values on the virtual measuring devices are obtained as a result of the registration of the rays falling on them. It is produced only for virtual instruments specified in the dialog in fig. 2. The results of the registration of the rays are stored in separate files for further analysis during the visualization of the rays. With multi-threaded ray tracing, the algorithm shown in Fig. 4, works almost independently in each computational thread for each computed portion of the rays. The only module in this algorithm that needs synchronization is the recording of portions of rays on a disk, since all rays are written to one file. This synchronization is provided by the usual critical section (CRITICAL_SECTION). It is clear that the algorithm will remain efficient as long as the recording of portions on the disk will be faster than the computational threads will produce them. Thus, a critical point in this formally simple algorithm is the efficient compression of the portions of the rays obtained by Monte-Carlo tracing.

 

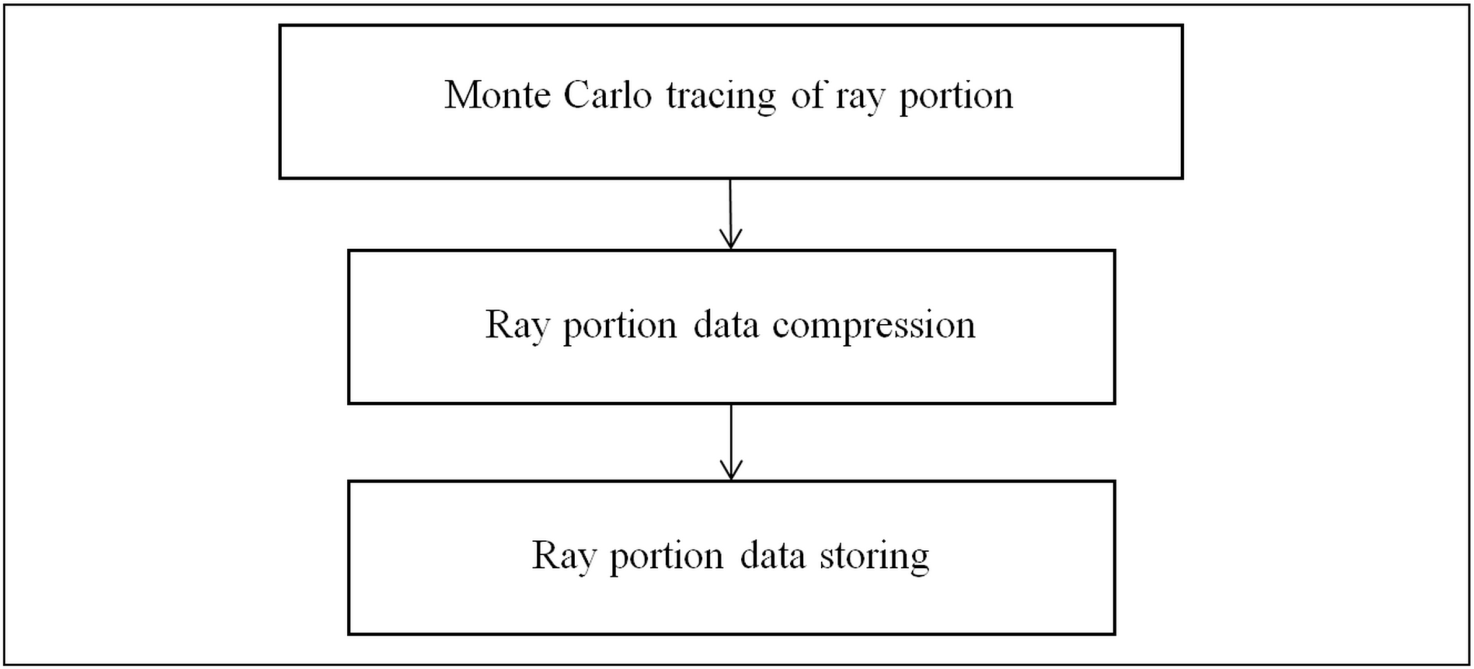
Fig. 4. Algorithm of storing rays during Monte Carlo raytracing

 

At first it is needed to minimize information amount for storing, but at the same time information should be sufficient for further analysis. For each ray segment the following information is being stored:

1.     Light source index (short);

2.     Object index (short);

3.     Triangle index (int). It is used for finding out the ray propagation medium and surface properties from both sides of the surface;

4.     Coordinates of starting point for the first (from light source) ray segment and the end point of the previous segment for the rest segments (float[3]);

5.     Surface normal in the segment starting point (short[3]);

6.     Event type in the end point of the segment (int);

7.     Index of the first descriptor of segment interrogation with virtual measuring device (int, -1 if there were no such event);

8.     Number of descriptors related to this segment (WORD).

Totally 36 bytes are used for recording a one ray segment. For each ray one more segment is recorded than they really exist. The last segment is used to record the coordinates of the end point of the previous segment, as well as event type and direction in case if the ray leaves the scene. To describe the type of event at the end point of the segment, int is used, since it can contain several events, and a separate bit is used for each event.

Since simulation can occur both in RGB and in spectral color space, the length of the array used to store the color of a ray segment depends on the color space used in the simulation. Therefore, the saving of the color of the ray segment occurs in a special array of short type elements. For the ray color in our Monte Carlo ray tracing, normalized values ​​are always used, i.e. the sum of the color components is equal to 1, therefore the accuracy provided by the short type (1.0 / 65535 = ~ 1.5e-5) is quite enough for our ray visualization task. The index of the first color element in an array of colors for a given segment is determined in a natural way as the product of the segment index and the number of values ​​that determine the color. These are three for simulation in RGB space, and the number of wavelengths during spectral simulation.

Similarly, an array of corresponding descriptors is used to describe the interaction of a ray with virtual measuring instruments. The descriptor includes the following:

1.     Index of virtual measuring device with which there was an interrogation at the specified ray segment (short);

2.     Index or the virtual measuring device cell where the interrogation was registered (WORD[2]);

3.     Cosine of the angle between the ray and direction of the virtual measuring device (short);

4.     Coordinates of the intersection point of the ray and virtual measuring device (or projection of the intersection point of ray and surface to the device) in the relative coordinates of the virtual detector (WORD[2]);

5.     Was the event registered (bool).

The compression itself in our algorithm is implemented using the shareware library for data compression zlib [12]. Each of the arrays – rays segments, events registered at virtual measuring devices and color components are compressed separately.

When saving to the file for each portion are recorded:

1.     Compression flag (for the purpose of debugging there is kept a possibility of saving non-compressed portion);

2.     Compressed segments array and its length;

3.     Compressed array of events registered at virtual measuring devices and its length (if present);

4.     Number of color channels used for simulation – 3 for RGB simulation and number of wavelengths for spectral simulation. The system allows to continue calculation and saving rays to the same file for new rays portions even after changing color space;

5.     Compressed array of color component values and its length.

This information is sufficient to recover all the rays received by Monte-Carlo ray tracing and to analyze them. Analysis allows you to select by a given criterion, visualize the selected rays in the window along with the scene geometry using natural or artificial colors, display all parameters of this segment in the dialog box for the corresponding user request. The implementation of this procedure allowed us to trace and save the rays at a speed of ~ 396720 rays per second instead of ~ 1266 rays per second for the old algorithm (Intel Core i7-4770 3.4GHz 32GB, 4 cores, 8 threads). That is an acceleration of ~ 300 times was obtained for ray storing.

Stored rays analysis

The resulting simulation file is in fact a three-dimensional ray map. These ray maps are used to quickly analyze the light characteristics of a radiation receiver with varying parameters, to study the features of light propagation in the scene, etc. One of the most important examples of the use of these maps is the visualization of the propagation of light rays in the design of complex optical systems [13]. To study the details of the propagation of light and obtain various statistical characteristics in some practical cases, three-dimensional maps of very large size are used. They can contain tens of millions of rays and hundreds of millions of segments, along with a large amount of information about optical events that have taken place along the ray trajectory. File sizes for storing these maps can reach several gigabytes.

When visualizing the propagation of light rays, a typical task that is crucial from the point of view of processing time is the selection for the further visualization of the ray trajectories that satisfy the given criterion. The criteria for this selection are the most diverse and quite complex. The following typical events occurring along the ray trajectory, which may be of interest in the study of the optical system [9]:

•        A ray was emitted by a given light source;

•        A ray was intersected or not intersected with specified object face (triangle);

•        A ray was intersected with specified part of a geometrical object of an optical system and a specific optical transformation took place;

•        There was registered an intersection of ray with specified virtual measuring device;

•        A ray was intersected with a surface which has specified optical parameters and a specific optical transformation took place;

•        A ray had undergone specified optical transformation (specular or diffuse reflection, absorption etc) at one of the optical system objects;

•        A ray was registered at the specified part of the virtual measuring device.

In the general case, a logical expression is constructed from these elementary events, represented as a tree of events shown in Fig. 6, which is the ray selection criterion for visualization. The expression is constructed using the logical intersection (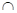), union (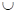) and logical negation (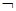). For each given optical conversion, you can choose which transformations took place and how many times. For each optical transformation one can specify which transformations took place and how many times.

For comfortable work it is needed to minimize the response time of the system after any changes of ray selection criterion. It is desirable to provide the real-time system response when it is possible. For three-dimensional ray maps of a huge size it is desirable that the response time does not exceed at least several minutes. Since practically all computers currently used are multi-core, it seems appropriate to parallelize the process of analyzing three-dimensional ray maps.

The subsystem of analysis of rays obtained with Monte Carlo ray tracing includes the following components:

1.     User interface which provides rays selection criteria creation and control of ray visualization parameters;

2.      Reading of a file with stored data and selection of rays satisfying to the created criterion;

3.     Visualization of selected rays and user interface for showing the information along the selected rays – coordinates of the start and the end of each segment, segment colors (RGB and spectral), name of the ray propagation medium for specified segment and its basic parameters, etc.

User interface

The user interface of the ray visualization subsystem is shown in Fig. 5. The left part shows the interface implemented in the CATIA system, and the right part shows the corresponding interface implemented in the Lumicept system. Some difference in the user interface is due to the use of different libraries (RADE in CATIA and QT in Lumicept), and the use of different objects. In CATIA, one can use the faces of objects, including curvilinear, in the criteria for selecting rays, while in the Lumicept system there is no such concept. CATIA also has the ability to use as a criterion the ray intersection of a virtual measuring instrument detector area, which is currently not implemented in the Lumicept system.

An additional, more complex criterion can be constructed using the visualization criterion editor, originally implemented in the basic Lumicept system. In CATIA, the implementation of this dialogue is provided through the I2 Server according to the scheme shown in Fig. 3 using the VR_RAY_CRITERIA command. The user interface of the complex ray selection criterion is shown in Fig. 6. Finally, the criterion combines all the events specified in dialogues shown in Figures 5 and 6.

 

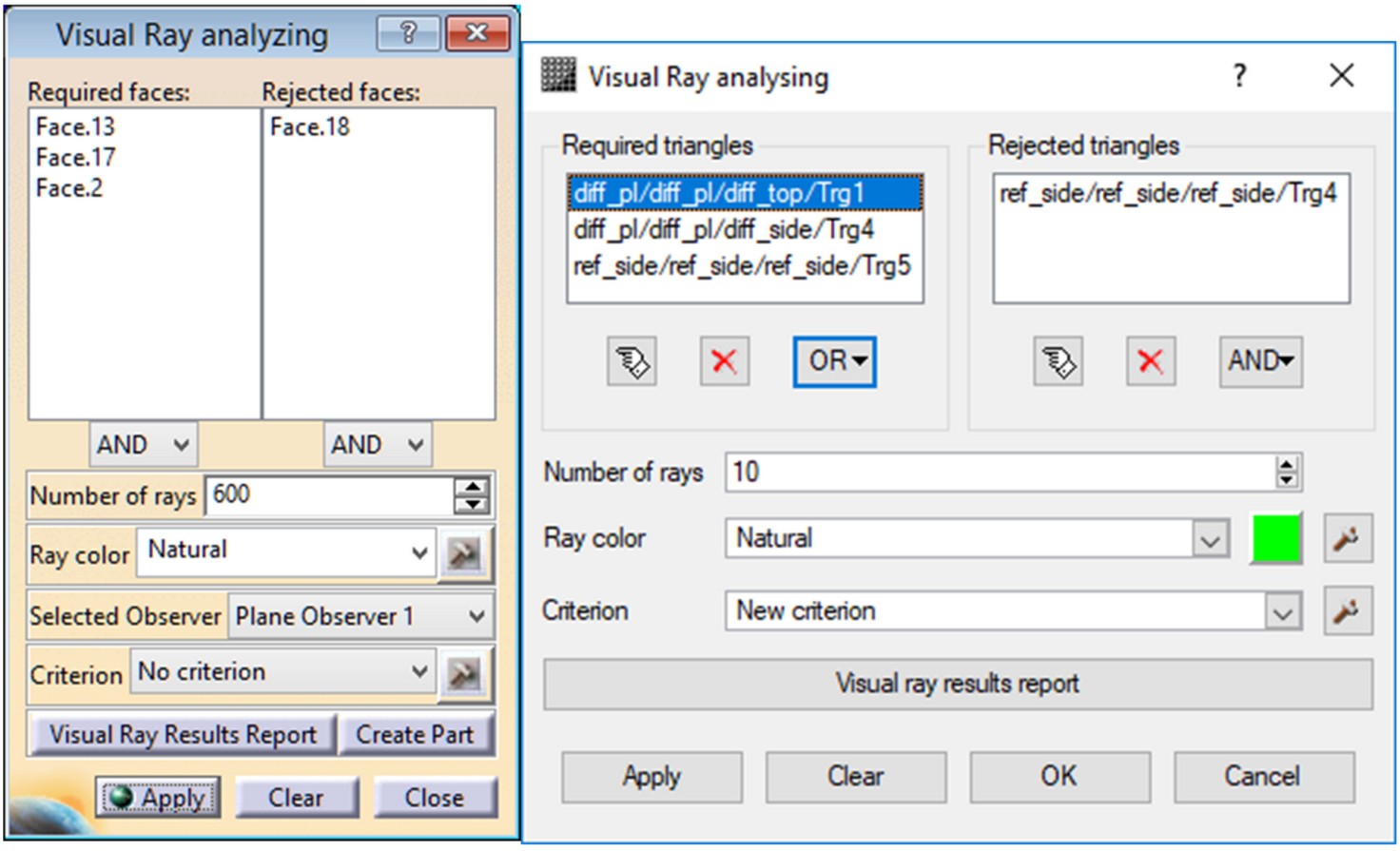
Fig. 5. User interface of ray visualization subsystem.

 

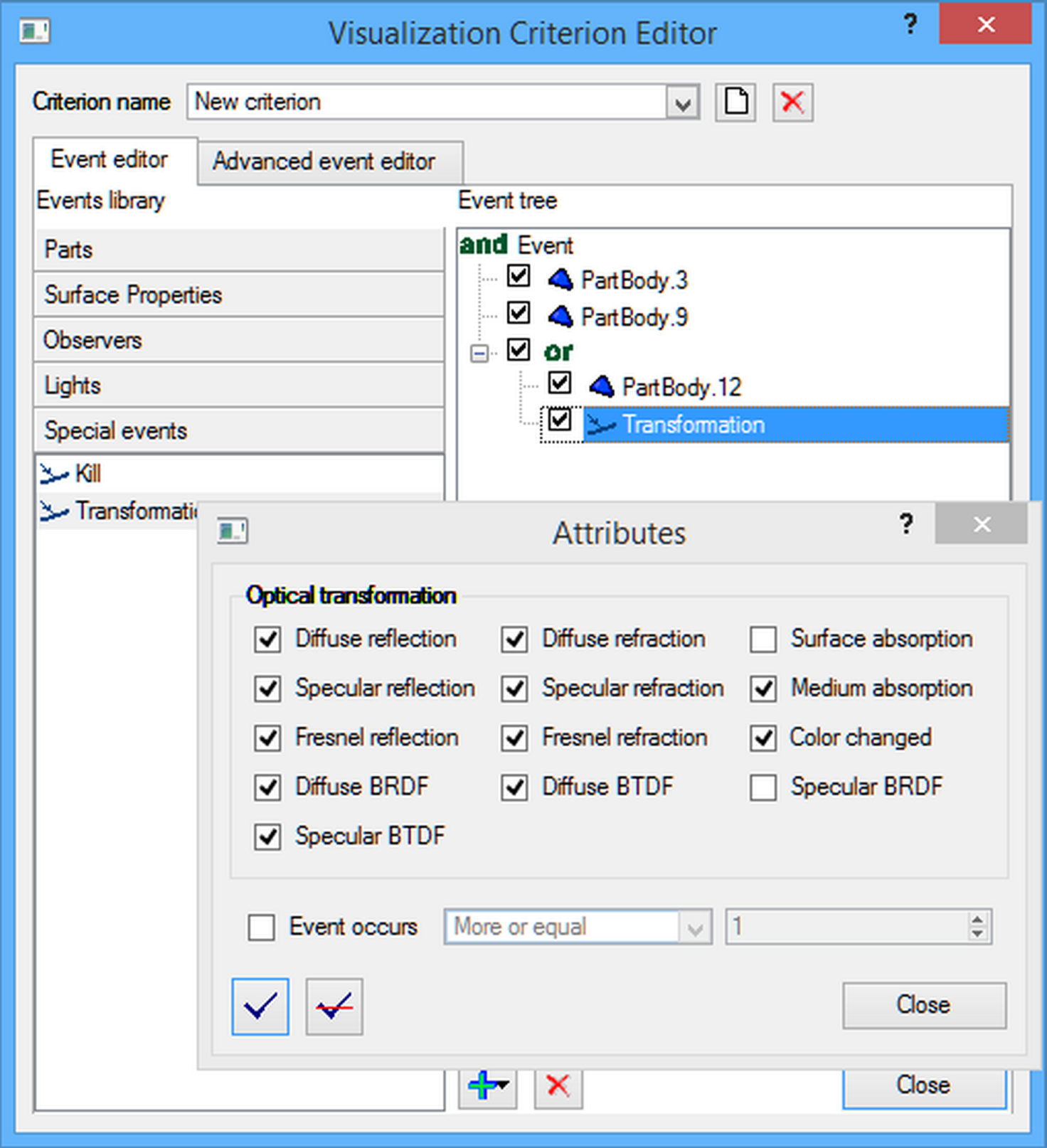
Fig. 6. User interface of a complicated criterion for ray selection.

 

For this purpose, the visual analysis module LumiVue is used, which allows you to select and edit the area on the virtual instrument image as a rectangle or ellipse. The registration of rays on this area can be considered as an additional criterion in the visualization of rays. An example of such a selected area is shown in Fig. 7. Additional possibilities of using the selected area for image analysis are given in [13].

 

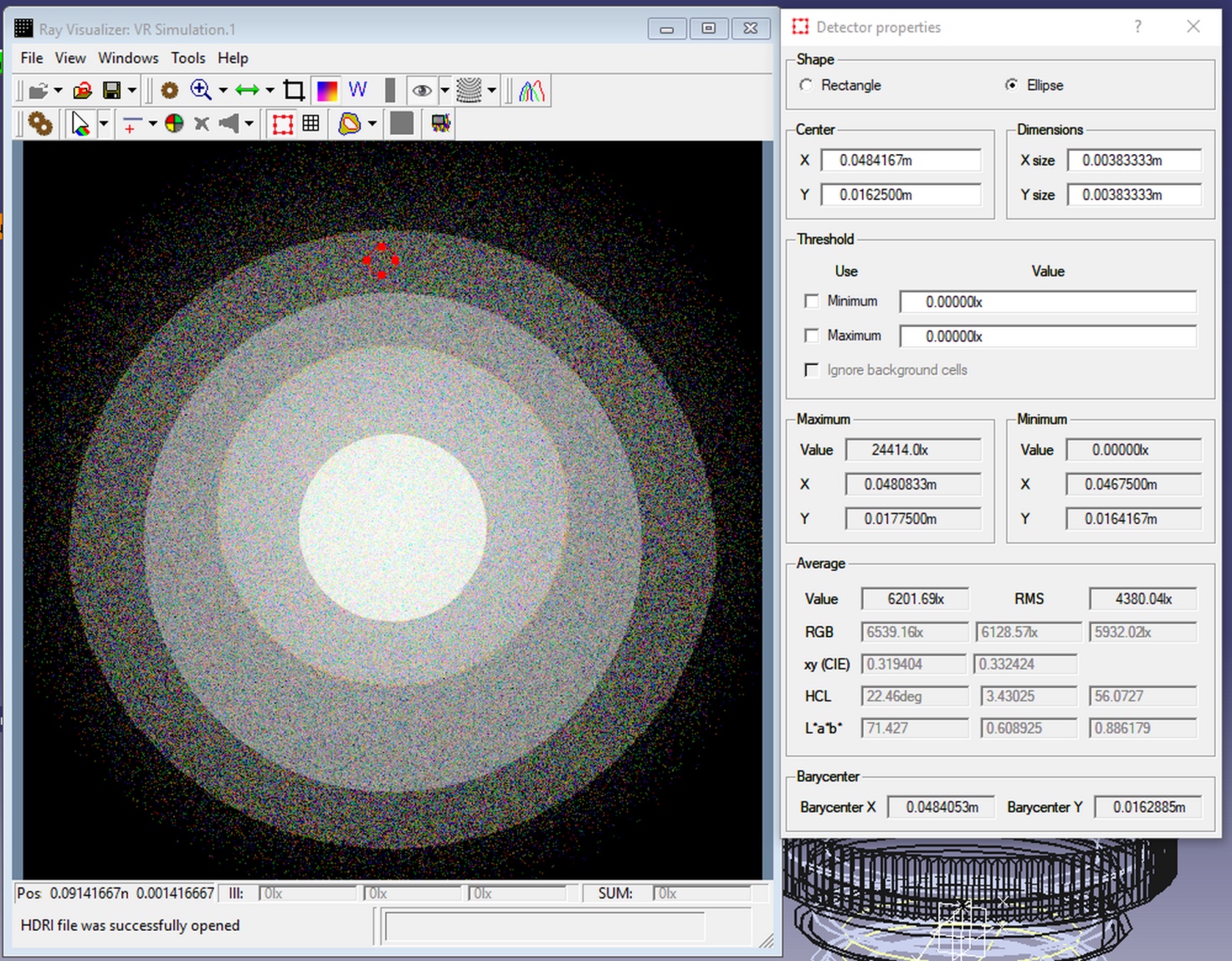
Fig. 7. Usage of selected region as a criterion

 

The image is loaded with the result of ray registration on this virtual measuring device and the LumiVue window is shown by the message LUMIVUE_LOAD, which is sent by CATIA (Fig. 3.) The path to the image file is transmitted through the shared memory used by the processes. The result of the simulation in the form of saved rays can use several virtual measuring devices. One can choose any of them, or even abandon the use of virtual measuring devices in the analysis. If the virtual device is replaced, the LUMIVUE_LOAD message is sent again and the path to the new file with the result of registration on the new device is sent through the shared memory. In case of refusal to use the measuring device, CATIA sends a message LUMIVUE_HIDE and LumiVue hides its window. To get the parameters of the selected area, CATIA sends a LUMIVUE_DETECTOR message, and LumiVue puts all the parameters of the selected area into shared memory. All other parameters necessary for the construction of the criterion, and the path to the file with the rays are already in shared memory. CATIA now sends a VR_RAY_HISTORY message. According to this message, the I2 Server reads the file with the rays and begins to select from them rays that satisfy the constructed criterion.

File reading and rays selection

Reading a file with a three-dimensional ray map and selecting rays from it that satisfy the constructed criterion is the most critical procedure for the speed of visualizing light rays. It is extremely important to provide a user-friendly response time for this procedure. It is desirable that it does not exceed a few seconds. The algorithm for selecting rays satisfying the constructed criterion is shown in Fig. 8.

On multi-core computers, a parallel approach to using multiple threads is a natural approach to speeding up processing. This approach is effectively used by us for direct Monte Carlo ray tracing [14]. The number of threads is chosen, as a rule, equal to the number of virtual computer cores.

 

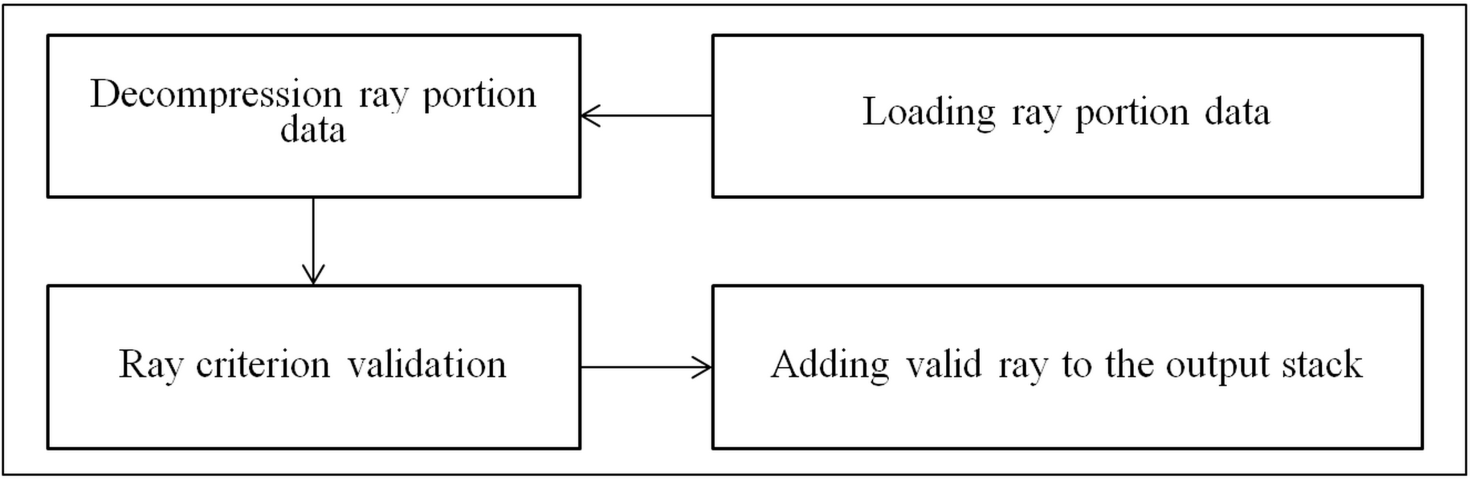
Fig. 8. General algorithm of selection of rays satisfying some criterion.

 

It is clear that in the procedure shown on Fig. 8 only unpacking of a portion and checking the ray against the criterion can be performed in parallel for different ray portions. Reading of ray portions from file must be performed sequentially because all threads work with the same file. Adding of a found ray that meets to the criterion to the output stack also cannot be performed in parallel because the stack is common for all threads. So a multithreaded scheme of selecting rays shown in Fig. 9 was elaborated.

 

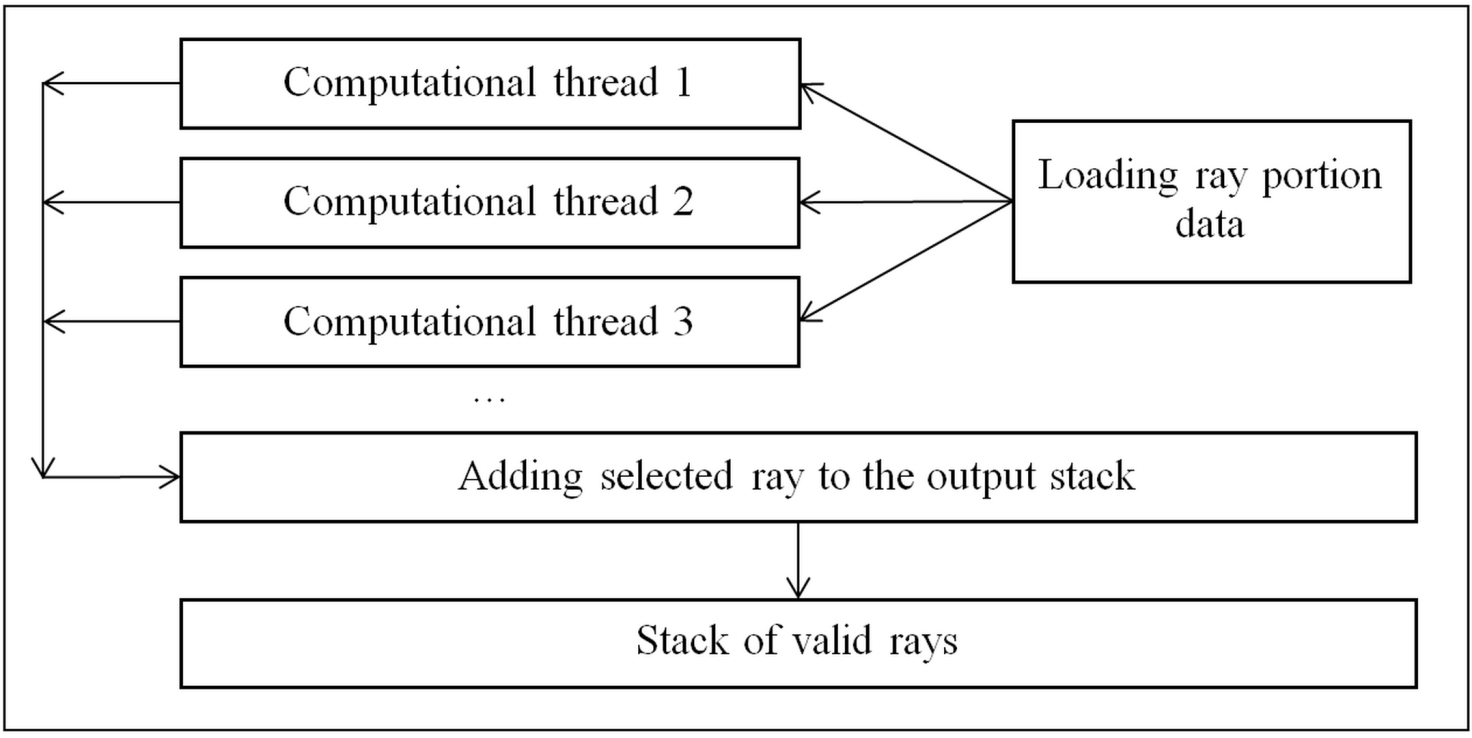
Fig. 9. Multithreaded algorithm of selection of rays satisfying to a criterion

 

The analysis procedure of the three-dimensional ray map starts after the user has specified the necessary parameters of the ray selection criterion. All necessary objects are created to store the results of data processing, in particular, the output stack of rays, a file with ray map is opened. Also computational threads for ray selection are created and started. Further, all data processing is carried out in computational threads, while the main thread only shows the progress of this processing, indicating the percentage of processed rays.

Rays processing in each thread is carried out according to algorithms shown on figures 8 and 9:

1.     A ray portion is loaded from the file. As all threads work with the same file a critical section is used for threads synchronization. As file reading in modern computers uses the special input/output coprocessor and a cache, this procedure almost does not restrict the work of the threads which unpack the portions and check the criterion.

2.     Obtained rays portion is being unpacked and searching of the rays satisfying to the specified criterion is performed.

3.     The found ray is added to the output stack in the format suitable for immediate visualization. As the output stack is common for all computational threads, this adding is also performed using a critical section. Since this procedure boils down mainly to adding a pointer to an object containing an array of segments to the stack, and quite rarely a large number of rays are required, the execution time is quite small and does not delay the operation of the main computational threads.

The effectiveness of this procedure can be characterized by the following values. For a three-dimensional ray map containing ~ 50 million rays (~ 450 million segments) the total processing time on an Intel Core (TM) i7–4770 computer (4 cores, 8 threads) is about 40 seconds. In this case, the file was processed completely, since the ordered number of rays that satisfy the specified criterion was not reached. The file contained spectral data, so the file size was about 6 Gb. In most practical cases it is sufficient to process only a few million rays. In this case the processing and visualization of the selected rays will be carried out in real time.

The Fig. 10 shows the dependence of the three-dimensional ray map processing speed on the number of used threads for the above computer. It can be seen that the proposed algorithm scales well with an increase in the number of processors used. Even the use of virtual processors (adding 5, 6, 7 and 8 threads) gives a noticeable increase in processing speed.

 

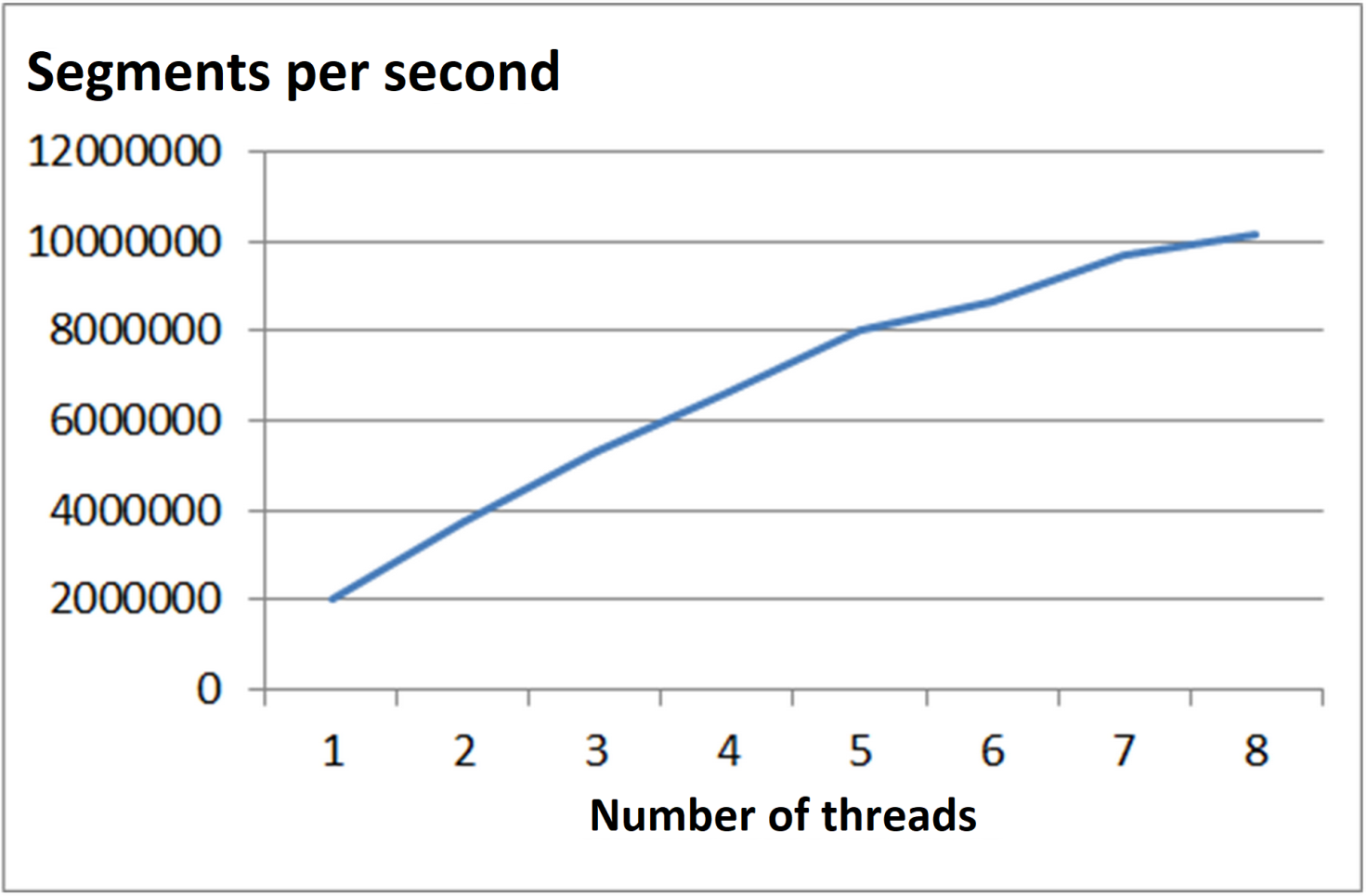
Fig. 10. Dependence of the three-dimensional ray map processing speed on the number of used threads

 

Examples of ray visualization

Examples of visualization of the ray paths in the lens system for different areas in the virtual device image are shown in Fig. 11. A parallel beam of white light falls on the lens, in the direction deflected from lens axis by an angle of ~ 2 degrees. The lens material has dispersion – the value of the refraction index depends on the wavelength of the light. Therefore after refraction of a ray at the boundary of two media, the ray is further traced with a value of a single wavelength selected from a set of wavelengths specified by the user. The wavelength (and accordingly the direction of the refracted ray) is selected from a given set of wavelengths with a probability proportional to the part of the ray energy corresponding to the selected wavelength. For this reason, after refraction the rays in Fig. 11 become colored if a natural color is selected for visualization. When one clicks the Visual Ray Results Report button, the dialog box shown in the upper right of the Fig. 11 opens, in which the user can analyze in detail all the events which took place along the path of the ray.

 

 

 

 

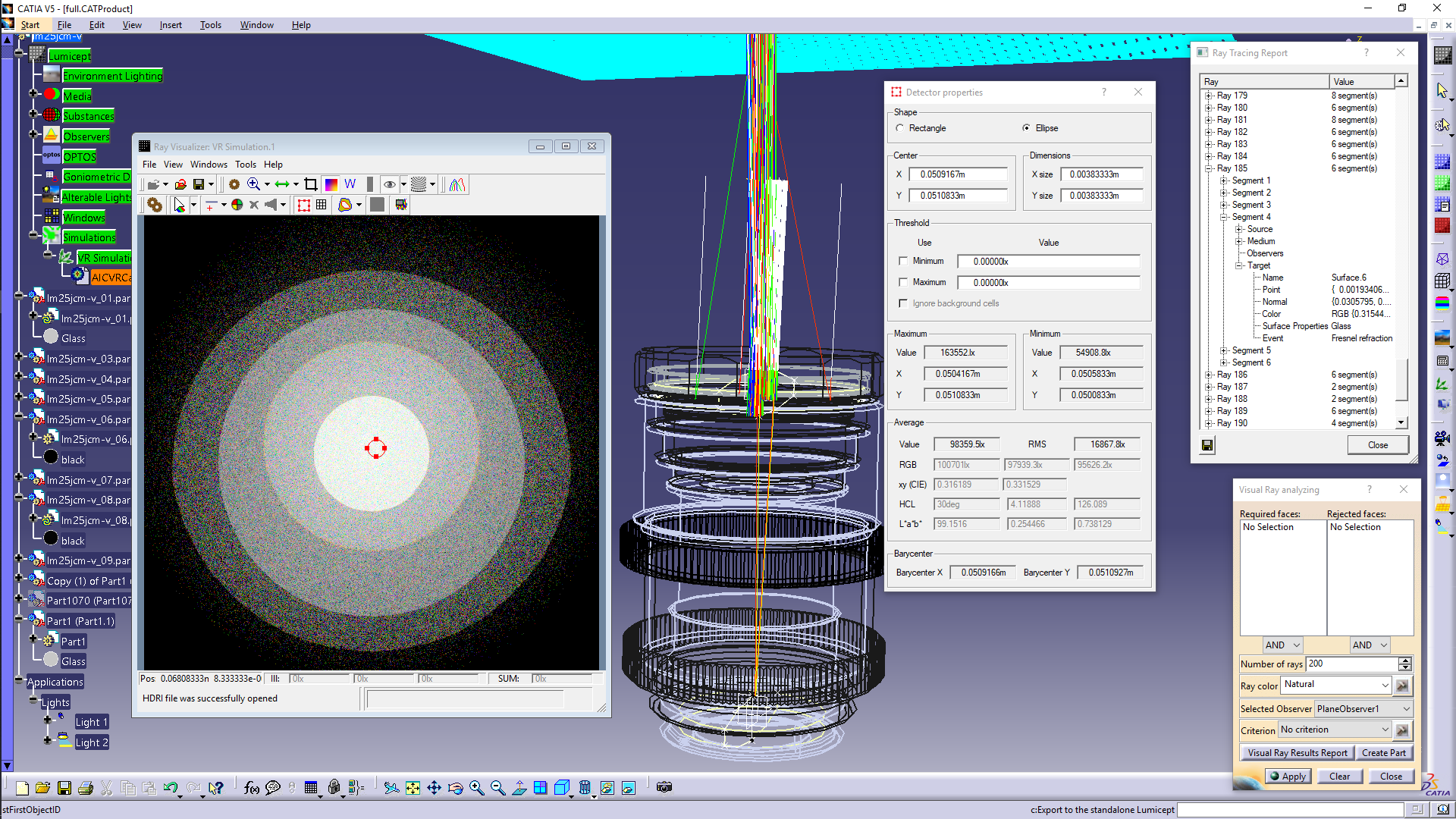
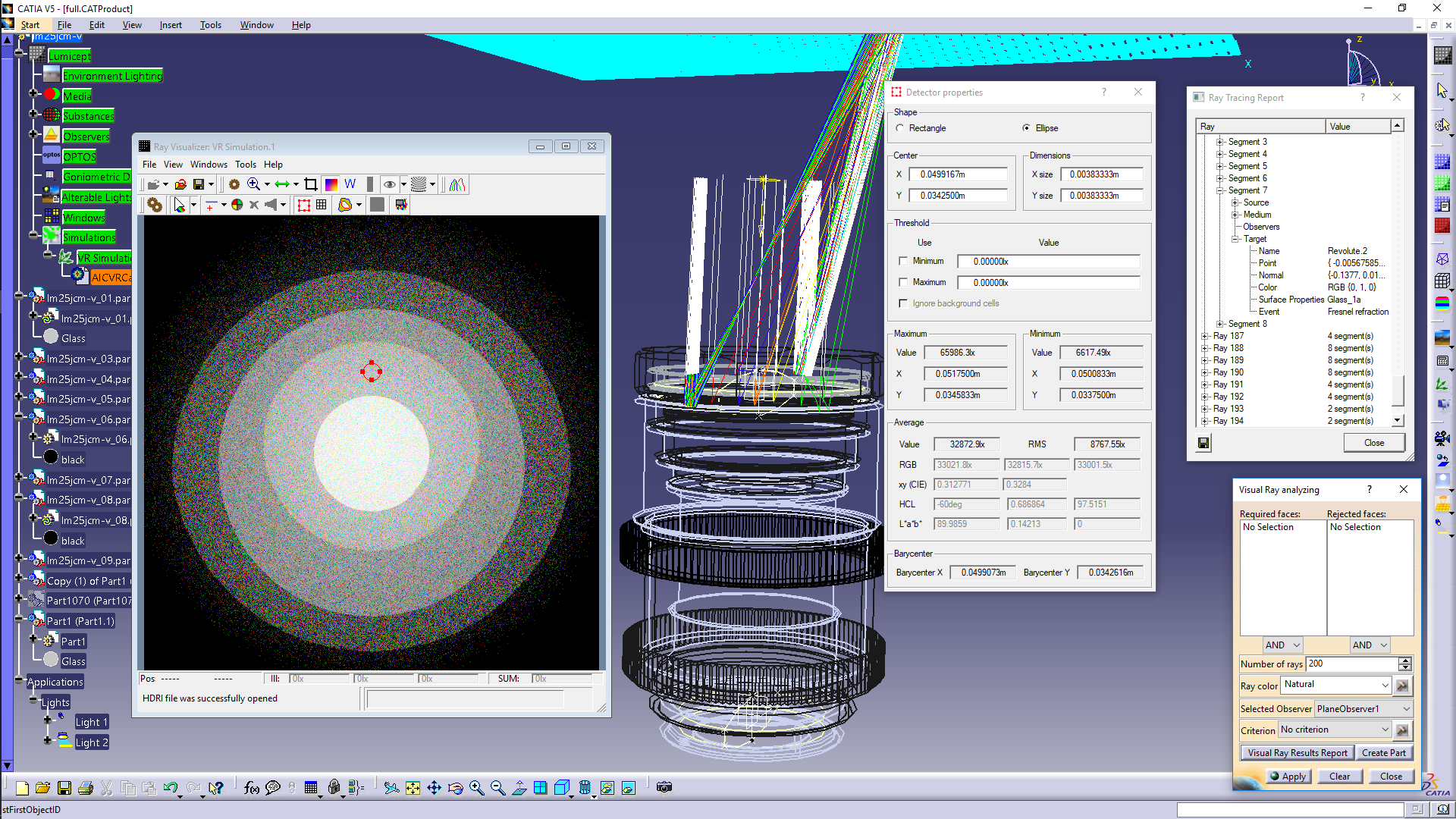
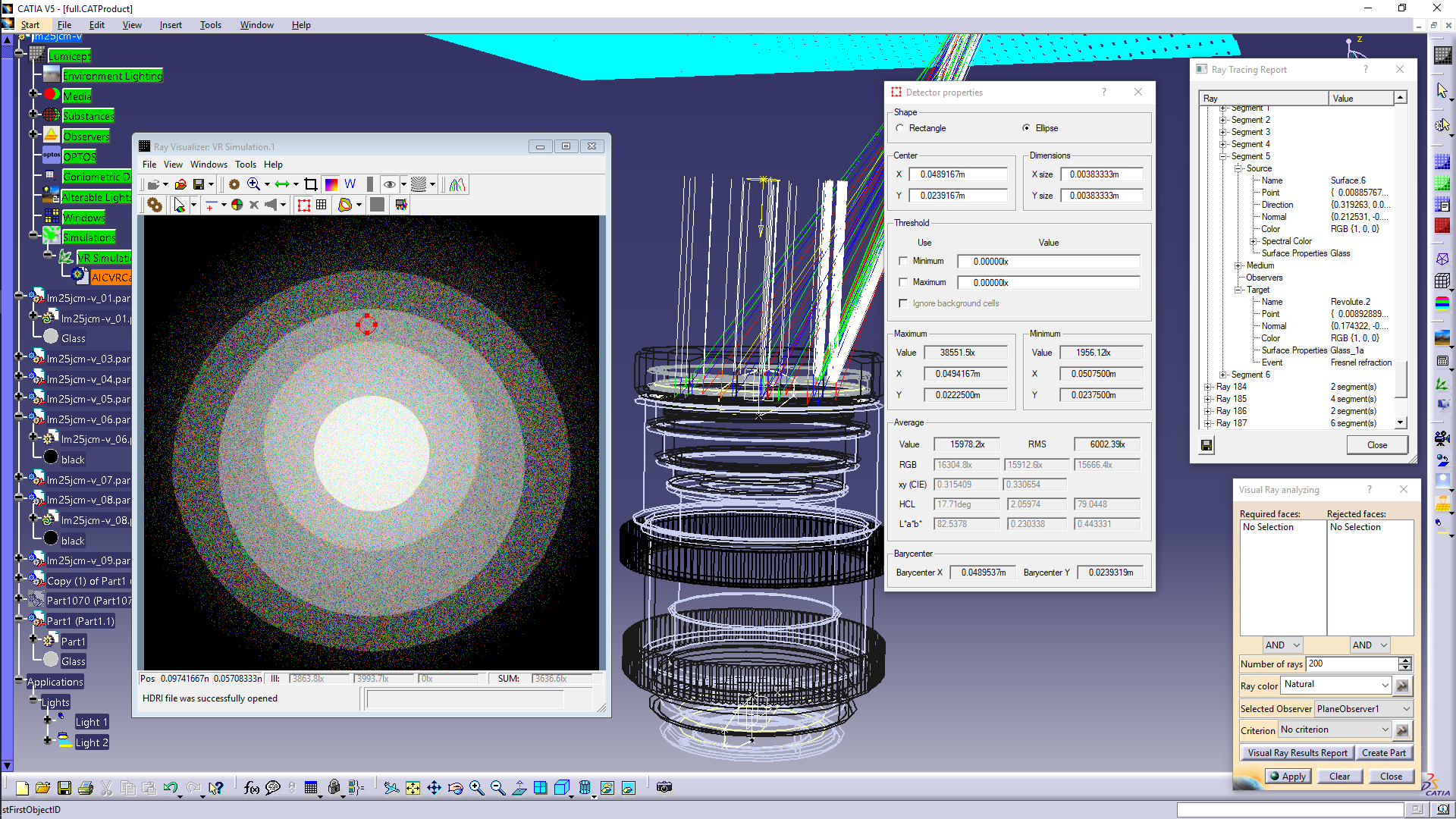
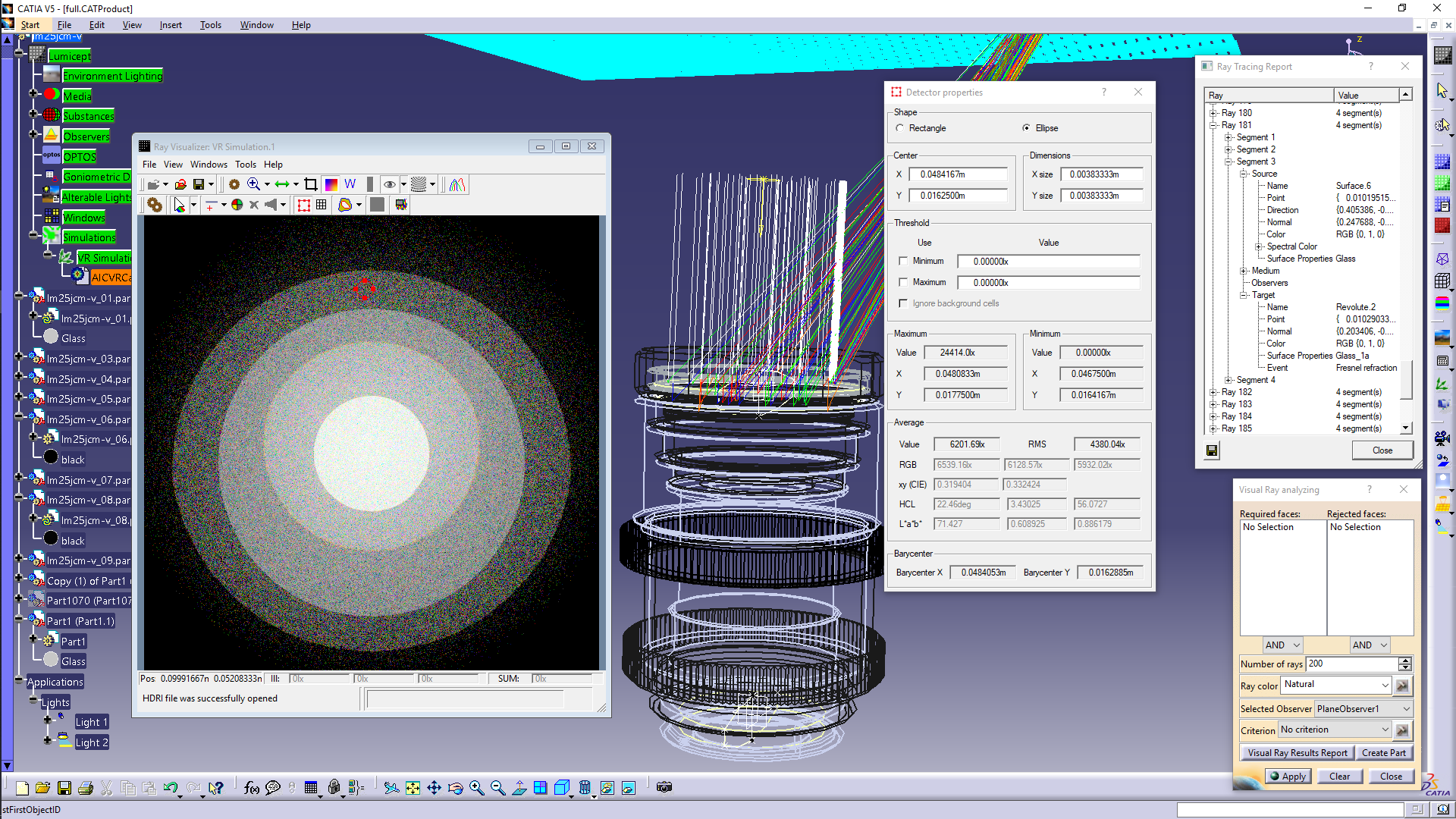
Fig. 11. Visualization of selected rays and report about the events along the ray path.

 

Conclusion

The visual representation of the trajectories of light rays has become in fact the basic functionality of modern optical simulation systems. The developed algorithms make it possible to efficiently use multi-core computers both for calculating the three-dimensional map of the rays obtained by Monte Carlo ray tracing and for their visualization using various criteria for the selection of rays. The developed algorithms are implemented in the standalone system for the synthesis of realistic images and optical simulation Lumicept, developed in KIAM, as well as in the corresponding system of ray visualization integrated into CAD systems CATIA.

Literature

 

[1]	Pharr M., Humphreys G., Physically Based Rendering: From Theory to Implementation. Second Edition. Morgan Kaufmann Publishers Inc., 2010.
[2]	Bogdanov N., Zhdanov D., Potemin I., Zhdanov A. Design of Ergonomic Illumination Systems for Cultural, Medical, Educational Facilities. The Educational Review, USA, 1(4), 85-90. http://dx.doi.org/10.26855/er.2017.04.001.
[3]	Wernert E., A unified environment for presenting, developing and analyzing graphicsalgorithms. Computer Graphics, т. 31, № 3, pp. 26-28, 1997.
[4]	Tsirikoglou A., Kronander J., Wrenninge M., UngerJ., Procedural Modeling and Physically Based Rendering for Synthetic Data Generation in Automotive Applications. arxiv.org. 2017.
[5]	McCormac J., Handa A., Leutenegger S., Davison A., SceneNet RGB-D: 5M Photorealistic Images of Synthetic Indoor Trajectories with Ground Truth. The IEEE International Conference on Computer Vision (ICCV 2017).
[6]	Rozantsev A., Lepetit V., Fua P., On rendering synthetic images for training an object detector. Comput. Vis. Image Underst. 137, C (August 2015), 24-37. DOI: http://dx.doi.org/10.1016/j.cviu.2014.12.006.
[7]	Voloboj A.G., Vishnyakov S.M., Galaktionov V.A., ZHdanov D.D., Sredstva vizualizacii rasprostraneniya sveta v zadachah proektirovaniya i analiza opticheskih sistem // Keldysh Institure of Applied Mathematics of RAS Preprints, № 54, 2007, 20 p [in Russian]
[8]	Kopylov E., Dmitriev K., Light propagation visualization as a tool for 3D scene analysis in lighting design. Computers & Graphics, т. 24, № 1, pp. 31-39, 2000.
[9]	Voloboj A.G., Galaktionov V.A., ZHdanov A.D., ZHdanov D.D., Sredstva vizualizacii rasprostraneniya svetovyh luchej v zadachah proektirovaniya opticheskih sistem. "Informacionnye tekhnologii i vychislitel'nye sistemy", № 4, c. 28-39, 2009. [in Russian]
[10]	Barladyan B., Shapiro L., Voloboy A., Ray maps technique for effective interrogation of results of MCRT simulation // Conference proceedings of 21-th International Conference on Computer Graphics and Vision GraphiCon-2011, Moscow State University, September 26-30, 2011, Moscow, Russia, pp. 46-49.
[11]	B.H. Barladyan, E.D. Biryukov, A.G. Voloboj, L.Z. SHapiro, «Effektivnyj algoritm vizualizacii predvaritel'no rasschitannyh luchej» // GraphiCon-2018, Tomsk, 24–27 september 2018, p. 36-39. [in Russian]
[12]	"zlib" general purpose compression library, http://zlib.net.ru/.
[13]	Barladian B.K., Potemin I.S., Zhdanov D.D., Voloboy A.G., Shapiro, I.V. Valiev L.S., Birukov E.D., Visual analysis of the computer simulation for both imaging and non-imaging optical systems // Proc. SPIE 10021, Optical Design and Testing VII, 100210T (October 31, 2016); doi:10.1117/12.2247751.
[14]	B.Kh. Barladian, L.Z. Shapiro, E.Yu. Denisov, A.G. Voloboy. An efficient mulithreading algorithm for the simulation of global illumination // Programming and Computer Software, 2017, Vol. 43, №. 4, pp. 217-223. DOI: 10.1134/S0361768817040028.