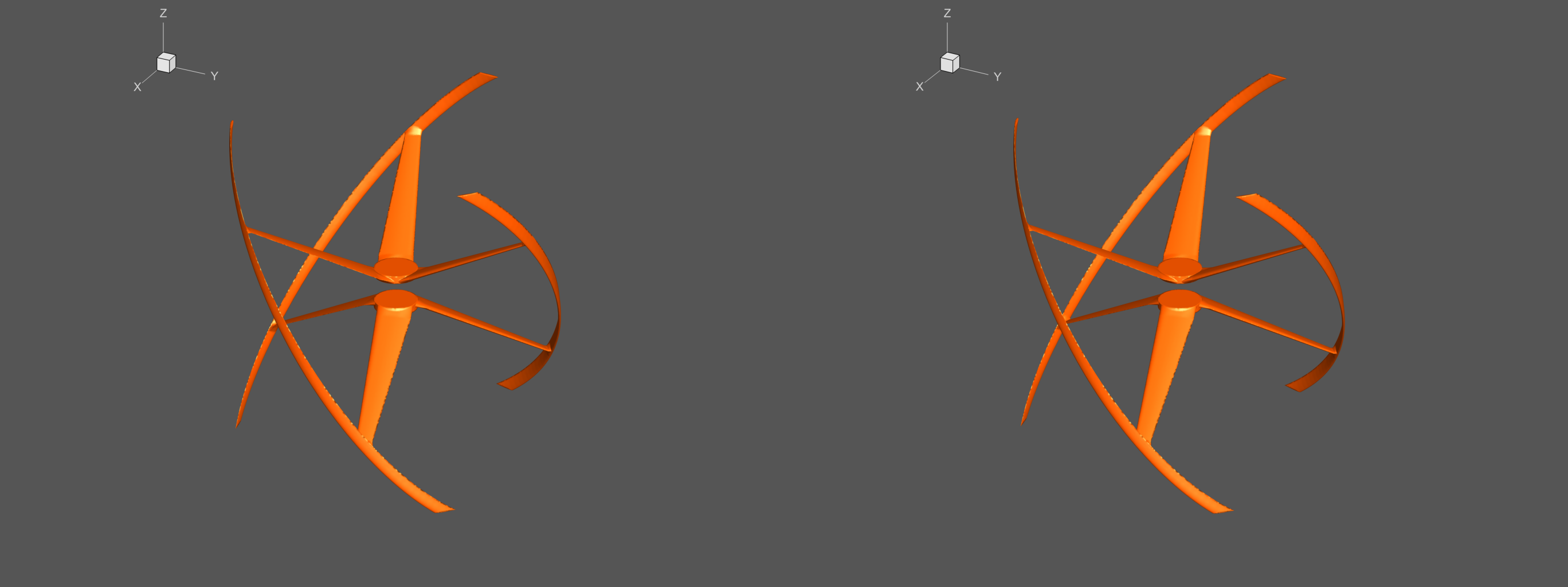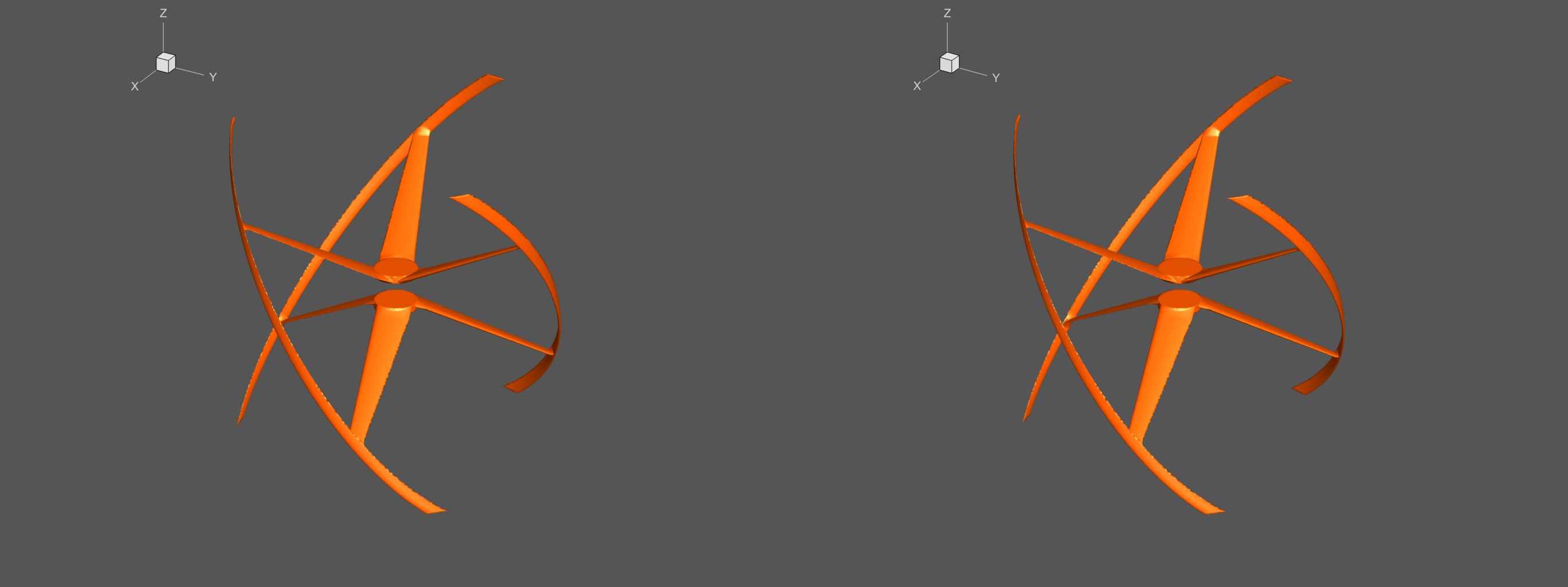The emergence, development and improvement
of modern stereo devices, both passive and active types, made it possible to
build stereo-animated presentations of scientific research results. The
significance and relevance of new opportunities opened up by using stereo
systems cannot be overestimated. Presentation of the numerical modeling
results, reflecting the flow of complex physical processes in time or showing
the operation of complex technical systems in a three-dimensional
representation, allows a lot. First, the three-dimensional representation of
the process development over time helps to verify the computational model and
the algorithms used. Secondly, it provides the observer with a full
understanding of the phenomenon being modeled. And finally, it promotes the
research and its results for society, including for decision makers. All of the
above makes theoretical and practical developments in the field of constructing
stereo representations very important.
With the emergence and development of
stereoscopes, more and more papers began to appear on the issues of constructing
stereo images. It is possible to refer to similar articles [1,6-8].At first,
most studies in the field of stereo images were related to the tasks of
building virtual reality, simulators and training systems. However, the issue
of building presentation complexes, which, among other things, made it possible
to demonstrate the results of scientific research in stereoscopic mode, became
very topical later [2-4, 11]. In [3], the results of the display of the
Supernova explosion in stereo mode are presented. The article [11] presents the
methods of stereovisualization for the task of displacing oil from porous
media. The paper [4] is devoted to the creation of computational technology for
modeling the operation of a three-dimensional node of the blades of a power
plant with a flow past a viscous compressible heat-conducting gas. The
construction of animated stereo representations of the calculation results was
one of the important components of the developed technology.
In general, systems for displaying images
in a volumetric representation (stereo) can be divided into two main types:
passive and active. Passive complexes are intended for demonstration of
material according to a predetermined scenario, when the viewer is deprived of
the opportunity to influence the process of the show; active (or interactive)
complexes are distinguished by the fact that the viewer in some way influences
the process of showing the displayed material.
Common to all these systems is the presence
of a large screen (and even several screens), so the typical monitor resolution
is often not enough to generate a frame displayed on the stereo screen. In
addition, such systems should provide a display in a three-dimensional
representation, that is, in stereo mode, when each frame is generated
separately for the left and right eyes (right and left stereo channels). Thus,
the requirements for computing resources for generating frames are doubled. Often,
such stereos are not controlled by a separate computer, the power of which is
not enough to generate frames in real time, but by a system of computers
connected to a local network and providing composite stereo frame output on
several screens. Specific problems that arise when using a computer system for
generating and visualizing a composite multi-screen stereo frame, and methods
for solving such problems are described in detail in [1,2].
The gradual spread of modern stereos has
generated great interest in the development of practical algorithms for the
stereo presentation of static and animated images, which is reflected in [3, 5
- 7]. This work relates to the general topic of building stereo images and
stereo animations of the results of mathematical modeling of complex technical
objects and physical processes in continuous media. This work presents a
practical experience in stereo animations constructing for specific devices for devices available in Keldysh Institute of Applied Mathematics (KIAM RAS). The first type of device is a 3D
projection stereo system for displaying stereo presentations, educational
applications, graphics and films. This device includes a graphic station, a
projection subsystem of two projectors (with a specialized screen), and a
speaker system. This system is a classic stereographic system using two
projectors, a screen and linear polarization glasses.
When creating stereo pairs required for
stereo film frames, systems of this type use either linear or angular camera
displacement, that is, linear or angular stereo base. In most cases, the linear
stereo image is used when rendering objects of the scene with a far distant
background. Linear displacement is used quite rarely, since most often you need
to get an idea about the object of visualization from all sides.
In most cases, the result of the
calculations is a rather encapsulated object that is not attached to the
environment, such as a part of an airplane or a car. And first of all it is
important for viewers to inspect this object from all sides. In such cases,
angular displacement, i.e. angular stereo base, is applied. Most often, the
center of spatial coordinates located inside the object is determined, and the
angular displacement of the camera occurs.
In order to show the object of
visualization from all sides, it is enough to fix the distance from the camera
to this center of coordinates and make a full rotation of 360 degrees in the
horizontal plane around the vertical axis OZ, successively changing only the
angle. As a result, we get a stereo effect for the visualization object that
"hangs in the air", and object center of coordinates is at a distance
from the viewer's eyes to the screen plane.
The second type of device is a Dimenco
DM654MAS autostereoscopic monitor. Autostereoscopic monitors provide stereo
images show without the need to track the observer’s position, that is, there
is no need to adjust the equipment depending on the observer’s position - as a
rule, such monitors allow you to observe stereo images, providing several fixed
segments in the observation space, so the viewer is able to see the displayed
object in 3D from different angles of view. The principle of operation of an
autostereoscopic monitor is the use of parallax partitions or Fresnel lenses
installed behind a protective glass screen.
One of the most important advantages of
autostereoscopic monitors is the fact that viewing images on such devices does
not require the use of special glasses. In past years, installations of this
type could not provide the quality of a stereo image, comparable to the classic
two-projector projection stereoscopic images. However, modern devices make it
possible to build stereo images on high-quality stereoscopic monitors, in no
way inferior to classic projection installations. The (Fig. 1) shows the modern
Dimenco autostereoscopic monitor with the following technical characteristics:
1) Weight - 72 kilograms;
2) Screen diagonal - 65 ”(165 cm);
3) Resolution - 3840 × 2160.
This monitor was used to build some of the
stereo images presented in this article.
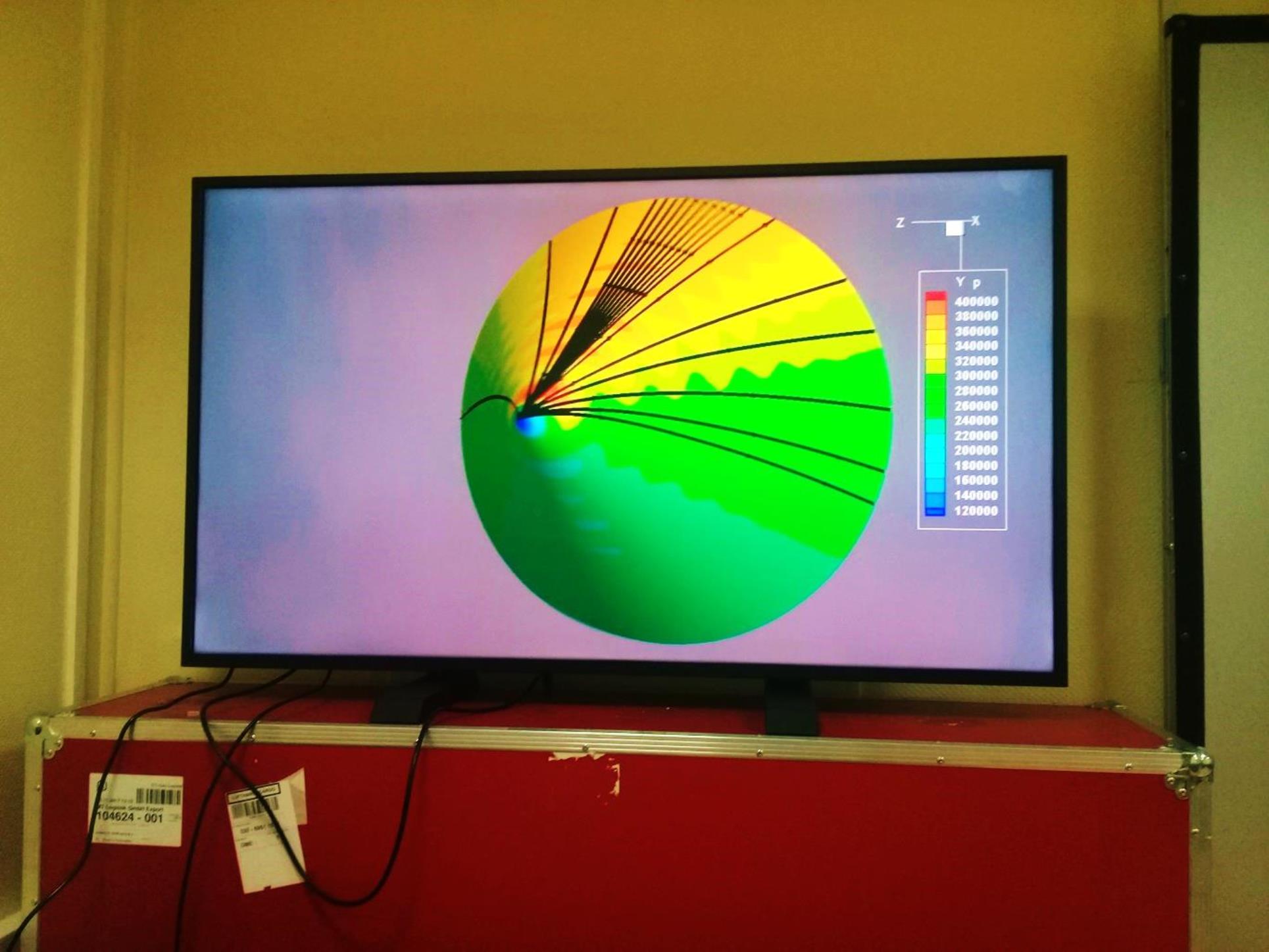
Fig.
1. Autostereoscopic monitor Dimenco DH654MAS.
To build a stereo frame on an
autostereoscopic monitor, such methods are used as the construction of depth
maps or the construction of a multi-view frame.
Next, we consider a number of methods and
approaches used in our research for the practical construction of stereo
animations on both types of modern stereos described above.
When creating stereo pairs required for
frames of stereo animation, either linear or angular camera displacement is
used, that is, linear or angular stereo base. In most cases, to visualize the
results of calculations, it is necessary to consider the object of
visualization from different sides, therefore, for these purposes, the most
suitable method is “camera flying around the object" method with using
angular stereo base.
Almost any CAD-system allows you to
visualize a three-dimensional object with given coordinates of the position
relative to the user. Therefore, the task is reduced to constructing a sequence
of images of a CAD model with a fixed Z axis passing through its geometric
center and offset by a certain angle. After each such shift, the model is
rendered, which allows to achieve photorealism, and the result is saved as a
graphic file in high resolution. For the left stereo channel, the initial
position is set, which differs from the right stereo channel by the angle
defining the parallax and allowing to achieve the volume of the object in the
resulting stereo film. This method is also attractive because for a static
model, that is, with a constant geometry and color distribution, it is possible
to reuse already calculated frames, for example, if for the left stereo channel
we use 1,2,3,4, ... frames, then for the right one a stereo channel is enough
to start the sequence from the second or third frame (2,3,4,5, ...),
automatically ensuring the object is shifted to the required stereo angle.
An additional gain of such a “camera flying
around the object” method also consists in the fact that having only 360 mono
frames you can organize a looping rotation of the visualization object in a
three-dimensional view, that is, organize its continuous and arbitrary long
time rotation, i.e. re-showing to the viewer all sides of the object (Fig. 2).
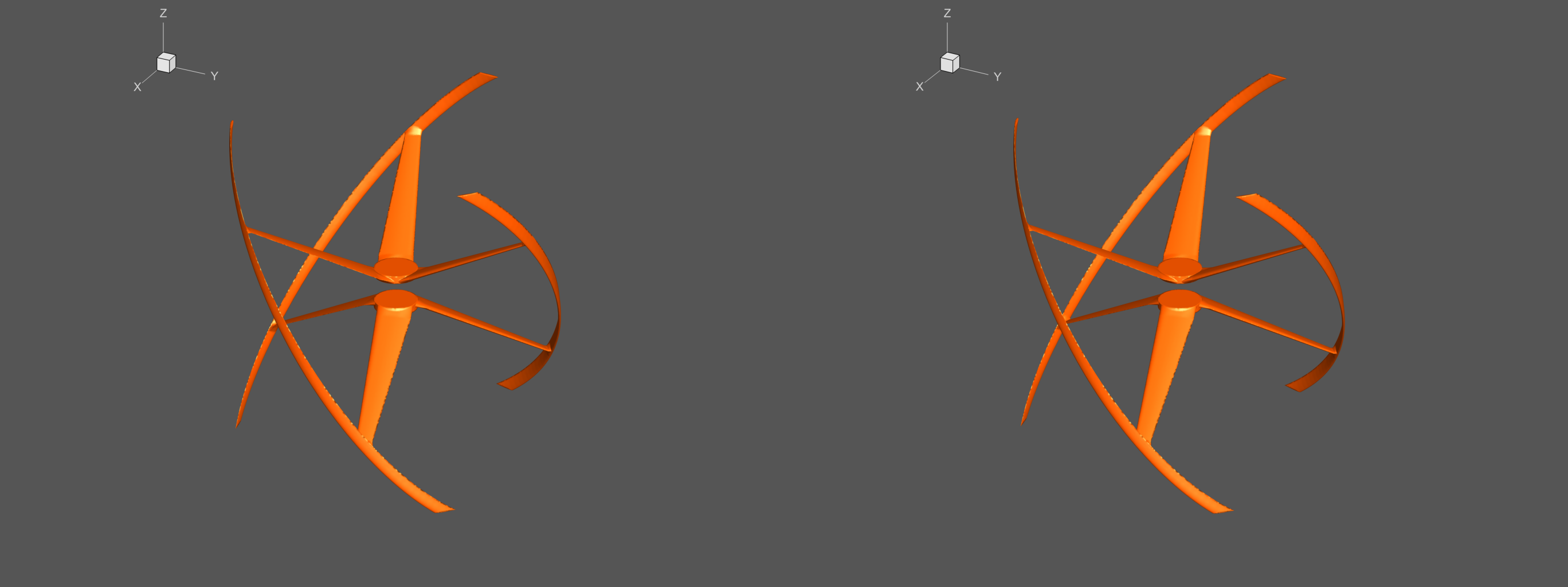
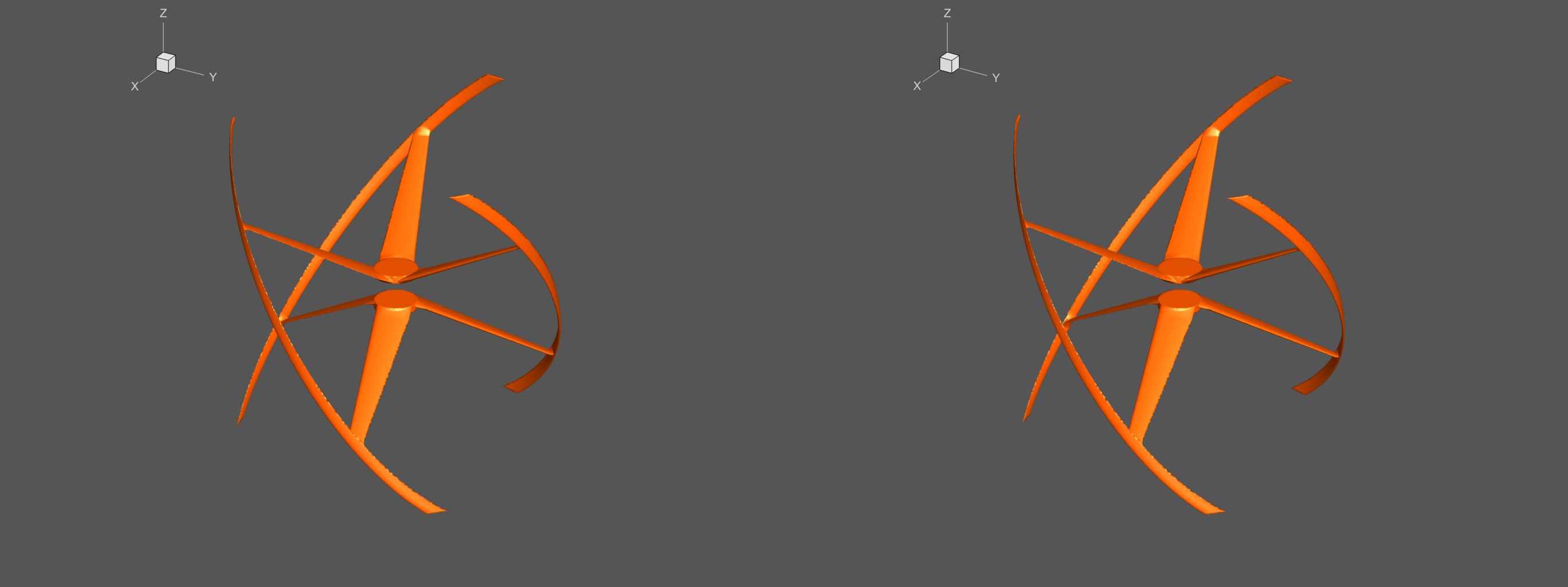
Fig.
2. Stereopairs with repeated use of calculated
frames with angular displacement.
This method was successfully implemented
when visualizing the modeling of the operation of a power plant with complex
shape in the stereo-animation mode for both classical stereoscopic projection
type and autostereoscopic monitor [4].
When creating a multi-view video for
autostereoscopic monitors, there is a need to store a large amount of data -
video streams for each angle. Even taking into account the fact that modern
methods of digital video compression can effectively take into account temporal
and spatial redundancy, the amount of data with multi-angle video increases
many times. This is especially critical for autostereoscopic monitors.
One of the effective ways to solve the
problem of large amounts of data is to use the so-called 2D + Z format. Any
conventional (2D) image can be matched with information about the distance of
each pixel from the observer (Z-coordinate). Such a representation of the image
is called "2D + Z format", and the plane of the coordinates Z is
called the "depth map". It can be represented as a monochrome image.
In the depth map, grayscale indicates the distance of the image points from the
observer. That is, the closest point to the viewer will turn white, and the
farthest to black. Figure 3 below shows an example of the original image and
its depth map.

Fig.
3. Original image and its depth map.
The 2D + Z format is a further development
of the concept of representing image information by component. It is widely
known that in analog and digital television the image is formed from brightness
and two color components. Adding a depth map to these components, which
characterizes the volume of the image, is a completely logical development and
is quite consistent with the principles of compatibility.
The idea underlying the construction of a
depth map using a stereopair is fairly obvious. For each point on one image, a
pair point is searched for it on another image. And by a pair of corresponding
points, you can determine the coordinates of their pre-image in three-dimensional
space. Having the same three-dimensional coordinates of the pre-image, the
depth is calculated as the distance to the camera plane.
The pair point must be sought on the
epipolar line [8]. Accordingly, to simplify the search, the images are aligned
so that all the epipolar lines are parallel to the sides of the image (usually
horizontal).
Moreover, the images are aligned so that
for the point with coordinates (x0, y0) the corresponding epipolar line is
given by the equation x = x0, then for each point the corresponding pair point
should be searched for in the same line in the image from the second camera.
This process of image alignment is called rectification.
After the images are rectified, the
corresponding pairs of points are searched.The simplest
method is as follows: for each pixel of the left image with coordinates (x0,
y0), a pixel is searched for in the right image. It is assumed that the
pixel in the right picture should have the coordinates (x0 - d, y0),
where d is a quantity called disparity. The search for the corresponding
pixel is performed by calculating the maximum of the response function, which
can be, for example, the correlation of neighborhoods of pixels. The result is
a disparity map.
Below Fig.4 presents a stereo-animation of
rotation for a synthesized image of a truck using a depth map.
Fig.
4. Stereo-animating the
rotation of a synthesized image of a truck using a depth map.
It should be noted that this method of
constructing a stereo image using a depth map when using it on an
autostereoscopic monitor provides more opportunities for the viewer compared to
conventional stereo animation, as the observer can view the image of the object
from different angles using the logic of the monitor processor.
An autostereoscopic monitor also has the
ability to show an object of visualization using a composite frame containing
views of the object of visualization from different angles that form a certain
viewing sector. Usually, the number of object views is
nine (Fig. 5).
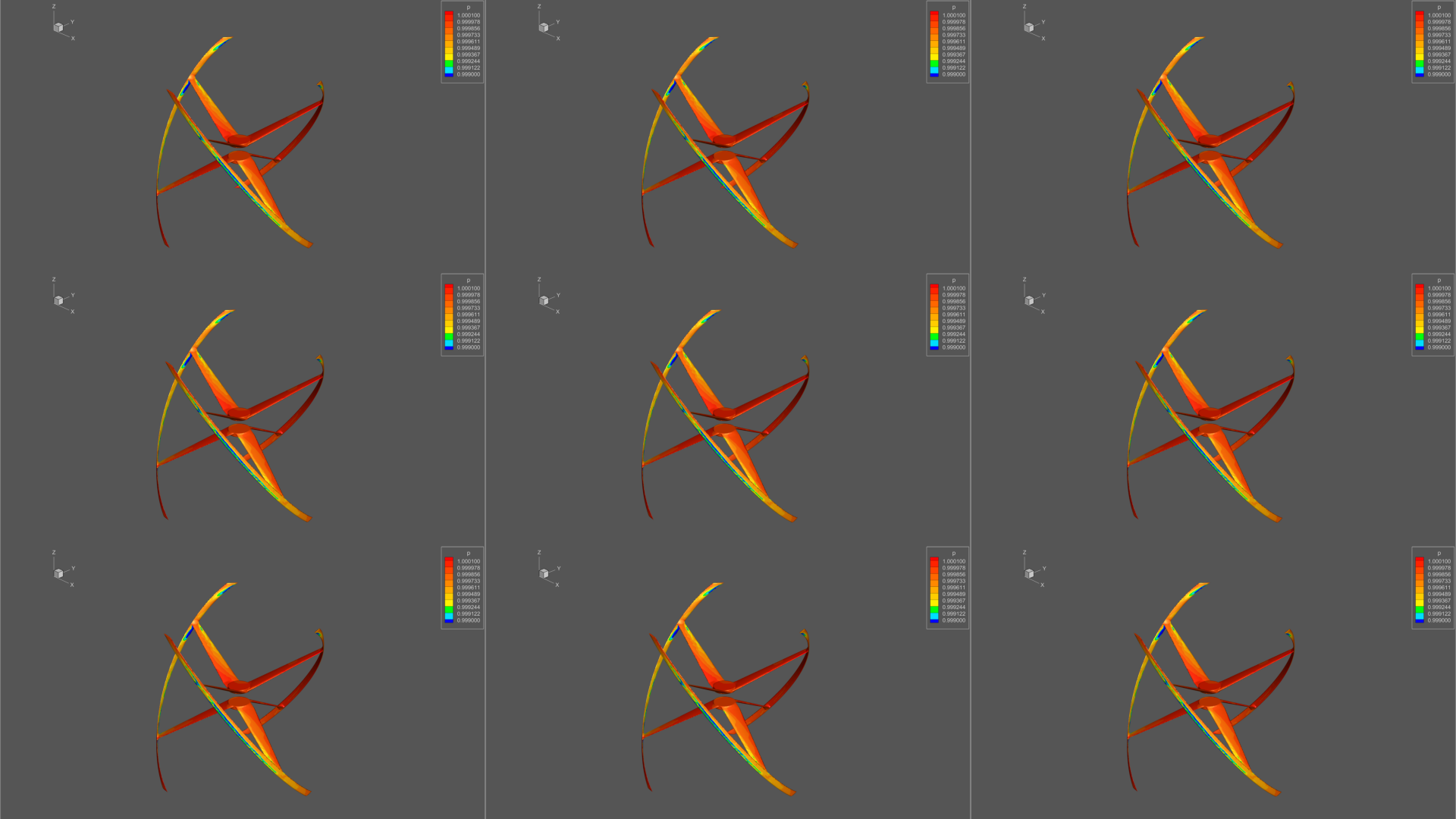
Fig.
5. Composite frame autostereoscopic monitor.
Moreover, these nine species form eight
stereo pairs ([1 | 2], [2 | 3], [3 | 4], ..., [8 | 9]), and the observer can
observe only one of the stereo pairs, depending on its position in angular
sector of observation. Moving from sector to sector, the observer receives 3D
information about the object, using all nine angles, that is, as if looking at
the object of visualization from different sides. At the same time, we note
that a “circling of the camera” actually occurs around the object, and,
therefore, the same method of reducing the necessary for visualizing mono
frames is quite applicable.
Indeed, in the case of an angular stereo
base of one degree and with a consistent angle of displacement around the axis
OZ, we get that the first frame consists of a sequence of angles with a
sequential change in the camera fly angle:
the second frame will be:
accordingly, the third frame will be:
and so on. The last frame looks like
allows one to loop the sequence of angles,
and, with a total of 360 mono-frames, you can get an arbitrarily long rotation
of the object of visualization in a multi-angle view on the autostereoscopic
monitor screen.
It should also be noted that this type of
representation of the object of visualization in a volumetric form on the
screen of an autostereoscopic monitor provides maximum quality compared to the
usual stereoscopic presentation and even the method using depth maps, allowing
you to view the object in a fairly wide viewing sector.
Building stereo animations using composite
multi-view frames made it possible to achieve stereo quality on an
autostereoscopic stereomonitor comparable to the quality obtained on a
classical projection device. Because of this, the construction of multi-view
frames has been applied in a whole range of computational technologies for
various problems of mathematical modeling in the construction of stereo
presentations of the results. We give below a number of examples illustrating
the application of this approach.
This visualization method was successfully
implemented when modeling the operation of a node of blades of complex shape in
a power plant [4]. The construction of stereoanimation was an integral part of
the computing technology organized in the form of a pipeline of algorithms:
from building a CAD model to presenting the results of calculations in the
stereo-animation mode (Fig.6). The overall goal of computing technology [4] was
to find the optimal, from the point of view of force, characteristics of the
blade node shape.
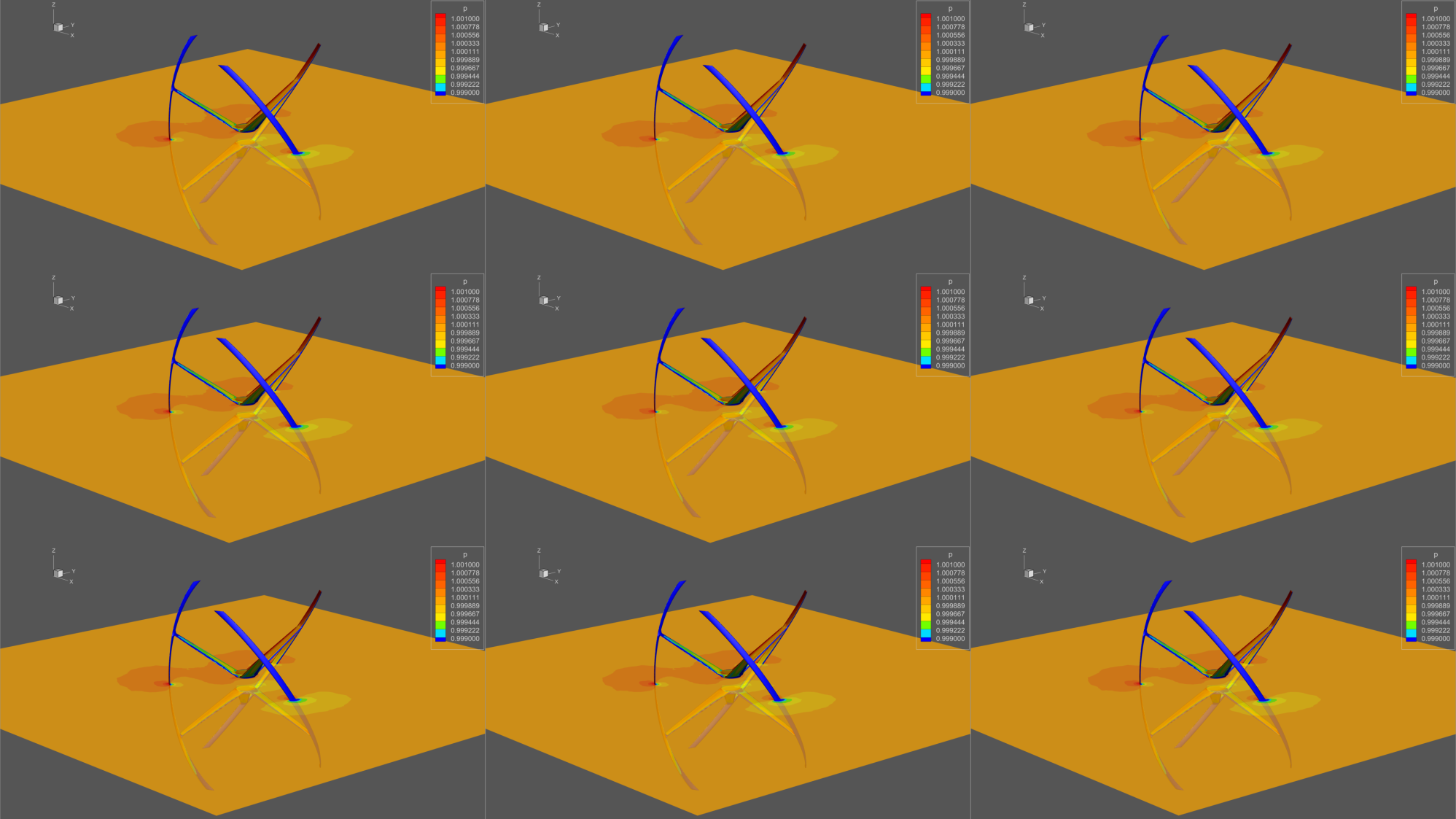
Fig.
6. A multi-view frame representing the simulation
results for a wind turbine blade assembly.
Another example is shown in Figure 7, where
a multi-view frame is shown for a blade node of another shape.
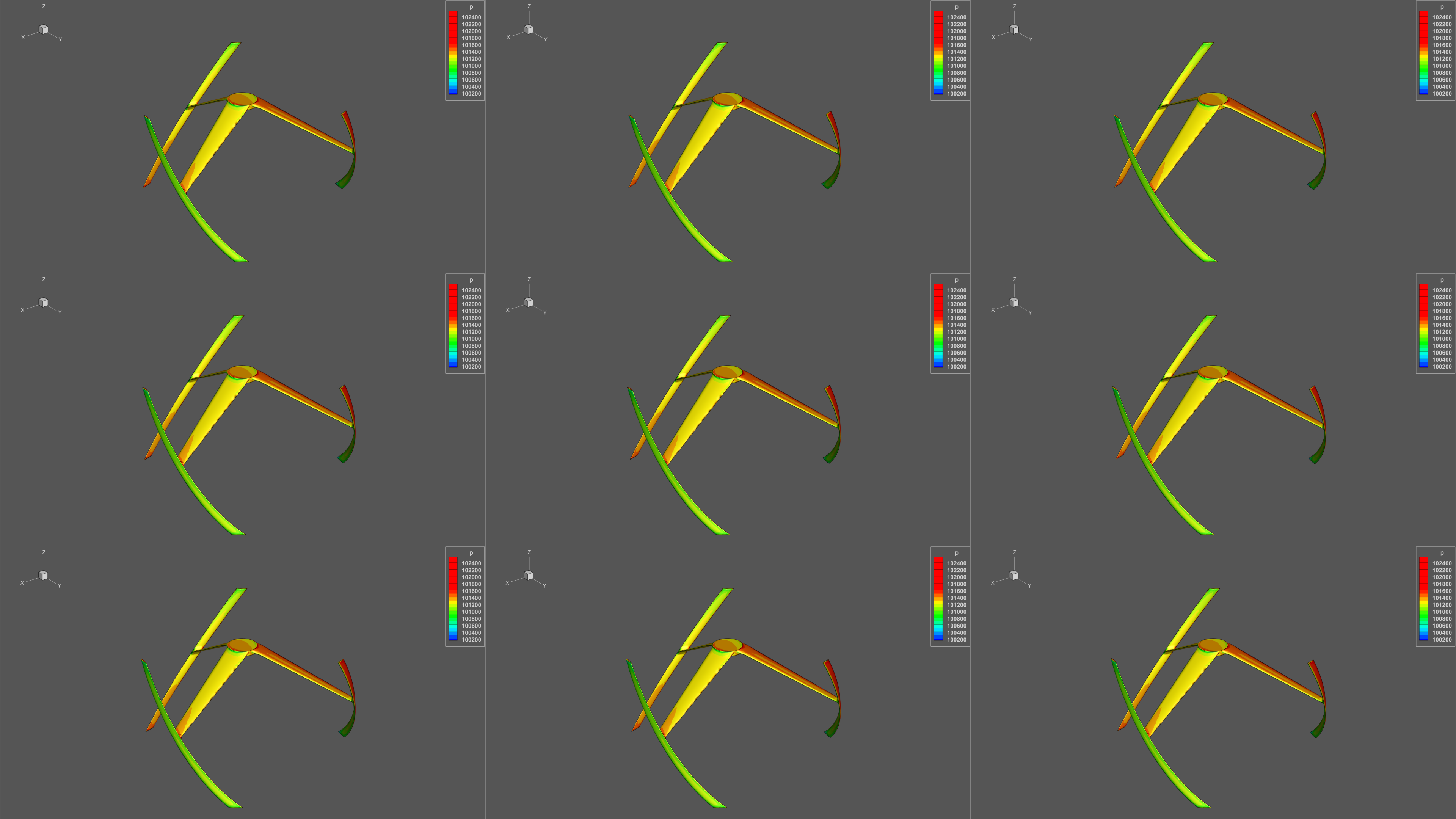
Fig.
7. A multi-view frame representing the simulation
results of a different form of a wind turbine blade assembly.
Figure 8 shows a “multi-view” frame for
stereo animation representing the results of a supersonic flow around a cone at
an angle of attack. The figure shows the distribution of
pressure on the surface of the cone and the streamlines.
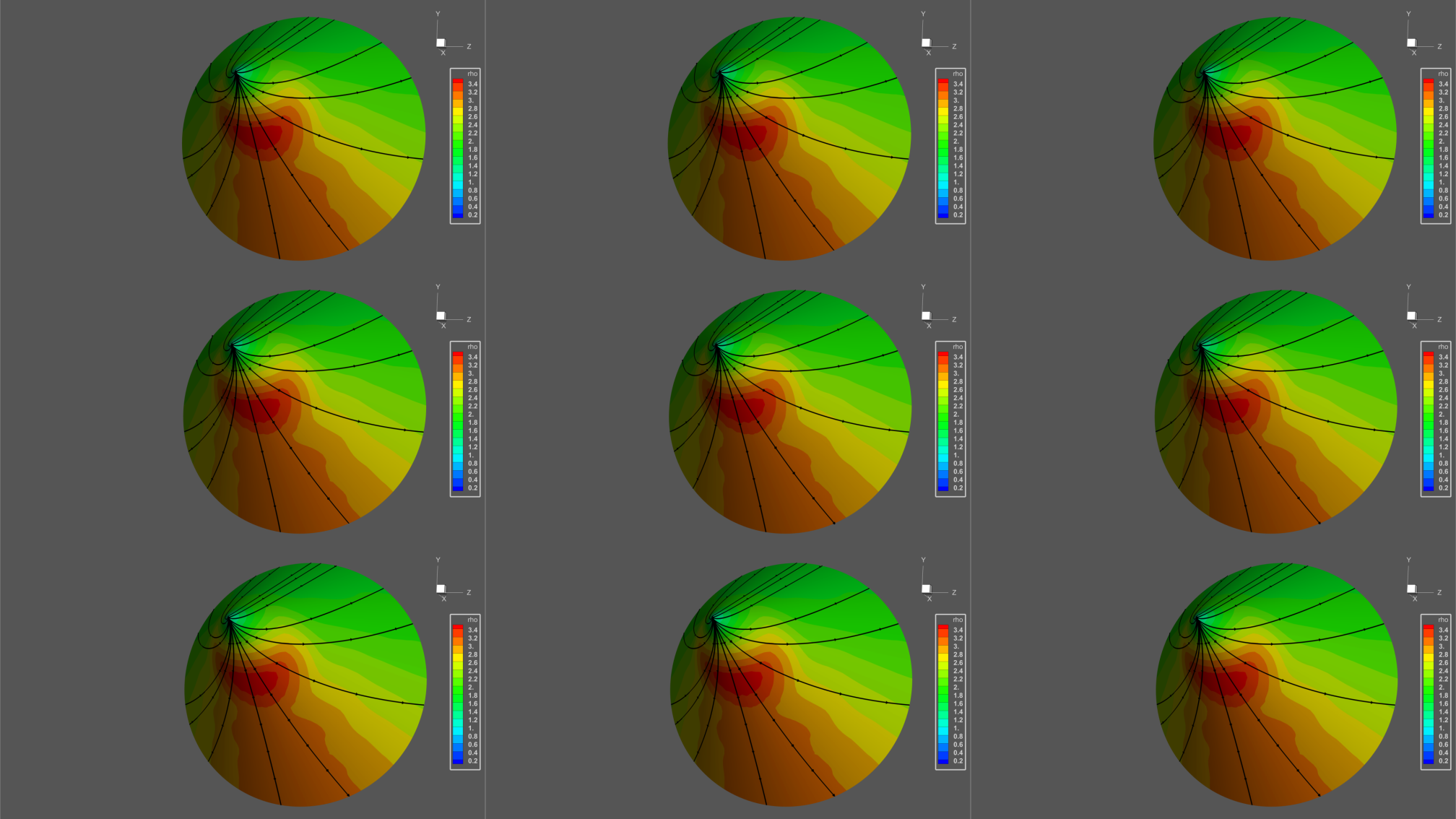
Fig.
8. A multi-view frame representing simulation
results of a flow around a cone.
When constructing stereo-animation, a
rather important private structural subtask arises. The standard presentation
of a scientific report, as a rule, includes not only the visualization of
complex geometry or fields of physical quantities, but also explanations,
usually represented by text and formulas. If for geometries and physical
quantities the problems of constructing stereo representations have been
developed sufficiently, then the tasks of constructing stereo images of texts
and formulas with sufficient expressiveness and the necessary stereo effect
remain open. Quite a few works are devoted to the development of specific
practical approaches in this area. Here we can mention only the work [12],
which describes the study in Japan of the perceptibility of stereo fonts on the
screens of stereoscopic mobile devices. However, this study was more social in
nature than it gave the recipes for constructing stereo images of texts and
formulas.
The construction of stereo-images of texts
and formulas in this research were carried out for the classical 3D projection
system, that is, for the device involving the use of linear polarization
glasses. The linear stereo image was chosen as the basis for constructing the
stereo image. Thus, the construction involved the creation of a left and right
frame for each text label.
When building the main goal was to follow a
number of fairly simple principles, originally assumed. These principles
include the following:
- The inscription should be
three-dimensional, i.e. to have a volume, according to the conclusions of [2],
where it was stated that the best stereo effect is obtained for
three-dimensional figures. Because of this, it was recommended that all lines
be presented in volumetric form. Therefore, to create labels and formulas, one
must use volume fonts or effects that create volume.
- The inscriptions should be clearly
readable, which is why it is recommended to use "strict" fonts.
- Inscriptions and formulas should clearly
stand out against the frame, therefore, the background can not be too bright.
- In a stereo animated film presenting the
results of scientific research, the main thing is the presentation of research
results. Explanations in the form of text inscriptions and mathematical
formulas play a secondary role. Therefore, the frame containing the
accompanying information in the form of labels and formulas should not be
brighter than the frames carrying the basic information.
Any program with a sufficient set of
built-in fonts, as well as a wide range of options and special effects to
ensure the creation of volumetric inscriptions and carrying out actions with
them, is suitable for building test inscriptions.
To vary the stereo base, a grid was used,
which made it possible to adjust the shear distance along the stereo base to arrange
the left and right frames.
This approach allowed us to carry out the
series of experiments to build the most appropriate frames with text labels and
formulas. About 200 variants of various representations of inscriptions and
formulas were built, where various parameters were varied.
Some of the constructed options are presented
in the figures below. Figure 9 shows a variant of the construction of the
inscription using the relief font Arial Black with the rotation of the entire
inscription. Figure 10 presents a similar construction using a Cambria embossed
font with a rotation of the entire lettering. The left and right frames are
marked in the figures below respectively with the letters “L” and “R”.


Fig.
9. An example of constructing an inscription based
on a relief font.
Arial
Black with turning inscriptions.


Fig.
10. An example of constructing an inscription based
on a relief font.
Cambria
with turning lettering.
For most of the test inscriptions, a variation
of the shift over the stereo base was performed. The general method for
constructing a test stereo image for the selected caption can be described as
follows:
- selection of the main font;
- selection of font color and background;
- choice of degree of relief;
- the choice of turning the inscription
entirely.
Next, from the created samples were
selected those that are most consistent with the principles set out at the
beginning of the section. For selected samples, the variation in the shear
distance along the grid, that is, along the linear stereo base, was studied.
Samples of stereo frames were checked on the stereo system in order to evaluate
the stereo effect.
It should be noted that due to the
inability to organize a full-fledged expert assessment, the selection of test
options was based on the initially selected principles and assessment of the
visual perception of the distance of the test inscription from the screen
plane. When the test inscription shifted to 3.5 intervals of the grid to the right
and left, the viewers who were 4 meters away from the screen perceived the
inscription as being approximately 1 meter away from the screen plane, which
was considered sufficient.
As a result, it was decided that the most
optimal way to represent the inscriptions is the representation based on the
relief font Arial Narrow on a light background, shaded at the bottom, without
turning the inscription. An example of such a representation of the inscription
is shown in Figure 11.

Fig.11. An inscription on the basis of the relief font Arial Narrow with
rotation of the inscription at a small angle.
The results of the experiments have found
practical application. When developing a computational technology that ensures
the construction of the optimum form of a blade for power plants [4, 9, 10], a
full cycle of power plant modeling was assumed from building the original CAD
model to organizing the visual presentation of the results in stereo. The
results of the experiments were used in the construction of stereo films in the
developed computing technology [9]. All titles, inscriptions and formulas in
this stereo film were made on the basis of experiments on the presentation of
inscriptions and formulas presented in this work. The version of the stereo
film is available using the link [9] and can be viewed on the classic
passive-type 3D projection stereo with linear polarization glasses.
This paper presents a part of the results
of a general project for organizing stereo-animated presentation of numerical
simulation results for mathematical physics problems. The implementation of
such animations is the final stage of computational technology for obtaining
and presenting the results of modeling complex physical processes and the
operation of complex technical systems. The results of animations for the
classic two-projector projection device and for autostereoscopic monitors are
presented. In the latter case, such methods were used as the construction of
depth maps and multiple frames. The experience of constructing textual
information, namely, texts and formulas, in stereo presentations for the
classical type of stereo device is presented also.
This work was supported by the Russian
Foundation for Basic Research (Projects 16-01-00553a and 17-01-00444a).
1.
Synthesis of photorealistic three-dimensional
images in modern presentation systems / Andreev S.V.[et al] //
Software&Systems 2007. ¹ 3. p. 37-40. [in Russian].
2.
Generation of Stereo-Presentations in
Photorealistic Rendering and Scientific Visualization /Andreev S.V.[et al] //
Keldysh Institute preprints, 2010. ¹ 61. 16 p.
http://library.keldysh.ru/preprint.asp?id=2010-61[in Russian].
3.
Andreev S., Filina A. Using stereo presentations
for visualization of scientific calculations results / Scientific
Visualization. 2012. v.4. ¹ 1. p.12-21.
4.
Modelling and visualisation of blade assembly
with complicated shape for power turbine / Andreev S.V.[et al] // Scientific
Visualization. 2015. v.7. ¹ 4. p.1-12.
5.
Hardware-software complex of 3D presentations
based on a virtual studio and virtual environment / Vandanov V.G. [è äð.] //
Proceedings of the 1-st international conference «3D visualization of
scientific, technical and social reality. Cluster technologies of modeling»
Izhevsk. 2009. P.73-77. [in Russian].
6.
Mezhenin A.V., Tozik V.G. 3D Visualization using
the stereo image effect // Proceedings of the 2-nd international conference «3D
visualization of scientific, technical and social reality. Cluster technologies
of modeling» Izhevsk. 2010. [in Russian].
7.
Mikhaylyuk M.V., Huraskin I.A. Synthesis of
stereo images for virtual reality systems using an optical tracking system /
Software&Systems 2006. ¹ 3. p. 10-14. [in Russian].
8.
Kalinichenko A.V., Sveshnikova N.V., Yurin D.V.
Epipolar geometry and evaluation of its reliability from the results of the
restoration of the three-dimensional scene by factorization algorithms //
Proceedings of the 16-th International Conference of Computer Graphics and
Vision GraphiCon-2006, 2006. [in Russian].
9.
Stereoanimation «Modeling and visualization of
the work of a power plant of complex shape in the stereoanimation mode»
https://yadi.sk/i/3CcYhlMB3TCH4r (last accessed 01.09.2018).
10. Modeling and visualization of the work of a power plant of complex
shape in the stereoanimation mode / Andreev S.V.[et al] // Proceedings of the
25-th International Conference of Computer Graphics and Vision GraphiCon-2015,
Protvino, Russia, 22-25 September 2015, p. 183-187. [in Russian].
11. Mikhaylyuk M.V., Maltsev A.V. Timokhin P.Yu. The methods of 3D
stereo visualizationof data obtainedin simulation of unstable oil displacement
from porous media / Proceedings of Scientific Research Institute for System
Analysis RAS, v.8, N 2, p. 125-129. [in Russian].
12. Visibility Experiment and Evaluation of 3D Character Representation
on Mobile Displays / Hiromu Ishio [et al.] // C. Stephanidis (Ed.): Posters,
Part II, HCII 2011, CCIS 174, pp. 46–51, 2011.