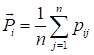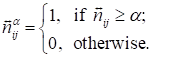The cognitive approach is one of approaches widely used to
modeling semi-structured systems and making controlling such systems decisions.
According to the definition given in [2], this approach focuses on the development
of formal models and methods supporting the intelligent problem-solving process
as they consider human cognitive capabilities (perception, conception,
cognition, understanding, explanation). Structure and target modeling, as well
as simulation modeling methods based on cognitive approach are commonly
subsumed under the umbrella term “cognitive modeling”. In general a cognitive
model is thought of as a model of expert knowledge about a system, processes
occurring in it, laws and principles of its functioning that are represented as
a cognitive map. A causal network reflects researcher's subjective notion of
the system (individual or collective) as a number of semantic categories known
as factors or concepts and a set of cause-and-effect relations between them is
referred to as a cognitive map. A cognitive model is an effective tool for
exploratory and estimative analysis of the situation. It does not give an
opportunity to obtain accurate quantitative characteristics of the system under
study, but it allows to assess trends related to its functioning and
development, and to identify the key factors influencing these processes.
As stated in [9], it is believed that knowledge of a crude,
perhaps even a hypothetical model of a system allows us to predict development scenarios
of initial situations under different control actions by varying the model
variables. This makes it possible to search and generate effective solutions to
control the system, as well as to identify risks and develop strategies to
reduce them.
Cognitive modeling starts with creating a cognitive map of a
system under study based on information received from experts or analysis of the
available system data [15]. At the next stage, the simulation takes place
directly. Its main objectives are forming and testing hypotheses about the structure
of the system under study that explain its behavior; developing behaviour
strategies for the specific situation in order to achieve target states.
Problems solved by cognitive modeling can be divided into two
groups:
– static (structure and target) analysis, which goals are finding
the key factors influencing the targets most, identification of contradictions between
the targets, feedback loops analysis, etc.;
– dynamic (scenario) analysis aimed at prediction of system
states under various control actions and search for control solutions bringing
the system to the target state.
Fuzzy logic is most commonly used as mathematical apparatus
to represent and analyze cognitive models. There is a whole class of cognitive
models based on different types of fuzzy cognitive maps (FCMs). A detailed
overview of such models can be found, for instance, in monograph [3]. One of
FCM varieties well-proven in practical problems of analyzing and modeling
semi-structured social, organizational, and economic systems is V.B. Sylov’s fuzzy
cognitive maps [11, 14].
One of the key ideas of effective application of a cognitive
model is to provide its visual representation. The paper proposes a
visualization metaphor for fuzzy cognitive maps (by the example of Sylov’s FCM)
which is based on graph visualization algorithms and the concept of cognitive
clarity. Examples of application of various visualization metaphors and the
possibility of interactive control of a FCM visual image in IGLA decision
support system developed with the participation of the authors are presented. A
more detailed description of IGLA system can be found in [10] and a demo
version can be found at http://iipo.tu-bryansk.ru/quill. The
system is a Windows application based on Microsoft .NET Framework, and a
network multi-user version is currently being developed.
As previously mentioned, the cognitive model is based on
formalization of cause-and-effect relations which occur between factors
characterizing a system under study. The result of the formalization represents
the system in the form of a cause-and-effect network, termed a cognitive map
and having the following form:
G = < E, W >,
where E = {e1, e2, …, eK } is a set
of factors (also called concepts), W is a binary relation on the set E,
which specifies a set of cause-and-effect relations between its elements.
Concepts can specify both relative (qualitative)
characteristics of the system under study, such as reliability, producibility,
and absolute, measurable values – time, labour intensity, cost, etc. Moreover,
every concept ei relates to a state variable vi,
which specifies the value of the corresponding index at a particular instant.
State variables can possess values expressed on a certain scale, within the
established limits. Value vi(t) of state variable at
instant t is called the state of concept ei at the
given instant. Thus, the state of the simulated system at any given instant is
described by the state of all concepts included in its cognitive map.
Concepts ei and ej are
considered to be connected by relation W (designated as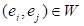 or
or 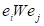 )
if changing the state of concept ei (cause) results in
changing the state of concept ej (effect). In this case we
say that concept ei influences concept ej.
Besides, if the value increase of the concept-cause state variable leads to the
value increase of the concept-effect state variable, then the influence is
considered positive (“strengthening”); if to the decrease – then negative
(“inhibition”). Therefore, the relation W can be represented as a union
of two disjoint subsets
)
if changing the state of concept ei (cause) results in
changing the state of concept ej (effect). In this case we
say that concept ei influences concept ej.
Besides, if the value increase of the concept-cause state variable leads to the
value increase of the concept-effect state variable, then the influence is
considered positive (“strengthening”); if to the decrease – then negative
(“inhibition”). Therefore, the relation W can be represented as a union
of two disjoint subsets 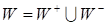 , where W+
is a set of positive relations and W– – is a set of negative
relations.
, where W+
is a set of positive relations and W– – is a set of negative
relations.
Fuzzy cognitive model assumes that the influence between
concepts may vary in intensity, whereas, intensity may be constant or variable
in time. Considering this assumption, W is set as a fuzzy relation,
however, its setting depends on the adopted approach to formalization of
cause-and-effect relations. A cognitive map with fuzzy relation W is
termed a fuzzy cognitive map.
Sylov’s fuzzy cognitive map represents FCM, characterized by
the following features.
1. State variables of concepts can possess values on the
interval [0, 1].
2. Influence intensity is considered constant, so relation W
is specified as a set of numbers wij, characterizing the
direction and degree of influence intensity (weight) between concepts ei
and ej:
wij = w(ei
, ej),
where w is a normalized index of influence intensity
(characteristic function of the relation W) with the following
properties:
a) –1 ≤ wij ≤ 1;
b) wij
= 0, if ej does not depend on ei (no
influence);
c) wij
= 1 if positive influence of ei on ej is
maximum, i.e. when any changes in the system related to concept ej
are uniquely determined by the actions associated with concept ei;
d) wij
= –1 if negative influence is maximum, i.e. when any changes related to concept
ej are uniquely constrained by the actions associated with
concept ei;
e) wij
possesses the value from the interval (–1, 1), when there is an intermediate
degree of positive or negative influence.
FCM of this structure can be graphically represented as a
weighted directed graph.The points correspond to elements of set E
(concepts) and arcs correspond to nonzero elements of relation W
(cause-and-effect relations). Each arc has a weight which is specified by the
corresponding value wij. In this case, relation W can
be represented as a matrix of dimension n´n
(where n is the number of concepts in the system), which can be
considered as the graph adjacency matrix and is termed a cognitive matrix.
Fig. 1 shows an example of a fuzzy cognitive map of choice of
a stamping manufacturing technology [8]. This FCM was built within the
framework of the decision support model in the field of computer-aided production
tooling design developed with direct participation of its authors. The colour
of the arc sets the sign of the corresponding cause-and-effect relation between
the concepts: red means a positive relation, blue indicates a negative one, and
the thickness of the arc determines the intensity of the relation.
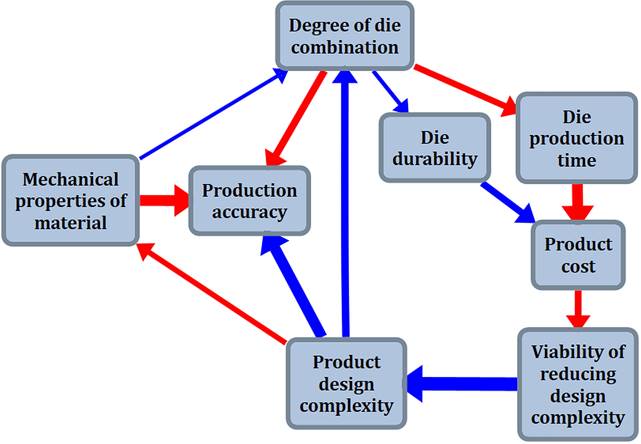
Fig.
1. Fuzzy cognitive map for the problem of choosing a stamping manufacturing
technology
Fig. 2 shows a diagram of a generalized algorithm for
constructing and analyzing a cognitive model of a semi-structured system based
on Sylov’s FCM. In the present paper, the stage of FCM visualization is studied.
A more detailed description of the other stages of this algorithm and methods
used at them can be found, for example, in [8, 10, 11, 14, 15].
Visual analysis is an integral part of the cognitive modeling
process, both at the stage of constructing a cognitive map and at the stages of
its verification and evaluation. The importance of clear and user-friendly
visual representation of the cognitive map is conditioned by the following
circumstances.
1. A visual representation of a cognitive map often provides
the researcher (expert, analyst) with the only opportunity to “grasp the model at
a glance,” with the result that he can quickly notice errors (for example, gaps
or redundancy) made when constructing it.
2. A visual representation is essential for presentation of cognitive
map verification results (at its simplest, verification is a search for
redundant transitive ways to transfer influence between concepts and closed
infinitely reinforcing or weakening influence cycles).
3. A visual representation can be used to present the
results of a structure and target and scenario analyses of a cognitive model.
However, in publications on cognitive modeling, the problem
of visualization of cognitive maps has received little attention. Certain
aspects of this problem were considered in [1, 12]. In previously published
paper [6], an approach was proposed that implies reduction of Sylov’s FCM visualization
problem to the graph visualization task. Several graph visualization algorithms
were investigated. In accordance with the idea underlying construction and
operation of these algorithms, we can distinguish algorithms based on physical
analogies (force algorithms), algorithms based on self-organizing principles,
and algorithms for level-by-level representation of directed graphs.
The most suitable for implementation in IGLA system were acknowledged
according to the results of experimental verification of the considered
algorithms in terms of real FCMs, the LinLog algorithm [17], belonging to the
class of force algorithms, and the ISOM algorithm [16], based on self-organizing
principles. . A further development of this approach is its expansion to the visualization
metaphor in accordance with the visual representation cognitive clarity requirements.
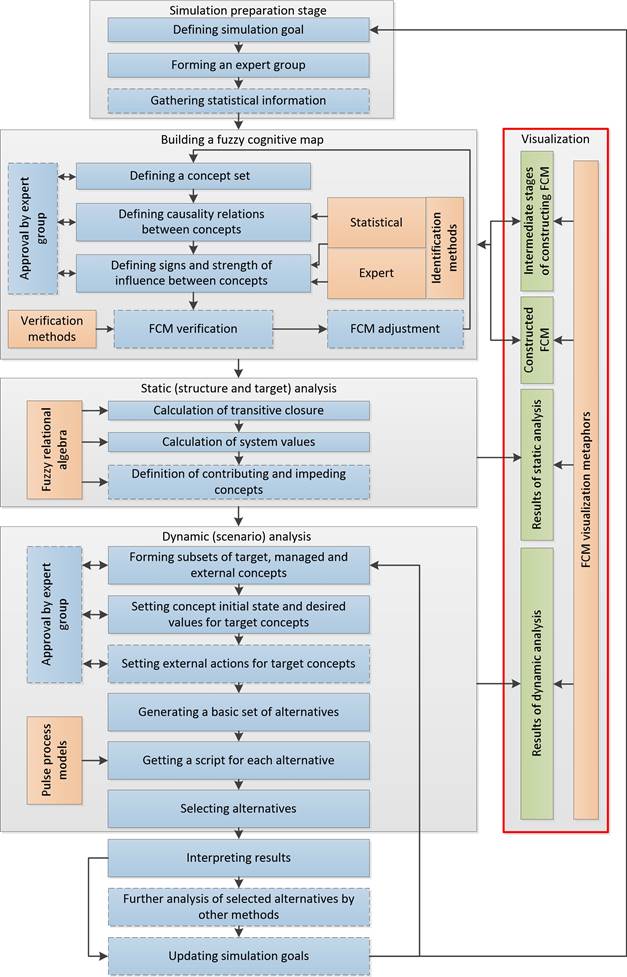
Fig.
2. Generalized algorithm for constructing and analyzing a cognitive model
In [5], visualization metaphor is defined as mapping of a visualized
object from the data space of the original task into the object of the representation
space, which occurs by conditional transfer of the elements attributes of one
set to elements of another set.
Moreover, according to [5], visualization metaphor can be
used at two stages of solving visualization problems. The first time is when
moving from the source data to the space of the visual model. For this case,
the term "spatial metaphor" is used. For the second time, the need to
apply this technique arises at the stage of clarifying the results of
visualization, strengthening the components necessary for problem solving,
filtering redundant components of the image created, etc. For this case, the
term “representation metaphor” is used. The actual role of the spatial metaphor
is to transform current problem data into data describing space elements of the
visual model. Representation metaphor is a means of uncovering potential
benefits of an already applied spatial metaphor.
Let us consider the proposed method of constructing two
components of a FCM visualization metaphor – spatial metaphor and
representation metaphor.
Since spatial metaphor implies transition to the visual
model space, it is necessary to determine the appearance of this space first – in
particular, its dimension.
In [12], a “cognitive cloud” model (that is actually a
spatial metaphor), implying the location of a cognitive map in
three-dimensional space, is presented. It is hypothesized that such visual
representation will contribute to a greater readability of a cognitive model (compared
to the location of the map on a plane). This hypothesis is supported by the
example of application of the proposed approach.
However, metaphor based on the “cognitive cloud” model is
not universal, since it focuses on visualization of cognitive maps of a
specific structure (namely, with the presence of pronounced “factor-cores”),
while the potential effectiveness of this metaphor for visualizing unstructured
maps is questionable. Besides, visualization in three-dimensional space is
obviously more resource-intensive than in two-dimensional one, which can
negatively affect the speed of model rendering and its response time to user
actions, especially with many concepts and cause-and-effect relations. Thus, it
seems appropriate to develop such a metaphor in a two-dimensional space (on a
plane), which, on the one hand, is free from the drawbacks and complications of
a three-dimensional metaphor, and on the other hand, is more universal and
suitable for an unstructured FCM.
As previously mentioned, the FCM visualization problem is
generally reduced to the graph visualization problem, which, in a
two-dimensional case, can be solved with the help of an extensive class of
graph tiling algorithms. Thus, the spatial metaphor of FCM visualization should
be based on these algorithms. However, the problems of human limited cognitive
abilities when reading graphs should also be considered (a detailed analysis of
this problem can be found, for example, in [13]). The approach proposed in the
above-mentioned work [6] allows obtaining satisfactory visualization results,
but it ignores an important aspect of the resulting image quality, namely,
achieving its cognitive clarity. The concept of cognitive clarity and related
criteria will be discussed further.
Application of the spatial metaphor to the source data
(cognitive graph structure) allows to obtain the optimal in some respects location
(i.e. coordinates on the plane) of its points and arcs, which is. Development
and description of specific criteria for the optimal location is beyond the
scope of this paper and is the direction for further research.
As stated above, the representation metaphor
is intended to “reveal the advantages” of the spatial metaphor being used,
which results in a transition from the visual model of the
object under study to its visual image. Based on the multi-stage process of
cognitive modeling (which includes construction of the model and its
verification, as well as various types of its analysis), it’s necessary to develop
several different representation metaphors. Moreover, each of these metaphors
must correspond to a certain stage of modeling and contribute to the
achievement by the researcher of the goal set at this stage. Thus, representation
metaphors should be built on the basis of the researcher’s perception emphases
at a particular stage of cognitive modeling.
Let us enumerate and exemplify
the main FCM representation metaphors implemented in IGLA system. We will use
the previously mentioned cognitive map of choice of a stamping manufacturing
technology (Fig. 1).
- The main metaphor that is used “by default”
corresponds to the cognitive map that presentedon Fig. 1. This
representation metaphor allows the researcher to focus on the structure of
the cognitive map as a whole, without being distracted by features of its
individual concepts. For this
metaphor, a single colour (gray-blue) is used to represent all concepts.
As noted above, the colour of the arc sets the sign
of the corresponding cause-and-effect relation between concepts: red means
a positive relation (“strengthening”) while blue means a negative relation
(“inhibition”). The thickness of the arc determines relation intensity.
- Metaphors implying visual differentiation of
concepts by their types or their belonging to certain
semantic groups, which are set by experts themselves when building a
cognitive model. Fig. 3 shows an example of visual differentiation for
focusing researcher’s attention on the relative position of managed
(yellow), observed (green) and target (gray-blue)
concepts. Note (following [10]) that managed are concepts the state of
which is directly manageable; observed are concepts which state cannot be
defined directly and is determined by the state changes of concept-causes;
the target ones are the concepts that need to be brought into a given
target state. So, in the example under consideration
it is assumed [8] that:
-
when choosing a stamping manufacturing
technology, the designer can directly influence such factors as
mechanical properties of material, product design complexity and the degree of die
combination;
-
the target states of the task of choice are
sufficient due to durability and high level of production accuracy while retaining
the required level of product design complexity;
-
finally, such parameters as die production time and product cost can not be influenced directly,
and their values depend on the state of the target and managed factors.
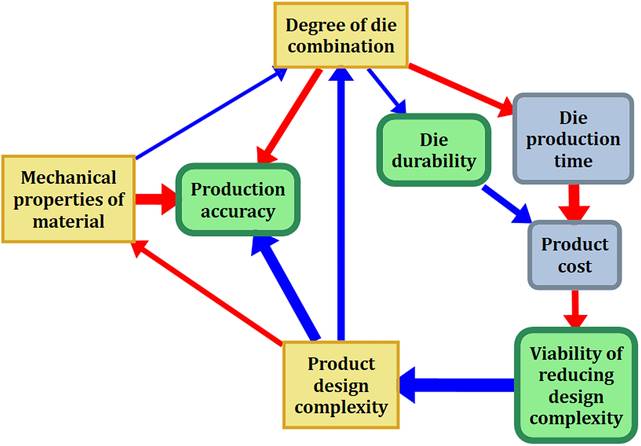
Fig. 3. Metaphor
of concept differentiation by type
- A group of metaphors that allow visualizing FCM
system indicators calculated as a result of structure and target analysis.
In addition to directly specified cause-and-effect relations, it is
necessary to consider all indirect mutual influences
of factors in the system in order to perform the structure and target
analysis. Transitive closure operation allows that by transforming the
initial matrix of influence intensity W into a transitively closed
matrix Z, elements of which are pairs (
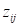 ,
,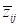 ), where
), where 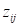 characterizes strength
of the positive influence and
characterizes strength
of the positive influence and 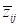 strength of the negative
influence of the i-th concept on the j-th one. The algorithm
for calculating fuzzy transitive closure is described in detail in
monograph [11]. Based on matrix Z, several FCM system indicators
can be calculated, a detailed description of which can be found, for
example, in [8, 10, 11]. In the example in Fig. 5 visualization objects include
comparative intensity and direction of influence of all concepts on the
system. The influence of the i-th concept on the system is
calculated by the following formula:
strength of the negative
influence of the i-th concept on the j-th one. The algorithm
for calculating fuzzy transitive closure is described in detail in
monograph [11]. Based on matrix Z, several FCM system indicators
can be calculated, a detailed description of which can be found, for
example, in [8, 10, 11]. In the example in Fig. 5 visualization objects include
comparative intensity and direction of influence of all concepts on the
system. The influence of the i-th concept on the system is
calculated by the following formula:
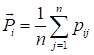 ,
,
where n is the number of concepts in
the system, pij is the influence (action) of the i-th
concept on the j-th one (i.e. dominating influence intensity between
concepts):
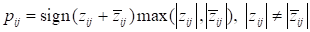 ,
,
where sign(x)
is a function, returning expression sign x.
Similar to the colours of the arcs, shades of
red are used to represent concepts that positively influence the system, and shades of blue represent those negatively affecting the system. Colour
saturation determines influence intensity. Thus, “Degree of die combination”
and “Die production time” concepts have the strongest positive influence on the
system, while “Product design complexity” concept has the strongest negative
influence. Meanwhile, white colour means that the concept has no significant influence
on the system, which is typical of target concepts that
are “stock” ones. In the example under consideration, “Production accuracy” is
such a concept.
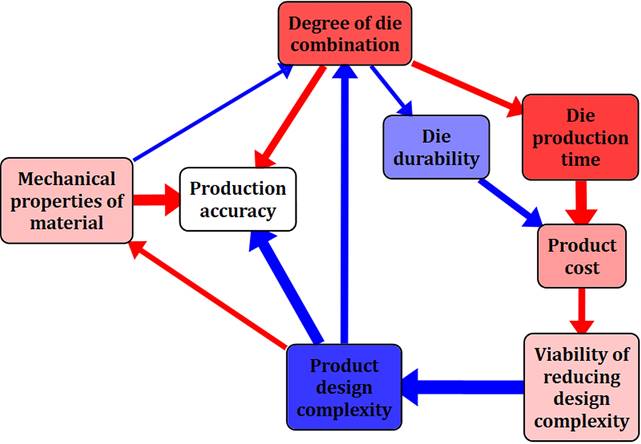
Fig. 4. Metaphor of
concept influence on the system
- “Alpha-cut” metaphor (Fig. 5), allowing to select groups
of interrelated concepts characterized by a given cut level relative to
the selected system indicator. Distinguishing such groups is possible only
for symmetrical indicators. One of such indicators is the indicator of
mutual negative influence of concepts, which is calculated by the formula:
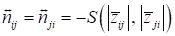 ,
,
where S is some S-norm operator used to
represent the operation of combining fuzzy sets (for example, maximum
operator). We will call matrix 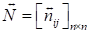 a cognitive
matrix of mutual negative influence. The α-cut of a cognitive map for some
symmetric system indicator is a binary relation corresponding to a level set of
a fuzzy relation defined based on a cognitive matrix associated with this indicator.
So, for the indicator of mutual negative influence and a given cut level
α, the corresponding binary relation is derived according to the rule:
a cognitive
matrix of mutual negative influence. The α-cut of a cognitive map for some
symmetric system indicator is a binary relation corresponding to a level set of
a fuzzy relation defined based on a cognitive matrix associated with this indicator.
So, for the indicator of mutual negative influence and a given cut level
α, the corresponding binary relation is derived according to the rule:
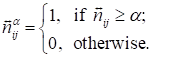
For other symmetric system indicators, α-cuts are derived
similarly.
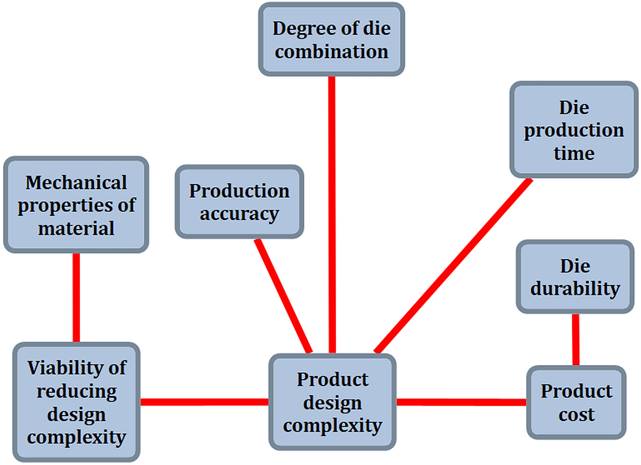
Fig. 5. Alpha-cut metaphor
in terms of mutual negative influence indicator
Note that for the alpha-cut, the
direction, sign and intensity of the cause-and-effect relation between concepts
are not taken into account, so in this case, we use undirected lines of the
same color and thickness to represent all the connections.
Cognitive clarity of some information is mainly
characterized by the ease of intuitive understanding of the corresponding
descriptions, messages, etc. Lack of cognitive clarity is manifested in the
fact that a person pauses to think, finds difficulties in trying to understand
what is said or written. This can be expressed in an observed slowdown of the comprehension
process. Another consequence can be the omission of meaningful information that
escapes notice [1].
On the other hand, in works dealing with graph
visualization, so-called “aesthetic criteria” are often cited, which are
associated with the increasing visual clarity of the resulting graph image. A
detailed review of such criteria is given in book [7]. Since FCM, as mentioned
above, is a weighted directed graph, it is logical that aesthetic criteria will
make a significant contribution to improving visual clarity of its image.
It can be noted that many aesthetic criteria are implicitly
aimed at improving cognitive clarity of a graph image, and, conversely, an
image that fully possesses the properties of cognitive clarity is most likely
to be aesthetically attractive. Thus, it is quite appropriate to include aesthetic
criteria with the cognitive clarity criteria, and we can further refer only to this
group of criteria.
Thus, the following cognitive clarity criteria are proposed
as the basis for constructing FCM visualization metaphor:
1) directionality of the arcs: more convenient (hereinafter – all other conditions being equal) for “reading” of FCM are the “top-down”
and “left-to-right” directions of the arcs (these directions coincide with the
usual reading directions);
2) unidirectionality
of consecutive arcs image: if it is not required to constantly change
gaze direction, then visual comprehension of paths and cycles of a graph
will be performed faster;
3) minimizing intersections of arcs: ideally they should be absent, and if
this is impossible (for a non-planar graph), their number should be minimized;
4) minimizing the number of curved arcs: images with straight arcs are
more convenient for perception;
5) minimizing length of arcs (both the aggregate length and maximum length): the shorter the arcs are, the easier it is to see which
concepts are connected to each other, and the more links can be seen simultaneously;
6) minimizing scatter in length of arcs: images in
which all the arcs are about the same length are more convenient for
perception;
7) maximizing angles between arcs incident with one point: at small angles between such arcs, they will “merge” with each other
near the points, which can hinder visual determination of their directions;
8) optimizing location area: for space efficiency,
graph should be placed in a rectangular area, the format of which (i.e. aspect
ratio) corresponds to the current format of a graphic area of visualization
subsystem;
9) emphasizing graph symmetry: images symmetrical about a certain axis or
center are more convenient for perception and analysis.
TurninThus for FCM visualization metaphor
described above, we conclude that its second most important component (after
graph visualization algorithms) should be the introduced criteria of cognitive
clarity. Analyzing these criteria, we can conclude that many of them contradict
each other, and it is usually impossible to ensure that the image conforms to
all the criteria from the algorithmic point of view. Thus, regardless of
specific features of FCM visualization metaphor implementation, it is necessary
to develop decision rules that simulate various forms of compromise between
criteria.
In [4], it is noted that interactive control of visual image
ensures user’s direct participation in manipulating the image and forms the
basis for in-depth data analysis. In addition, interactive model control system
is one of the ways to verify the obtained solutions and therefore it ensures
accelerated achievement of analysis goal in the case when this method is
convenient for the user. Thus, the interactivity of the visual model becomes a
condition for its high performance.
The mechanism of interactive control of the FCM visual representation
by a cognitive model in IGLA system provides the following features:
1) editing cognitive model structure by editing its visual
image;
2) restructuring of spatial metaphor taking into account the
chosen algorithm for graph visualization;
3) transformation of a cognitive model image;
4) switching between representation metaphors and adjustment
of individual metaphors.
Editing model structure implies the possibility to add,
delete, and change concepts and relations by manipulating elements of graphical
interface and visual image of the model itself.
Transformation of the image affects neither the structure of
the model nor the currently used representation metaphor, however, it allows
flexibility to change properties of the final displayed image (thus performing
a kind of post-processing). Possibilities of transformation include: smooth
image scaling; image rotation at a given angle clockwise or counterclockwise; image
mirroring relative to the horizontal or vertical axis; image compressing and spreading
along selected directions (Fig. 6).
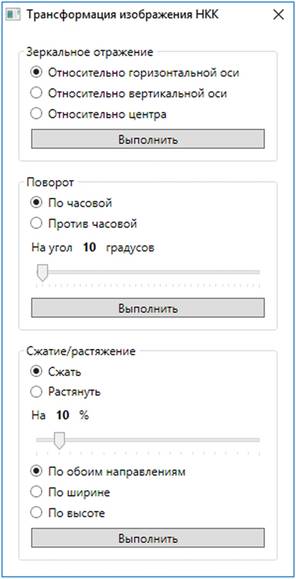
Fig. 6. User
interface of FCM image transformation in IGLA system
Finally, due to the possibility to switch between representation
metaphors, the researcher can direct his attention at any time to the aspects
of the model that are of greatest interest to him at the current stage of the
analysis. Besides, functions of adjusting visual characteristics of representation
metaphors also contribute to increasing flexibility of this tool and its
convenience for the researcher (Fig. 7).
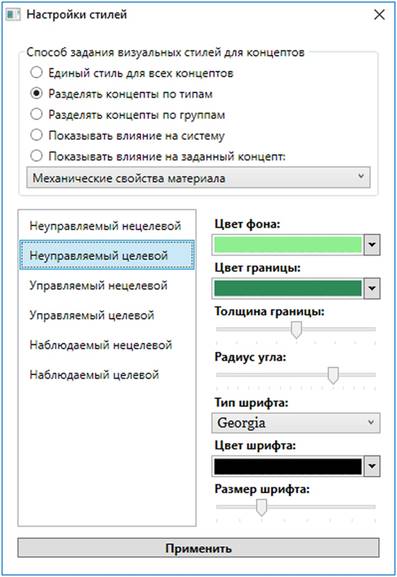
Fig.7. User interface
for selecting and adjusting representation metaphors in IGLA system
The paper presents a visualization metaphor of
fuzzy cognitive maps. Two components of the visualization metaphor are defined –
spatial metaphor and representation metaphor. The concept of cognitive clarity
is considered. As follows from the analysis, there is a link between the
quality of the FCM visualization metaphor and the level of cognitive clarity of
the obtained visual image: the higher the level of cognitive clarity provided
by the visualization metaphor is, the simpler the process of expert
understanding of a cognitive model is when visualy analyzing it. To assess the
level of cognitive clarity, a set of criteria has been proposed.
Thus, along with graph visualization algorithms,
indicators of cognitive clarity form the basis for constructing a FCM visualization
metaphor and at the same time they are the most natural quality assessment tool
for a constructed metaphor.
We have studied the possibilities of
interactive control of FCM visual representation in IGLA system providing
flexible adjustment of representation metaphor visual characteristics. They
allow the researcher’s focusing on the aspects most relevant at a particular
stage of analysis.
The possibilities of using visualization
metaphors and interactive control of FCM visual representation in IGLA system
are exemplified by a cognitive model of decision support in production
tooling design [8].
Let us consider directions for further
research:
The first on is formalization of the criteria
of cognitive clarity described above and the development of a quality assessing
method for the FCM visualization metaphor based on formalized criteria, with
the implementation of this method in the visualization subsystem of IGLA
system.
The second one improving the mechanism of
interactive control of FCM visual image in IGLA system, in particular,
implementation of the function of optimal spatial metaphor automatic selection with
regard to the priorities indicated by the user according to the
cognitive clarity criteria.
- Abramova N.A., Voronina T.A., Portsev R.Y. O metodah
podderzhki postroeniya i verifikacii kognitivnyh kart s primeneniem idej
kognitivnoj grafiki [Ideas of Cognitive Graphics to Support Verification
of Cognitive Maps] // Upravlenie bol'shimi sistemami. Special issue 30.1
“Setevye modeli v upravlenii”. – Moscow: ICS RAS, 2010. – pp. 411-430 [in
Russian].
- Avdeeva Z.K., Kovriga S.V., Makarenko D.I. Kognitivnoe
modelirovanie dlya resheniya zadach upravleniya slabostrukturirovannymi
sistemami (situaciyami) [Cognitive Modeling for Solving Problems of
Control of Semi-structured Systems (Situations)] // Upravlenie bol'shimi
sistemami. – 2007. – Issue. 16. – pp. 26-39 [in Russian].
- Borisov V.V., Kruglov V.V., Fedulov A.S. Nechetkie modeli
i seti [Fuzzy Models and Networks]. – M.: Goryachaya Liniya – Telekom,
2012. – 284 p. [in Russian]
- Zakharova A.A., Vekhter E.V., Shklyar A.V. Metodika
resheniya zadach analiza dannyh pri ispol'zovanii analiticheskih vizual'nyh
modelej [Methods of Solving Problems of Data Analysis Using Analytical
Visual Models] // Scientific Visualization. – 2017. – Vol. 9. – ¹ 4. – pp.
78-88 [in Russian].
- Zakharova A.A., Shklyar A.V. Metafory vizualizacii
[Visualization Metaphors] // Scientific Visualization. – 2013. – Vol. 5. –
¹ 2. – pp. 16-24.
- Isaev R.A., Podvesovskii A.G. Sovershenstvovanie
mekhanizma vizualizacii nechetkih kognitivnyh modelej v sisteme podderzhki
prinyatiya reshenij «IGLA» [Improvement of the Mechanism of Fuzzy Cognitive
Models Visualization in Decision Support System «IGLA»] // Proceedings of
the International Conference “Sovremennye tekhnologii v nauke i
obrazovanii – STNO-2017” [Up-to-date Technologies in Science and
Education], Vol.1. – Ryazan: Ryazan State Radioengineering University,
2017. – p. 138-142.
- Kasyanov V.N., Evstigneev V.A. Grafy v programmirovanii:
obrabotka, vizualizaciya i primenenie [Graphs in Programming: Processing,
Visualization and Application]. – Saint Petersburg: BHV-Peterburg, 2003. –
1104 p. [in Russian]
- Kopeliovich D.I., Podvesovskii A.G., Safonov A.L.,
Vilyukha A.V., Isaev R.A. Primenenie nechetkih kognitivnyh modelej v
avtomatizacii proektirovaniya tekhnologicheskoj osnastki [Application of
Fuzzy Cognitive Models in Computer-Aided Production Tooling Design] //
Vestnik komp'yuternyh i informacionnyh tekhnologij [Herald of Computer and
Information Technologies]. – 2018. – ¹ 3. – pp. 20-35 [in Russian].
- Kulinich A.A. Situacionnyj, kognitivnyj i semioticheskij
podhody k prinyatiyu reshenij v organizaciyah [Contingency, Cognitive and
Semiotic Approaches to Decision-Making in the Organizations] // Otkrytoe
obrazovanie. – 2016. – Vol. 20. – ¹ 6. – pp. 9-17 [in Russian].
- Podvesovskii A.G., Lagerev D.G., Korostelev D.A.
Primenenie nechetkih kognitivnyh modelej dlya formirovaniya mnozhestva
al'ternativ v zadachah prinyatiya reshenij [Application of Fuzzy Cognitive
Models for Alternatives Set Generation in Decision Problems] // Vestnik
Bryanskogo gosudarstvennogo tekhnicheskogo universiteta [Bulletin of
Bryansk State Technical University]. – 2009. – ¹ 4 (24). – pp. 77-84 [in
Russian].
- Silov V.B. Prinyatie strategicheskih reshenij v nechetkoj
obstanovke [Strategical Decision Making in Fuzzy Environment] – Moscow:
INPRO-RES, 1995. – 228 p. [in Russian]
- Ferreira Opaso E.V., Terelyanskij P.V. Predstavlenie
kognitivnyh kart v trekhmernom prostranstve [Presentation of Cognitive
Maps in Three-Dimensional Space] // Proceedings of the XII All-Russian
Conference on Control Science. M.: ICS RAS, 2014. – pp. 6149-6154 [in
Russian].
- Huang W., Hong S.H., Eades P. Predicting Graph Reading
Performance: A Cognitive Approach // Proc. Asia Pacific Symposium on
Information Visualization (APVIS2006). – Tokyo, Japan, 2006. – Ð. 207–216.
- Isaev R.A., Podvesovskii A.G. Generalized Model of Pulse
Process for Dynamic Analysis of Sylov’s Fuzzy Cognitive Maps // CEUR
Workshop Proceedings of the Mathematical Modeling Session at the
International Conference Information Technology and Nanotechnology
(MM-ITNT 2017), Vol. 1904. – P. 57-63.
- Isaev R.A., Podvesovskii A.G. Application of time series
analysis for structural and parametric identification of fuzzy cognitive
models // CEUR Workshop Proceedings of the International Conference
Information Technology and Nanotechnology. Session Data Science (DS-ITNT
2018), Vol. 2212. – P. 119-125.
- Meyer B. Self-Organizing Graphs – A Neural Network
Perspective of Graph Layout // Whitesides S.H. (eds) Graph Drawing. GD
1998. Lecture Notes in Computer Science, vol 1547. Springer, Berlin,
Heidelberg.
- Noack A. An energy model for visual graph clustering //
Proceedings of the 11th International Symposium on Graph Drawing.
Springer-Verlag, 2004. – P. 425-436.