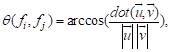1. Introduction

3D models have known a significant growth in the past years; this is due to the fact that scanning and modelling tools and techniques become more popular and were extensively studied, in addition to the fact that many fields now make use of such models (medicine, biology, mechanical engineering, augmented reality). The availability of such models over the World Wide Web and the ease to create them made indexing such data for retrieving or comparing be a complicated task, requiring considerable amounts of algorithms and tools to extract a good shape similarity/dissimilarity measure that represents or describe the 3D model in a compact way.

A retrieval system can be defined as a system that given a query model can return the most similar models to the query based on a signature or a descriptor that represent the 3D object. The final goal would be to provide results that match as much as possible the humane perception. Many methods and techniques have been proposed during the past years to solve this problem; the majority of these approaches propose to extract some local or global geometric or topologic information directly from the 3D object or from its 2D representation (binary images, projection, depth images). Once these features are extracted, they are then used as a descriptor to be compared with the descriptor of other 3D objects and return the models with the biggest similarity. We encourage readers to refer to the works of Lara López et al. [1], Yang et al. [2]  and Tangelder et al. [3] were the authors provide an extensive state of the art of existing method and a comparison of performance between them. Recently researchers oriented their effort to the use of machine learning techniques in this field; the majority of these methods uses features extracted from 3D projections and use them for the training step. We can mention, for example, the work of [4], [5]  who uses a convolutional neural network (CNN) trained over many 2D projections for the same 3D object, the objective of the training is to make the CNN able to classify the 3D object into the correct class. Finally, once the CNN is well trained the authors extract a signature form the CNN corresponding to each 3D model. This kind of approach is very powerful and provides excellent results since generally machine learning methods can resolve classification problem with outstanding accuracy, but the problem with such approach is that they need lots of data to use in training step which imply the need of powerful machine and lots of time to do this task.

In this paper, we present a new retrieval method that uses an artificial neural network (ANN), which will be trained to classify 3D objects, and then extract a descriptor from the trained ANN, representing each 3D object. The main contribution of the proposed approach is during the training step, we extract features directly from the 3D object without using 2D projection. The extracted features will be transformed to histograms then used to feed our ANN. The use of histogram directly extracted from the 3D object helps our ANN to train fast with useful data (since histograms have been used in many previous works as descriptors and they succeed to provide satisfactory results). Finally, the proposed approach does not need to be executed in powerful machine, since the size of the used data is relatively small.

The present paper is organized as follows: In section 2, we review a brief state-of-the-art of the existing descriptors in the literature. In section 3, we describe our proposed approach. The experimental results are discussed in section 4. Finally, in the last section, we present a conclusion and some perspectives.

2. Related works

Due to the importance of the Content-based 3D model retrieval field, many methods and approaches have been proposed in the last decades trying to provide results that match as much as possible the human perception. Since textual descriptions are not a good solution because of the huge time and the resources needed to achieve this task, and even the results are not quite good (many facts can impact the results), the best solution is to extract a signature or a descriptor that compactly represent the 3D model. Many descriptors have been proposed in the literature; generally, we can classify them into two broad categories: 3D shape descriptors and view-based descriptors.

2.1 3D shape descriptors

This category gathers all methods that use any 3D representation (polygon, point cloud, voxel) as it is, to extract any geometric or topological properties (distances, angles, curvatures). Many methods have been proposed with this logic, we can mention the work of Osada et al. [6] who proposed five shape distribution based on global characteristics of the 3D object which are (Fig.1) angle, Euclidian distance, area and volume computed on randomly selected points on the surface of the 3D mesh. These distributions are quite fast and easy to compute, but they still cannot give a good representation of the 3D object.

 

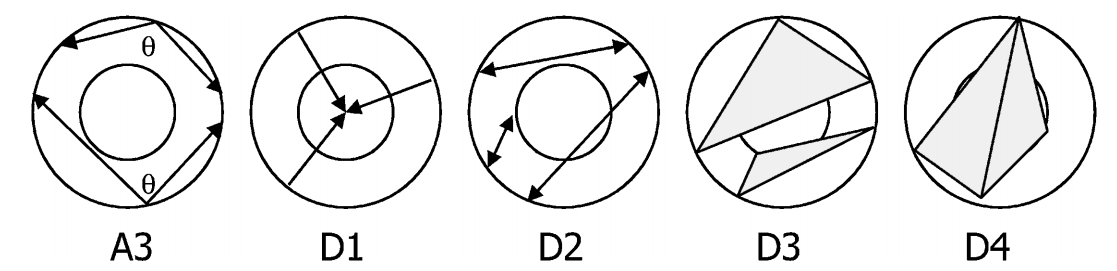
Fig. 1. The five distibution proposed by Osada et al.[6] based on angles (A3), distance (D1 and D2), areas (D3), and volumes (D4)

 

Zaharia et al. [7] proposed a descriptor called Shape Spectrum Descriptor (SSD) which computes a histogram of shape index over the whole 3D mesh. This method provides satisfactory results but its main inconvenient is that it needs a pretreatment step for meshes that are not topologically correct or not orientable, and also the shape index is not defined for flat faces. Funkhouser et al. [8] proposed an approach based on spherical harmonics, which helps to transform any descriptor to rotation independent ones. This is done by decomposing the function into spherical harmonics then summing the harmonics with the same frequency finally computing the L2-norm for each frequency component. Recently we proposed a new retrieval approach [9] the main idea behind this new approach is to propose a way to combine any features extracted from the 3D object to extract a final hybrid descriptor that regroup all the inputs features. To achieve this task we choose to use Data envelopment analysis (DEA) [10] which can extract a final score or descriptor (based on the inputs features), to test this approach we use DEA to combine the dihedral angle, shape index, and the shape diameter function (SDF), the obtained results were very satisfactory.

2.2 View-based descriptors

This kind of descriptors assumes that two 3D models are similar if these models look the same from all viewing angles. These descriptors use any 2D projection (binary images, 2D projection or depth images) to represent the 3D model and extract a 2D descriptor based on the projections. The main inconvenient of this kind of approaches is the choice of the number and the representative views, which can heavily affect the results. Papadakis et al. [11] proposed a new shape descriptor based on panoramic views, these views are extracted by projecting the 3D object to the lateral surface of a cylinder parallel to one of its three principal axes, for each projection the authors propose to compute its corresponding 2D Discrete Fourier Transform as well as 2D Discrete Wavelet Transform. Chen et al. [12] introduced a LightField descriptor, which is based on extracting silhouette images from ten viewing angles distributed on a regular dodecahedron. Each silhouette image is encoded by a combination of 35 coefficients for the Zernike moments descriptor, and 10 coefficients for the Fourier descriptor. Finally, the authors define the dissimilarity as the minimum dissimilarity between each LightField descriptor and other LightField descriptors. Atmosukarto et al. [13] presented a descriptor based on learning shape characteristics to extract salient 2D views, finally to compute the similarity between extracted views of two 3D object the authors use measure developed by Chen et al. [12]. Su et al. [5] proposed a novel Multiview method for retrieving and classifying 3D objects. This method is based on Convolutional neural network, which learns to combine many 2D views to extract a final descriptor. The authors tested two setups the first one using 12 representative views and the second one using 80.

3. The propose approach

The proposed approach aims to combine any sets of features without any imposed order, using an artificial neural network, and finally extract a signature or a descriptor to represent the 3D model effectively, in a reasonable time and without the need of a powerful machine to run it. The proposed method can be summed in the following steps.

3.1 Features extraction

To train our neural network we need to feed it with input data, almost all previous works using neural network in the 3D field, are view based [4], [5], that’s mean they extract features from many 2D projections of the 3D object. The main inconvenient of such methods is that it takes lots of time to extract, choose and stock good and relevant 2D projections which imply the need for a very powerful machine to train the neural network. In the proposed approach, we decide to extract vectors of feature directly from the 3D object and use the histogram extracted from these feature vector as input for our neural network. Using this technique our neural network uses less memory and perform the training in a small amount of time. For our experiment, we choose to use three features extracted from the 3D object, which are:

Shape index: proposed by Koenderink et al. [14] in 1992 the shape index is a value between 0 and 1, this value represents the curvature or the topology of the local surface based on the principal curvatures (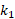 and 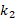). The index is widely used in the 3D field. The shape index is formulated as follow:

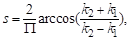
(1)

 

where 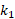 and 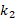 are the principal curvatures with  ≥  .

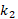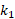It is noteworthy that we didn't take into consideration the case where 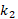=  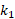which imply a plan surface since the shape index isn't defined in this case and the number of perfectly plan faces are very small, so the final generated descriptor won't be affected

Dihedral angle:  this one of the most feature used in many 3D fields (segmentation, indexation, classification), this measures the angle between two adjacent faces. Mathematically the dihedral angle between two adjacent faces 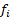 and 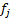 is defined as follow:

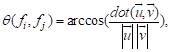
(2)

 

where 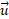 and 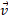  are respectively the normal vector of the face  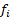and 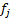.  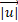is the norm of the vector .

 

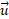Shape Diameter Function (SDF) [15] : proposed by Shapira et al. it’s a scalar value that represent the thickness on each face on the 3D object. The SDF is computing by a cone centered on each face and sampling rays within the cone, finally we take the average of the lengths of all the rays.

The choice of these features is made because they are easy to compute, they can give a satisfactory representation of the 3D model (all these measures have been previously used as a descriptor), they are pose-invariant, and finally to make it easy to compare the results with our previous work.

3.2 Artificial neural networks usage

As mentioned before we use the three features of each 3D object as the input of our artificial neural network, to generate a descriptor for each 3D model. The choice of using an ANN was made because of their parallel structure and their ability to solve complex classification problems. To use the ANN classifier, we have to specify some parameters, which can heavily affect the final results, such as the network architecture, network type, and the training algorithm.

For the network type, we choose to use the feedforward network, which is one of the most used ones, and also known for its excellent results, and does not need a big amount of training data to provide satisfactory results. The backpropagation algorithm is used to improve the accuracy of the predictions of our ANN, by finding the best weight of each connection in the neural network.

Since there is no general rule on how to set and choose the architecture, we tried many of them, and the one that seems to provide the best result is the following: we choose to use four-layer neural network, an input and output layer and two hidden layers. The number of neurons in the input layer is the same as the input data (three features each one is represented with a histogram of 64 elements), the output layer is composed of 19 neurons each neuron correspond to a class of the 3D objects. Finally, and after several tests, the number of hidden neurons on the hidden layer was chosen empirically to maximize the effectiveness of the proposed approach. Figure 2 summarizes the entire process of the proposed method.

 

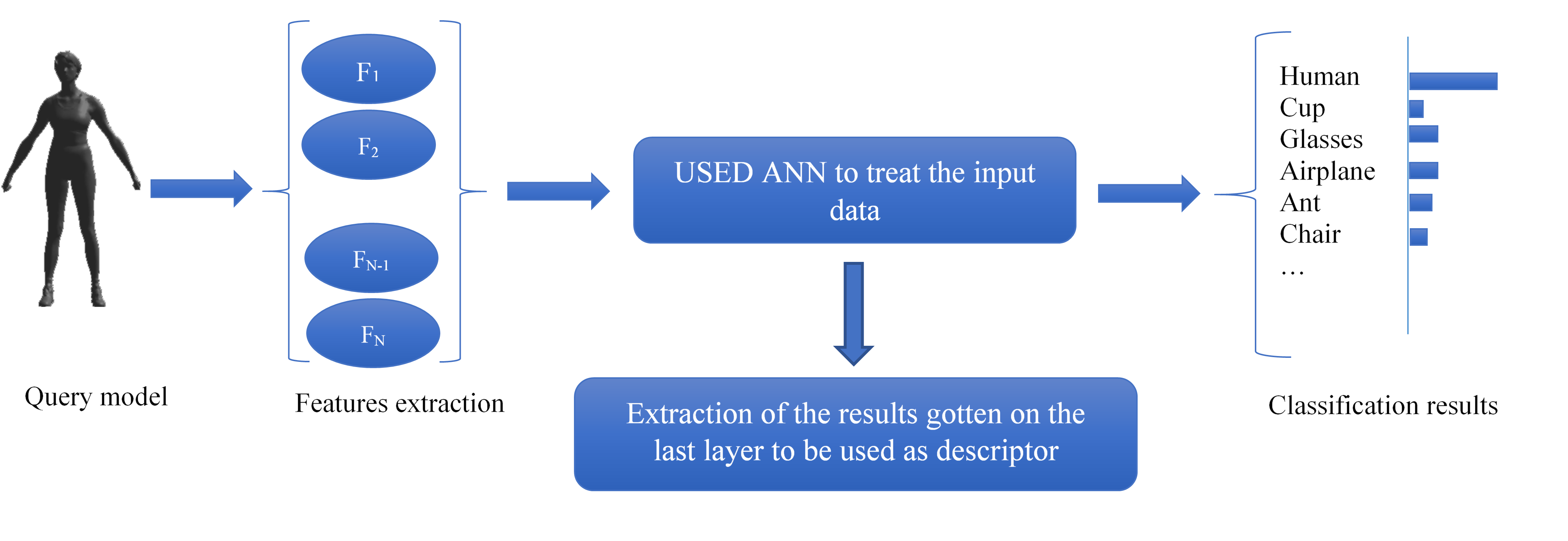
Fig. 2. Illustration that summarizes the whole process of the proposed approach

 

4. Experimental results

The fourth section of this paper is dedicated to the experimental studies, through several tests we will validate the proposed method and show its discriminative power compared to other well-known methods founded in the literature.

Before starting our test, we need to choose a database, which will be used during our tests. Many databases can be considered. We can mention Princeton shape benchmark (PSB) [16], Shape Recognition Contest (SHREC), National Taiwan University database (NTU) [12], Konstanze 3D Model Benchmark (CCCC) [17], or NIST Generic Shape Benchmark (NSB) [18]. For our experiments, we choose to use Princeton's segmentation benchmark database [19], which is a modified version of the Watertight Track of the 2007 SHREC Shape-based Retrieval Contest [20] and expand it with some models taken from the Princeton shape benchmark and the National Taiwan University database. Our choice went to these databases for many facts, the first one was the diversity of this database, it contains over 570 3D models divided into 19 classes (Human, Cup, Glasses, Airplane, Ant, Chair, Octopus, Table, Teddy, Hand, Plier, Fish, Bird, Armadillo, Bust, Mech, Bearing, Vase, and Fourleg). The second reason is that many models from different classes share the same geometric aspect even if they are not semantically similar, for example, birds and airplanes, tables and chairs, which will be a challenging task to detect in the retrieval process.

From the used database we choose N meshes randomly from each category to be used to train the ANN, the rest of the meshes are used for the tests. In our experiments, we chose to set N=10 and N=15 and call the resulting database respectively DB10 and DB15.

The first test is a classic one in the information retrieval field, which is the precision and recall diagram. The recall measures the relevant results retrieved over the total relevant in the database, and the precision measures the relevant results among the retrieved instances.

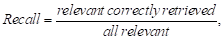
(3)

 

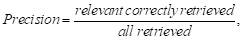
(4)

 

Figures 3 and 4 represent the precision-recall curves obtained using the proposed approach along with PANORAMA [11], LightField [12] , Harmonics [8], and multicriteria with DEA [9]. The obtained results show that our method provides very satisfactory results, it did almost as good as the PANORAMA method for the DB10, and it outperforms LightField, Harmonics, and even DEA even if it combines the same features. In the other hand for DB15, the proposed method outperformed all four methods. These results are excellent considering the small number of models used in the training step respectively 10 and 15 models per class.

 

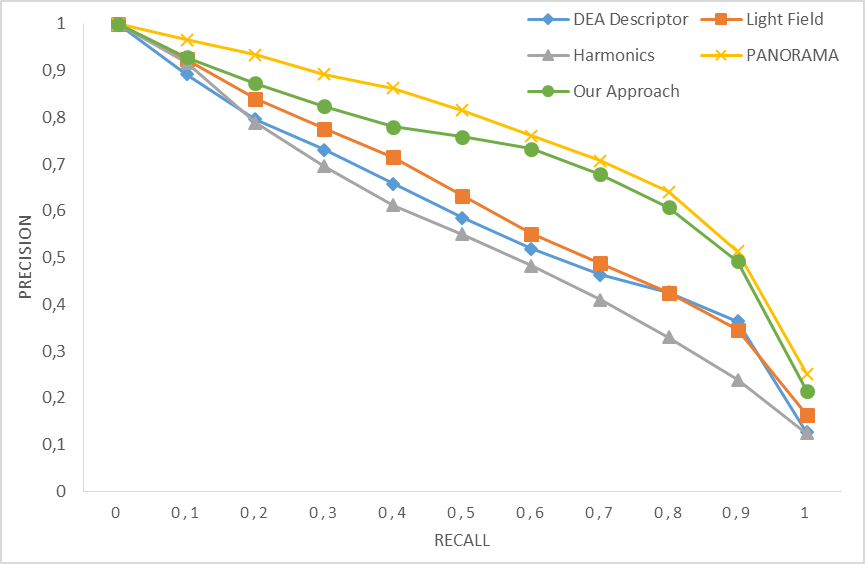
Fig. 3. Precision-Recall graph using four different descriptors along with the proposed one on the database DB10

 

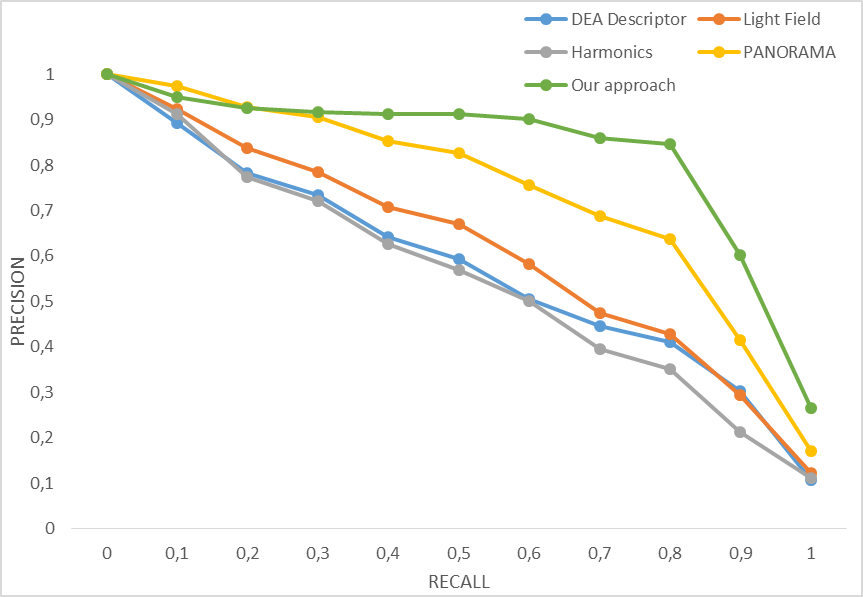
Fig. 4. Precision-Recall graph using four different descriptors along with the proposed one on the database DB15

 

The second test will quantify the performance of our proposed method by computing some evaluation metrics, which are:

·         Nearest Neighbor (NN):  represent the percentage of the top K-relevant items belonging to the retrieval results where K=1.

·         First Tier (FT) and Second Tier (ST): computes the recall for the top C−1 and 2*(C−1) correctly retrieved objects in the result list, where C represents the number of item in each class.

·         Discounted Cumulative Gain (DCG): a scalar that focuses on the items that are correctly retrieved and are in the front of the results list, since generally, a low ranking position has a low probability to be discovered by the user.

·         F-Measure: The F-Measure simply generate a measure that combines the recall and precision values to express the overall performance of the retrieval system. It is computed as follow:

 

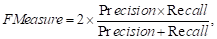
(5)

 

Table 1 represents the obtained results along with those of the following methods PANORAMA, LightField, Harmonics and multicriteria with DEA. The obtained results are the same deduced from the precision-recall curves, for the DB10 the panoramic provides the best results for all metrics, our approach followed behind closely, LightField and DEA come after, finally Harmonics with the less relevant results from all the tested methods. For DB15 our method performed very well and outperformed all the tested approach since it got the best scores for almost all the metrics.

 

Table 1: Performance comparison on DB10 and DB1 using the proposed approach, PANORAMA, LightField , multicriteria with DEA and Harmonics

 

The third test is done to show a global overview of the results obtained for all models in the test set. To do so we compute the dissimilarity matrix which consists in computing the dissimilarity between all pairs of 3D objects in the test database (DB15) using our approach, PANORAMA, LightField, multicriteria with DEA and Harmonics; the resulting matrix can be divided into 19×19 blocks (for the 19 classes), also it should be symmetric and square. A robust retrieval method should have a smaller dissimilarity score in the diagonal’s blocks, which imply a higher similarity between objects in the same class and higher dissimilarity between objects in different classes. As can be observed from the figure 5, our proposed method provides excellent results since the dissimilarity results in the diagonal blocks range from 0 to 0.35 and it is higher in other parts of the matrix. We can also observe a small dissimilarity (0.25 to 0.4) between some objects in different classes for example airplane and bird, ant and octopus this is due to a big similarity from a geometric point of view between these categories. PANORAMA did also well with a small dissimilarity score in the diagonal (between 0.3 to 0.5) and higher scores elsewhere. For the LightField, Harmonics and DEA they got a good dissimilarity scores for same classes, but they did detect a false similarity between some classes for example cup and armadillo or hand and plier which is not correct neither from a geometric nor from a semantic point of view.

 

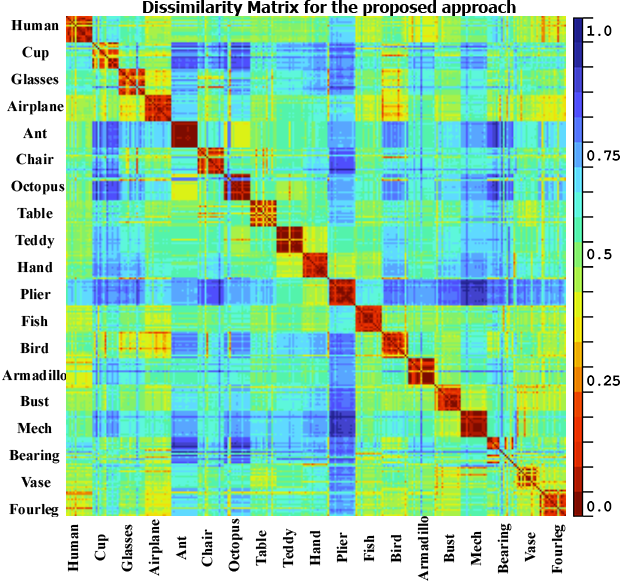
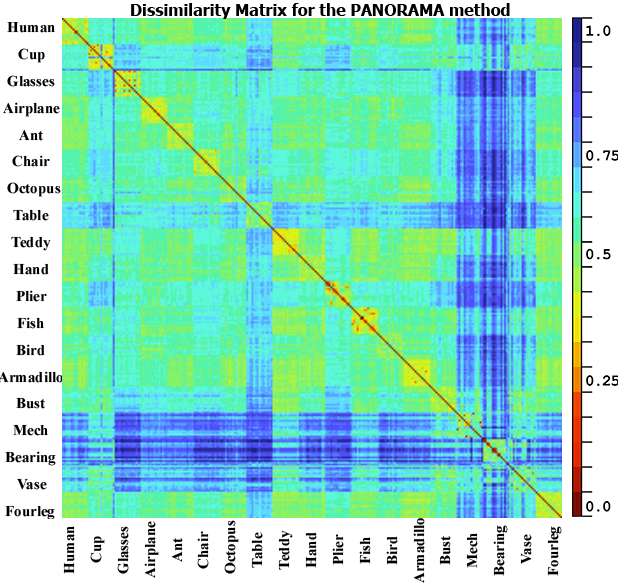
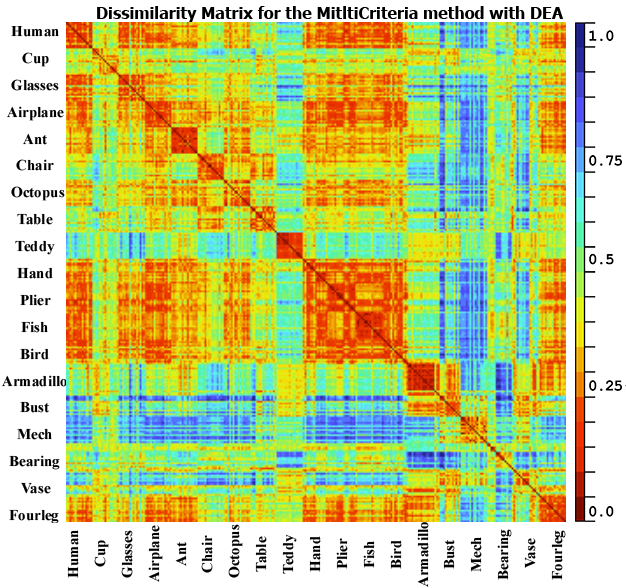
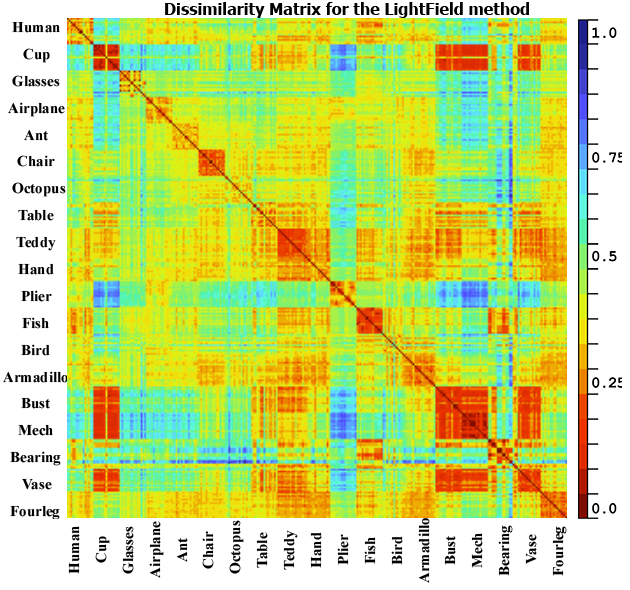
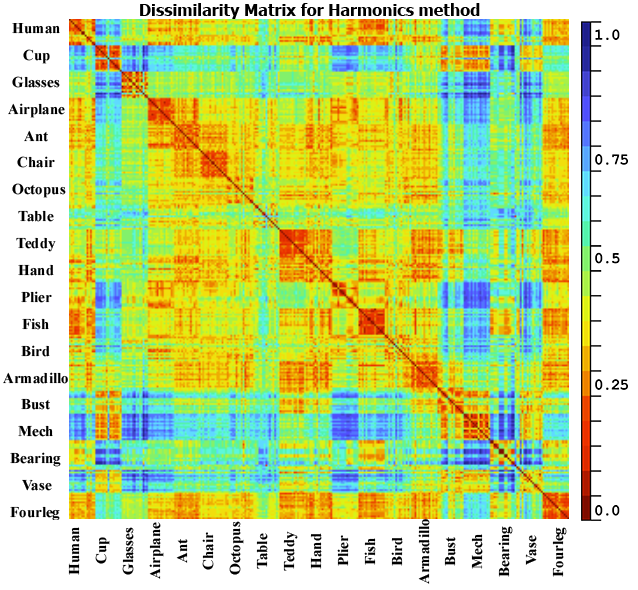
Fig. 5. Dissimilarity matrix for the database DB15 using the proposed approach, PANORAMA, LightField and multicriteria with DEA

 

Finally, the last test will present the top six nearest neighbor for eight query (one per class) selected randomly. Our approach will be compared again with the same four methods as before. The obtained results in Fig. 6 show that our method succeeds to give very good results for the entire tested queries followed once again by PANORAMA which also provides very good results except for a query representing a table it gives a score of four out of six correctly retrieved models. Followed with DEA, LightField and Harmonics with almost the same performance they both got a full score for the following queries: chair, teddy, armadillo and fish for the other classes they obtain a score that ranges from 0% to 66% of correct similar objects.

 

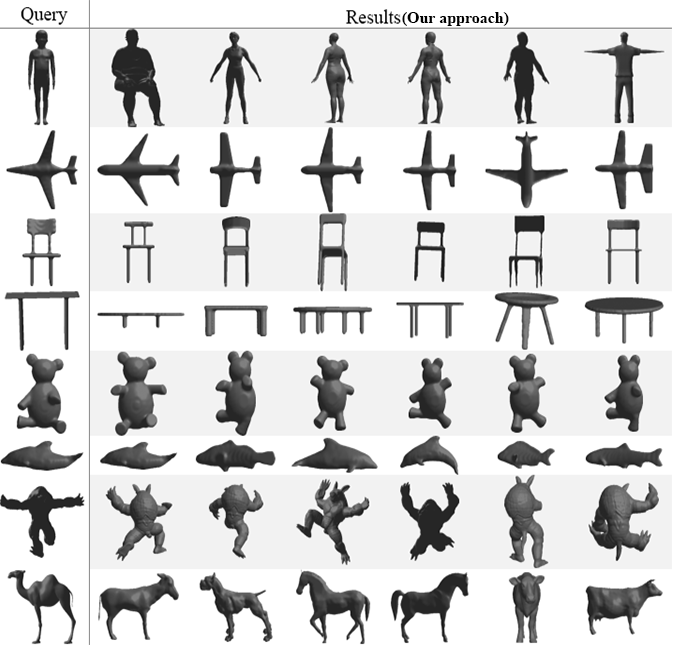
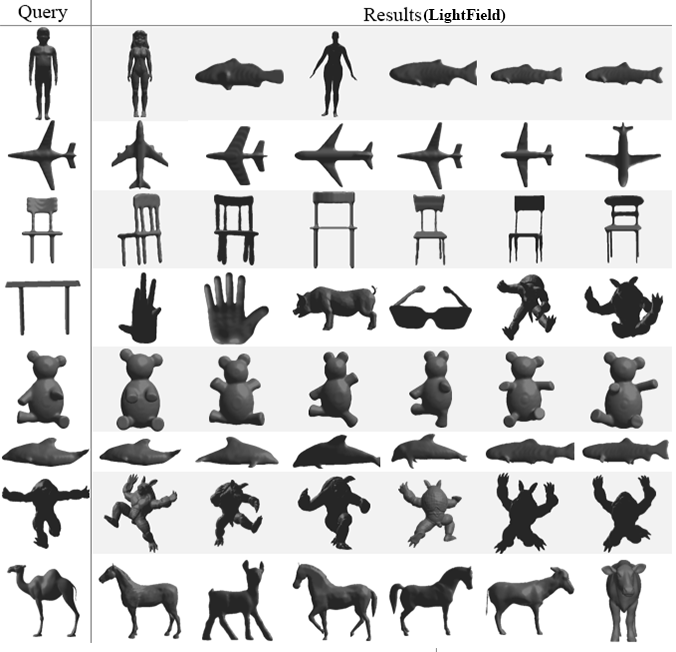
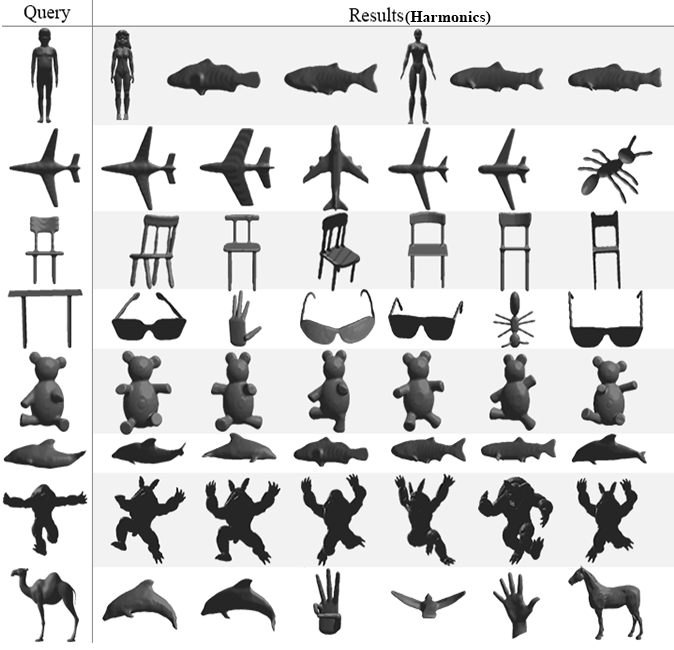
Fig. 6. Top 6 retrieved 3D models using the proposed approach and four other methods

 

 From all the previous tests, we demonstrate the excellent performance and the efficiency of the proposed method, which consist in training a simple artificial neural network with a histogram of features, extracted directly from the 3D object, without going through 2D projections representing the 3D model. This approach is less time and memory consuming, since the whole process of training take between 15 to 25 minutes, and can run on low to medium specification, the tests in this paper were run on two computers with following specification:

·         Intel Core I5 (second generation) 2.50 GHz and 4Gb of Ram;

·         Intel Core 2 Duo 3.00 GHz, with 3Gb of Ram.

5. Conclusion

In the present paper, we propose a new retrieval method, based on an artificial neural network. We propose to train the ANN with a histogram of features extracted directly from the 3D object. Using this method, we can train our ANN fast and with consistent data without going through any 2D views. Once our ANN trained, we can use the resulted knowledge to extract a signature that can be used to compare between models. The experimental results show an excellent result obtained by the proposed approach compared with other well-known methods. For future works, we plan to investigate other features to be combined using the same approach and compare the performance.

Acknowledgments

The authors would like to thank Michael Kazhdan, Papadakis Panagiotis, and Chen Ding-Yun for making available the executable code for their methods respectively the Spherical Harmonics, PANORAMA, and LightField. We would also like to thank George Ioannakis et al. [21] for their online platform (http://retrieval.ceti.gr/) which made it easy for us to evaluate our method.

References

[1]          G. Lara López, A. Peña Pérez Negrón, A. De Antonio Jiménez, J. Ramírez Rodríguez, and R. Imbert Paredes, “Comparative analysis of shape descriptors for 3D objects,” Multimedia Tools and Applications, vol. 76, no. 5, pp. 6993–7040, Mar. 2017.

[2]          Y. Yang, H. Lin, and Y. Zhang, “Content-Based 3-D Model Retrieval: A Survey,” IEEE Transactions on Systems, Man and Cybernetics, Part C (Applications and Reviews), vol. 37, no. 6, pp. 1081–1098, Nov. 2007.

[3]          J. W. H. Tangelder and R. C. Veltkamp, “A survey of content based 3D shape retrieval methods,” Multimedia Tools and Applications, vol. 39, no. 3, pp. 441–471, Sep. 2008.

[4]          Fang Wang, Le Kang, and Yi Li, “Sketch-based 3D shape retrieval using Convolutional Neural Networks,” in 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015, pp. 1875–1883.

[5]          H. Su, S. Maji, E. Kalogerakis, and E. Learned-Miller, “Multi-view Convolutional Neural Networks for 3D Shape Recognition,” in 2015 IEEE International Conference on Computer Vision (ICCV), 2015, pp. 945–953.

[6]          R. Osada, T. Funkhouser, B. Chazelle, and D. Dobkin, “Shape distributions,” ACM Transactions on Graphics, vol. 21, no. 4, pp. 807–832, Oct. 2002.

[7]          T. Zaharia and F. J. Preteux, “3D-shape-based retrieval within the MPEG-7 framework,” in Nonlinear Image Processing and Pattern Analysis, 2001.

[8]          T. Funkhouser et al., “A search engine for 3D models,” ACM Trans. Graph., 2003.

[9]          M. Bouksim, F. R. Zakani, K. Arhid, M. Aboulfatah, and T. Gadi, “New Approach for 3D Mesh Retrieval Using Data Envelopment Analysis,” International Journal of Intelligent Engineering and Systems, vol. 11, no. 1, pp. 1–10, 2018.

[10]        A. Charnes et al., “Measuring the efficiency of decision making units,” European Journal of Operational Research, vol. 2, no. 6, pp. 429–444, Nov. 1978.

[11]        P. Papadakis, I. Pratikakis, T. Theoharis, and S. Perantonis, “PANORAMA: A 3D Shape Descriptor Based on Panoramic Views for Unsupervised 3D Object Retrieval,” International Journal of Computer Vision, vol. 89, no. 2–3, pp. 177–192, Sep. 2010.

[12]        D.-Y. Chen, X.-P. Tian, Y.-T. Shen, and M. Ouhyoung, “On Visual Similarity Based 3D Model Retrieval,” Computer Graphics Forum, vol. 22, no. 3, pp. 223–232, Sep. 2003.

[13]        I. Atmosukarto and L. G. Shapiro, “3D object retrieval using salient views,” International Journal of Multimedia Information Retrieval, vol. 2, no. 2, pp. 103–115, Jun. 2013.

[14]        J. J. Koenderink and A. J. van Doorn, “Surface shape and curvature scales,” Image and Vision Computing, 1992.

[15]        L. Shapira, A. Shamir, and D. Cohen-Or, “Consistent mesh partitioning and skeletonisation using the shape diameter function,” The Visual Computer, vol. 24, no. 4, pp. 249–259, Apr. 2008.

[16]        P. Shilane, P. Min, M. Kazhdan, and T. Funkhouser, “The princeton shape benchmark,” in Proceedings Shape Modeling Applications, 2004., 2004, pp. 167–388.

[17]        D. V. Vranic, “3D Model Retrieval,” Ph.D. thesis, University of Leipzig, 2004.

[18]        R. Fang, A. Godil, X. Li, and A. Wagan, “A new shape benchmark for 3D object retrieval,” in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2008.

[19]        X. Chen, A. Golovinskiy, and T. Funkhouser, “A benchmark for 3D mesh segmentation,” ACM Transactions on Graphics, vol. 28, no. 3, p. 1, 2009.

[20]        D. Giorgi, D. Giorgi, S. Biasotti, and L. Paraboschi, “SHape REtrieval Contest 2007: Watertight Models Track.”

[21]        G. Ioannakis, A. Koutsoudis, I. Pratikakis, and C. Chamzas, “RETRIEVAL—An Online Performance Evaluation Tool for Information Retrieval Methods,” IEEE Transactions on Multimedia, vol. 20, no. 1, pp. 119–127, Jan. 2018.