There is a growing tendency in
architectural computer-aided design practice and education to use parametric
design systems for implementing design concepts [1]. Parametric rules and
strategies constitute the core of parametric design systems. They are operated
through symbolic (scripting) or analogue (visual) programming languages, which
are used as the means to actualise an idea-to-form translation [2]. In spite of
the fact that the logics of human and computer translations do not follow the
same patterns, the paradigm of applying the parametric design principles
(variables, arithmetic, data structures and logical operations) to one’s idea
is rather easy to understand: you compose a form-making algorithm – software
generates a form. It is the implementation of programming that is frustrating
and causes most difficulties for both novice and advanced users. Recent studies
indicate that some barriers have significantly decreased with the development
of such software as Grasshopper and Generative Component’s Symbolic Diagram,
which support visual programming [1]. Even with this apparently more accessible
analogue modelling method, the accessibility issues of the algorithmic
functions and syntax of CAD programming languages are far from being resolved.
Many designers find it difficult to
integrate algorithmic thinking and programming into design process [3].
Understanding and learning the programing framework syntax rules can be very
frustrating to novel users [1]. This fact is relatively easy to explain. There
is a distinct gap between traditional design principles and algorithmic
modelling methods and rules. Most architects and architectural students find it
problematic to shift from conventional freehand drawing and modelling to
describing their ideas through the language of algorithms and codes (Pilot
study). They have to perform the familiar role of translator of data into form
in a different and apparently remote or distancing manner. Translation of site
characteristics, programme, and design objectives into form is a familiar act.
Identifying an algorithm that will do this translation retaining the familiar
act, whilst enriching it with parametric exploration is where the new and the
expert user both find difficulty.
The idea of design knowledge-sharing and
the re-use of the effective solutions as a means to overcome programming issues
and support parametric modelling underlines both Design Patterns (DP) and
Dynamic Knowledge Repository (DKR) approaches. None of these approaches is a
research target in itself, but they are a vehicle through which this research
is going to investigate the impact of each system on the design process. The
comparative study aims to address the following criteria of parametric
modelling performance, which outlines designers’ ability to use generative CAD
environments:
- amount of programming difficulties
(mistakes);
- explored solution space;
- re-use of generative logic;
- learning precedents;
- programming efficiency;
- degree of algorithm sophistication;
- speed of algorithmic modelling.
The target group of this research refers to
a rather broad category of people who are engaged in parametric computer-aided
architectural design. This study has identified a list of criteria for
selecting participants. The following participant selection criteria were
established:
- people who are doing architectural
design;
- design experience of at least one year (to
ensure certain fluency and confidence in architectural design);
- interest in learning how to use
parametric modelling systems / usage parametric modelling systems;
- openness (flexiblility) towards new
design methods and ideas;
- keenness in mastering and experimenting with
generative CAD technologies.
Parametric computer-aided design systems
are operated by algorithmic modelling methods, which are represented by either
textual or visual programming languages. The key difference between those
methods of representation is a difference of level of abstraction [2]. Visual
or diagrammatic (analogue) programming languages (Fig. 1) are represented by so-called
‘box-and-wire’ modelling environments. The examples of visual programming
environments are: Grasshopper (Rhino), Generative Components’ (GC) Symbolic
Diagram and Houdini (Sidefx) (http://www.grasshopper3d.com/).
A recent study, which compares these three
systems, was conducted by Janssen and Chen [4]. The research, based on
qualitative assessment, explored the cognitive stress associated with iterative
construct of visual dataflow modelling (VDM) environments. VDM refers to a
modelling approach that uses visual programming languages to create computer
programs (which in our case generate geometry). Visual programming progresses
through manipulating graphical elements rather than entering text (scripting).
In order to test the VDM systems an
exercise was conducted: each platform was used to build the same complex
parametric model. The research states that all three programming environments
have completed the modelling task successfully. The approximate number of nodes
used to generate the model was: 80-90 for Grasshopper, 90-100 for GC and 70-80
for Houdini. The authors indicate that in order to perform certain iterations
in GC a user is forced to follow a reverse-order modelling method, which causes
additional cognitive stress. Grasshopper and Houdini, in contrast to GC, both
use the forward-order modelling method. It is also noted that GC heavily relies
on scripted (textual) expressions for manipulating such data as: lists, sets or
arrays. Thus it is not possible to avoid scripting while working with GC [4].
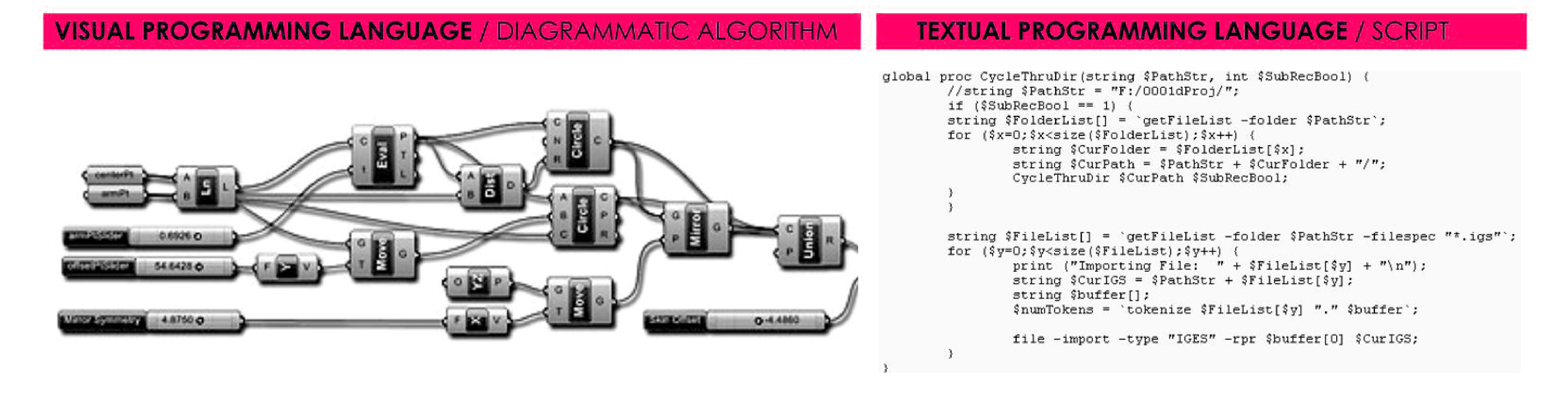
Figure
1. Visual and Textual programming languages (Latest Grasshopper for Rhino 5.0
(Windows only))
There are advantages and disadvantages in
both (textual and visual) types of programming languages. The biggest
disadvantage of scripting is that it has very strict syntax rules, which are extremely
hard to follow [1]. Syntax mistakes, which inevitably occur during the
scripting process, can discourage the majority of architects who are willing to
use generative CAD systems. CAD scripting, cannot be done intuitively, it
requires the user to have a comprehensive amount of knowledge and skills in
programming language rules and syntax. The disadvantages of a visual
programming environment are related to the limitations that this ‘box-and-wire’
system inflicts on the variety of available functions and components. Each
‘box’ contains a script that can be a function, an action or a component and
the amount of ‘boxes’ is limited. Nevertheless, these limitations can be
overcome when combined with textual programming capabilities, through adding a
script ‘box’, for example [5]. Recent research in the field of CAD programming
languages and platforms indicates that users (especially novices) are more
enthusiastic and successful in understanding and realising design concepts when
they use visual programming [1].
With visual programming environments one
can expect to have tangible design outcomes after a short series of practical
tutorials, even from people who are new to parametric CAD technology. That is
why it was decided that both Design Patterns and Dynamic Knowledge Repository
approaches will be tested on the Grasshopper (visual programming plugin for
Rhinoceros) software platform. Grasshopper ‘box-and-wire’ environment is user
friendly and can be explored and operated intuitively. Both Rhinoceros and Grasshopper
are available in Victoria University of Wellington computer labs.
The design scope and constraints of the
case studies were developed according to the two main strategies. The first
strategy is to keep the design tasks simple but open to various
interpretations, thus ensuring an easily controlled, short-term experimental
framework, and fast and efficient analysis of the outcome results. This
strategy also gives an opportunity to test the identified parametric modelling
criteria, such as the amount of programming difficulties, explored solution
space, CAD programming efficiency, degree of algorithm sophistication, speed of
modelling, etc. The second strategy is to use practical exercises which allow
the potential of parametric design to be expressed to its full extent, hence
the choice of the exercises: “an abstract composition” and “a parametric
canopy”. Though the implementation of parametric modelling can, hypothetically,
be implemented within the context of almost any design scenario, in design
studios it is typically used to create such geometries as parametric surfaces
(including canopies and building envelopes), algorithmic ornaments, urban or
landscape planning, etc.
The first practical exercise will consist
of designing a simple abstract composition (Fig. 2.1). Participants are
expected to develop short definitions (modelling algorithms), which will
generate intended outcome geometry. The objective of the first exercise is to
introduce and get users familiar with practical implementation of parametric
modelling assisted by DP and DKR approaches. It is anticipated that
participants will most likely use, change parameters and modify existing codes
to explore design alternatives.
Figure
2.1. Examples of simple abstract parametric models
The second exercise will consist of a
slightly more sophisticated and specific task: a parametric canopy system
(complex parametric surface). In both cases participants will be asked to
describe their design ideas prior modelling, in order to track the relations
between the design concept and the resulting model. It is anticipated that
participants will develop more complex algorithms, functions and geometries,
while the amount of variations could decrease, compared to the first exercise (Fig.
2.2).
Similar design scope (exercises) was used
by Celani and Vaz for a comparative study of the use of scripting and visual
programming in computational design [1], as well as by Jasses and Chen for
their experimental study, which compares three visual dataflow modelling (VDM)
systems [4].
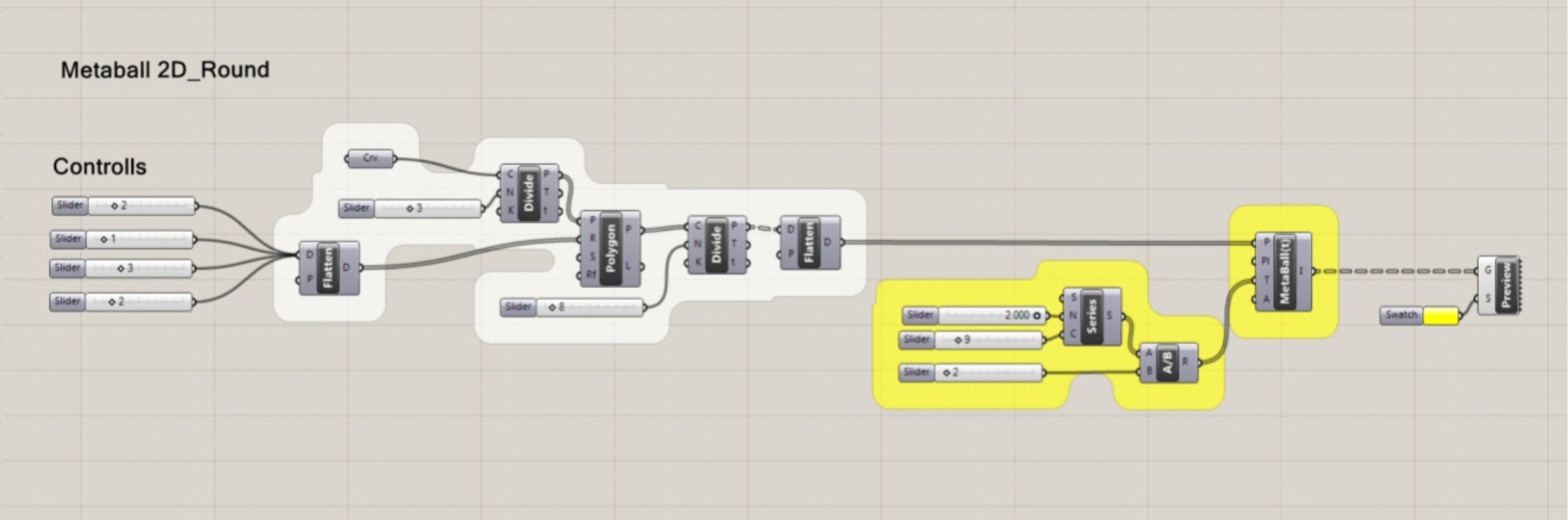
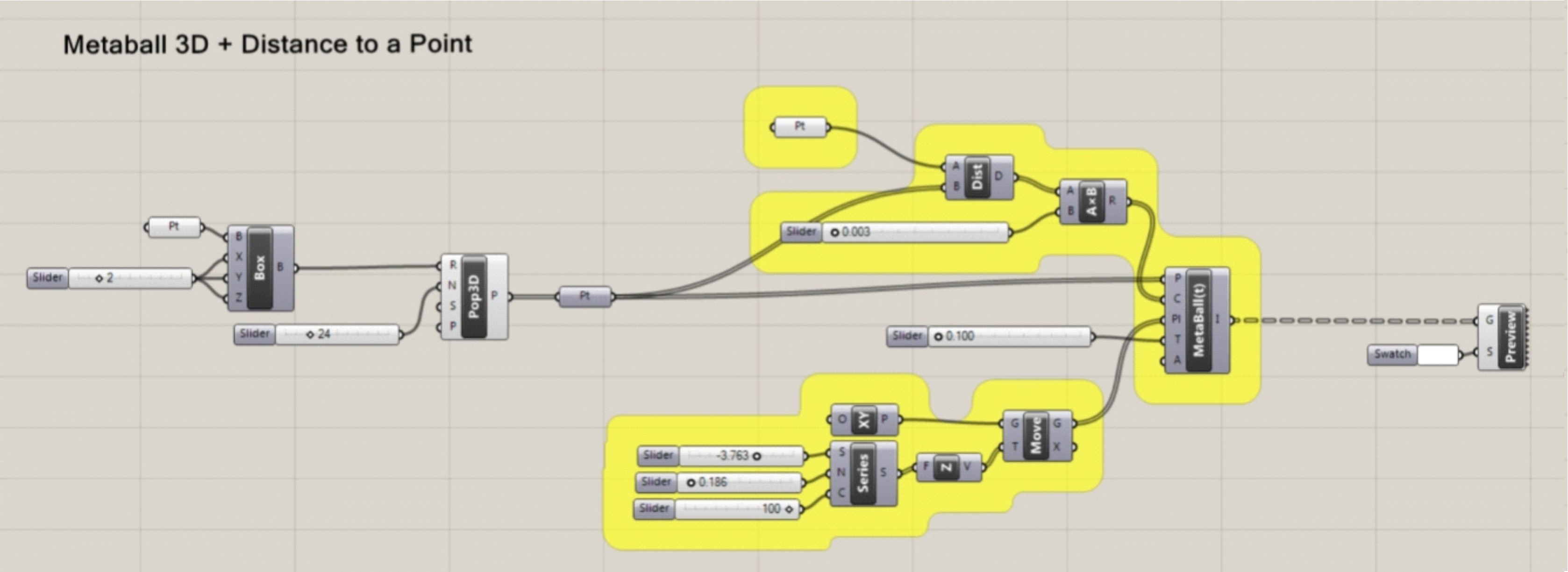

Figure
2.2. Examples of the second exercise sophisticated and specific task (Metaballs
2D, 3D).
The proposed methodology has been drawn
from a range of studies, which have examined the application of CAD
technologies through case studies of the software in use. The criteria related
to the fluency and novelty of design ideation were inspired by the work titled
‘Metrics for measuring ideation effectiveness’ [7]. The experimental setup was
influenced by the recent [1] and relevant research work by Gabriela Celani and
Carlos Vaz: ‘Cad Scripting and visual programming Languages for implementing
computational design concepts’. The overall methodology has drawn from Groat
and Wang's [8] guidelines for the development of experimental studies: a
carefully controlled study with at least two groups, random selection of
participants, no systematic differences between groups, and with the same
treatment applied for all groups.
After careful consideration and comparison
between research objectives and the relevance of available methods (which deal
with design process) it is concluded that the experimental methodology suits
this study the best. There are several experimental methods to study and
evaluate design processes such as controlled tests [9], protocol studies [10], [11]
and case studies [12]. Case studies analysis (namely students’ design works,
which will be produced during a proposed parametric programming workshop) meets
all the research requirements and objectives and therefore was chosen as the
most suitable. The data gathering methodology will be based on two types of
approaches:
- outcome-based analysis [7];
- questionnaire.
This systematic approach will cover all
possible angles of information extraction from this particular type of
‘parametric design’ experiment.
The data, namely values for each identified
parametric modelling criteria, obtained from questionnaires and outcome-based
analysis will be used to compare how each key criteria of parametric modelling
effectiveness (see Detailed Research Methodology section) vary when designers
use Design Patterns / Dynamic Knowledge Repository for Parametric Modelling.
The evaluation criteria data will be interpreted as a metrics of numerical
values, allowing explicit comparison between the approaches, thus we will be
able to answer the main research question, which is to what extent and in which
particular aspects each approach improves designers’ ability to use parametric
modelling environments more effectively.
In order to test and evaluate the
effectiveness of parametric modelling and a change in design ideation, two sets
of criteria have been established. The first set of criteria tests the
effectiveness of algorithmic modelling via visual programming. The study has to
consider the relation between experimental results and the initial level of
participants’ skills in parametric design. The questionnaire will have a design
background section, where respondents indicate their level of experience and
knowledge in architectural design and parametric modelling. Each category will
be divided into five identified levels [13]:
- non-existent;
- basic;
- average;
- strong;
- advanced.
The first set of criteria refers to the
main research question. Their objective is to measure and compare the
effectiveness of parametric modelling.
The second set of design ideation criteria
refers to rate their satisfaction with the design outcome.
It is estimated at the seven point scale
[15]:
- completely dissatisfied (0 point);
- not satisfied (1-3 point);
- satisfied (4-6 point);
- completely satisfied (7 point).
Method of information extraction
Amount of programming difficulties (mistakes) / Questionnaire
Participants will be asked to indicate how
often they have come across programming difficulties (including any kind of
mistakes), which they could not overcome. The study takes into account the fact
that almost every algorithmic modelling problem or mistake can be eventually
found and solved (corrected). That is why the cases when users have spent a
significant amount of time (more than 30 minutes) on solving a particular
programming issue will be counted as a programming difficulty.
Explored solution space /Algorithm and outcome 3D model analysis
Two criteria: novelty and variety, were
identified to evaluate the boundaries of explored solution space. The methods
of measuring these criteria were inspired by research work ‘Metrics for
measuring ideation effectiveness’ [7].
- ‘Novelty’ refers to how unusual or
unexpected an idea is compared to other ideas. In order to measure an
individual idea’s novelty we have to work on a group level. During the
first stage there is a collection and analysis of all of the ideas
generated by participants. During analysis we identify key functions of
the algorithms, which generate the form, such as: surface/curve
subdivision, Voronoi pattern, morphing, lofting, etc. After that we will
be able to count the number of times each solution re-occurs in the pool
of ideas. The less a characteristic is identified, the higher is its
novelty (Ibid).
- ‘Variety’ refers to the amount of
explored alternative solutions during the idea generation process. This
criterion applies only to the group level. Similarly to the novelty
measurement we will analyse generative algorithms to track the amount of
various generative approaches. The bigger is the count of various
programming functions and instructions used by participants, the higher is
the variety.
Generative logic to re-use (useful work) / Questionnaire
This criterion refers to the cases when
participants have used (copy/paste/modify) the algorithm (or part of the
algorithm). Term ‘re-use’ is only relevant towards the cases when the user was
aware of the borrowed algorithm’s existence. It also applies in cases when
users copy algorithms because they do not want to spend time on building some
particular algorithms from scratch, or if they have borrowed because they have
forgotten some specific instructions, parameters or structural rules of the
algorithm.
Learning curve / Questionnaire
Amount of times when the implementation of
new (never used before) function or command occurred.
CAD programming efficiency / Algorithm and outcome 3D model analysis
- Check the presence of positive generative
output of the algorithm. This means that at least one geometry or process
should be generated [14];
- Check if each instruction or function
implemented in the algorithm can be carried out in principle and check if
their presence is justified. The example of unjustified instruction is
shown in the diagram. The highlighted set of components does not
contribute to the positive design outcome and leads to a ‘dead end’ (Fig.
3).
Figure
3. Example of the ‘dead end’ instruction of the generative algorithm
Degree of algorithm sophistication / Algorithm and outcome 3D model analysis
It is possible to evaluate the level of
algorithm sophistication by analysing the complexity of used (mathematical or
geometrical) functions and components. The grading scale will consist of five
levels of complexity (where ‘one’ will represent such simple functions as:
create a primitive, move, rotate, scale; and ‘seven’ will refer to more
complex mathematical functions with several variables in the equation (x
× sin y / 2) or ‘MetaBall(t)’ function in Grasshopper (Fig.4, 5).
Figure
4. Example of the Algorithm composed of rather simple components (functions)
Figure
5. Example of the Algorithm composed of more advanced components (functions)
Speed of algorithmic modelling / Algorithm and outcome 3D model analysis
- In order to evaluate design speed we have
to calculate the quantity of generated ideas (total amount of algorithms
(idea-to-form translations)) modelled during a designated amount of time (Fig.6).
During the experimental workshop participants will be asked to submit each
design idea separately [7].

Figure
6. Example of the Outcome geometry with different level of development
- It is anticipated that some participants
will produce a smaller amount of alternative designs, but will invest more
time in the thorough development of one algorithm (model). In order to
take this into account, all algorithms will be compared to the level of
the average algorithm and outcome model development of the group.
Algorithms, which greatly exceed this level of development, will be
counted as two, three, four or five ideas – accordingly. The next diagram
shows the outcome models generated by Algorithm A and B (see the examples
of simple and more advanced algorithms).
These criteria refer to the evaluation of a
feedback process when the approaches influence the initial idea. The aim is to
evaluate the degree to which each approach can alter a design outcome (compared
to the initial design intent). Due to the limitations of the programming
environment it is expected that the initial idea will be often modified in any
case. Nevertheless we will be able to compare results against each other and
see the overall tendency. Regardless of the cause of changes in the initial
idea, this study aims to evaluate whether the user is still satisfied with the
final design outcome.
Change in the design intent / Questionnaire
This criterion indicates an ability to
model an algorithm, which generates a desired intent (direct idea-to form
translation) rather than shift the idea and use some available algorithms or
change design strategy according to the possibilities and limitations of the
tool (parametric modelling environment). The participants will be asked to
describe their initial ideas prior to modelling. After the completion of a
design task, when the outcome model is generated, participants will be asked to
describe their design outcome one more time.
Degree of satisfaction with the design
outcome / Questionnaire
Participants will be asked to rate their
degree of satisfaction with the design outcome on a seven point scale [1].
The exploratory ‘Pilot study’ has already
been undertaken. One group of students (counting 19 people) enrolled in the
course ARCI 211 (Victoria University of Wellington, New Zealand) was briefed
with the basics of generative design and was given a series of basic tutorials
(Grasshopper/Rhino). Each student was provided with a small collection of
tagged basic algorithmic definitions taken from the code database (you can
found more details about the experiment parameters in [15]). The logic of each
algorithm was explained to students during a lecture.
It was observed that initially almost all
students were encouraged by the opportunities of parametric modelling
environments. It was also discovered that motivation was not strong enough.
Programming design logic appeared to be too complicated, and even frightening
for the majority of students (≈ 70 %). This stopped many of them from
even trying to use the new parametric modelling tool [15]. The actual
‘icebreaker’ was a series of short-term personal talks, where students were
shown examples of how to deal with some particular modelling tasks they had in
mind. After these personal talks students have shown progress in development of
their own algorithms and implementing existing algorithms. The focus of this
stage was to explore how effectively CAD users are able to operate within a
generative programming environment and to access algorithms, not learning
software.
At this moment the following research
criteria are set up: software platform, case study framework, research
methodology, detailed criteria for comparing the two approaches to support of
parametric design, parametric modelling criteria, design ideation criteria,
etc. The next step is the experimental phase of the research. A number of
studies (test studies, parametric workshops with DP and DKR) were carried out
in 2013 and 2014. One of the objectives of the experimental phase is to
empirically test the methods to measure established evaluation criteria. This
research stage will test the implementation of proposed evaluation criteria on
case studies, measuring the effectiveness of algorithmic modelling and design
ideation patterns.
This evaluation metrics and methodology
should be applicable in various studies operating within the domains of
parametric computer-aided design.
- Celani G., Vaz C. E. V., 2012, “CAD Scripting
and Visual Programming Languages for Implementing Computational Design
Concepts: A Comparison from a Pedagogical Point Of View”, International
journal of architectural computing, Volume 10, Number 1 / March 2012,
Multi Science Publishing, pp. 121-138
- Mitchell, W.J., The theoretical
foundation of computer-aided architectural design,Environment and Planning
B, 1978, 2(2), 127 - 150.
- Woodbury, R. (2010) Elements of
Parametric Design. Routledge, New York.
- Janssen and Chen, 2011, Visual Dataflow
Modelling; A Comparison Of Three Systems, CAAD Futures 2011:Designing
together, ULg, 2011
- Leitao, A., Santos, L., Programming
Languages for Generative design.Visual or Textual, in: Zupancic,T.,
Juvancic, M.,Verovsek., S. and Jutraz, A., eds., Respecting Fragile Places,
29th eCAADe Conference
- Proceedings, University of Ljubljana,
Faculty of Architecture (Slovenia), Ljubljana, 2011, 549-557.
- Shah, Jami J.; Smith, Steve M.;
Vargas-Hernandez, Noe, 2003, Metrics for measuring ideation effectiveness,
Design Studies, Volume 24 (2) Elsevier, Mar 1, 2003
- Groat, Linda N. & David Wang, 2002,
Architectural Research Methods, New York: Wiley
- Schon, D., 1991, ‘Teaching and Learning
as a Design Transaction’ in Research in Design Thinking, Delft Press
- Christiaans, H and Dorst,K, 1991 ‘An
Empirical Study Into Design Thinking’ in Research in Design Thinking,
Delft Press
- Sobek, D and Ward, 1996, A‘Principles
from Toyota’s Set- Based Concurrent Engineering Process’ in Proceedings of
ASME Computers in Engineering Conference, Irvine, CA
- Ericsson, K and Simon, H, 1984, Protocol
Analysis—Verbal Reports as Data MIT Press
- Hamade R. F., Artail H. A., 2008, “A
study of the influence of technical attributes of beginner CAD users on
their performance” Computer aided design 40 (2008) 262 – 272
- Kozen D., 1991, “The Design and Analysis
of Algorithms” (Monographs in Computer Science), USA.
- Globa A.A., Donn M., Ulchitskiy O.A.,
2016, Metrics for measuring complexity of geometric models, Scientific
Visualization, Volume 8, Number 5 / Quarter 4, 2016, National Research
Nuclear University "MEPhI", pp. 74-82.










