Previewing and pre-selecting images from track cameras is one of the most
time-consuming and lengthy stages of the results of an experiment processing.
Optical and holographic methods of data processing are distinguished by high
information capacity of the carrier - light field and holographic memory
blocks, naturalness of information representation in two-dimensional form, high
speed of direct processing, possibility of multichannel analysis of input data.
Therefore, almost immediately after the appearance of one of the most important
coherent-optical processing circuits - holographic correlation, an image
recognition by the method of spatial frequency filtering [1], there was a rise
of interest to its application for images processingfrom bubble chambers [2].
In the joint project of the laboratory FNAL (USA) and the Center for Data
Analysis of Track Detectors of Tohoku University (Japan), there are 5.104 holograms of
three-dimensional track objects registered on a 30-inch camera. With such data
volumes, manual visualization (Fig. 1) becomes so labor-consuming [3] that the
search for an informative event is practically unrealizable.

Fig.1.
Laboratory of manual visualization of holograms
of
track detectors - Tohoku University (Japan)
The analysis of the data processing problems for tracked detectors for solving
optical methods shows that the practical interest may not be the measurement of
the geometric parameters of events or the search for these features. Primarily
the problem of accelerating the viewing of images and recognizing events based
on topological features, for example, the presence of stars, the number of
tracks in the stars, the end of tracks, the suppression of background tracks.
The introduction of high-efficiency low-volume track cameras as vertex
detectors [4,5] into experimental practice and the consequent need for
holographic information retrieval from such cameras gave a tangible impulse to
closer research into the possibilities of optical data processing from track
cameras under new conditions [6 , 7]. The range of such studies includes a
rethinking of the methods and schemes proposed earlier for coherent processing
systems [8-10], the study of optical methods for recognizing events with
non-fixed geometry [11-12], the development and creation of systems of
partially coherent photonics [13-15].
Experiments to determine the type of signal correlation and the discrimination
selectivity carried out on the models of track events. The experimental setup
was a variant of Vander Lugt's holographic correlator, supplemented with a
scheme for recording holographic filters and recording equipment. Our system of
holographic pattern recognition (Fig. 2.3) allows comparison of two images
(banners) - recognizable, installed in the input plane, and a reference image
recorded on a holographic filter, by their mutual correlation function.
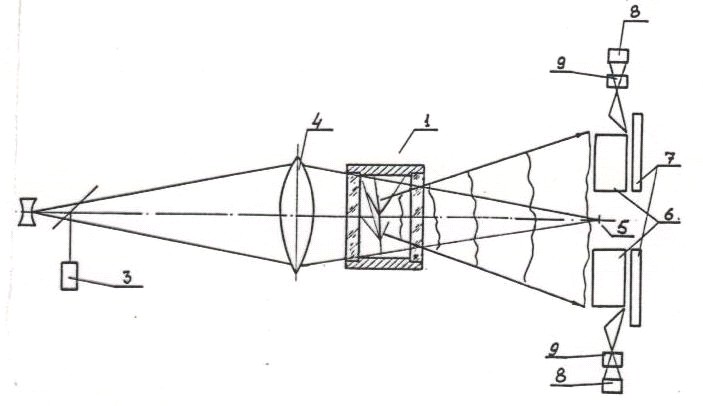
Fig.2.
Scheme of holographic recognition of traces of particles in a track detector
1-track detector, 2-pulse laser, 3-incoherent
light source, 4-condenser, 5-spatial filter, 6-Fourier = interferometers,
7-hologram recorders, 8 service information slots, 9- The scheme also shows
mirrors, a lens = a beam expander and a beam-splitter, but for the sake of
simplicity, these elements are omitted

Fig.3.
Device of holographic recognition of traces of particles in a track detector.
Objects that arise during the track detector data processing are formed, being
abstracted from their microstructure, by straight lines, arcs and combinations
of their small number. The higher is the efficiency of the recognition system for
a given class of objects, the less time-consuming the operations that must be
performed on the input signals to establish the difference or identity of the
objects to be recognized. In cases the object is formed by a set of elements of
different configurations, the operation is the simplest: the presence is
established (if the objects coincide) or the absence (in case of a mismatch) of
the light point in the output plane. For the objects considered, belonging to
the class of objects formed by a small number of simple elements , it is
necessary to analyze the features of the form of the correlation signals, that
allows to detect events with given parameters among the others. Figure 4 shows
an example of the result of recognition of an event in the form of a three-beam
star.
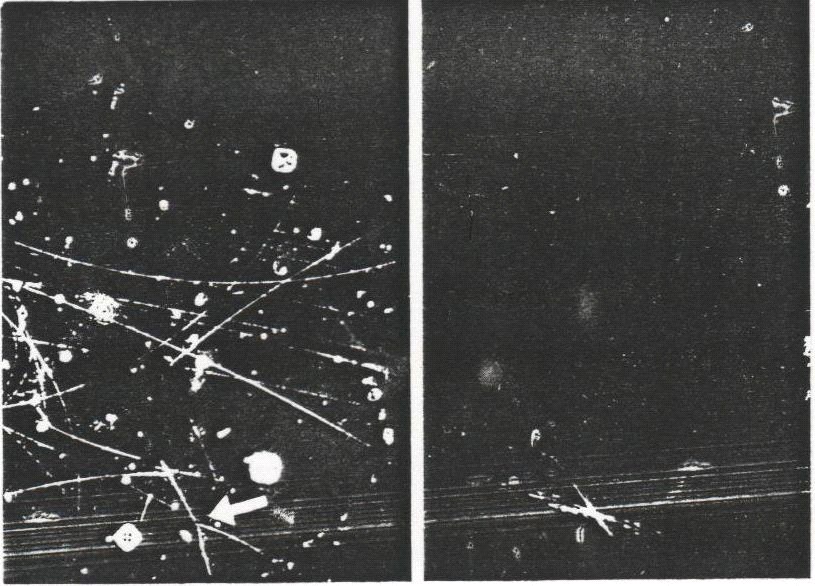
a b
Fig.4.
Example of holographic recognition of an event in the form of a three-beam star
a - the input object, b - the signal in the correlation plane
• Detection of a direct track of a given direction.
If the direction of the track does not
coincide with the direction of the reference segment, the cross-correlation
signal is transformed into a parallelogram. Using this signal sign, you can
select all the segments of the given direction. In addition, there is a
difference in the intensity of the correlation signals as a function of the
angle between the reference and the given segments. By selecting the parameters
of the reference segment researcher can control the selectivity of the
detection.
• Detection of the preset angle formed by two tracks.
The considered objects have the length of the
correlation signal comparable to the intrinsic size, so their difference or
coincidence most clearly manifested in the form of the signal, while measuring
the peak intensity of cross-correlation and autocorrelation signals becomes
inconvenient, since it is necessary to set the coordinates of the measurement
point on an extended signal. The correlation signals represent the sum of the
signals over individual segments. For these objects, it is also possible to
detect the shape of the signal if the angles do not coincide in the case of the
same orientation of one of the sides of the required and reference angles. It
is possible to adjust the selectivity of the detection by choosing the width
and length of the segments that form the reference image of the angle recorded
on the holographic filter.
• Detection of events formed by curvilinear tracks.
In this case, the recognized objects have
additional information signs that complicate their structure. The correlation signal localized and
recognition reduced to establishing the presence or absence of a localized
light response. Compared to objects having an extended correlation signal, it
is easy to measure its magnitude, since integral spot measurement is possible,
which makes it possible to use the dependence of the values of
the correlation signal against the mismatch of the curvature of the recognized
and reference arcs.
When objects recognized in the holographic correlator, the characteristics of
the signals close to the calculated ones can obtained, and consequently, a
quantitative evaluation of the signals and adjustment of the recognition modes
are possible. The events in the pictures detected may appear in a variety of
variants due to the limited number of kinematic links and arbitrary
orientation. In this case it is necessary either to create a holographic filter
that can recognize an event by topological characteristics or use multichannel
processing for a set of filters in which a set of standards overlapping the
entire range of possible event configurations in pictures is recorded with a
step determined by the selectivity of a single reference. The second approach
may require a sequential-parallel comparison, i.e. in addition to a parallel in
time comparison with a group of standards recorded on a single hologram, the
operational replacement of such holograms. A concrete example is the
construction of the elastic scattering cross section of π + by He3. Taking
into account the arbitrary orientation of the plane in which the scattering
fork is located, shows that more than 102 standards
should use.
Such a number of standards can technically recorded on one hologram, but
filters corresponding to other ranges of scattering angles should recorded on
other holograms. The task of rapidly changing hologram filters in circuits with
coherent illumination becomes difficult to achieve, because is necessary to
provide positioning accuracy of about 10μ. This is one of the essential
limitations on the use of holography with the emission of high spatial
coherence.
Holographic correlation analysis makes it possible to determine the
quantitative parameter - the degree of localization of the autocorrelation
signal of the object L = δ / D, where D is the largest object size, and
δ is the extent of the function of its autocorrelation. For L << 1,
recognition objects are "complex", with L ≤ 1 -
"simple". In the case of "simple" objects - direct tracks
and stars, the spatial structure of autocorrelation signal coincidence that
they form is similar to the objects themselves. However, a small change in the
parameter of the object shown drastically changes the shape of the signal,
while the difference in the image of the object itself is difficult to detect.
This is what determines the appropriateness of using a system of partially
coherent recognition, even for objects belonging to the class of
"simple" ones.
Recognition of "simple" objects imposes features on the elements of
the optical system. The recording of a holographic filter intended for use in
coherent illumination is hampered by the narrow spectrum of the spatial
frequencies of the reference object and the large dynamic range of the spectrum
components. Since real tracks are formed by separate bubbles, it is necessary
to ensure undistorted recording of low spatial frequencies of the standard,
which results in low diffraction efficiency of the holographic filter (<I%)
and high noise level. In part, this difficulty can circumvented by applying the
methods of element-by-element and two-step recording.
In spatially coherent illumination, one of the most stringent is the
requirement for phase homogeneity of the base of the processed images. The size
of the processed image can not significantly exceed the correlation radius of
carrier phase noise, because otherwise the magnitude of the signal will be
determined not by the useful information, but by the nature of the phase noise.
This limitation can also overcome by using a laser radiation with a transformed
coherence function in a holographic correlator.
• The use of holographic systems for recognition of events recorded in track
detectors is possible at the stage of primary selection according to the form
or intensity of the correlation signal.
• The use of holographic systems for visualizing events in track detectors has
significant merits.
• It is advisable to develop methods for detecting events with non-fixed
geometry. Orientation and exact geometry of events are usually unknown in
advance, and therefore the number of required holographic filters may be
excessively large - more than 102.
• Three factors make it necessary to transform the coherence of laser radiation
and transition to holographic visualization and processing of information by
radiation of partial spatial coherence.
1. With coherent illumination, the practical realization of the potential
capabilities of holographic systems significantly hampered by stringent
requirements for phase homogeneities.
2. With coherent illumination, the sensitivity of the recognition result to the
accuracy of the installation of the holographic filter is extremely high.
3. With coherent illumination, it is
practically impossible to recognize "simple" objects due to the lack
of localization of the correlation signal in the output plane of the system.
1. Vander Lugt A. Signal Detection by Complex Spatial Filtering. IEEE Trans.
Inform. Theory, v.IT-10, N.2, p.139-145, 1964
2. Bykovsky Y.A., Larkin A.I., Markilov A.A., Starikov S.N. Holographic
processing of track chamber data. Nuclear Instruments and Methods, 131 (1), pp.
129-132, 1975
3. Kitagaki T., Yuta H. Holographic chamber for neutrino experiments. Nuclear
Instruments and Methods. V. A281. P. 81, 1989
4. Stefanini G., Hall G., Dowell J.D. Optoelectronic analogue signal transfer
for LHC detectors CERN / DRDC / 91-41., October 1991
5. Bjelckhagen H., Harigel G. Nuclear Instruments and Methods. V. 227. P. 437,
1984
6. Falconer D.G. Optical Processing of Bubble Chamber. Appl. Opt., V.5, N.9, p.
1365-1369, 1996
7. Averianov S.G., Dolgoshein B.A., Larkin A.I. Physical properties of the
coherent laser radiation and its employment for high energy physics
experiments, CERN Workshop on Electronics for LHC Experiments. Lisbon, 11−15
September, 1995
8. Becker A.M., Bukhtoyarova N.I. Opredelenie geometrii sobytija v puzyr'kovyh kamerah kogerentno-opticheskimi metodami [Determination of the geometry of the event in
bubble chambers by coherent-optical methods]. Te.s.d. Vses.Shkola for Optical
Processing of Information, Kiev, KSU, p. 122, 1984. [In Russian]
9. Larkin A.I., Rusakov V.A., Starikov S.N. Preprint of JINR P1-86-669. Dubna, 1986. [In Russian]
10. Larkin A.I., Rusakov V.A., Starikov S.N. Preprint of JINR B1-1-86-670. Dubna,
1986. [In Russian]
11. Larkin A.I., Matveev A.K., Zarubin A.M., Optical in the processing with the
transformation of the laser radiation of the spatial coherence. In: Proc. 15th
Int. Congress on High Speed Photography and Photonics, San Diego,
USA, SPIE, v.348, pt.2, p. 970-975. 1982
12. Larkin A.I., Zarubin A.M. OSA Technical digest online. Optical Society of
America, Frontiers in Optics. Paper JTu3A.23.
Https://doi.org/10.1364/FIO.2014.JTu3A.23, 2014
13. Grosmann M., Larkin A. Laser Photonics in the world, in Russia, in Moscow
Engineering Physics Institute. II Conference on Plasma and Laser Research and
Technologies. MEPhI, 2016
14. Larkin A. I., Starikov S.N. Laser photonics as a tool of experimental
physics. Instruments and Experimental Techniques, in print, 2017
15. Larkin A. I., Yu F.T.S. Kogerentnaja fotonika [Coherent photonics]. Second edition, Moscow: BINOM,
2015. [In Russian]




