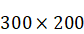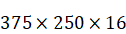Internal
waves are may be the most common types of waves in oceans, since even if the
ocean surface seems to be calm, the deep-ocean waves [1,2] are always present1.
Oceanologists, biologists, ecologists, and technician have specific interests
in the study of internal waves. This phenomenon is partly responsible for the
vertical mixing of the stratified fluids, the migration of living organisms,
the redistribution of energy in the ocean, and the propagation of various kinds
of impurities and pollution.
Despite
a great diversity of experimental approaches for visualisation of weakly
compressible flows [4,5], the experiments are often bounded by the possibility
to assess some interesting propriety at certain time and location. Concerning
the internal attractors and accompanying phenomena, remarkable advantages have
been achieved since 1990s. Besides the successful application of traditional
approaches based on synthetic schlieren, particle image velocimetry (PIV) and
planar laser-induced fluorescence (PLIF), some methods based on signal
analysis, which traditionally were more applied to electromagnetic fields,
showed remarkable relevance for description of the internal or inertial wave
dynamics [6–9]. Meanwhile, the time and space resolution of these methods
is limited, and sometimes the laboratory data do not allow to reconstruct the
hydrodynamic fields, as mentioned in [10] concerning the reconstruction of
the stream function based on laboratory data near the boundaries.
Internal
wave appears as a result of perturbations of stably stratified fluid. One of
the major sources of the external forcing, resulting in internal waves, is the
tidal effect produced by the orbital motions of the Moon and the Sun. These
global flows interact with the ocean bottom irregularities and generate
internal waves. The very special feature of the internal waves is that in case
of constant stratification the angle of the wave beams and the law of
reflection are defined by the dispersion relation:
|
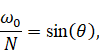
|
(1)
|
where
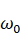 is
the forcing frequency determined by external forcing on the fluid;
is
the forcing frequency determined by external forcing on the fluid;
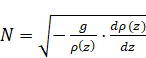 buoyancy frequency
which determine distribution of density
buoyancy frequency
which determine distribution of density
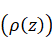 .
.
Due
to these properties internal waves can be focused upon reflection from the
oblique wall. As a consequence, the internal wave wavelength is reduced upon
reflection but its amplitude increases.
The
great interest is the result of the consecutive reflections. It can be obtained
by the monochromatic excitation of the internal waves in the closed domain with
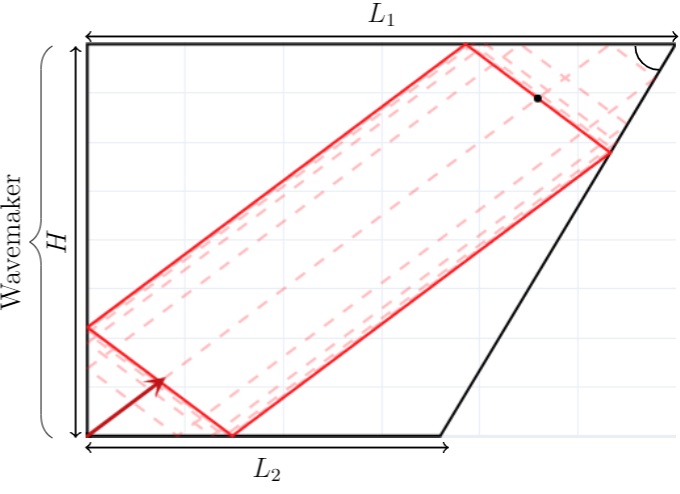
the oblique boundaries, the simplest example of which is the trapeze with one
inclined boundary. A remarkable property of the billiard in trapezoid geometry
is that focusing prevails over defocusing. If the internal waves beams
propagate in trapezoid tank, focusing occurs continuously and all the wave
beams converge to closed trajectory. The simplest one is a parallelogram with
four reflection points located at the sides of the trapeze (Fig. 1a).
For
the first time the phenomenon of wave attractors was described by Leo Maas [11,
12] who studied the convergence of wave beams in different geometries.
First
attempts of numerical study [13] of internal wave attractors successfully
reproduced qualitatively the 2D structure of internal wave attractors in
trapezoidal domains, though quantitatively the velocity amplitude was too high
as compared with the experiment. 3D numerical simulations [14, 15]
resolved this discrepancy through estimation of dissipation and boundary layers
effects.
In
this paper we apply the before-mentioned methods for the results of numerical
experiments, and discuss the methods, which were not yet widely used for
analysis of internal wave attractors.
|
|
|
|
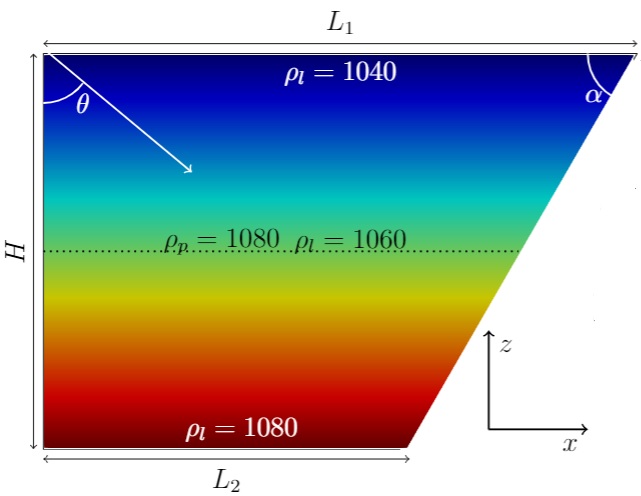
(a) Initial
distribution of density.
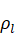 –
density of liquid,
–
density of liquid,
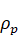 – density of
particles,
– density of
particles,
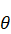 =
=
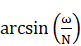 ,
where ,
where
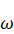 is frequency of
wavemaker and
is frequency of
wavemaker and
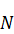 is the buoyancy
frequency.
is the buoyancy
frequency.
|
(b) Ray-tracing of an
internal wave beam subject to the dispersion relation (1).
|
|
Figure 1: Scheme of
computational domain for 2D attractor of internal waves. Initial distribution
of density (a), and shape of attractor in ideal fluid (b).
|
Laboratory
and numerical study of linear and nonlinear dynamics of wave attractors in
three-dimensional setup showed a good agreement in terms of major hydrodynamic
properties both in laminar and turbulent regimes [14, 15]. High order spectral
element approach, which was used in these simulations is still hard to adopt
for multi-phase flows. In this study we consider the processes of
sedimentation, and numerical simulation with the help of quasihydrodynamic
approach [16, 17].
Equations
for mass, momentum, and salinity transport and diffusion in quasihydrodynamic
approach can be written in the following form [16]:
where reduced pressure
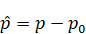 ,
restoring force
,
restoring force
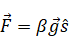 ,
,
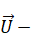 velocity
field.
velocity
field.
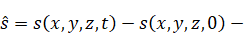 salinity destribution,
salinity destribution,
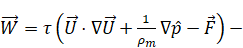 additional velocity
according to quasihydrodynamic approach,
additional velocity
according to quasihydrodynamic approach,
 viscosity,
viscosity,
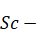 Schmidt
number.
Schmidt
number.
Geometrically the
computational domain is a rectangular trapeze, with the wavemaker located at
the left wall, and inclined right wall, as in the experiments [14; 18].
Boundary conditions at
the fixed walls:
|
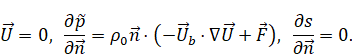
|
(5)
|
The initial conditions for a passive
scalar are chosen so that the buoyancy frequency is equal to 1
|
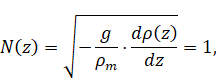
|
(6)
|
where
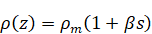 ,
,
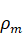 is
minimal density, and
is
minimal density, and
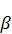 –
coefficient of salinity contraction.
–
coefficient of salinity contraction.
Equations (2 – 4)
were approximated with the help of finite
volume method and open-source code OpenFOAM v2012 with QHDFoam solver [19]
The
results of numerical simulation were approximated at a regular rectangular grid
with the help of openFoam functionObject and processed by python scripts.
Hydrodynamic fields were visualised with the help of open-source,
multi-platform data analysis and visualization platform
paraview
[20].
Parameters
of the simulation are chosen to be close to the corresponding laboratory
experiments. As follows from the theoretical predictions and laboratory
experiments, it is expected that internal waves energy will concentrate in the
zone of attraction (Fig.
1b).
Geometry
of the tank filled with salty water is given by:
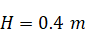 ,
,
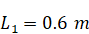 ,
,
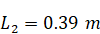 .
The buoyancy frequency
.
The buoyancy frequency
 .
.
Boundary
conditions at the left wall with the wavemaker read:
|
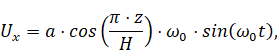
|
(7)
|
where
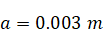 ,
,
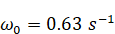 .
.
In the figures below we
will use wavemaker frequency
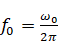 and
corresponding period
and
corresponding period
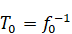 .
.
|
|
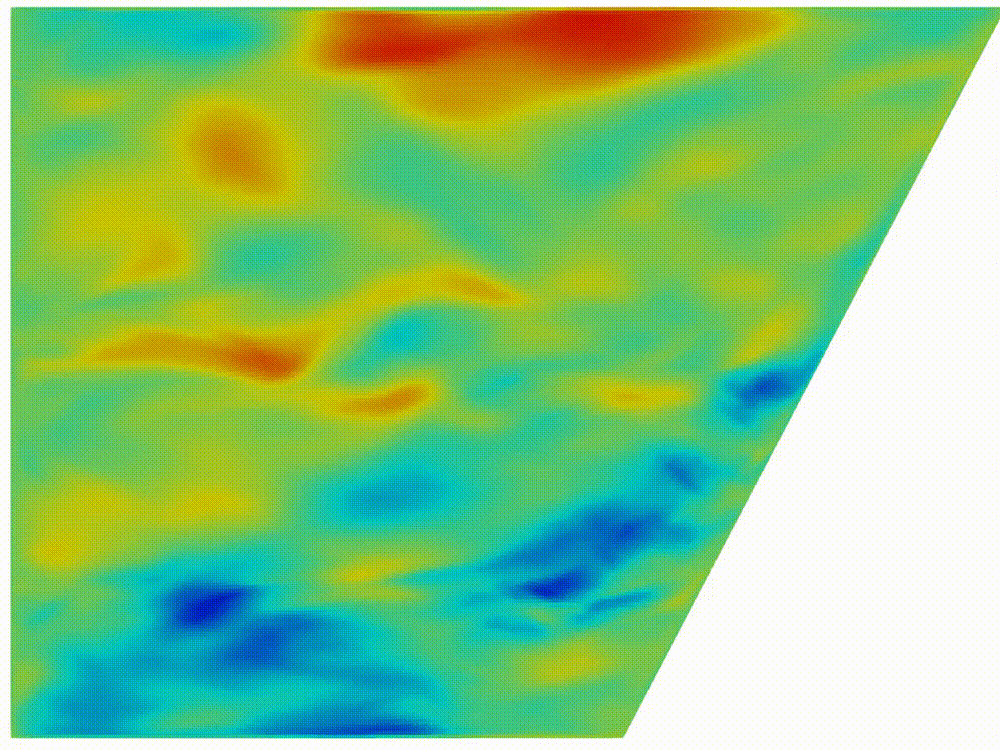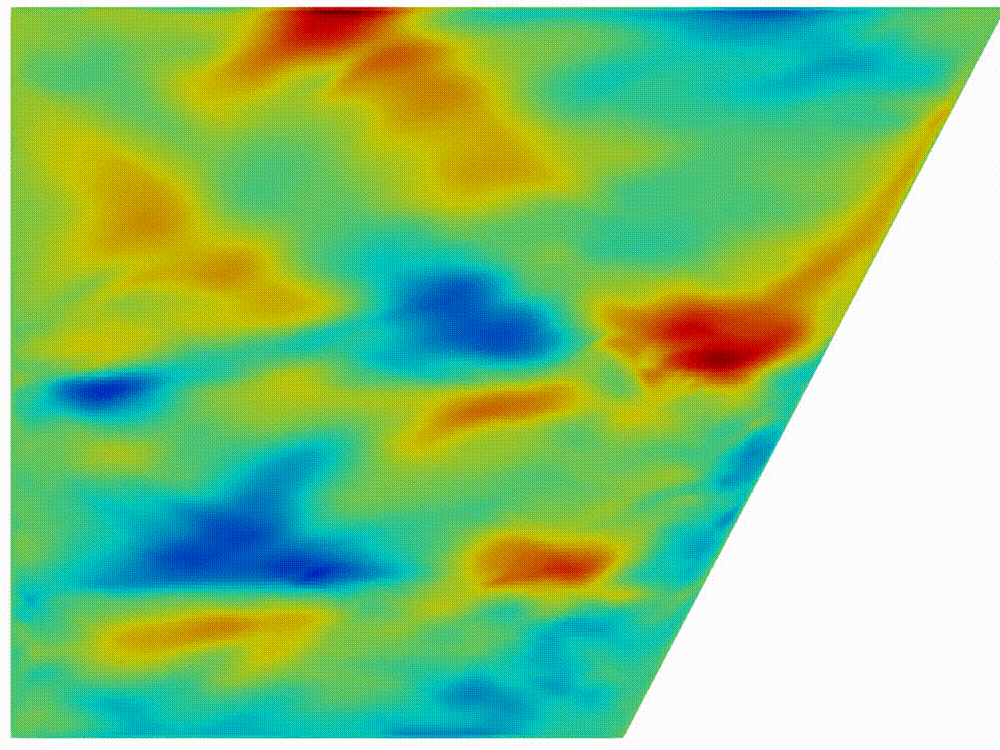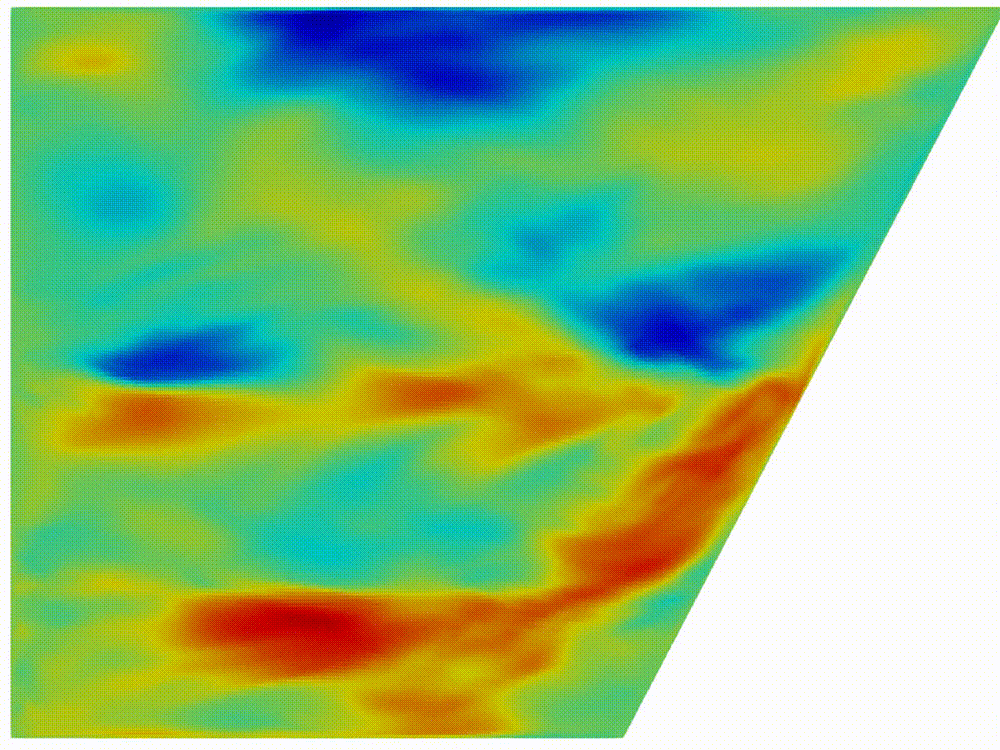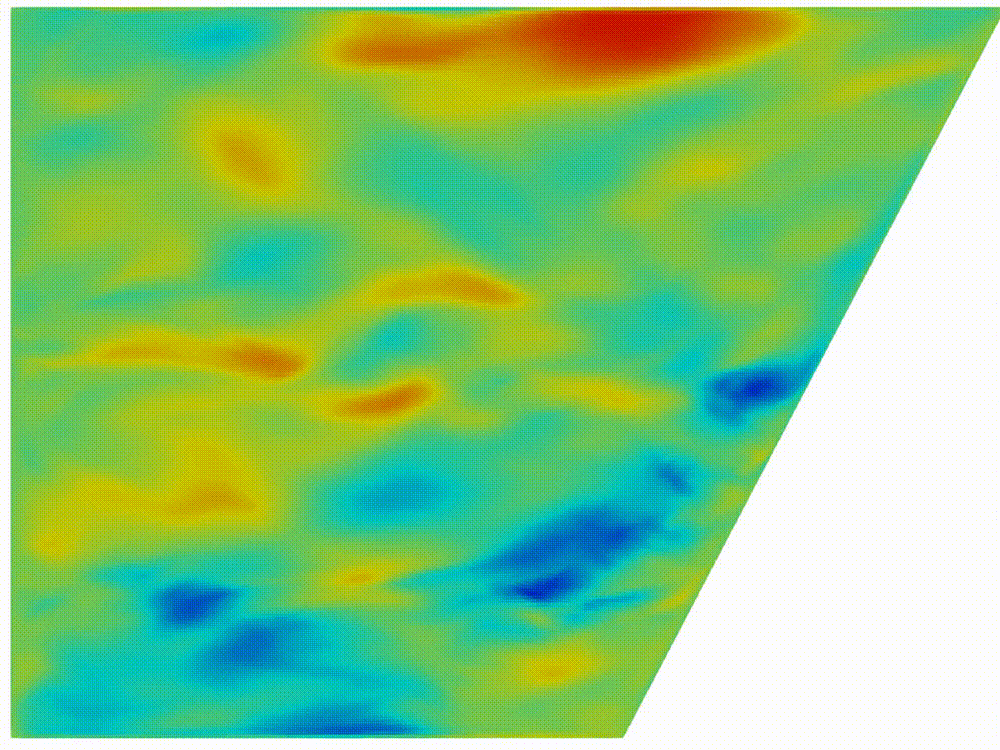
|
|
(a) Internal waves
attractor formation
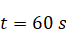 to
to
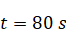
|
(b) Internal waves
turbulence
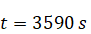 to
to
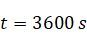
|
|
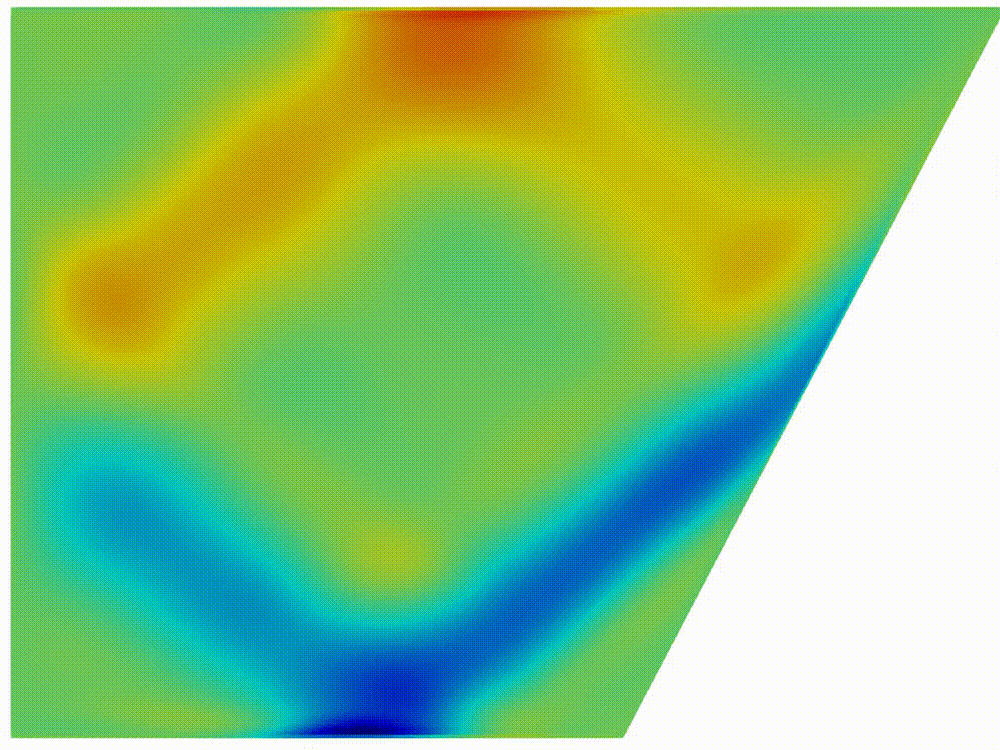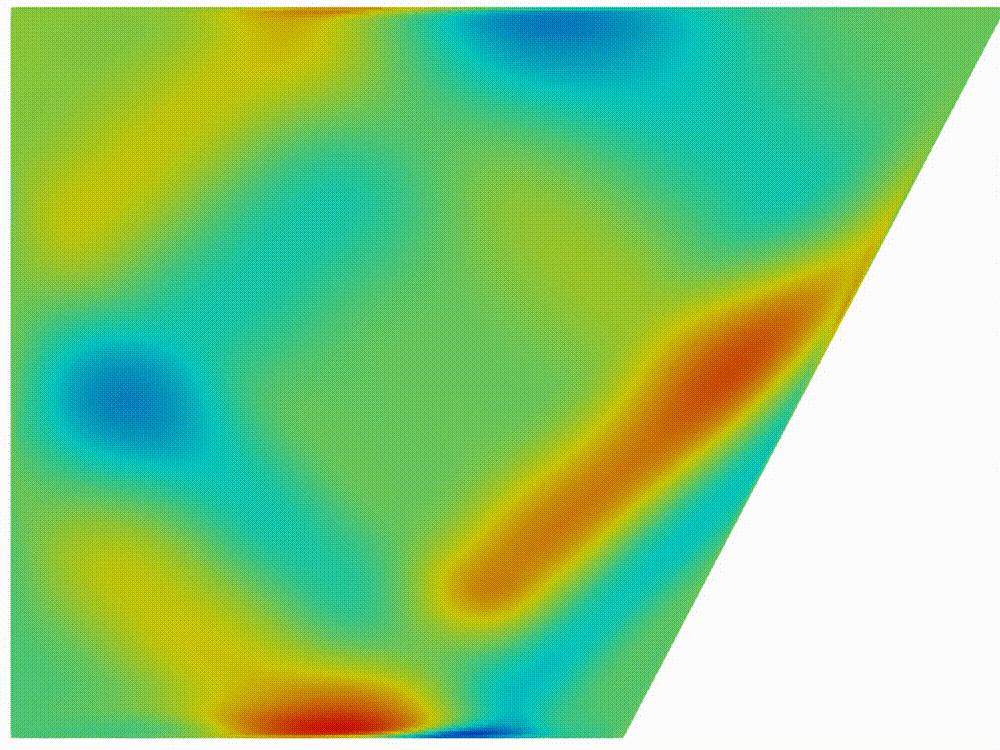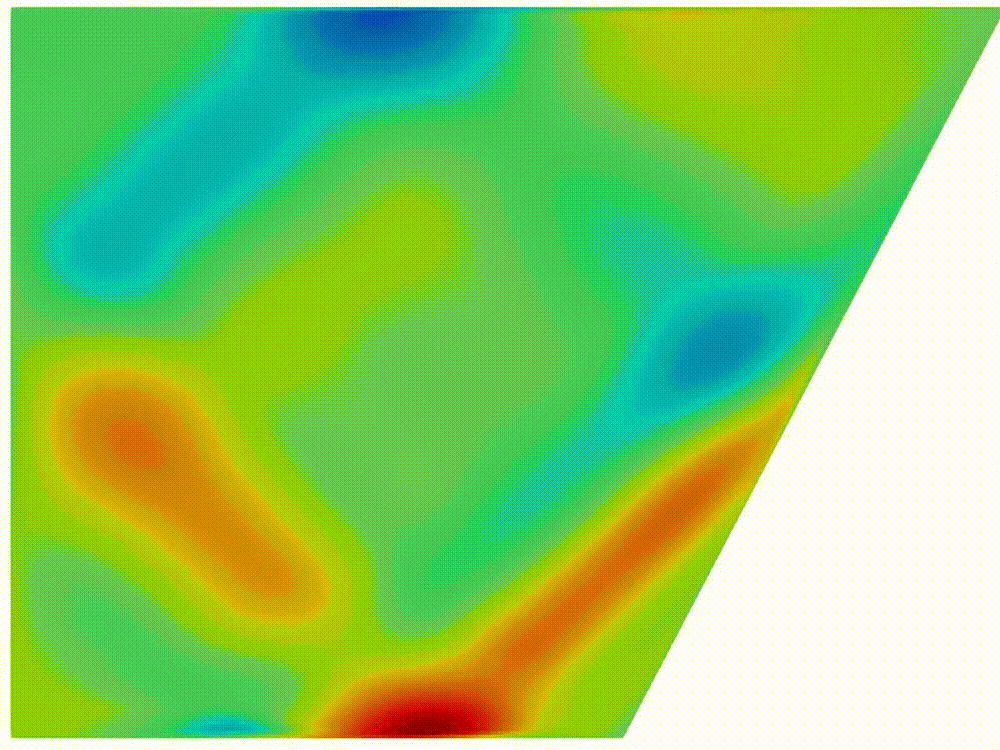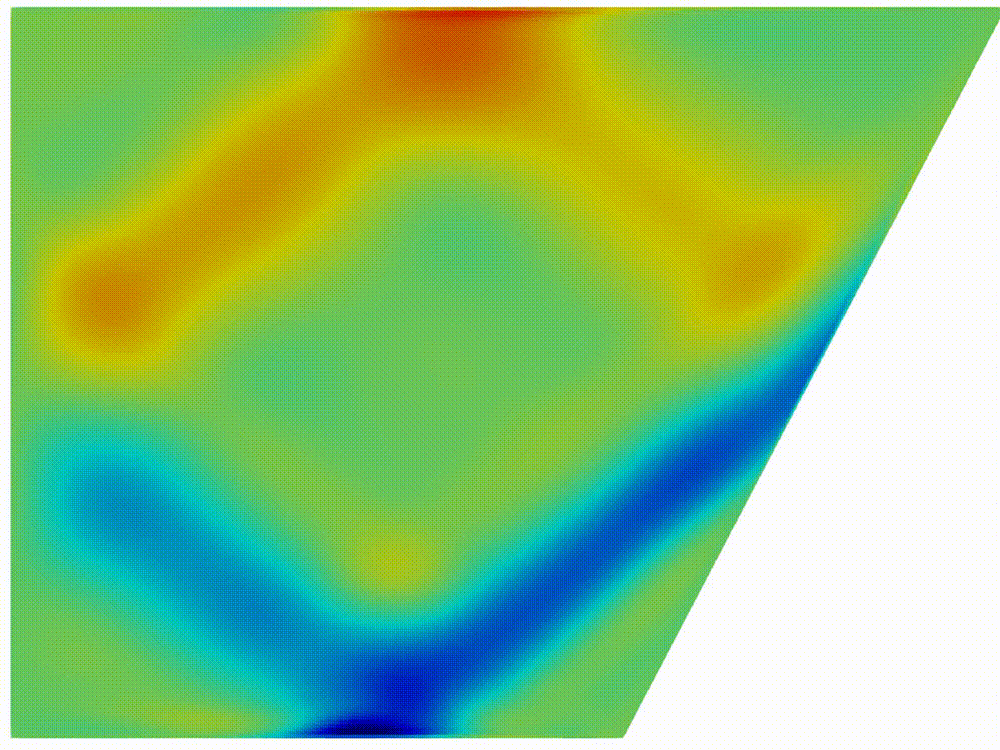
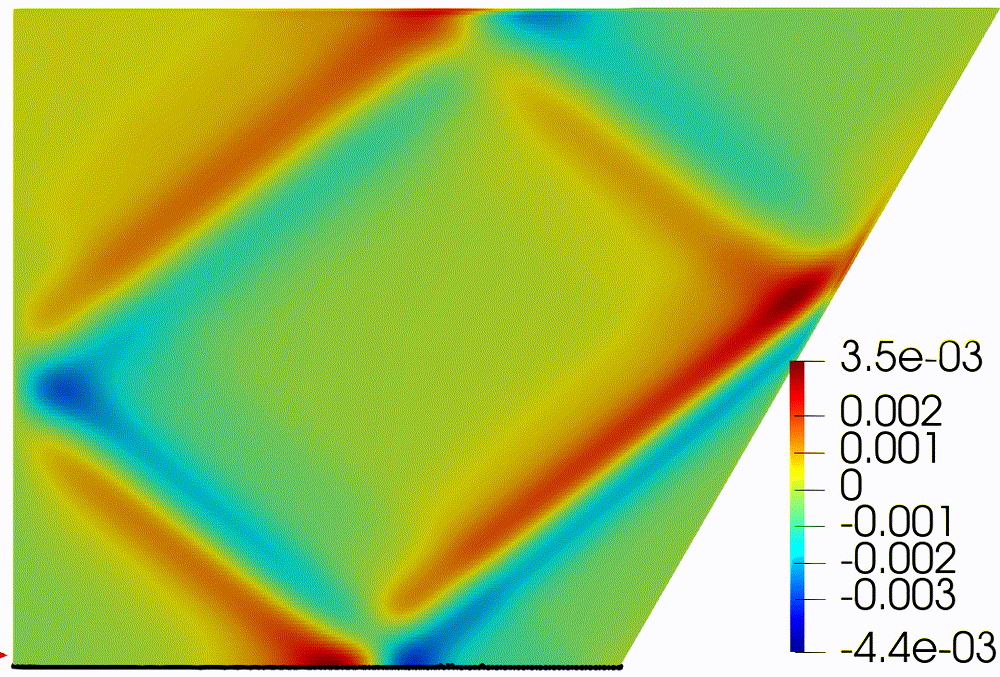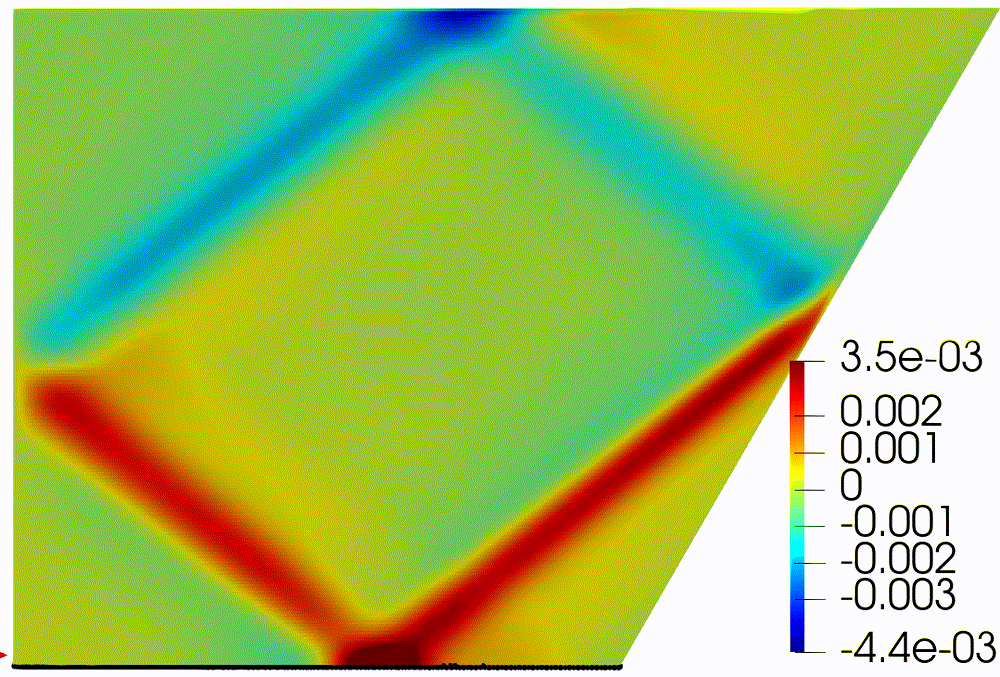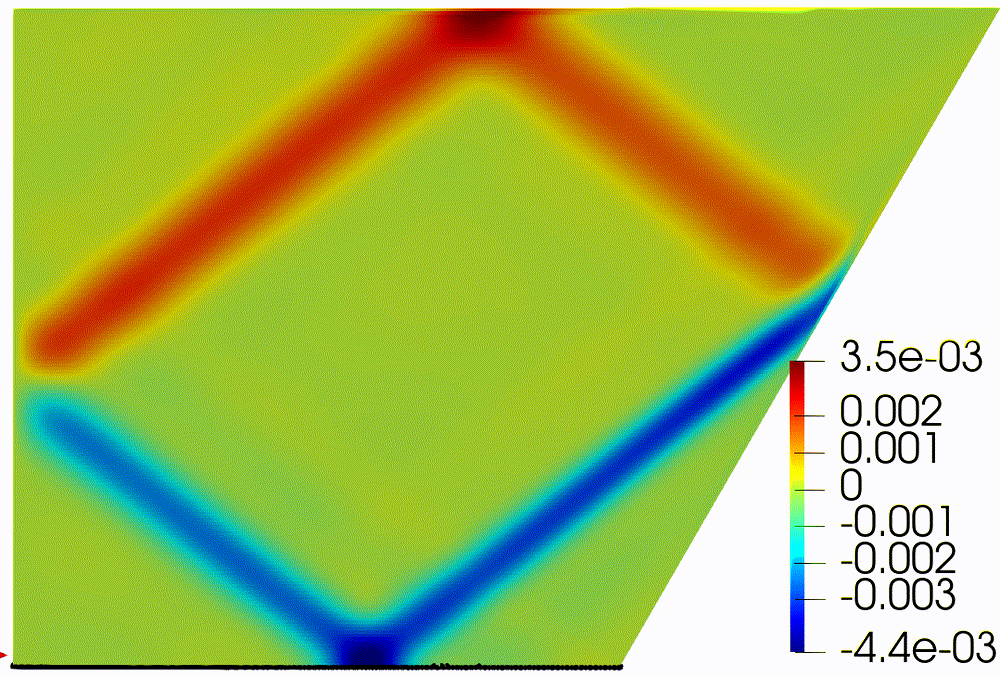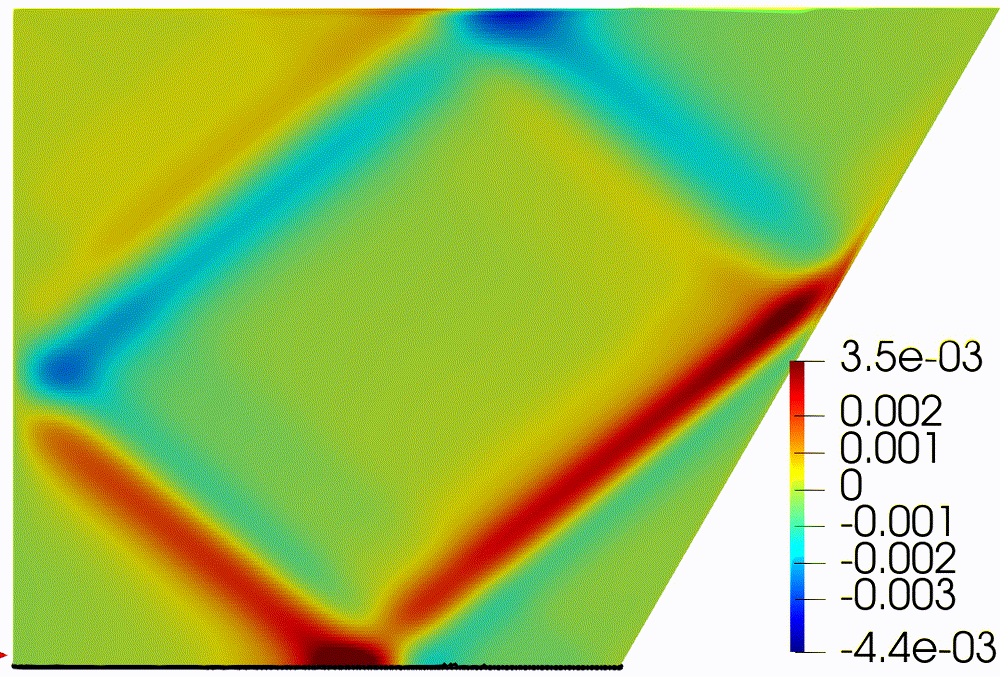
Figure 2: Horizontal
component of velocity, (a) after formation of internal wave attractor with
finite width, (b) instability development and transition to fully turbulent
motion.
|
Visualization
of velocity field was provided by open-source software paraview [20]. In figure
2
the horizontal component
is shown. About 20 first wavemaker periods attractor is being formed, next the
attractor holds the shape during about 30 periods, after 50 periods the
perturbation are grown enough to initiate the cascade of the triadic
instabilities.
As
the one of main method of flow motions analysis time-frequency diagram which
shows dynamic of spectrum is considered (Fig.
3).
It is defined by the Fourier-transform made with a sliding time window. Hence,
a vertical slice of the diagram is the spectrum taken over the neighbourhood of
time moment
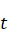 ,
so one can trace the evolution of the spectrum. At the start of the wavemaker
the fluid has one clear frequency, but then the attractor becomes prone to
hydrodynamic instabilities and the generation of the cascade of secondary
waves.
,
so one can trace the evolution of the spectrum. At the start of the wavemaker
the fluid has one clear frequency, but then the attractor becomes prone to
hydrodynamic instabilities and the generation of the cascade of secondary
waves.
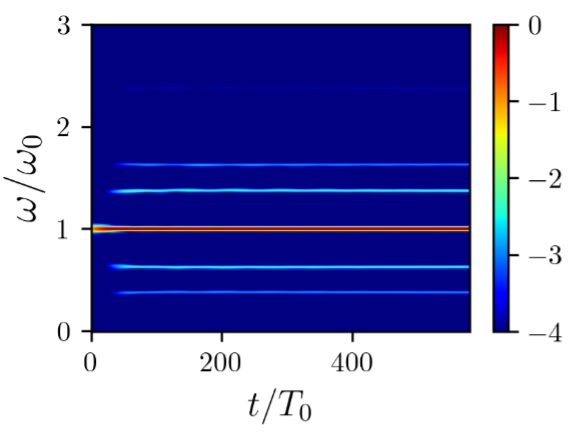
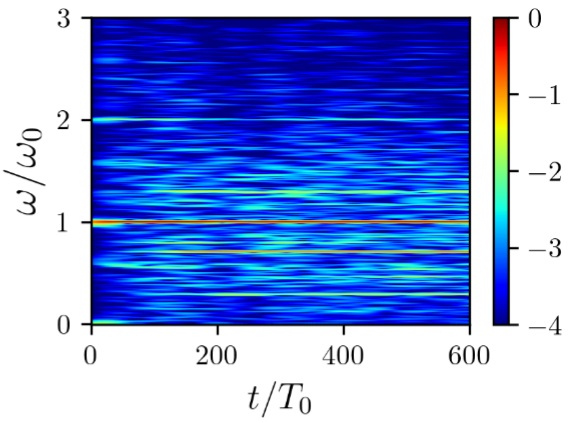
Figure
3 illustrate dependence of time-frequency diagrams on the forcing amplitude
(log-scale of amplitude, normalized by maximum value). If the amplitude is not
high enough, spectrum almost doesn’t evolve and has discrete peaks; with the
increase of the amplitude the spectrum combines discrete peaks and continuous
background and fluctuates with the time, which indicates the transition to the
turbulent regime.
|
|
|
|
(a) Time-frequency diagram
of superharmonics presence
(
|
(b)
Time-frequency diagram of attractor destruction
|
|
Figure 3: Time-frequency
diagrams
|
One
of the important problems with applications in oceanology is the sedimentation
of suspended particles and their interaction with the internal waves. To
describe qualitatively the influence of wave attractors on sedimentation of
suspended particles we have made visualization for laminar and turbulent
regimes of wave attractors. Initial density profile in the tank is linear. At
the initial state spherical particles with diameter
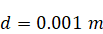 were distributed
uniformly over the horizontal middle line (Fig.
1a).
The model does not account for feedback from the particles on the flow. Such a
setup showed drastic differences in the sedimentation properties for laminar
and turbulent wave attractors.
were distributed
uniformly over the horizontal middle line (Fig.
1a).
The model does not account for feedback from the particles on the flow. Such a
setup showed drastic differences in the sedimentation properties for laminar
and turbulent wave attractors.
Two
questions arise: a) redistribution of the particles in the bulk flow before the
particles approach the bottom, b) redistribution of the particles near the
bottom.
Numerical
experiments were carried out for two different regimes, corresponding to
wavemaker
(7)
amplitudes
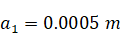 – regime of stable
attractor without wave instabilities, and
– regime of stable
attractor without wave instabilities, and
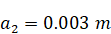 – fully turbulent
regime.
– fully turbulent
regime.
Numerical
experiment has shown that particles experience oscillation while falling, and
in laminar regime they continue to oscillate near the bottom along horizontal
direction (Fig. 4). First part of the experiment shows movement of particles
until they touch the bottom. Internal waves make weak oscillation of “particles
line” (Fig. 4a). And even attractor of internal waves does not affect to
particle distribution due to small amplitude (Fig. 4b). For the turbulent
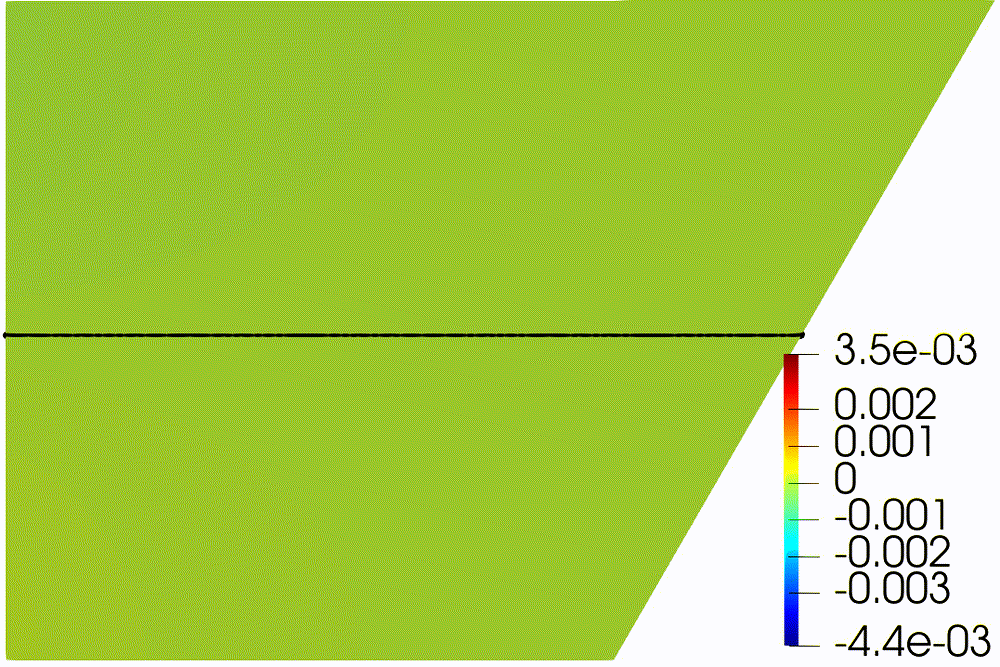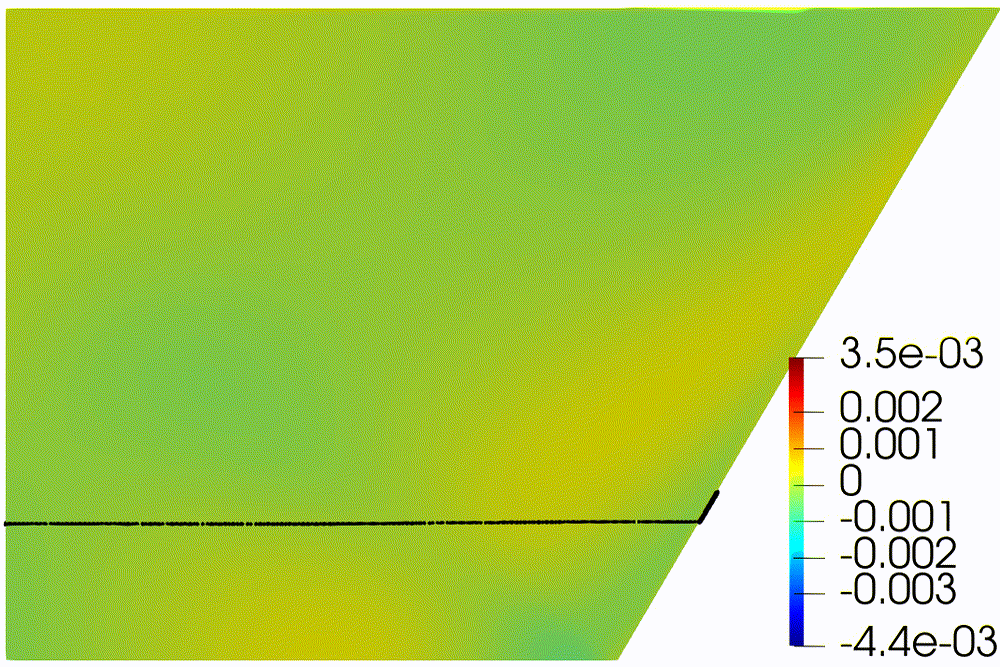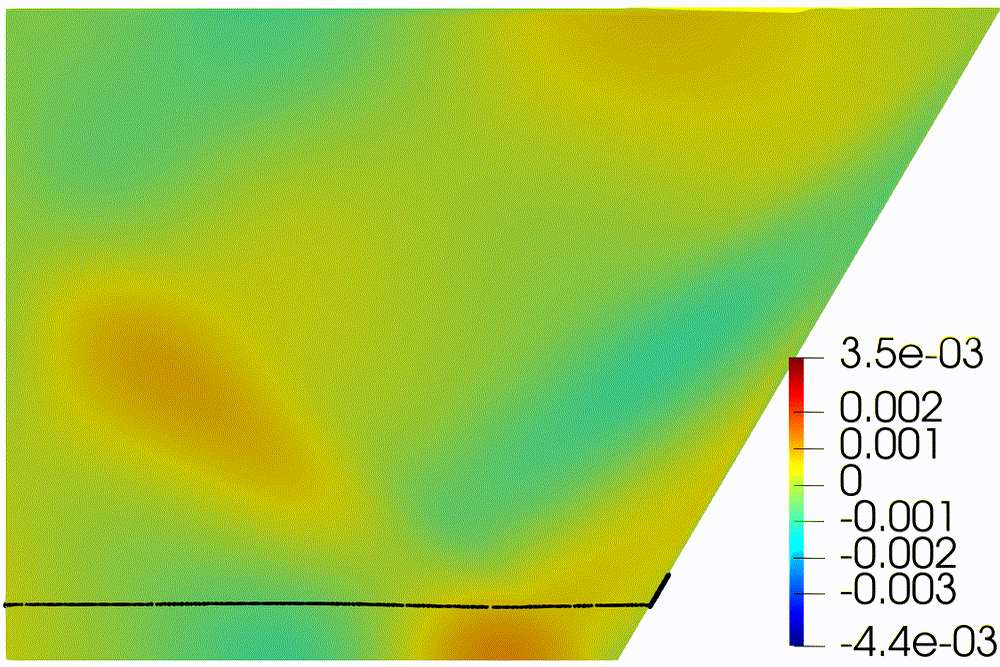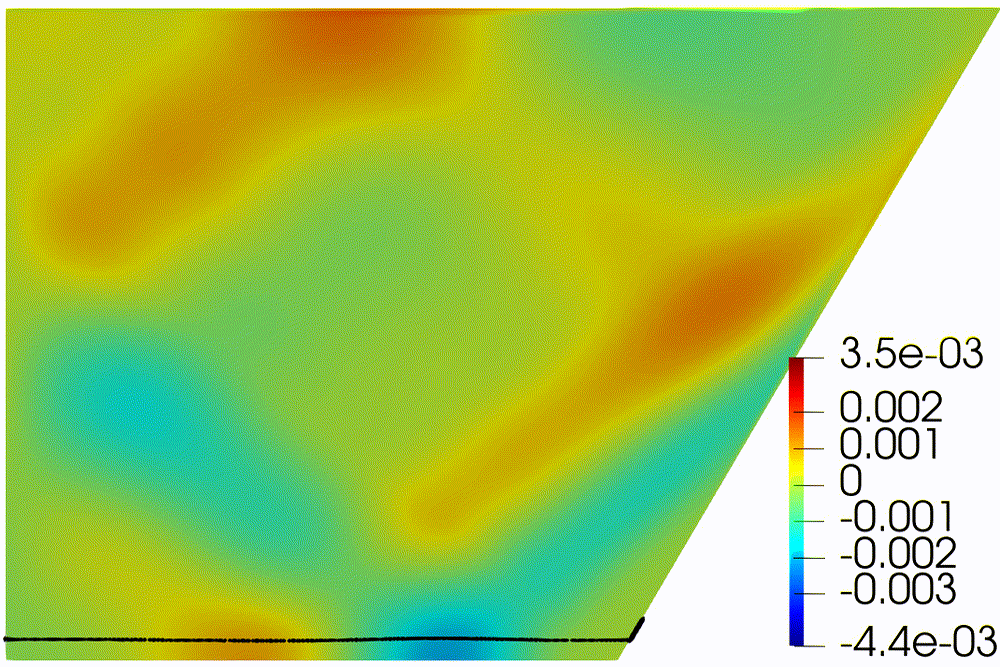
regime the long-time behavior of the particles near the bottom is completely
different: all the particles are attracted by two points at the bottom during
the period
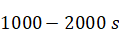 (Fig. 5). At the initial
phase of sedimentation (Fig. 5a) internal waves focusing produce intense
movement of particles around the bottom of the tank, which leads to a
redistribution of particles around two points (Fig. 5b).
(Fig. 5). At the initial
phase of sedimentation (Fig. 5a) internal waves focusing produce intense
movement of particles around the bottom of the tank, which leads to a
redistribution of particles around two points (Fig. 5b).
|
|
|
|
(a) Sedimentation from
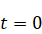 s
to s
to
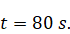 Initial phase, particles slowly moving to the bottom.
Initial phase, particles slowly moving to the bottom.
|
(b) Redistribution from
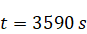 to
to
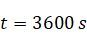 .
Ending stage, particles lie evenly at the bottom. .
Ending stage, particles lie evenly at the bottom.
|
|
Figure 4: Sedimentation in presence of stable (''laminar'')
wave attractor.
|
|

|
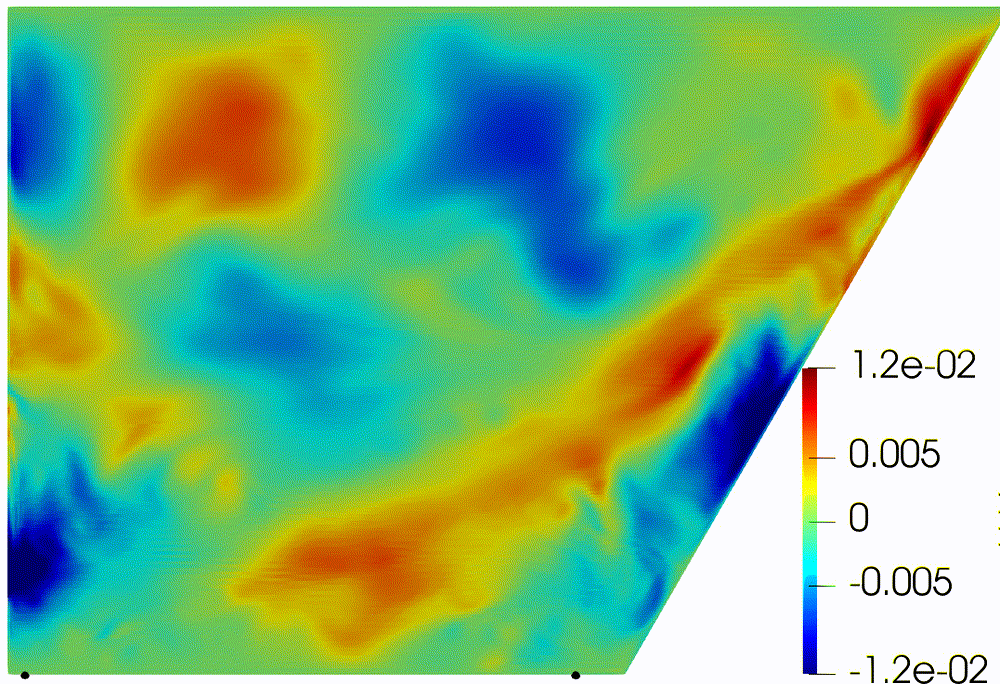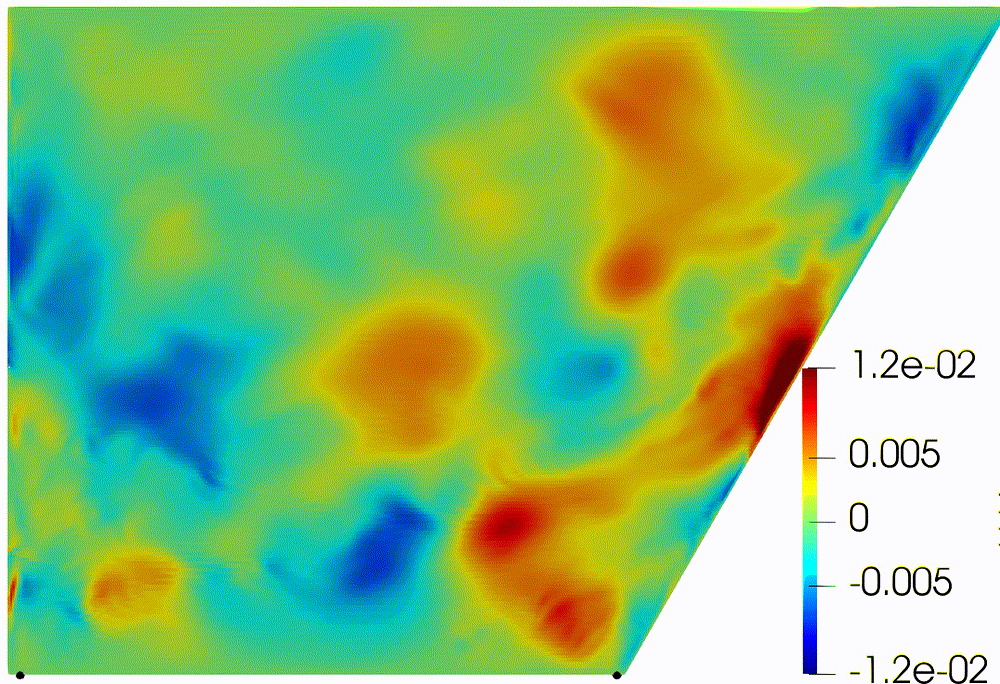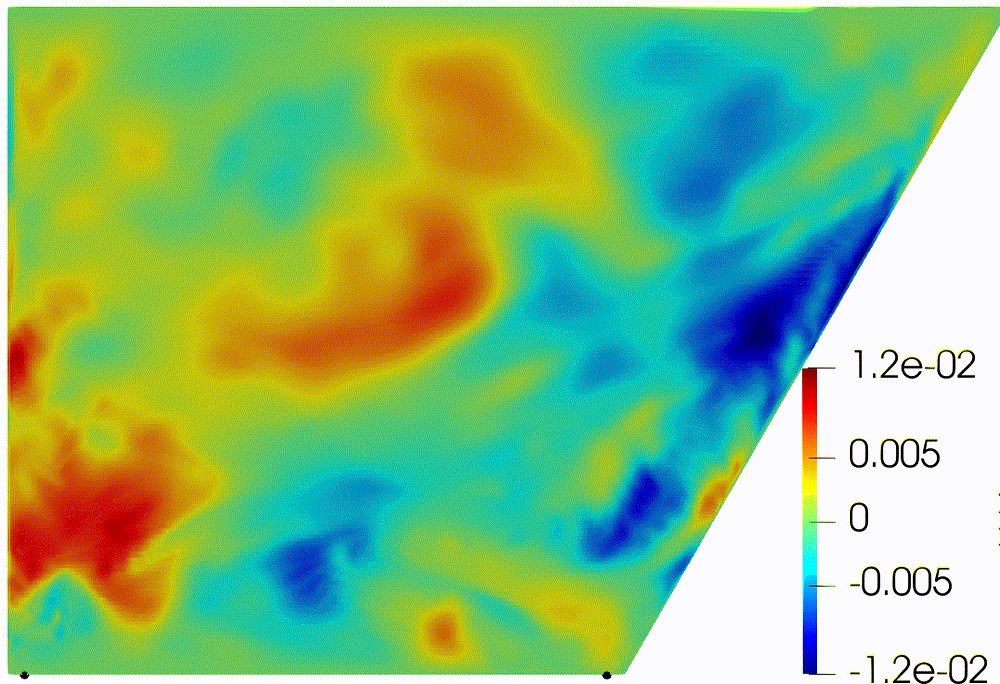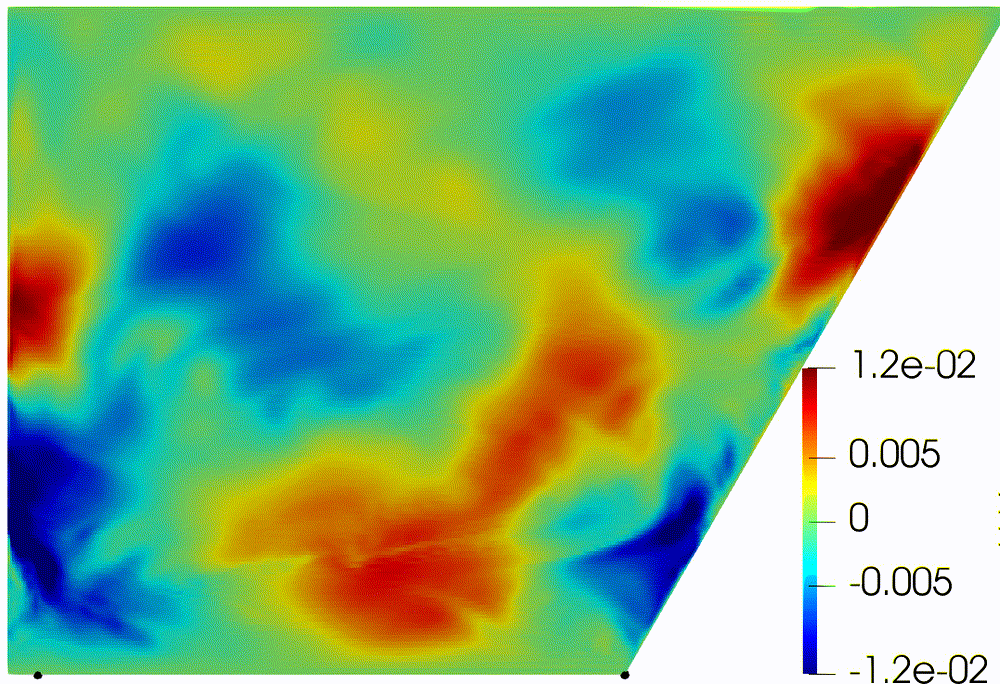
|
|
(a) Sedimentation from
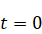 s
to s
to
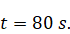 Initial phase, particles slowly moving to the bottom.
Initial phase, particles slowly moving to the bottom.
|
(b) Redistribution from
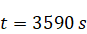 to
to
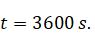 Ending stage, particles concentrate around two points at
the bottom.
Ending stage, particles concentrate around two points at
the bottom.
|
|
Figure 5: Sedimentation in presence of turbulent wave
attractor.
|
Three-dimensional
setup may result in additional focusing along the transverse direction [21].
Despite the fact that attractor may be located at only part of the left wall,
the visualisation of numerical simulation in figure 7 shows almost perfect
two-dimensional structure.
With
addition third dimension the simulation problem was complicated significantly.
There are difficulties in visualizing a three-dimensional velocity field. For
showing destruction of internal waves attractor paraview filter ’threshold’ was
used. It allows to see values from gap and detect areas with intensive motion
(Fig.
7).
Emptiness is proposed to fill in salinity field with interprocess patches
(glares). And finally, with ’slice’ filter select closest to wavemaker area for
visualisation of wavemaker motion.
Visual
analysis of simulation shows internal waves attractors destruction procedure.
The attractor is formed in the period from 0 to 10 oscillation periods, then
from 10 to 30 oscillation periods stable and attractor structure is observed
and finally from 30 to 300 and belong difference of velocities become too big
that waves overturn and incoming energy produce secondary waves.
|
|
|
Figure 7: Life cycle of internal waves attractor from
stability to chaos. Color visualization of velocity horizontal component.
Flare in reservoir is an interprocessors interfaces painted in salinity
colorbar where 1
is a blue and 2
is a red. Wall with wave maker has a different color
scale: from
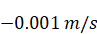 to
to
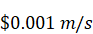 . .
|
As a result of direct numerical
simulation of internal wave turbulence, one gets a large volume of data. It is
now possible to get high-resolution data, and resolve the small-scale flows. At
the same time, it requires more computational resources to generate and process
it. Raw data is difficult to interpret without special software. In this paper
we consider some open-source software for flow analysis and visualization. The
open-source software complies with the principles of scientific credibility,
ability to modify and reuse the code, and source code transparency.
To obtain hydrodynamic
fields OpenFOAM was used, but raw data takes up a lot of space on hard drives
and generate a lot of files especially in simulations with particles. Sometimes
it can be critical. At this paper functionObject ’vtkWrite’ was used to resolve
this problem. For simulation with particles ’cloudWrite’ function object was
used which generate much fewer files then raw pure OpenFOAM output.
Additionally, data was collected at key nodes for Fourier analysis and
construction of time-frequency diagrams with ’postProcWrite’ functionObject.
Problem of internal
gravity waves attractor simulation is complicated by the fact that it is
required to simulate significant periods of model time. 24 processors for
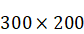 computational
domain needs for simulation of 2D problem. Simulation of a 2D problem lasted
for 5 days on Unihub cluster [22]. 3D problem required more detailed mesh
additionally to the 3-d dimension. 196 processors for
computational
domain needs for simulation of 2D problem. Simulation of a 2D problem lasted
for 5 days on Unihub cluster [22]. 3D problem required more detailed mesh
additionally to the 3-d dimension. 196 processors for
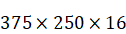 domain. Simulation of
450 seconds lasted for 7 days on The Lobachevsky supercomputer.
domain. Simulation of
450 seconds lasted for 7 days on The Lobachevsky supercomputer.
Processing of simulation
results required many different instruments for calculations and visualisation.
Fourier analysis was provided with python package scipy [23], and drawing with
matplotlib [24]. Visualisation was obtained by paraview [20]. Scripts for
vortices visualisation was developed with python [25].
The research was supported by RSF
(project No. 19-11-00169). The authors thank Elizarova T. G. for continuous
support.
1.
Munk, W.
Abyssal recipes // Deep-Sea Res. – 1966. – Vol. 13. – P. 707-730.
2.
W. Munk, C. Wunsch // Deep Sea Research Part I: Oceanographic Research Papers.
– 1998. – Vol. 45. – Abyssal recipes II. – ¹ 12. – P. 1977-2010.
3.
Munk, W.H.
9 internal waves and small-scale processes – 2005.
4.
Znamenskaya, I.A.
Methods for panoramic visualization and digital analysis of thermophysical flow
fields // Scientific Visualization. – 2021. – Vol. 13. – ¹ 3. –
P. 125-158.
5. B. Sutherland,
T. Dauxois, T. Peacock // Modeling atmospheric and oceanic flows. – American
Geophysical Union (AGU), 2014. – P. 193-212.
6.
Bourget, B.
Experimental study of parametric subharmonic instability for internal plane
waves – 2013. – Vol. 723. – P. 1-20.
7.
Dossmann, Y.
Mixing by internal waves quantified using combined
PIV/PLIF technique // Experiments in Fluids. – 2016. – Vol. 57. –
¹ 8. – P. 132.
8.
Davis, G.
Energy budget in internal wave attractor experiments //
Journal of Fluid Mechanics. – 2019. – Vol. 880. – P. 743-763.
9.
Husseini, P.
Experimental study on superharmonic wave generation by
resonant interaction between internal wave modes // Phys. Rev. Fluids. – 2020.
– Vol. 5. – P. 074804.
10.
Lee, F.M.
Experimental determination of radiated internal wave
power without pressure field data // Physics of Fluids. – 2014. – Vol. 26.
– ¹ 4. – P. 046606.
11.
Maas, L.R.M.
Geometric focusing of internal waves // Journal of
Fluid Mechanics. – 1995. – Vol. 300. – P. 1-41.
12.
Maas, L.R.M.
Observation of an internal wave attractor in a
confined, stably stratified fluid // Nature. – 1997. – Vol. 388. –
P. 557-561.
13.
Grisouard, N.,
C.
Staquet, I. Pairaud, Numerical simulation
of a two-dimensional internal wave attractor // Journal of Fluid Mechanics. –
2008. – Vol. 614.
14.
Brouzet, C.
Internal wave attractors examined using laboratory
experiments and 3D numerical simulations // Journal of Fluid Mechanics. – 2016.
– Vol. 793. – P. 109-131.
15.
Brouzet, C.
Energy cascade in internal-wave attractors // EPL
(Europhysics Letters). – 2016. – Vol. 113. – ¹ 4.
16.
Elizarova, T.G.
Quasi-gas dynamic equations – Springer, 2009.
17.
Sheretov, Y.V.
Continuum dynamics under spatiotemporal averaging //
SPC Regular; Chaotic Dynamics. (Moscow-Izhevsk, 2009, in Russian), 2009.
18.
Scolan, H., E. Ermanyuk, T. Dauxois
Nonlinear Fate of Internal
Wave Attractors // Physical Review Letters. – 2013. – Vol. 110. – ¹ 23.
– P.
19.
OpenFOAM framework for simulation of fluid flows using regularized (QGD/QHD)
equations approach. –
https://github.com/unicfdlab/QGDsolver,
2019
20.
Open-source, multi-platform data analysis and visualization application. –
https://https://www.paraview.org/,
2000.20.
21.
Pillet, G.
Internal wave attractors in three-dimensional geometries: trapping by oblique
reflection // Journal of Fluid Mechanics. – 2018. – Vol. 845. –
P. 203-225.
22.
Samovarov, O.I., S.S. Gaysaryan.
The web-laboratory architecture
based on the cloud and the UniHUB implementation as an extension of the
OpenStack platform – 2014. – Vol. 26. – ¹ 1. – P. 403-420.
23.
scipy official website. –
https://www.scipy.org/.
24.
matplotlib official github. –
https://github.com/matplotlib/matplotlib.
25.
python official website. –
https://www.python.org/.
[1]
“Gravity waves in the ocean’s interior are as common as waves at
the sea surface – perhaps even more so, for no one has ever
reported an interior calm” [3]

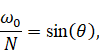
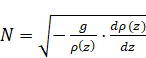
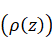 .
.


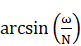 ,
,
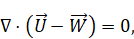
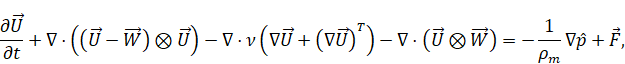
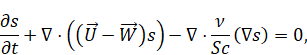
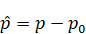 ,
,
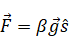 ,
,
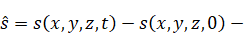
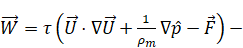
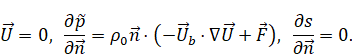
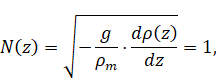
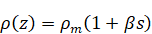 ,
,
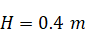 ,
,
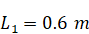 ,
,
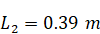 .
.
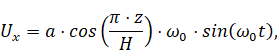
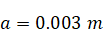 ,
,
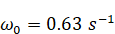 .
.
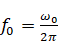
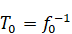 .
.


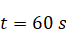
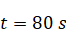
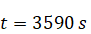
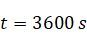


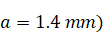
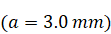
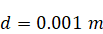
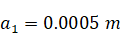
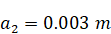
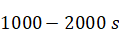


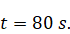
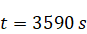


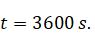

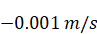
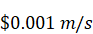 .
.