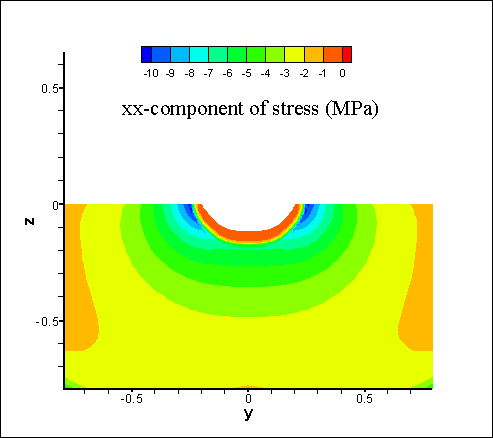
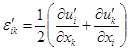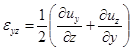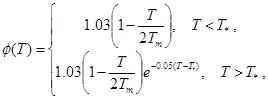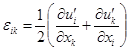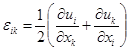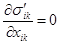 ,(1)
,(1)
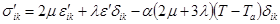 ,
,
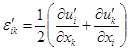 ,
,
where 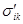 is the full stress tensor;
is the full stress tensor; 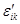 is the strain tensor;
is the strain tensor; 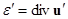 is deformation of the
material;
is deformation of the
material; 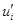 are the components of the displacement vector
are the components of the displacement vector 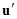 of the material;
of the material; 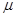 ,
, 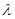 are the elastic moduli (Lame
coefficients);
are the elastic moduli (Lame
coefficients); 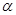 is the thermal expansion coefficient;
is the thermal expansion coefficient; 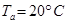 is the reference temperature;
the indices
is the reference temperature;
the indices 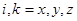 .
.
We assume that
evolution occurs via a series of plane strain states. This means that there are
no displacements of the material along the direction of the laser beam movement
(i.e. 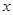 -direction) at each moment. In this case the problem becomes
two-dimensional and
-direction) at each moment. In this case the problem becomes
two-dimensional and 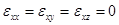 . The non-zero strain tensor components are
related with the components of displacements by the following relations:
. The non-zero strain tensor components are
related with the components of displacements by the following relations:
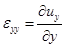 ,
, 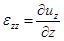 ,
, 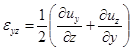 ,
,
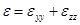 .
.
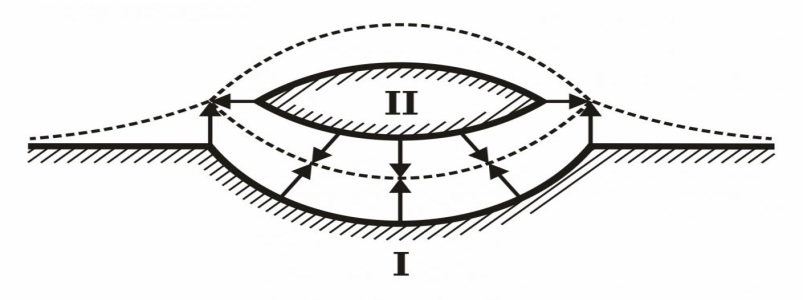
Fig. 1. Schematic representation of the two-step algorithm for residual stresses calculations.
The problem is
solved in the domain, composed of two subdomains (Fig. 1). A subdomain I
contains the material at the temperature 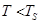 . In a subdomain II the temperature is
. In a subdomain II the temperature is 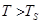 . The subdomain II is not considered, as it is assumed that there are no
stresses in it. The thermal stresses in the subregion
I lead to area stretching relative to the reference state at temperature
. The subdomain II is not considered, as it is assumed that there are no
stresses in it. The thermal stresses in the subregion
I lead to area stretching relative to the reference state at temperature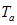 . Subregions
I and II are joined (have no gaps and overlaps) and
have a temperature distribution calculated at the first stage of modeling.
. Subregions
I and II are joined (have no gaps and overlaps) and
have a temperature distribution calculated at the first stage of modeling.
In Fig. 1 the
shaded areas I and II represent the material of the substrate and the bead
under the reference conditions (not heated or strained). Heated up to the first
stage temperature, the material expands and fills a region those boundaries are
shown by the dashed lines. In this state the subdomains I and II densely adjoin
to each other.
The material,
returning to its initial reference temperature, would return to the reference
state with the gap between the subdomains. But since the actual gaps and
overlapping do not exist after cooling to the reference temperature, the
subdomains can not return to their initial states
free from the stresses. In other words, the material of the substrate and the
weld should contain residual stresses.
At the lower
boundary of the computational domain we apply the Dirichlet
boundary condition for the displacements 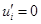 . At the other boundaries we apply
the Newmann boundary condition
. At the other boundaries we apply
the Newmann boundary condition 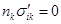 , i.e. the absence of the normal to
the boundary total stresses.
, i.e. the absence of the normal to
the boundary total stresses.
The equations
contain the elastic modulus 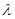 and the shear modulus
and the shear modulus 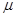 . These quantities depend linearly
on the Young’s modulus
. These quantities depend linearly
on the Young’s modulus 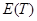 as
as
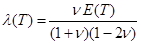 ,
, 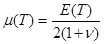 .
.
The temperature
dependence is introduced into the Young’s modulus as 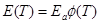 . Here
. Here 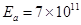 dyn/cm2 is the Young’s modulus at the reference temperature
dyn/cm2 is the Young’s modulus at the reference temperature 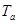 ; Poisson’s ratio
; Poisson’s ratio 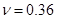 is considered
temperature-independent. As a specific example, the temperature dependence of
the Young’s modulus is taken in the following calculations as [10]:
is considered
temperature-independent. As a specific example, the temperature dependence of
the Young’s modulus is taken in the following calculations as [10]:
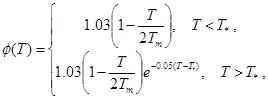
where 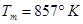 is the melting temperature.
is the melting temperature.
The temperature
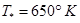 is chosen as it provides the
best agreement between the empirical relation and experimental measurements. It
is assumed that the thermal expansion coefficient does not depend on the
temperature and is equal to
is chosen as it provides the
best agreement between the empirical relation and experimental measurements. It
is assumed that the thermal expansion coefficient does not depend on the
temperature and is equal to 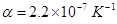 .
.
At the second stage
of the simulation it is assumed that the temperature in the whole region is
reduced to its reference value 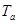 . At the same time due to the
differences in strains in the ”melted” and ”unmelted” subdomains, the residual stresses appear. At this
stage the equation (1) is solved numerically in both subdomains I and II. As
. At the same time due to the
differences in strains in the ”melted” and ”unmelted” subdomains, the residual stresses appear. At this
stage the equation (1) is solved numerically in both subdomains I and II. As 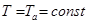 , the thermal stresses are absent. In the same way as it is at the first
stage of simulation, at the lower boundary of the joint computational domain
I+II the Derichlet’s boundary condition
, the thermal stresses are absent. In the same way as it is at the first
stage of simulation, at the lower boundary of the joint computational domain
I+II the Derichlet’s boundary condition 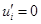 for the displacements is
applied. On the other boundaries the Newmann’s
boundary condition
for the displacements is
applied. On the other boundaries the Newmann’s
boundary condition 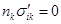 is applied.
is applied.
The problem (1)
is solved for the displacements. The temperature field and the thermal term are
assumed to be defined. At the first stage the displacements of the elastic
material particles are calculated.
After the
temperature in the both regions returns to the initial reference value at fixed
particle displacements, obtained at the first stage. In order to the particles
do not shift from now on, they must be under the action of ”virtual”
force with density
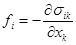 ,
, 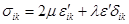 ,
, 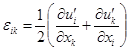 ,
,
where the
elastic moduli are calculated at the temperature 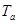 ;
; 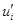 are the displacements obtained at the
first stage.
are the displacements obtained at the
first stage.
Note that in
the subdomain II the ”virtual” force acts only on the surface and provides a
uniform tension of this subdomain, in accordance with the thermal expansion
obtained at the first stage.
At the second
stage the ”virtual” force disappears, and the
particles of the elastic material, enclosed within the subdomains I and II,
relax to the ”natural” state. This state, however, does not coincide with the
initial one for the reasons mentioned above. At this point, the following
problem is considered
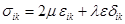 ,
,
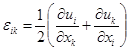 ,
(2)
,
(2)
The
displacements of the material particles (after the stages ”heating+melting” and ”solidification+cooling”)
obtain finally the following values
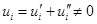 .
.
The residual
stresses are calculated for these residual displacements by the formula (2),
where the elastic moduli are calculated at the reference temperature
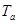 .
.
The output data for the proposed mathematical
model are temperature fields, components of the stress tensor (as well as the
main directions and stresses calculated from them), components of the
displacement vector. For greater clarity, when analyzing the results of numerical
modeling, it is proposed to use a joint flat technology as representation of
the fields of scalar quantities. This is done by filling the vector quantities
shown by streamlines with color and the direction field. To implement this
visual presentation method, the well-known graphic visualization package TecPlot [11] and the corresponding data file format were
used.
The difference scheme that approximates the Lame equations
on a curvilinear mesh is based
on the support
operators method [12]. The method provides
self-adjointness and positivity of an
approximation difference operator, if the
parent operator of the initial
differential problem has the same
properties. The matrix of the
set of linear
equations for the displacements is inversed by
conjugate gradient method.
Calculations were performed for silumin powder.
The laser radiation power is 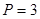 kW, the laser beam radius
is 1.67 mm, the laser light
absorption factor is 0.45, the radius
of the powder
jet is 4 mm, the capture
efficiency of powder is 0.7, the mass discharge
of the powder
is 20 g/min.
kW, the laser beam radius
is 1.67 mm, the laser light
absorption factor is 0.45, the radius
of the powder
jet is 4 mm, the capture
efficiency of powder is 0.7, the mass discharge
of the powder
is 20 g/min.
The temperature distribution in the substrate
at the heating
stage is presented in Fig.
2. Here, the lines indicate the direction of
the displacements. Fig. 3 shows the
distribution of the main stresses
in the substrate
at the heating
stage. The lines indicate the direction the
main stresses, color represents the corresponding values.
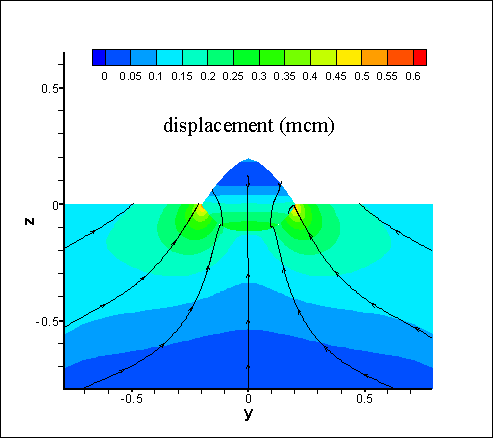
The distribution of the residual displacements
in the substrate
and the weld
bead after cooling is shown
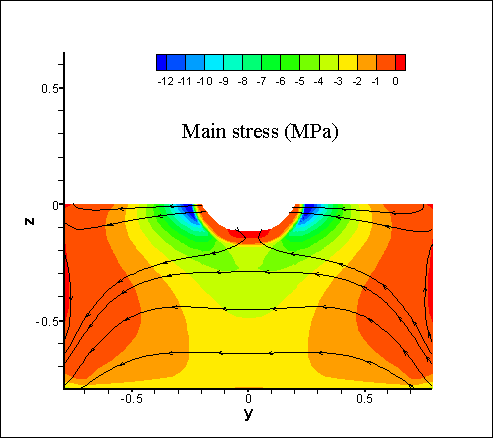
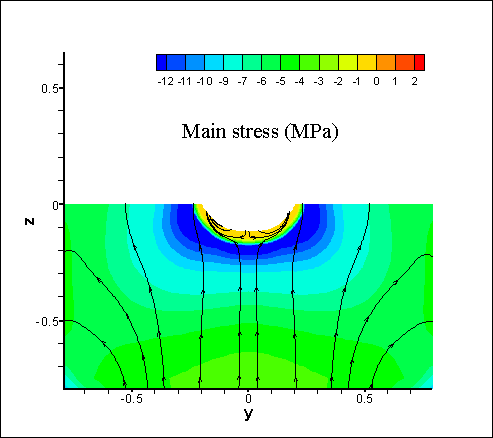
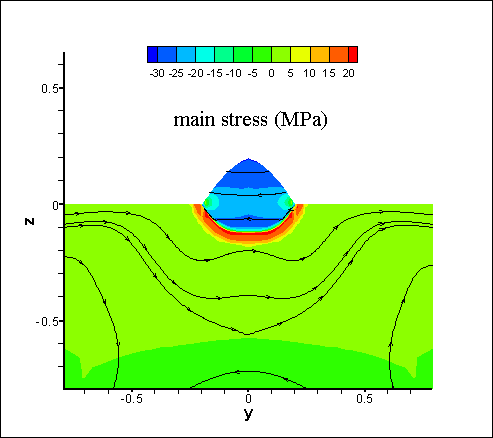
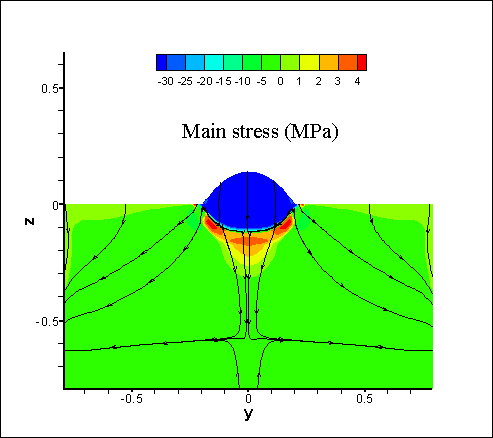
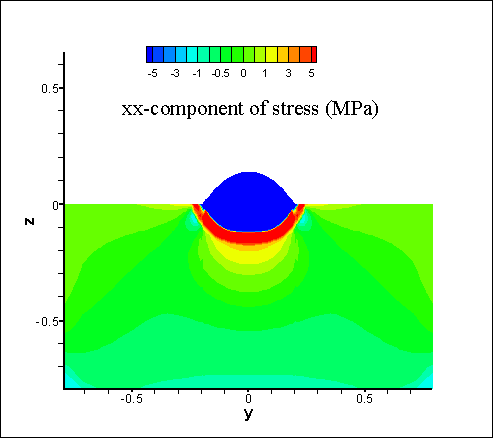
in Fig. 4. Fig. 5 shows the
distribution of the main stresses
in the substrate
and the weld
bead after cooling. The lines
indicate the direction of the
main stresses, color represents the corresponding values.
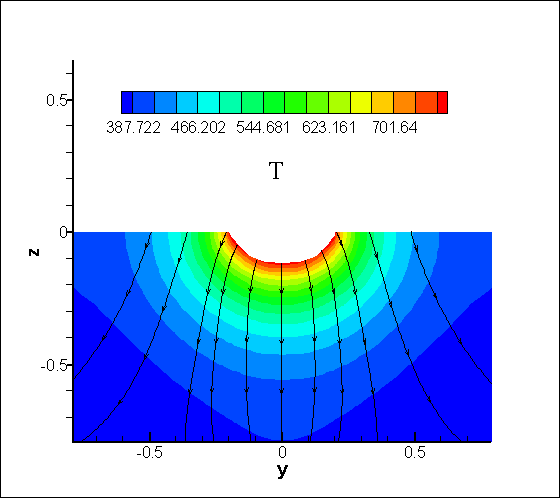
Fig. 2. The temperature distribution, established in the substrate at the heating stage. The lines show
the direction of the displacements.
Fig. 3. Distributions of main stresses in the substrate at the heating stage. The lines indicate the
direction of the stresses, color represents the corresponding values (MPa). Cases A, B: the stresses at the
section y-z.Case C: the same along the scanning direction of the laser beam (x-axis).
Fig. 4. Distribution of residual displacements (mcm) in the substrate and the weld bead at the
cooling stage. The lines show the direction of the displacements,
color represents the corresponding values in microns.
Fig. 5. Distributions of main stresses in the substrate and the weld bead at the cooling stage. The
lines indicate the direction of the color represents the corresponding values (MPa). Cases A, B: the
stresses at the section y-z.Case C: the same along the scanning
direction of the laser beam (x-axis).
Study the
stress-strain state that occurs in LS of metal in weld bead and substrate, a
mathematical model and the corresponding computational algorithm are developed.
A technique is proposed for visual presentation of the results of numerical
simulation of the stress-strain state (deformation and stress fields) arising
from local heating, partial melting and subsequent cooling of the product.
Using the developed computer technology, the stress fields were calculated and
visualized for a specific mode of the LS process. It was found that in the
boundary layers of the weld layer, the stress level is the highest. Perhaps
this is due to large temperature gradients inin these zones. In numerical
experiments, it was shown that taking the temperature dependence of Young's
modulus into account when determining the stress-strain state in products leads
to a decrease in the calculated stress levels. In addition, taking this dependence
into account can lead to noticeable qualitative differences in the pattern of
stress state evolution compared with the elastic setting. The resulting
patterns of residual stresses make it possible to predict the appearance of microcracks arising in the product after the process of
laser powder deposition, depending on the processing mode. The presented
numerical model can be used to calculate the residual stresses of a real
process in the presence of physical parameters of the material.
1. I.
V. Shishkovsky. Laser Synthesis of
Functional Mesostructures and 3D Parts.
2. V.
G. Niz’ev, F. Kh. Mirzade, V. Ya. Panchenko, V. M.
Chechetkin, and G. V. Ustiugova.
Heat and mass transfer under laser sintering of a powder mixture. Mathematical
Models and Computer Simulations, 4(2):163-171, 2012.
3.
V. G. Niz’ev, F. Kh.
Mirzade, and V. Ya. Panchenko.
Numerical modeling of laser sintering metallic powders // Collective monograph:
Modern laser and information technologies.
4.
F. Brückner, D. Lepski,
and E. Beyer. Modeling the Influence of
Process Parameters and Additional Heat Sources on Residual Stresses in Laser
Cladding. Journal of Thermal Spray Technology, 16:355–373, September
2007.
5. R.
Jendrzejewski, G. ´ Sliwi´nski,
M. Krawczuk, andW. Ostachowicz.
Temperature and stress fields induced during laser cladding. Computers &
Structures, 82(7-8):653–658, 2004.
6.
V. Ocelík, J. Bosgra,
and J.Th.M. de Hosson. In-situ strain observation in high power laser cladding.
Surface and Coatings Technology, 203(20-21):3189–3196, 2009.
7.
A. V. Gusarov, M. Pavlov, and I. Smurov. Residual
Stresses at Laser Surface Remelting and Additive
Manufacturing. Physics Procedia, 12:248-254, 2011.
8.
A. V. Gusarov, I. S. Malakhova-Ziablova,
and M. D. Pavlov. Thermoelastic
Residual Stresses and Deformations at Laser Treatment. Physics Procedia,
41:896–903, 2013.
9. L.
Hua,W. Tian,W.
Liao, and C. Zeng. Numerical Simulation of Temperature Field
and Residual Stress Distribution for Laser Cladding Remanufacturing.
Advances in Mechanical Engineering, 6:id291615, 2014.
10. J.F.
Bell and C. Truesdell. Mechanics of
Solids: Volume I: The Experimental Foundations of Solid Mechanics. Springer Berlin Heidelberg, 1984.
11. TecPlot – CFD
Visualization & Analysis Software URL: https://www.tecplot.com/
12. A.
V. Koldoba, Yu. A. Poveshchenko,
I. V. Gasilova, and E. Yu. Dorofeeva. Numerical schemes
of the support operators method for elasticity theory
equations. Mathematical Modelling, 24:86–96, 2012.