Тема 3. Многомерная научная визуализация
- 3.1 О многомерных научных данных
- 3.2 Типовые задачи анализа многомерных научных данных
- 3.3 Визуальные методы
- 3.3.1 Метод лиц чернова
- 3.3.2 Метод главных компонент
- 3.3.3 Метод проекции отрезков
3.1. О многомерных научных данных
Под многомерными научными данными мы будем понимать данные об исследуемых объектах той или иной природы, которые исходно представлены (или могут быть представлены) в виде таблиц, строки которых соответствуют отдельным объектам, а элементы строк соответствуют числовым значениям признаков этих объектов. Причем число столбцов в рассматриваемой таблице n (количество признаков объектов) больше трех, а число строк m – произвольно. Такие многомерные данные встречаются при проведении как теоретических, так и экспериментальных исследований.
Не трудно видеть, что каждой j-ой строке такой таблицы может быть поставлена в соответствие точка 
в n-мерном евклидовом пространстве, где
координаты 
представляют собой числовые значения i-ых признаков
рассматриваемого j-ого объекта.
Например, многомерные данные могут получится в результате измерения векторного поля в различных точках. Подобные измерения дают нам тройки значений координат начальных точек векторов и тройки значений длин, составляющих вектора по трем осям. В результате получаются шестимерные данные.
3.2. Типовые задачи анализа многомерных научных данных
Существует несколько типовых задач анализа многомерных научных данных – задачи кластерного анализа, регрессионного анализа, корреляционного анализа и др. Примером таких задач, часто встречающимся на практике, является задача кластерного анализа. Рассмотрим эту задачу анализа многомерных научных данных.
Задача кластерного анализа заключается в разбиении исходного набора строк многомерных научных данных на непересекающиеся подмножества (кластеры) со схожими параметрами. Формально, эту задачу, используя упомянутую выше естественную геометризацию строк таблицы исходных научных данных, можно поставить следующим образом:
Дано:
Многомерный набор точек: 
Необходимо разбить исходное множество на непересекающиеся
группы 
, 
… 
, такие что расстояния между точками внутри каждой группы меньше
наперед заданного числа d, а расстояния между любыми
точками разных групп больше d.
Рис.3.1. Задача кластеризации.
Частным случаем кластерного анализа является задача поиска аномалий. Данная задача сконцентрирована на поиске единичных кластеров (кластеров мощностью 1), т.е. Точек многомерного пространства не похожих ни на одну другую точку.
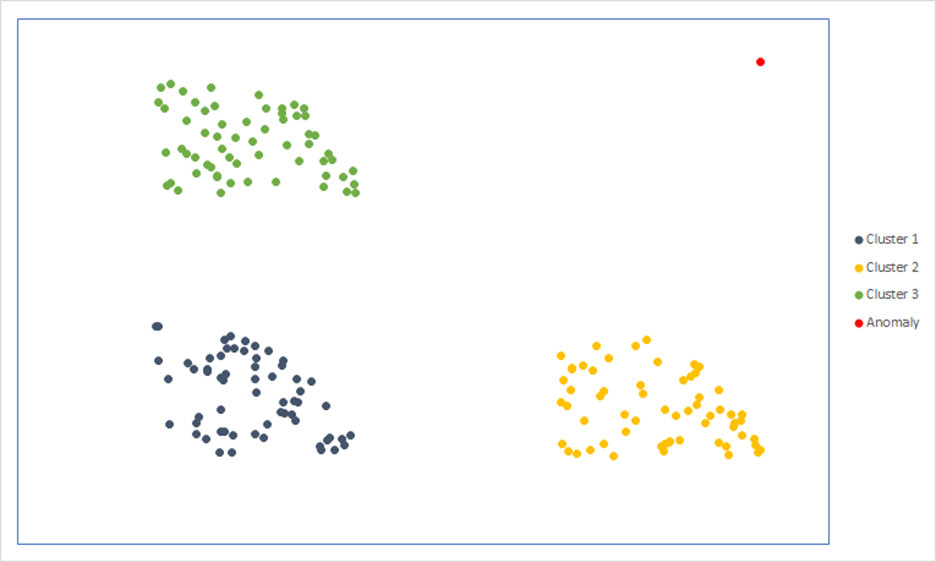
Рис.3.2. Задача поиска аномалий.
Рассмотрим визуальные методы решения задач кластерного анализа.
3.3. Визуальные методы
Визуальные методы для решения задач кластерного анализа основаны на отображении параметров объектов в виде удобном для зрительного восприятия человеком. Разбиение на кластеры выполняется непосредственно человеком, поэтому результаты могут отличаться при использовании данных методов разными аналитиками. Каждый из методов является частным случаем метода визуализации (рассмотренного в предыдущих главах) и описывает только часть шагов конвейера визуализации, которые характеризуют этот метод.
3.3.1. Метод лиц Чернова
Одним из ярких примеров визуальных методов решения задачи анализа является метод лиц Чернова.
Лица Чернова основаны на отображении совокупности признаков исходных объектов в виде лица человека, при этом признаки отображаются как формы и размеры отдельных черт лица (например, длина носа, угол между бровями и т.д.). Таким образом, метод лиц Чернова в конвейере визуализации определяет конкретный вид мэппинга. В силу особенности человеческого восприятия лица, данные черты бросаются в глаза, и группировка (кластеризация) выполняется на подсознательном уровне. [Низаметдинов Ш.У. “Анализ данных”, 248 с.]
Рис.3.3. Лица чернова
3.3.2. Метод главных компонент
С математической точки зрения метод главных компонент представляет собой ортогональное линейное преобразование, которое отображает данные из исходного пространство признаков в новое пространство меньшей размерности. При этом первая ось новой системы координат строится таким образом, чтобы дисперсия данных вдоль неё была бы максимальна. Вторая ось строится ортогонально первой так, чтобы дисперсия данных вдоль неё, была бы максимальной их оставшихся возможных и т.д. Первая ось называется первой главной компонентой, вторая - второй и т.д. [Низаметдинов Ш.У. “Анализ данных”, 248 с.] Данный метод определяет конкретный вид фильтрации данных конвейера визуализации.
Рис.3.4. Метод главных компонент
После перехода к новым осям, выполняется ортогональная проекция на часть осей. В случае, когда выполняется ортогональная проекция на трехмерное пространство, появляется возможность обычной трехмерной визуализации. Далее можно визуально выделить кластеры.
3.3.3. Метод проекции отрезков
В методе проекции отрезков используются дополнительные построения в исходном многомерном пространстве. Рассмотрим этот метод более подробно.
Задача кластерного анализа-одна из классических задач анализа данных. Как было сказано выше, постановка задачи кластерного анализа включает в себя следующее:
Дано: множество
точек 
, где 
Необходимо: разбить
множество 
таким образом, что:
В классической постановке задачи кластерного
анализа подмножество 
называется кластером и должно удовлетворять следующим свойствам
(при наперед заданной функции вычисления расстояния 
и максимальном внутрикластерном расстоянии d):
Рассмотрим расширенную постановку задачи кластерного анализа.
В зависимости от расстояния между точками и параметра d,
изменяемого во время анализа, можно визуально выделять следующие подмножества
многомерных точек:
- Кластер — классический кластер.
- Удаленная (аномальная) точка — точка
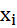является удаленной, если 
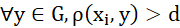. Можно сказать, что удаленная точка — это кластер мощностью 1. Однако,
данные точки могут представлять определенный интерес для аналитика. - Сгусток — подмножество точек, большая часть расстояний между которыми не превышает заданное d.
- Квазиудаленная точка — точка, не являющаяся удаленной, но и не входящая в кластер или сгусток при данном разбиении.
Отметим, что выделение сгустков и квазиудаленных точек осуществляется аналитиком в процессе решения указанной выше задачи анализа. Введенные понятия оказываются полезными аналитику в процессе решения задачи анализа геометрических интерпретаций исходных табличных данных.
Выделение сгустков и квазиудаленных точек позволяет аналитику в процессе изменения параметра d сконцентрировать внимание на данных объектах. Таким образом, если выделена квазиудаленная точка, то необходимо постепенно изменять значение d, чтобы узнать при каких условиях точка станет аномальной. При выделении сгустка, необходимо попробовать изменить d так, чтобы в результате данный сгусток преобразовался в кластер.
В процессе решения задачи аналитиком формируются суждения следующих типов:
- Точка
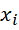относится к подмножеству
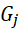при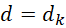 
- Подмножество 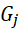является кластером
- Подмножество 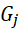является сгустком
- Точка 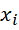является аномальной (удаленной) точкой
- Точка 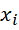является квазиудаленной точкой
Таким образом, решается задача разбиения многомерных геометрических интерпретаций исходных табличных данных на подмножества, в качестве которых могут выступать кластеры и удаленные точки, а также выделение вспомогательных в процессе решения этой задачи сгустков и квазиудаленных точек при изменении аналитиком максимального внутрикластерного расстояния d.
Описание общей идеи алгоритма
В рамках рассматриваемого метода проекции
отрезков предложен оригинальный алгоритм решения задачи визуализации. Основная
идея состоит в том, чтобы в исходном n-мерном пространстве 
провести дополнительное построение. Если расстояние между двумя
n-мерными точками ,
не превышает наперед заданное d (
),
то в исходном пространстве проводится отрезок между точками. Таким
образом, исходными анализируемыми данными являются 
многомерных точек и некоторое количество многомерных отрезков (в
зависимости от d). Затем осуществляется
проецирование исходного пространства на выбираемое аналитиком 3-х мерное
пространство 
.
Далее строится пространственная сцена по следующим правилам:
- точкам ставится в соответствии сфера с заданным радиусом;
- отрезкам ставятся в соответствие цилиндр с заданным радиусом.
При этом цвет сфер задается одинаковым, а цвет цилиндров зависит от расстояния в исходном пространстве. Чем меньше расстояние, тем более красным будет цилиндр между сферами. При задании сферы в палитре RGB, цвет будет задаваться следующим образом:
Задание различных цветов цилиндрам позволит аналитику делать суждения о расстоянии в исходном n-мерном пространстве при визуальном анализе пространственной сцены 3-х мерного пространства.
Как следует из сказанного выше, данный метод определяет конкретный вид мэппинга конвейера визуализации, включающий дополнительные построения в исходном многомерном пространстве.
Подробное описание алгоритма
Алгоритм решения задачи анализа взаимного расположения представлен следующими шагами:
Ввод исходных данных.
Выбор используемого расстояния.
Задание максимального внутрикластерного расстояния d просчет расстояний между каждой парой исходных точек в исходном пространстве.
Ввод параметров визуализации (радиусы сфер и
цилиндров, пространство для проекции).
Проецирование объектов исходного n-мерного пространства на 3-х мерное пространство.
Построение пространственной сцены сцена.
Пространственная сцена визуализируется и анализируется.
Если не вся необходимая информация получена, то необходимо вернутся к шагу 3.
Выполняется интерпретация полученных результатов анализа по отношению к исходным многомерным геометрическим данным.
Таким образом, алгоритм решения задачи является интерактивным и итеративным.