Тема 2. Инструментальные средства анализа данных методом визуализации

• 2.1 Общие характеристики инструментальных средств.
• 2.2 Программный продукт 3ds Max.
• 2.3 Программный продукт HyperFun.
• 2.4 Программный продукт VTK.

2.1 Общие характеристики инструментальных средств.

Как было указано в параграфе 1.2., процесс решения задачи анализа тех или иных данных методом визуализации включает в себя 2-а этапа. На первом этапе осуществляется разработка и реализация алгоритма визуализации исходных данных. Этот алгоритм реализуется с использованием компьютера.

Реализация осуществляется путем написания прикладной программы визуализации на некотором входном языке программирования используемого инструментального средства (совокупности средств) в виде некоторого программного продукта (совокупности программных продуктов). Соответственно в прикладной программе визуализации должны быть описаны используемые шаги конвейера визуализации (отметим, что в общем случае, в прикладной программе визуализации могут описываться не все шаги конвейера визуализации, подобные ситуации рассмотрены ниже при описании примеров инструментальных средств). Отметим также, что прикладная программа визуализации может быть непосредственно написана человеком, решающим задачу анализа данных, либо он использует «чужую», написанную ранее прикладную программу.

Общим для рассматриваемых инструментальных средств является то, что при их использовании они рассматриваются как совокупность некоторых программных функциональных процедур. Соответственно эти функциональные процедуры в общем случае можно подразделить на несколько групп:

1. функциональные процедуры задание исходных данных;
2. функциональные процедуры фильтрации;
3. функциональные процедуры мэппинга;
4. функциональные процедуры рендеринга.

Прикладная программа визуализации обрабатывается компьютером и инициирует выполнение этих функциональных процедур при реализации соответствующих шагов алгоритма визуализации. Результаты выполнения функциональных процедур доступны прикладной программе визуализации для последующего использования (рис.2.1).

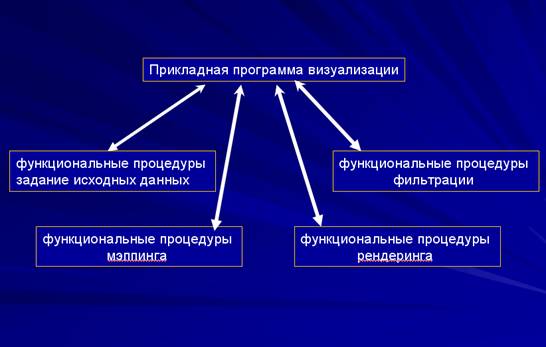
Рис. 2.1

Результатом выполнения функциональных процедур 1-й группы является представление исходных данных в памяти компьютера (компьютерная модель этих данных).

Результатом выполнения функциональных процедур 2-й группы является компьютерная модель отфильтрованных данных.

Результатом выполнения функциональных процедур 3-й группы является компьютерная модель пространственной сцены.

Результатом выполнения функциональных процедур 4-й группы является проекционное графического изображение на используемом графическом терминале.

Вид компьютерных моделей, являющихся результатом выполнения соответствующих функциональных процедур, зависит от используемого инструментального средства.

Отметим, что то или иное инструментальное средство визуализации может располагать не всем набором функциональных процедур. При отсутствии необходимой функциональной процедуры, эта функциональная процедура описывается человеком в теле прикладной программы визуализации.

Рассмотрим примеры программных продуктов, которые могут быть использованы в качестве инструментальных средств (причем как автономно, так и совместно) для решения прикладных задач анализа данных методом визуализации.

2.2 Программный продукт 3ds Max

3ds Max — широко известный программный продукт, обладающий развитыми функциональными возможностями для моделирования и визуализации произвольных сложных пространственных сцен, которые могут быть использованы при написании сложных прикладных программ визуализации.

Разработка 3ds Max (тогда этот программный продукт назывался 3d Studio Max) была начата в 1993 году, когда входящей в состав компании Autodesk группе Kinetix поручили создать новый продукт на базе пакета 3d Studio для MS DOS. Главными особенностями программного продукта должны были стать: графический интерфейс, объектно-ориентированная архитектура и полная поддержка системой Windows.

Структура 1-й версии программного продукта, вышедшая в 1995 году, подразумевала, что любая функциональная процедура, задаваемая человеком, может быть выполнена дополнительным модулем (плагин). Следует отметить, что основные концепции программного продукта, в том числе объектно-ориентированная архитектура и «мертвая» привязка к платформе Windows актуальна и по сей день. Название программного продукта менялось, в настоящее время он называется 3ds Max.

Рассмотрим основные характеристики функциональных процедур 3ds Max, используемого в качестве инструментального средства при написании прикладных программ визуализации. В начале, рассмотрим основные характеристики входного языка программирования 3ds Max - языка MaxScript, используемого для написания прикладной программы визуализации.

Программирование на языке MaxScript

Язык Maxscript - язык программирования, созданный специально для работы в среде 3ds Max. Данный язык имеет простую структуру и синтаксис, он является языком интерпретируемого типа (программа на этом языке не требует компиляции и сборки исходного кода, а может выполняться сразу в режиме интерпретации). Программа на языке MaxScript представляет собой последовательность операторов. Можно выделить следующие типы операторов:

1. арифметические операторы
2. логические операторы
3. условные операторы
4. циклические операторы
5. операторы функций

При написании прикладной программы визуализации для инициации (вызова) той или иной функциональной процедуры используется синтаксическая конструкция в виде одного или нескольких операторов функции. Эта синтаксическая конструкция одного оператора в общем случае имеет вид:

1-й вариант: <название функции> _ <параметр 1>_ <параметр 2>_..._<параметр n>

2-й вариант: <название функции> _ <ключевое слово 1>:<параметр 1>_ <ключевое слово 2>:<параметр 2>_..._<ключевое слово n>:<параметр n>

В 1-м варианте порядок перечисления параметров важен, во 2-м варианте параметры перечисляются в произвольном порядке

Значения параметров текущей выполняемой функциональной процедуры в прикладной программе визуализации определенным образом связываются с результатом выполнения предыдущей функциональной процедуры.

Параметры могут представлять собой:

• Числовые значения
• Символьные значения
• Сложные типы данных MaxScript

Рассмотрим примеры использования этой синтаксической конструкции для вызова функциональных процедур. Начнем с рассмотрения функциональных процедур задания исходных данных.

Функциональные процедуры задания исходных данных

При использовании языка MaxScript функциональными процедурами задания исходных данных в 3ds Max являются процедуры открытия файла, чтения данных из файла, закрытия файла. Вызов функциональной процедуры осуществляется с помощью соответствующего оператора функции. В качестве таких операторов могут использоваться операторы:

openFile_”<наименование файла>” - оператор открытия текстового файла.

<readValue>_<наименования переменной – указателя на файл> - оператор чтения значения из файла.

<close>_<наименования переменной – указателя на файл> - оператор закрытия файла.

Пример 2.1.

Пусть в файле c:\\textfile.txt хранятся в виде данных численные значения координат десяти пространственных точек ( X Y Z). Задание исходных данных в этом случае будет состоять в открытие этого файла, считывании из него числовых значений координат точек и занесении их в массивы чисел ArrayX, ArrayY, ArrayZ . Приведем в качестве примера фрагмент прикладной программы визуализации.

…………………….

fs=openFile ”c:\\textfile.txt” --- открытие файла с именем ”c:\\textfile.txt” , и присвоение переменной fs значения указателя на данный файл . Здесь в качестве параметра функции используется символьное значение ”c:\\textfile.txt” .

ArrayX = # ()

ArrayY = # ()

ArrayZ = # ()

for i = 1 to 10 do ----- оператор цикла,

( ----- где значение переменной i изменяется от 1 до 10

x = readValue fs ------ считывание текущего значения координаты x из файла

y = readValue fs ------ считывание текущего значения координаты y из файла

z = readValue fs ------ считывание текущего значения координаты z из файла

append ArrayX x ------ занесение текущего значения переменной x в массив ArrayX

append ArrayY y ------ занесение текущего значения переменной y в массив ArrayY

append ArrayZ z ------ занесение текущего значения переменной z в массив ArrayZ

)

close fs --- закрытие файла

……….

Функциональные процедуры фильтрации данных

В программном продукте 3ds Max отсутствуют программные средства которые можно было бы использовать в качестве программных функциональных процедур фильтрации. Поэтому эти функциональные процедуры необходимо включать в тело прикладной программы визуализации, написанной на языке MaxScript. Для этого могут быть использованы различные типы операторов MaxScript, упомянутые выше.

Пример 2.2

Будем рассматривать в качестве исходных данных численные значения координат десяти пространственных точек из предыдущего примера. Пусть фильтрация исходных данных состоит в том, чтобы из числа исходных 10-ти точек нужно для последующей визуализации отобрать только те из них, которые лежат внутри куба. Грани этого куба параллельны координатным плоскостям, координаты левого нижнего угла (-5,-5,-5), координаты правого верхнего (5,5,5). Отфильтрованные данные заносятся в массивы ArrayX2, ArrayY2, ArrayZ2 соответственно. Фрагмент прикладной программы визуализации, описывающий функциональную процедуру фильтрации, будет иметь следующий вид:

……….

ArrayX2 = # ()

ArrayY2 = # ()

ArrayZ2 = # ()

for i = 1 to 10 do ----- оператор цикла,

( ----- где значение переменной i изменяется от 1 до 10

x = ArrayX [i] ------ присвоение переменной x значения текущего элемента массива

y = ArrayY [i] ------ присвоение переменной y значения текущего элемента массива z = ArrayZ [i] ------ присвоение переменной z значения текущего элемента массива

if (x > -5 and x < 5 and y > -5 and y< 5 and z > -5 and z < 5) --- оператор условия

--- проверка нахождения точки

--- внутри куба

then

(

append ArrayX2 x ------ занесение выбранного значения переменной x в массив

append ArrayY2 y ------ занесение выбранного значения переменной y в массив

append ArrayZ2 z ----- занесение выбранного значения переменной z в массив

)

)

……….

Следует отметить, что необязательно размещение функциональной процедуры фильтрации в теле прикладной программы (как мы это сделали в рассмотренном примере). Данная процедура может быть размещена в теле оператора функции и вызываться из прикладной программы визуализации с помощью этого оператора функции. Это замечание справедливо не только в отношении функциональных процедур фильтрации, но и любых других нештатных функциональных процедур, определяемых человеком.

Функциональные процедуры мэппинга

Отличительной чертой 3ds Max является богатый набор штатных функциональных процедур мэппинга. Напомним, что под функциональными процедурами мэппинга (как указывалось ранее, мы рассматриваем 3d мэппинг) понимаются процедуры формирования компьютерных представлений описаний пространственных сцен, которое включает в себя описание геометрии (геометрической модели) этой сцены и описание ее графических характеристик (текстуры).

Выше было отмечено, что геометрическая модель пространственной сцены представляет собой совокупность пространственных геометрических примитивов или/и сложных геометрических объектов (являющихся результатом выполнения некоторых геометрических операций над пространственными геометрическими примитивами или другими сложными объектами). В качестве таких геометрических примитивов в 3ds Max могут использоваться:

• cфера
• конус
• цилиндр
• параллелепипед
• тор
• пирамида
• призма
• многогранник
• отсек поверхности
• NURBS-поверхность
• поверхность Безье

Из этих примитивов можно формировать сложные пространственные геометрические объекты, которые, в свою очередь, могут использоваться как операнды других геометрических операций. В качестве таких геометрических операций в 3ds Max могут использоваться:

• сдвиг
• поворот
• масштабирование
• теоретико-множественное объединение
• теоретико-множественное пересечение
• теоретико-множественное вычитание
• лофтинг
• морфинг
• изгиб
• шум
• сглаживание
• сжатие
• растяжение
• скручивание
• скос

Для задания графических характеристик пространственной сцены в 3ds Max предоставляется возможность использовать обширную библиотеку различных текстур. Помимо этого с помощью программного средства «Редактор материалов» можно создавать и использовать нештатные текстуры.

Как было отмечено выше, вызов функциональных процедур из прикладной программы визуализации на языке MaxScript осуществляется с помощью операторов функций. Это справедливо и для мэппинга. Приведем примеры операторов функций, используемых для обращения к функциональным процедурам мэппинга. Напомним, что значения параметров в этих операторах функций в прикладной программе визуализации определенным образом связываются с ранее отфильтрованными данными.

Пример 2.3

<box> _height: <числовое значение> _ width: < числовое значение > _ length: < числовое значение > _ pos: [< числовое значение >,_ < числовое значение >_ < числовое значение >]

Эта функциональная процедура ставит в соответствие отфильтрованным данным компьютерное представление геометрической модели пространственной сцены в виде параллелепипеда (box). Задаваемые параметры:

height – высота параллелепипеда

width – ширина параллелепипеда

length – длина параллелепипеда

pos – координаты центра параллелепипеда

В прикладной программе значения этих параметров связываются определенным образом (так как это задано человеком) с отфильтрованными данными.

Пример 2.4

<sphere> _radius: <числовое значение> _ pos: [< числовое значение >,_ < числовое значение >_ < числовое значение >]

Эта функциональная процедура аналогична предыдущей. Она ставит в соответствие отфильтрованным данным компьютерное представление геометрической модели пространственной сцены в виде cферы (sphere). Задаваемые параметры:

radius – радиус сферы

pos – координаты центра сферы

Как и в предыдущем примере, значения этих параметров в прикладной программе визуализации связываются определенным образом (так как это задано человеком) с отфильтрованными данными.

Пример 2.5

<move> <указатель на геометрический объект – операнд операции> _[<числовое значение>, числовое значение >, числовое значение >]

Эта функциональная процедура ставит в соответствие ранее созданному геометрическому объекту компьютерное представление геометрической модели пространственной сцены в виде сдвинутого геометрического объекта. Задаваемые параметры:

1-е числовое значение - величина сдвига по оси x

2-е числовое значение - величина сдвига по оси y

3-е числовое значение - величина сдвига по оси z

Пример 2.6

<boolObj.createBooleanObject>_ <указатель на геометрический объект – 1-й операнд операции> <boolObj.SetOperandB> _<указатель на геометрический объект – 1-й операнд операции> _ <указатель на геометрический объект – 2-й операнд операции >_ 1

Эта функциональная процедура ставит в соответствие двум ранее созданным геометрическим объектам компьютерное представление геометрической модели пространственной сцены в виде сложного геометрического объекта, являющегося результатом теоретико-множественного объединения этих объектов.

Инициация этой функциональной процедуры осуществляется с помощью двух операторов функций. 1-й оператор служит для задания 1-го операнда теоретико-множественной операции объединения (эта операция является двуместной). 2-й оператор служит для задания 2-го операнда теоретико-множественной операции объединения. В качестве операндов здесь могли бы выступать, например, ранее созданные сфера и параллелепипед. Здесь «1» - идентификатор теоретико-множественной операции объединения.

Пример 2.7

Рассмотрим фрагмент прикладной программы визуализации, в котором отфильтрованным исходным данным из примера 2.2 ставится в соответствие компьютерное представление геометрической модели пространственной сцены в виде совокупности cфер.

……….

for i = 1 to ArrayX2.count do ----- оператор цикла,

( ----- где значение переменной i изменяется от 1 до

----- числа элементов массива ArrayX2 (т.е. числа точек,

----- отобранных на шаге фильтрации)

x = ArrayX2 [i] -- присвоение переменной x значения текущего элемента массива

y = ArrayY2 [i] -- присвоение переменной y значения текущего элемента массива

z = ArrayZ2 [i] ---присвоение переменной z значения текущего элемента массива

Sphere radius:0.4 pos: [x,y,z] --- создание сферы с выбранным радиусом 0.4 и

--- с центров в точке с координатами x,y,z

)

--- по завершению цикла создается соответствующее

--- размерности массива ArrayX2

--- количество сфер с именами Sphere01, Sphere02…,

--- задаваемыми по умолчанию

……….

Выше мы рассмотрели характеристики и примеры инициации функциональных процедур мэппинга, служащих для задания геометрической модели сцены. Следует отметить, что при создании геометрической модели, графические характеристики создаваемого объекта в 3ds Max, а именно цвет, задаются по умолчанию, если они не определены с помощью соответствующих функциональных процедур мэппинга. Перейдем к функциональной процедуре мэппинга, с помощью которой можно задавать графические характеристики, а именно, текстуру.

Пример 2.8

<Standard> ambient: [<числовое значение>, <числовое значение>, <числовое значение>] wire: <логическое значение> faceted: <логическое значение> opacity: <числовое значение>

Эта функциональная процедура служит для задания компьютерного представления 2-й составляющей описания (модели) пространственной сцены - текстуры. Задаваемые параметры:

аmbient –цвет покрытия

wire – наличие/отсутствие решетчатой текстуры

faceted – наличие/отсутствие ребристой текстуры

opacity – процент прозрачности

В прикладной программе визуализации значения перечисленных параметров могут задаваться произвольно, либо они связываются определенным образом (так как это нужно человеку) с отфильтрованными данными.

Пример 2.9

Рассмотрим фрагмент прикладной программы визуализации, в котором задается компьютерное представление текстурного покрытия cфер из примера 2.7.

……….

select $Sphere* -- вспомогательная операция выделения всех сфер из примера 2.7

-- (после этого над ними могут выполняться те или иные операции)

ArraySphere = for b in $* collect ( b ) --- оператор цикла, в теле которого из ранее

--- выделенных сфер формируется

--- массив сфер ArraySphere

---вспомогательной переменной b в цикле

-- присваивается в качестве значения текущая

-- сфера

for i = 1 to ArraySphere.count do ----- оператор цикла,

( ----- где значение переменной i изменяется от 1 до

----- числа элементов массива ArraySphere

----- (т.е. числа сфер)

ArraySphere[i].material = standard ambient: [150, 250, 150] wire: false faceted: true

opacity: 50 ---- создание полупрозрачной ребристой текстуры салатового цвета

)

……….

Отметим, что помимо рассмотренной функциональной процедуры задания текстуры в программном продукте 3ds Max предусмотрены также другие функциональные процедуры аналогичного назначения.

Отметим также, что в 3ds Max предусмотрена программные средства для быстрого и несложного создания нештатных функциональных процедур мэппинга в виде плагинов 3ds Max.

Функциональные процедуры рендеринга

Напомним, что функциональные процедуры рендеринга ставят в соответствие компьютерному представлению описания (модели) пространственной сцены ее проекционное графическое изображение на используемом графическом терминале.

Рендеринг имеет ряд параметров (здесь, как было оговорено ранее, имеется в виду 3D рендеринг), в частности, к ним относятся - камера, источники освещения и среда. Рассмотрим примеры функциональных процедур задания этих параметров.

Пример 2.10

<targetCamera>_<pos>: [<числовое значение>,< числовое значение >, < числовое значение >] _ <target>:(<targetObject> _<pos>:[<числовое значение>,< числовое значение >,< числовое значение >])_<fov>: < числовое значение >

Результатом выполнения данной функциональной процедуры будет создание компьютерного представлений направленной камеры (камера направлена на цель (target)). Задаваемые параметры:

pos – координаты камеры в пространстве

target – объект-цель (в виде точки), на который будет направлена камера, задается с помощью параметра pos – координаты объекта-цели камеры в пространстве

fov – поле зрения камеры (величина обратная фокусному расстоянию камеры)

Пример 2.11

<Omnilight>_<rgb>:(<color> [<числовое значение>,< числовое значение >, < числовое значение >)_<shadowColor>:(<color> <числовое значение>,< числовое значение >, < числовое значение >)_<pos>: [<числовое значение>,< числовое значение >, < числовое значение >]

Результатом выполнения данной функциональной процедуры будет создание компьютерного представления точечного источника света, излучающего свет во все стороны. Задаваемые параметры:

rgb – цветовая окраска света, излучаемого источником освещения

shadowColor – цветовая окраска тени, отбрасываемой объектами, освещенными данным источником освещения

pos – координаты источника освещения в пространстве

Пример 2.12

<addAtmospheric> _(<Fog>_<Fog_Color>:_(<color> <числовое значение>_< числовое значение >_< числовое значение>)_<Density>:< числовое значение>)

Результатом выполнения данной функциональной процедуры будет создание компьютерного представления среды типа «туман». Задаваемые параметры:

Color – цвет тумана

Density – плотность тумана

Вызов самой функциональной процедуры рендеринга, также как и вызов рассмотренных процедур задания параметров рендеринга, осуществляется с помощью оператора функции.

Пример 2.13

<render>_<camera>:<указатель на камеру>_ <outputwidth>: <числовое значение> _< outputheight>: <числовое значение> _ < outputfile>: <"название файла">

Результатом выполнения данной функциональной процедуры будет статическое проекционное графическое изображение текущей (сформированной к данному моменту времени) сцены на графическом терминале, в качестве которого в 3ds Max используется монитор. Одновременно компьютерное представление проекционного графического изображения сцены сохраняется в файл. Задаваемые параметры:

camera – камера, с помощью которой будет осуществляться рендеринг

outputwidth – ширина получаемого графического проекционного изображения в пикселях

outputheight – высота получаемого графического проекционного изображения в пикселях

outputfile – название файла, в котором будет сохранен результат рендеринга (необязательный параметр)

Результатом рендеринга может быть также и анимационное (динамическое, зависящее от времени) проекционное графическое изображение, которое представляет собой соответствующую временную последовательность статических проекционных графических изображений рассматриваемой сцены. Так, например, если каждое такое статическое проекционное изображение получено с помощью перемещающейся в пространстве камеры (т.е. камера, как параметр рендеринга, задана для ряда фиксированных значений времени), то результатом такой «фотосъемки» будет анимационное проекционное графическое изображение (упорядоченная совокупность соответствующих статических проекционных графических изображений).

Пример. 2.14

Рассмотрим фрагмент прикладной программы визуализации, содержащий вызов функциональных процедур рендеринга для создания анимационного проекционного графического изображения.

……….

c = targetCamera pos:[10,0,0] target:(targetObject pos:[0, 0, 0]) fov: 45

set animate on

at time ti move c [10,0,0] ---- расположение камеры в выбранный начальный дискретный

---- момент времени (ti=i*dt) в точке с

---- координатами 10,0,0

at time tj move c [20,0,0] ---- расположение камеры в выбранный конечный дискретный

---- момент времени (tj=j*dt) в точке с

---- координатами 20,0,0

……….

Здесь показано обращение к функциональной процедуре задания компьютерного представления камеры, меняющейся во времени. Отметим, что в общем случае таких моментов времени может быть несколько, более чем 2 в рассмотренном примере.

Следует отметить, что в общем случае анимационное проекционное графическое изображение может быть получено в результате задания аналогичным образом любого параметра рендеринга для ряда фиксированных значений времени. Анимационное проекционное графическое изображение может быть также получено, если задано описание динамической пространственной сцены (т.е. если заданы соответствующие описания статических пространственных сцен для ряда фиксированных значений времени в рамках процедуры мэппинга).

Получить такое анимационное проекционное графическое изображение сцены можно с помощью вызова ранее рассмотренной функциональной процедуры:

<render>_<camera>:<указатель на камеру>_<fromframe>: <числовое значение>_<toframe>: <числовое значение>_ <outputwidth>: <числовое значение> _< outputheight>: <числовое значение> _ < outputfile>: <"название файла">

Здесь дополнительно задаются параметры:

fromframe – задаваемый номер k начального проекционного графического изображения , соответствующего моменту времени tk=k*dt, k>=i.

toframe – задаваемый номер l конечного проекционного графического изображения , соответствующего моменту времени tl=l*dt, l>=j.

Т.е. в процессе выполнения этой функциональной процедуры на графическом терминале последовательно воспроизводятся статические проекционные графические изображения с номерами, изменяющимися от k до l из числа сформированных статических проекционных графических изображений с номерами от i до j.

Приведем пример прикладной программы визуализации исходных данных из примера 2.1. Результатом работы этой программы будет статическое проекционное графическое изображение пространственной сцены, получаемое в результате мэппинга, описанного в примере 2.7.

Фрагменты этой программы, соответствующие вызовам функциональных процедур задания исходных данных, фильтрации и мэппинга, были приведены выше в примерах 2.1, 2.2, 2.7

Пример 2.15

Задание исходных данных		fs=openFile ”c:\\textfile.txt” --- открытие файла с именем ”c:\\textfile.txt” , и присвоение переменной fs значения указателя на данный файл . Здесь в качестве параметра функции используется символьное значение ”c:\\textfile.txt” . ArrayX = # () ArrayY = # () ArrayZ = # () for i = 1 to 10 do ----- оператор цикла, ( ----- где значение переменной i изменяется от 1 до 10 x = readValue fs ------ считывание текущего значения координаты x из файла y = readValue fs ------ считывание текущего значения координаты y из файла z = readValue fs ------ считывание текущего значения координаты z из файла append ArrayX x ------ занесение текущего значения переменной x в массив ArrayX append ArrayY y ------ занесение текущего значения переменной y в массив ArrayY append ArrayZ z ------ занесение текущего значения переменной z в массив ArrayZ ) close fs --- закрытие файла
Фильтрация исходных данных		ArrayX2 = # () ArrayY2 = # () ArrayZ2 = # () for i = 1 to 10 do ----- оператор цикла, ( ----- где значение переменной i изменяется от 1 до 10 x = ArrayX [i] ------ присвоение переменной x значения текущего элемента массива y = ArrayY [i] ------ присвоение переменной y значения текущего элемента массива z = ArrayZ [i] ------ присвоение переменной z значения текущего элемента массива if (x > -5 and x < 5 and y > -5 and y< 5 and z > -5 and z < 5) --- оператор условия --- проверка нахождения точки --- внутри куба then ( append ArrayX2 x ------ занесение выбранного значения переменной x в массив append ArrayY2 y ------ занесение выбранного значения переменной y в массив append ArrayZ2 z ----- занесение выбранного значения переменной z в массив ) )
Мэппинг отфильтрованных данных		for i = 1 to ArrayX2.count do ----- оператор цикла, ( ----- где значение переменной i изменяется от 1 до ----- числа элементов массива ArrayX2 (т.е. числа точек, ----- отобранных на шаге фильтрации) x = ArrayX2 [i] -- присвоение переменной x значения текущего элемента массива y = ArrayY2 [i] -- присвоение переменной y значения текущего элемента массива z = ArrayZ2 [i] ---присвоение переменной z значения текущего элемента массива Sphere radius:0.4 pos: [x,y,z] --- создание сферы с выбранным радиусом 0.4 и --- с центров в точке с координатами x,y,z ) --- по завершению цикла создается соответствующее --- размерности массива ArrayX2 --- количество сфер с именами Sphere01, Sphere02…, --- задаваемыми по умолчанию
Рендеринг		c = targetCamera pos:[10,0,0] target:(targetObject pos:[0, 0, 0]) fov: 45 render camera:c

При заданных в файле textfile.txt исходных данных

0 0 0

1 3 0

2 2 0

3 3 0

0 4 0

5 3 0

1 7 0

1 0 2

0 1 0

0 -1 0

получим проекционное графическое изображение, представленное на Рис.2.3

Рис.2.3

Анализ этого изображения позволяет предварительно выделить 2 кластера пространственных точек, координаты которых лежат в диапазоне от -5 до 5, заданного в прикладной программе (исходное количество точек равнялось 10).

Следует отметить, что в 3ds Max функциональные процедуры рендеринга доступны не только из прикладной программы. Так, например, человек может модифицировать полученное проекционное графическое изображение сцены, описанной в прикладной программе, в интерактивном режиме с использованием языка диалога 3ds Max.

Заканчивая рассмотрение использования программного средства 3ds Max в качестве инструментального средства для решения прикладных задач анализа данных методом визуализации, отметим, что более подробное описание 3ds Max можно найти, например, в учебнике «Основы 3ds Max 8. MaxScript».

2.3 Программный продукт HyperFun

HyperFun является открытым программным продуктом, разрабатываемым в рамках одноименного проекта. Это программный продукт обладает широкими функциональными возможностями для моделирования и визуализации пространственных объектов, которые могут быть использованы в различных приложениях.

Проект HyperFun является международным. Участниками этого проекта являются ученые и студенты из различных стран (Великобритания, США, Россия, Франция, Япония, Норвегия и др.). В декабре 2009 года проект HyperFun «отметил» 10-летие своего существования.

Отметим, что в HyperFun для определения геометрических объектов служит описывающая функция этих объектов f(x,y,z). Под описывающей функцией понимается функция, используемая в неравенстве рассматриваемой фигуры: f(x,y,z)>=0 (смысл этого неравенства заключается в том, что оно истинно только для координат тех и только тех точек, которые принадлежат этой фигуре).

Рассмотрим основные характеристики функциональных процедур программного продукта HyperFun, используемого в качестве инструментального средства при написании прикладных программ визуализации. В начале, рассмотрим основные характеристики входного языка программирования этого программного продукта HyperFun – языка HyperFun, используемого для написания прикладной программы визуализации.

Программирование на языке HyperFun

Язык HyperFun является простым языком программирования, созданным специально для работы в среде HyperFun. Данный язык, как и рассмотренный выше язык maxScript, имеет простую структуру и синтаксис, он является языком интерпретируемого типа. Программа на языке HyperFun представляет собой последовательность операторов. Можно выделить следующие типы операторов:

1. арифметические операторы
2. логические операторы
3. условные операторы
4. циклические операторы
5. операторы функций

При написании прикладной программы визуализации для инициации (вызова) той или иной функциональной процедуры используется, в основном, синтаксическая конструкция в виде одного или нескольких операторов функции:

Общий вид оператора функции:

<название функции> (<параметр 1>, <параметр 2>,...,<параметр n>)

Значения параметров текущей выполняемой функциональной процедуры в прикладной программе визуализации определенным образом связываются с результатом выполнения предыдущей функциональной процедуры.

Параметры могут представлять собой:

• Числовые значения
• Символьные значения

Вся прикладная программа визуализации на HyperFun должна начинаться с синтаксической конструкции my_model(x[3], a[1], s[3]){, и заканчиваться конструкцией my_model = y ;}. Здесь x[3] – массив входных переменных описывающей функции (в обем случае, размерность может быть больше трех). a[1] – параметр описывающей функции (или массив параметров, например, a[7]). s[3] – массив атрибутов. Эти атрибуты, как правило, используются для задания цвета моделируемого пространственного объекта. y – выходная переменная этой функции.

Рассмотрим примеры использования различных функциональных процедур. Начнем с рассмотрения функциональных процедур задания исходных данных.

Функциональные процедуры задания исходных данных

При использовании языка HyperFun функциональными процедурами задания исходных данных в 3ds Max являются процедуры открытия файла, чтения данных из файла, закрытия файла. Эти процедуры являются нештатными процедурами расширения HyperFun, используемые для написания прикладных программ визуализации. Вызов функциональной процедуры осуществляется с помощью соответствующего оператора функции. В качестве таких операторов могут использоваться операторы:

openfile("r"/"w","<наименование файла>")	– оператор открытия текстового файла (r – чтения из файла, w – запись в файл)
readfile(n,"<наименование файла>")	– чтение значения из файла (n – номер позиции значения)
rfile("<наименование файла>")	– чтение значения из файла
reservefile(n,"<наименование файла>")	– резервирование памяти для считывания значений из файла (n – количество значений, которые будут считаны из файла)
closefile("<наименование файла>")	– оператор закрытия текстового файла

Пример 2.16.

Пусть в файле «textfile.txt» хранятся в виде данных численные значения координат шести пространственных точек ( X Y Z). Задание исходных данных в этом случае будет состоять в открытии этого файла, считывании из него числовых значений координат точек и занесении их в массивы чисел «x0», «y0», «z0» . Рассмотрим фрагмент программы, осуществляющий задание исходных данных.

………………

array x0[10], y0[10], z0[10]; - - массивы исходных данных

fs = openfile("r","1.txt") ; - - открытие файла с именем «textfile.txt», присвоение переменной fs значения либо 0, либо 1 в случае удачного или неудачного открытия файла. Здесь в качестве параметра функции используется символьное значение "1.txt". 

r=reservefile(30,"1.txt") ; - - резервирование в памяти места для считывания 30 значений

i = 1;

while (i < 11) loop - - оператор цикла считывания данных из файла, где значение i изменяется от 1 до 10

x0[i] = rfile("1.txt"); - - считывание и занесение текущего значения переменной x в массив x0 из файла

y0[i] = rfile("1.txt"); - - считывание и занесение текущего значения переменной y в массив y0 из файла

z0[i] = rfile("1.txt"); - - считывание и занесение текущего значения переменной z в массив z0 из файла

i = i+1;

endloop; - - окончание цикла

fs = closefile("1.txt"); - - закрытие файла

……………………

Функциональные процедуры фильтрации данных

В программном продукте HyperFun, также как и в 3ds Max, отсутствуют программные средства, которые можно использовать в качестве программных функциональных процедур фильтрации. Эти функциональные процедуры надо описывать в теле программы, используя существующие возможности на языке HyperFun. Для этого могут быть использованы различные типы операторов MaxScript, упомянутые выше.

Пример 2.17

Будем рассматривать в качестве исходных данных численные значения координат десяти пространственных точек из предыдущего примера. Пусть фильтрация исходных данных состоит в том, чтобы из числа исходных 10-ти точек нужно для последующей визуализации отобрать только те из них, которые лежат внутри куба. Грани этого куба параллельны координатным плоскостям, координаты левого нижнего угла (-5,-5,-5), координаты правого верхнего (5,5,5). Отфильтрованные данные заносятся в массивы x2, y2, z2 соответственно. Фрагмент прикладной программы визуализации, описывающий функциональную процедуру фильтрации, будет иметь следующий вид:

……………………………

array x2[10], y2[10], z2[10]; - - массив значений отфильтрованных точек

……………………………

i=1;

numsp=1; - - переменная, задающая количество отфильрованных точек

while (i < 11) loop - - оператор цикла, где значение переменной i меняется от 1 до 10

if ((x0[i] >-5) and (x0[i]<5) and (y0[i]>-5) and (y0[i]<5) and (z0[i]<5) and (z0[i]>-5)) then

- - оператор условия, проверка нахождения точки внутри куба

x2[numsp] = x0[i]; - - занесение выбранного значения переменной x в массив

y2[numsp] = y0[i]; - - занесение выбранного значения переменной y в массив

z2[numsp] = z0[i]; - - занесение выбранного значения переменной z в массив

numsp=numsp+1;p>

endif; - окончание оператора условия

i=i+1;

endloop; - окончание цикла

……………..

Следует отметить, что, также как и в 3ds Max, необязательно размещение функциональной процедуры фильтрации в теле прикладной программы (как мы это сделали в рассмотренном примере). Из прикладной программы визуализации могут вызываться с помощью оператора функции также и нештатные процедуры фильтрации. Это замечание справедливо не только в отношении функциональных процедур фильтрации, но и любых других нештатных функциональных процедур, определяемых человеком.

Функциональные процедуры мэппинга

HyperFun, также как и MaxScript, обладает богатым набором функциональных процедур мэппинга. Как упоминалось выше, под функциональными процедурами мэппинга (как указывалось ранее, мы рассматриваем 3d мэппинг) понимаются процедуры формирования компьютерных представлений описаний пространственных сцен, которое включает в себя описание геометрии (геометрической модели) этой сцены и описание ее графических характеристик (текстуры).

Геометрическая модель пространственной сцены представляет собой совокупность пространственных геометрических примитивов или/и сложных геометрических объектов (являющихся результатом выполнения некоторых геометрических операций над пространственными геометрическими примитивами или другими сложными объектами). В качестве таких геометрических примитивов в HyperFun могут использоваться:

• cфера
• эллипсоид
• цилиндр
• эллиптический цилиндр
• конус
• эллиптический конус
• тор
• суперэллипсоид
• параллелепипед
• конволюционная поверхность на основе треугольников
• конволюционная поверхность на основе каркасных отрезков линии
• блобби
• метабол
• и др.

Из этих примитивов можно формировать сложные пространственные геометрические объекты, которые, в свою очередь, могут использоваться как операнды других геометрических операций. В качестве таких геометрических операций в HyperFun могут использоваться:

• сдвиг
• поворот
• масштабирование
• скручивание
• растяжение
• кубическое отображение
• сглаживающее объединение
• сглаживающее пересечение
• теоретико-множественное объединение
• теоретико-множественное пересечение
• теоретико-множественное вычитание
• и др.

Как было отмечено выше, вызов функциональных процедур из прикладной программы визуализации на языке HyperFun осуществляется в основном с помощью операторов функций. Это справедливо и для мэппинга. Приведем примеры операторов функций, используемых для обращения к функциональным процедурам мэппинга. Напомним, что значения параметров в этих операторах функций в прикладной программе визуализации определенным образом связываются с ранее отфильтрованными данными.

Пример 2.18

 

Оператор функции «сфера»:

 

hfSphere(x,center,R);

 

Эта функциональная процедура ставит в соответствие отфильтрованным данным компьютерное представление геометрической модели пространственной сцены в виде сферы. Задаваемые параметры:

x – массив входных переменных x,y,z описывающей функции f(x,y,z)

сenter – массив координат центра сферы

R – радиус сферы

Для сферы описывающая функция имеет вид:

f(x,y,z) = R^2 – (x – center[1])^2 + (y – center[2])^2+(z – center[3])^2

Нетрудно видеть, что величины center[1], center[2], center[3] и R по отношению к описывающей функции f(x,y,z) являются ее параметрами.

Следует отметить, что задание сферы может осуществляться также с помощью следующей синтаксической конструкции:

 

Sphere = R^2 – (x – center[1])^2 + (y – center[2])^2+(z – center[3])^2 ;

 

Это замечание справедливо для задания любого примитива в HyperFun.

 

 

Пример 2.19

 

Оператор функции «эллипсоид»:

 

hfEllipsoid(x,center,a,b,c);

Эта функциональная процедура ставит в соответствие отфильтрованным данным компьютерное представление модели пространственной сцены в виде эллипсоида. Задаваемые параметры:

x – массив входных переменных x,y,z описывающей функции f(x,y,z)

сenter – массив координаты центра эллипсоида

a,b,c – полуоси эллипсоида

 

Пример 2.20

 

Операторы сдвига сферы на величины dx,dy,dz вдоль координатных осей.

 

hfShift3D(x,dx,dy,dz);

s2 = hfSphere(x,center,R);

Первый оператор обеспечивает преобразование значений входных переменных x,y,z по формулам:

x=x - dx

y=y - dy

z=z - dz

Второй оператор обеспечивает построение компьютерного представления новой описывающей функции сферы f(x,y,z) с учетом преобразованных x,y,z.

 

Пример 2.21

 

Как было указано выше, для инициации функциональных процедур могут использоваться не только операторы функций. Так, для инициации функциональной процедуры объединения двух ранее созданных геометрических объектов используется геометрический оператор теоретико-множественного объединения:

 

f3 = f1|f2;

 

Эта функциональная процедура ставит в соответствие двум ранее созданным геометрическим объектам f1 и f2 компьютерное представление геометрической модели пространственной сцены в виде сложного геометрического объекта f3, являющегося результатом геометрической операции теоретико-множественного объединения этих объектов.

 

Пример 2.22

 

Рассмотрим фрагмент прикладной программы визуализации, которая ставит в соответствии ранее отфильтрованным данным пространственную сцену в виде совокупности сфер.

 

………………………..

array sph[10]; - - массив сфер

array center[3]; - - массив центра сферы

…………………………

center[1]=x2[1]; - - заполнение значений массива центра сферы первыми значениями массивов координат x2,y2,z2

center[2]=y2[1];

center[3]=z2[1];

sph[1]=hfSphere(x,center,0.5); - - создание сферы с радиусом 0.5 и центров с точке со значениями массива center

i=2;

while (i <numsp) loop - - начало оператора цикла, переменная i меняется от 1 до числа отфильтрованных точек

center[1]=x2[i]; - - заполнение значений массива центра сферы текущими значениями массивов координат x2,y2,z2

center[2]=y2[i];

center[3]=z2[i];

sph[i] = hfSphere(x,center,0.5); - - создание сферы с радиусом 0.5 и центров с точке со значениями массива center

sph[1]=sph[1]|sph[i]; - - объединение ранее созданных сфер, начиная с первой, с текущей и присвоение результата объединения переменной sph[1]

i=i+1;

endloop; - - окончание цикла

……………………………

До этого мы рассматривали характеристики и примеры инициации функциональных процедур мэппинга, служащих для задания геометрической модели сцены. Перейдем к функциональной процедуре мэппинга, с помощью которой можно задавать цветовые атрибуты.

Как уже было отмечено выше, в HyperFun используется массив атрибутов s[3] для задания графических характеристик. Приведем пример использования этого массива для задания цвета пространственного объекта.

 

Пример 2.23

……………………………

s=[0,0,1]; - - задание значений массива, которые будут использованы в качестве значений составляющих цвета (красный, зеленый, синий) по модели RGB

……………………………

Функциональные процедуры рендеринга

Как было упомянуто выше, функциональные процедуры рендеринга ставят в соответствие компьютерному представлению описания (модели) пространственной сцены ее проекционное графическое изображение на используемом графическом терминале.

Рендеринг имеет ряд параметров, к ним относятся: камера, источники освещения и среда. В HyperFun инициация функциональных процедур рендеринга осуществляется не в прикладной программе, а через командную строку или диалоговый режим. Например, можно управлять параметрами камеры (позиция, направление зрения), размерами обрамляющего параллелепипеда, определяющего визуализируемую область пространственной сцены, цветом фона и т.д.

Результатом рендеринга может быть также и анимационное (динамическое, зависящее от времени) проекционное графическое изображение, которое представляет собой соответствующую временную последовательность статических проекционных графических изображений рассматриваемой сцены. Так, например, если каждое такое статическое проекционное изображение получено с помощью меняющейся во времени пространственной сцены – шара, постепенно превращающегося в куб. Приведем пример такой анимации. Отметим, что в этом примере, в отличие от примера 2.14 в предыдущем параграфе, последовательность проекционных графических изображений получается не за счет изменения позиции камеры, а за счет изменения самой пространственной сцены (шара, превращающегося в куб).

Пример 2.24

anim(x[4],a[1]){

array xx[3],center[3], vertex[3]; - - инициализация массивов текущих точек, центров сферы и кубика

xx[1]=x[1]; xx[2]=x[2]; xx[3]=x[3]; - - присвоение массиву значений координат текущей точки

center = [0,0,0]; - - задание центра сферы

object0 = hfSphere(xx,center,6); - - задание сферы

vertex=[-8,-8,-8]; - - задание центра кубика

object1 = hfBlock(xx,vertex,16,16,16); - - задание кубика

anim = object0*(1-x[4]) + object1*x[4]; - - метаморфозис (линейная интерполяция с использованием двух обетов: шара и куба)

}

Здесь переменная x[4] задается дискретным набором чисел и интерпретируется как время.

Пример 2.25

Приведем пример прикладной программы визуализации исходных данных из примера 2.16. Результатом работы этой программы будет статическое проекционное графическое изображение пространственной сцены, получаемое в результате фильтрации из примера 2.17, и мэппинга, описанного в примерах 2.22,2.23.

Фрагменты этой программы, соответствующие вызовам функциональных процедур задания исходных данных, фильтрации и мэппинга, были приведены выше в соответствующих примерах.

		my_model(x[3], a[1],s[3]) { array center[3]; array x0[10], y0[10], z0[10]; array x2[10], y2[10], z2[10]; array sph[10]; center = [3,0,0];
Задание исходных данных		fs = openfile("r","1.txt") ; r=reservefile(10,"1.txt") ; i = 1; while (i < 11) loop x0[i] = rfile("1.txt"); y0[i] = rfile("1.txt"); z0[i] = rfile("1.txt"); i = i+1; endloop; fs = closefile("1.txt");
Фильтрация исходных данных		i=1; numsp=1; while (i < 11) loop if ((x0[i] >-5) and (x0[i]<5) and (y0[i]>-5) and (y0[i]<5) and (z0[i]<5) and (z0[i]>-5)) then x2[numsp] = x0[i]; y2[numsp] = y0[i]; z2[numsp] = z0[i]; numsp=numsp+1; endif; i=i+1; endloop;
Мэппинг отфильтрованных данных		center[1]=x2[1]; center[2]=y2[1]; center[3]=z2[1]; sph[1]=hfSphere(x,center,0.5); i=2; while (i <numsp) loop center[1]=x2[i]; center[2]=y2[i]; center[3]=z2[i]; sph[i] = hfSphere(x,center,0.5); sph[1]=sph[1]|sph[i]; i=i+1; endloop; s=[0,0,1]; my_model = sph[1]; }

При заданных значениях в файле «1.txt»:

0 4 0

3 0 0

2 3 0

0 2 -8

12 3 -10

4 -5 7

5 15 0

-8 -5 -5

15 -4 9

7 12 5

получается следующее статическое проекционное графическое изображение:

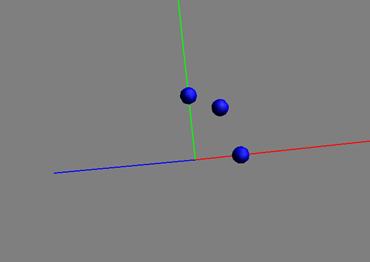
При запуске этой программы из командной строки задавались следующие размеры обрамляющего параллелепипеда: x,y,z меняются в пределах от -10 до 10 (цвет фона и камера в прикладной программе задаются по умолчанию).

Анализ этого изображения позволяет предварительно выделить 2 кластера пространственных точек, в одном кластере сосредоточено две точки, а в другом одна (исходное количество точек равнялось 10).

Заканчивая рассмотрение использования программного средства HyperFun в качестве инструментального средства для решения прикладных задач анализа данных методом визуализации, отметим, что более подробное описание HyperFun можно посмотреть на официальном сайте проекта HyperFun www.hyperfun.org.

2.4 Программный продукт VTK

VTK — широко известный программный продукт, который, в отличие от рассмотренных в предыдущих параграфов 3ds Max и HyperFun, является специализированным инструментарием, предназначенным для решения задач визуализации.

VTK представляет собой широкий набор функциональных процедур визуализации. Эти функциональные процедуры подразделяются на 4-ре рассмотренные ранее группы функциональных процедур визуализации, а именно процедуры задания исходных данных, процедуры фильтрации, процедуры мэппинга и процедуры рендеринга.

Первая версия VTK была разработана в 1993 году сотрудниками компании GE Corporate R&D. VTK распространяется как открытое программное обеспечение. В его дальнейшем развитии принимали участие пользователи из различных стран. На сегодняшний день VTK принято считать наиболее развитым программным инструментальным средством с объектно-ориентированной архитектурой, предназначенным для написания прикладных программ визуализации.

Рассмотрим основные характеристики функциональных процедур VTK, используемого в качестве инструментального средства при написании прикладных программ визуализации. В начале, рассмотрим основные характеристики наиболее часто используемого входного языка программирования VTK – языка C++, используемого для написания прикладной программы визуализации.

Программирование на языке C++

Язык C++ - язык программирования общего назначения, он обеспечивает гибкие эффективные средства для написания любых программ, в том числе программ визуализации. Язык является объектно-ориентированным, предусматривающим использование классов. Функциональные процедуры визуализации представлены в VTK как классы, описываемые на языке C++. Эти функциональные процедуры инициируются с помощью языковой конструкции - оператора функции. В общем случае может использоваться несколько операторов функции. Наряду с этим язык C++ предоставляет возможность использования всех типов операторов, описанных ранее при рассмотрении 3ds Max и HyperFun.

Оператор функции может описываться с помощью синтаксической конструкции, которая в общем случае имеет вид:

<название класса>::<название функции>(<параметр функции>,<параметр функции>,…<параметр функции>);

Как правило, в прикладной программе визуализации экземпляр класса VTK задается с помощью оператора функции New(), после чего ему присваивается имя и вызов всех последующих операторов функций происходит через это имя. Более подробную информацию о синтаксических конструкциях С++, используемых для задания и последующей работы с экземплярами классов, можно найти в документации по С++.

Обращение к результатам выполнения функциональных процедур задания исходных данных, фильтрации и мэппинга при написании прикладных программ визуализации с использованием программного инструментального средства VTK, как правило, происходит с помощью оператора функции GetOutputPort(). Получение функциональными процедурами фильтрации и мэппинга результатов выполнения соответствующих функциональных процедур, как правило, происходит с помощью оператора функции SetInputConnection(..). Фрагметры прикладных программ визуализации с использованием этиъ операторов функций приведены в приерах 2.26 и 2.28.

Рассмотрим примеры использования операторов функций для вызова функциональных процедур VTK. Начнем с рассмотрения функциональных процедур задания исходных данных.

Функциональные процедуры задания исходных данных

При использовании языка C++ функциональными процедурами задания исходных данных являются процедуры открытия файла, чтения данных из файла, закрытия файла. Инициация этих функциональных процедур может быть выполнена с помощью стандартных операторов функций С++ fopen(..), fread(..), fclose(..) и т.д. Более подробную информацию об этих операторах функций можно найти в любой документации по языку С++. Помимо этого, VTK предоставляет также набор специализированных функциональных процедур задания исходных данных, более простых в использовании по сравнению с указанными выше. Как правило, это функциональные процедуры открытия, чтения исходных данных и закрытия файлов определенного типа: xyz, pdb, Gaussian Cube и т.д. Как и для всех групп функциональных процедур VTK, инициация этих функциональных процедур происходит с помощью операторов функций.

Рассмотрим фрагмент программы с использованием оператора функции, инициирующего функциональную процедуру открытия, чтения исходных данных и закрытия файла в формате XYZ. В файле такого формата хранится информация о молекулярной структуре в виде совокупности точек - центров атомов, а также типе атомов.

Пример 2.25

……………..

vtkXYZMolReader *pdb0= vtkXYZMolReader::New(); // выбор функциональной процедуры чтения исходных данных как задание экземпляра (c именем pdb0) класса (с именем vtkXYZMolReader)

pdb0-> SetFileName ("caffeine.xyz"); // оператор функции SetFileName(), инициирующий выполнение выбранной функциональной процедуры открытия, чтения исходных данных и закрытия файла с именем "caffeine.xyz". Результат выполнения данной функциональной процедуры доступен, по умолчанию, для последующих функциональных процедур через соответствующий оператор функцию GetOutputPort().

………………

Результатом выполнения этой функциональной процедуры будет компьютерное представление исходных данных в виде совокупности четверок (x,y,z,s), где x,y,z – координаты точки, s –числовое значение, соответствующие типу атома.

Функциональные процедуры фильтрации данных

Также как и языки MaxScript и HyperFun, язык С++ дает возможность написания различных функциональных процедур фильтрации данных в теле программы. Однако, помимо этого, в отличие от 3ds Max и HyperFun, в VTK существует широкий набор специализированных функциональных процедур фильтрации данных.

Приведем фрагмент программы фильтрации исходных данных, описанных в примере 2.25 с использованием таких функциональных процедур.

Пример 2.26

Пусть фильтрация исходных данных состоит в том, чтобы из числа исходных четверок (x,y,z,s) нужно для последующей визуализации отобрать только те из четверки, для которых выполняется условие:

-2<=x<=2 -2<=y<=2 -2<=z<=2

В качестве исходных данных возьмем результат выполнения функциональной процедуры из примера 2.25.

……………………..

vtkBox * box = vtkBox::New(); // выбор функциональной процедуры фильтрации данных, определяющей параметр фильтрации (решающее правило отбора точек, заданное аналитически в виде F(x,y,z)>=0, где F – описывающая функция примитива параллелепипед, x,y,z – координаты точки), как задание экземпляра (с именем box) класса (с именем vtkBox).

box-> SetXMin (-2, -2, -2); // задание параметров выбранного экземпляра класса

box ->SetXMax (2, 2, 2); // задание параметров выбранного экземпляра класса и инициация функциональной процедуры

vtkClipPolyData* clipper= vtkClipPolyData::New(); // выбор функциональной процедуры фильтрации данных как задание экземпляра (с именем clipper) класса (с именем vtkClipPolyData).

 

clipper-> SetInputConnection (pdb0-> GetOutputPort());// задание параметров экземпляра clipper класса (с именем vtkClipPolyData) – передача исходных данных (массива точек) для фильтрации

clipper-> SetClipFunction (box); // задание параметров экземпляра clipper класса (с именем vtkClipPolyData) – задание решающего правила отбора точек, заданного аналитически в виде F(x,y,z)>=0

clipper-> InsideOutOn(); // инициация функциональной процедуры отбора точек, попадающих в заданный куб

……………………..

Функциональные процедуры мэппинга

Приведем в качестве примера функциональные процедуры мэппинга VTK.

В качестве геометрических примитивов в VTK могут использоваться:

• cфера
• конус
• цилиндр
• параллелепипед
• плоскость
• и др.

Из этих примитивов можно формировать сложные пространственные геометрические объекты, которые, в свою очередь, могут использоваться как операнды других геометрических операций. В качестве таких геометрических операций в VTK могут использоваться:

• сдвиг
• поворот
• масштабирование
• теоретико-множественное объединение
• теоретико-множественное пересечение
• теоретико-множественное вычитание
• и др.

Для задания графических характеристик пространственной сцены в VTK предоставляется возможность использовать функциональные процедуры задания цвета и текстуры.

Приведем примеры операторов функций, используемых для обращения к функциональным процедурам мэппинга.

Пример 2.28

…………………

vtkSphereSource* Sphere0= vtkSphereSource::New();

Sphere0-> SetCenter (0, 0, 0);

Sphere0-> SetRadius (1);

vtkGlyph3D* Glyph0= vtkGlyph3D::New();

Glyph0 ->SetInputConnection(clipper-> GetOutputPort());

Glyph0-> SetOrient (1);

Glyph0-> SetColorMode (1);

Glyph0-> ScalingOn();

Glyph0-> SetScaleMode (2);

Glyph0-> SetScaleFactor (.25);

Glyph0-> SetSource (Sphere0 ->GetOutput());

………………………

Эта языковая конструкция, построенная в соответствии с синтаксисом С++ и использующая операторы функций, инициирует выполнение функциональной процедуры, которая ставит в соответствие отфильтрованным данным компьютерное представление геометрической модели пространственной сцены в виде совокупности сфер таким образом, что каждой четверке чисел (x,y,z,s), , ставится в соответствие сфера с центром в точке x,y,z.

Приведем пример использования функциональной процедуры объединения двух примитивов.

Пример 2.29

……………………………………

vtkBox * box1=vtkBox::New(); // инициация функциональной процедуры создания параллелепипеда box1

box1-> SetXMin (-5, -5, -5);

box1 ->SetXMax (5, 5, 5);

vtkBox * box2=vtkBox::New();// инициация функциональной процедуры создания параллелепипеда box2

box2-> SetXMin (0, 0, 0);

box2->SetXMax (15, 15, 15);

vtkImplicitBoolean* b= vtkImplicitBoolean::New(); // инициация функциональной процедуры объединения этих двух примитивов

b-> SetOperationTypeToUnion();

b->AddFunction (box1);

b-> AddFunction (box2);

……………………..

Выше мы рассмотрели характеристики и примеры инициации функциональных процедур мэппинга, служащих для задания геометрической модели сцены. Перейдем к функциональной процедуре мэппинга, с помощью которой можно задавать цвет и текстуру.

Пример 2.30

……………………..

vtkPolyDataMapper* Mapper5= vtkPolyDataMapper::New();

Mapper5 ->SetInputConnection (Glyph0 ->GetOutputPort());

Mapper5-> SetImmediateModeRendering (1);

Mapper5-> UseLookupTableScalarRangeOff();

Mapper5-> SetScalarVisibility (1);

Mapper5-> SetScalarModeToDefault();

………………….

Эта синтаксическая конструкция служит для задания графических характеристик пространственной сцены. Здесь цвет каждой сферы, поставленной в соответствие отфильтрованным данным в примере 2.29, связываются определенным образом с этими данными, а именно, определяется в соответствии с числовым значением s в «четверке» (x,y,z,s).

Функциональные процедуры рендеринга

Функциональные процедуры рендеринга ставят в соответствие компьютерному представлению описания (модели) пространственной сцены ее проекционное графическое изображение на используемом графическом терминале.

Рендеринг имеет ряд параметров, в частности, к ним относятся - камера и источники освещения. Рассмотрим примеры функциональных процедур задания этих параметров.

Пример 2.31

…………………

vtkCamera* camera= vtkCamera::New();

camera-> SetViewAngle(30); // задание угла зрения камеры

camera-> SetPosition (8.3761, 4.94858, 4.12505); // задание позиции камеры

………………..

Результатом выполнения данной функциональной процедуры будет создание компьютерного представлений камеры.

Пример 2.32

……………

vtkLight* light= vtkLight::New();

light-> SetPosition (8.3761, 4.94858, 4.12505); // задание позиции источника освещения

……………

 

Результатом выполнения данной функциональной процедуры будет создание компьютерного представления источника освещения.

Пример 2.33

……………..

vtkActor* Actor5= vtkActor::New();

Actor5 ->SetMapper (Mapper5);

…………….

Результатом выполнения данной функциональной процедуры будет выбор описания конкретной пространственной сцены из числа имеющихся описаний для последующего рендеринга.

Приведем пример фрагмента прикладной программы, содержащего вызов самой функциональной процедуры рендеринга.

Пример 2.34

………………….

vtkRenderer* ren1 = vtkRenderer::New(); // задание функциональной процедуры рендеринга

// задание параметров рендеринга

vtkRenderWindow* renWin= vtkRenderWindow::New(); // задание области отрисовки проекционного изображения

renWin-> AddRenderer(ren1);

 

ren1->SetActiveCamera (camera);

ren1->AddLight (light);

ren1-> AddActor (Actor5);

ren1->SetBackground(0,0,0); // задание параметра рендернинга - цвета фона

ren1->Render() ; //инициация функциональной процедуры рендеринга

……………………

Результатом выполнения данной функциональной процедуры будет статическое проекционное графическое изображение текущей (сформированной к данному моменту времени) сцены на графическом терминале.

Результатом рендеринга может быть также и анимационное (динамическое, зависящее от времени) проекционное графическое изображение, которое представляет собой соответствующую временную последовательность статических проекционных графических изображений рассматриваемой сцены. Так, например, если каждое такое статическое проекционное изображение получено с помощью перемещающейся в пространстве камеры (т.е. камера, как параметр рендеринга, задана для ряда фиксированных значений времени), то результатом такой «фотосъемки» будет анимационное проекционное графическое изображение (упорядоченная совокупность соответствующих статических проекционных графических изображений).

Приведем фрагмент программы визуализации, содержащий вызов функциональной процедуры рендеринга, результатом которой будет построение такого анимационного проекционного графического изображения пространственной сцены.

Пример 2.35

………………

int i;

for (i = 0; i < 360; ++i)

{

// render the image

renWin->Render();

// rotate the active camera by one degree

ren1->GetActiveCamera()->Azimuth( 1 );

}

…………….

Здесь показано обращение к функциональной процедуре задания компьютерного представления камеры, меняющейся во времени.

Приведем пример прикладной программы визуализации исходных данных из примера 2.25. Результатом работы этой программы будет статическое проекционное графическое изображение пространственной сцены, описание которой получается в результате мэппинга, описанного в примере 2.28.

Пример 2.36

		#include "vtkXYZMolReader.h" #include "vtkBox.h" #include "vtkClipPolyData.h" #include "vtkSphereSource.h" #include "vtkGlyph3D.h" #include "vtkTubeFilter.h" #include "vtkPolyDataMapper.h" #include "vtkRenderWindow.h" #include "vtkCamera.h" #include "vtkActor.h" #include "vtkLight.h" #include "vtkCamera.h" #include "vtkRenderer.h" #include "vtkRenderWindowInteractor.h" #include "vtkProperty.h" int main() {
Задание исходных данных		vtkXYZMolReader *pdb0= vtkXYZMolReader::New(); pdb0-> SetFileName ("caffeine.xyz");
Фильтрация данных		vtkBox * box=vtkBox::New(); box-> SetXMin (-2, -2, -2); box ->SetXMax (2, 2, 2); vtkClipPolyData* clipper= vtkClipPolyData::New(); clipper-> SetInputConnection (pdb0-> GetOutputPort()); clipper-> SetClipFunction (box); clipper->InsideOutOn();
Мэппинг отфильтрованных данных		vtkSphereSource* Sphere0= vtkSphereSource::New(); Sphere0-> SetCenter (0, 0, 0 ); Sphere0-> SetRadius (0.5); Sphere0-> SetThetaResolution (18); Sphere0-> SetStartTheta ( 0); Sphere0-> SetEndTheta (360); vtkGlyph3D* Glyph0= vtkGlyph3D::New(); Glyph0 ->SetInputConnection(clipper-> GetOutputPort()); Glyph0-> SetOrient (1); Glyph0-> SetColorMode (1); Glyph0-> ScalingOn(); Glyph0-> SetScaleMode ( 2); Glyph0-> SetScaleFactor (.25); Glyph0-> SetSource (Sphere0 ->GetOutput());
Мэппинг отфильтрованных данных		vtkPolyDataMapper* Mapper5= vtkPolyDataMapper::New(); Mapper5 ->SetInputConnection (Glyph0 ->GetOutputPort()); Mapper5-> SetImmediateModeRendering (1); Mapper5-> UseLookupTableScalarRangeOff(); Mapper5-> SetScalarVisibility (1); Mapper5-> SetScalarModeToDefault();
Рендеринг		vtkActor* Actor5= vtkActor::New(); Actor5 ->SetMapper (Mapper5); vtkCamera* camera= vtkCamera::New(); camera-> SetViewAngle(30); camera-> SetPosition (8.3761, 4.94858, 4.12505); vtkLight* light= vtkLight::New(); light-> SetPosition (8.3761, 4.94858, 4.12505); vtkRenderer *ren1 = vtkRenderer::New(); vtkRenderWindow *renWin = vtkRenderWindow::New(); renWin->AddRenderer(ren1); vtkRenderWindowInteractor *iren = vtkRenderWindowInteractor::New(); iren->SetRenderWindow(renWin); ren1-> AddActor (Actor5); ren1->SetActiveCamera (camera); ren1->AddLight (light); ren1->SetBackground(0,0,0); renWin->Render(); iren->Start(); }

При заданных в файле « caffeine.xyz» исходных данных

24

Caffeine

H -3.3804130 -1.1272367 0.5733036

N 0.9668296 -1.0737425 -0.8198227

C 0.0567293 0.8527195 0.3923156

N -1.3751742 -1.0212243 -0.0570552

C -1.2615018 0.2590713 0.5234135

C -0.3068337 -1.6836331 -0.7169344

C 1.1394235 0.1874122 -0.2700900

N 0.5602627 2.0839095 0.8251589

O -0.4926797 -2.8180554 -1.2094732

C -2.6328073 -1.7303959 -0.0060953

O -2.2301338 0.7988624 1.0899730

H 2.5496990 2.9734977 0.6229590

C 2.0527432 -1.7360887 -1.4931279

H -2.4807715 -2.7269528 0.4882631

H -3.0089039 -1.9025254 -1.0498023

H 2.9176101 -1.8481516 -0.7857866

H 2.3787863 -1.1211917 -2.3743655

H 1.7189877 -2.7489920 -1.8439205

C -0.1518450 3.0970046 1.5348347

C 1.8934096 2.1181245 0.4193193

N 2.2861252 0.9968439 -0.2440298

H -0.1687028 4.0436553 0.9301094

H 0.3535322 3.2979060 2.5177747

H -1.2074498 2.7537592 1.7203047

получим проекционное графическое изображение, представленное на Рис.2.5

1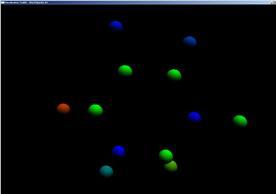	2
3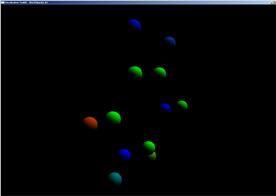	4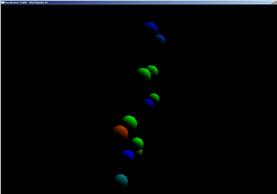

Рис.2.5

Анализ четырех проекционных графических изображений позволяет сделать вывод , что количество отфильтрованных точек равняется 12-ти при параметрах фильтрации, от (-2, -2, -2) до (2, 2, 2), заданных в прикладной программе (исходное количество точек равнялось 24). Точки размещаются в пространстве в виде «плоской» пятиконечной «звезды».

Заканчивая рассмотрение использования программного средства VTK в качестве инструментального средства для решения прикладных задач анализа данных методом визуализации, отметим, что более подробное описание VTK можно найти на официальном сайте www.vtk.org.

Заканчивая рассмотрение использования инструментальных средств визуализации, отметим, что при написании прикладных программ визуализации возможно использование этих средств как автономно, так и совместно, что позволяет наиболее эффективно использовать достоинства каждого из них. Примеры такого использования приведены в части 3.

---

Наверх