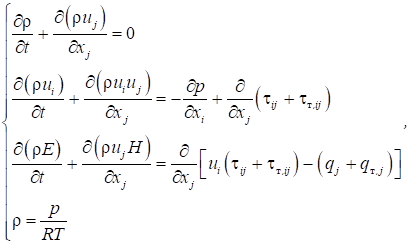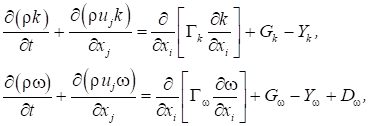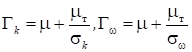Особенности
движения дисперсной примеси в виде частиц в турбулентных потоках газа и ее
обратное влияние на характеристики турбулентности несущей фазы являются
ключевыми проблемами теории двухфазных течений [1
–
4].
Обратная задача заключается в изучении влияния частиц на характеристики
несущего их газового потока. Решение этой задачи предполагает определение
характеристик газа в присутствии частиц: полей скоростей и температур,
коэффициентов трения и теплоотдачи и т.д. [5
–
7].
Течение с крупными частицами характеризуется тем, что время релаксации частиц
значительно превышает характерное время крупномасштабных турбулентных вихрей, т.е.
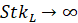 .
Такие частицы не будут реагировать на турбулентные пульсации скорости несущей
фазы, а распределения их осредненных скоростей будут практически однородными по
сечению канала (трубы). Наглядным подтверждением этого могут служить данные [8].
.
Такие частицы не будут реагировать на турбулентные пульсации скорости несущей
фазы, а распределения их осредненных скоростей будут практически однородными по
сечению канала (трубы). Наглядным подтверждением этого могут служить данные [8].
Цель
настоящей работы
–
визуализации
течения, формирующегося в следах за крупными частицами, движущимися в восходящем
турбулентном потоке воздуха в канале на основе численного моделирования.
Характерной
особенностью турбулентных течений является наличие беспорядочных флуктуаций
всех параметров потока. В силу переменности параметров не только в
пространстве, но и во времени при изучении турбулентных потоков используют
различные методы осреднения и сглаживания, позволяющие перейти от вероятностных
полей характеристик к их регулярным средним значениям.
Полная
система уравнений, осредненных по Рейнольдсу (RANS), описывающая движение
вязкой жидкости в тензорной форме:
|
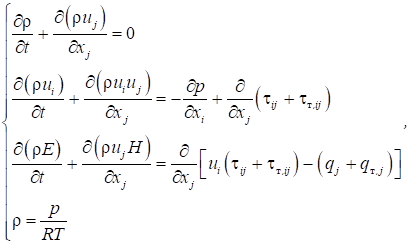
|
(1)
|
где
xj
–
декартовы
координаты;
ui,
uj
–
компоненты
вектора скорости осредненного течения,
E
–
удельная
полная энергия,
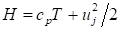 –
удельная
полная энтальпия газа,
Т
– температура,
–
удельная
полная энтальпия газа,
Т
– температура,
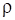 –
плотность
газа,
р
– давление,
R
– газовая
постоянная.
–
плотность
газа,
р
– давление,
R
– газовая
постоянная.
Компоненты
тензора рейнольдсовых напряжений
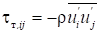 и вектора
рейнольдсового теплового потока
и вектора
рейнольдсового теплового потока
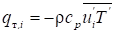 появляются при
осреднении нелинейных конвективных членов исходных уравнений Навье-Стокса и
переноса энергии, и их связь с параметрами осредненного течения неизвестна.
появляются при
осреднении нелинейных конвективных членов исходных уравнений Навье-Стокса и
переноса энергии, и их связь с параметрами осредненного течения неизвестна.
Поскольку
уравнения
RANS
незамкнуты за счет
тензора рейнольдсовых напряжений и вектора турбулентного теплового потока
необходимо использовать дополнительные соотношения (модели турбулентности),
связывающие эти величины с характеристиками осредненного течения.
В работе для замыкания
уравнений Навье-Стокса, осредненных по Рейнольдсу, применяется модель
турбулентности
SST
k
-
ω-модель
Ментера [9]. Данная модель турбулентности выбрана потому, что дополнительные
(источниковые) слагаемые в уравнениях переноса двухпараметрической модели
Ментера, учитывающие генерацию турбулентности крупными частицами, отсутствуют.
Собственно, дополнительная генерация энергии турбулентности происходит не за
счет дополнительного источникового члена в уравнении, а за счет того, что
обтекание крупных частиц рассчитывается напрямую, как объектов с твердыми
стенками.
Модель Ментера
реализуется в следующем виде:
|
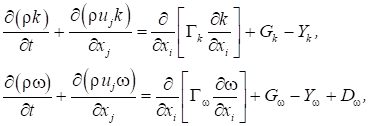
|
(2)
|
где
Gk
‑ генерация
кинетической энергии турбулентности
k,
G
ω
–
генерация
диссипации кинетической энергии турбулентности
ω
на единицу
k,
<
Yk
–
диссипация
кинетической энергии турбулентности,
Y
ω
–
диссипация
ω,
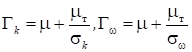 ,
,
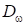 ‑
перекрестный
диффузионный член.
‑
перекрестный
диффузионный член.
Для
решения задачи была построена расчетная сетка с 1.11 млн ячеек. Исследование
сеточной сходимости было выполнено в части достаточности сгущения сетки у
частиц. Значение
y+ при обтекании частиц не
превышает 3, что позволяет говорить, что первая ячейка находится в вязком
подслое, пристеночные функции не используются.
Авторами
работы для визуализации течения в следах за крупными частицами было выбрано
программное обеспечение
Ansys
Fluent,
так как данное ПО является мощным
инструментом при моделировании сложных задач в области гидрогазодинамики.
Ansys
Fluent
позволяет
моделировать поведение жидкостей и газов в различных условиях, включая
ламинарные и турбулентные потоки, с учетом вязкости, плотности и других
свойств, а также обладает множеством инструментов для визуализации результатов
расчета [10].
Моделирование
крупных частиц реализовано при помощи модуля Dynamic Mesh в Ansys Fluent.
Сглаживание осуществлялось методом Spring/Laplace/Boundary Layer – это функция
сглаживания при перестроении расчетной сетки. В используемом методе ребра ячеек
представляются как пружины и задается коэффициент, который фактически является
коэффициентом пропорциональности в законе Гука, тем самым можно регулировать
сгущение сетки при перестроении. Динамическая сетка отслеживает движение частиц
и перестраивается, функции сглаживания используются, чтобы качество сетки
оставалось близким к начальному. Перестроение сетки осуществлено методом
локальной ячейки с минимальным масштабом 0.0005 м и максимальным масштабом 0.1
м. Движение частиц задавалось одной степенью свободы при помощи модуля Six DOF
(degree
of
freedom), который позволяет
вычислять силы и моменты, действующие на объект, которые приводят к изменению
его положения в пространстве с заданным шагом по времени. В работе
предполагается, что у частиц одна степень свободы – они могут двигаться только
вдоль оси
Y
без
вращения. Соответственно, дополнительно к граничным и начальным условиям для
частиц задается масса для учета гравитации (в работе масса каждой частицы 0.5
г.).
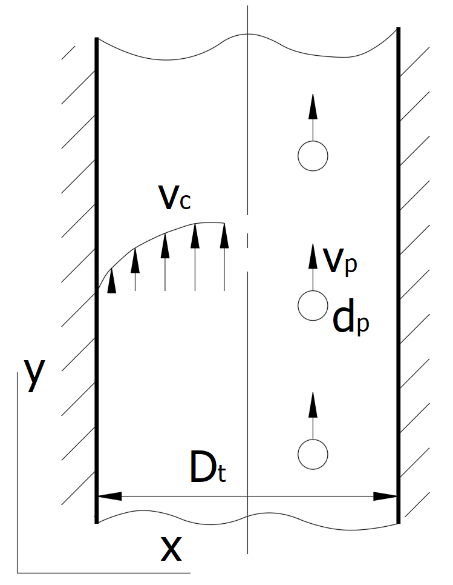
Рис.1
Схема движения частиц в несущем газе
На
рисунке 1, показана схема движения частиц со скоростью
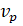 в
несущем газе
в
несущем газе
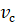 .
Центр системы прямоугольной координат
(x
–
y)
находится на оси симметрии канала
диаметром
.
Центр системы прямоугольной координат
(x
–
y)
находится на оси симметрии канала
диаметром
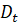 .
Крупными частицами являются сферы диаметром
.
Крупными частицами являются сферы диаметром
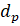 ,
которые размещаются вертикально друг за другом по длине канала
L
на различном расстоянии друг от друга, чтобы исключить взаимное влияние
вихревых следов за сферами. Сферы расположены со смещением относительно оси
симметрии канала на 5 мм.
,
которые размещаются вертикально друг за другом по длине канала
L
на различном расстоянии друг от друга, чтобы исключить взаимное влияние
вихревых следов за сферами. Сферы расположены со смещением относительно оси
симметрии канала на 5 мм.
Таблица 1. Основные
характеристики исследуемого потока
|
Скорость воздуха
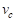 , м/с , м/с
|
Скорость частиц
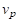 , м/с , м/с
|
Диаметр частиц
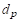 , м , м
|
Диаметр трубы
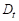 , м , м
|
Длина трубы
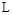 , м , м
|
Число Рейнольдса
Rep
|
Число Рейнольдса
Rec
|
|
14.9
|
5.7
|
0.003
|
0.0305
|
0.2
|
1120
|
3
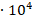
|
Для детального анализа процесса
дополнительной генерации энергии турбулентности воздуха в выборочном сечении трубы
был предложен оригинальный методический прием, заключающийся в расположении
частиц на одной линии (рис. 1).
Использование
настоящего приема позволило получить наглядные распределения энергии
турбулентности по длине канала и выделить качественно отличные области (рис. 2):
1) начальный участок, характеризующийся повышенными значениями энергии
турбулентности «чистого» воздуха (однофазное течение); 2) области роста энергии
турбулентности газовой фазы за отдельными частицами; 3) область
«квазистационарного» однофазного течения.
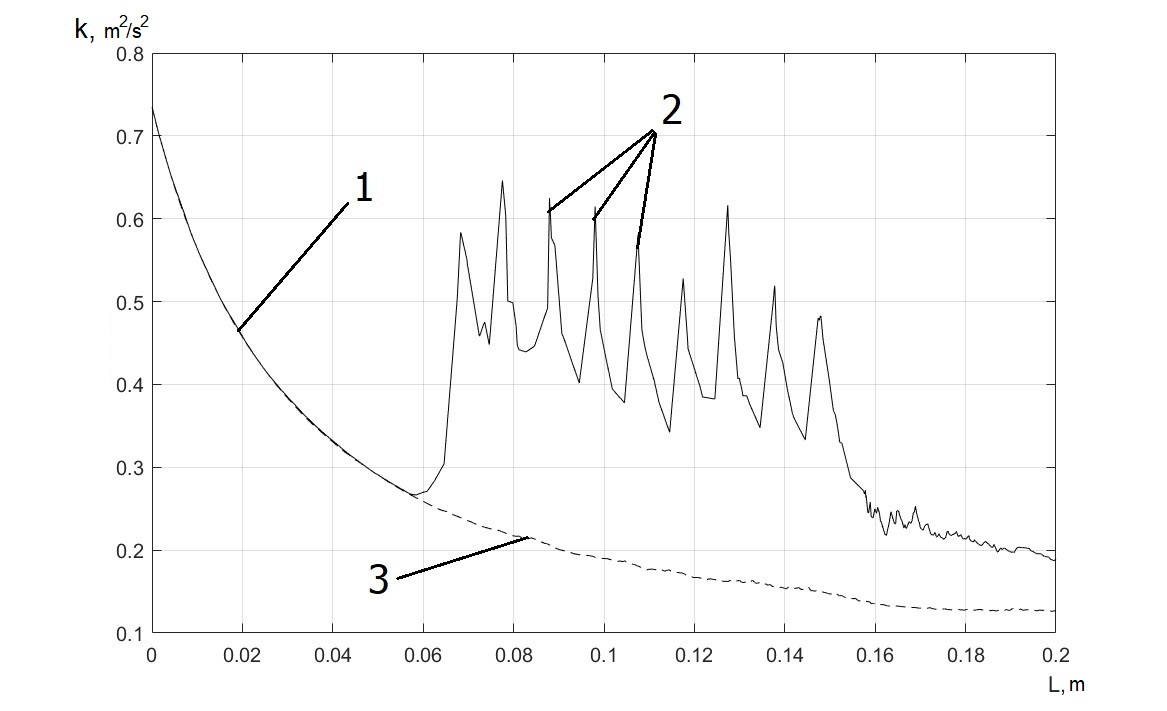
Рис.
2 Распределение энергии турбулентности
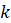 по
длине канала для
по
длине канала для
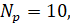 цифрами
обозначены: 1 – начальный участок с повышенной
цифрами
обозначены: 1 – начальный участок с повышенной
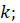 2
– рост
2
– рост
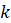 в
случае за отдельными частицами; 3 – «квазистационарное» однофазное течение
в
случае за отдельными частицами; 3 – «квазистационарное» однофазное течение
Данные
рис. 2 свидетельствуют в пользу того, что за крупными частицами образуются
развитые турбулентные следы, которые характеризуются наличием нестационарных
трехмерных вихревых структур.
На
рисунках 3–5 приведены типичные распределения энергии турбулентности
 в
несущем газе в канале и в следах за частицами. Визуализация течения газа и
частиц выполнена в программном обеспечении
Ansys
Fluent.
Необходимо отметить, что уравнения
движения частиц не интегрировались, а сами частицы двигались с одинаковыми
скоростями. Таким образом был реализован упрощенный вариант подхода,
называемого в англоязычной литературе «two–way coupling»,
т.е. учитывающий обратное влияние частиц на характеристики газа. Назовем его
квазиподходом или, используя англоязычную аббревиатуру, «quasi
–
two–way
coupling»,
TWC(Q).
В такой постановке, когда производится расчет обтекания газом каждой одиночной
частицы и разрешается межфазная граница (такие расчеты называются «particle
–
resolved» (PR)).
Таким образом, используемый в данной работе подход может быть классифицирован
как
PR
–
TWC(Q)
–
RANS.
в
несущем газе в канале и в следах за частицами. Визуализация течения газа и
частиц выполнена в программном обеспечении
Ansys
Fluent.
Необходимо отметить, что уравнения
движения частиц не интегрировались, а сами частицы двигались с одинаковыми
скоростями. Таким образом был реализован упрощенный вариант подхода,
называемого в англоязычной литературе «two–way coupling»,
т.е. учитывающий обратное влияние частиц на характеристики газа. Назовем его
квазиподходом или, используя англоязычную аббревиатуру, «quasi
–
two–way
coupling»,
TWC(Q).
В такой постановке, когда производится расчет обтекания газом каждой одиночной
частицы и разрешается межфазная граница (такие расчеты называются «particle
–
resolved» (PR)).
Таким образом, используемый в данной работе подход может быть классифицирован
как
PR
–
TWC(Q)
–
RANS.
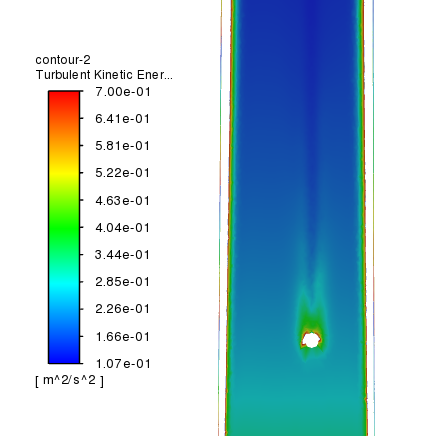
Рис.
3 Распределение кинетической энергии турбулентности за одиночной частицей,
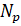 =
0.1, 1/см3
=
0.1, 1/см3
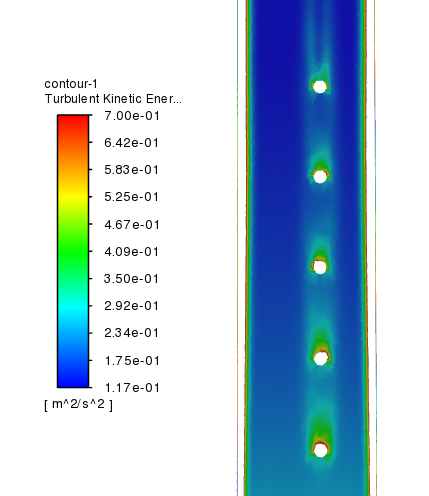
Рис.
4 Распределение кинетической энергии турбулентности за группой частиц,
 =
0.5, 1/см3
=
0.5, 1/см3
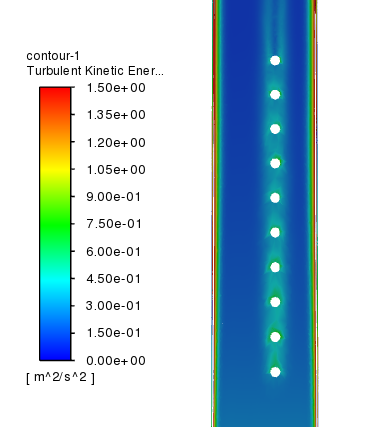
Рис.
5 Распределение кинетической энергии турбулентности за группой частиц,
 =
1, 1/см3
=
1, 1/см3
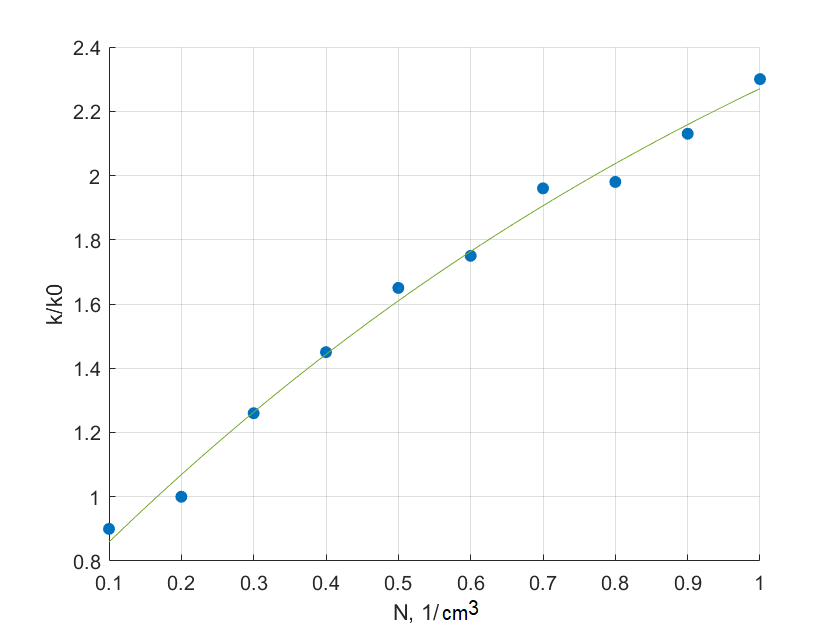
Рис.
6 Рост генерации энергии турбулентности в зависимости от счетной концентрации
частиц
На
рис. 6 приведены данные по росту энергии турбулентности несущего газа от величины
счетной концентрации частиц (количество частиц в единице объема).
В
работе выполнена визуализация течения за крупными частицами, движущимися в восходящем
турбулентном потоке воздуха в канале. Численное моделирование выполнено с использованием
упрощенного варианта
TWC(Q).
Приведены
некоторые результаты численного моделирования характеристик турбулентных следов
за крупными движущимися частицами на основе осредненных по Рейнольдсу уравнений
Навье-Стокса (RANS). Выявлена зависимость величины
энергии турбулентности от счетной концентрации частиц.
Работа выполнена за счет
гранта Российского научного фонда № 23-19-00734.
1. Crowe C., Sommerfeld M., Tsuji Y. (Eds.). Multiphase Flows with Droplets and Particles. Boca Raton, FL, USA: CRC Press, 1998. 471 p.
2. Michaelides E.E., Crowe C.T., Schwarzkopf J.D. (Eds.). Multiphase Flows Handbook, 2nd ed. Boca Raton, FL, USA: CRC Press, 2017. 1396 p.
3. Zaichik L.I., Alipchenkov V.M., Sinaisky E.G. Particles in Turbulent Flows. Darmstadt, Germany: Wiley-VCH, 2008. 320 p.
4. Varaksin A.Y. Collisions in Particle-Laden Gas Flows. New York, NY, USA: Begell House, 2013. 370 p.
5. Varaksin A.Yu. Hydrogasdynamics and Thermal Physics of Two-Phase Flows with Solid Particles, Droplets, and Bubbles. High Temperature, 2023, vol. 61, p. 852–870.
6. Yu Z.S., Xia Y., Guo Y., Lin J.Z. Modulation of Turbulence Intensity by Heavy Finite-Size Particles in Upward Channel Flow. J. Fluid Mech., 2021, vol. 913, paper no. A3.
7. Yang B., Peng C., Wang G.C., Wang L.P. A Direct Numerical Simulation Study of Flow Modulation and Turbulent Sedimentation in Particle-Laden Downward Channel Flows. Phys. Fluids, 2021, vol. 33, paper no. 093306.
8. Varaksin A.Yu., Mochalov A.A., Zhelebovsky A.A. Flow Characteristics in the Wake of a Large Moving Particle. High Temperature, 2022, vol. 60, p. 639–644.
9. Menter F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J., 1994, vol. 32, p. 1598–1605.
10. Басов К.А. Ansys для конструкторов. – М.: ДМК Пресс, 2009 – С. 248
Numerical Visualization of Vortex Wakes Behind Large Particles
Authors: А.А. Mochalov1,A,B, А.Yu. Varaksin2,A,B
A Bauman Moscow State Technical University, Moscow, Russia
B Joint Institute for High Temperature, Moscow, Russia
1 ORCID: 0000-0003-3078-1277, artem.mochalov@yandex.ru
2 ORCID: 0000-0002-8799-6378, varaksin_a@mail.ru
Abstract
An attempt has been made to visualize the flow formed in the wake of large particles moving in an ascending turbulent air flow in the channel. Numerical modeling was performed using a simplified version of the approach called "two–way coupling" (TWC) in English literature and taking into account the inverse effect of particles on gas characteristics. The particle motion was calculated in an approximate manner, therefore the method used is called "quasi – two–way coupling", TWC(Q). The results of numerical modeling of the characteristics of turbulent trails behind large moving particles based on the Reynolds averaged Navier-Stokes equations (RANS) are presented.
Keywords: visualization, numerical simulation, two – phase flows, turbulent wake, turbulence, RANS.
1. Crowe C., Sommerfeld M., Tsuji Y. (Eds.). Multiphase Flows with Droplets and Particles. Boca Raton, FL, USA: CRC Press, 1998. 471 p.
2. Michaelides E.E., Crowe C.T., Schwarzkopf J.D. (Eds.). Multiphase Flows Handbook, 2nd ed. Boca Raton, FL, USA: CRC Press, 2017. 1396 p.
3. Zaichik L.I., Alipchenkov V.M., Sinaisky E.G. Particles in Turbulent Flows. Darmstadt, Germany: Wiley-VCH, 2008. 320 p.
4. Varaksin A.Y. Collisions in Particle-Laden Gas Flows. New York, NY, USA: Begell House, 2013. 370 p.
5. Varaksin A.Yu. Hydrogasdynamics and Thermal Physics of Two-Phase Flows with Solid Particles, Droplets, and Bubbles. High Temperature, 2023, vol. 61, p. 852–870.
6. Yu Z.S., Xia Y., Guo Y., Lin J.Z. Modulation of Turbulence Intensity by Heavy Finite-Size Particles in Upward Channel Flow. J. Fluid Mech., 2021, vol. 913, paper no. A3.
7. Yang B., Peng C., Wang G.C., Wang L.P. A Direct Numerical Simulation Study of Flow Modulation and Turbulent Sedimentation in Particle-Laden Downward Channel Flows. Phys. Fluids, 2021, vol. 33, paper no. 093306.
8. Varaksin A.Yu., Mochalov A.A., Zhelebovsky A.A. Flow Characteristics in the Wake of a Large Moving Particle. High Temperature, 2022, vol. 60, p. 639–644.
9. Menter F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J., 1994, vol. 32, p. 1598–1605.
10. Басов К.А. Ansys для конструкторов. – М.: ДМК Пресс, 2009 – С. 248