1.   Введение

Методы гильберт-оптики и интерферометрии составляют одно из направлений невозмущающей диагностики реагирующих струй и пламён [1, 2].Они основаны на визуализации и анализе фазовых возмущений, индуцированных исследуемой средой в зондирующем световом поле. В работах [3, 4] исследовалось диффузное горение струи водорода методами гильберт-оптики. Использовался оптический диагностический комплекс на основе прибора ИАБ–463М [5], оснащённого модифицированными модулями гильберт-фильтрации, интерференции, светового источника, регистрации гильберт-изображения и обработки информации. В работе [6] описан метод оценки распределения температуры в асимметричном пламени с применением высоконтрастной стереоскопической фотосъемки. Сообщается о спектральной реконструкции температурных полей с использованием пирометрии цветовых соотношений и интерферометрической томографии [7]. Струйное пламя предварительно перемешанных пропано-воздушных смесей имеет широкий спектр применений в научных исследованиях и практических приложениях, успешное развитие которых требует развития методов оптической диагностики с возможностью реконструкции пространственной фазовой и температурной структуры горящего факела. Целью данной работы является адаптация методов гильберт-оптики к решению задач диагностики с реконструкцией пространственной фазовой и температурной структуры пламени. Исследования мотивируются научной и практической значимостью проблемы, состоящей в поиске методов управления структурными и термодинамическими параметрами факела [8].

2.   Метод исследования

Комплекс оптической диагностики создан на основе прибора ИАБ–463М [5] с модифицированными под задачи эксперимента модулями гильберт-фильтрации, источника зондирующего поля, регистрации и обработки оптического сигнала.

 

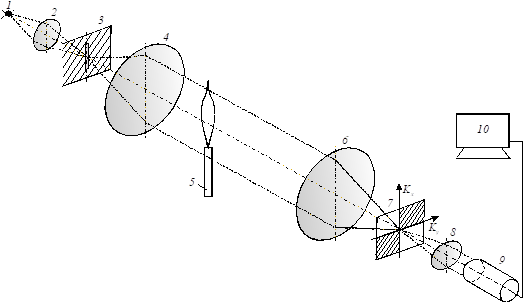
Рис. 1. Схема гильберт-визуализатора.

 

На рис. 1 показана упрощённая схема комплекса оптической диагностики пламени для метода гильберт-визуализации. Он содержит осветительный модуль, состоящий из источника света 1, линзы 2 и щелевой диафрагмы 3, помещённой в передней фурье-плоскости объектива 4, формирующего зондирующее поле. Фурье-спектр фазовых возмущений, индуцируемых в исследуемой среде 5, локализуется в частотной плоскости объектива 6, где помещён квадрантный гильберт-фильтр 7, ориентация которого согласована с диафрагмой 3. Объектив 8 выполняет обратное фурье-преобразование фильтрованного поля, формируя, в зависимости от спектральных характеристик светового источника, аналитический или гильберт-сопряжённый оптические сигналы, которые регистрируются цифровой видеокамерой 9, подключенной к компьютеру 10.

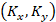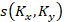В частотной плоскости  для фурье-спектра фазовой оптической плотности светового поля , возмущённого исследуемой средой (пламенем), имеем непосредственно после фильтра 7:

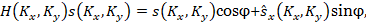
(1)

где 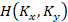 – передаточная функция фильтра, 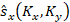 – гильберт-сопряжённый фурье-спектр оптического сигнала:

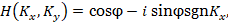
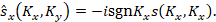
Фазовый сдвиг 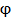 является функцией длины волны 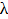 зондирующего светового поля, .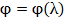

Объектив 8 выполняет обратное фурье-преобразование фильтрованного сигнала (1):

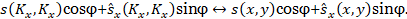
(2)

Интенсивность сигнала (2) регистрируется фотоматрицей камеры 9:

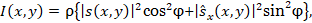
(3)

где 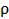 – коэффициент, учитывающий чувствительность фотоматрицы. На длине волны 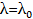, удовлетворяющей условию 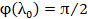, фурье-фильтр выполняет одномерное преобразование Гильберта.

Гильберт-преобразование обладает свойствами перераспределения энергии из области низких пространственных частот в высокочастотную область. Экстремумы и градиенты фазовой оптической плотности исследуемой среды трансформируются в визуализированные структуры гильберт-полос. Пространственное распределение гильберт-полос несёт информацию о возмущениях фазовой оптической плотности, индуцированных температурным полем.

Пламя свечи и спиртовки выбрано в качестве классического объекта для апробации метода диагностики. На рис. 2 представлены результаты измерения температурного профиля в сечениях пламённа различных расстояниях от конца фитиля, выполненные с помощью ХА-термопары. Гильберт-изображения пламён показаны на рис. 3а и 3б.

 

a)                                                         б)

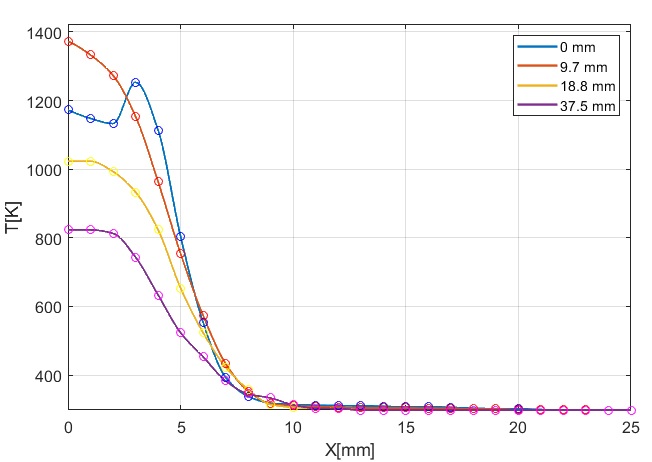
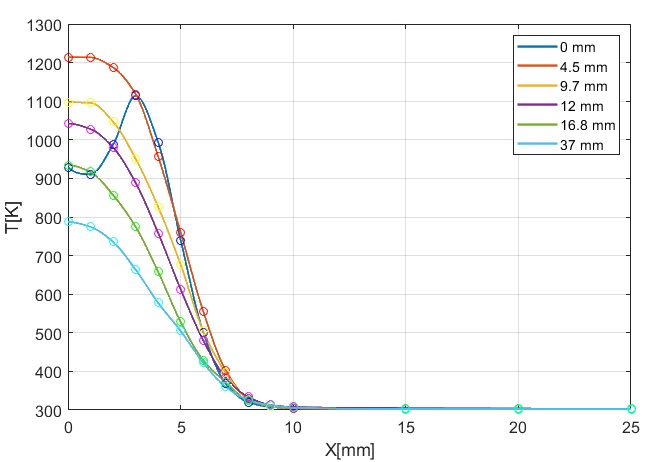
Рис. 2. Температурные профили пламени: (а) – свечи в сечениях 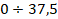на расстояниях  мм от фитиля; (б) – спиртовки на расстояниях 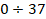 мм от фитиля.

 

Фазовая структура зондирующего светового поля, возмущённого исследуемой средой, определяется как:

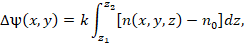
(4)

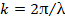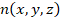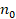где  – волновое число зондирующего поля;  – показатель преломления среды в пространственной структуре пламени; – показатель преломления невозмущённой среды. Ось 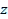 задаётся направлением зондирующего светового пучка, сечение факела описывается в координатах 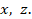 Выбор положения сечения определяется координатой 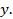 Координаты 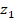,  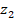задают размер сечения пламени по направлению зондирующего пучка.

В случае осевой симметрии пламени формула (4) трансформируется в уравнение Абеля:

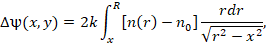
(5)

где 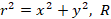 – радиус сечения рассматриваемой зоны,  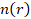– показатель преломления на расстоянии 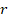 от оси факела. Уравнение Абеля решается приближённым методом, основанным на аппроксимации экспериментальных данных температуры кривыми Безье (частный случай B-сплайнов).

  

a)                                 б)                               в)

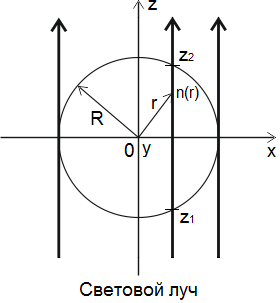
Рис. 3. Экспериментальные гильбертограммы: (а) – пламени свечи, (б) – спиртовки; (в) – схема сечения исследуемого осесимметричного пламени в плоскости .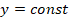

 

Полный фазовый сдвиг 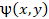 для светового луча в сечении 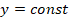 зависит от коэффициента преломления 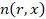 на отрезке (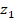, 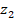), (рис.3в).

Найденные из уравнения Абеля осесимметричные распределения коэффициента преломления 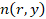 в сечении  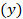факела позволяют определить радиальные поля температуры 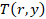. Для этого можно воспользоваться уравнением Гладстона–Дейла:

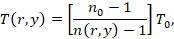
(6)

На рис. 4 представлены графики, иллюстрирующие, согласно уравнениям (5) и (6), восстановление радиального распределения температуры пламени свечи и спиртовки в сечениях, расположенных на расстояниях 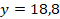 мм и 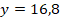 мм от конца фитиля. Красная линия на рис. 4(2) отображает фазовую функцию 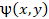 в выбранных сечениях, полученную из уравнения Абеля, зелёная и чёрная линии – интерферограмму и гильбертограмму, реконструированные из фазовой функции 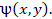 Синяя линия – экспериментальная гильбертограмма.

Из сравнения экспериментальной и реконструированной гильбертограмм в выбранных сечениях видно, что точки локальных минимумов совпадают. Это означает совпадение фазовой функции, полученной из решения уравнения Абеля, и реальной фазовой функции. Следовательно, совпадают реальное и восстановленное поля температур в выбранных сечениях пламени. Критерием правильности полученных результатов является фазовая идентичность реконструированной и экспериментальной гильбертограмм, которая достигается повторением описанной процедуры.

 

a)

 

б)

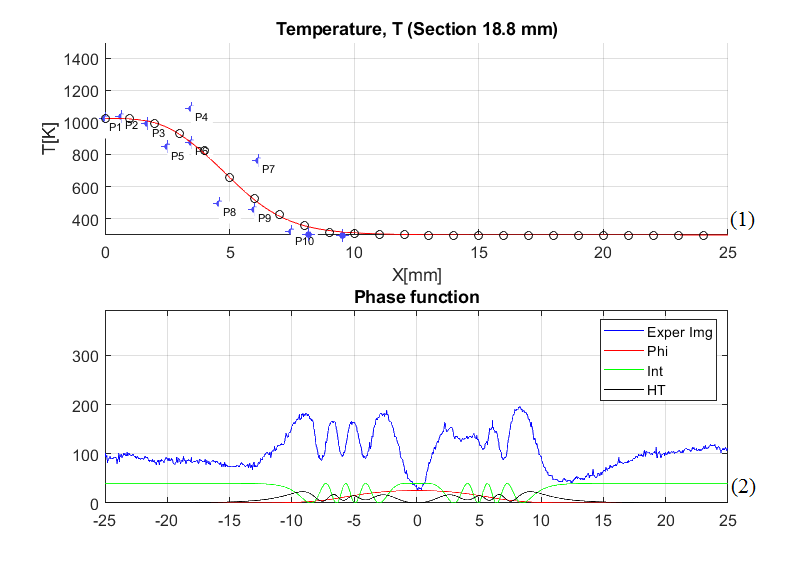
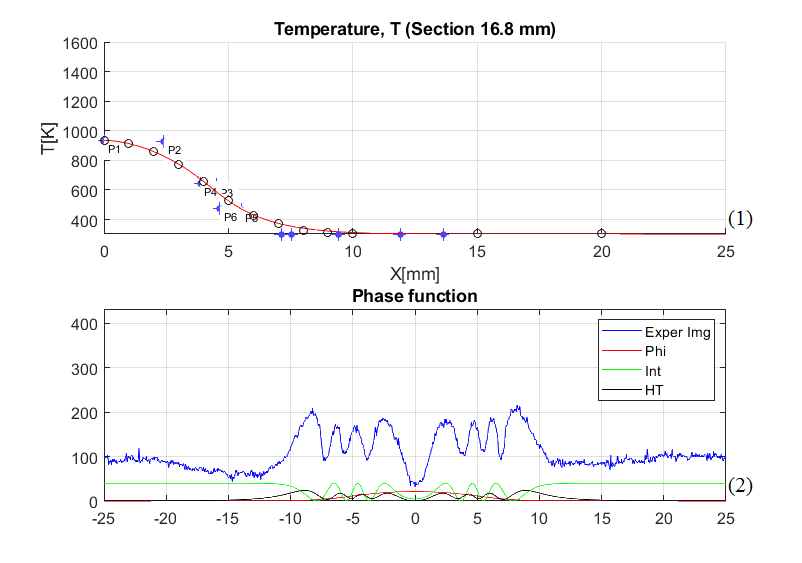
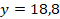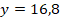Рис. 4. Реконструкция фазовой структуры и температуры пламени свечи (а) и спиртовки (б) в сечениях  мм и  мм:

(1) красная линия – восстановленная температура (кружочки – данные термопары); (2) красная линия – фазовая функция, зелёная – интерферограмма, реконструированная из фазовой функции, чёрная – реконструированная гильбертограмма, синяя – экспериментальная гильбертограмма.

 

На рис. 5 и рис. 6 представлены температурные поля, восстановленные по результатам измерений с помощью термопар (рис. 5а и 6а), и температурные поля, реконструированные из гильберт-изображений (рис. 5б и 6б). Сходство реконструированных и исходных температурных полей вполне удовлетворительное.

В качестве верификации полученных результатов решена обратная задача: из реконструированных температурных полей (рис. 5б и 6б) восстановлены гильберт-изображения (рис. 7б и 7г), которые сопоставлены изображениям, полученным в эксперименте (рис. 7а и 7в).

Из рис. 7 видно, что структуры, полученные в эксперименте, и реконструированные, имеют сходный характер. Этим подтверждается достоверность результатов. Некоторое расхождение обусловлено искажением осевой симметрии пламени в реальном эксперименте из-за влияния динамических возмущений воздушной среды, окружающей пламя.

 

 

a)                                                    б)

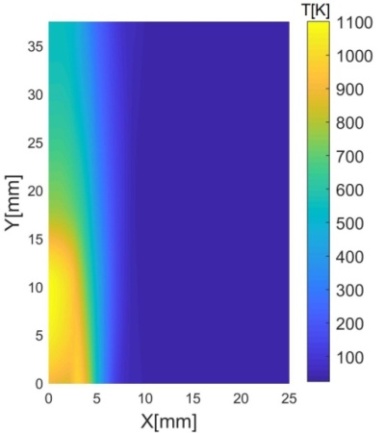
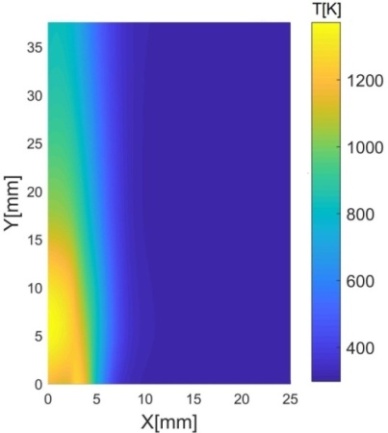
Рис. 5. Температурное поле пламени свечи: (а) – реконструированное по данным термопары, (б) – реконструированное из гильберт-изображения.

 

 

a)                                                   б)

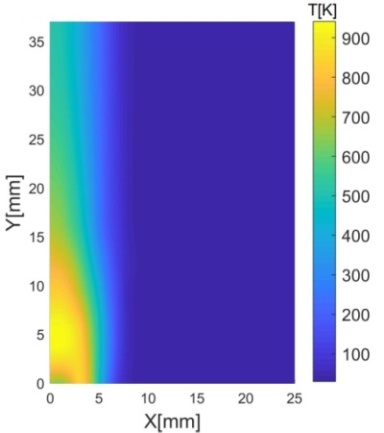
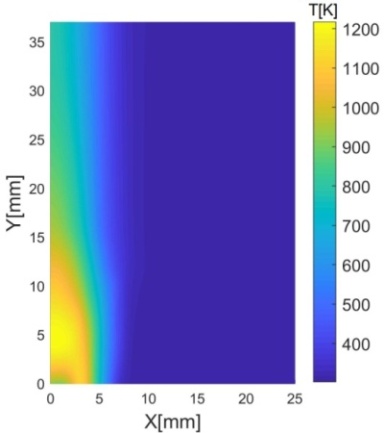
Рис. 6. Температурное поле пламени спиртовки: (а) – реконструированное по данным термопары, (б) – реконструированное из гильберт-изображения.

 

   

a)                             б)                                в)                                г)

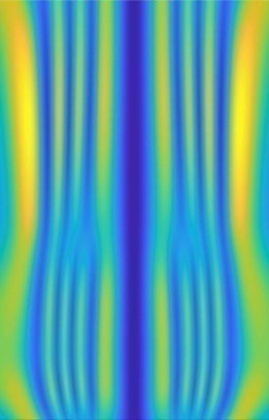
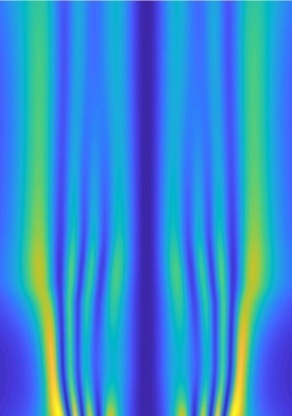
Рис. 7. (а) и (в) – гильберт-изображения пламени свечи и спиртовки, полученные в эксперименте; (б) и (г) – гильберт-изображения пламени свечи и спиртовки, численно смоделированные по реконструированным температурным полям.

 

Разработанный метод оптической диагностики был успешно применён в исследованиях струйного горения предварительно перемешанного пропано-воздушного пламени.

На рис. 8а показано гильберт-изображение струйного горения предварительно перемешанной пропано-воздушной смеси (концентрация пропана 25%) в неподвижной атмосфере (воздухе). Визуализирована градиентная фазовая структура зондирующего светового поля, индуцированная температурным полем в факеле. На рис. 8б представлены результаты измерения температурного профиля факела в сечениях на расстояниях 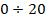 мм от торца трубки. Измерения выполнены с помощью TПР-термопары. На рис. 8в представлен график, иллюстрирующий восстановление радиального распределения температуры в сечении факела 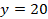 мм от торца трубки.

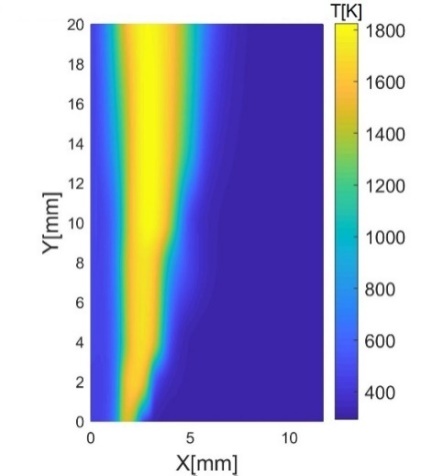
На рис. 9а и 9б – температурные поля, полученные по результатам измерений термопары, и реконструированные из гильберт-изображений, соответственно.

Рис. 10а и 10б иллюстрируют сравнение гильберт-изображений, восстановленного и полученного в эксперименте температурных полей.

 

 

a)                                                    б)

 

в)

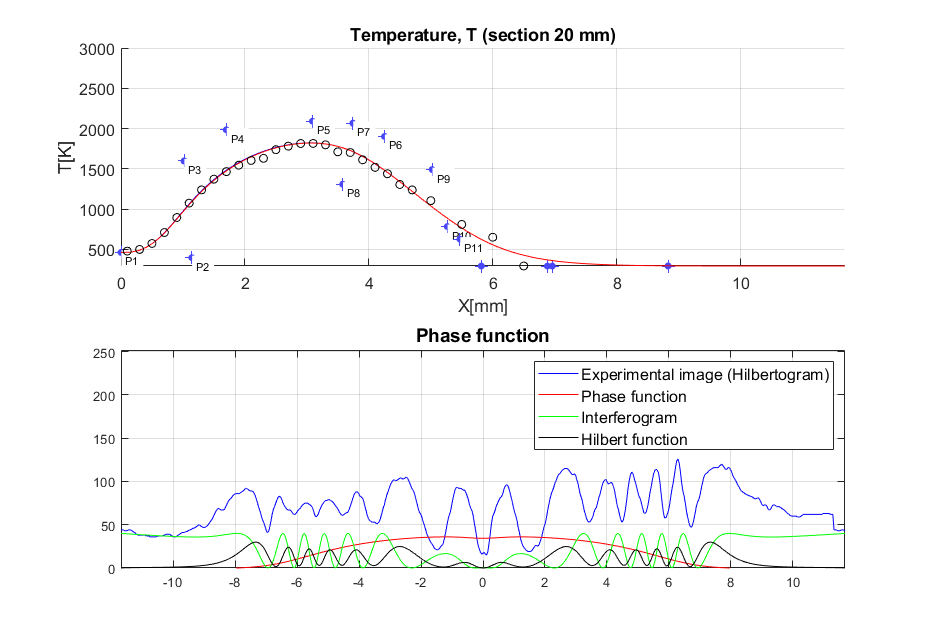
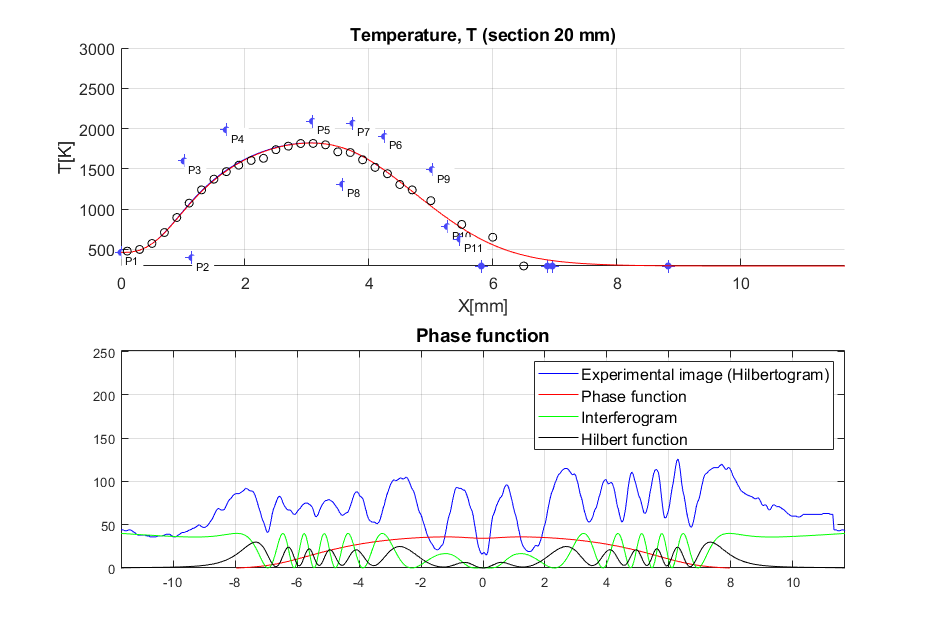
Рис. 8. (а) – Гильбертограмма струйного горения предварительно перемешанной пропано-воздушной смеси 25% в воздухе; (б) – температурные профили струйного горения пропано-воздушной смеси 25% на расстояниях 0÷20 мм; (в) – реконструкция фазовой структуры и температуры факела в сечении 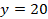 мм.

 

 

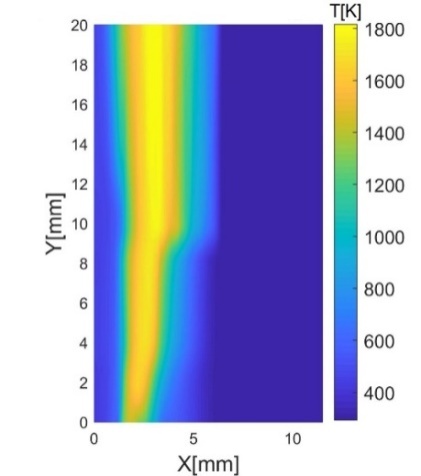
a)                                                    б)

Рис. 9. (а) – температурное поле, восстановленное по термопарным измерениям, (б) – температурное поле, реконструированное из гильберт-изображения.

 

 

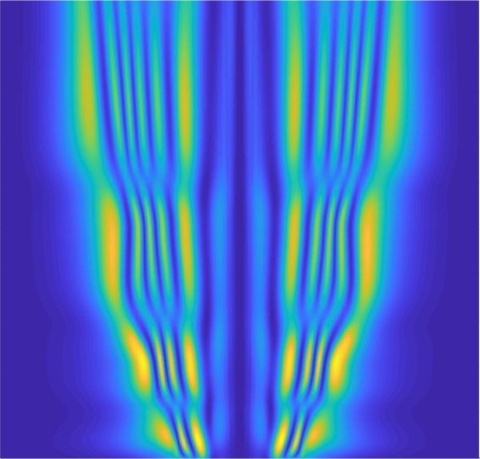
a)                               б)

Рис. 10. (а) – гильберт-изображение пропано-воздушного факела, полученное в эксперименте; (б) – гильберт-изображение, численно смоделированное из реконструированного температурного поля.

 

3.   Заключение

В представленной работе выполнено исследование пламени свечи, спиртовки и предварительно перемешанного пропано-воздушного факела с применением методов гильберт-оптики в приближении осевой симметрии с использованием преобразования Абеля. Достоверность результатов подтверждается сравнением гильбертограмм, полученных в эксперименте, и реконструированных из фазовой структуры по Абелю. Результаты сравнения используются как критерий качества моделирования фазовой структуры и температурного поля при исследовании процесса горения.

Авторы выражают благодарность Н.С. Буфетову за помощь в работе

Работа выполнена в рамках государственного задания ИТ СО РАН (Гос. рег. АААА–А17–117030310010–9) и при поддержке комплексной Программы фундаментальных научных исследований СО РАН II.1 (проект 0314-2018-0010).

Список литературы

1.    Дубнищев Ю. Н., Арбузов В. А., Белоусов П. П., Белоусов П. Я. Оптические методы исследования потоков. Новосибирск: Сибирское университетское издательство, 2003, 418 С.

2.   Дубнищев Ю.Н. Теория и преобразование сигналов в оптических системах. СПб.: Издательство «Лань», 2011, 368 С.

3.   Dubnishchev Yu. N., Lemanov V. V., Lukashov V. V., Arbuzov V. A., Sharov K. A. Hydrodynamic vortex structure sinadiffusion jet flame (Электронное издание) // «Swirling Flows and Flames», pp. 1 – 21. DOI: 10.5772/intechopen.80610. https://www.intechopen.com/online-irst/hydrodynamic-vortex-structures-in-a-diffusion-jet-flame. Published: November 5th 2018.

4.   Дубнищев Ю. Н., Арбузов В. А., Леманов В. В., Лукашов В. В., Шаров К. А. Исследование струйного горения водорода с помощью гильберт-диагностики // Автометрия, 2019. 55, № 1, С. 21 – 25.

5.   Белозёров А. Ф. Оптические методы визуализации потоков. Казань: издательство КГТУ, 2007, 747 С.

6.   Qunxing Huang, Fei Wang, Jianhua Yan, and Yong Chi. Simultaneous estimation of the 3-D soot temperature and volume faction distributions in asymmetric flames using high-speed stereoscopics images // Applied Optics, 2012, 51 (15), pp. 2968 – 2978.

7.    Jochen A. H. Dreyer, Radomir I. Slawchov, Eric J. Rees, Jethro Akroyd, Maurin Salamanca, Sebastian Mosbach, and Markus Kraft. Improved methodology for performing the inverse Abel transform of flame images for cilir ratio pyrometry // Applied Optics, 2019, 58 (10), pp. 2662 – 2670.

8.   Литвиненко Ю. А. Устойчивость дозвуковых макро- и микроструктурных течений и микроструйное горение (обзор) // Сибирский физический журнал, 2017, 12 (3), С. 83 – 89.

---

Optical diagnostics of temperature field of an axisymmetric flame

Authors: Yu.N.  Dubnishchev^1,А,C,D, V.A.  Arbuzov^2,A,C, E.V.  Arbuzov^3,B,C, O.S.  Zolotukhina^4,C, V.V.  Lukashov^5,A

^A Kutateladze Institute of Thermophysics, Siberian Branch of the Russian Academy of Sciences

^B Sobolev Institute of Mathematics of the Siberian Branch of the Russian Academy of Sciences

^C Novosibirsk State Technical University

^D Technological Design Institute of Scientific Instrument Engineering of the Siberian Branch of the Russian Academy of Sciences

¹ ORCID: 0000-0001-7874-039X, dubnistchev@itp.nsc.ru

² ORCID: 0000-0003-2404-326X, arbuzov@itp.nsc.ru

³ ORCID: 0000-0001-9488-8650 , arbuzov@math.nsc.ru

⁴ ORCID: 0000-0003-3486-4459 , melexinaolga17@yandex.ru

⁵ ORCID: 0000-0001-8178-7607, luka@itp.nsc.ru

 

Abstract

The structure of the temperature field of an axisymmetric flame using an example of a candle, spiritlamp, and propane-air torch was studied. The optical diagnostics adapted to the study of combustion problems is based on the visualization by methods of Hilbert-optics of phase disturbances induced by the medium under study in a probe light field. The diagnostic complex is implemented on the basis of the IAB–463M device with modified blocks of optical filtration, light source, registration and information processing. The dynamic phase structure of the candle flame and spiritlamp was visualized as a classic object for approbation the diagnostic method. The dynamic phase structure of the propane-air torch was investigated. The temperature was measured using thermocouples at the reference points. The phase function was restored on axisymmetric sections from the obtained hilbertograms, and the temperature field of flame was reconstructed using the inverse Abel transform.

 

Keywords: optical diagnostics of flames, propane-air flame, Hilbert-optics.

 

References

               

1.       Dubnishchev Yu. N., Arbuzov V. A., Belousov P. P., Belousov P. Ya. Opticheskie metody issledovaniya potokov [Optical Methods of Flow Investigation]. Sib. Univ. Izd., Novosibirsk, 2003, 418 p. [in Russian]

2.      Dubnishchev Yu. N. Teoriya i preobrazovanie signalov v opticheskih sistemah [Theory and Transformation of Signals in Optical Systems]. St.–Petersburg: Publishing house «Lan», 2011, 368 p. [in Russian]

3.      2.Dubnishchev Yu. N., Lemanov V. V., Lukashov V. V., Arbuzov V. A., Sharov K. A.  Hydrodynamic vortexs tructure sinadiffusi on jet flame (electronic edition) // «Swirling Flows and Flames», pp. 1 – 21. DOI: 10.5772/intechopen.80610. https://www.intechopen.com/online-irst/hydrodynamic-vortex-structures-in-a-diffusion-jet-flame. Published: November 5th 2018.

4.      Yu. N. Dubnishchev, V. A. Arbuzov, V. V. Lukashov, K. A. Sharov, V. V. Lemanov. Optical Hilbert Diagnostics of Hydrogen Jet Burning// Optoelectron., Instrum. Data Process., 2019, 55: pp. 16 - 19. https://doi.org/10.3103/S8756699019010035

5.      Belozerov A. F. Opticheskie metody vizualizacii potokov [Optical Methods of Gas Flow Visualization]. Izd. Kazan. Gos. Tekh. Univ., Kazan’, 2007, 747 p. [in Russian]

6.      Qunxing Huang, Fei Wang, Jianhua Yan, and Yong Chi. Simultaneous estimation of the 3-D soot temperature and volume faction distributions in asymmetric flames using high-speed stereoscopics images // Applied Optics, 2012, 51 (15), pp. 2968 – 2978.

7.      Jochen A. H. Dreyer, Radomir I. Slawchov, Eric J. Rees, Jethro Akroyd, Maurin Salamanca, Sebastian Mosbach, and Markus Kraft. Improved methodology for performing the inverse Abel transform of flame images for cilir ratio pyrometry // Applied Optics, 2019, 58 (10), pp. 2662 – 2670.

8.     Yu. A. Litvinenko Yu. A. “Stability of Subsonic Macro- and Microjets and Microjet Burning (Review),” Sib. Fiz. Zh. 12 (3), 2017, pp. 83 – 99.