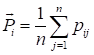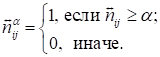Одним из широко применяемых в настоящее время подходов к моделированию
слабоструктурированных систем и принятию решений в управлении такими
системами является когнитивный подход. В соответствии с определением,
приведенным в [2], данный подход ориентирован на разработку формальных моделей
и методов, поддерживающих интеллектуальный процесс решения проблем благодаря
учету в этих моделях и методах когнитивных возможностей человека (восприятие,
представление, познание, понимание, объяснение) при решении управленческих
задач. Методы структурно-целевого и имитационного моделирования систем на
основе когнитивного подхода принято объединять под общим термином «когнитивное
моделирование». В общем виде под когнитивной моделью понимается модель
экспертных знаний о системе, происходящих в ней процессах, а также законах и
закономерностях ее функционирования, представленная в виде когнитивной карты.
Когнитивной картой называется причинно-следственная сеть, которая отражает
субъективное представление исследователя о системе (индивидуальное или
коллективное) в виде множества семантических категорий, называемых факторами
или концептами, и множества причинно-следственных связей между ними.
Когнитивная модель представляет собой эффективный инструмент
для разведочного, оценочного анализа ситуации. Она не позволяет получить
точные, количественные характеристики исследуемой системы, но позволяет оценить
тенденции и тренды, связанные с ее функционированием и развитием, и выявить
значимые факторы, оказывающие наибольшее влияние на указанные процессы. Как
отмечено в [9], считается, что знание грубой, возможно даже гипотетической
модели системы позволяет прогнозировать сценарии развития начальных ситуаций
при различных управляющих воздействиях путем варьирования переменных модели. Благодаря
этому появляется возможность поиска и генерации эффективных решений по
управлению системой, а также выявления рисков и разработки стратегий их
снижения.
Процесс когнитивного моделирования начинается с построения
когнитивной карты исследуемой системы на основе информации, получаемой от экспертов
или путем анализа имеющихся данных о системе [15]. На следующем этапе
происходит непосредственно моделирование, основными целями которого являются
формирование и проверка гипотез о структуре исследуемой системы, позволяющих
объяснить ее поведение, а также выработка стратегий поведения в той или иной
ситуации с целью достижения заданных целевых состояний.
Задачи, решаемые с помощью когнитивного моделирования, можно
разделить на две группы:
– статический (структурно-целевой) анализ, целью которого
является нахождение факторов, оказывающих наиболее значимое влияние на целевые,
выявление противоречий между целями, анализ циклов обратной связи и др.;
– динамический (сценарный) анализ, направленный на прогнозирование
состояния системы при различных управляющих воздействиях и поиск решений по
приведению системы в целевое состояние.
В качестве математического аппарата, применяемого для
представления и анализа когнитивных моделей, чаще всего используется нечеткая
логика. Существует целый класс когнитивных моделей, основанный на различных
типах нечетких когнитивных карт (НКК) – достаточно подробный обзор таких
моделей можно найти, например, в монографии [3]. Одной из разновидностей НКК,
хорошо зарекомендовавшей себя в практических задачах анализа и моделирования
слабоструктурированных социальных, организационных, и экономических систем
являются нечеткие когнитивные карты В.Б. Силова [11, 14].
Одним из условий эффективной работы с когнитивной моделью
является обеспечение ее визуального представления. В статье предлагается
метафора визуализации нечетких когнитивных карт (на примере НКК Силова), в
основе которой лежат алгоритмы визуализации графов и понятие когнитивной
ясности. Рассматриваются примеры применения различных метафор визуализации и
возможности интерактивного управления визуальным образом нечеткой когнитивной
карты в разработанной с участием авторов системе поддержки принятия решений
«ИГЛА». Более подробное описание системы «ИГЛА» можно найти в [10], а
демо-версию – по адресу http://iipo.tu-bryansk.ru/quill. Система представляет
собой Windows-приложение на платформе Microsoft .NET Framework, и в настоящее
время ведется разработка сетевой многопользовательской версии.
Как уже отмечалось, когнитивная модель основана
на формализации причинно-следственных связей, которые имеют место между
факторами, характеризующими исследуемую систему. Результатом формализации
является представление системы в виде причинно-следственной сети, называемой
когнитивной картой и имеющей вид:
G
= < E, W >,
где E = {e1, e2, …, eK}
– множество факторов (называемых также концептами), W – бинарное
отношение на множестве E, которое задает набор связей между его
элементами.
Концепты могут задавать как относительные (качественные)
характеристики исследуемой системы, такие как надежность, технологичность, так
и абсолютные, измеримые величины – время, трудоемкость, себестоимость
и т.п. При этом с каждым концептом ei связывается
переменная состояния vi, которая задает значение
соответствующего показателя в определенный момент времени. Переменные состояния
могут принимать значения, выраженные в некоторой шкале, в пределах
установленных ограничений. Значение vi(t) переменной
состояния в момент времени t называется состоянием концепта ei
в данный момент времени. Таким образом, состояние моделируемой системы в любой
момент времени описывается состоянием всех концептов, входящих в ее
когнитивную карту.
Концепты ei и ej
считаются связанными отношением W (обозначается 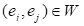 или
или 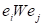 ), если изменение значения концепта ei
(причины) приводит к изменению значения концепта ej
(следствия). В этом случае говорят, что концепт ei оказывает
влияние на концепт ej. При этом если увеличение значения
переменной состояния концепта-причины приводит к увеличению значения переменной
состояния концепта-следствия, то влияние считается положительным («усиление»),
если же значение уменьшается – отрицательным («торможение»). Тем самым, отношение
W можно представить в виде объединения двух непересекающихся подмножеств
), если изменение значения концепта ei
(причины) приводит к изменению значения концепта ej
(следствия). В этом случае говорят, что концепт ei оказывает
влияние на концепт ej. При этом если увеличение значения
переменной состояния концепта-причины приводит к увеличению значения переменной
состояния концепта-следствия, то влияние считается положительным («усиление»),
если же значение уменьшается – отрицательным («торможение»). Тем самым, отношение
W можно представить в виде объединения двух непересекающихся подмножеств
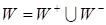 , где W +
– множество положительных, а W – – множество
отрицательных связей.
, где W +
– множество положительных, а W – – множество
отрицательных связей.
Нечеткая когнитивная модель основана на предположении о том,
что влияния между концептами могут различаться по интенсивности, при этом
интенсивность может быть постоянной либо переменной во времени. Для учета
данного обстоятельства W задается как нечеткое отношение, при этом
способ его задания зависит от применяемого подхода к формализации
причинно-следственных связей. Когнитивная карта с нечетким отношением W
называется нечеткой когнитивной картой.
Нечеткая когнитивная карта Силова представляет собой НКК, характеризующуюся
следующими особенностями.
1. Переменные состояния концептов могут принимать значения
на отрезке [0, 1].
2. Интенсивность взаимовлияний считается постоянной, и таким
образом, отношение W задается в виде набора чисел wij,
характеризующих направление и степень интенсивности (вес) влияния между
концептами ei и ej:
wij
= w(ei
, ej),
где w – нормированный
показатель интенсивности влияния (характеристическая функция отношения W), обладающий следующими свойствами:
а)
–1 ≤ wij ≤ 1;
б) wij = 0, если ej
не зависит от ei (влияние
отсутствует);
в) wij = 1 при максимальном положительном влиянии
ei на ej,
т.е. когда любая реализация изменений в системе,
связанных с концептом ej, однозначно
определяется действиями, связанными с концептом ei;
г) wij = –1 при максимальном отрицательном
влиянии, т.е. когда любая реализация изменений, связанных с концептом ej, однозначно сдерживается действиями,
связанными с концептом ei;
д) wij принимает значение из интервала (–1, 1)
при промежуточной степени положительного или отрицательного влияния.
Легко заметить, что НКК данной структуры может быть наглядно
представлена в виде взвешенного ориентированного графа, вершины которого
соответствуют элементам множества E (концептам), а дуги – ненулевым
элементам отношения W (причинно-следственным связям). Каждая дуга имеет
вес, задаваемый соответствующим значением wij. При этом само
отношение W представимо в виде матрицы размерности n´n (где n – число
концептов в системе), которая может рассматриваться как матрица смежности
данного графа и называется когнитивной матрицей.
На рис. 1 показан пример нечеткой когнитивной карты выбора
технологии изготовления штампованного изделия [8]. Данная НКК построена в
рамках разработанной при непосредственном участии авторов модели поддержки
принятия решений в области автоматизации проектирования технологической
оснастки. Цвет дуги задает знак соответствующей причинно-следственной связи
между концептами: красный цвет означает положительную связь, синий –
отрицательную, толщина дуги задает интенсивность связи.
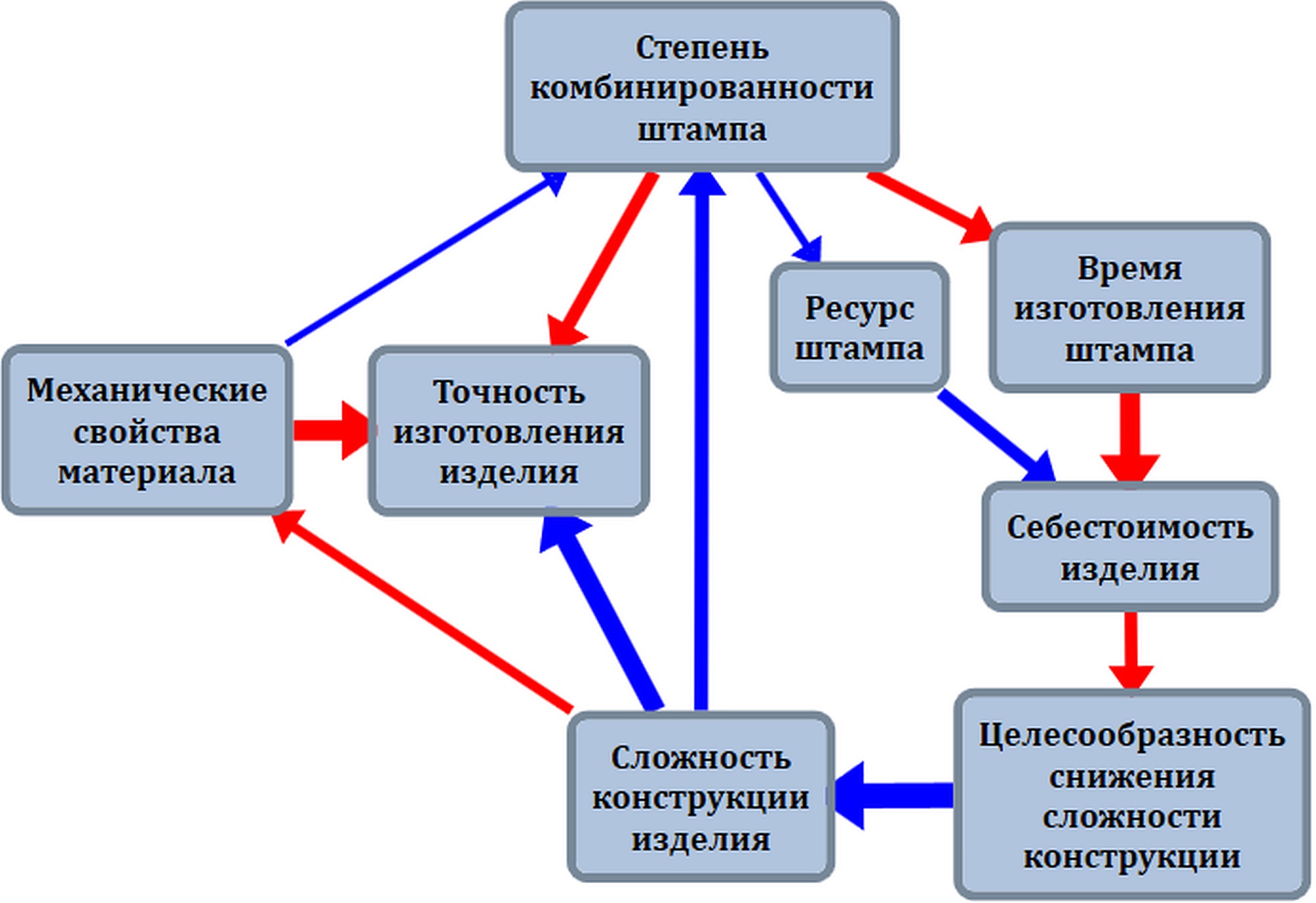
Рис. 1. Нечеткая
когнитивная карта для задачи выбора технологии изготовления штампованного
изделия
На рис. 2 показана схема обобщенного алгоритма построения и
анализа когнитивной модели слабоструктурированной системы на основе НКК Силова.
В настоящей работе исследуется этап визуализации НКК. Более подробное описание других
этапов данного алгоритма и применяемых на них методов можно найти, например, в
работах [8, 10, 11, 14, 15].
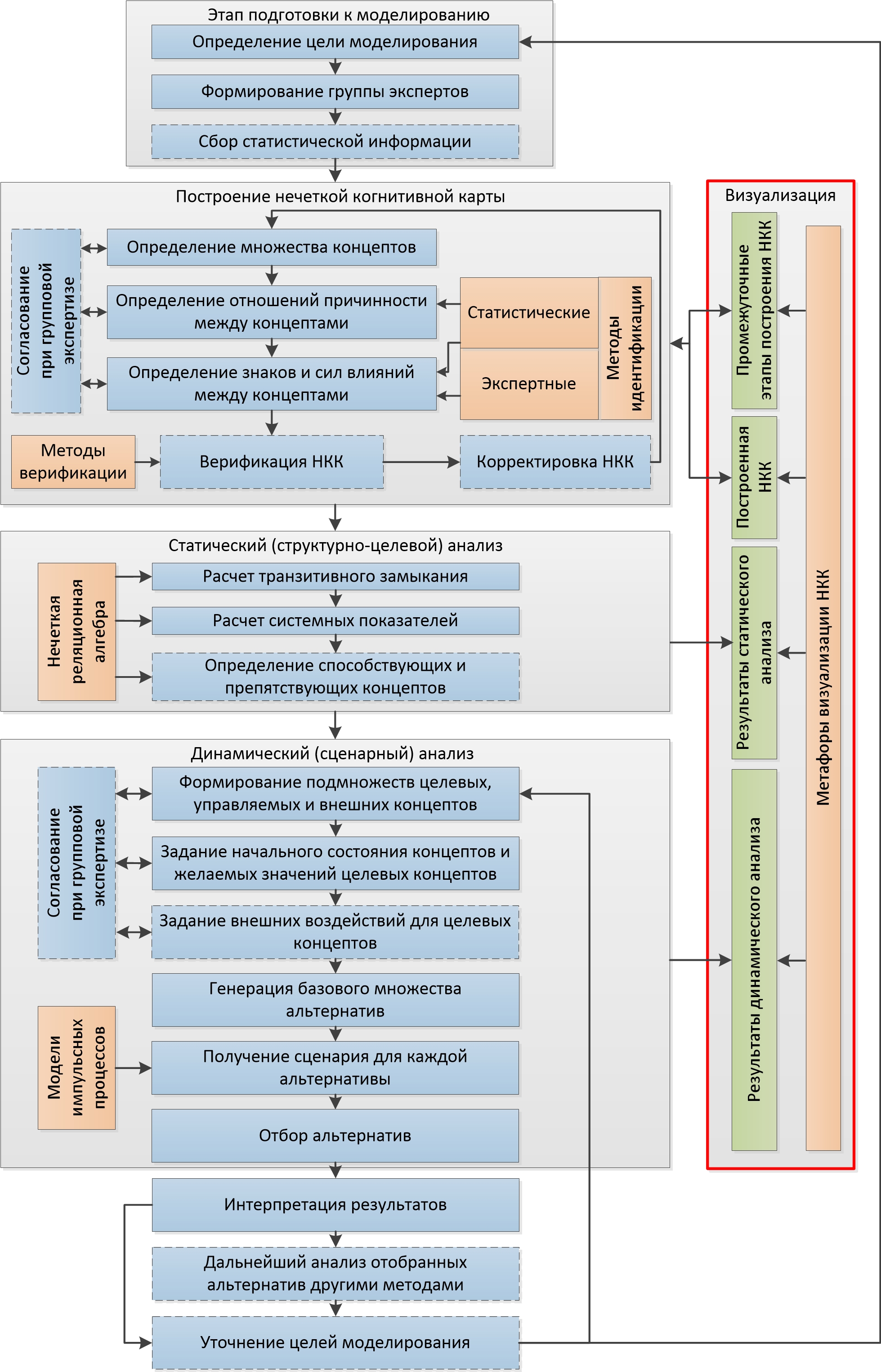
Рис. 2. Обобщенный
алгоритм построения и анализа когнитивной модели
Визуальный анализ является неотъемлемой составляющей
процесса когнитивного моделирования, как на этапе построения когнитивной карты,
так и на этапах ее верификации и исследования. Важность обеспечения наглядного
и удобного для восприятия визуального представления когнитивной карты
обусловлена следующими обстоятельствами.
1. Визуальное
представление когнитивной карты предоставляет исследователю (эксперту,
аналитику) зачастую единственную возможность «охватить модель одним взглядом»,
в результате чего тот способен быстро заметить ошибки (например, пробелы или
избыточность), допущенные при ее построении.
2. Наличие
визуального представления является необходимым условием для обеспечения
возможности отображения результатов верификации когнитивной карты (в простейшем
случае верификация представляет собой поиск избыточных транзитивных путей
передачи влияния между концептами и замкнутых бесконечно усиливающих или
ослабляющих циклов влияния).
3. Визуальное
представление может быть использовано для отображения результатов
структурно-целевого и сценарного анализа когнитивной модели.
Тем не менее, в публикациях по когнитивному моделированию
проблеме визуализации когнитивных карт уделяется достаточно мало внимания.
Отдельные аспекты данной проблемы рассматривались в работах [1, 12].
В опубликованной авторами ранее работе [6] был предложен подход,
подразумевающий сведение задачи визуализации НКК Силова к задаче визуализации
графов. Исследовался ряд алгоритмов визуализации графов. В соответствии с
идеей, лежащей в основе построения и работы этих алгоритмов, среди них можно
выделить алгоритмы, основанные на физических аналогиях (силовые алгоритмы),
алгоритмы, основанные на принципах самоорганизации, и алгоритмы поуровневого
изображения ориентированных графов.
По результатам экспериментальной проверки рассмотренных
алгоритмов на реальных НКК, наиболее подходящими для реализации в системе
«ИГЛА» были признаны алгоритм LinLog [17], относящийся
к классу силовых алгоритмов, и алгоритм ISOM [16],
основанный на принципах самоорганизации.
Дальнейшим развитием данного подхода является его расширение до метафоры
визуализации, с учетом требований обеспечения когнитивной ясности визуального
представления.
В работе [5] метафора визуализации определяется как
отображение визуализируемого объекта из пространства данных исходной задачи в
объект пространства представления, происходящее посредством условного переноса
признаков элементов одного множества на элементы другого множества.
При этом, согласно [5], метафора визуализации может
использоваться на двух стадиях решения задач визуализации. Первый раз – при
переходе от исходных данных к пространству визуальной модели. Для этого случая
используется термин «пространственная метафора». Второй раз необходимость в
применении этого приема возникает на стадии уточнения результатов визуализации,
усиления необходимых для решения составляющих, фильтрации избыточных компонент
созданного образа и т.д. Для данного случая используется термин «метафора
представления». Фактическая роль пространственной метафоры состоит в
преобразовании данных решаемой задачи в данные, описывающие элементы
пространства визуальной модели. Метафора представления используется как
средство, раскрывающее потенциальные преимущества уже примененной
пространственной метафоры.
Рассмотрим предлагаемый способ построения двух составляющих
метафоры визуализации НКК – пространственной метафоры и метафоры представления.
Поскольку пространственная метафора подразумевает переход к
пространству визуальной модели, необходимо определить в первую очередь вид
этого пространства – в частности, его размерность.
В работе [12] приводится модель «когнитивное облако»
(фактически это пространственная метафора), подразумевающая расположение
когнитивной карты в трехмерном пространстве. Выдвигается гипотеза о том, что
такое визуальное представление в большей степени (по сравнению с расположением
карты на плоскости) будет способствовать пониманию когнитивной модели при ее
чтении. В подтверждение выдвинутой гипотезы приводится пример применения
предложенного подхода.
Вместе с тем, метафора, основанная на модели «когнитивное
облако», не является универсальной, поскольку она ориентирована на визуализацию
когнитивных карт специфичной структуры (а именно, с наличием ярко выраженных
«факторов-ядер»), в то время как потенциальная эффективность применения данной
метафоры для визуализации карт произвольной структуры вызывает сомнения. Помимо
этого, визуализация в трехмерном пространстве, очевидно, является более
ресурсоемким процессом, чем в двумерном, что может негативно сказаться на
скорости отрисовки модели и времени ее отклика на действия пользователя,
особенно при большом количестве концептов и причинно-следственных связей. Таким
образом представляется целесообразной разработка такой метафоры в двумерном
пространстве (на плоскости), которая, с одной стороны, свободна от недостатков
и усложнений трехмерной метафоры, а с другой, является более универсальной и
подходящей для НКК произвольной структуры.
Как упоминалось ранее, задача визуализации НКК в целом
сводится к задаче визуализации графа, которая, в двумерном случае, может быть
решена при помощи обширного класса алгоритмов укладки графов. Таким образом, в
основе пространственной метафоры визуализации НКК должны лежать указанные
алгоритмы. Однако при этом также должны быть учтены проблемы ограниченности
когнитивных возможностей человека при чтении графов (подробный анализ данной
проблемы можно найти, например, в [13]). Предложенный в упомянутой выше работе
[6] подход позволяет получить удовлетворительные результаты визуализации,
однако при этом не учитывается важный аспект качества получаемого изображения,
а именно, достижение его когнитивной ясности. Понятие когнитивной ясности и
связанные с ним критерии будут рассмотрены далее.
В результате применения к исходным данным (структуре
когнитивного графа) пространственной метафоры будет получено расположение (т.е.
координаты на плоскости) его вершин и дуг, являющееся оптимальным в некотором
отношении. Разработка и описание конкретных критериев оптимального расположения
выходит за рамки настоящей работы и является направлением дальнейших исследований.
Метафора представления, как уже отмечалось, призвана
«раскрыть преимущества» используемой пространственной метафоры, в результате
чего совершается переход от визуальной модели исследуемого объекта к его
визуальному образу. Исходя из многоэтапности процесса когнитивного
моделирования (включающего в себя как построение модели и ее верификацию, так и
различные виды ее анализа), возникает потребность в разработке нескольких
различных метафор представления. При этом каждая из этих метафор должна
соответствовать определенному этапу моделирования и способствовать достижению
исследователем поставленной на данном этапе цели. Таким образом, метафоры
представления должны строиться, исходя из акцентов восприятия исследователя на
том или ином этапе когнитивного моделирования.
Перечислим с примерами основные метафоры представления НКК,
реализованные в системе «ИГЛА». Для примеров будем использовать упоминавшуюся
ранее когнитивную карту выбора технологии изготовления штампованного изделия
(рис. 1).
1. Основная
метафора, используемая «по умолчанию», соответствует когнитивной карте, которая
была показана выше, на рис. 1. Данная метафора представления позволяет
исследователю акцентировать внимание на структуре когнитивной карты в целом, не
отвлекаясь на особенности отдельных ее концептов. В рамках данной метафоры для представления
всех концептов используется единый цвет (серо-голубой). Как уже отмечалось
выше, цвет дуги задает знак соответствующей причинно-следственной связи между
концептами: красный цвет означает положительную связь («усиление»), синий –
отрицательную («торможение»). Толщина дуги определяет интенсивность связи.
2. Метафоры,
подразумевающие визуальное разделение концептов в зависимости от их типов либо
их принадлежности к тем или иным смысловым группам, которые задаются самими экспертами
при построении когнитивной модели. На рис. 3 показан пример визуального
разделения с целью акцентировать внимание исследователя на взаимном
расположении управляемых (желтый цвет), наблюдаемых (зеленый цвет) и целевых
(серо-голубой цвет) концептов. Отметим (следуя [10]), что управляемыми являются
концепты, состояние которых поддается непосредственному управлению,
наблюдаемыми – концепты, состояние которых не может задаваться непосредственно
и определяется изменением состояний концептов-причин, целевыми – концепты,
которые необходимо привести в заданное целевое состояние. Так, в рассматриваемом
примере предполагается [8], что:
-
при выборе технологии изготовления штампованного изделия
проектировщик может непосредственно воздействовать на такие факторы, как
механические свойства материала, сложность конструкции изделия и степень
комбинированности штампа;
-
целевыми состояниями задачи выбора являются обеспечение
достаточного уровня ресурса штампа и высокой точности изготовления изделия при
сохранении требуемого уровня сложности его конструкции;
-
наконец, такие параметры, как время изготовления штампа и
себестоимость изделия, не поддаются непосредственному влиянию, и их значения
зависят от состояния целевых и управляемых факторов.
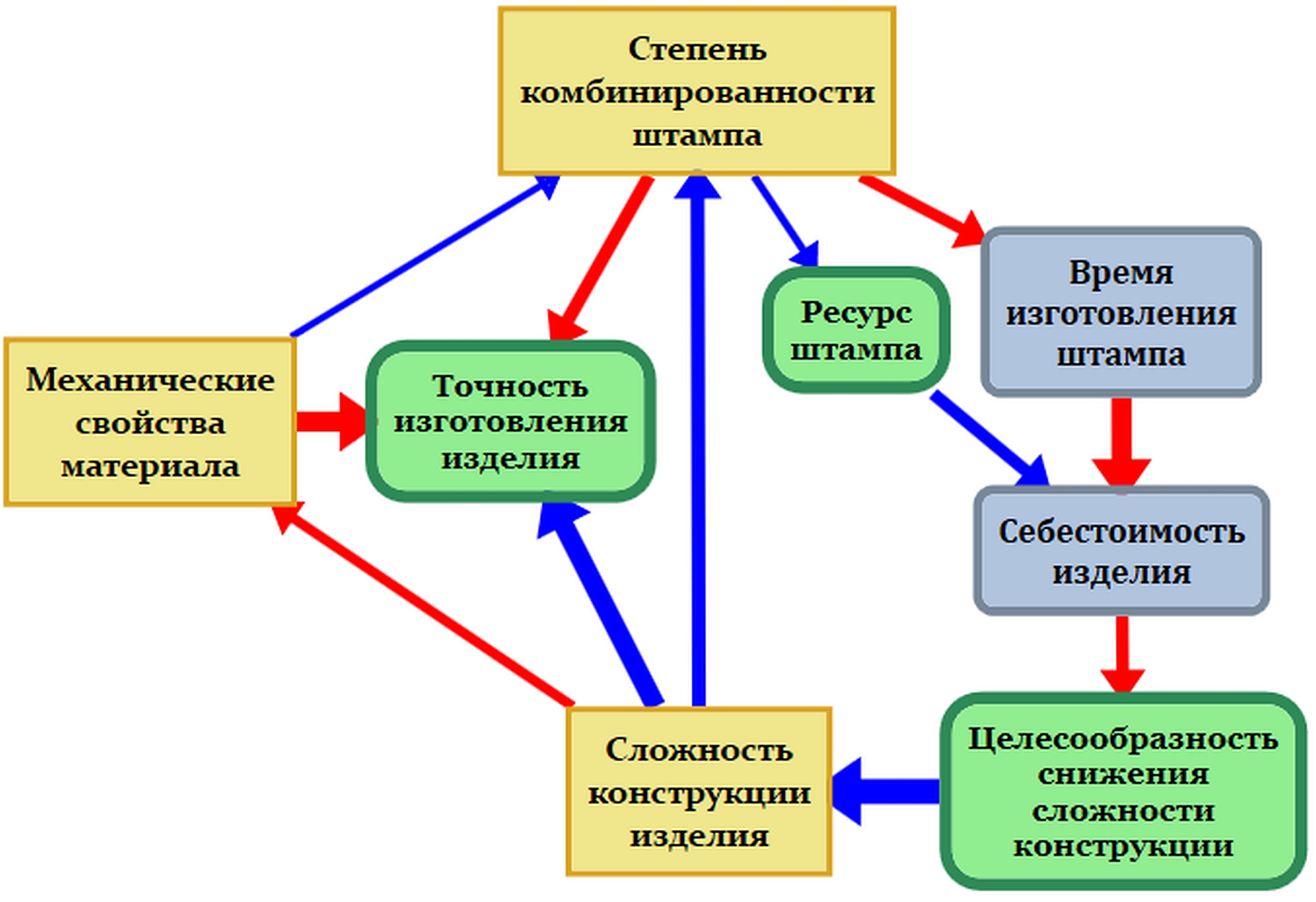
Рис. 3. Метафора разделения
концептов по типам
3. Группа метафор, позволяющих визуализировать в наглядной
форме системные показатели НКК, рассчитанные в результате ее
структурно-целевого анализа. Для выполнения структурно-целевого анализа помимо
непосредственно заданных причинно-следственных связей необходимо учесть все
имеющиеся в системе опосредованные взаимовлияния факторов друг на друга. Это
позволяет сделать операция транзитивного замыкания, преобразующая исходную
матрицу интенсивности взаимовлияний W в
транзитивно замкнутую матрицу Z, элементами которой являются пары
(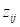 ,
,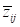 ), где
), где 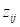 характеризует силу положительного влияния, а
характеризует силу положительного влияния, а 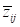 – силу
отрицательного влияния i-го концепта на j-й. Алгоритм расчета
нечеткого транзитивного замыкания подробно описан в монографии [11].
На основе матрицы Z может быть рассчитан ряд системных показателей
НКК, подробное описание которых можно найти, например, в работах [8, 10,
11]. В примере на рис. 4 объектами визуализации являются сравнительная
интенсивность и направление влияния всех концептов на систему. Влияние i-го
концепта на систему рассчитывается по следующей формуле:
– силу
отрицательного влияния i-го концепта на j-й. Алгоритм расчета
нечеткого транзитивного замыкания подробно описан в монографии [11].
На основе матрицы Z может быть рассчитан ряд системных показателей
НКК, подробное описание которых можно найти, например, в работах [8, 10,
11]. В примере на рис. 4 объектами визуализации являются сравнительная
интенсивность и направление влияния всех концептов на систему. Влияние i-го
концепта на систему рассчитывается по следующей формуле:
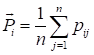
где n – количество концептов в системе, pij – влияние
(воздействие) i-го концепта на j-й (т.е. доминирующее по силе
влияние между концептами):
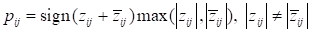
где sign(x) – функция, возвращающая знак выражения x.
По аналогии с цветами дуг, для представления концептов,
положительно влияющих на систему, используются оттенки красного цвета,
а отрицательно влияющих – оттенки синего цвета. Насыщенность цвета определяет
интенсивность влияния. Таким образом, наиболее сильное положительное влияние на
систему оказывают концепты «Степень комбинированности штампа» и «Время
изготовления штампа», а наиболее сильное отрицательное влияние – концепт
«Сложность конструкции изделия». При этом белый цвет означает, что данный
концепт не оказывает существенного влияния на систему, что характерно для
целевых концептов, являющихся «стоковыми» – в рассматриваемом примере таким
концептом является «Точность изготовления изделия».
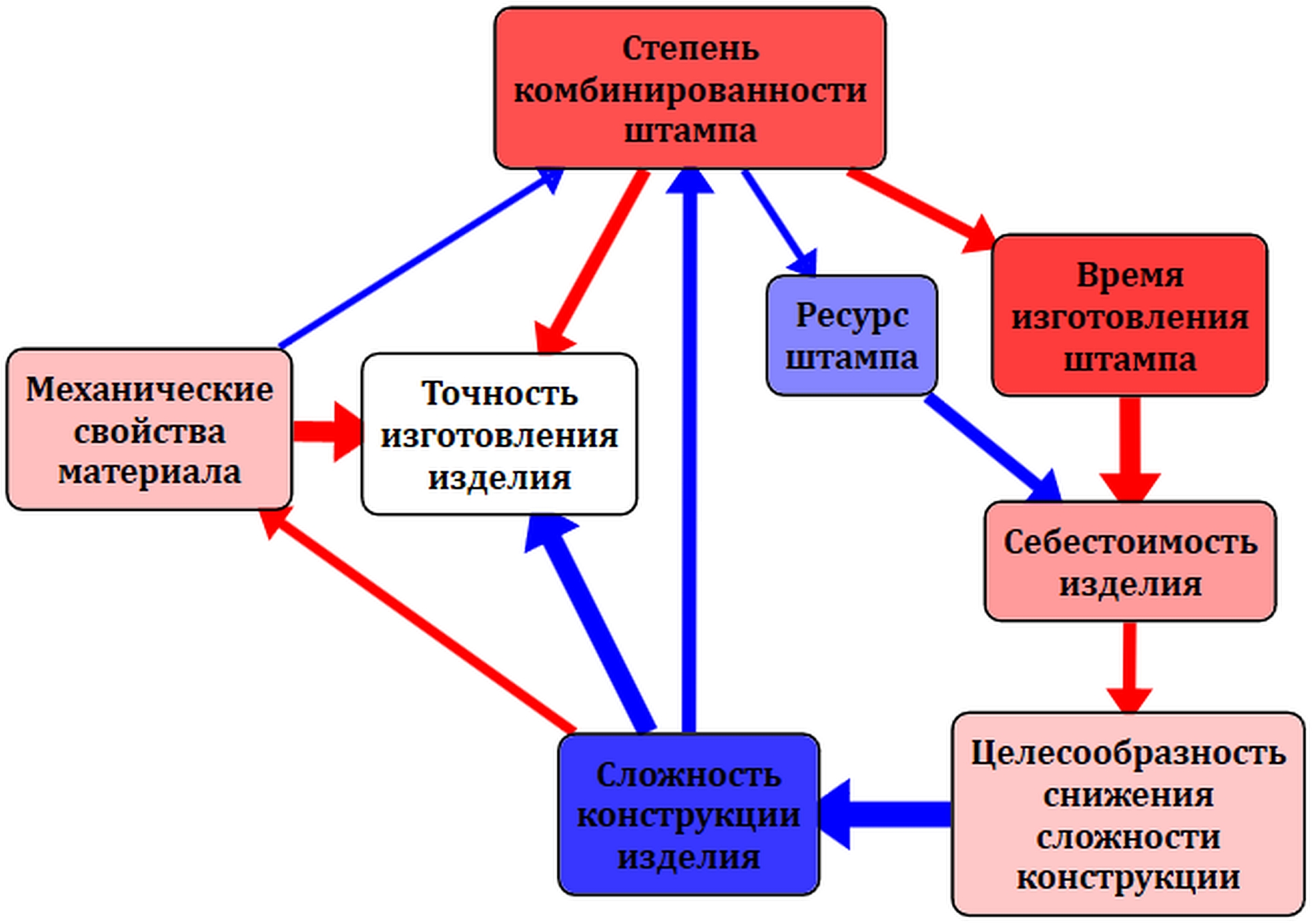
Рис. 4. Метафора
влияния концептов на систему
4. Метафора «альфа-срез» (рис. 5), позволяющая выделять группы
взаимосвязанных концептов, характеризуемых заданным уровнем среза относительно
выбранного системного показателя. Выделение таких групп возможно только для
показателей, являющихся симметричными. Одним из таких показателей является
показатель взаимного отрицательного влияния концептов, который рассчитывается
по формуле:
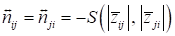
где S – некоторый оператор S-нормы, используемый для представления операции объединения
нечетких множеств (например, оператор максимума). Матрицу 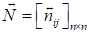 будем называть когнитивной матрицей
взаимного отрицательного влияния. α-срезом когнитивной карты по некоторому
симметричному системному показателю называется бинарное отношение,
соответствующее уровневому множеству нечеткого отношения, заданного на основе
когнитивной матрицы, связанной с данным показателем. Так, для показателя
взаимного отрицательного влияния и заданного уровня среза α
соответствующее бинарное отношение строится по правилу:
будем называть когнитивной матрицей
взаимного отрицательного влияния. α-срезом когнитивной карты по некоторому
симметричному системному показателю называется бинарное отношение,
соответствующее уровневому множеству нечеткого отношения, заданного на основе
когнитивной матрицы, связанной с данным показателем. Так, для показателя
взаимного отрицательного влияния и заданного уровня среза α
соответствующее бинарное отношение строится по правилу:
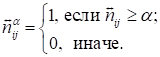
Для остальных симметричных системных показателей
α-срезы строятся аналогично.
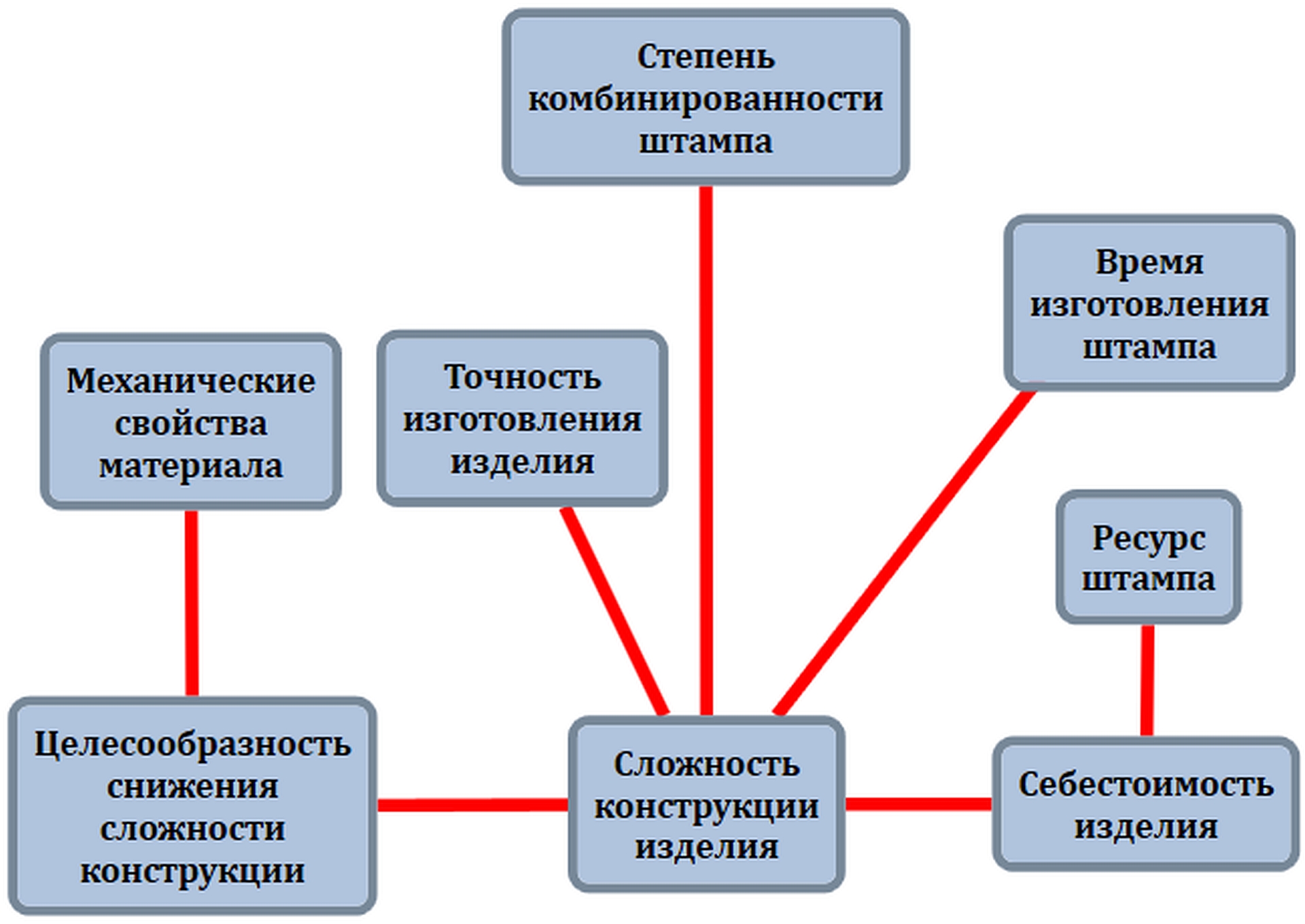
Рис. 5. Метафора
альфа-срезов по показателю взаимного отрицательного влияния
Отметим, что для альфа-среза не учитываются направленность,
знак и интенсивность причинно-следственной связи между концептами, поэтому в данном
случае для представления всех связей используются ненаправленные линии единого
цвета и толщины
Понятие когнитивной ясности некоторой информации
в основном характеризуется легкостью интуитивного понимания
соответствующих описаний, сообщений и т.п. Отсутствие когнитивной ясности
проявляется в том, что человек задумывается, чувствует затруднения, пытаясь
понять сказанное или написанное. Это может выражаться в наблюдаемом
замедлении процесса понимания. Другим последствием может быть упущение значимой
информации, которая остается незамеченной [1].
С другой стороны, в работах, затрагивающих тематику
визуализации графов, зачастую приводятся так называемые «эстетические
критерии», связанные с повышением наглядности получаемого изображения графа.
Достаточно подробный обзор таких критериев приведен в книге [7]. Поскольку НКК,
как упоминалось выше, является взвешенным ориентированным графом, то вполне
логично, что эстетические критерии будут вносить существенный вклад в повышение
наглядности ее изображения.
При этом можно заметить, что многие эстетические критерии
неявно направлены на повышение когнитивной ясности изображения графа, и,
напротив, изображение, в полной мере обладающее свойствами когнитивной ясности,
вероятнее всего, будет привлекательным в эстетическом отношении. Таким образом,
эстетические критерии будет вполне целесообразным также относить к критериям
когнитивной ясности, и в дальнейшем можно говорить только об этой группе
критериев.
С учетом сказанного, в качестве основы для построения
метафоры визуализации НКК предлагаются следующие критерии когнитивной ясности:
1) направленность
дуг: более удобными (здесь и далее – при прочих равных условиях) для
«прочтения» НКК являются направления дуг «сверху-вниз» и «слева-направо»
(именно эти направления совпадают с привычными для многих направлениями чтения);
2) однонаправленность
изображения последовательных дуг: если не требуется постоянно менять
направление взгляда, то зрительный обхват путей и циклов графа будет
совершаться быстрее;
3) минимизация
пересечений дуг: в идеале они должны отсутствовать, а при невозможности этого
(для непланарного графа) их число следует минимизировать;
4) минимизация
количества искривленных дуг: более удобными для восприятия являются изображения
с прямыми дугами;
5) минимизация
длины дуг (как совокупной длины, так и наибольшей из длин): чем короче дуги,
тем проще увидеть, какие концепты связаны друг с другом, и тем больше связей
можно увидеть одновременно;
6) минимизация
разброса длины дуг: более удобными для восприятия являются изображения, в
которых все дуги имеют примерно одинаковую длину;
7) максимизация
углов между дугами, инцидентными одной вершине: при небольших углах между
такими дугами они будут «сливаться» друг с другом вблизи вершин, что может
существенно затруднить визуальное определение их направлений;
8) оптимизация
области размещения: для эффективного использования пространства граф должен
быть размещен в прямоугольной области, формат которой (т.е. соотношение ширины
и высоты) соответствует текущему формату графической области подсистемы
визуализации;
9) подчеркивание
симметрии графа: изображения, симметричные относительно некоторой оси или
центра, более удобны для восприятия и анализа.
Возвращаясь к описанной ранее метафоре визуализации НКК,
можно теперь сказать, что вторым по важности ее компонентом (после алгоритмов
визуализации графов) должны стать введенные критерии когнитивной ясности.
Анализируя эти критерии, можно прийти к выводу, что многие из них противоречат
друг другу, и обеспечить соответствие изображения одновременно всем критериям
с алгоритмической точки зрения, как правило, невозможно. Таким образом,
независимо от конкретных особенностей реализации метафоры визуализации НКК,
необходима разработка решающих правил, моделирующих различные формы компромисса
между критериями.
В работе [4] отмечается, что наличие интерактивного
управления визуальным образом обеспечивает прямое участие пользователя в
манипулировании образом и является основанием для глубокого анализа данных.
Кроме того, система интерактивного управления моделью является одним из
способов верификации полученных решений и потому обеспечивает ускоренное
достижение цели анализа в случае, когда этот способ удобен для пользователя.
Таким образом, интерактивность визуальной модели становится условием ее высокой
результативности.
Механизм интерактивного управления визуальным представлением
НКК в системе «ИГЛА» обеспечивает следующие возможности:
1) редактирование
структуры когнитивной модели посредством редактирования ее визуального образа;
2) перестройка
пространственной метафоры с учетом выбранного алгоритма визуализации графов;
3) трансформация
изображения когнитивной модели;
4) переключение
между метафорами представления, а также настройки отдельных метафор.
Редактирование структуры модели подразумевает возможность
добавления, удаления и изменения концептов и связей путем манипулирования
элементами графического интерфейса и визуального образа самой модели.
Трансформация изображения не затрагивает ни структуру
модели, ни используемую в текущий момент метафору представления, однако
позволяет гибко изменять свойства конечного изображения, выводимого на экран
(таким образом, выполняя своего рода постобработку). К возможностям
трансформации относятся: плавное масштабирование изображения; поворот
изображения на заданный угол по часовой стрелке или против нее; зеркальное
отражение изображения относительно горизонтальной или вертикальной оси; сжатие
и растяжение изображения вдоль выбранных направлений (рис. 6).
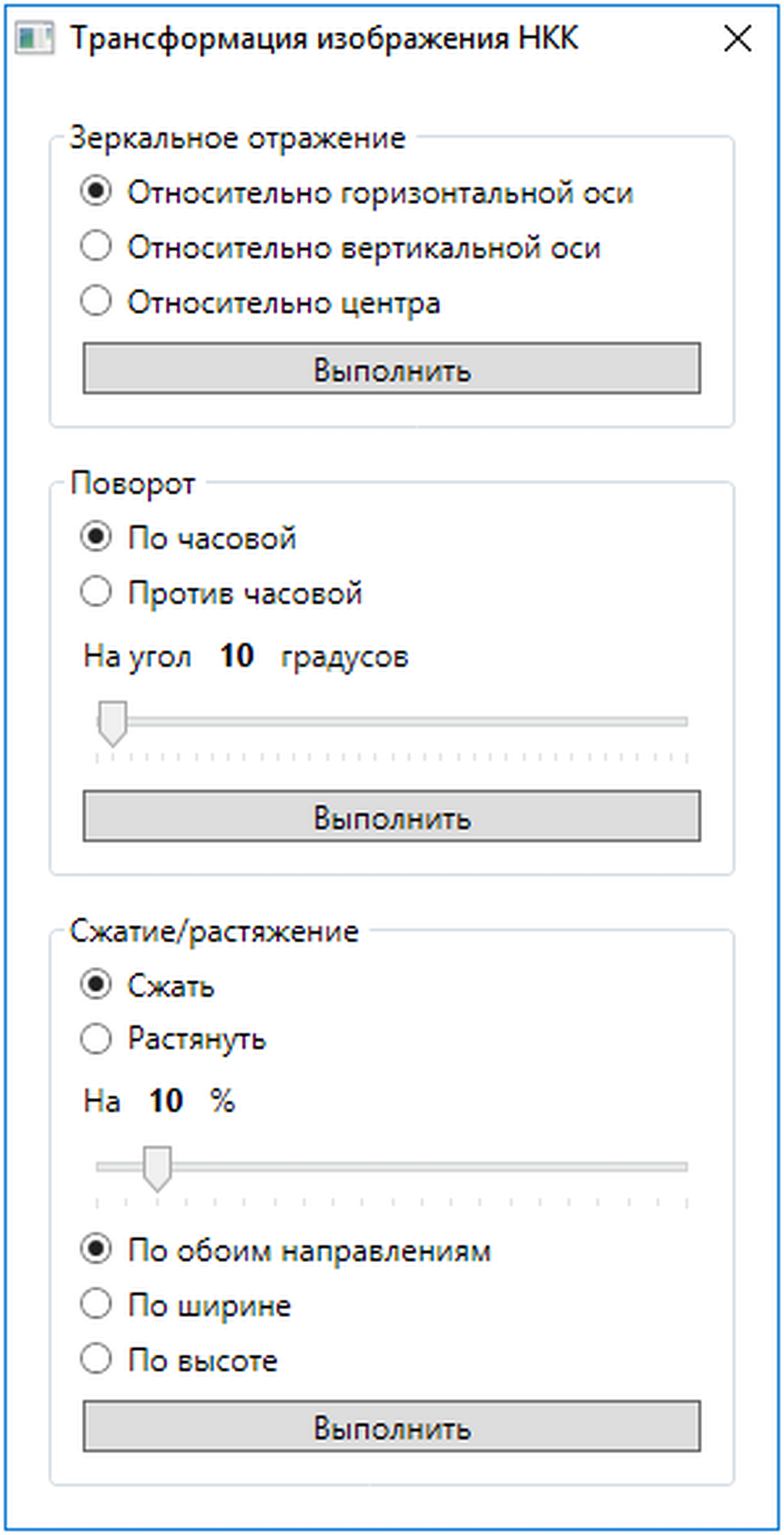
Рис. 6. Пользовательский
интерфейс трансформации изображения НКК в системе «ИГЛА»
Наконец, благодаря возможности переключаться между
метафорами представления исследователь в любой момент может направить внимание
на те аспекты модели, которые представляют для него наибольший интерес на
текущем этапе анализа. При этом функции настройки визуальных характеристик
метафор представления также способствуют повышению гибкости этого инструмента и
его удобства для исследователя (рис. 7).
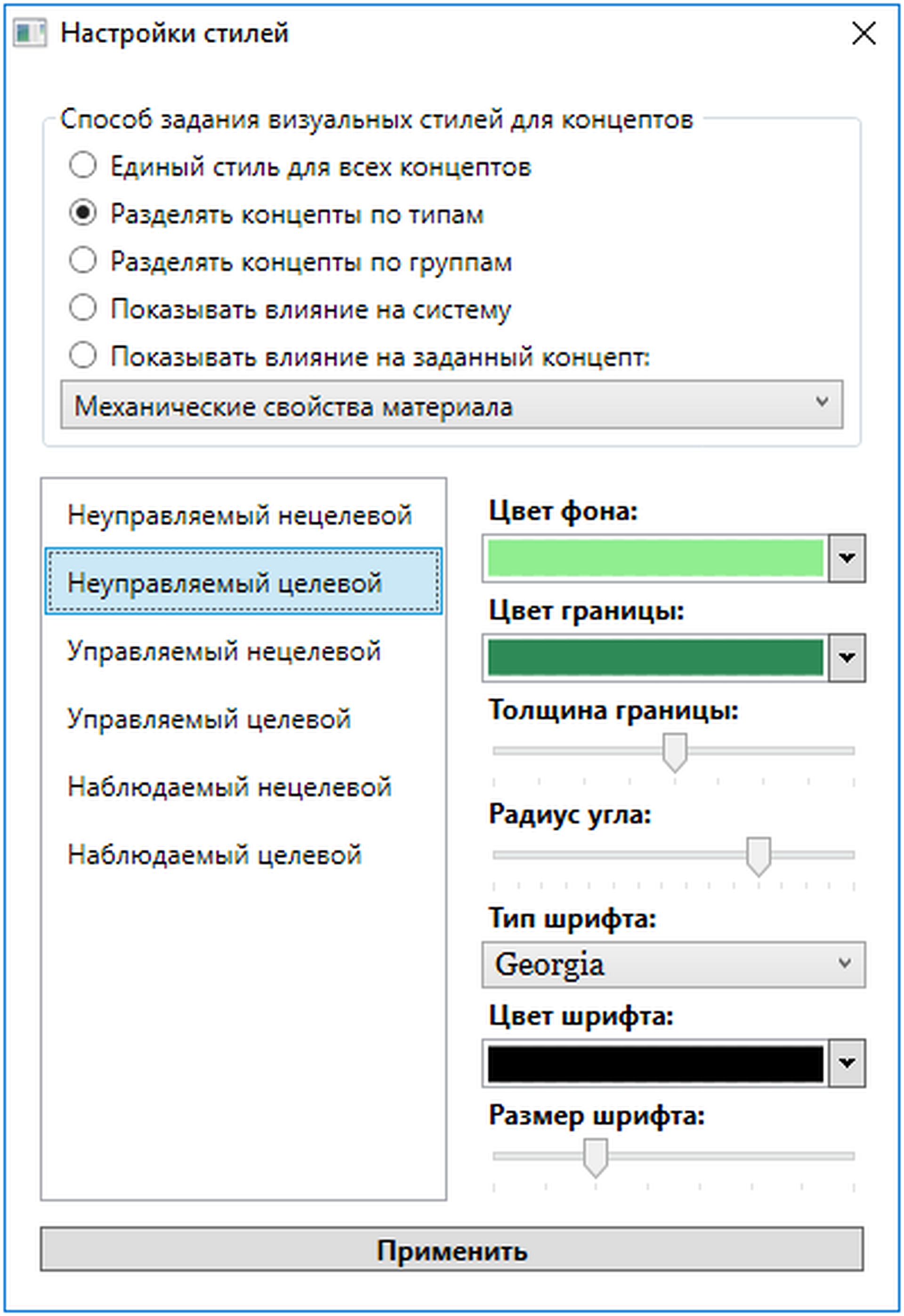
Рис.7.
Пользовательский интерфейс выбора и настройки метафор представления в системе
«ИГЛА»
В работе представлена метафора визуализации нечетких
когнитивных карт. Определены две составляющие метафоры визуализации –
пространственная метафора и метафора представления. Рассмотрено понятие когнитивной
ясности, в результате анализа которого сделан вывод о наличии связи между
качеством применяемой метафоры визуализации НКК и уровнем когнитивной ясности
полученного визуального образа: чем более высокий уровень когнитивной ясности
обеспечивает метафора визуализации, тем более простым является процесс
экспертного понимания когнитивной модели при ее визуальном анализе. Для оценки
уровня когнитивной ясности предложен набор критериев.
Таким образом, наряду с алгоритмами визуализации графов,
показатели когнитивной ясности составляют основу для построения метафоры
визуализации НКК и одновременно с этим являются средством наиболее естественной
оценки качества построенной метафоры.
Также рассмотрены возможности интерактивного управления
визуальным представлением НКК в системе «ИГЛА», обеспечивающие гибкую настройку
визуальных характеристик метафор представления, что позволяет исследователю в
ходе анализа когнитивной модели фокусировать внимание на тех ее аспектах,
которые представляют для него наибольший интерес на том или ином этапе анализа.
Возможности использования метафор визуализации и
интерактивного управления визуальным представлением НКК в системе «ИГЛА»
проиллюстрированы на примере когнитивной модели поддержки принятия решений в
области проектирования технологической оснастки [8].
Укажем направления дальнейших исследований.
Во-первых, это формализация описанных выше критериев
когнитивной ясности и разработка метода оценки качества метафоры визуализации
НКК на основе формализованных критериев, с реализацией этого метода в
подсистеме визуализации системы «ИГЛА».
Во-вторых, совершенствование механизма интерактивного
управления визуальным образом НКК в системе «ИГЛА», в частности, реализация
функции автоматического подбора оптимальной пространственной метафоры с учетом
указанных пользователем приоритетов по критериям когнитивной ясности.
1. Абрамова
Н.А., Воронина Т.А., Порцев Р.Ю. О методах поддержки построения и верификации
когнитивных карт с применением идей когнитивной графики // Управление большими
системами. Специальный выпуск 30.1 «Сетевые модели в управлении». – М.: ИПУ
РАН, 2010. – С. 411-430.
2. Авдеева
З.К., Коврига С.В., Макаренко Д.И. Когнитивное моделирование для решения задач
управления слабоструктурированными системами (ситуациями) // Управление
большими системами. – 2007. – Вып. 16. – С. 26-39.
3. Борисов
В.В., Круглов В.В., Федулов А.С. Нечеткие модели и сети. – М.: Горячая линия –
Телеком, 2012. – 284 с.
4. Захарова
А.А., Вехтер Е.В., Шкляр А.В. Методика решения задач анализа данных при
использовании аналитических визуальных моделей // Научная визуализация. – 2017.
– Т. 9. – № 4. – С. 78-88.
5. Захарова
А.А., Шкляр А.В. Метафоры визуализации // Научная визуализация. – 2013. – Т. 5.
– № 2. – С. 16-24.
6. Исаев
Р.А., Подвесовский А.Г. Совершенствование механизма визуализации нечетких
когнитивных моделей в системе поддержки принятия решений «ИГЛА» // Современные
технологии в науке и образовании – СТНО-2017: сб. тр. междунар. науч.-техн. и
науч.-метод. конф.: в 9 т. Т.1. – Рязань: Рязан. гос. радиотехн. ун-т, 2017. –
С. 138-142.
7. Касьянов
В.Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и
применение. – СПб.: БХВ-Петербург, 2003. – 1104 с.
8. Копелиович
Д.И., Подвесовский А.Г., Сафонов А.Л., Вилюха А.В., Исаев Р.А. Применение
нечетких когнитивных моделей в автоматизации проектирования технологической
оснастки. // Вестник компьютерных и информационных технологий. – 2018. – № 3.
– С. 20-35.
9. Кулинич
А.А. Ситуационный, когнитивный и семиотический подходы к принятию решений в
организациях // Открытое образование. – 2016. – Т. 20. – № 6. – С. 9-17.
10. Подвесовский А.Г., Лагерев
Д.Г., Коростелев Д.А. Применение нечетких когнитивных моделей для формирования
множества альтернатив в задачах принятия решений // Вестник Брянского государственного
технического университета. – 2009. – № 4 (24). – С. 77-84.
11. Силов, В.Б. Принятие
стратегических решений в нечеткой обстановке / В.Б. Силов – М.: ИНПРО-РЕС,
1995. – 228 с.
12. Феррейра Опасо Е.В.,
Терелянский П.В. Представление когнитивных карт в трехмерном пространстве //
XII Всероссийское совещание по проблемам управления ВСПУ-2014: Труды совещания.
М.: ИПУ РАН, 2014. – С. 6149-6154.
13. Huang W., Hong S.H., Eades
P. Predicting Graph Reading Performance: A Cognitive Approach // Proc. Asia
Pacific Symposium on Information Visualization (APVIS2006). – Tokyo, Japan,
2006. – Р. 207–216.
14. Isaev R.A., Podvesovskii
A.G. Generalized Model of Pulse Process for Dynamic Analysis of Sylov’s Fuzzy
Cognitive Maps // CEUR Workshop Proceedings of the Mathematical Modeling
Session at the International Conference Information Technology and
Nanotechnology (MM-ITNT 2017), Vol. 1904. – P. 57-63.
15. Isaev R.A., Podvesovskii
A.G. Application of time series analysis for structural and parametric
identification of fuzzy cognitive models // CEUR Workshop Proceedings of the
International Conference Information Technology and Nanotechnology. Session
Data Science (DS-ITNT 2018), Vol. 2212. – P. 119-125.
16. Meyer B. Self-Organizing
Graphs – A Neural Network Perspective of Graph Layout // Whitesides S.H. (eds)
Graph Drawing. GD 1998. Lecture Notes in Computer Science, vol 1547. Springer,
Berlin, Heidelberg.
17. Noack A. An energy model for
visual graph clustering // Proceedings of the 11th International Symposium on
Graph Drawing. Springer-Verlag, 2004. – P. 425-436.
Visualization Metaphors for Fuzzy Cognitive Maps
Authors: A.G. Podvesovskii1, R.A. Isaev2
Bryansk State Technical University
1 ORCID: 0000-0002-1118-3266, apodv@tu-bryansk.ru
2 ORCID: 0000-0003-3263-4051, ruslan-isaev-32@yandex.ru
Abstract
At present, a cognitive approach is widely used for modeling and decision support in semi-structured systems. This approach focuses on the development of formal models and methods supporting the intelligent problem-solving process as they take into account human cognitive capabilities (perception, conception, cognition, understanding, explanation). In general terms, a cognitive model is thought of as a model of expert knowledge about a system, processes occurring in it and laws and principles of its functioning represented as a cognitive map. A causal network which reflects researcher's subjective notion of the system as a number of semantic categories known as factors or concepts and a set of cause-and-effect relations between them is referred to as a cognitive map.
One of the key ideas in effective dealing with a cognitive model is providing its visual representation. In the paper, a visualization metaphor for fuzzy cognitive maps is proposed and its two components, namely spatial metaphor and representation metaphor, are defined. Graphs visualization algorithms and cognitive clarity notion form the basis for constructing a visualization metaphor. To assess the level of cognitive clarity, a set of criteria is proposed.
The mechanism of interactive control of a visual image of a fuzzy cognitive map in the cognitive modeling support system IGLA is considered. This mechanism provides flexible adjustment of representation metaphors visual characteristics, which allows the researcher to focus on the aspects of a cognitive model that are of most interest to him at a particular stage of the analysis.
The possibilities of using visualization metaphors and interactive control of the fuzzy cognitive maps visual representation in IGLA system are illustrated by the example of a cognitive model of decision support in tooling design.
Keywords: fuzzy cognitive map, graph visualization, cognitive clarity, visualization metaphor.
1. Abramova
N.A., Voronina T.A., Portsev R.Y. O metodah podderzhki postroeniya i
verifikacii kognitivnyh kart s primeneniem idej kognitivnoj grafiki [Ideas of
Cognitive Graphics to Support Verification of Cognitive Maps] // Upravlenie
bol'shimi sistemami. Special issue 30.1 “Setevye modeli v upravlenii”. –
Moscow: ICS RAS, 2010. – pp. 411-430 [in Russian].
2. Avdeeva
Z.K., Kovriga S.V., Makarenko D.I. Kognitivnoe modelirovanie dlya resheniya
zadach upravleniya slabostrukturirovannymi sistemami (situaciyami) [Cognitive
Modeling for Solving Problems of Control of Semi-structured Systems
(Situations)] // Upravlenie bol'shimi sistemami. – 2007. – Issue. 16. – pp.
26-39 [in Russian].
3. Borisov
V.V., Kruglov V.V., Fedulov A.S. Nechetkie modeli i seti [Fuzzy Models and
Networks]. – M.: Goryachaya Liniya – Telekom, 2012. – 284 p. [in Russian]
4. Zakharova
A.A., Vekhter E.V., Shklyar A.V. Metodika resheniya zadach analiza dannyh pri
ispol'zovanii analiticheskih vizual'nyh modelej [Methods of Solving Problems of
Data Analysis Using Analytical Visual Models] // Scientific Visualization. –
2017. – Vol. 9. – № 4. – pp. 78-88 [in Russian].
5. Zakharova
A.A., Shklyar A.V. Metafory vizualizacii [Visualization Metaphors] //
Scientific Visualization. – 2013. – Vol. 5. – № 2. – pp. 16-24.
6. Isaev
R.A., Podvesovskii A.G. Sovershenstvovanie mekhanizma vizualizacii nechetkih
kognitivnyh modelej v sisteme podderzhki prinyatiya reshenij «IGLA»
[Improvement of the Mechanism of Fuzzy Cognitive Models Visualization in
Decision Support System «IGLA»] // Proceedings of the International Conference
“Sovremennye tekhnologii v nauke i obrazovanii – STNO-2017” [Up-to-date
Technologies in Science and Education], Vol.1. – Ryazan: Ryazan State
Radioengineering University, 2017. – p. 138-142.
7. Kasyanov
V.N., Evstigneev V.A. Grafy v programmirovanii: obrabotka, vizualizaciya i
primenenie [Graphs in Programming: Processing, Visualization and Application].
– Saint Petersburg: BHV-Peterburg, 2003. – 1104 p. [in Russian]
8. Kopeliovich
D.I., Podvesovskii A.G., Safonov A.L., Vilyukha A.V., Isaev R.A. Primenenie
nechetkih kognitivnyh modelej v avtomatizacii proektirovaniya tekhnologicheskoj
osnastki [Application of Fuzzy Cognitive Models in Computer-Aided Production
Tooling Design] // Vestnik komp'yuternyh i informacionnyh tekhnologij [Herald
of Computer and Information Technologies]. – 2018. – № 3. – pp. 20-35 [in
Russian].
9. Kulinich
A.A. Situacionnyj, kognitivnyj i semioticheskij podhody k prinyatiyu reshenij v
organizaciyah [Contingency, Cognitive and Semiotic Approaches to
Decision-Making in the Organizations] // Otkrytoe obrazovanie. – 2016. – Vol.
20. – № 6. – pp. 9-17 [in Russian].
10. Podvesovskii A.G., Lagerev
D.G., Korostelev D.A. Primenenie nechetkih kognitivnyh modelej dlya
formirovaniya mnozhestva al'ternativ v zadachah prinyatiya reshenij
[Application of Fuzzy Cognitive Models for Alternatives Set Generation in
Decision Problems] // Vestnik Bryanskogo gosudarstvennogo tekhnicheskogo
universiteta [Bulletin of Bryansk State Technical University]. – 2009. – № 4
(24). – pp. 77-84 [in Russian].
11. Silov V.B. Prinyatie
strategicheskih reshenij v nechetkoj obstanovke [Strategical Decision Making in
Fuzzy Environment] – Moscow: INPRO-RES, 1995. – 228 p. [in Russian]
12. Ferreira Opaso E.V.,
Terelyanskij P.V. Predstavlenie kognitivnyh kart v trekhmernom prostranstve
[Presentation of Cognitive Maps in Three-Dimensional Space] // Proceedings of
the XII All-Russian Conference on Control Science. M.: ICS RAS, 2014. – pp.
6149-6154 [in Russian].
13. Huang W., Hong S.H., Eades
P. Predicting Graph Reading Performance: A Cognitive Approach // Proc. Asia
Pacific Symposium on Information Visualization (APVIS2006). – Tokyo, Japan,
2006. – Р. 207–216.
14. Isaev R.A., Podvesovskii
A.G. Generalized Model of Pulse Process for Dynamic Analysis of Sylov’s Fuzzy
Cognitive Maps // CEUR Workshop Proceedings of the Mathematical Modeling
Session at the International Conference Information Technology and
Nanotechnology (MM-ITNT 2017), Vol. 1904. – P. 57-63.
15. Isaev R.A., Podvesovskii
A.G. Application of time series analysis for structural and parametric
identification of fuzzy cognitive models // CEUR Workshop Proceedings of the
International Conference Information Technology and Nanotechnology. Session
Data Science (DS-ITNT 2018), Vol. 2212. – P. 119-125.
16. Meyer B. Self-Organizing
Graphs – A Neural Network Perspective of Graph Layout // Whitesides S.H. (eds)
Graph Drawing. GD 1998. Lecture Notes in Computer Science, vol 1547. Springer,
Berlin, Heidelberg.
17. Noack A. An energy model for
visual graph clustering // Proceedings of the 11th International Symposium on
Graph Drawing. Springer-Verlag, 2004. – P. 425-436.