“Нет преград
человеческой мысли.”
Сергей Павлович Королёв
Существует обширный класс изделий с функциональными кривыми
и поверхностями, определяющими их существенные проектные характеристики. Это, к
примеру, внешние обводы летательных аппаратов, судов, рабочие поверхности
почвообрабатывающих агрегатов, профили кулачков, осевые линии трассы дорог,
профили крыльев летательных аппаратов, лопасти турбин и компрессоров.
В работах [1-2] базовые требования к качеству функциональных
кривых строятся на основе анализа движения материальной точки по траектории
пространственной кривой. Эти базовые требования, обобщённые в работе [3],
базируются на критериях плавности и инвариантны относительно специфики
эксплуатации конкретного изделия:
1. Порядок
гладкости не ниже 4-х;
2. Отсутствие
или минимальное количество экстремумов кривизны;
3. Малые
значения вариации кривизны и скорости ее изменения;
4. Малое
значение потенциальной энергии кривой;
5. Эстетический
анализ с позиций законов технической эстетики.
Кривые высокого качества, удовлетворяющие вышеперечисленным
критериям плавности, были названы кривыми класса F (Functional) [3-5], в
отличие от термина кривые класса A (Aussenhaut),
который был позаимствован Джеральдом Фарином из описания САПР SYRKO
фирмы «Daimler-Benz AG» для моделирования внешних (в
переводе с нем. языка aussenhaut
– внешний) поверхностей автомобиля [6].
Известно, что всё проектируется для людей, так как главным
объектом внимания является человек – потребитель опредмеченных в изделиях
свойств своих жизненных потребностей. Данные изделия создаются средствами
материального и духовного производства, образуют наполнение жизненного
пространства человека, в котором он раскрывает их содержание и даёт им
соответствующую оценку. Но человек оценивает готовый продукт жизненной
необходимости не узконаправленно, а в совокупности всех его качеств. Главный
сигнал о полезных свойствах изделия он получает через зрительный канал связи. В
этом смысле форма продукта, которую человек воспринимает на уровне сенсорного
приёма информации, выражает в своих характеристиках основные качественные
показатели. Как правило, гармоничная форма является адекватным отражением
основных технико-эксплуатационных свойств и эстетических качеств промышленного
изделия. В свою очередь, эстетические качества формы, воплощённые средствами
дизайна, играют важную роль в продвижении промышленного изделия на рынке сбыта.
«…Коммерческий успех любого из продуктов, которые человек использует, с
которыми работает или которые видит, в значительной степени зависит от их
дизайна» [23]. В этом смысле наиболее ярким образцом выраженного формообразования
с качественной геометрией поверхности может служить эстетика автомобиля ‑
объекта проектирования промышленного дизайна как самого наукоёмкого вида
художественного конструирования. Высокие эстетические качества формы являются
показателем хорошего уровня дизайна изделия и служат важнейшей характеристикой
при оценке автомобиля покупателем, а также становятся значимыми и для множества
других объектов промышленного дизайна. В контексте дизайна автомобиля под его
основным эстетическим аспектом понимается способность формы, основанной на
высоком качестве геометрических связей отдельных формообразующих участков между
собой, положительно воздействовать на психоэмоциональную сферу человека и
формировать необходимый для покупки товара рекламоспособный эстетический образ.
Его содержание зависит от заданной композиционной структуры формы, различные
аспекты которой ориентированы на обеспечение положительного эмоционального
восприятия геометрии поверхности изделия человеком в разных
предметно-пространственных условиях и при любом характере освещения. В данном
случае, подразумевается то, что независимо от характера и условий освещения
(рассеянное, прямой падающий свет, дневное, ночное и т.д.) стабильно ровное
движение светового блика по поверхности формы автомобиля должно являться
показателем идеальной плавности соединения отдельных формообразующих участков
изделия. Высокая культура плавности перехода между отдельными поверхностями
создаёт визуальную чистоту формы, которая уже на уровне зрительного канала связи
трансформируется в эстетическое качество.
Важно подчеркнуть, что эстетические свойства формы продукта
дизайна с идеальными сопряжениями формообразующих поверхностей остаются
постоянными в любых предметно-пространственных ситуациях и не разрушаются в
зависимости от условий восприятия, которые только меняют картину
психологического переживания эстетического образа изделия, так как в разном
предметно-пространственном окружении опосредованно преобразовывается
эмоционально-психологическое состояние реципиента.
Таким образом, эстетика становится важной составляющей
потребительских свойств изделия. Очевидно, что более плавные кривые и
поверхности более эстетичны [25]. Собственно, сам термин плавная кривая
несет в себе эстетическую составляющую. В настоящей работе предлагается базовые
критерии плавности считать и эстетическими критериями при оценке качества форм.
В работе [3] кривые, формообразующие поверхность,
эстетические качества которой являются важной составляющей потребительских
свойств изделия, были определены как эстетические функциональные кривые. К
оценке качества эстетических функциональных кривых предлагается
многокритериальный подход. Авторы работы [3] считают, что приоритетным является
оценка по критериям плавности. Экспертная оценка с позиций законов технической
эстетики правомерна только после оценки на плавность или при отсутствии
возможности проведения такого анализа.
Для визуализации кривых линий и поверхностей класса F разработан программный комплекс FairCurveModeler,
реализованый в виде приложений AutoCAD [7], Fusion360
[8], nanoCAD, КОМПАС [9], Mathematica
[4], в виде облачного продукта Web FairCurveModeler [10]. Перевод программы под
другие САПР с использованием их API представляет трудоемкую задачу. Также
трудоемко одновременное расширение функционала программного комплекса
FairCurveModeler во всех его реализациях.
В [11] предлагается идея о возможности использования
универсальной программной платформы, инвариантной относительно специфики
конкретных САПР. В качестве такой программной платформы предлагается
использовать сочетание из Microsoft Excel VBA,
программного комплекса FairCurveModeler и систем компьютерной математики.
Программная платформа предназначена для выполнения следующих задач:
•
Для визуализации кривых линий и поверхностей высокого качества
для любых САПР. При этом нет необходимости переноса функционала
FairCurveModeler на другие САПР, используя их API. Достаточно написать утилиты
обмена геометрическими моделями между Microsoft Excel и САПР или использовать
стандартный обмен через DXF-файл.
•
Для разработки специализированных приложений (прикладных САПР),
использующих функционал FairCurveModeler. Для этого предоставляется набор
программ с открытым кодом, реализующих интерфейс между Microsoft Excel и
FairCurveModeler.
Необходимым компонентом программной платформы и, вообще,
САПР, также являются системы компьютерной математики. Необходимость и важность
математического аппарата для САПР прекрасно понимали Самуэл Гейсберг и Майк
Пейн, которые ввели пакет Mathcad в состав продуктов корпорации PTC [12].
Системы компьютерной математики совместно с программным
комплексом FairCurveModeler используются
•
для вычисления геометрического определителя Эрмита, необходимого
для аппроксимации аналитической кривой посредством NURBS-кривой и ввода в САПР
аналитической кривой в виде NURBS шаблона [13]. Геометрический определитель
Эрмита представляется в виде таблицы координат точек опорной ломаной, векторов
первых производных, положительных значений кривизны, длин сегментов кривой
между опорными точками и единичных векторов кривизны;
•
для глубокого и всестороннего анализа построенных NURBS кривых по
критериям плавности;
•
для анализа NURBS кривой на предмет соответствия инженерной цели
(например, для анализа геометрических параметров профиля кулачка на
соответствие заданным макропараметрам и динамическим характеристикам
кулачкового механизма).
Таким образом, программная платформа представляет собой
интегрированную систему, объединяющую Microsoft Excel VBA, FairCurveModeler и системы
компьютерной математики.
Универсальная программная платформа для визуализации кривых
и поверхностей класса F и разработки прикладных САПР изделий с
функциональными кривыми и поверхностями состоит из следующих компонентов:
•
FairCurveModeler – программный комплекс для визуализации кривых
класса F;
•
Microsoft Excel VBA;
•
Системы компьютерной математики Mathcad и Mathematica;
Метод построения кривой высокого качества состоит из
следующих этапов.
•
На двух видах геометрического определителя вида опорной ломаной
или касательной ломаной строится виртуальная кривая (v-кривая) класса C5.
•
На v-кривой формируется геометрический определитель Эрмита
в виде таблицы координат точек, касательных векторов и значений кривизны.
•
На геометрическом определителе Эрмита изогеометрически и с
сохранением качества v-кривой строятся NURBzS кривая (рациональная
сплайновая кривая Безье) или NURBS кривая (неоднородный рациональный B-сплайн
высокой чётной степени m, где m ={6,8,10}).
Теоретические основы программного комплекса подробно описаны
в работах [14-17]. Программный комплекс состоит из двух частей: COM-компонента FairCurve.exe и интерфейсной части.
Системы компьютерной математики Mathcad и Mathematica
необходимы для анализа NURBS кривых, подготовки данных для аппроксимации
аналитических кривых в FairCurveModeler, для решения вычислительных задач в
прикладных САПР.
Концепция применения универсальной программной платформы
позволяет без особых трудозатрат перенести функционал программного комплекса
FairCurveModeler в любую САПР. Например, эта концепция легко реализуется для
перспективной САПР Fusion360, являющейся амбициозным
проектом Autodesk. Функционал Fusion360 обеспечивает
все стадии проектирования изделия. Fusion360 - это, по
существу, автоматизированное рабочее место инженера. Поэтому, если дополнить
функционал Fusion360 функциями визуализации кривых класса F, то Fusion360 станет самодостаточной высококлассной САПР,
способной моделировать функциональные и эстетические кривые и поверхности
изделий, вплоть до внешних обводов суперкаров.
Программный комплекс FairCurveModeler имеет реализацию под Fusion360
[8]. Платформа используется для расширения функционала приложения “FairCurveModeler
app Fusion360” и для возможности разработки прикладных САПР в интегрированной
системе программная платформа + Fusion360. Для
обеспечения интеграции средствами API (Application Programming Interface) Fusion360 разработан
плагин, который обеспечивает обмен геометрическими объектами с Microsoft Excel.
В составе программной платформы представлена книга Microsoft Excel
‘FCModeler+Fusion360.xlsm’, которая обеспечивает передачу NURBS
моделей в Fusion360.
Ниже опишем технологию работы с программной платформой для визуализации
кривых класса F в САПР Fusion360.
1. Построение v-кривой на опорной ломаной
a) В
Fusion360 постройте ломаную.
b) Вызовите
плагин кнопкой [plug_in_FairCurveModeler] во вкладке ADD-INS рабочего
пространства Model.
c) В
диалоговом окне 'FAIRCURVEMODELER' приложения в области ‘Exchange Options’
включите переключатель на 'Points'.
d) Выберите
последовательно вершины ломаной.
e) Нажмите
кнопку 'Exchange' в дилоговом окне 'FAIRCURVEMODELER'.
f)
В текстовом окне 'Exchange Box' появится текст модели объекта.
Установите курсор в текстовое окно 'Exchange Box', выделите весь текст
(используйте кнопки 'End', 'Shift + Home') и скопируйте в буфер обмена ( 'Ctrl
+ Insert').
g) Перейдите
в книгу Microsoft Excel ‘FCModeler.xlsm’ на страницу 'Polyline' . Вставьте
содержимое буфера обмена в область листа, начиная с ячейки Set_XYZ (C12).
h) В
области Topology включите переключатель Unclosed (ломаная незамкнута). В
области 'Type GD' включите Basic (опорная ломаная).
i)
Для построения v-кривой на опорной ломаной нажмите [Create Curve].
Программа построит график кривой функции её кривизны на странице Graphics (рис.
1) и сформирует NURBzS модель кривой на странице NURBS.

Рис. 1. График
кривой ее кривизны на странице Graphics.
Для ввода NURBS-модели в проект Fusion360 используются два
способа:
•
ввод NURBS модели в проект посредством плагина;
•
ввод NURBS модели в проект через DXF-файл.
Ввод NURBS модели в проект посредством плагина
a) Для
переноса кривой в Fusion360 перейдите в книгу Microsoft Excel ‘FCModel + Fusion360.xlsm’ (папка ‘apps
Fusion360’) на страницу Fusion360. Нажмите на кнопку [from
NURBS to Fusion360] (рис. 2). Программа скопирует NURBS-модель в буфер обмена.

Рис. 2. Книга Microsoft Excel ‘FCModel + Fusion360.xlsm’, страница Fusion360.
b) Перейдите
в Fusion360.
c) Вставьте
текст в ‘Exchange Box’.
d) Приложение
выведет сообщение ‘Press OK to create Object’.
e) Нажмите
OK в окне сообщения. Нажмите OK в диалоговом окне FAIRCURVEMODELER.
Средства API Fusion360 предоставляют средства для ввода в
Fusion360 NURBS моделей кривых в т.н. формате ‘transient’ (промежуточный).
Однако, в API Fusion360 отсутствует метод прямого ввода кривой из формата
‘transient’ в проект. Для ввода кривой в проект кривая в плагине
интерполируется, и на интерполированных точках генерируется сплайн внутреннего
представления.
f)
Приложение выведет сообщение 'Standard сurve successfully created on
points of a fair curve, number of points = ...'
g) Нажмите
OK. Кривая построена.
h) Проверьте
качество кривой. Выделите кривую. В контекстном меню выберите 'Toggle Curvature
Display'.
i)
Программа построит график кривизны над кривой.
Импорт NURBS моделей в формате ‘transient’ дает возможность
вычислить любой параметр, но не позволяет включить в проект точную модель
построенной кривой. Можно модель ввести в проект только опосредованно путем
аппроксимации сплайном внутреннего представления.
Главным недостатком сплайна внутреннего представления является то, что он не
сохраняет значения граничных параметров исходной кривой.
Для построения незамкнутых кривых с сохранением качества v-кривой
предлагается следующая техника.
Ввод NURBS модели в проект через DXF-файл
a) После
построения кривой в книге Microsoft Excel ‘FCModel.xlsm’ перейдите на страницу
NURBS.
b) Нажмите
на кнопку [ViewCVT]. Программа интерполирует кривую и строит графики кривизны.
Программа также формирует DXF-файл NURBS кривой. DXF-файл сохраняется в папке
C://FairCurveModeler_TEMP/temp/ с именем 'r_out_dxf.dxf'.
c) Далее
перейдите в Fusion360.
d) Вызовите
приложение plug_in_FairCurveModeler.
e) Установите
переключатель на 'Curve from DXF'.
f)
Очистите 'Change Box'.
g) Программа
выдаст сообщение 'Press OK to create Object'.
h) Нажмите
OK в окне сообщения. Нажмите OK в диалоговом окне FAIRCURVEMODELER.
i)
Программа сгенерирует кривую из DXF-файла.
j)
Из-за разности единиц измерения в Fusion360 и в DXF-файле, кривая будет
в 10 раз меньше оригинала.
k) Выберите
> Modify > Scale.
l)
Выберите кривую в дереве построения.
m) Установите
параметры масштабирования.
Scale Type = Uniform
Scale Factor = 10
n) Кривая
проходит по вершинам исходной ломаной.
Импорт NURBS модели через DXF-файл сохраняет геометрию
кривой.
2. Построение v-кривой на касательной ломаной
a) В
Fusion360 постройте произвольную ломаную.
b) Запустите
плагин plug_in_FairCurveModeler из Add-Ins.
c) В
диалоговом окне 'FAIRCURVEMODELER' приложения включите переключатель на
'Points'.
d) Выберите
последовательно вершины ломаной.
e) Нажмите
кнопку 'Exchange' в дилоговом окне 'FAIRCURVEMODELER'.
f)
В текстовом окне 'Exchange Box' появится модель объекта. Установите
курсор в текстовое окно 'Exchange Box', выделите весь текст (используйте кнопки
'End', 'Shift + Home') и скопируйте в буфер обмена ( 'Ctrl + Insert').
g) Перейдите
в книгу Microsoft Excel ‘FCModeler.xlsm’ на страницу 'Polyline'.
h) Вставьте
содержимое буфера обмена в область листа, начиная с ячейки Set_XYZ (C12). В
области Topology включите переключатель Closed (ломаная замкнута). В области
'Type GD' включите Tangent (ломаная касательная).
i)
Для построения v-кривой на ломаной нажмите 'Create Curve'.
j)
Программа построит кривую и сформирует NURBzS модель кривой на странице
NURBS.
k) Для
переноса кривой в Fusion360 перейдите в книгу Microsoft Excel ‘FCModel +
Fusion360.xlsm’ (папка ‘apps Fusion360’) на страницу Fusion360. Нажмите на
кнопку [from NURBS to Fusion360]. Программа скопирует NURBS-модель в буфер
обмена.
l)
Перейдите в Fusion360.
m) Введите текст в
'Exchange Box’.
n) Приложение
выдает сообщение 'Press OK to create Object'.
o) Нажмите
OK в окне сообщения. Нажмите OK в диалоговом окне FAIRCURVEMODELER.
p) NURBS
из формата ‘transient’ конвертируется в сплайн внутреннего представления.
q) Приложение
выведет сообщение 'Standard сurve successfully created on points of a fair
curve, number of points = ...'
r) Нажмите
OK в сообщении. Кривая построена (рис. 3).
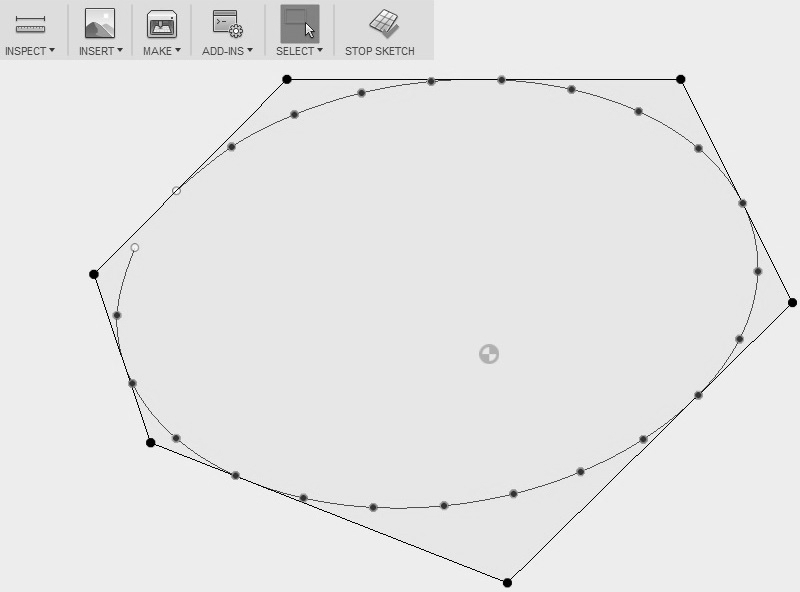
Рис. 3. NURBS
модель аппроксимирована сплайном внутреннего представления.
Если кривая замкнута, то при конвертировании в сплайн
внутреннего представления программа сгенерирует незамкнутую кривую. Замкните
ее, выделив кривую, затем в контекстном меню выберете ‘Open/Close Spline
Curve’. Проверьте качество кривой. Выделите кривую и в контекстном меню
выберите 'Toggle Curvature Display'. Замкнутые кривые конвертируются с
сохранением качества v-кривой (рис. 4).
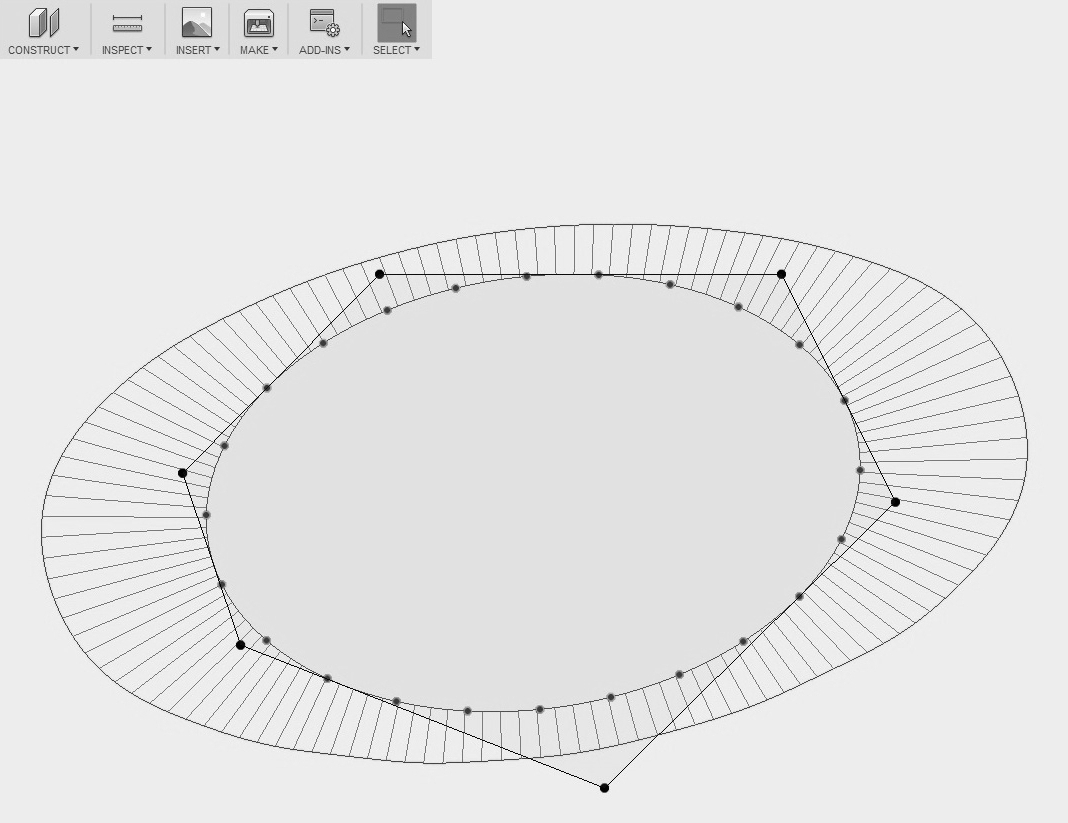
Рис. 4.
Замыкание кривой и проверка качества построением графика кривизны.
Безусловно, кривые класса F
эстетичны сами по себе. Однако, наряду с просто красивыми кривыми, существуют
“топ-модели” - эстетические кривые. Оценка эстетических кривых основывается на
математических характеристиках форм, выявленных у объектов реального мира
(например, крылья бабочек) [18-19]. Эстетическая оценка кривых проводится с
позиций законов технической эстетики и призвана выявить эстетическую
целесообразность кривой в единстве со способностью отвечать требованиям
рациональности [24]. Ввиду композиционной упорядоченности и структурной
согласованности эстетическая кривая обладает и выразительными качествами. В
этом смысле плавность как геометрическое свойство кривой формирует её
выразительную основу и визуальную чистоту. В эмоционально-психологическом
аспекте плавность является фактором обретения человеком психологического
комфорта, так как ассоциируется со спокойствием, постоянством, отсутствием
агрессивности, в противовес линии изломанной, рождающей противоположные
ассоциации. Для моделирования эстетических форм предлагаются так называемые
log-эстетические кривые [20], имеющие линейный график кривизны в
логарифмической шкале. Множество известных спиралей, в том числе клотоида,
являются частными случаями этого класса кривых. В [21] был предложен самый
широкий класс кривых с монотонной функцией кривизны, называемых cуперспиралями.
Уравнения этих кривых выражаются через Гауссовы гипергеометрические функции и
численно интегрируются адаптивными методами типа Гаусса-Кронрода. Уникальная
формула cуперспирали позволяет варьированием трех параметров формы (a, b, c)
получить любую из известных спиралей и, вообще, любую спиралевидную кривую с
монотонным изменением кривизны. В частности, при значениях параметров a
= 0.5, b = 1, c = 1 суперспираль представляет собой клотоиду.
Для введения аналитических кривых в САПР их целесообразно
аппроксимировать NURBS кривыми. Таким образом, создается NURBS-шаблон
аналитической кривой. В предлагаемой программной платформе для вычисления
сложнейшей формулы суперспирали используется Mathematica. В СКМ Mathematica
разработана динамическая процедура аппроксимации и визуализации суперспирали
(рис. 5). В динамической процедуре формируется геометрический определитель
Эрмита в виде таблицы координат точек опорной ломаной, векторов первых
производных, положительных значений кривизны, длин сегментов кривой между
опорными точками и единичных векторов кривизны. Динамическая процедура
использует непосредственно компонент FairCurve.exe и
выполняет не только подготовку геометрического определителя Эрмита для
аппроксимации аналитической кривой, но и ее аппроксимацию посредством NURBS, а
также оценку точности аппроксимации. При надлежащем выборе параметров
аппроксимации и использовании методики золотой середины (отсечения концевых
участков с возмущением формы) можно добиться высокой точности аппроксимации.
На рис. 5 показана суперспираль, представляющая клотоиду при
значениях a = 0.5, b = 1, c = 1. Клотоида аппроксимирована
B-сплайновой кривой восьмой степени при
параметрах аппроксимации Number of Points =
16, начальное значение параметра s0 = -1, первый шаг
приращения параметра hs0 = 0.1, последний шаг приращения hsk
= 1. Для устранения возмущения формы на конечном участке B-сплайновой
кривой последние три сегмента удалены.
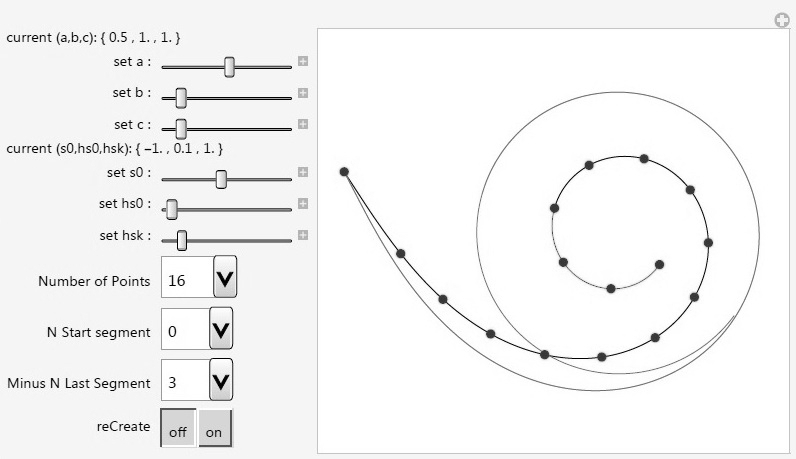
Рис. 5. Суперспираль,
представляющая клотоиду. Аппроксимация клотоиды B-сплайном.
Динамическая процедура позволяет обеспечить высокое качество
и точность построения NURBS-шаблона. B-сплайновая кривая визуально
совпадает с исходной клотоидой. Визуально совпадают и графики кривизны B-сплайновой
кривой и исходной кривой. Программа также дает численную оценку максимальных
отклонений NURBS-шаблона от оригинала: max = max[0.00140453],
min = min[-0.00417795]. Программа формирует NURBS-модель кривой в формате Microsoft Excel и экспортирует её во внешний файл.
Далее для переноса NURBS-модели из внешнего файла в
Fusion360 необходимо выполнить следующие действия:
a) Откройте
этот файл в Microsoft Excel, выделите область с моделью и скопируйте в буфер
обмена. Перейдите в книгу FCModeler.xlsm на страницу NURBS. Вставьте текст из
буфера обмена, начиная с ячейки A2.
b) Удалите
последние три сегмента сплайна. В области 'Extract segments' установите параметры
'Start segment = 0', ‘Number of segments = 12’. Нажмите кнопку [Extract segments].
Далее выполните интерполяцию кривой для формирования DXF-файла (кнопка [ViewCvt]).
c) Перейдите
в Fusion360.
d) Вызовите
приложение plug_in_FairCurveModeler in Excel.
e) Установите
переключатель на 'Curve from DXF'.
f)
Очистите 'Change Box'.
g) Программа
выдаст сообщение 'Press OK to create Object'. Нажмите OK в окне сообщения.
Нажмите OK в диалоговом окне FAIRCURVEMODELER.
h) Программа
сгенерирует кривую из DXF-файла.
i)
Из-за разности единиц измерения в Fusion360 и в DXF-файле, кривая будет
в 10 раз меньше оригинала.
j)
Выберите Modify- Scale. Выберите кривую в дереве построения. Установите
следующие параметры масштабирования: Scale Type = Uniform, Scale Factor = 10.
k) Суперспираль
отобразится в проекте. Проверьте качество cуперспирали построением графика её
кривизны (рис. 6).
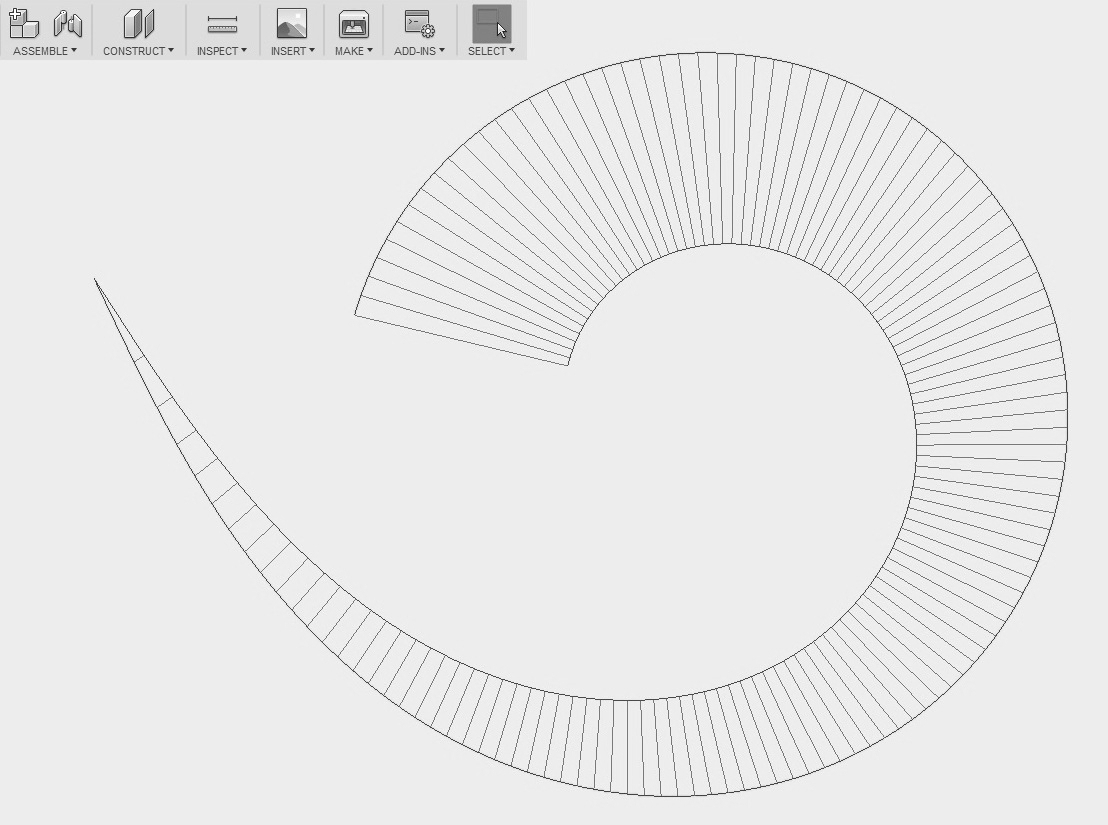
Рис. 6.
Суперспираль и её функция кривизны в проекте Fusion360.
Несмотря на самодостаточность Fusion360, рекомендуется
дополнительно к Fusion360 использовать AutoCAD [22]. Авторы настоящей работы представляют
необходимым использовать AutoCAD для фиксации кривых
высокого качества в трехмерных моделях, чтобы избежать аппроксимации кривых
сплайном внутреннего представления и сохранить высокое качество кривых класса F. Также рекомендуется использовать приложение
‘FairCurveModeler app AutoCAD’ [7], обладающее наиболее полным функционалом и
позволяющее моделировать кривые и поверхности. Приложение имеет развитый
инструментарий редактирования кривых и поверхностей для различных видов
геометрического определителя.
Программная платформа поставляется в комплекте с
приложениями FairCurveModeler к САПР (Fusion360,
AutoCAD, nanoCAD и КОМПАС 3D). Перед началом работы
необходимо перенести код активации Code_Activation.txt из папки приложения в
папку программной платформы ‘FairCurveModeler app Excel VBA’.
1. Разработан
программный комплекс FairCurveModeler для визуализации кривых линий и
поверхностей высокого качества по критериям плавности.
2. Предложена
универсальная программная платформа для визуализации кривых класса F и
разработки специализированных прикладных приложений для любых САПР, основанная
на использовании Microsoft Excel VBA, FairCurveModeler и систем компьютерной
математики.
3. Продемонстрирована
интеграция программной платформы с Fusion360. Выявлены ограничения API
Fusion360 при включении NURBS-модели в проект. Показана техника переноса точной
NURBS-модели c программной платформы в Fusion360 через DXF-файл.
4. Показано
применение программной платформы для визуализации функциональных и эстетических
кривых в интеграции с Fusion360.
1. Мударисов
С. Г., Муфтеев В. Г., Фархутдинов И. М. Оптимизация геометрии лемешно-отвальной
поверхности плуга. Механизация и электрификация сельского хозяйства. 2009. №4.
С. 17-19.
2. Обоснование
выбора оптимальной формы функциональной кривой динамической поверхности
технического изделия / В.Г.Муфтеев, С.Г.Мударисов, И.М.Фархутдинов,
А.Р.Марданов, А.С.Семенов, М.А.Талыпов // Известия международной академии
аграрного образования. 2013. Выпуск 17. С. 90-93.
3. Муфтеев
В. Г., Зиатдинов Р. А. Функциональность и эстетичность кривых линий в
промышленном дизайне: многокритериальный подход к оценке качества форм в CAD-системах
будущего. Вестник машиностроения (№ 5/940, в публикации).
4. Muftejev
V. Modeling class F NURBS curves in the integrated environment - CAD-system +
web-app FairCurveModeler + Mathematica / Wolfram Library Archive. MathSource.
2013-07-26. URL: http://library.wolfram.com/infocenter/MathSource/8465/ (дата
обращения: 01.07.2017).
5. Моделирование
кривых и поверхностей класса F в интегрированной среде CAD-система + FairCurveModeler
+ Mathematica / Муфтеев В.Г., Михалкина Н., Романюк А.Н., Марданов А.Р.,
Семенов А.С.// Материалы научно-практической конференции, посвященной 60-летию
кафедры "Трактора и Автомобили" ФГБОУ ВПО БГАУ. 19-20 декабря 2013 г.
С. 282-297
6. Farin,
G. Class A Bézier curves // Computer Aided Geometric Design. 2006. N.
23. P. 573–581.
7. Муфтеев
В. Г., Марданов А. Р., Талыпов М. А. Программа ‘FairCurveModeler app AutoCAD’
// Autodesk App Store. Release Date: 8/5/2016. URL:
https://apps.autodesk.com/ACD/en/Detail/Index?id=4526969846340104233&appLang=en&os=Win32_64
(дата обращения: 01.07.2017).
8. Муфтеев
В. Г., Марданов А. Р., Талыпов М. А. Программа ‘FairCurveModeler app Fusion360’
// Autodesk App Store. Release Date: 4/10/2016. URL:
https://apps.autodesk.com/FUSION/en/Detail/Index?id=3245146306164013809&appLang=en&os=Win64
(дата обращения: 01.07.2017).
9. Муфтеев
В. Г., Зелев А. П, Тархова Л. М. Интеграция Mathematica + FairCurveModeler с CAD-системой
КОМПАС 3D // Материалы научно-практической конференции, посвященной 60-летию
кафедры "Трактора и Автомобили" ФГБОУ ВПО БГАУ. 19-20 декабря 2013 г.
С. 282-297.
10. Программа
изогеометрического моделирования кривых линий высокого качества. Web-приложение
CAD-систем / В.Г.Муфтеев, А.Р.Марданов, А.Н.Романюк, В.Г.Турта, И.М.Фархутдинов
// Компьютерная графика и распознавание изображений. Материалы международной
научно-технической интернет-конференции. Винница. 2012. С. 127-139.
11. Открытая платформа для
разработки прикладных САПР изделий с функциональными кривыми и поверхностями /
Муфтеев В.Г., Аминев Р.И., Гизатова Д.Х., Талыпов М.А. // В сборнике: ПРОБЛЕМЫ
СТРОИТЕЛЬНОГО КОМПЛЕКСА РОССИИ. Материалы XX Международной научно-технической конференции.
2016. С. 115-117.
12. URL: https://ru.wikipedia.org/wiki/Parametric_Technology_Corporation
(дата обращения: 01.07.2017).
13. Подготовка NURBS
шаблонов аналитических кривых в Mathematica+FairCurveModeler для CAD-cистем /
Муфтеев В.Г., Марданов А.Р., Семенов А.С., Урманов В.Г. // Материалы
научно-практической конференции, посвященной 60-летию кафедры "Трактора и
Автомобили" ФГБОУ ВПО БГАУ. 19-20 декабря 2013 г. С. 275-282.
14. Муфтеев В.Г.
Конструирование плоских кривых методом огибающей // Изв. ВУЗов. Авиационная
техника. 1980. № 4. С. 43-47.
15. Osipov, V.A.,
Muftejev, V.G. Modelling Curvilinear Lines and Surfaces via Modified B-Splines.
Computers in Industry. 1989. N. 13. P. 61-67.
16. Муфтеев В. Г.
Моделирование кривых высокого качества на основе v-кривых // Прикладная
геометрия. Applied Geometry [Электронный ресурс]: науч. журн. / Моск.
авиационный ин-т (гос.техн.университет) "МАИ". - Электрон. журн. -
Москва : МАИ. 2007. №19. вып.9. –Режим доступа к журн.: http://www.mai.ru. –
Загл. с титул. экрана. С. 25-74. (дата обращения: 01.07.2017).
17. Муфтеев В. Г.,
Марданов А. Р. Изогеометрическое моделирование кривых линий и поверхностей
высокого качества по базовым критериям плавности / Сборник трудов ДонНТУ серии
"Информатика, кибернетика и вычислительная техника". 2009. Вып. 10.
№153. С. 131-145.
18. Harada, T. Study of
quantitative analysis of the characteristics of a curve. Forma. 1997. V. 12. N.
1. P. 55-63.
19. Kineri, Y., Endo, S.,
Maekawa, T. Surface design based on direct curvature editing. Computer-Aided Design.
2014. V. 55. P. 1 - 12.
20. Ziatdinov, R.,
Yoshida, N., Kim, T. Analytic parametric equations of log-aesthetic curves in
terms of incomplete gamma functions. Computer Aided Geometric Design, V. 29, N.
7. P. 129-140.
21. Ziatdinov, R. Family
of superspirals with completely monotonic curvature given in terms of Gauss
hypergeometric function. Computer Aided Geometric Design. 2012. V. 29. N.7. P.
510-518.
22. URL: http://fusion-360.ru/features.html#fabricate
(дата обращения: 01.07.2017).
23. Ульрих, К.
Промышленный дизайн: создание и производство продукта / Карл Ульрих, Стивен
Эппингер; пер. с англ. М. Лебедева, под общ. ред. А. Матвеева. – Москва:
Вершина, 2007.
24. Nabiyev, R. I.,
Ziatdinov, R. The mathematical design and evaluation of the peculiarities of
the shape features of Bernstein-Bézier curves from the standpoint of the
laws of technical aesthetics, Mathematical Design & Technical Aesthetics.
2014. V. 2. N. 1. P. 6-11.
25. Ziatdinov, R.,
Yoshida, N., & Kim, T. Visualization and analysis of regions of monotonic
curvature for interpolating segments of extended sectrices of Maclaurin.
Computer Aided Geometric Design. 2017. V. 56. P. 35-47.
Universal software platform for visualizing class F curves, log-aesthetic curves and development of applied CAD systems
Authors: R.A. Ziatdinov1,A, V.G. Muftejev2,B, R.I. Akhmetshin3,B, A.P. Zelev4,B, R.I. Nabiyev5,B, A.R. Mardanov6,B
A Department of Industrial and Management Engineering, Keimyung University, Daegu, Republic of Korea
B Ufa State Aviation Technical University, Ufa, Russian Federation
1 ORCID: 0000-0002-3822-4275, ziatdinov@kmu.ac.kr
2 ORCID: 0000-0003-4352-3381, muftejev@mail.ru
3 ORCID: 0000-0003-2448-0654, ahmetshin@bk.ru
4 ORCID: 0000-0002-1999-9729, zelev7@mail.ru
5 ORCID: 0000-0002-0920-6780, dizain55@yandex.ru
6 ORCID: 0000-0002-6635-8887, systems@list.ru
Abstract
This article describes the capabilities of a universal software platform for visualizing class F curves and developing specialized applications for CAD systems based on Microsoft Excel VBA, the software complex FairCurveModeler, and computer algebra systems. Additionally, it demonstrates the use of a software platform for visualizing functional and log-aesthetic curves integrated with CAD Fusion360. The value of the curves is evident in visualizing the qualitative geometry of the product shape in industrial design. Moreover, the requirements for the characteristics of class F curves are emphasized to form a visual purity of shape in industrial design and to provide a positive emotional perception of the visual image of the product by a person.
Keywords: high-quality curve, superspiral, class F curve, shape modeling, CAD system.
1.
Mudarisov S.G., Muftejev V.G., Farkhutdinov I.M.
Optimization of the geometry of the plowshare-dump surface. Mechanization and
Electrification of Agriculture. 2009. No. 4. pp. 17-19.
2.
Muftejev V.G., Mudarisov S.G., Farhutdinov I.M.,
Mardanov A.R., Semenov A.S., Talypov M.A. Justification of the optimal shape
choice for the functional curve of dynamic surface in industrial product. News
of the International Academy of Agrarian Education. 2013. Issue 17. pp. 90-93.
3.
Muftejev V.G., Ziatdinov R.A. Functionality and
aesthetics of curves in industrial design: a multi-criteria approach to the
evaluation of the quality of shapes in CAD systems of the future. Vestnik
Mashinostroeniya, 2018 (No. 5/940, accepted for publication).
4.
Muftejev V.G. Modeling class F NURBS curves in
the integrated environment - CAD-system + web-app FairCurveModeler +
Mathematica / Wolfram Library Archive. MathSource. 2013-07-26. URL:
http://library.wolfram.com/infocenter/MathSource/8465/ (Accessed on
01.07.2017).
5.
Muftejev V.G., Mikhalkina N., Romanyuk A.N.,
Mardanov A.R., Semenov A.S. Class F curves and surfaces modeling in integrated
environment - CAD system + FairCurveModeler + Mathematica // Proceedings of the
scientific-practical conference devoted to the 60th anniversary of the Tractors
and Cars Department, Ufa State Aviation Technical University. 2013. pp.
282-297.
6.
Farin, G. Class A Bézier curves //
Computer Aided Geometric Design. 2006. No. 23. pp. 573–581.
7.
Muftejev V.G., Mardanov A.R., Talypov M.A.
‘FairCurveModeler app AutoCAD’ software package // Autodesk App Store. Release
Date: 8.5.2016. URL:
https://apps.autodesk.com/ACD/en/Detail/Index?id=4526969846340104233&appLang=en&os=Win32_64
(Accessed on 01.07.2017).
8.
Muftejev V.G., Mardanov A.R., Talypov M.A.
‘FairCurveModeler app Fusion360’ software package // Autodesk App Store.
Release Date: 4.10.2016. URL:
https://apps.autodesk.com/FUSION/en/Detail/Index?id=3245146306164013809&appLang=en&os=Win64
(дата обращения: 01.07.2017).
9.
Muftejev V.G., Zelev A.P., Tarkhova L.M.
Integration of Mathematica + FairCurveModeler with COMPAS 3D computer-aided
design system // Proceedings of the scientific-practical conference devoted to
the 60th anniversary of the Department of Tractors and Cars, Ufa State Aviation
Technical University. pp. 282-297.
10. Muftejev V.G., Mardanov A.R., Romanyuk A.N., Turt V.G., Farkhutdinov
I.M. Program for isogeometric modeling of a high-quality curves.
Web-application for CAD systems // Materials of the International Scientific
and Technical Internet-Conference "Computer graphics and image
recognition". Vinnitsa. 2012. pp. 127-139.
11. Muftejev V.G., Aminev R.I., Gizatova D.H., Talypov M.A. Open
platform for developing applied CAD systems for the products with functional
curves and surfaces // Materials of the 20th International Scientific and
Technical Conference "Problems of the Russian Construction Industry".
2016. pp. 115-117.
12. URL: https://ru.wikipedia.org/wiki/Parametric_Technology_Corporation
(Accessed on 01.07.2017).
13. Muftejev V.G., Mardanov A.R., Semenov A.S., Urmanov V.G. Developing
NURBS templates of analytical curves in Mathematica + FairCurveModeler for CAD
systems // Proceedings of the scientific-practical conference devoted to the
60th anniversary of the Tractors and Cars Department, Ufa State Aviation
Technical University. 2013. pp. 275-282.
14. Muftejev V.G. The construction of plane curves by the envelope
method // Izvestiya Vuzov. Aviatsionnaya Tehnika. 1980. No, 4. pp. 43-47.
15. Osipov V.A., Muftejev, V.G. Modelling Curvilinear Lines and Surfaces
via Modified B-Splines. Computers in Industry. 1989. No. 13. pp. 61-67.
16. Muftejev V.G. Modeling of a high-quality curves on the basis of v-curves.
Applied Geometry. 2007. No. 19. Issue 9. pp. 25-74.
17. Muftejev V.G., Mardanov A.R. Isogeometric modeling of a high-quality
curves and surfaces based on basic smoothness criteria / Collection of works of
DonNTU, Informatics, Cybernetics and Computer Science series. 2009. Issue 10.
No. 153. pp. 131-145.
18. Harada, T. Study of quantitative analysis of the characteristics of
a curve. Forma. 1997. Vol. 12. No. 1. pp. 55-63.
19. Kineri, Y., Endo, S., Maekawa, T. Surface design based on direct
curvature editing. Computer-Aided Design. 2014. Vol. 55. pp. 1 - 12.
20. Ziatdinov, R., Yoshida, N., Kim, T. Analytic parametric equations of
log-aesthetic curves in terms of incomplete gamma functions. Computer Aided
Geometric Design, Vol. 29, No. 7. pp. 129-140.
21. Ziatdinov, R. Family of superspirals with completely monotonic
curvature given in terms of Gauss hypergeometric function. Computer Aided
Geometric Design. 2012. Vol. 29. No.7. pp. 510-518.
22. URL: http://fusion-360.ru/features.html#fabricate (Accessed on
01.07.2017).
23. Eppinger S., Ulrich K. Product design and development. McGraw-Hill
Higher Education, 2015.
24. Nabiyev, R. I., Ziatdinov, R. The mathematical design and evaluation
of the peculiarities of the shape features of Bernstein-Bézier curves
from the standpoint of the laws of technical aesthetics, Mathematical Design
& Technical Aesthetics. 2014. Vol. 2. No. 1. pp. 6-11.
25. Ziatdinov, R., Yoshida, N., Kim, T. Visualization and analysis of
regions of monotonic curvature for interpolating segments of extended sectrices
of Maclaurin. Computer Aided Geometric Design. 2017. Vol. 56. pp. 35-47.






