Механика деформированного твердого тела – это техническая
наука, которая проводит исследования и решает задачи преимущественно
прикладного характера. В настоящее время одной из многочисленных актуальных
задач, решаемых механикой деформированного твердого тел является, задача по определению
собственных частот и визуализации форм колебаний элементов конструкций.
Цель данного исследования заключается в определении набора параметров
и характеристик при динамическом нагружении для элементов ядерных
энергетических установок различной конфигурации.
Для достижения поставленной цели поставлены следующие
задачи:
- Определение собственных частот и форм колебаний элементов
конструкций расчетным методом.
- Определение собственных частот и форм колебаний элементов
конструкций экспериментальным методом.
- Сравнение результатов, полученных расчетным и
экспериментальным методами.
В статье рассматриваются две методики для определения
собственных частот и форм колебаний: метод конечных элементов (далее по тексту
МКЭ) в программном комплексе ANSYS, и экспериментальный метод – голографическая
интерферометрия.
К достоинствам МКЭ относится его универсальность по
отношению к геометрии и свойствам рассчитываемых объектов. Область применения
МКЭ не ограничивается линейно-упругим анализом напряженно-деформированного
состояния при статическом нагружении. В настоящее время МКЭ успешно применяют
для расчетов в упругопластической области, решения задач устойчивости,
динамического нагружения, механики разрушения, задач тепло- и массопереноса,
электромагнитных полей и т.п. В связи с этим открываются дополнительные
возможности и в области прочностных расчетов – при решении комбинированных
задач. Главным недостатком МКЭ является необходимость составления
вычислительных программ и применения вычислительной техники.
Экспериментальные методы исследования колебаний служат для
определения параметров (частот, коэффициентов затухания, собственные форм)
колебаний линейных не зависящих от времени механических систем. Поскольку
параметры колебаний можно определить аналитическими методами (формулы) и
численными методами (метод конечных элементов), то экспериментальные методы
исследований колебаний служат для проверки результатов, полученных
аналитическими, численными методами и решения сложных инженерных задач, когда
расчет затруднен. Если аналитическим и численным методами не удается определить
параметры колебаний, то найденные экспериментально параметры колебаний служат в
качестве основы при последующих расчетах и модификации конструкций.
Экспериментальные методы исследования колебаний используются
главным образом при решении сложных динамических задач, которые не удается
проанализировать с помощью аналитических моделей или на основе накопленного
опыта для аналогичных систем.
Для определения собственных частот и форм колебаний рассмотрим
две методики, представленные на рисунке 1.
Рисунок 1 - Схема методик определение собственных
частот и форм колебаний
Первая методика является расчетным методом в программном комплексе
ANSYS, реализованный с помощью метода конечных элементов, который часто используется
для аналитического решения актуальных задач механики деформированного твердого
тела. Для примера, иллюстрирующего эту методику, рассмотрим определение
собственных частот и форм колебаний консольной балочки.
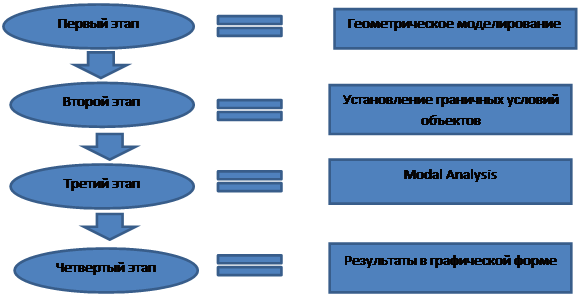
Реализация методики заключается в последовательных этапах
решения задачи в программном комплексе ANSYS (рисунок 2).
Рисунок 2 - Схема первой
методики определения собственных частот и форм колебаний
Первый этап заключался в геометрическом моделировании.
Для создания геометрической модели образца задаются геометрические размеры
объекта и механические характеристики материала, а именно: модуль Юнга,
коэффициент Пуассона, значение плотности материала. Далее выбирается конечные
элементы из библиотеки элементов в программном комплексе. В качестве конечного
элемента для трехмерного (3D) моделирования объемных конструкций использовался
восьми узловой гексагональный элемент SOLID185. Выбранный элемент определяется
узлами, имеющими три степени свободы в каждом узле, перемещения в направлении
осей X, Y, Z узловой системы координат. Элемент имеет свойства пластичности,
гиперупругости, изменения жесткости приложения нагрузок, ползучести, больших
перемещений и больших деформаций, смешанную формулировку для расчета почти
несжимаемых упругопластических материалов и полностью несжимаемых гиперупругих
материалов [1]. Рисунок 3 отражает первый этап геометрического моделирования
объекта.

Рисунок 3 – Геометрическая модель объекта
После создания геометрической модели объекта наносится,
конечно – элементная сетка, результат ее нанесения представлен на рисунке 4

Рисунок 4 – Конечно – элементная сетка объекта
Второй этап заключается в задании граничных условий объектов.
В расчете использовались ограничения перемещений объектов по трем осям по
внешнему контору, с целью моделирования жесткого защемления образцов. Рисунок 5 отражает результат второго этапа, заданы граничных условий объекта
моделирования.

Рисунок 5 – Граничные условия объекта
На третьем этапе расчета выполняется Modal Analysis. Modal
Analysis используется для определения характеристик вибраций (собственных
частот и форм колебаний) конструкции в целом или отдельных сборочных единиц в
процессе проектирования. Такой расчет может также являться начальной фазой
другого, более подробного расчета, в том числе расчета переходных процессов,
исследования вынужденных колебаний или случайных колебаний [2].
В четвертом этапе осуществляется обработка
результатов, включающая представление результатов в графическом виде. В итоге получаем
результат в виде графического изображения – рисунок 6.
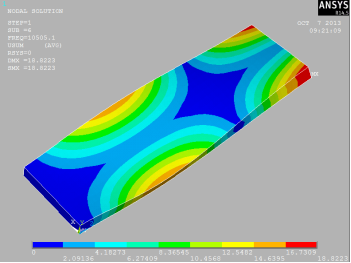
Рисунок 6 – Результат решения модального анализа для
консольной балки
Вторая методика определения собственных частот и форм
колебаний использует метод голографической интерферометрии.
Для примера, иллюстрирующего эту методику, рассмотрим
определение собственной частоты и формы колебаний плоского днища с двумя
круговыми вырезами.
Проведение экспериментальной части исследование собственных
частот и форм колебаний состоит из трех этапов эксперимента - Рисунок 7.
Рисунок 7 - Схема второй методики определения
собственных частот и форм колебаний
Первый этап заключается в том, что используя
оптическую схему в сходящихся пучках на фотопластинке, установленной на
специальном кинематическом устройстве, регистрируют голограмму неподвижного исследуемого
объекта. Голограмму возвращают в оптическую схему интерферометра и изменяют
направление освещения, в результате чего на поверхности тела в реальном
масштабе времени наблюдают систему несущих полос. На рисунке 8 отражен первый этап экспериментального исследования голографическая интерферограмма с несущими
полосами, наблюдаемая методом реального времени.

Рисунок 8 – Голографическая интерферограмма с
несущими полосами, наблюдаемая в реальном масштабе времени
На втором этапе эксперимента, при плавном изменении
частоты внешнего возбуждения колебаний исследуемого объекта, фиксируют момент
возникновения резонанса по изменению (уничтожению) картины несущих
интерференционных полос в местах расположения пучностей. Несущие полосы
конечной ширины наблюдаются только в местах расположения узловых линий. Полученные
частоты резонансных колебаний исследуемого объекта фиксируются
экспериментатором. Типичная картина несущих интерференционных полос,
наблюдаемая в момент резонанса представлена на рисунке 9.
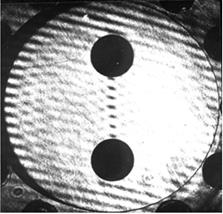
Рисунок 9– Резонансная форма колебаний,
визуализированная эталонными полосами
В третьем этапе эксперимента голографическая
интерферограмма неподвижного объекта убирается из схемы интерферометра и на ее
место устанавливается новая фотопластинка, и на нее методом усреднения во
времени регистрируется голограмма колебаний исследуемого объекта на найденной
собственной частоте. На рисунке 10 показан результат третьего этапа
эксперимента.

Рисунок 10 – Резонансная форма колебаний, записанная
методом усреднения во времени
Таким образом, на практике для решения задач механики
деформированного твердого тела используются оба метода. Экспериментальные
методы исследования колебаний служат для определения параметров (частот,
коэффициентов затухания, собственные форм) колебаний линейных не зависящих от
времени механических систем. Поскольку параметры колебаний можно определить
численными методами (метод конечных элементов), то экспериментальные методы
исследований колебаний служат для проверки результатов, полученных
аналитическими, численными методами. Если численным методами не удается
определить параметры колебаний, то найденные экспериментально параметры
колебаний служат в качестве основы при последующих расчетах и модификации
конструкций. Экспериментальные методы исследования колебаний используются
главным образом при решении сложных динамических задач, связанных с вибрациями
или акустикой, которые не удается проанализировать с помощью аналитических
моделей или на основе накопленного опыта для аналогичных систем.
В данном исследовании определялись собственные частоты и
формы колебаний для четырех типов образцов с разными конфигурациями, изготовленными
из материала Д16Т с помощью двух методов, расчетного в программном комплексе ANSYS,
и экспериментального методом голографической интерферометрии.
Визуализация (от лат visualis, «зрительный») – общее
название примеров представления числовой информации или физического явления в
виде, удобным для зрительного наблюдения и анализа [4].
В рамках проводимого исследования рассматривается
компьютерная визуализация в программном комплексе ANSYS, и оптическая
визуализация форм колебаний методом голографической интерферометрии.
Компьютерная визуализация представляет собой методику перевода
абстрактных представлений об объектах в геометрические образцы, что дает
возможность наблюдать результаты компьютерного моделирования явлений и
процессов.
В данном исследовании при использовании метода усреднения по
времени оптическая визуализация реализована на голограммах, узловая линия
визуализируется в виде светлой интерференционной полосы максимальной
интенсивности, а темные интерференционные полосы дают распределение амплитуд
вибраций в пучностях.
Использовались четыре типа образцов с разными конфигурациями
из материала Д16Т, а именно:
- тонкая квадратная пластина, жестко защемленная по контору.
- тонкая квадратная пластина, с центральным отверстием
жестко защемленная по контору.
- тонкая прямоугольная пластина, жестко защемленная с одной
стороной (консоль).
- тонкая прямоугольная пластина, жестко защемленная по
контору.
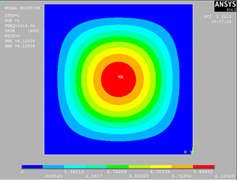
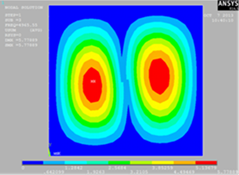
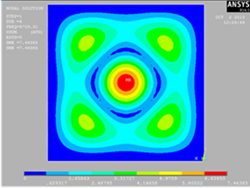
Первый образец в виде тонкой квадратной пластины
жестко защемленной по контору. В таблице 1 визуализированы компьютерные и
оптические формы колебаний квадратной пластины.
Таблица 1. – Визуализация
форм колебаний квадратной пластины
|
Число полуволн nхm
|
Метод конечных
элементов в программном комплексе ANSYS
|
Голографическая интерферометрия
|
|
1-1
|
|

|
|
2-1
|
|

|
|
3-3
|
|

|
Полученные результаты свидетельствует о том, что экспериментальное
решение собственных форм колебаний для тонкой квадратной пластины дает
аналогическое визуальное представление с расчётным методом.
Также в таблице 2 результаты значений собственных частот
колебаний для квадратной пластины, полученные экспериментальным (обозначенные в
таблице fэксп) и расчетным (обозначенные в таблице fANSYS) методами.
Таблица 2 . – Значение
частот собственных колебаний квадратной пластинки
|
Число полуволн nхm
|
1-1
|
1-2
|
2-1
|
2-2
|
3-3
|
|
fэксп,
Гц
|
2275
|
4773
|
4773
|
6730
|
8294
|
|
fANSYS,
Гц
|
2377
|
4965
|
4965
|
7116
|
8759
|
|
δmax,
%
|
4
|
3
|
3
|
5
|
5
|
Необходимо отметить, что значения собственных частот с
числом полуволн nхm 1-2 и 2-1 одинаковы.
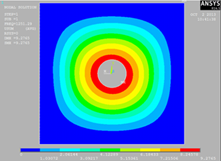
Далее рассмотрим второй образец в виде тонкой квадратной
пластины с центральным отверстием жестко защемленной по контору. В таблице 3 визуализированы
компьютерные и оптические формы колебаний квадратной пластины с центральным
отверстием.
Таблица 3. –
Визуализация форм колебаний квадратной пластины с центральным отверстием
|
Число полуволн nхm
|
Метод конечных
элементов в программном комплексе ANSYS
|
Голографическая интерферометрия
|
|
1-1
|
|

|
|
1-2
|
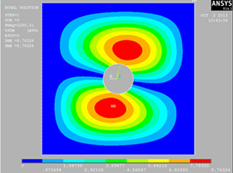
|

|
|
2-2
|
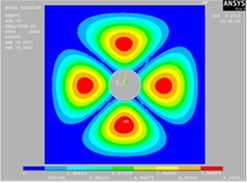
|

|
Полученные результаты свидетельствует о том, что
экспериментальное решение собственных форм колебаний для тонкой квадратной
пластины с центральным отверстием дает аналогическое визуальное представление с
расчётным методом.
В таблице 4 приведены результаты значений собственных частот
колебаний квадратной пластины с центральным отверстие, полученные
экспериментальным (обозначенные в таблице fэксп),
так и расчетным (обозначенные в таблице fANSYS)
методами.
Таблица 4. – Значение
частот собственных колебаний квадратной пластинки с центральным отверстием
|
Число полуволн nхm
|
1-1
|
1-2
|
2-2
|
2-3
|
3-3
|
|
fэксп,
Гц
|
1221
|
2215
|
3366
|
4051
|
4674
|
|
fANSYS,
Гц
|
1251
|
2281
|
3266
|
3899
|
4600
|
|
δmax,
%
|
3
|
3
|
3
|
4
|
2
|
С увеличением собственных частот с одинаковом количеством
полуволн nхm 2-2 учитывается
метод суперпозиции.
Исследуется так же третий образец в
виде тонкой прямоугольной пластины жестко защемленной с одной стороной
(консоль). В таблице 5 визуализированы компьютерные и оптические определения
форм колебаний прямоугольной консольной пластины.
Таблица 5. –
Визуализация форм колебаний прямоугольной консольной пластины
|
Число полуволн nхm
|
Метод конечных
элементов в программном комплексе ANSYS
|
Голографическая интерферометрия
|
|
2-0
|

|

|
|
0-1
|
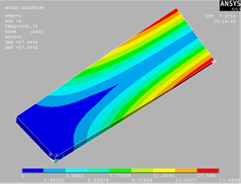
|

|
|
1-1
|

|

|
|
4-0
|
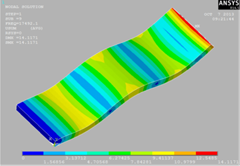
|

|
Полученные результаты свидетельствует о том, что
экспериментальное решение собственных форм колебаний для прямоугольной
консольной пластины дает аналогическое визуальное представление с расчётным
методом.
В таблице 6 представлены значения собственных частот
колебаний прямоугольной пластины консоли, полученные экспериментальным
(обозначенные в таблице fэксп), так и
расчетным (обозначенные в таблице fANSYS)
методами.
Таблица 6. – Значение
частот собственных колебаний прямоугольной пластины консоли
|
Число полуволн nхm
|
2-0
|
0-1
|
3-0
|
1-1
|
4-0
|
|
fэксп, Гц
|
3337
|
3508
|
8708
|
10377
|
17595
|
|
fANSY ,
Гц
|
3286
|
3392
|
9085
|
10505
|
17492
|
|
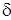 max,
% max,
%
|
2
|
3
|
4
|
2
|
1
|
Решение задачи определение собственных частот и форм
колебаний консоли является ключевой, так как при рассмотрении сложных систем
конструкции можно упростить до консоли, внося вклад в запас расчетов и использовать
модель в виде консоли.
Четвёртый образец в виде тонкой прямоугольной
пластины жестко защемленной по контору. В таблице 7 визуализированы
компьютерные и оптические формы колебаний прямоугольной пластины.
Таблица 7. –
Визуализация форм колебаний прямоугольной пластины
|
Число полуволн nхm
|
Метод конечных
элементов в программном комплексе ANSYS
|
Голографическая интерферометрия
|
|
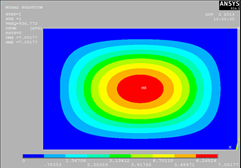
1-1
|
|

|
|
2-1
|
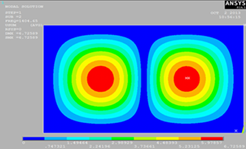
|

|
|
4-1
|
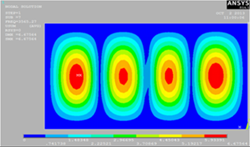
|

|
|
3-3
|
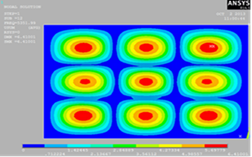
|

|
Полученные результаты свидетельствует о том, что
экспериментальное решение нахождение собственных форм колебаний для прямоугольной
пластины дает аналогическое визуальное представление с расчётным методом.
В таблице 8 представлены значения собственных частот
колебаний прямоугольной пластины, полученные экспериментальным (обозначенные в
таблице fэксп), так и расчетным
(обозначенные в таблице fANSYS)
методами.
Таблица 8. – Значение
частот собственных колебаний прямоугольной пластины
|
Число полуволн nхm
|
1-1
|
2-1
|
1-2
|
4-1
|
3-3
|
|
fэксп,
Гц
|
910
|
1383
|
2320
|
3367
|
5541
|
|
fANSYS,
Гц
|
936
|
1405
|
2362
|
3565
|
5352
|
|
δmax,
%
|
3
|
2
|
2
|
5
|
4
|
Зная первые низкие собственные частоты элементов конструкции использовать
для решения задач нахождения сейсмических напряжений, случайных колебаний, и
так далее.
Таким образом, компьютерная и оптическая визуализация форм колебаний
элементов конструкций идентичная, что дает возможность использовать один из
методов не зависимо от другого.
Результаты определения собственных частот и форм колебаний элементов
конструкций полученные с помощью экспериментального метода, голографической
интерферометрии сопоставлялись с результатами, полученными расчетным методом
конечных элементов в программном комплексе ANSYS.
Анализировались значения собственных частот колебаний образцов, полученных
экспериментальным и расчетным методами для одинаковых форм колебаний.
Таким образом, относительная погрешность (обозначенная в таблицах 1-3 δmax, %) для значений частот собственных
колебаний, полученных двумя разными методами исследования, для каждого образца
не превышает 5%.
Целью данного исследования заключалось в проведение
экспериментального анализа поведения деформируемых твердых тел различной
конфигурации при динамическом нагружении. В результате проведенного
исследования получены следующие выводы.
- Определены собственные частоты, и формы колебаний
расчетным методом конечных элементов в программном комплексе ANSYS и
экспериментальным – методом голографической интерферометрией, для четырех
типов пластин.
- Полученные результаты сопоставлялись как в графическом
формате, так и в табличном виде для анализа показателей собственных частот
и форм колебаний элементов конструкций, имеющих различную конфигурацию.
Расхождение значений собственных частот вычисленных методом конечных
элементов с экспериментально полученными результатами, методом
голографической интерферометрии, не превышает 5%, что позволяет
использовать предложенные методы, дополняя друг друга и получить
достоверные результаты.
В ходе проведенного исследование можно отметить, что знание
значений собственных частот и вида форм колебаний, позволяет существенно
уменьшать амплитуды вибраций, изменять собственные частоты путем введения
дополнительных конструктивных элементов или замены материала.
- Басов К.А. ANSYS: справочник пользователя. М.: ДМК Пресс,
2005. - 640.
- Каплун А.Б., Морозов Е.М., Олферьева М.А. ANSYS в руках
инженера. Практическое руководство. М.: Едиториал УРСС, 2003. - 272 с.
- Островский Ю.И., Щепинов В.П., Яковлев В.В. Голографические
интерференционные методы измерения деформаций. М.: Наука, 1988. - 248 с.
- https://ru.wikipedia.org
- И. А. Биргера, Я. Г. Пановко Прочность, устойчивость,
колебания Т. 3. М.: Машиностроение, 1968 страницы .
- Бутусов М.М., Туркевич Ю.Г Простая схема для получения
голографических интерферограмм в реальном масштабе времени - Журн. науч. и
прикл. фотогр. и кинематограф. – 1971. - №4. – С. 303 – 305.
- Гонткевич B.C. Собственные колебания пластин и оболочек.
-Киев: Наукова думка, 1964. 288 с.
- Зенкевич О. Метод конечных элементов в технике. М.: Мир,
1975.541 с.
- Козачок А.Г. Голографические методы исследования в
экспериментальной механике. М.: Машиностроение, 1984. - 175 с.
- Крылов О.В. Метод конечных элементов и его применение в
инженерных расчетах: Учебн. пособие для вузов-М.: Радио и связь, 2002.-104
с.
Determination natuxal freguencies and mode shapes imaging element structures
Authors: E.A. Zheleznyakova1, A.V. Osintsev2
NRNU «MEPhI», Moscow, Russia
1 ORCID: 0000-0002-0471-011X, remi.vivi@gmail.com
2 ORCID: 0000-0001-8077-9082, avosintsev@yandex.ru
Abstract
Currently, the problem of strength and stability of various complex structures is relevant and paramount for manufacturing, industrial, construction and other spheres of material production. This article discusses two methods of determining the eigenfrequencies and visualize the mode shapes, namely: the method of holographic interferometry and finite element method. Knowing the kind of shape oscillations and the corresponding frequency, it is possible to significantly reduce the amplitude of the vibrations change the natural frequencies by introducing additional elements or replacement of the material. This article presents the determination of natural frequencies and visualized mode shapes of structural elements with various configurations are widely used in the industry of high-temperature structural material of duralumin D16T.
Keywords: holographic interferometry, finite element method, natural frequencies, mode shape, visualization.
- Basov K. A. ANSYS: user's guide. M.:
DMK Press, 2005. - 640.
- Kaplun A. B., Morozov E. M., the Shape of
M. A. ANSYS in the hands of the engineer. A practical guide. M.:
editorial URSS, 2003. - 272.
- Ostrovsky, Y. I., Sainov V. P., Yakovlev
V. V. Holographic interferometric deformation measurement methods. M.:
Nauka, 1988. - 248 p.
- https://ru.wikipedia.org
- A. Birger, Y. G. Panovko Strength,
stability, vibrations vol. 3. M.: engineering, 1968 pages .
- Butusov, M. M., turkiewicz, Y. G Simple
scheme for obtaining holographic interferograms in real time - Sib.
scientific. and PM. photograph. and cinema. – 1971. - No. 4. – P. 303 –
305.
- Gantsevich B. C. natural oscillations of
plates and shells. -Kiev: Naukova Dumka, 1964. 288 p.
- Zenkevich O. finite element Method in
engineering. M.: Mir, S. 1975.541
- Kozachok, A. G., Holographic research
methods in experimental mechanics. M.: Mashinostroenie, 1984. - 175
p
- Krylov O. V. finite element Method and
its application in engineering calculations: Uchebn. manual for
schools-M.: Radio and communication, 2002.104 p