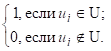Теорема о четырёх красках была доказана в 1976 году К.
Аппелем и В. Хакеном из Иллинойского университета. Это была первая крупная
математическая теорема, доказанная с помощью компьютера. Первым шагом
доказательства была демонстрация того, что существует определенный набор из
1936 карт, ни одна из которых не может содержать карту меньшего размера,
которая опровергала бы теорему. Аппель и Хакен использовали специальную
компьютерную программу чтобы доказать это свойство для каждой из 1936 карт.
Изначально доказательство было принято не всеми математиками, поскольку его
невозможно было проверить вручную. В дальнейшем оно получило более широкое
признание, хотя у некоторых долгое время оставались сомнения [1,2]. Чтобы
развеять оставшиеся сомнения, в 1997 году Робертсон, Сандерс, Сеймур и Томас
опубликовали более простое доказательство, использующее аналогичные идеи, но
по-прежнему проделанное с помощью компьютера. Кроме того, в 2005 году
доказательство было проделано Д. Гонтиром с использованием специализированного
программного обеспечения (Coq v7.3.1). Таким образом, существование раскраски вершин
плоского графа четырьмя красками было обосновано с помощью компьютерного
перебора [3].
Однако для полноты картины не хватает строго математического
описания механизма раскраски вершин плоского графа, способа описания
вычислительных аспектов раскраски плоских графов. Такой механизм имеет и
практическое значение. И хотя вычислительные методы раскраски плоских графов
мало используются в картографии, с которой эту задачу, как правило, связывают,
то в естественных науках и инженерных приложениях она представляет весьма
большой интерес. Например, раскраска плоских графов используется при изучении
свойств кристаллов [4]. Достаточно рассмотреть свойства кристалла FexTaS2.
Это слоистая структура, принадлежащая к классу дихалькогенидов переходных
металлов (TMD), такую структуру можно обнаружить под микроскопом в сплавах
металлов и магнитах. Другой пример использования – проектирование плоских
конструктивов [5]. Поэтому выявление естественного
механизма раскраски и вопрос дедуктивного доказательства данной теоремы
представляет практический интерес. Данная работа ставит своей целью произвести
дедуктивное доказательство теоремы о четырех красках и описать вычислительный
процесс раскраски плоских графов.
Рассмотрим произвольный связный плоский граф G, у
которого степень каждой вершины больше двух. В графе G каждую
нетреугольную грань путем добавления ребер разобьем на несколько треугольных
граней. В итоге получим максимально плоский граф G', все грани которого будут
треугольными. И хотя данный процесс неоднозначен, но если граф G'
раскрашен, то удаление из него вновь введенных ребер не нарушит его раскраску
[6]. Поместим внутри каждой грани s графа G' вершину x0.
Каждому ребру u графа G' поставим в соответствие
ребро u0,
соединяющее те вершины x0i
и x0j,
которые соответствуют граням si и sj
по обе стороны ребра u. Полученный таким образом топологический граф
является плоским, связным и называется или двойственным к G', или однородным
графом H степени три, или кубическим графом H.
Понятно, что в плоском кубическом графе вершины
соответствуют граням, а грани – вершинам
максимально плоского графа. Количество ребер в максимально плоском графе равно
количеству ребер двойственного плоского кубического графа. Количество ребер в
кубическом графе Н c n вершинами определяется по формуле:
m =
3n/2
(1)
Следовательно, количество ребер в таком графе всегда кратно
трем:
m ≡ 0 (mod 3)
(2)
Так как в кубическом графе количество ребер m – целое число,
то количество вершин n в однородном кубическом графе должно быть четным числом:
n ≡ 0 (mod
2)
(3)
С точки зрения раскраски, между максимальным плоским графом G'
и двойственным к нему плоским кубическим графом Н существует связь,
устанавливаемая следующей теоремой (Тэйта) [7].
Теорема 1. (Тэйт). Пусть Н –
плоский однородный кубический граф без перешейков. Необходимое и достаточное
условие возможности такой раскраски граней графа четырьмя цветами, при котором
никакие две смежные грани не окрашиваются в одинаковый цвет, состоит в том,
чтобы хроматический класс графа Н был равен трем.
Теорема Тэйта устанавливает связь между раскраской вершин
для максимально плоского графа и раскраской ребер двойственного к нему
кубического графа Н. Однако она не утверждает, что любой кубический граф
без мостов имеет хроматический класс равный трем. Тэйт высказал предположение,
что всякий плоский кубический граф без перешейков имеет гамильтонов цикл. Если
бы ему удалось это доказать, то тем самым была бы решена проблема четырех
красок, хотя сам Тэйт и не обнаружил этой зависимости. Однако Татт [8,9,10]
показал, что это предположение неверно, и привел пример кубического графа с 46
вершинами, не являющегося гамильтоновым (рис. 1).
|
|
|
|
Рис. 1. Граф Татта
|
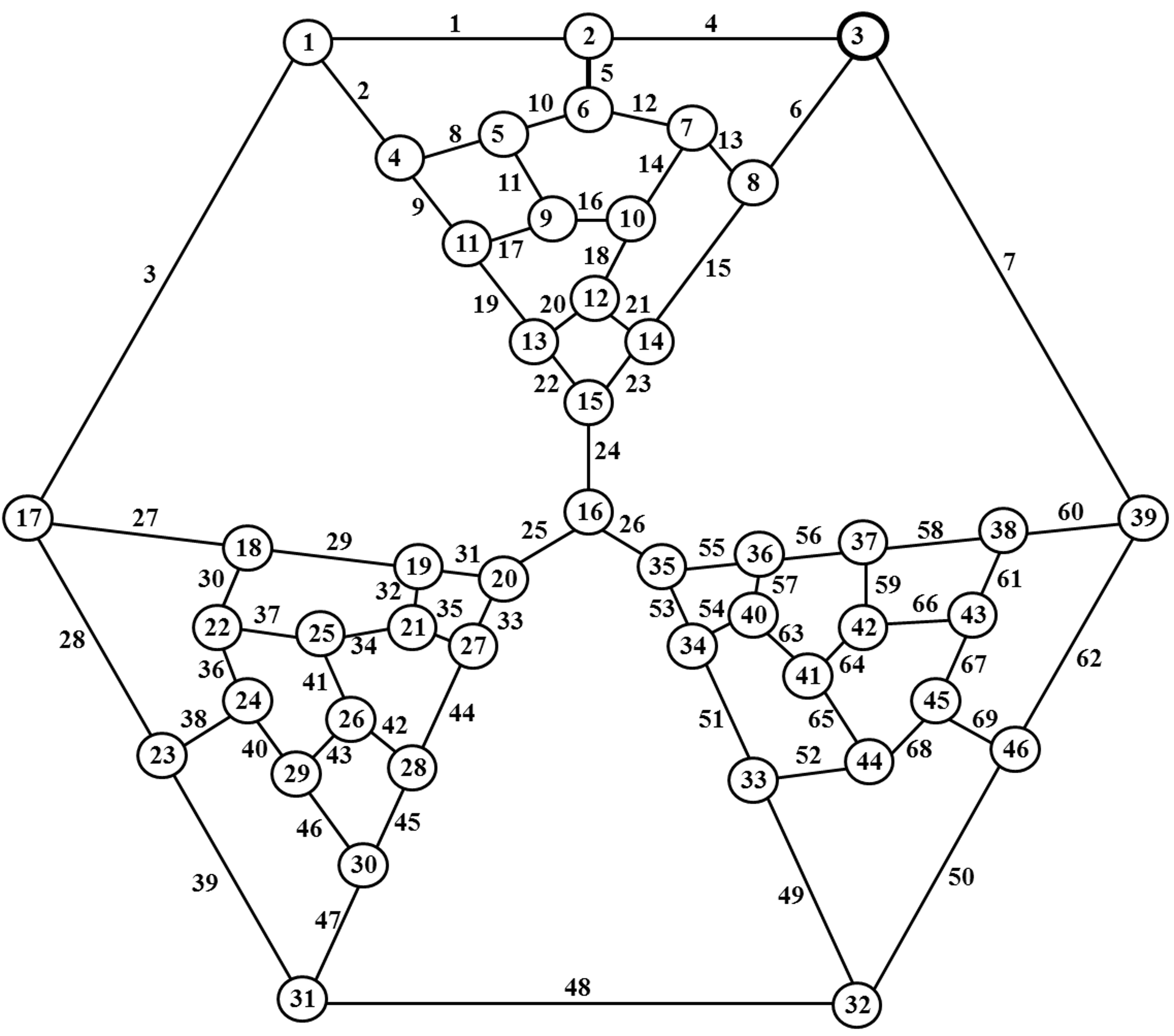
Рис. 2. Раскраска
ребер в кубическом графе Н
|
Если кубический граф Н имеет хроматический класс
равный трем, то его ребра должны быть раскрашены в три цвета. Раскраска
предполагает наличие трех разноцветных ребер для каждой вершины графа Н.
Кубический граф имеющий хроматический класс равный трем
будем называть раскрашенным плоским кубическим графом Н. Например,
кубический граф представленный на рис. 2 является раскрашенным кубическим
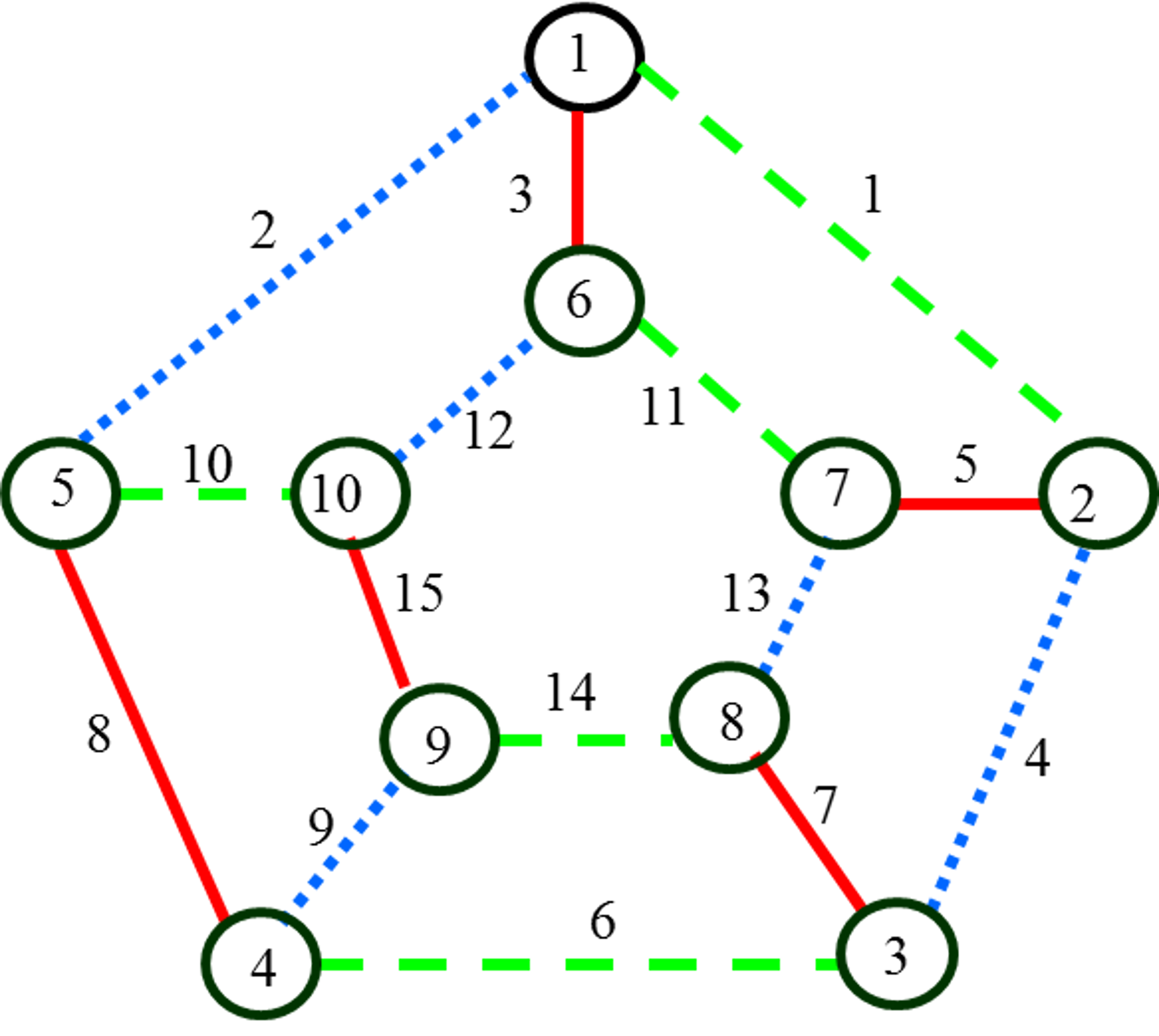
графом Н. Здесь белый цвет будем обозначать буквой W
или цифрой 0, а на рисунках графа ребра данного цвета будем представлять
штрихпунктирной линией. Красный цвет будем обозначать буквой R
или цифрой 1, а на рисунках графа ребра данного цвета будем представлять
сплошной линией. Синий цвет, будем обозначать буквой B
или цифрой 2, а на рисунках графа ребра данного цвета будем представлять точечной
линией. Зеленый цвет будем обозначать буквой G или цифрой 3, а на рисунках графа ребра данного цвета будем
представлять пунктирной линией. Согласно теореме Тэйта раскраска ребер
индуцирует раскраску граней плоского кубического графа Н, а раскраска
граней, в свою очередь, индуцирует раскраску ребер. На рис. 4 представлены 4
способа раскраски граней в зависимости от раскраски ребер.
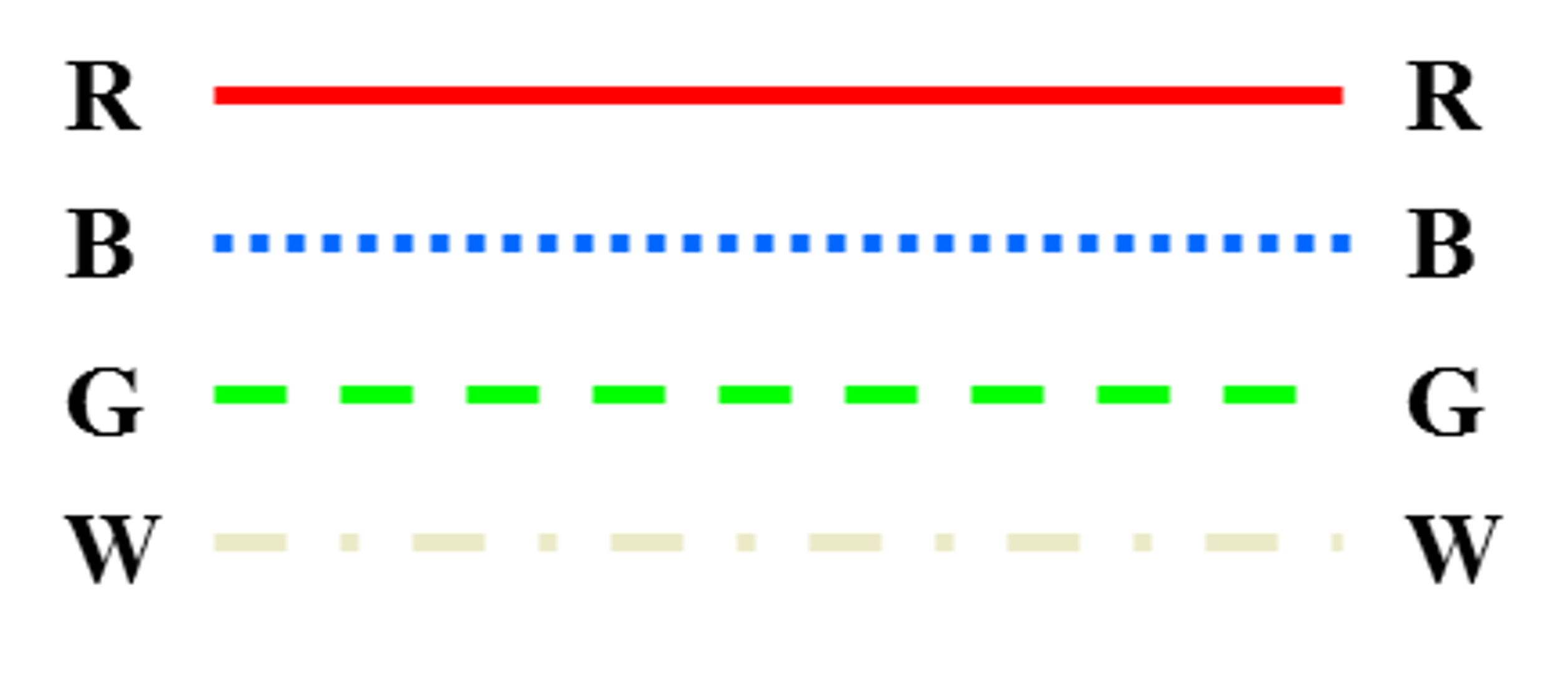
Рис. 3. Обозначение
цветных линий
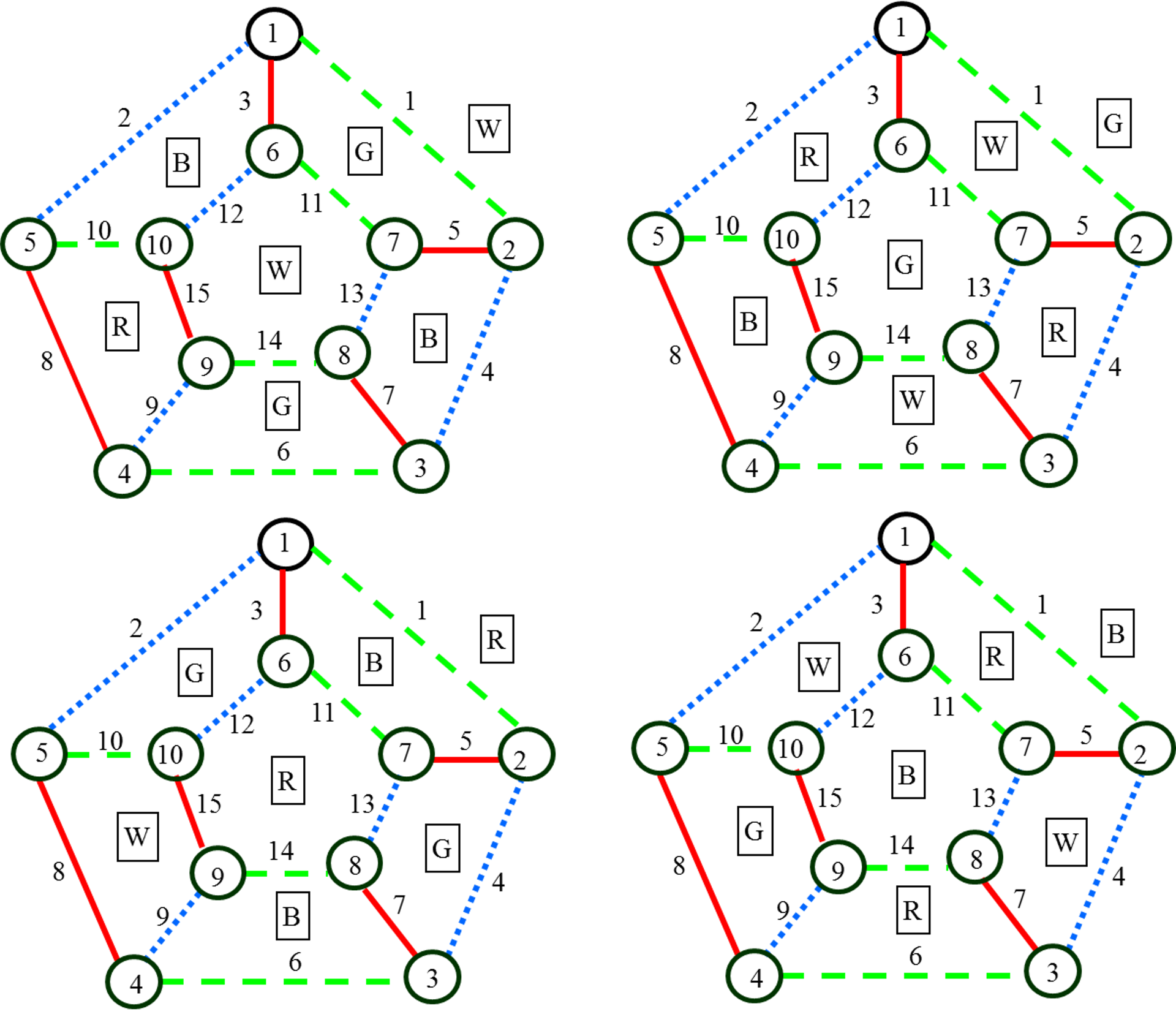
Рис. 4. Раскраска
граней плоского кубического графа
В свою очередь вершине максимального плоского графа может
быть поставлена в соответствие грань двойственного плоского кубического графа.
Следовательно, нужна математическая структура, одновременно описывающая
раскраску и ребер плоского кубического графа без мостов, и граней. Такая
математическая структура существует и называется группой Клейна четвертого
порядка. Её образует множество цветов при операции преобразования. Таблица
преобразования цветов для этой группы имеет вид [11].
|
+
|
0
|
1
|
2
|
3
|
|
W
|
W
|
R
|
B
|
G
|
|
R
|
R
|
W
|
G
|
B
|
|
B
|
B
|
G
|
W
|
R
|
|
G
|
G
|
B
|
R
|
W
|
(4)
Поставим в соответствие границе грани цикл из базиса
квазициклов плоского кубического графа. Квазициклом будем
называть цикл с четной валентностью вершин. Гамильтоновым квазициклом
будем называть квазицикл с валентностью вершин равной двум, проходящий по всем
вершинам графа [12]. Пусть G = (X,U) – граф с пронумерованным множеством
ребер U = {u1, u2,...,um}, a LG – множество
всех суграфов этого графа. Относительно операции сложения (будем называть ее
кольцевой суммой) множество LG
образует абелеву группу [13].
(X, U1) ⊕ (X, U2) =
(X,(U1 ∪ U2)\(U1∩ U2))
(5)
Действительно, LG заведомо является группоидом. Относя каждому
суграфу G = (X, U) строку чисел (α1,α2,...,αi,...,αm),
в которой i = (1,2,...,m), и определяя сложение строк как покомпонентное
по модулю 2, мы получим изоморфный LG группоид, элементами которого служат все
возможные строки длины m из нулей и единиц и который уже представляет
собой абелеву группу.
|
αi =
|
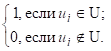
|
В дальнейшем группу LG удобно рассматривать как
линейное пространство над полем коэффициентов GF(2) = {0,1}, называемое
пространством суграфов данного графа G.
Размерность этого пространства dim LG = m, ибо множество элементов (1,0,....0),
(0.1.....0),....(0.0....,1), представляющих однореберные суграфы, образует
базис.
С другой стороны, каждый гамильтонов квазицикл есть 2-фактор
графа, так как n-фактор – это регулярный суграф
степени n. Тогда имеет место следующая теорема
для кубических графов (теорема Петерсена) [14].
|
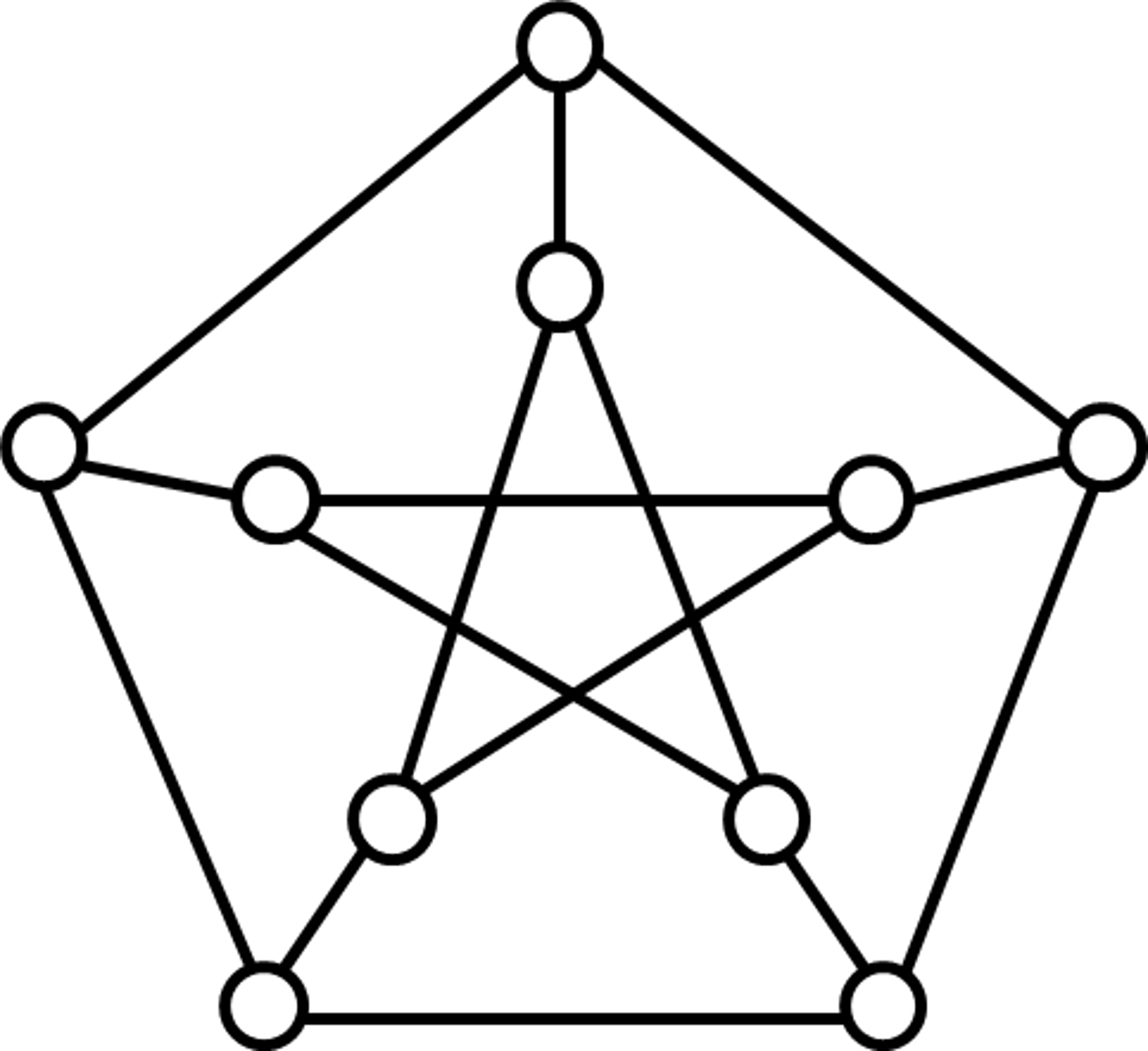
а) Граф Петерсена
|
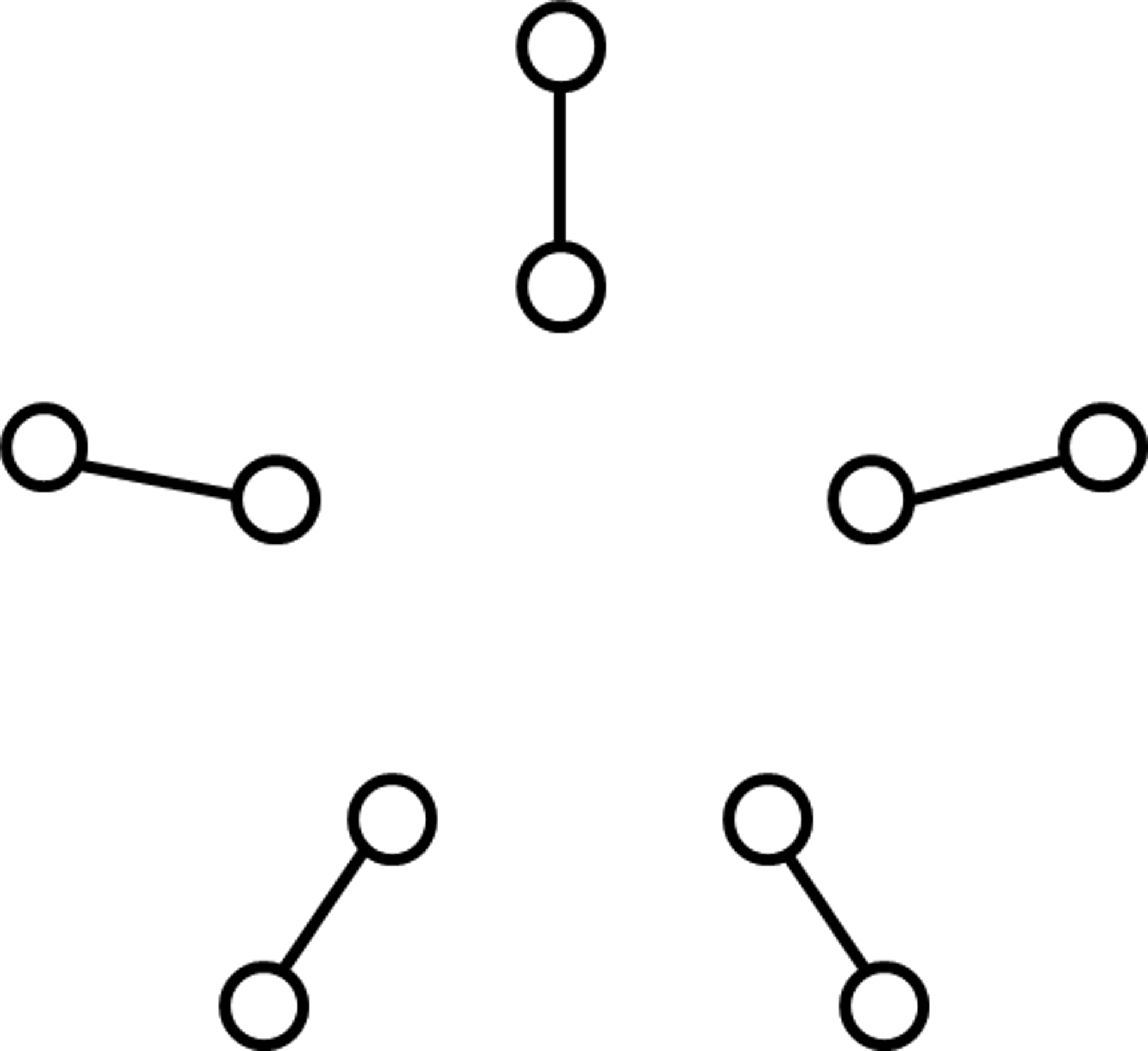
б) 1-фактор графа
Петерсена
|
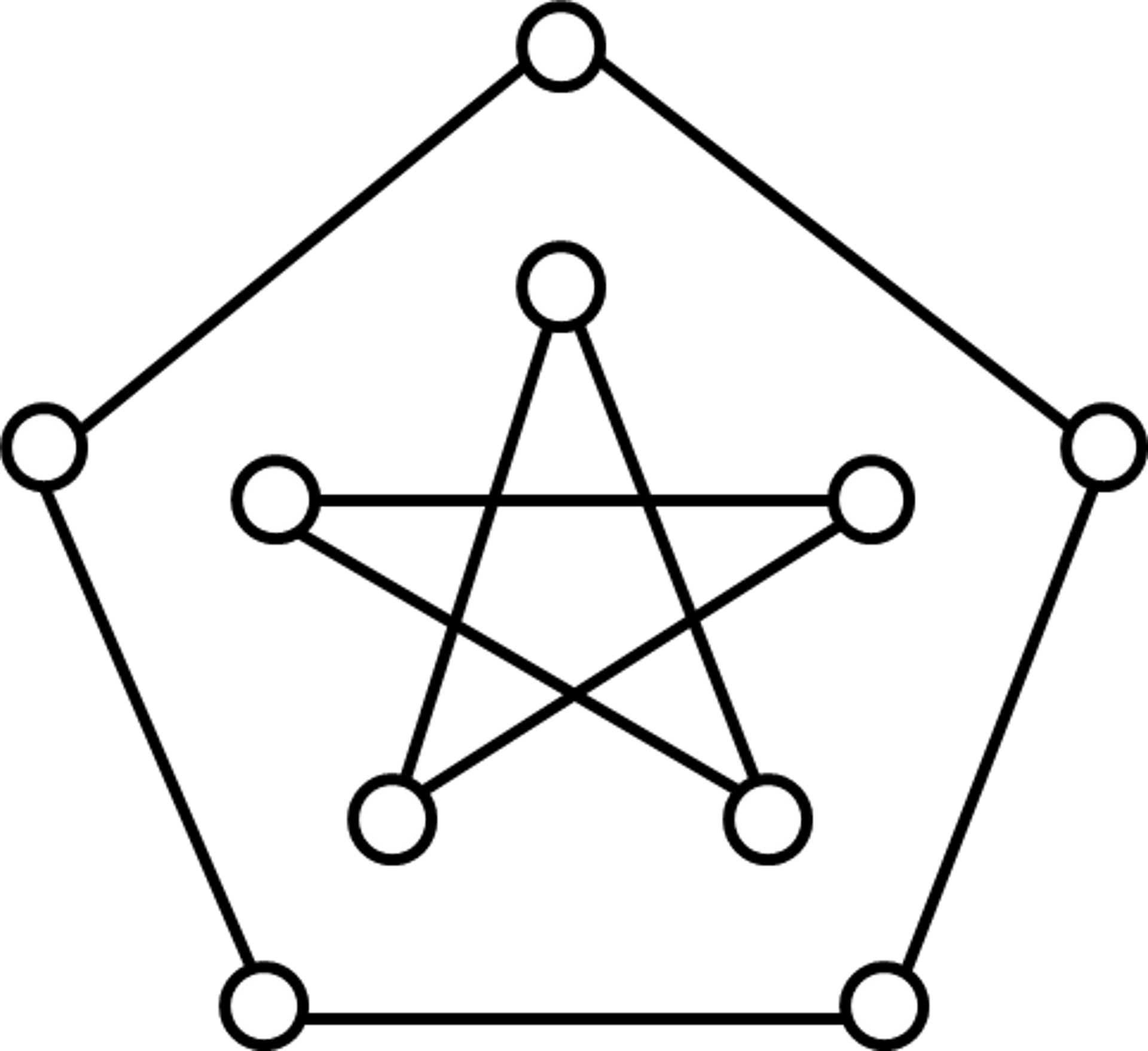
в) 2-фактор графа
Петерсена
|
Рис. 5. Кубический
граф Петерсена
Теорема 2. (Петерсен). Любой кубический граф,
не содержащий мостов, можно представить в виде суммы 1-фактора и 2-фактора.
В свою очередь, гамильтонов квазицикл (2-фактор) может
состоять из нескольких простых циклов (см. рис. 5,в). Каждый такой простой цикл
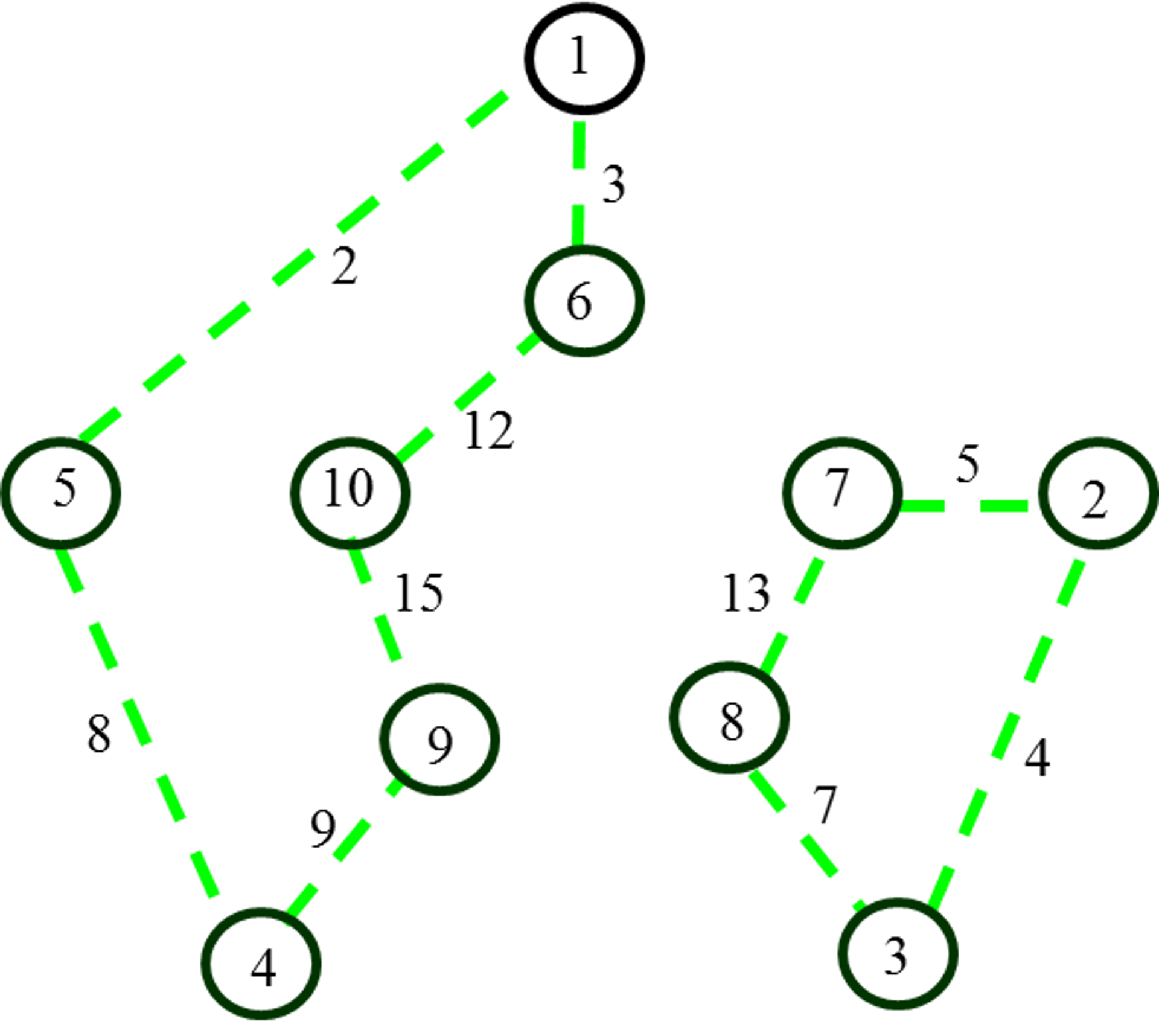
четной длины будем называть цветным диском. На рис. 6г показаны два
диска одного цвета: один проходит по ребрам {u2,u3,u8,u9,u12,u15}, а другой – по ребрам {u4,u5,u7,u13}.
Гамильтонов квазицикл, состоящий из цветных дисков, будем называть цветным
гамильтоновым квазициклом или цветным 2-фактором. В
раскрашенном кубическом графе обязательно существует цветная конфигурация,
состоящая из цветных 2-факторов имеющих диски только четной длины и цветных
1-факторов. Любой цветной гамильтонов квазицикл состоит из дисков. Если цветной
диск один, то такой гамильтонов квазицикл – гамильтонов цикл.
Раскрашенные плоские кубические графы обладают следующими
свойствами:
Свойство 1. В любом цветном диске число
вершин четно. Действительно, для того чтобы диск был цветным необходимо
чтобы его ребра были раскрашены в два цвета. Это возможно только в том случае,
когда количество вершин в цикле четно.
Свойство 2. Любой цветной гамильтонов
квазицикл (2-фактор) порождает два других цветных гамильтоновых квазицикла и
производит раскраску графа Н. Если задан цветной гамильтонов
квазицикл, то ребра графа этого 2-фактора можно раскрасить в два цвета отличных
от его цвета, а нераскрашенные ребра – в цвет самого гамильтонова квазицикла
(2-фактора). Таким образом, кубический граф будет раскрашен, а раскраска ребер,
в свою очередь, порождает три цветных гамильтоновых квазицикла (2-фактора).
Свойство 3. Сумма по модулю 2 трех цветных
гамильтоновых квазициклов (2-факторов), порожденных раскраской кубического
графа Н, есть пустое множество. Так как по каждому ребру проходит
два цветных гамильтоновых квазицикла и каждое ребро в сумме появляется дважды,
что при сложении по модулю 2 тождественно равно ∅, то сумма цветных гамильтоновых квазициклов, порожденных
правильной раскраской кубического графа Н, есть пустое множество.
|
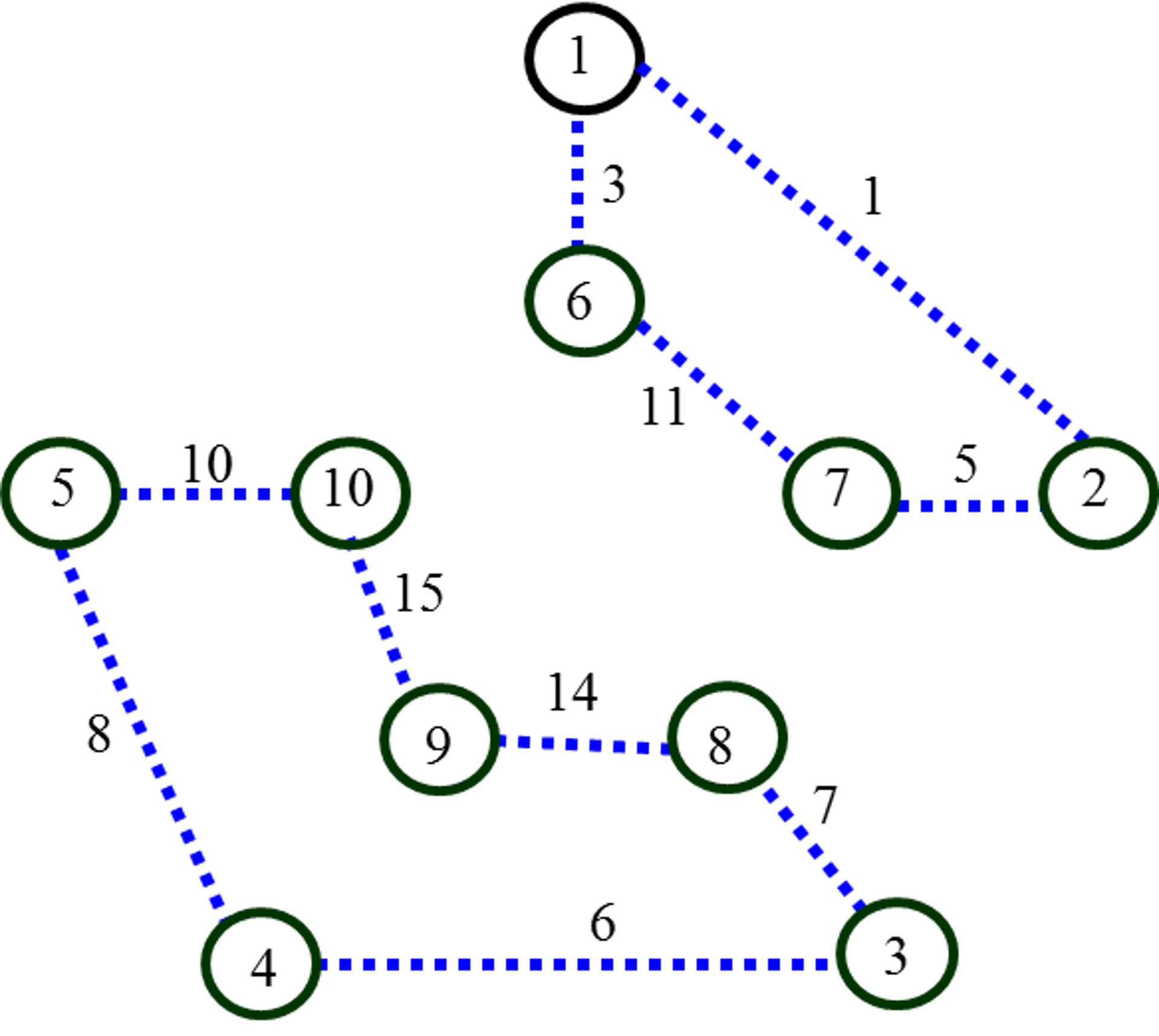
|
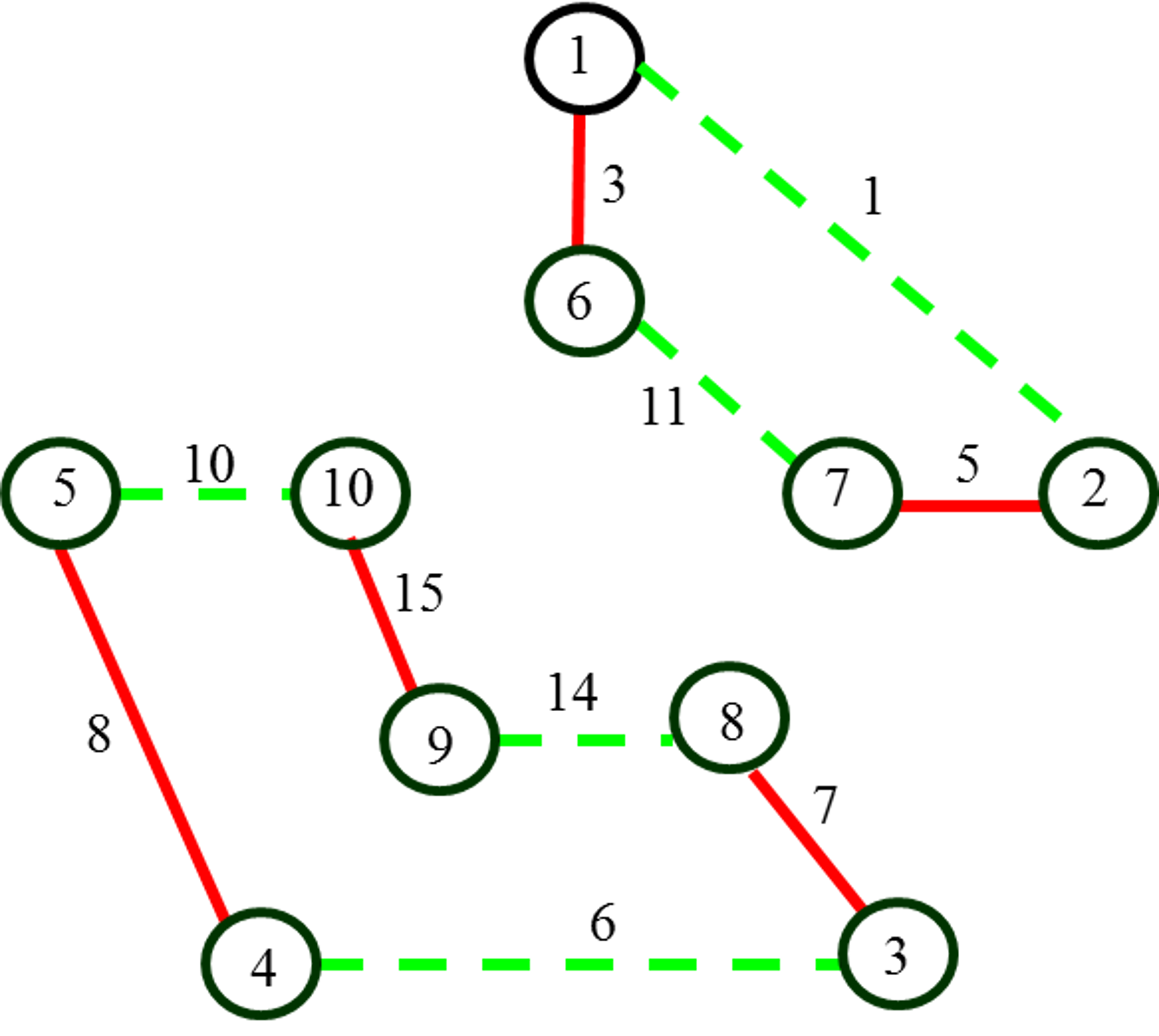
|
|
а) синий гамильтонов квазицикл
(2-фактор)
|
б) тот же квазицикл состоящий из красных и зеленых ребер
|
|
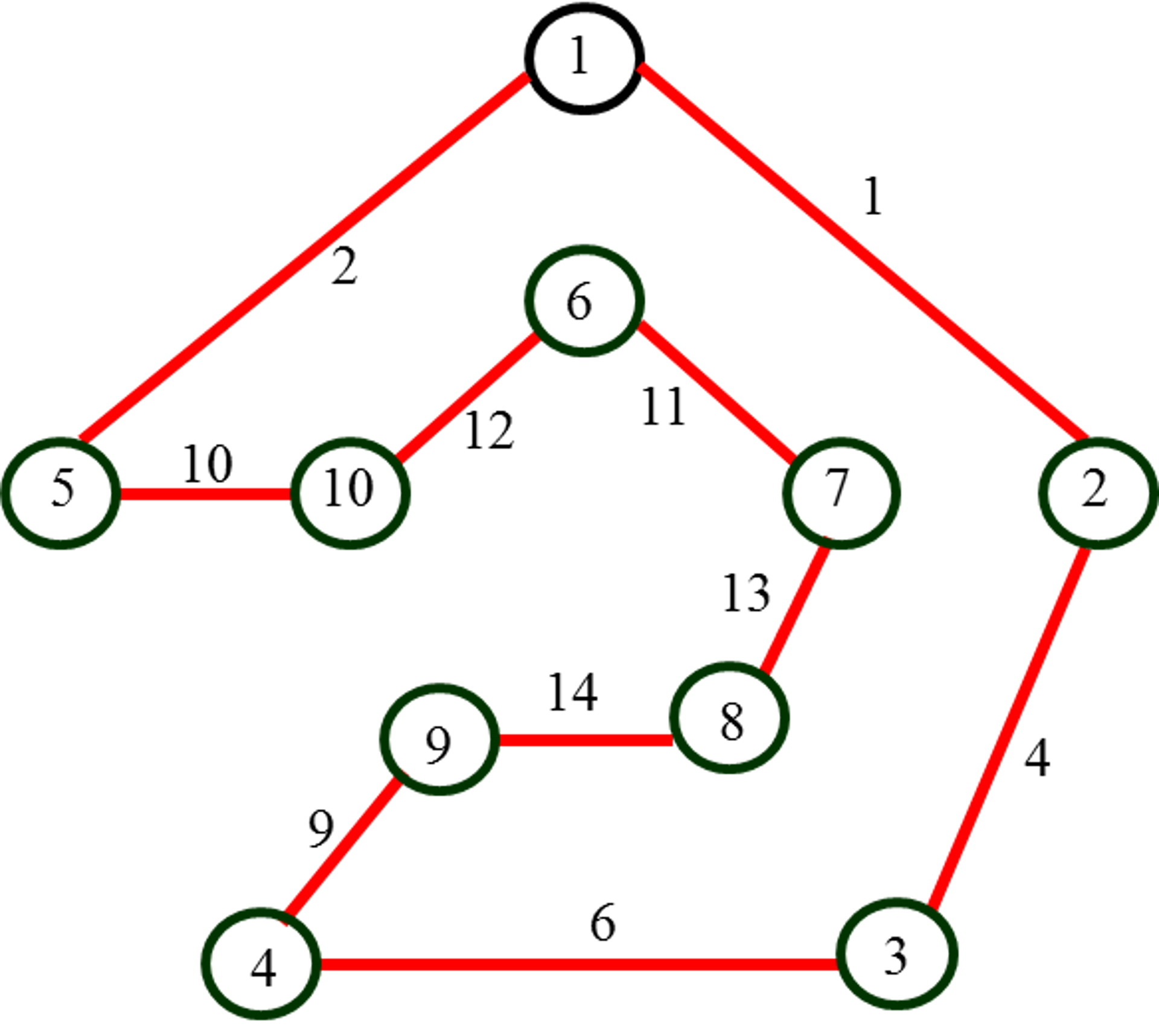
|
|
|
в) красный гамильтонов квазицикл
|
г) зеленый гамильтонов квазицикл
|
Рис. 6. Цветные
2-факторы (гамильтоновы квазициклы)
На базисе подпространства циклов графа G можно
определить функционал Мак Лейна принимающий нулевое значение, если граф
планарен [15]:
| F(С) = |
 |
= |
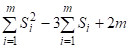 |
. |
(6)
Здесь Si
– количество изометрических циклов [16] проходящих по ребру i.
С учетом сказанного и введенной операции сложения циклов,
цветные гамильтоновы квазициклы и цветные 1-факторы обладают следующими
свойствами:
Rc ⊕ Gc ⊕ Bc = ∅;
(7)
Rf ⊕ Gf ⊕ Bf = H;
(8)
Rf
⊕ Rc
=
H;
(9)
Gf
⊕ Gc
=
H;
(10)
Bf ⊕ Bc = H.
(11)
Здесь индекс с
обозначает множество ребер, принадлежащих 2-фактору (гамильтонову квазициклу),
индекс f обозначает множество ребер,
принадлежащих 1-фактору, а Н –
множество ребер исходного плоского кубического графа. Кроме того, в
раскрашенном кубическом графе любой цветной 2-фактор образуется как конечная
кольцевая сумма базисных циклов [13]: Rc –
сумма базисных циклов образующих красный 2-фактор; Bc – сумма базисных циклов образующих синий 2-фактор; Gc – сумма базисных х циклов образующих зеленый
2-фактор; Wc – сумма
базисных циклов не вошедших ни в красный, ни в синий и ни в зеленый 2-факторы.
Проявление свойства двойственности построения цветных 2-факторов описывается
следующими выражениями:
Rc = Rc ,
Bc = Bc ,
Gc = Gc ,
(12)
где  ,
, 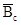 ,
, 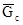 являются соответственными дополнениями базисных
циклов Rc, Bc,
Gc до полного базиса плоского графа и обода
графа Н. То есть:
являются соответственными дополнениями базисных
циклов Rc, Bc,
Gc до полного базиса плоского графа и обода
графа Н. То есть:
Rc ⊕ Rc =
Bc ⊕ Bc =
Gc ⊕ Gc =
∅
(13)
Будем называть гранью клетку ограниченную базисным циклом.
Три цветных 2-фактора порождают (индуцируют) раскраску граней плоского
кубического графа Н. В свою очередь, раскраска граней порождает
раскраску базисных циклов в цвет грани, так как границей грани служит базисный
цикл. Для раскрашенных плоских кубических графов кольцевая сумма базисных
циклов и обода согласно теореме Мак Лейна [15] равна
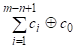 |
= ∅. |
(14)
С другой стороны, кольцевая сумма трех цветных гамильтоновых
квазициклов
Rc ⊕ Bc ⊕ Gc = ∅,
(15)
согласно выражению (2).
Следующее равенство связывает условие планарности Мак Лейна,
записанное в виде суммы базисных циклов и обода, с кольцевой суммой трех
цветных 2-факторов для плоского кубического графа H
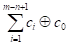 |
= Rc ⊕ Gc ⊕ Bc =
Rc ⊕ Bc ⊕
Gc =
Rc ⊕ Bc ⊕ Gc =
Rc ⊕ Bc ⊕ Gc =
|
|
= Rc ⊕ Bc ⊕ Gc =
Rc ⊕ Bc ⊕
Gc =
Rc ⊕ Bc ⊕ Gc =
Rc ⊕ Bc ⊕
Gc = ∅.
|
(16)
Если в раскрашенном плоском кубическом графе Н
кольцевую сумму базисных циклов, описывающих границы всех граней красного
цвета, обозначить как 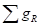 , кольцевую сумму базисных циклов, описывающих
границы граней синего цвета – как
, кольцевую сумму базисных циклов, описывающих
границы граней синего цвета – как 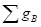 , кольцевую сумму базисных циклов, описывающих
границы граней зеленого цвета – как
, кольцевую сумму базисных циклов, описывающих
границы граней зеленого цвета – как 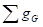 , а кольцевую сумму всех базисных циклов,
описывающих границы граней белого цвета – как
, а кольцевую сумму всех базисных циклов,
описывающих границы граней белого цвета – как 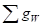 , то с учетом обода можно записать следующие
выражения:
, то с учетом обода можно записать следующие
выражения:
Gc
=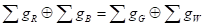 ;
;
(17)
Bc
=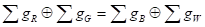 ;
;
(18)
Rc
=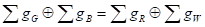 .
.
(19)
В свою очередь, три цветных 2-фактора индуцируют раскраску П
граней, где границы граней суть базисные циклы и обод плоского графа Н,
а раскраска граней описывается соответствием Г = {П, С, К}.
Здесь П – множество пар кортежей <ci,
ai,1 ✕ 1 + ai,2 ✕ 2 + ai,3
✕ 3 + ai,4
✕ 0>, C
– множество базисных циклов и обода плоского кубического графа Н, а К
– множество четырех цветов. Множество П характеризует раскраску граней
плоского кубического графа Н и представляет собой произведение элементов
множества С и элементов множества К, а его элементы – это кортежи
записанные в виде:
{<c1,
a1,1 ✕ 1 + a1,2 ✕ 2 + a1,3 ✕ 3 + a1,4 ✕ 0>,
<c2,
a2,1 ✕ 1 + a2,2 ✕ 2 + a2,3 ✕ 3 + a2,4 ✕ 0>,
……………………….……………………
(20)
<cm-n+1,
am-n+1,1 ✕1 + a m-n+1,2 ✕ 2 + a m-n+1,3 ✕ 3 + a m-n+1,4 ✕ 0>,
<c0,
am-n+2,1 ✕ 1 + a m-n+2,2 ✕ 2 + a m-n+2,3 ✕ 3 + a m-n+2,4 ✕ 0>}.
Здесь ai,j 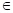 {0,1}; i
=(1,2,…,m-n+2); j = (1,2,3,4). Коэффициенты ai,j при базисных циклах
определяют принадлежность описывающего границу грани базисного цикла
соответствующему цветному 2-фактору. Сложение выполняется по законам операции
преобразования группы Клейна, а умножение – по обычным правилам арифметики.
Множество базисных циклов и обода С = {c1,c2,…,cm-n+1,c0}. Множество
цветов К = {1,2,3,0}. Следующие пары трех цветных 2-факторов индуцируют
разную раскраску граней:
{0,1}; i
=(1,2,…,m-n+2); j = (1,2,3,4). Коэффициенты ai,j при базисных циклах
определяют принадлежность описывающего границу грани базисного цикла
соответствующему цветному 2-фактору. Сложение выполняется по законам операции
преобразования группы Клейна, а умножение – по обычным правилам арифметики.
Множество базисных циклов и обода С = {c1,c2,…,cm-n+1,c0}. Множество
цветов К = {1,2,3,0}. Следующие пары трех цветных 2-факторов индуцируют
разную раскраску граней:
(Rc ⊕ Bc ⊕ Gc ) ∨ (Rc ⊕
Bc ⊕ Gc) индуцирует раскраску Г1 = {П1,
С, К},
(21)
(Rc ⊕ Bc ⊕ Gc)
∨ (Rc ⊕ Bc ⊕ Gc) индуцирует раскраску Г2 = {П2,
С, К},
(22)
(Rc ⊕ Bc ⊕ Gc)
∨ (Rc ⊕
Bc ⊕ Gc) индуцирует раскраску Г3 = {П3,
С, К},
(23)
(Rc ⊕ Bc ⊕ Gc) ∨
(Rc ⊕Bc ⊕
Gc) индуцирует раскраску Г4
= {П4, С, К}.
(24)
Произвольный плоский кубический граф без мостов можно
построить на плоскости путем введения новых ребер в предыдущий граф следующими
способами:
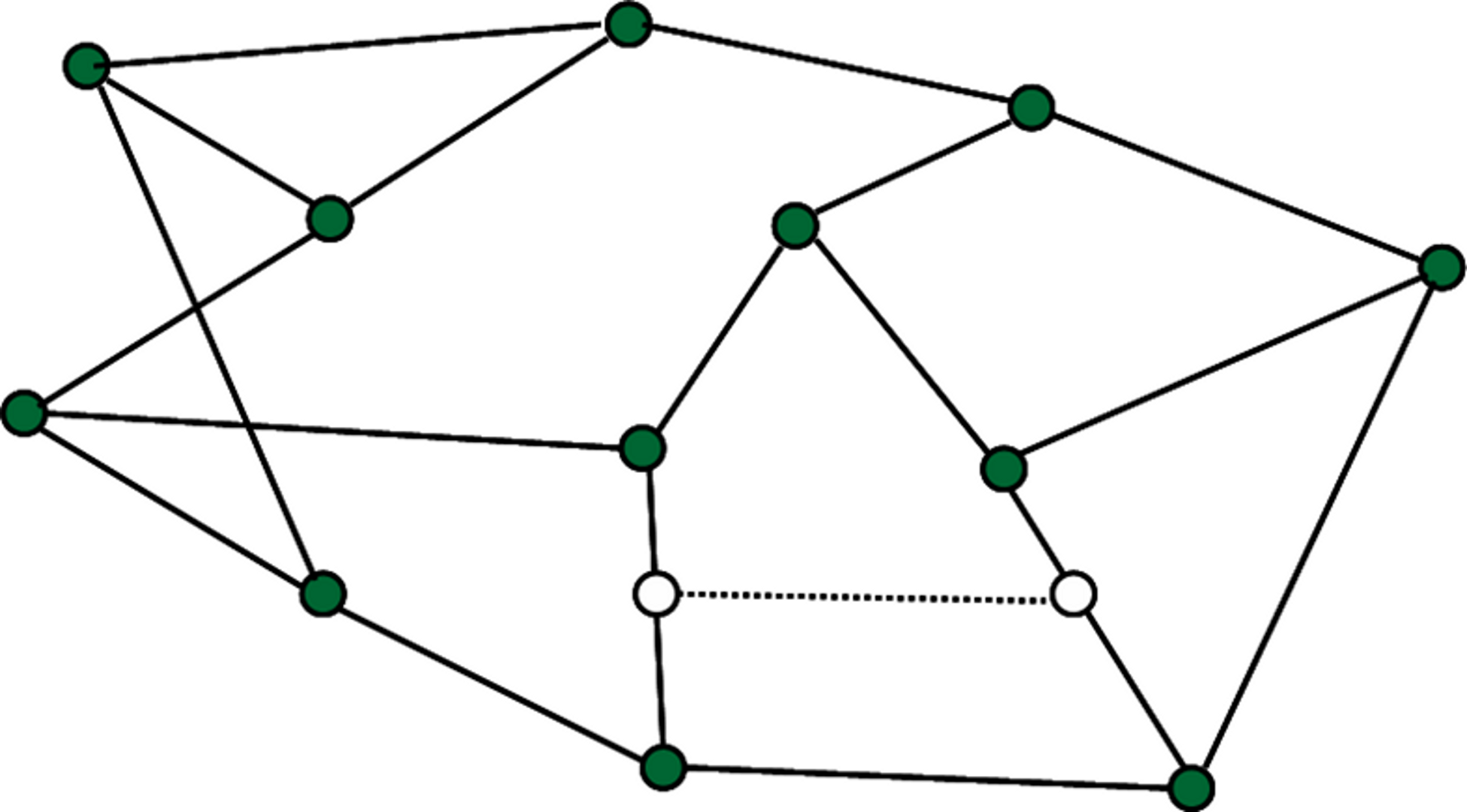
Способ 1. Расположить две новые вершины на
двух ребрах принадлежащих одному базисному циклу исходного кубического графа
без мостов и провести новое ребро, соединяющее эти вершины (см. рис. 7).
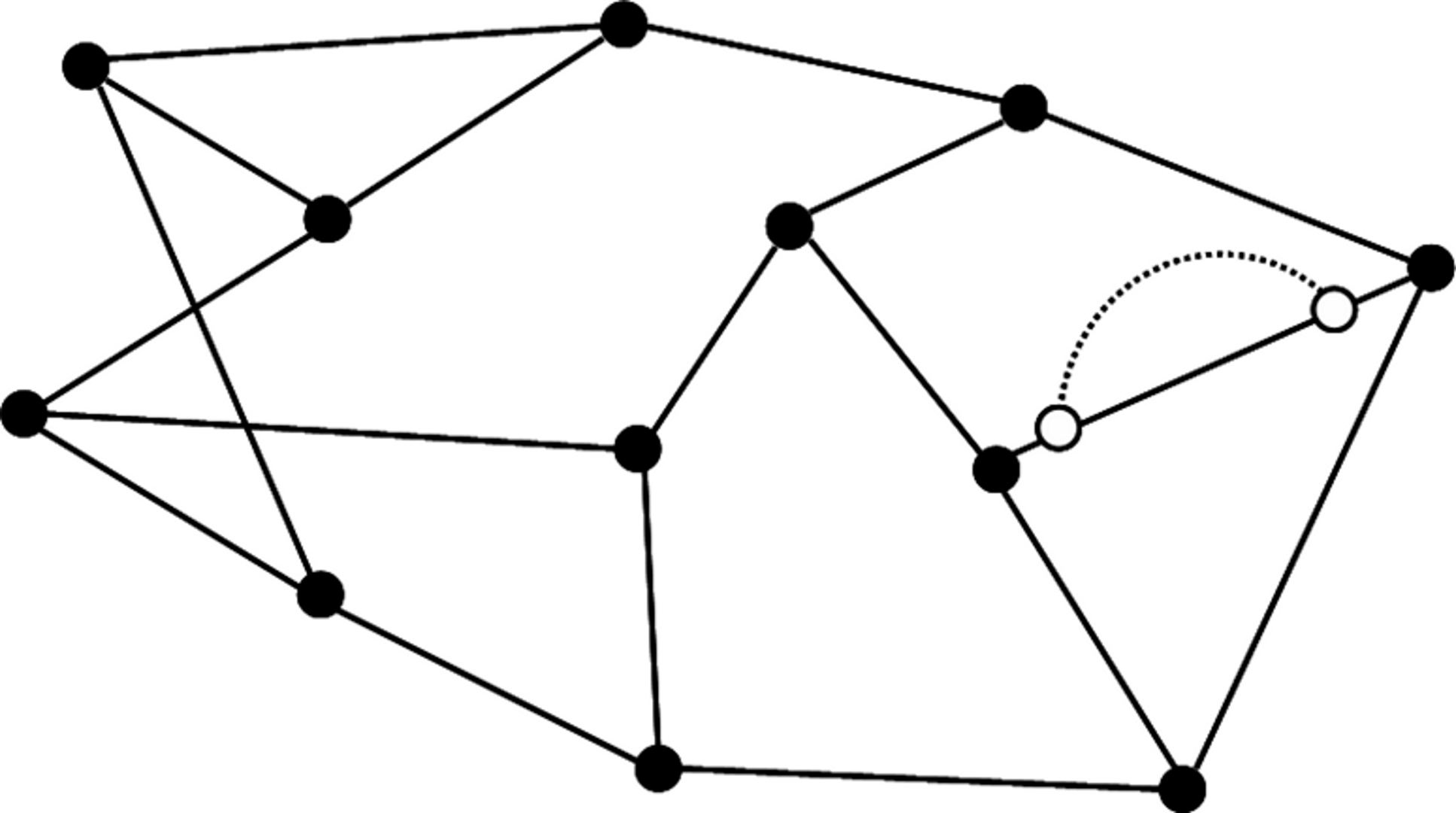
Способ 2. Расположить две новые вершины на
одном ребре исходного кубического графа без мостов и провести новое ребро,
соединяющее эти вершины (см. рис. 8).
|
|
|
|
|
Рис. 7. Первый
способ построения кубического графа H
|
Рис. 8. Второй
способ построения кубического графа H
|
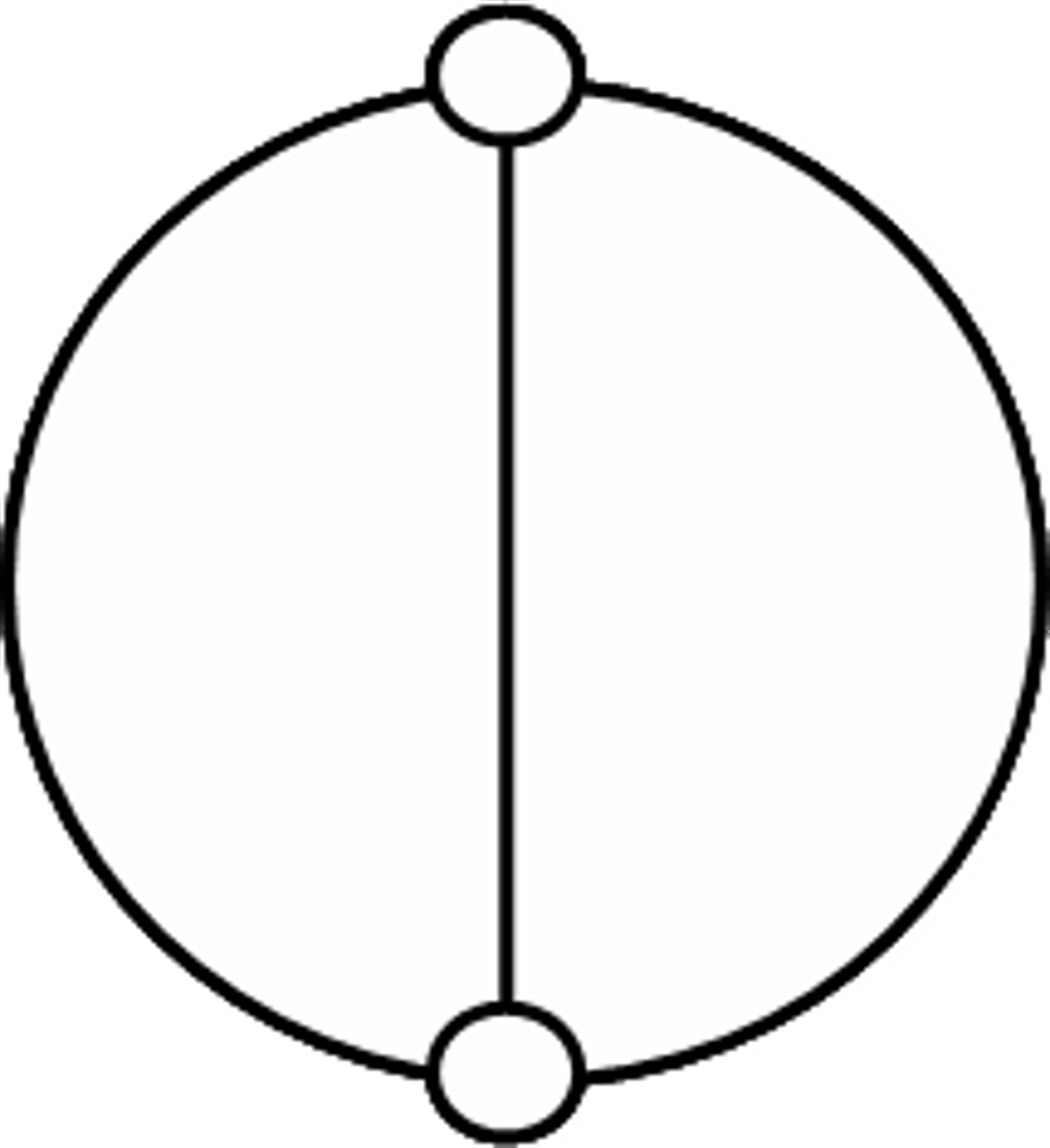
Рис. 9. Минимальный
кубический граф
|
Плоский кубический граф без мостов с количеством вершин n-2 до введения нового ребра будем называть предыдущим,
полученный после введения нового ребра c количеством вершин n – последующим. Ребра, на которых находятся вершины
вновь вводимого ребра для предыдущего графа, будем называть сцепленными.
Для получения последующего плоского кубического графа сцепленные ребра должны
принадлежать базисному циклу. Минимальным графом для первоначального построения
является кубический граф с двумя вершинами и тремя ребрами (см. рис. 9).
Заметим, что цвет вновь вводимого ребра соответствует цвету
гамильтонового диска (диска 2-фактора), на котором находятся концы вновь
вводимого ребра. Действительно, вновь введенное ребро увеличивает количество
вершин диска ровно на 2, что не влияет на цвет диска. Это относится также и к
удаленным ребрам, не принадлежащим ободу, т. к. удаление ребра уменьшает
количество вершин в диске ровно на 2. Если ребро введено или удалено с учетом
последнего факта, то в результате получим раскраску нового плоского кубического
графа. С учетом описанного, раскраску любого плоского кубического графа можно
свести к последовательному рекурсивному процессу:
-
удаление ребер из исходного плоского кубического графа без
мостов, с целью получения плоского кубического графа, раскраска которого
известна;
-
определение сцепленных ребер для введения ребра из множества
удаленных;
-
поиск цветного диска проходящего по сцепленным ребрам;
-
раскраска введенного ребра в цвет диска, проходящего по
сцепленным ребрам;
-
перекраска ребер диска, проходящего по сцепленным ребрам
после ввода ребра.
Так как по каждому из сцепленных ребер проходит два разных
цветных диска, то обязательно имеется один цветной 2-фактор, принадлежащий
обоим сцепленным ребрам. И тогда возможны следующие комбинации: сцепленные
ребра принадлежат одному цветному диску соответствующего цветного 2-фактора
(1); сцепленные ребра принадлежат двум разным дискам соответствующего цветного
2-фактора (2).
Если сцепленные ребра одного цвета, то выбор цветного
2-фактора из двух других цветных 2-факторов тривиален, если различного – то
общий цветной 2-фактор будет третьего цвета. В 1-ом случае (тривиальный случай)
вновь введенное ребро может быть легко раскрашено. Покажем, что оно может быть
раскрашено и во втором случае.
Докажем теорему о существовании цветного диска, проходящего
по сцепленным ребрам принадлежащим базисному циклу в произвольном плоском
кубическом раскрашенном графе без мостов. Будем обозначать предыдущий граф Gpr, а последующий Gsu.
Лемма 1. Если в предыдущем раскрашенном
кубическом графе без мостов Gpr существует цветной диск, проходящий по двум
сцепленным ребрам, то последующий кубический граф Gsu раскрашен.
Доказательство. По теореме Петерсена
последующий кубический граф Gsu состоит из 1-фактора и 2-фактора. Если в предыдущем
раскрашенном кубическом графе Gpr существует цветной диск, проходящий по сцепленным ребрам,
то соответствующий цветной диск, проходящий по вершинам вновь введенного ребра
в графе Gsu,
увеличивается на две единицы и может быть раскрашен в цвет соответствующего
диска в графе Gpr. Естественно,
что вновь введенное ребро в Gsu принадлежит 1-фактору и тоже раскрашивается в цвет
диска, проходящего по вершинам введенного ребра. Следовательно, в этом случае,
граф Gsu –
раскрашиваем.
Лемма 2. Если в предыдущем
раскрашенном кубическом графе без мостов Gpr не существует цветного диска, проходящего по двум
сцепленным рёбрам, то последующий кубический граф Gsu без мостов не плоский и не раскрашиваемый.
Доказательство. Предположим, что в
предыдущем раскрашенном кубическом графе Gpr не существует цветного диска, проходящего по
сцепленным рёбрам. Тогда существует два одинаково раскрашенных цветных диска,
проходящих по сцепленным ребрам. После введения нового ребра в последующий граф
Gsu, в
соответствующем диске какое-то рядом стоящее ребро должно быть окрашено в белый
цвет для соответствия правилам раскраски. Так как в этом случае каждый диск,
проходящий по вершине нового ребра, увеличится в длину на одну единицу и станет
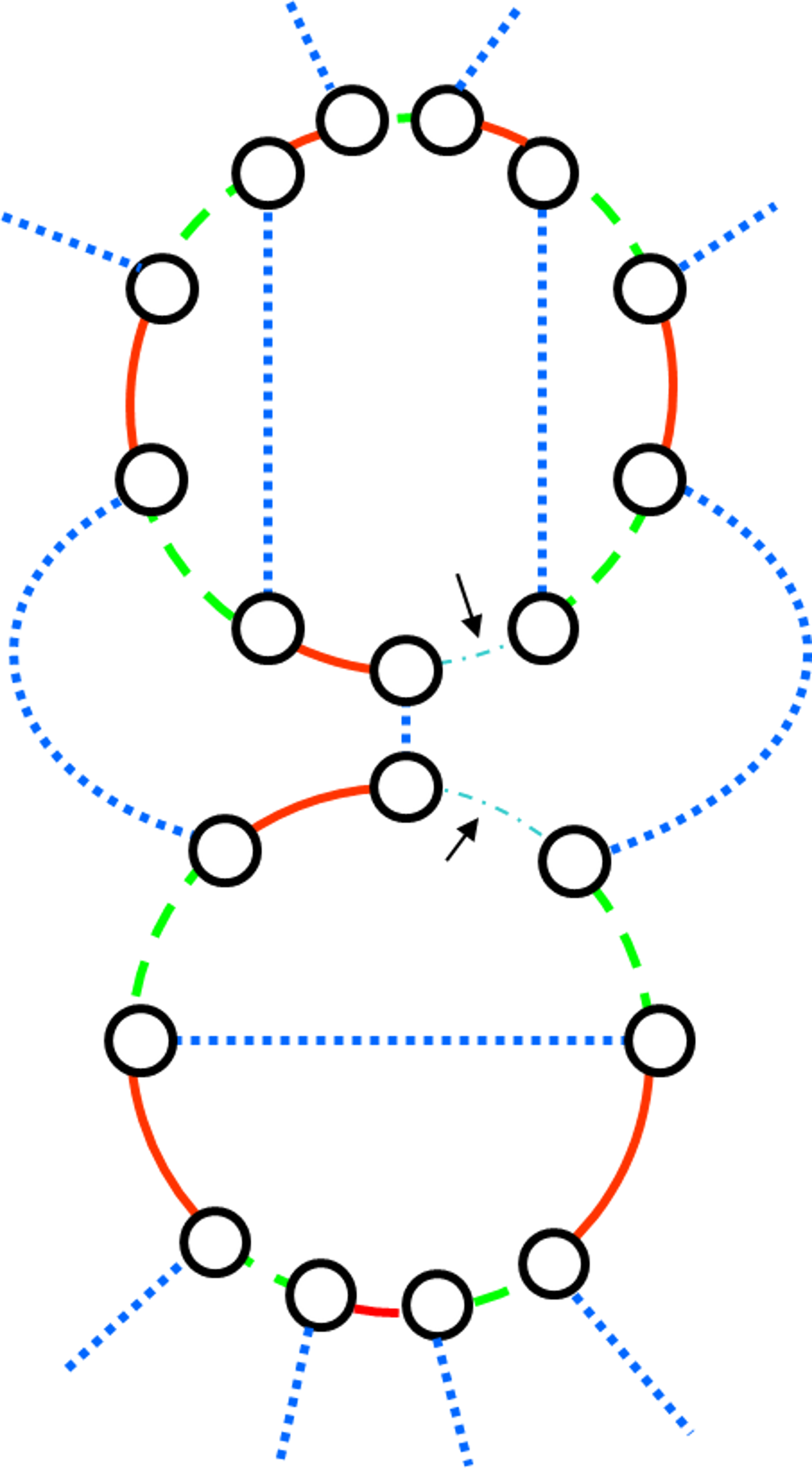
диском нечетной длины (рис. 10). Но тогда ребро, окрашенное в белый цвет,
должно индуцироваться тремя разноцветными базисными циклами для удовлетворения
группового преобразования Клейна:
W = (R + B + G).
Но последнее высказывание нарушает условие планарности
(напомним, что по теореме Маклейна, граф планарен тогда и только тогда, когда
существует базис циклов такой, что по каждому ребру проходит не более двух
циклов). Следовательно, полученный граф не плоский.
|
|
|
|
Рис. 10. Введение белых рёбер в последующий плоский
кубический граф (на рисунке белые ребра указаны стрелками)
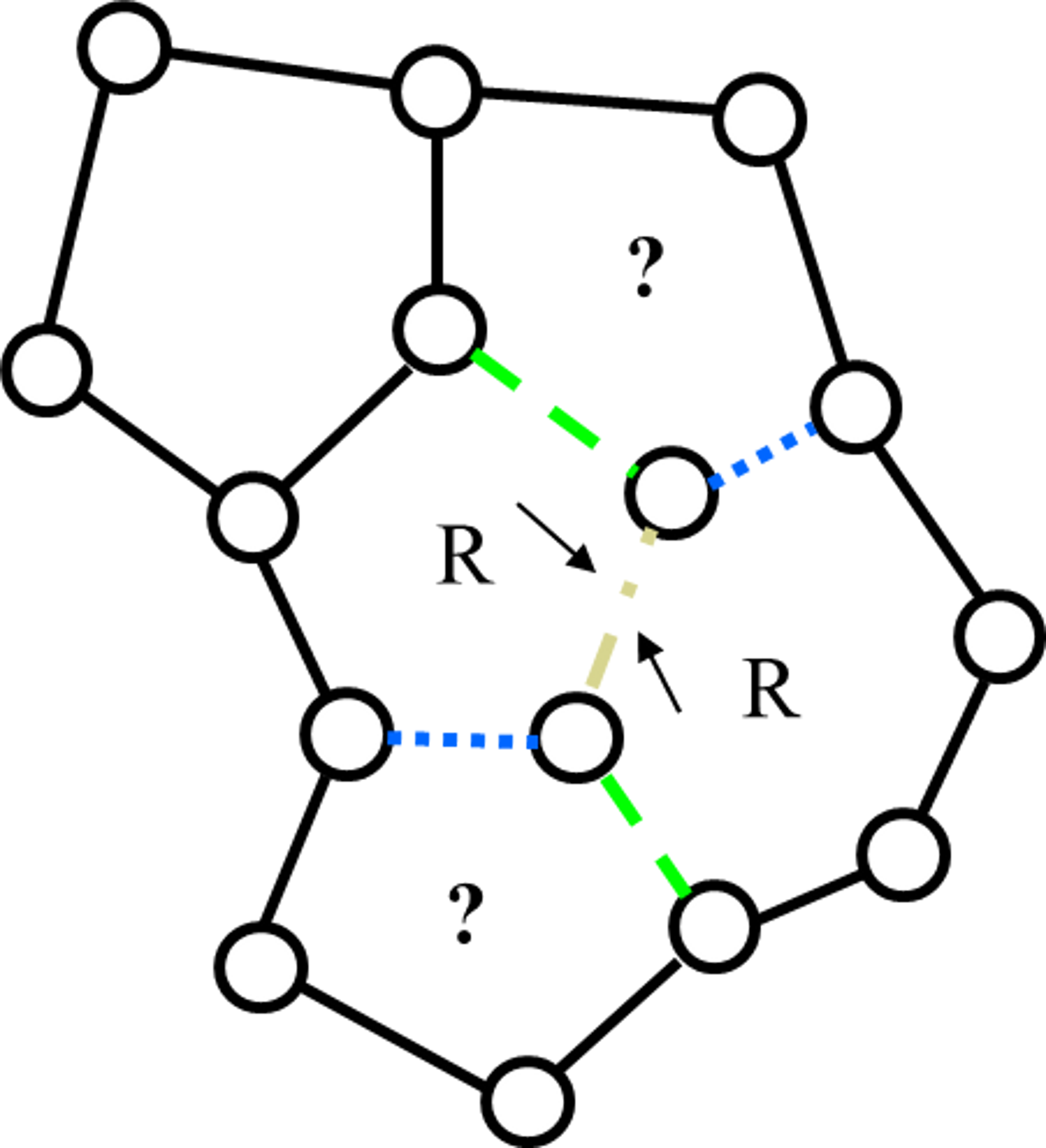
|
Рис. 11. Случай неопределенной раскраски смежных циклов
|
Рассмотрим случай, когда белое ребро может быть индуцировано
двумя разноцветными базисными циклами (гранями) имеющими одно общее ребро для
удовлетворения группового преобразования Клейна:
W = (R + R) 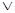 (B
+ B)
(B
+ B) 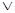 (G
+ G)
(G
+ G) 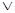 (W
+ W),
(W
+ W),
В этом случае возникает противоречие в раскраске циклов
(граней) смежных с раскрашенными циклами (гранями). Эти циклы должны со стороны
одного ребра быть раскрашены в один цвет, а со стороны другого ребра – в другой
цвет (эти циклы на рис. 11 обозначены знаком вопроса). То есть, циклы должны
быть раскрашены двумя цветами одновременно, что невозможно. Мы пришли к
противоречию. Следовательно, полученный граф не раскрашиваем. Лемма
доказана.
Данная лемма утверждает, что появление ребра белого цвета в
последующем кубическом графе Gsu характеризует не плоский и не раскрашенный
кубический граф.
Теорема 3. В предыдущем плоском
раскрашенном кубическом графе без мостов Gpr, существует
цветной диск, проходящий по сцепленным ребрам.
Доказательство. Если вновь введенное
ребро принадлежит базисному циклу предыдущего раскрашенного плоского
кубического графа, то последующий кубический граф Gsu является плоским по построению. Но тогда в плоском
графе не возможно существование белого ребра, т.к. по теореме Маклейна
невозможно существование трех циклов проходящих по ребру графа. Следовательно,
ребра графа могут быть раскрашены только в три цвета. А это значит, что в
предыдущем плоском раскрашенном кубическом графе без мостов Gpr существует цветной
диск, проходящий по сцепленным ребрам. Понятие предыдущего раскрашенного
плоского кубического графа можно распространить на все множество раскрашенных
плоских кубических графов. Теорема доказана.
Теорема 4. Хроматический класс произвольного плоского
кубического графа без мостов равен трем.
Доказательство проведем методом математической индукции.
а) очевидно, что ребра минимального плоского кубического
графа всегда можно раскрасить тремя цветами (см. рис. 9);
б) предположим, что имеется предыдущий плоский раскрашенный
кубический граф без мостов. Вводим новое ребро в произвольном базисном цикле
или ободе для получения последующего раскрашенного плоского кубического графа
без мостов. Согласно Теореме 3, данное ребро обязательно раскрашено. Тем самым
произведена раскраска последующего плоского кубического графа без мостов.
Следствие 4.1. В плоском кубическом графе без мостов
существует цветной 2-фактор с дисками четной длины.
Теорема 5. (Визинг) [17,18]. Рёбра любого
неориентированного графа могут быть раскрашены в число цветов, максимум на
единицу большее максимальной степени 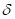 вершин графа.
вершин графа.
По меньшей мере, 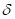 цветов
необходимо всегда, так что неориентированные графы можно разбить на два класса
– графы "первого класса", для которых
цветов
необходимо всегда, так что неориентированные графы можно разбить на два класса
– графы "первого класса", для которых 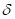 цветов
достаточно, и "второго класса", для которых необходимо
цветов
достаточно, и "второго класса", для которых необходимо 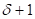 цветов. Из доказанной
теоремы 4 следует, что плоские кубические графы без мостов следует отнести к
"первому классу".
цветов. Из доказанной
теоремы 4 следует, что плоские кубические графы без мостов следует отнести к
"первому классу".
Теперь можно доказать теорему о четырех красках.
Теорема 6. Хроматическое число максимально
плоского графа равно четырем.
Это следует из теорем 1 (Тэйта) и 4, а также того факта, что
базисные циклы и обод плоского кубического графа Н дуальны вершинам
максимально плоского графа G.
Для поиска диска проходящего по сцепленным ребрам нам
понадобится операция перекраски ребер.
|
|
|
|
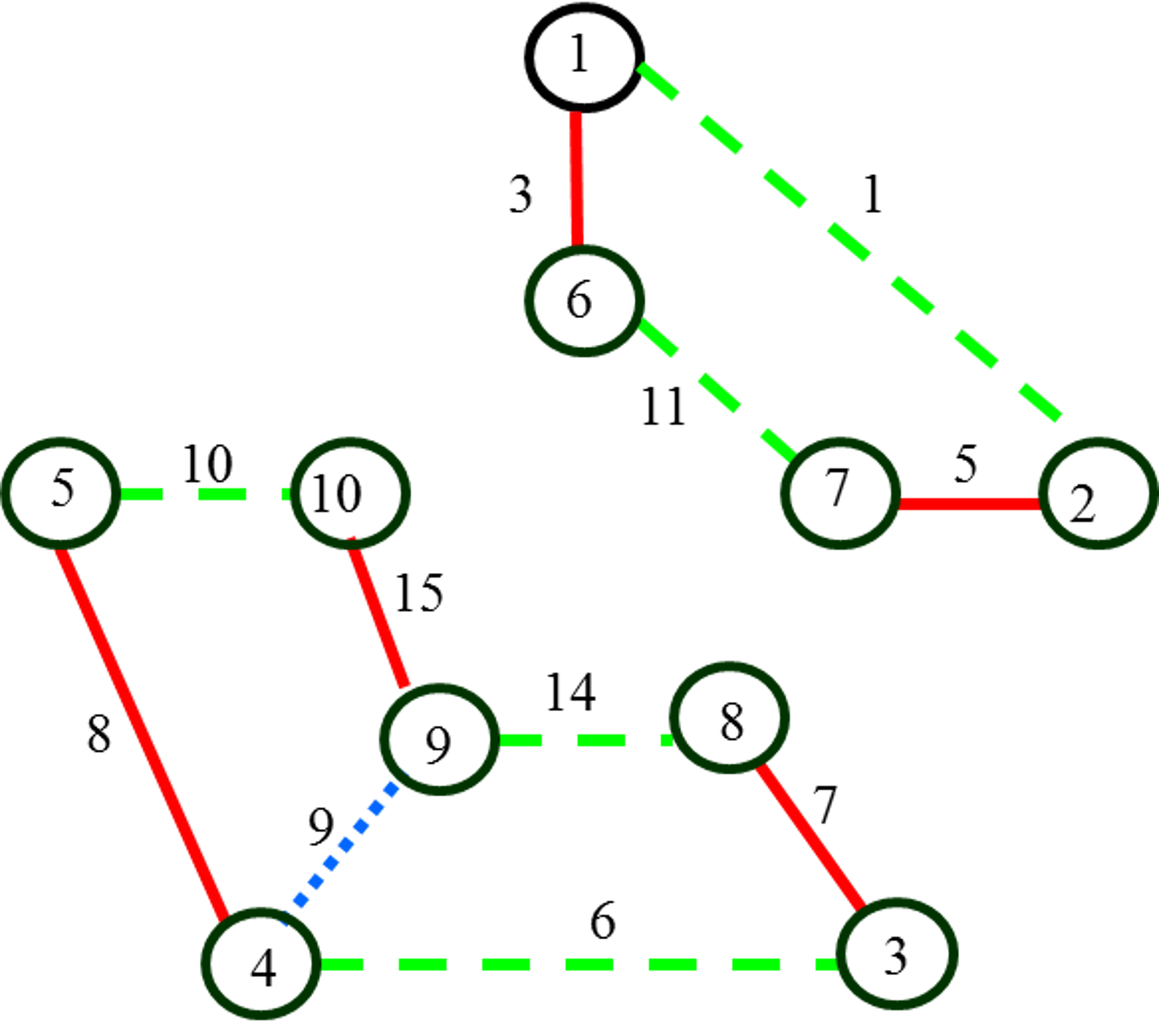
Рис. 12. Синий диск
до ротации
|
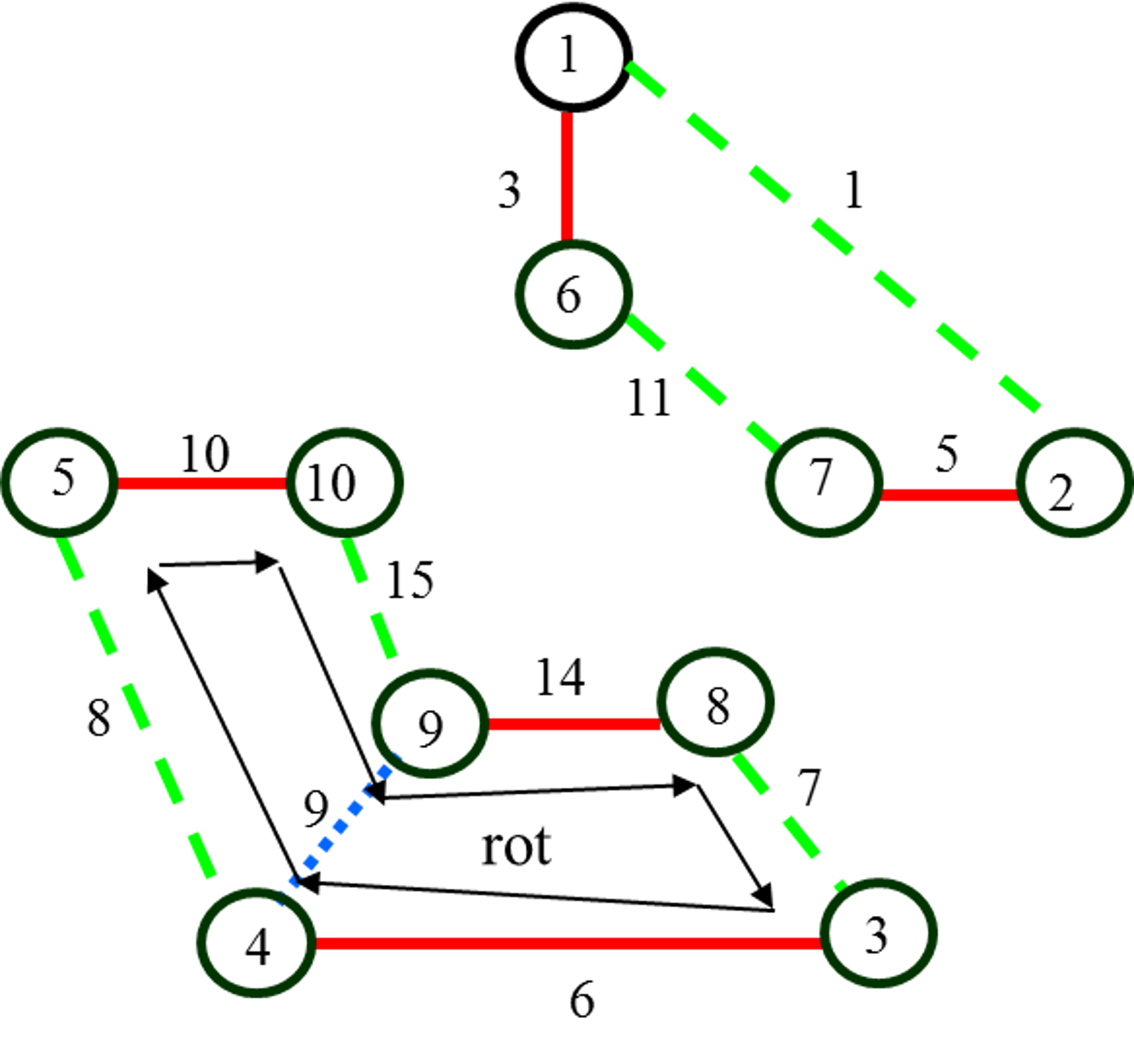
Рис. 13. Синий диск
после ротации
|
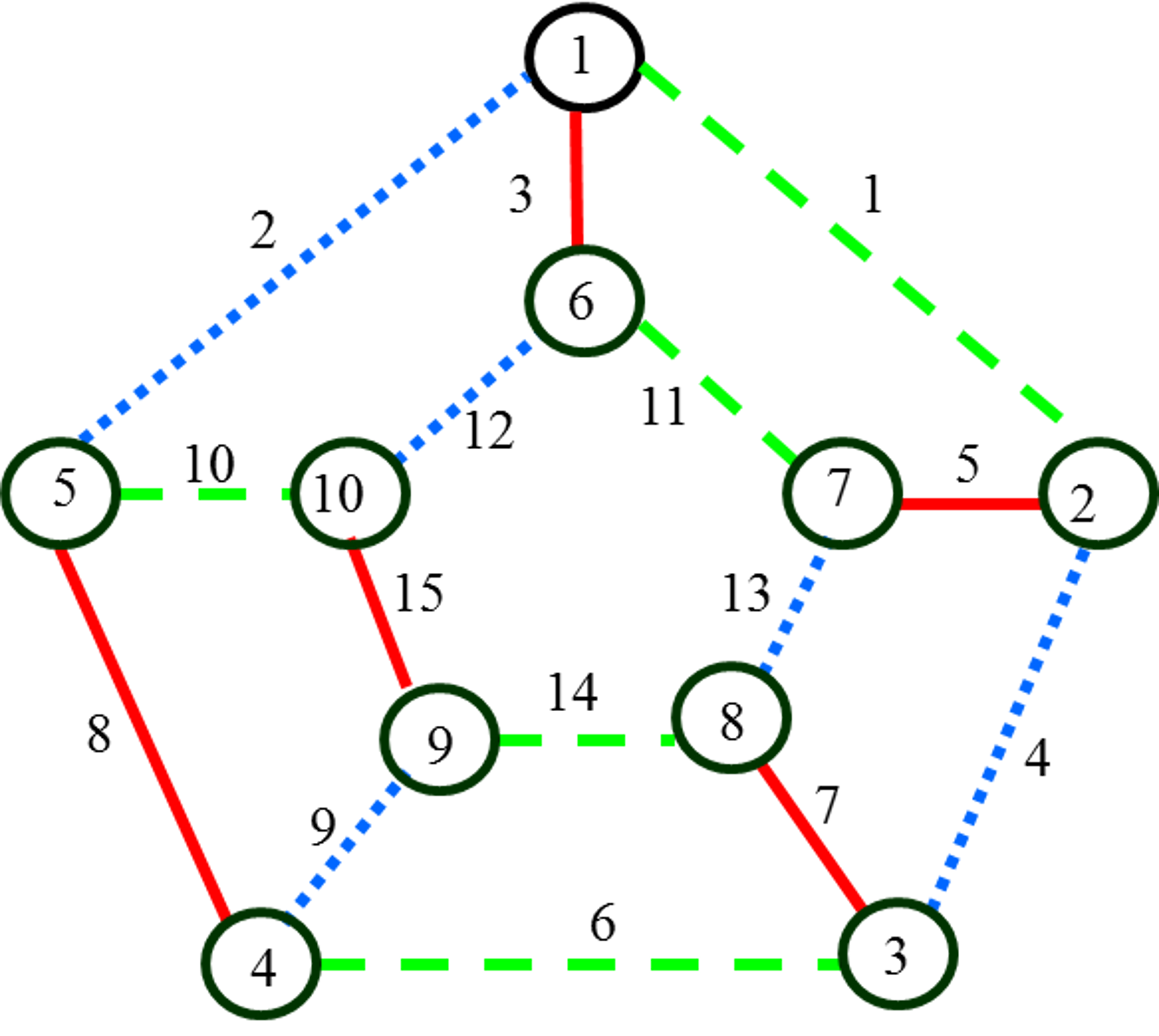
Для перекраски ребер введем операцию ротации. Под ротацией
цветного гамильтонова диска будем понимать изменение последовательности
раскраски ребер данного диска. Ротация диска приводит к изменению других
цветных гамильтоновых квазициклов. На рис. 12 представлен синий диск до
ротации, а на рис. 13 – после ротации. Операция ротации дисков может быть
описана как перестановка двух ребер в других цветных 2-факторах. Например, для
графа, представленного на рис. 6, цветные 2-факторы до ротации синего диска
имеют вид:
синий 2-фактор – {e1,e3,e5,e6,e7,e8,e10,e11,e13,e14},
красный 2-фактор – {e1,e2,e4,e6,e9,e10,e11,e12,e13,e15},
зеленый 2-фактор – {e2,e3,e4,e5,e7,e8,e9,e12,e14,e15}.
|
|
|
|
Рис. 14. Раскраска
графа до ротации
|
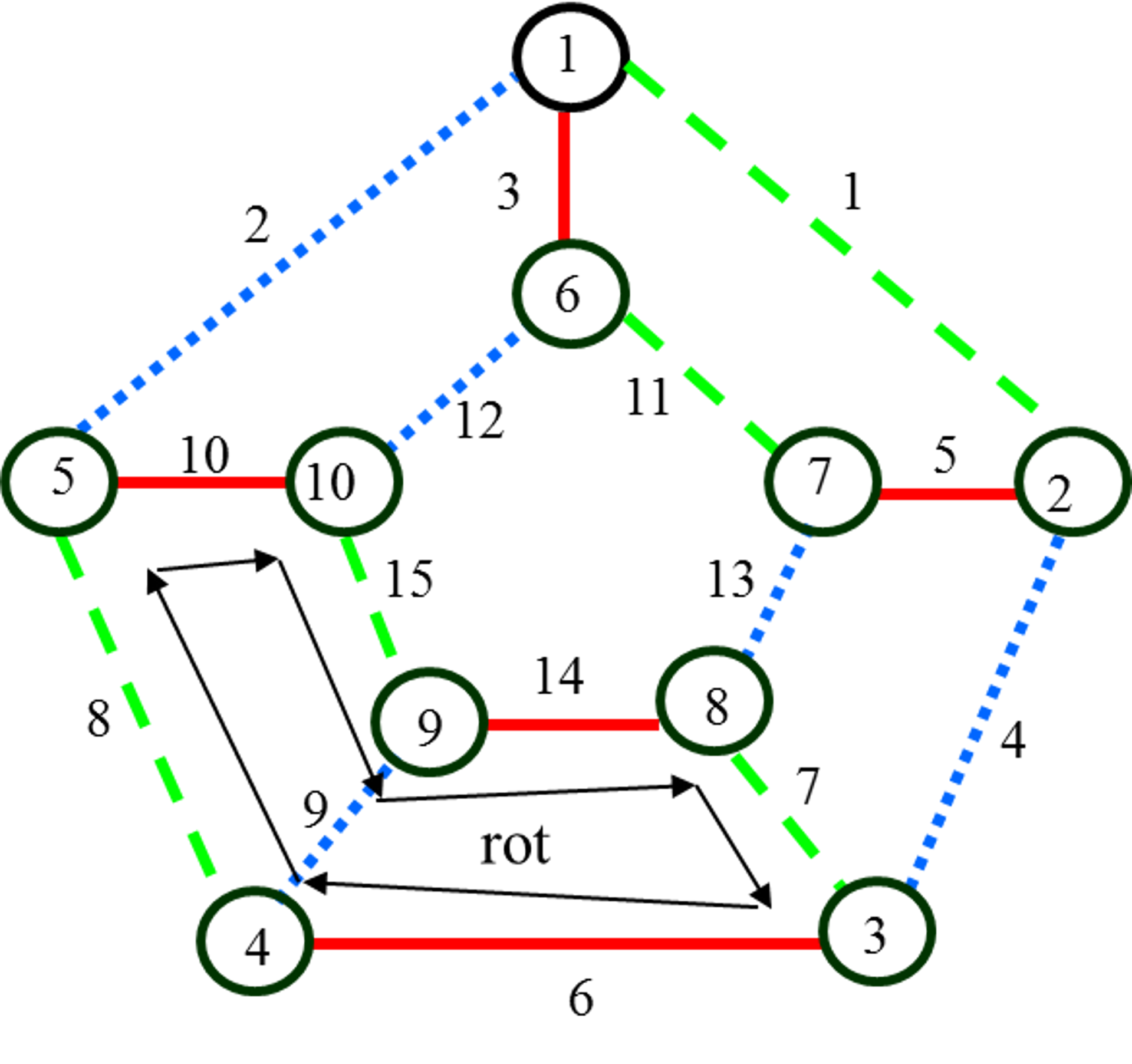
Рис. 15. Раскраска
графа после ротации
|
После ротации синего диска:
синий 2-фактор – {e1,e3,e5,e6,e7,e8,e10,e11,e13,e14},
красный 2-фактор – {e1,e2,e4,e7,e8,e9,e11,e12,e14,e15},
зеленый 2-фактор – {e2,e3,e4,e5,e6,e9,e10,e12,e13,e15}.
В красном и зеленом 2-факторах произошла перестановка
следующих пар ребер (e6 «e7),
(e8
«e10), (e13 «e14).
Рассмотрим пример, когда для раскраски нового ребра
необходимо применить операцию ротации дисков.
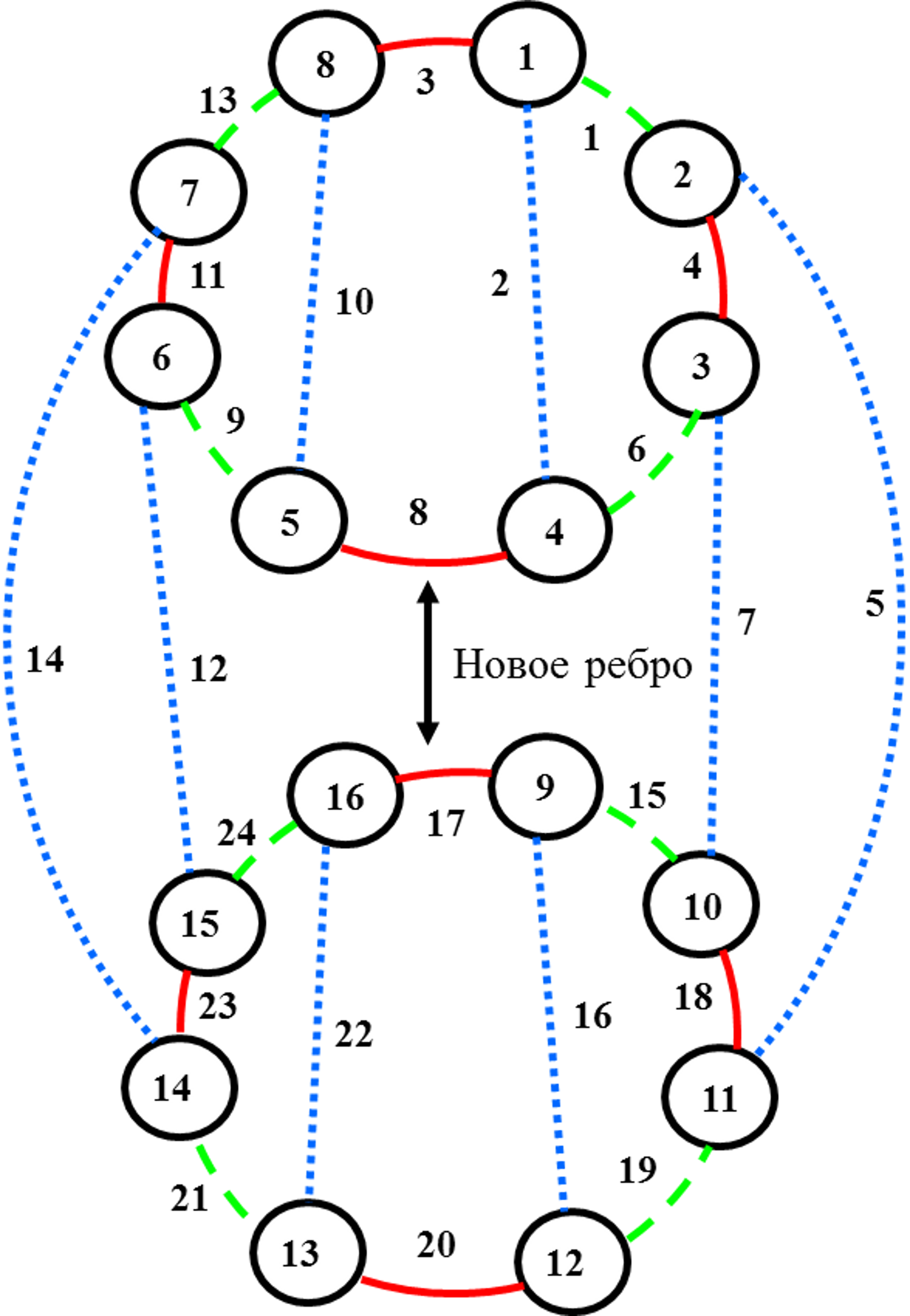
Пример 1. На рисунке 16 представлена раскраска
кубического графа, где концы вновь введенного ребра принадлежат двум дискам
синего цвета и двум дискам зеленого цвета [19,20]. Рассмотрим способы раскраски
в этом особом случае. Для данного кубического графа Н (см. рис. 17)
выберем базисные циклы:
c1 = {e2,e3, e8, e10}, c2 = {e1, e2, e4, e6}, c3 = {e9, e10, e11, e13}, c4 = {e4, e5, e7, e18},
c5 = {e11, e12, e14, e23}, c6 = {e6, e7, e8, e9, e12, e15, e17, e24}, c7 = {e16, e17, e20, e22},
c8 = {e15, e16, e18, e19}, c9 = {e21, e22, e23, e24}.
Формируем обод, c0 = {e1, e3, e5, e13, e14, e19, e20, e21}.
|
|

|
|
Рис.16. Два диска
одного цвета и введение нового ребра.
|
Рис. 17. Раскраска
базисных циклов.
|
Тогда цветные 2-факторы можно записать в виде:
Rc = (c2 ⊕ c4 ⊕
c8) ⊕ (c3 ⊕ c5 ⊕
c9) = ({e1, e2, e4, e6} ⊕ {e4, e5, e7, e18} ⊕
{e15, e16, e18, e19}) ⊕ ({e9, e10, e11, e13} ⊕ {e11, e12, e14, e23} ⊕ {e21, e22, e23, e24}) = {e1, e2, e5, e6, e7, e9, e10, e12, e13, e14, e15, e16, e19, e21, e22, e24};
Bc = (c1 ⊕ c2 ⊕
c3) ⊕ (c7 ⊕ c8 ⊕
c9)
= ({e2, e3, e8, e10} ⊕ {e1, e2, e4, e6} ⊕ {e9, e10, e11, e13}) ⊕ ({e16, e17, e20, e22} ⊕
{e15, e16, e18, e19} ⊕
{e21, e22, e23, e24}) = {e1, e3, e4, e6, e8, e9, e11, e13, e15, e17, e18, e19, e20, e21, e23, e24};
Gc = c1 ⊕ c4 ⊕
c5 ⊕ c7 = {e2, e3, e8, e10} ⊕
{e4, e5, e7, e18} ⊕ {e11, e12, e14, e23} ⊕ {e16, e17, e20, e22} = {e2, e3, e4, e5, e7, e8, e10, e11, e12, e14, e16, e17, e18, e20, e22, e23};
Wc = c6 ⊕ c0 = {e6, e7, e8,e9, e12, e15, e17, e24} ⊕
{e1, e3, e5, e13, e14, e19, e20, e21} = {e1, e3, e5, e6, e7, e8, e9, e12, e13, e14, e15, e17, e19, e20, e21, e24};
 = c1 ⊕ c6 ⊕ c7 ⊕ c0 = {e2, e3, e8, e10} ⊕ {e6, e7, e8, e9, e12, e15, e17, e24} ⊕ {e16, e17, e20, e22} ⊕
{e1, e3, e5, e13, e14, e19, e20, e21} = {e1, e2, e5, e6, e7, e9, e10, e12, e13, e14, e15, e16, e19, e21, e22, e24};
= c1 ⊕ c6 ⊕ c7 ⊕ c0 = {e2, e3, e8, e10} ⊕ {e6, e7, e8, e9, e12, e15, e17, e24} ⊕ {e16, e17, e20, e22} ⊕
{e1, e3, e5, e13, e14, e19, e20, e21} = {e1, e2, e5, e6, e7, e9, e10, e12, e13, e14, e15, e16, e19, e21, e22, e24};
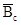 = c4 ⊕ c5 ⊕ c6 ⊕
c0= {e4, e5, e7, e18} ⊕ {e11, e12, e14, e23} ⊕ {e6, e7, e8, e9, e12, e15, e17, e24} ⊕ {e1, e3, e5, e13, e14, e19, e20, e21} = {e1, e3, e4, e6, e8, e9, e11, e13,e15, e17, e18, e19, e20, e21, e23, e24};
= c4 ⊕ c5 ⊕ c6 ⊕
c0= {e4, e5, e7, e18} ⊕ {e11, e12, e14, e23} ⊕ {e6, e7, e8, e9, e12, e15, e17, e24} ⊕ {e1, e3, e5, e13, e14, e19, e20, e21} = {e1, e3, e4, e6, e8, e9, e11, e13,e15, e17, e18, e19, e20, e21, e23, e24};
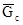 = c2 ⊕ c3 ⊕ c6 ⊕
c8 ⊕ c0 = {e1, e2, e4, e6} ⊕
{e9, e10, e11, e13} ⊕ {e6, e7, e8, e9, e12, e15, e17, e24} ⊕ {e15, e16, e18, e19} ⊕ {e1, e3, e5, e13, e14, e19, e20, e21} = {e2, e3, e4, e5, e7, e8, e10, e11, e12, e14, e16, e17, e18, e20, e22, e23}.
= c2 ⊕ c3 ⊕ c6 ⊕
c8 ⊕ c0 = {e1, e2, e4, e6} ⊕
{e9, e10, e11, e13} ⊕ {e6, e7, e8, e9, e12, e15, e17, e24} ⊕ {e15, e16, e18, e19} ⊕ {e1, e3, e5, e13, e14, e19, e20, e21} = {e2, e3, e4, e5, e7, e8, e10, e11, e12, e14, e16, e17, e18, e20, e22, e23}.
Осуществим операцию ротации дисков. Будем вращать два
единичных диска зеленого цвета с1 = {e2, e3, e8, e10} и c7 = {e16, e17, e20, e22}.
Новая раскраска характеризуется другим набором цветных
2-факторов и 1-факторов и позволяет раскрасить вновь введенное ребро красным
цветом.
Rc = c1 ⊕ c2 ⊕
c3 ⊕ c4 ⊕
c5 ⊕ c7 ⊕ c8 ⊕ c9 = {e2, e3, e8, e10} ⊕
{e1, e2, e4, e6} ⊕
{e9, e10, e11, e13} ⊕ {e4, e5, e7, e18} ⊕ {e11, e12, e14, e23} ⊕ {e16, e17, e20, e22} ⊕ {e15, e16, e18, e19} ⊕ {e21, e22, e23, e24} =
{e1, e3, e5, e6, e7, e8, e9, e12, e13, e14, e15, e17, e19, e20, e21, e24};
|
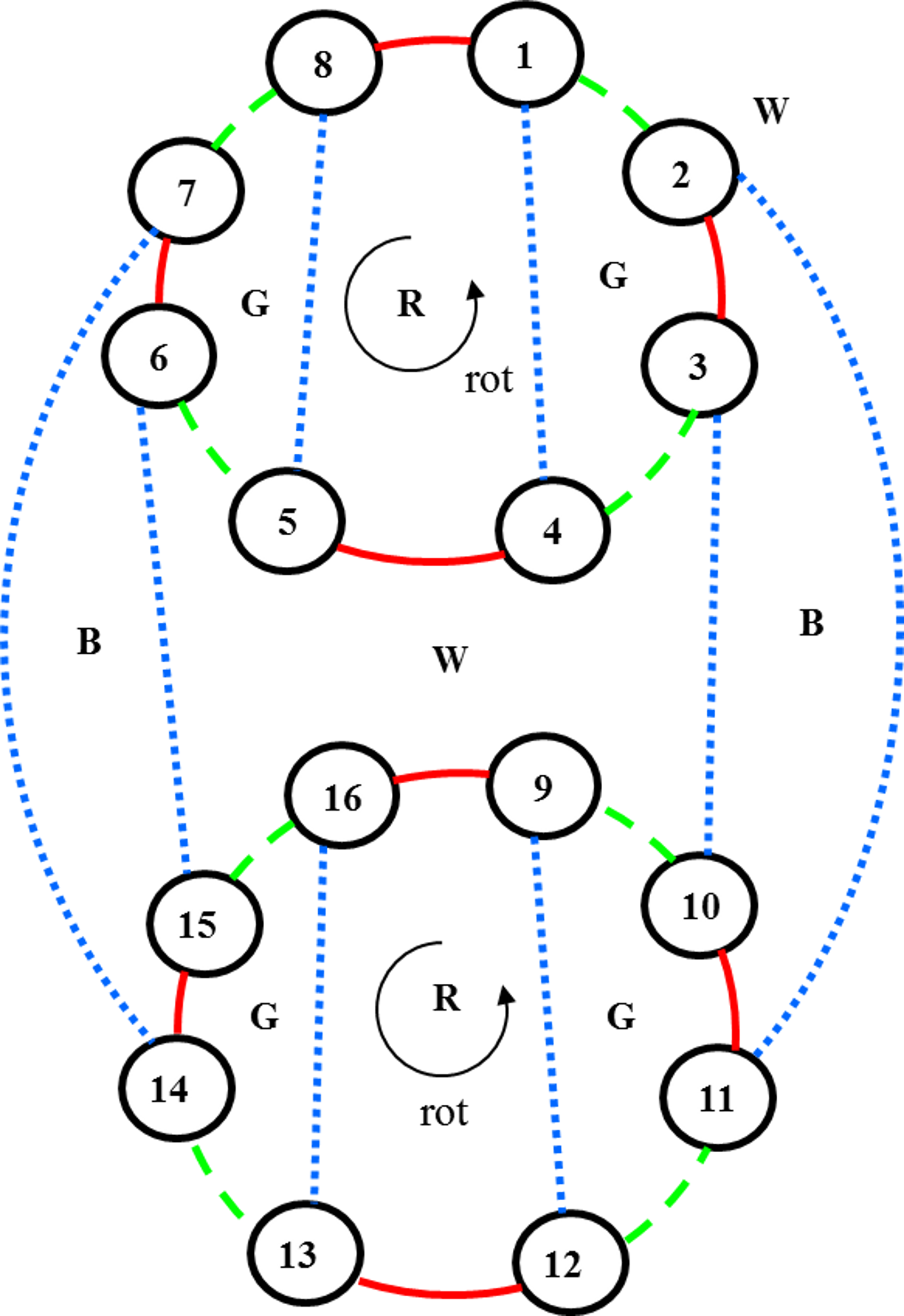
|
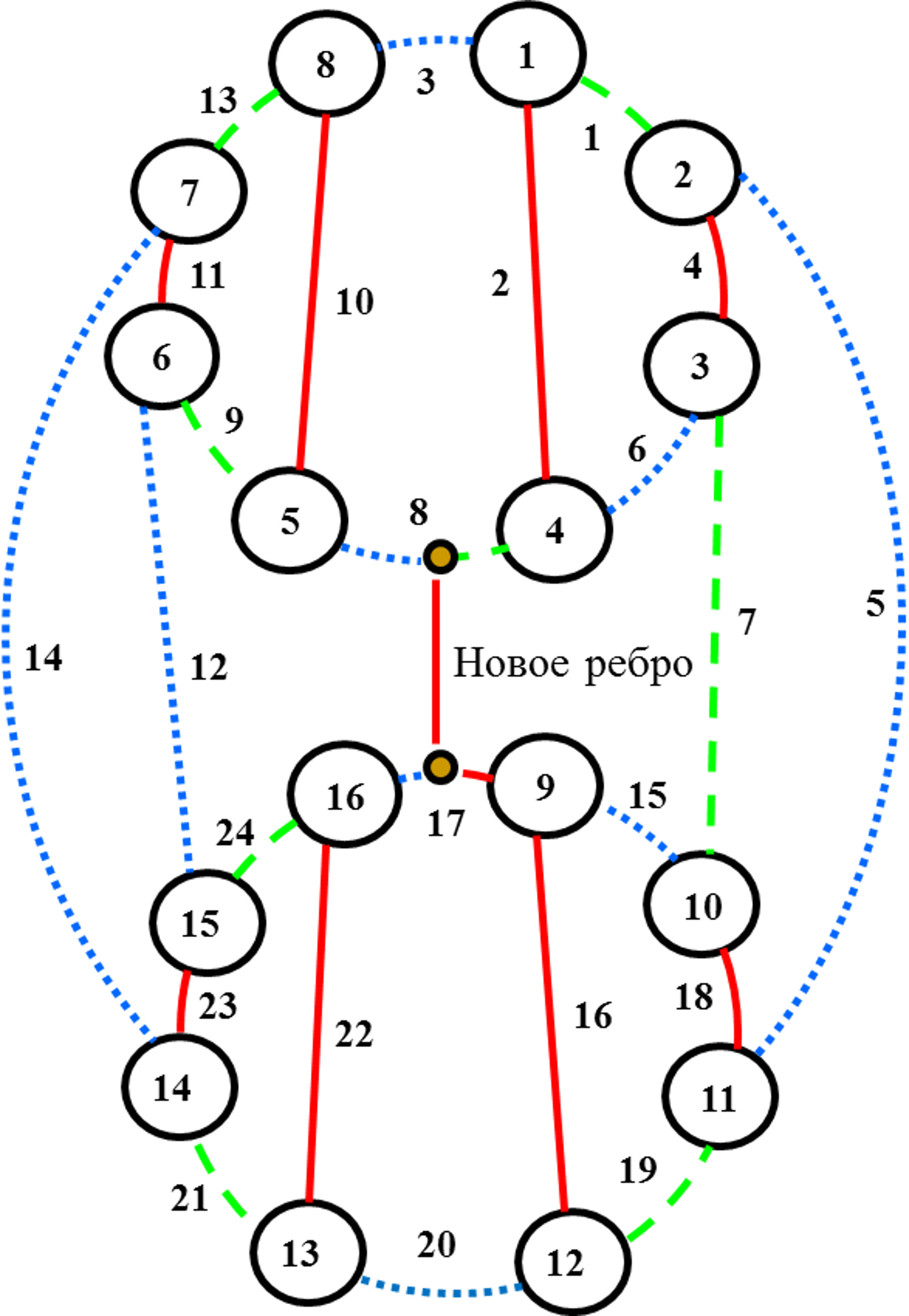
|
|
Рис. 18. Новая
раскраска ребер и базисных циклов.
|
Рис. 19. Новая
раскраска ребер и базисных циклов.
|
Bc = c2 ⊕ c3 ⊕
c8 ⊕ c9 = {e1, e2, e4, e6} ⊕ {e9, e10, e11, e13} ⊕
{e15, e16, e18, e19} ⊕
{e21, e22, e23, e24}) = {e1, e2, e4, e6, e9, e10, e11, e13, e15, E16, E18, E19, E21, E22, E23, E24};
Gc = c1 ⊕ c4 ⊕
c5 ⊕ c7 = {e2, e3, e8, e10} ⊕
{e4, e5, e7, e18} ⊕ {e11, e12, e14, e23} ⊕ {e16, e17, e20, e22} = {e2, e3, e4, e5, e7, e8, e10, e11, e12, e14, e16, e17, e18, e20, e22, e23}.
Применение операции ротации двух зеленых дисков изменяет
цвета базисных циклов с красного на синий (см. рис. 18), и тогда вновь вводимое
ребро можно окрасить в красный цвет (см. рис. 19).
Приведем примеры раскраски плоских кубических графов, не
имеющих гамильтонового цикла. Раскраска плоских кубических графов имеющих
гамильтонов цикл тривиальна. Ребра гамильнового цикла раскрашиваются
последовательно двумя цветами. Оставшиеся ребра, принадлежащие 1-фактору графа,
раскрашиваются третьим цветом.
Пример 2. Рассмотрим раскраску ребер для плоского
кубического негамильтонового графа G44
(см. рис. 20).
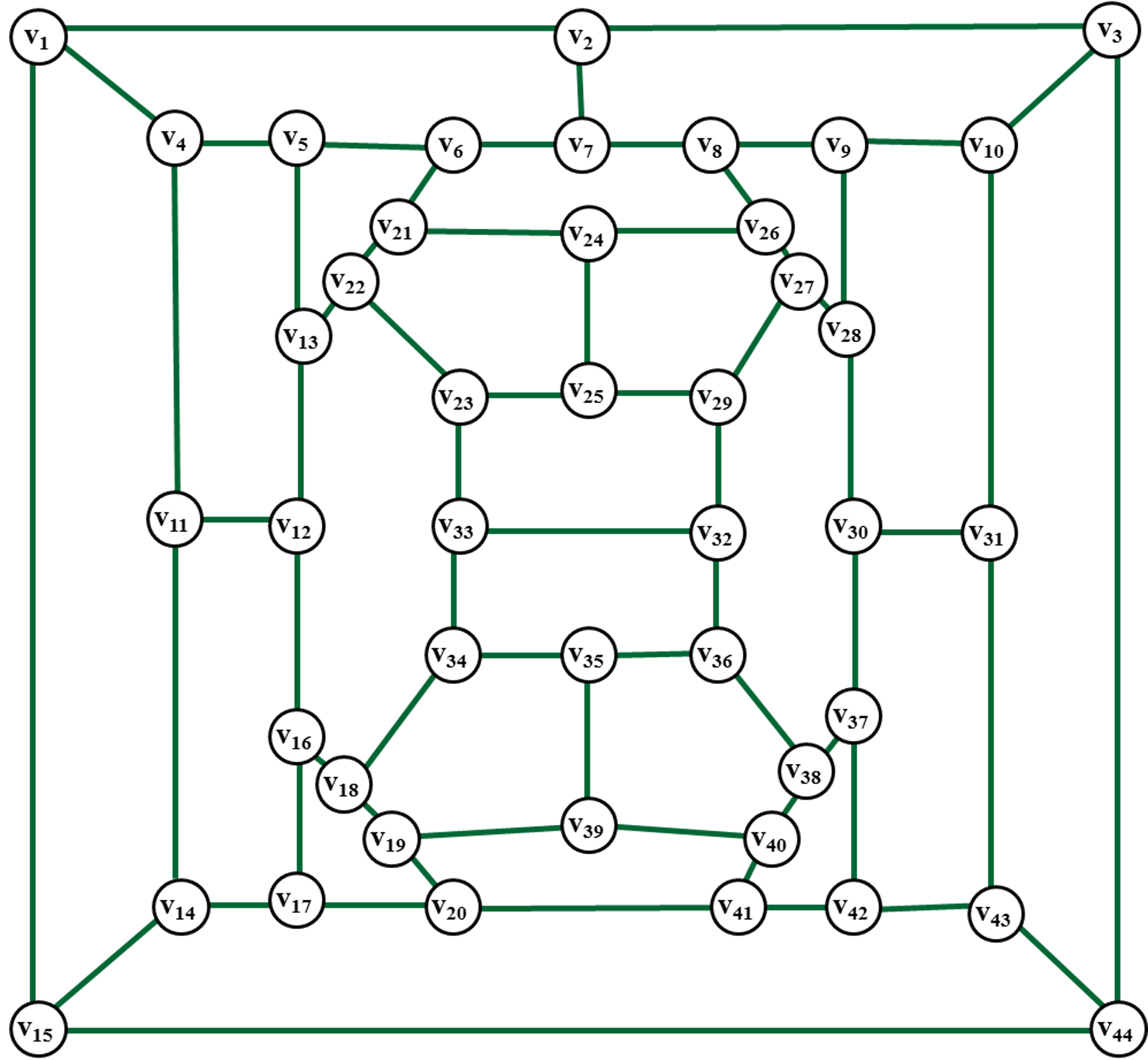
Рис. 20. Плоский
кубический негамильтонов граф G44.
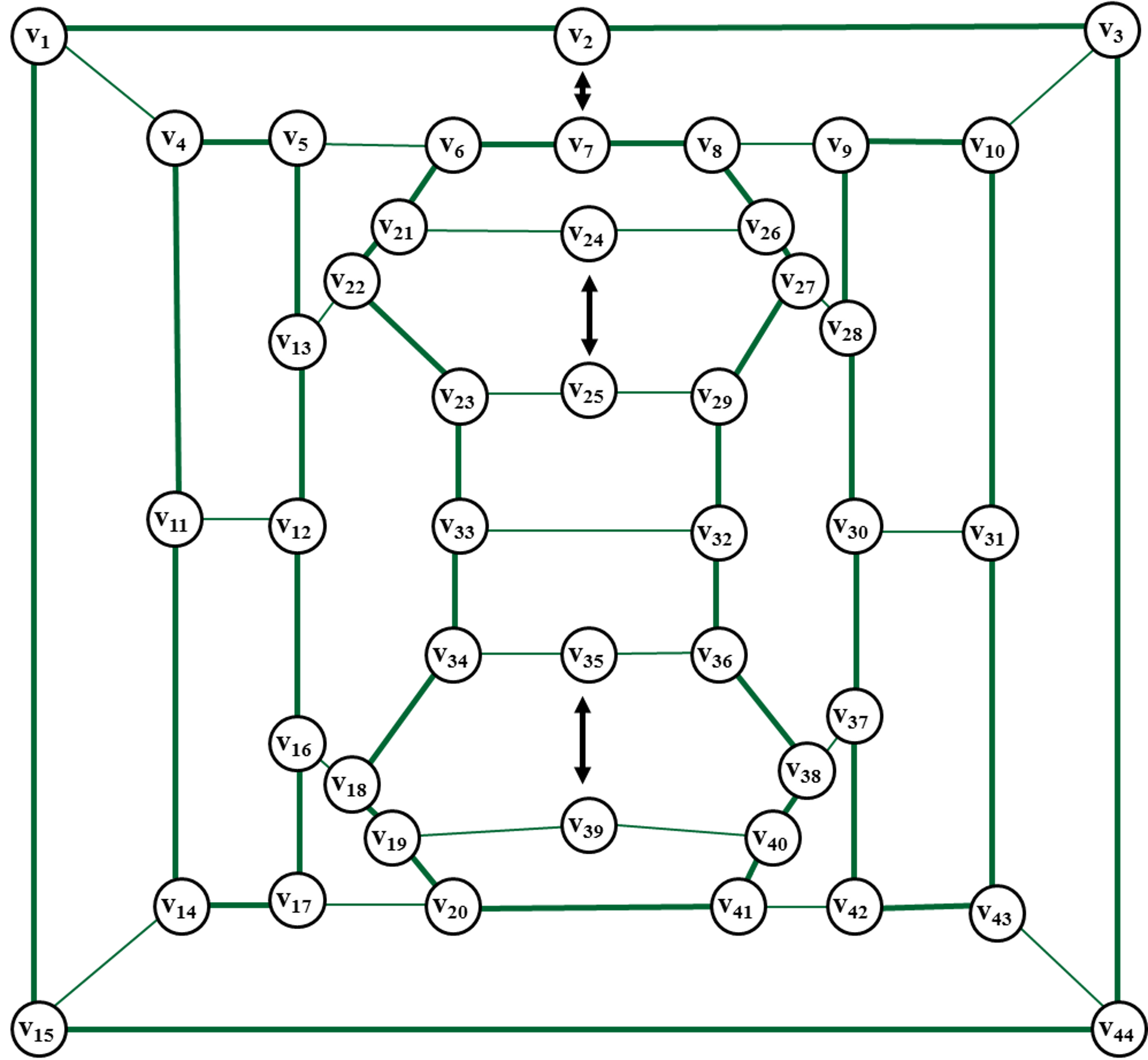
Рис. 21. Удаление
ребер в плоском кубическом негамильтоновом графе G44.
С целью получения совокупности циклов четной длины (дисков)
удаляем из графа ребра (v2,v7),(v24,v25),(v35,v39).
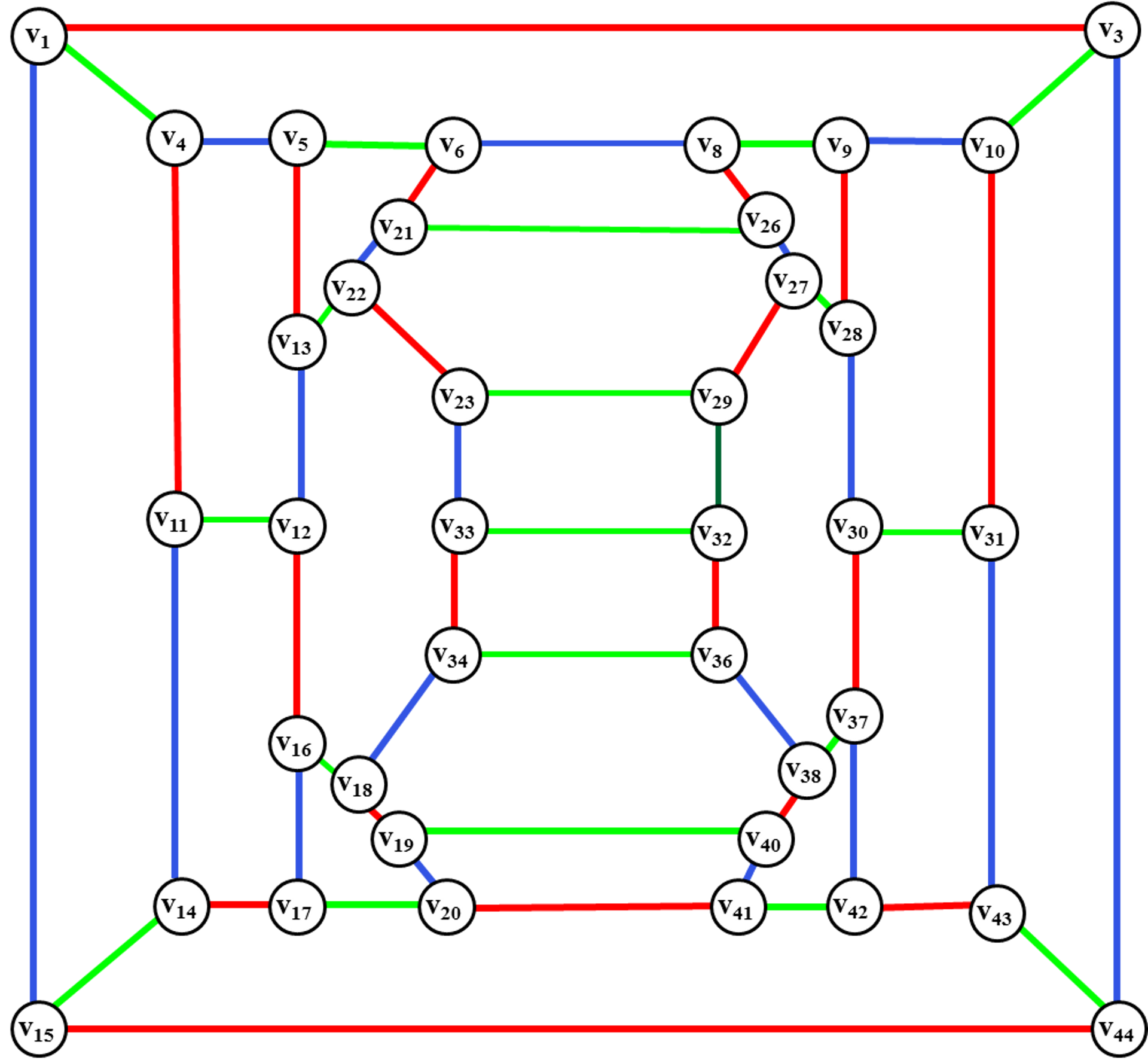
Рис. 22. Раскраска
ребер в выделенных дисках (пусть диски будут зеленые).

Рис. 23. Определение
цветного диска для введения ребра (v24,v25).
Визуально, находим цветной диск для введения ребра (v24, v25).
Это диск <v5, v13,v22, v23,v29, v27,v28, v9,v8, v26,v21, v6>.

Рис. 24. Введение и
раскраска ребра (v24,v25).
Введение и раскраска ребра (v24, v25)
представлена на рис. 24. Осуществляется перекраска ребер цветного диска <v5,
v13, v22, v23, v25, v29, v27, v28, v9, v8, v26, v24, v21, v6>.

Рис. 25. Определение
цветного диска для введения ребра (v35,v39).
Визуально определяем диск <v16, v17,
v20, v19, v40, v41,
v42, v37, v38, v36,
v34, v18> (см.
рис. 25) для введения ребра (v35,
v39).
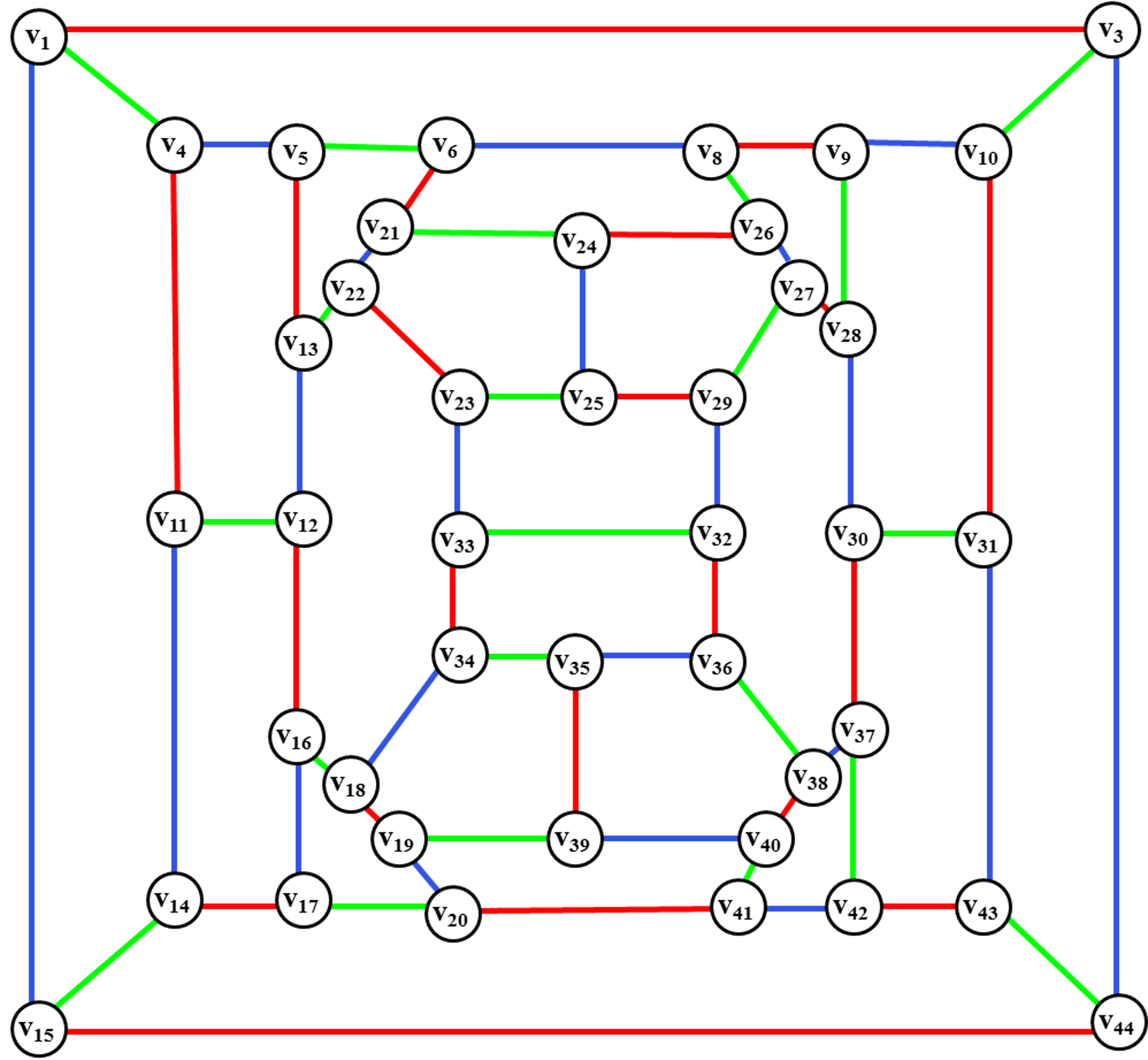
Рис. 26. Введение и
раскраска ребра (v35,v39).
Вводим и раскрашиваем ребро (v35,v39), перекрашиваем ребра в цветном диске (см. рис. 26) <v16,v17,v20,v19,v39,v40,v41,v42,v37,v38,v36,v35,v34,v18>.
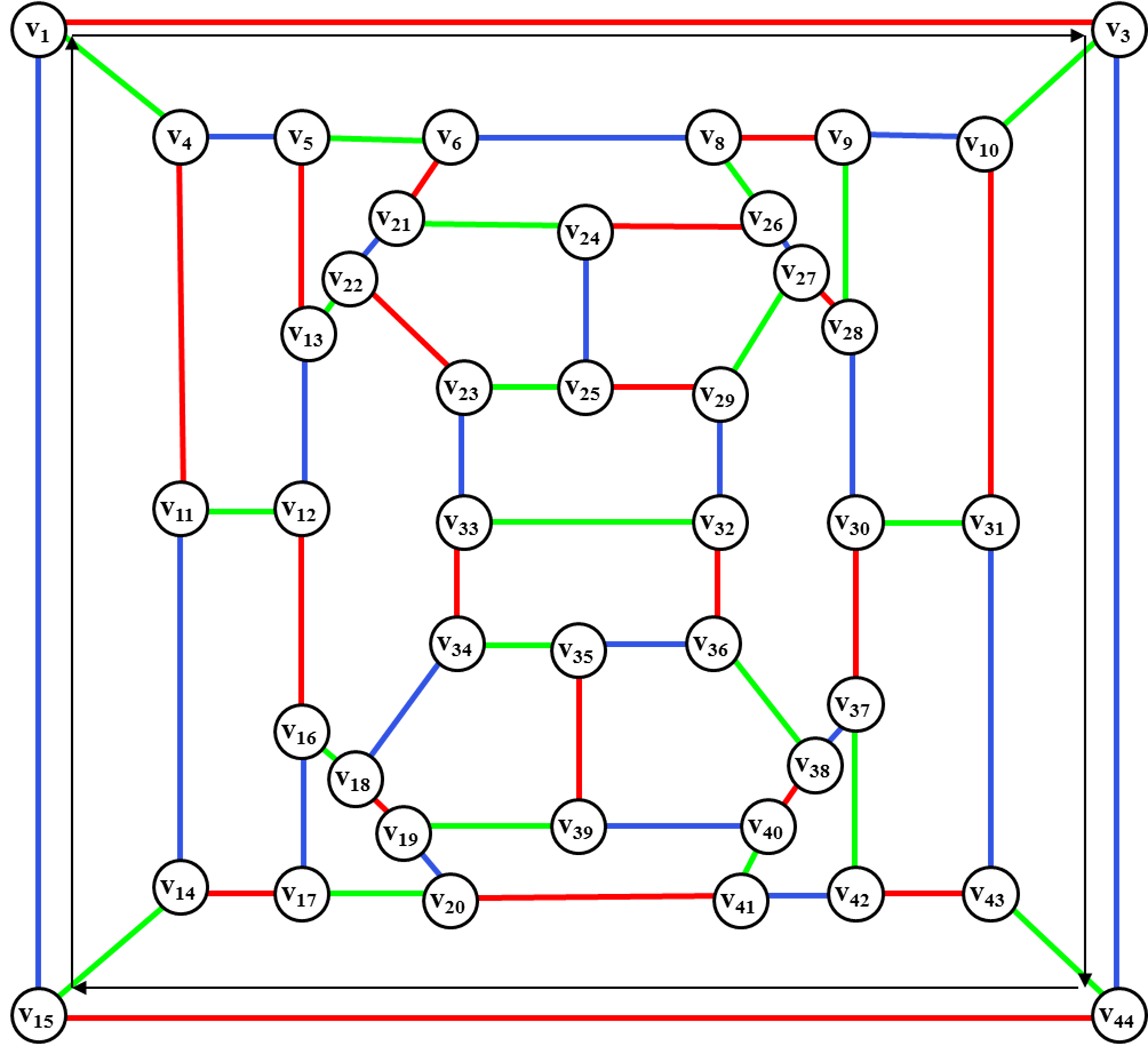
Рис. 27. Определение
ротации цветного диска для введения ребра (v2,v7).
Осуществляем ротацию цветного диска <v15,v1, v3,v44> с целью введения ребра (v2, v7).
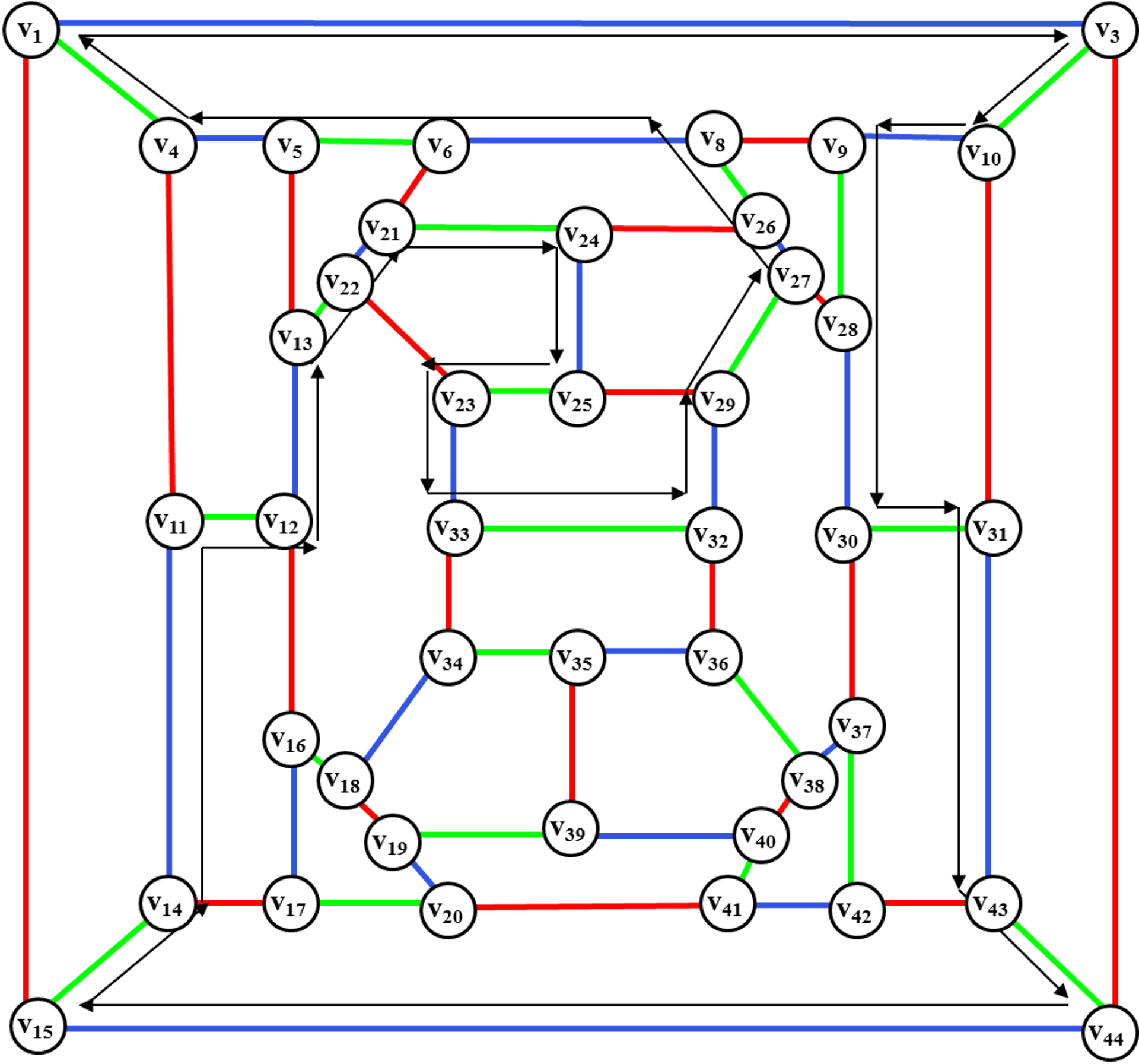
Рис. 28. Нахождение
цветного диска для введения ребра (v2,v7) после ротации.
Находим цветной диск <v1, v3, v10, v9, v28, v30, v31, v43,
v44, v15, v14, v11, v12, v13, v22, v21, v24, v25, v23, v33, v32, v29, v27, v26,
v8, v6, v5, v4> для введения ребра (v2, v7). Окончательная раскраска
негамильтонового графа G44 представлена на рис. 29.
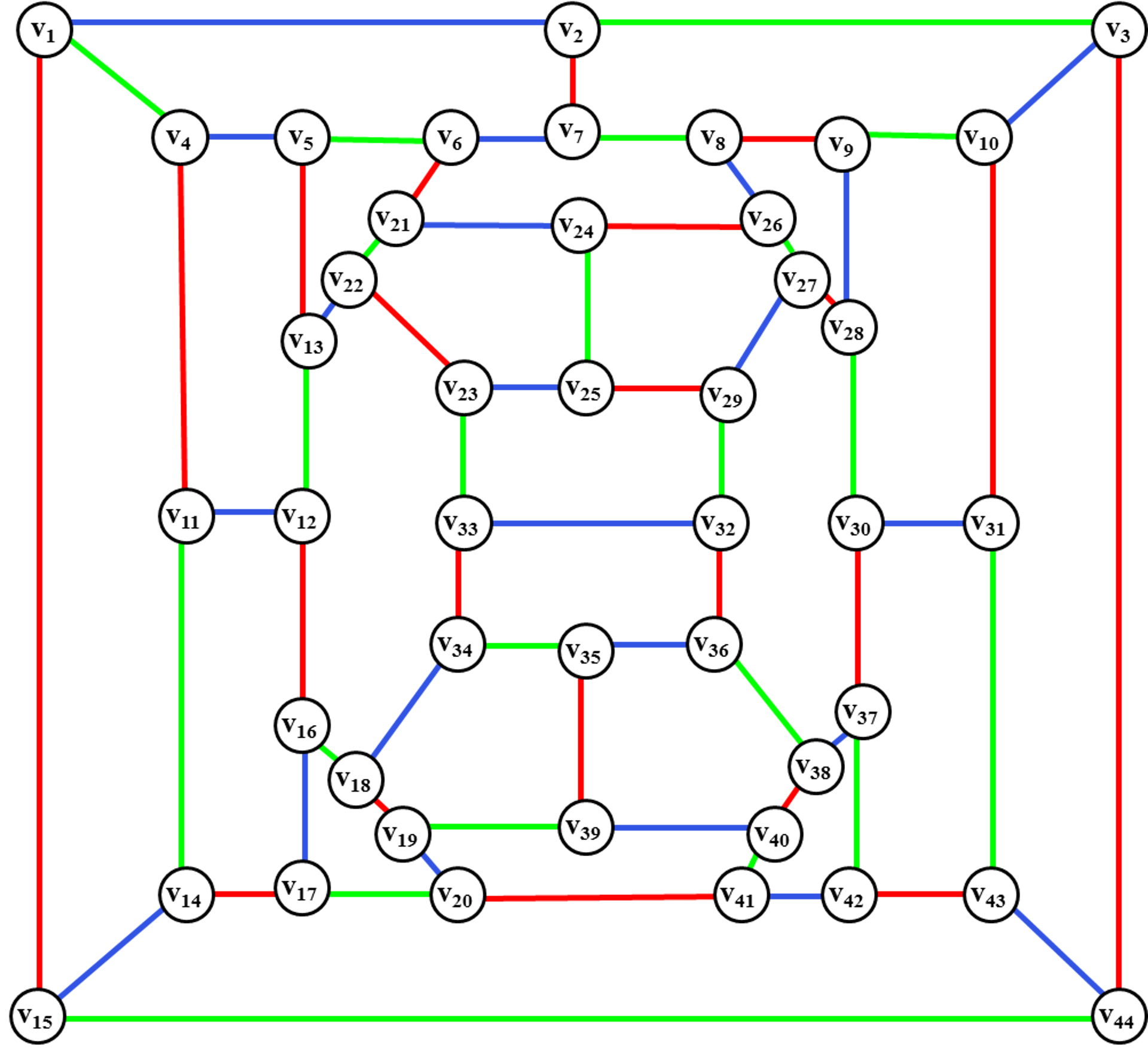
Рис. 29. Окончательная раскраска
негамильтонового графа G44.
Пример 3. Произведем раскраску ребер в негамильтоновом
графе G46.
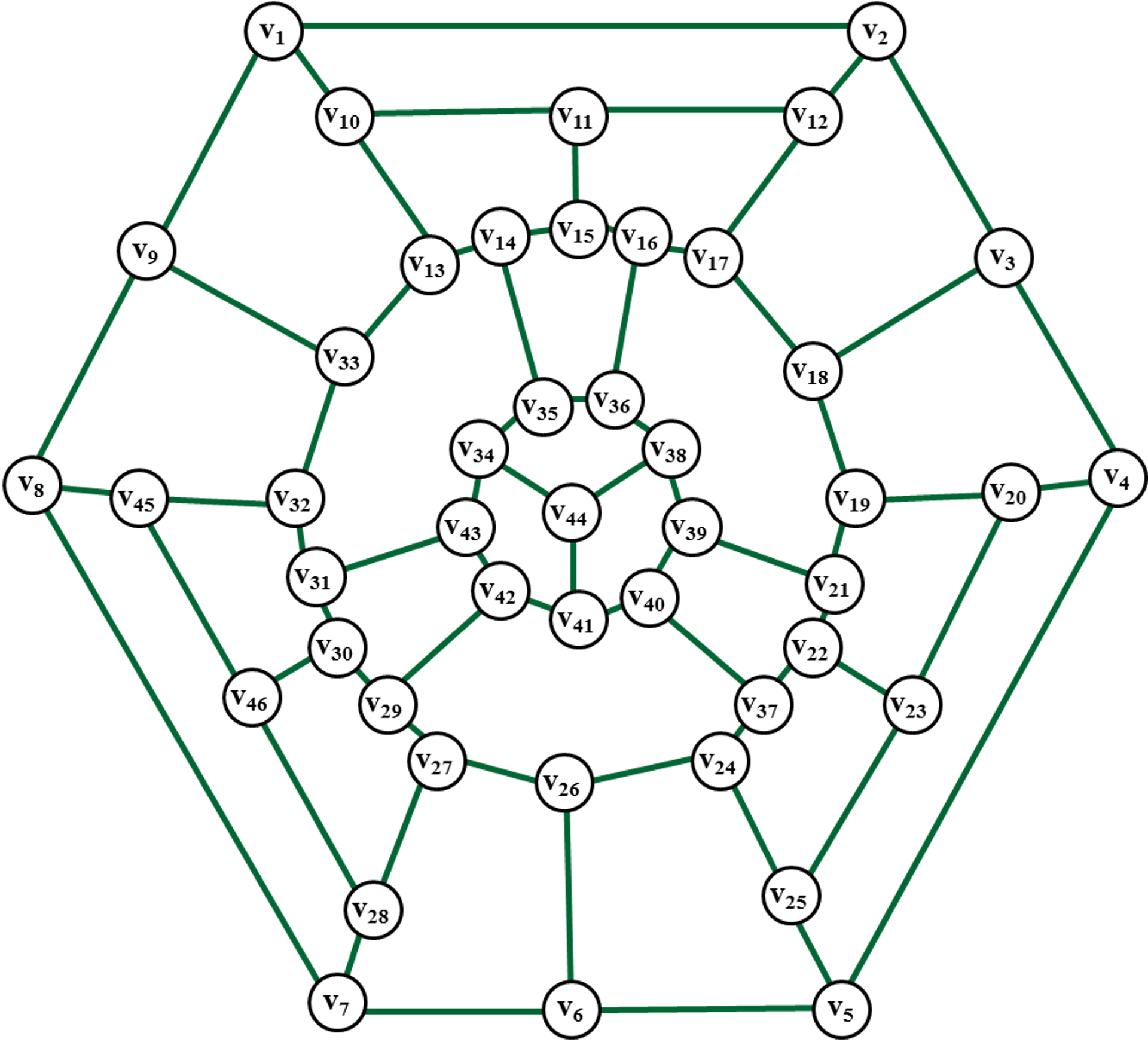
Рис. 30. Кубический
негамильтонов граф G46.

Рис. 31. Удаление
ребер с целью получения дисков четной длины.
Удаляем из графа ребра (v9,v33), (v3,v18), (v30,v46), (v6,v26), (v38,v44) с целью получения дисков четной длины.
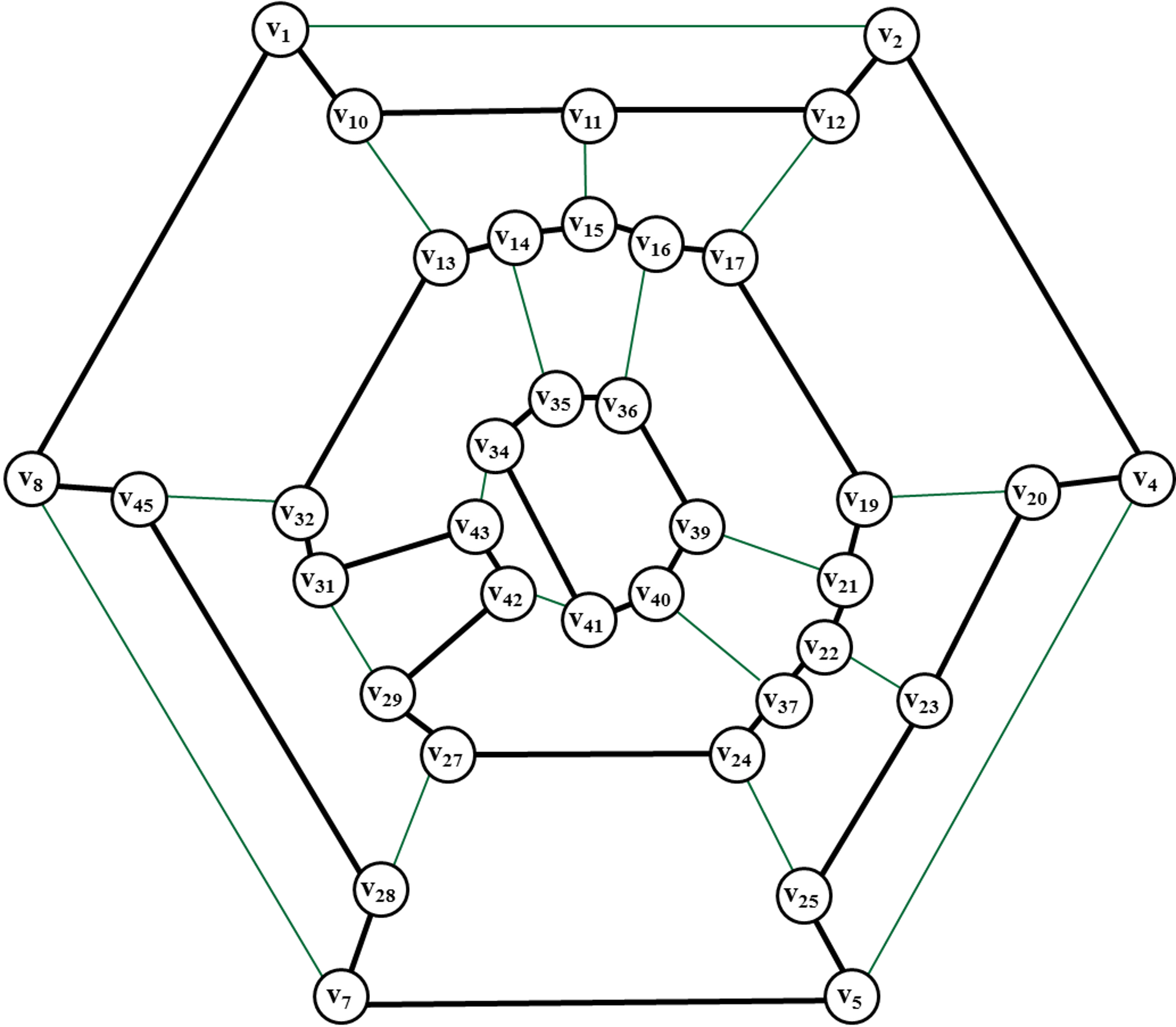
Рис. 32. Диски четной длины.
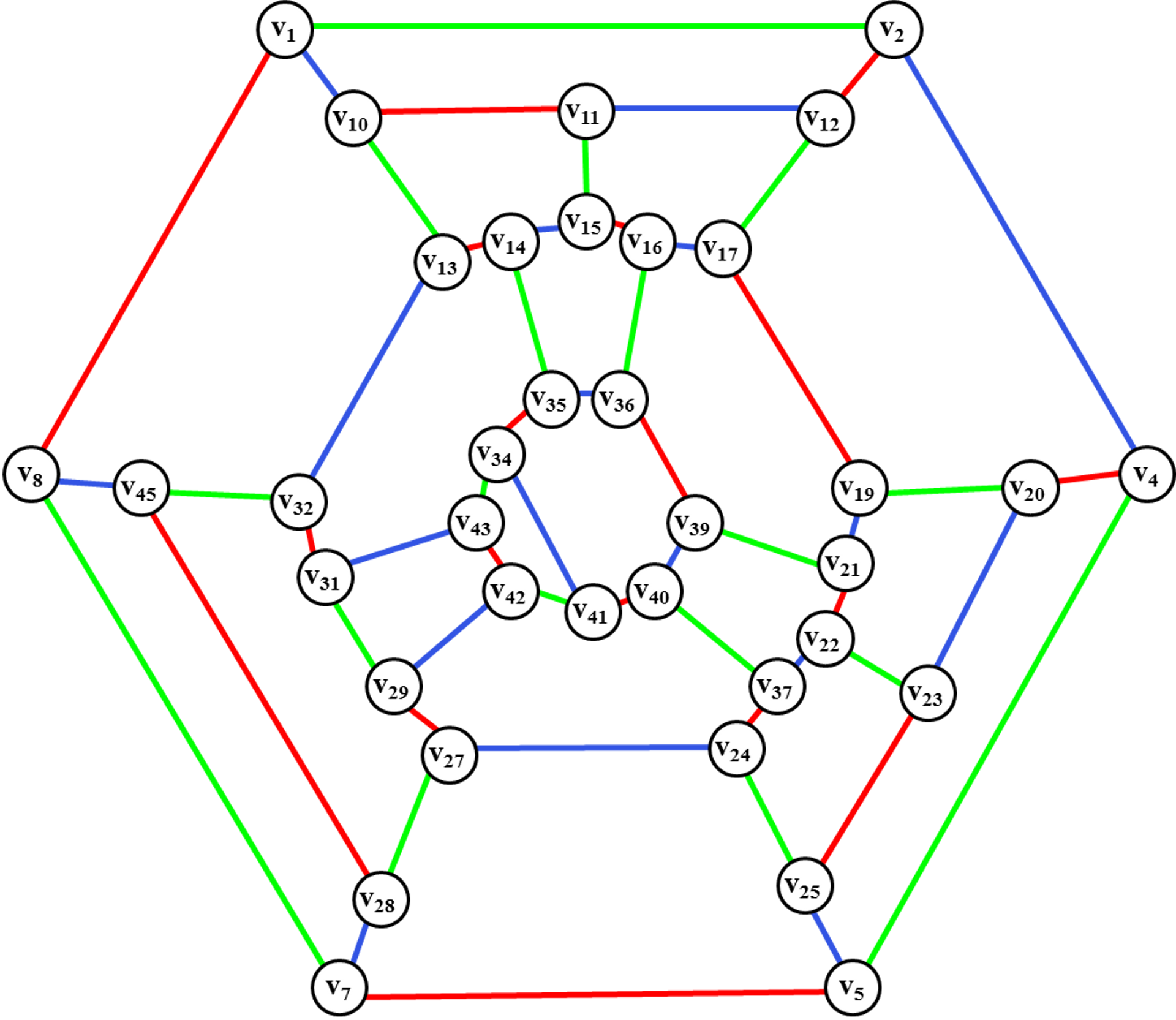
Рис. 33. Раскраска
дисков четной длины.
Раскрашиваем диски четной длины в зеленый цвет. Тогда ребра
данного цветного диска раскрашиваются в красный и синий цвета. Ребра,
принадлежащие зеленому 1‑фактору графа, также раскрашиваем в зеленый
цвет.
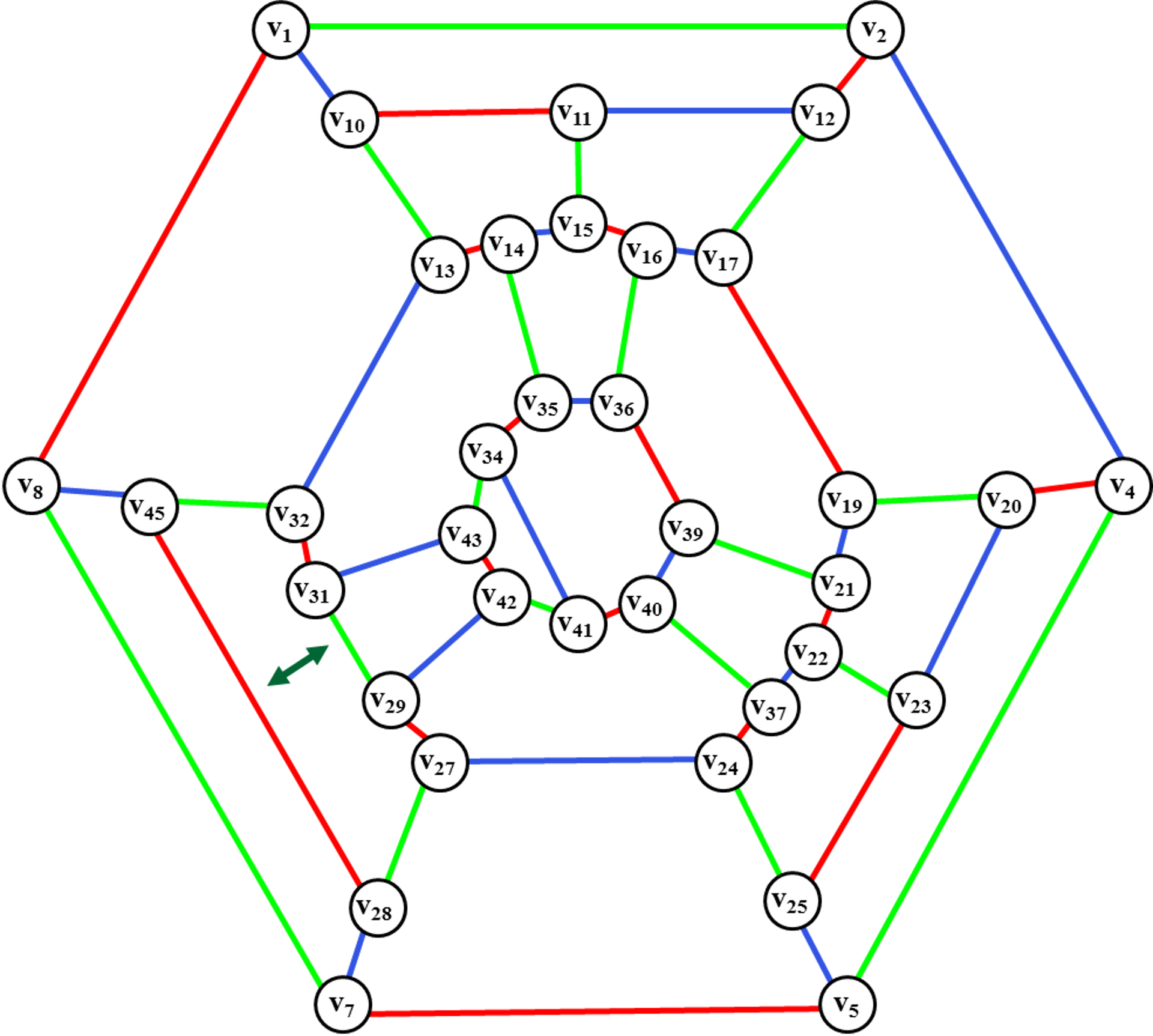
Рис. 34. Введение
ребра (v30, v46).
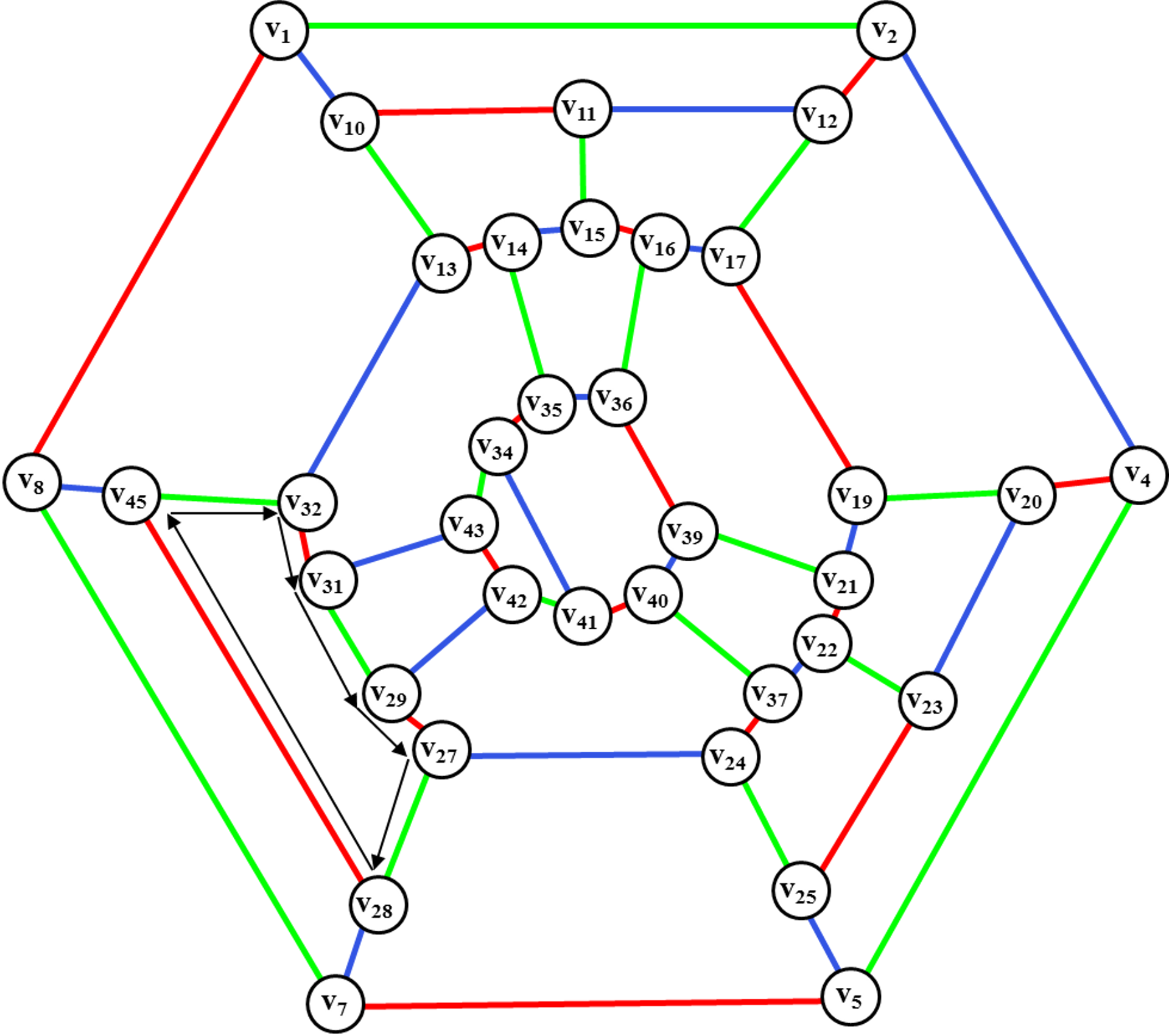
Рис. 35. Поиск диска
для введения ребра (v30,v46).
Осуществляем поиск цветного диска для введения ребра (v30, v46).
Это синий диск <v45,v32, v31,v29, v27,v28>.
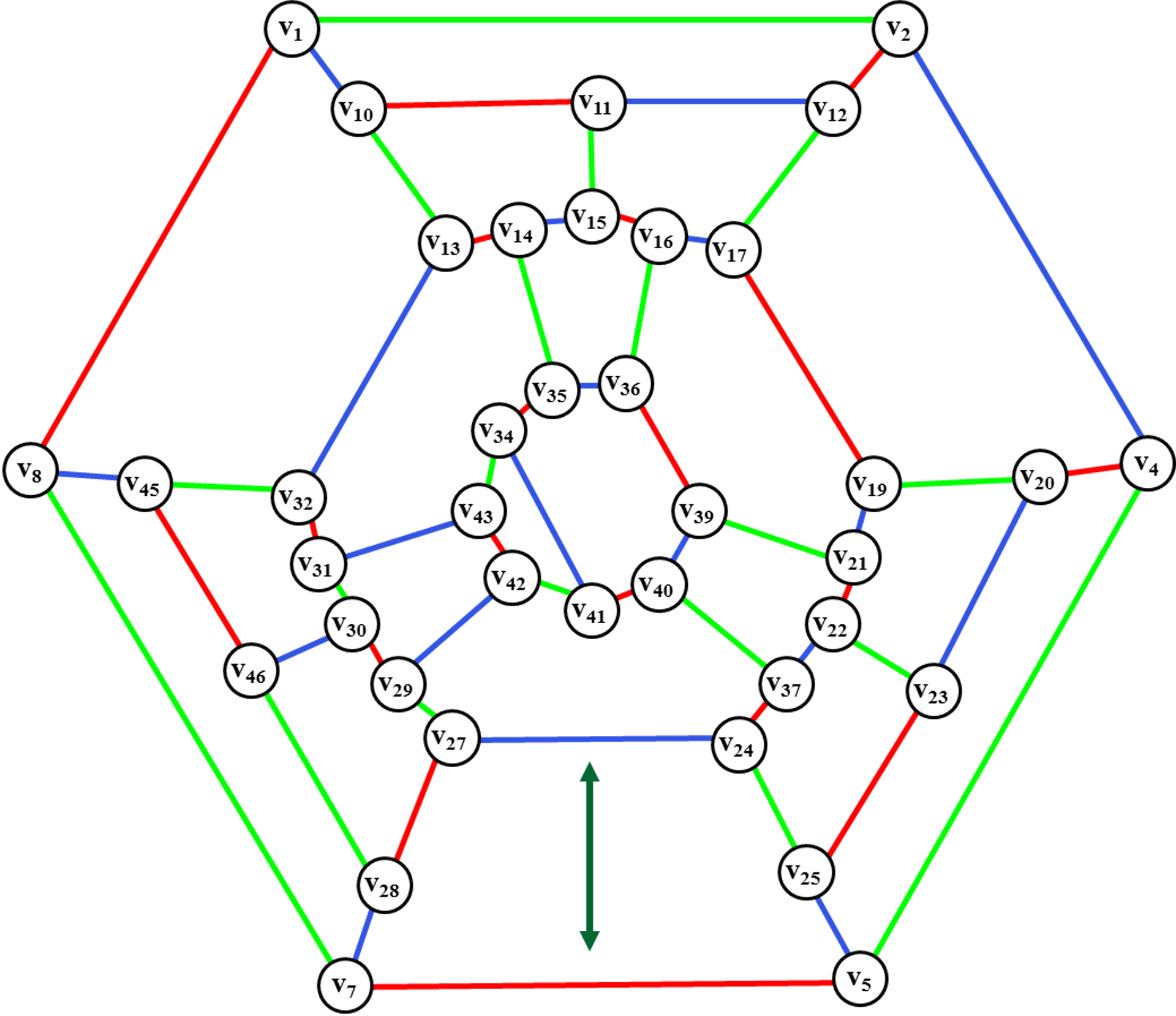
Рис. 36. Введение
ребра (v30, v46)
и перекраска ребер диска.
Вводим ребро (v30, v46)
и осуществляем перекраску ребер диска <v45,v32, v31,v30, v29,v27, v28,v46>. Определяем цветной диск <v27,
v28, v7, v5, v25, v23, v20, v4, v2, v12, v11, v10, v1, v8, v45, v46, v30, v29, v42, v43, v31, v32, v13, v14, v15, v16, v17, v19, v21, v22, v37, v24>
с сцепленными ребрами для введения ребра (v6, v26))
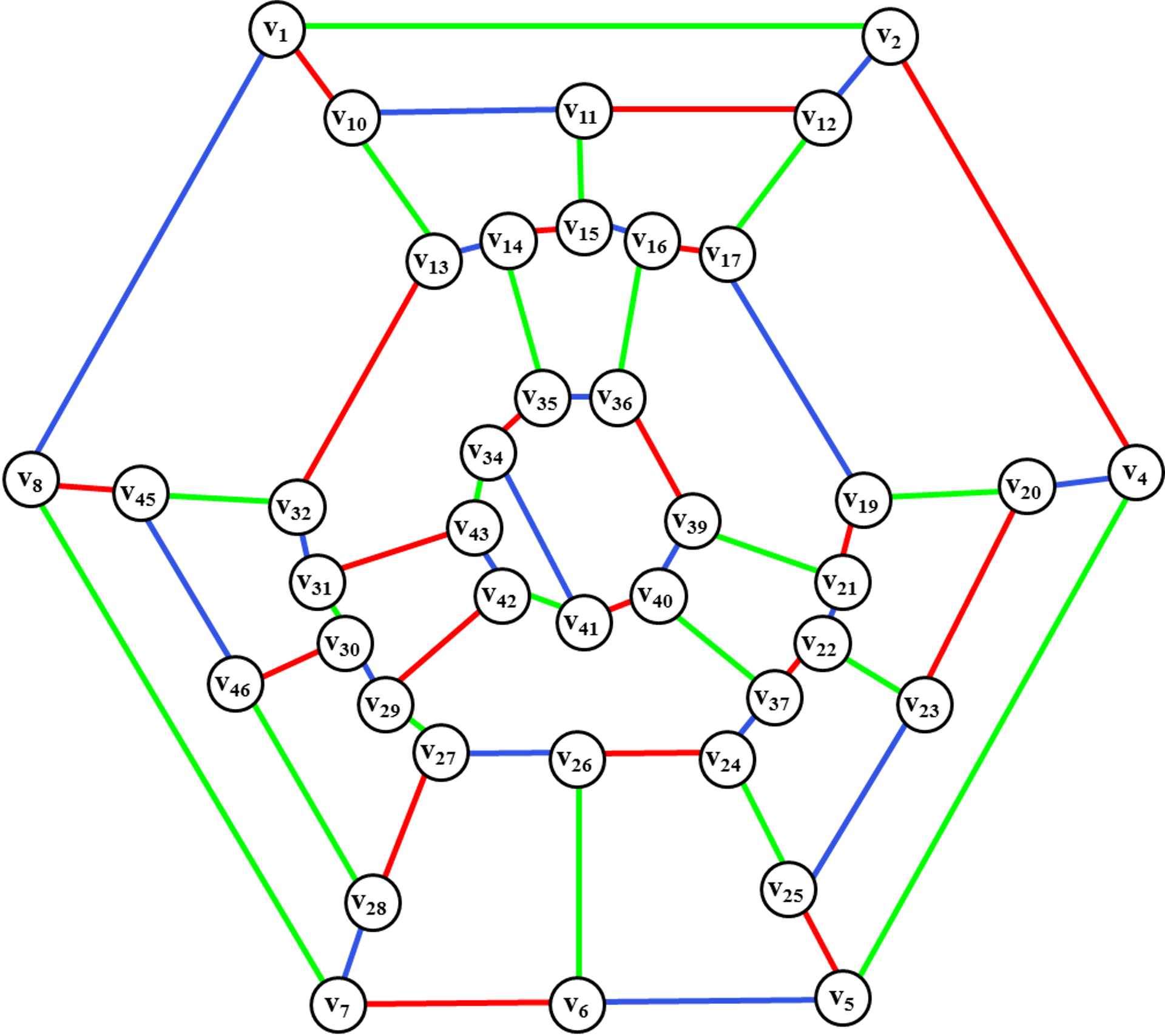
Рис. 37. Введение
ребра (v6, v26)
и перекраска ребер диска.
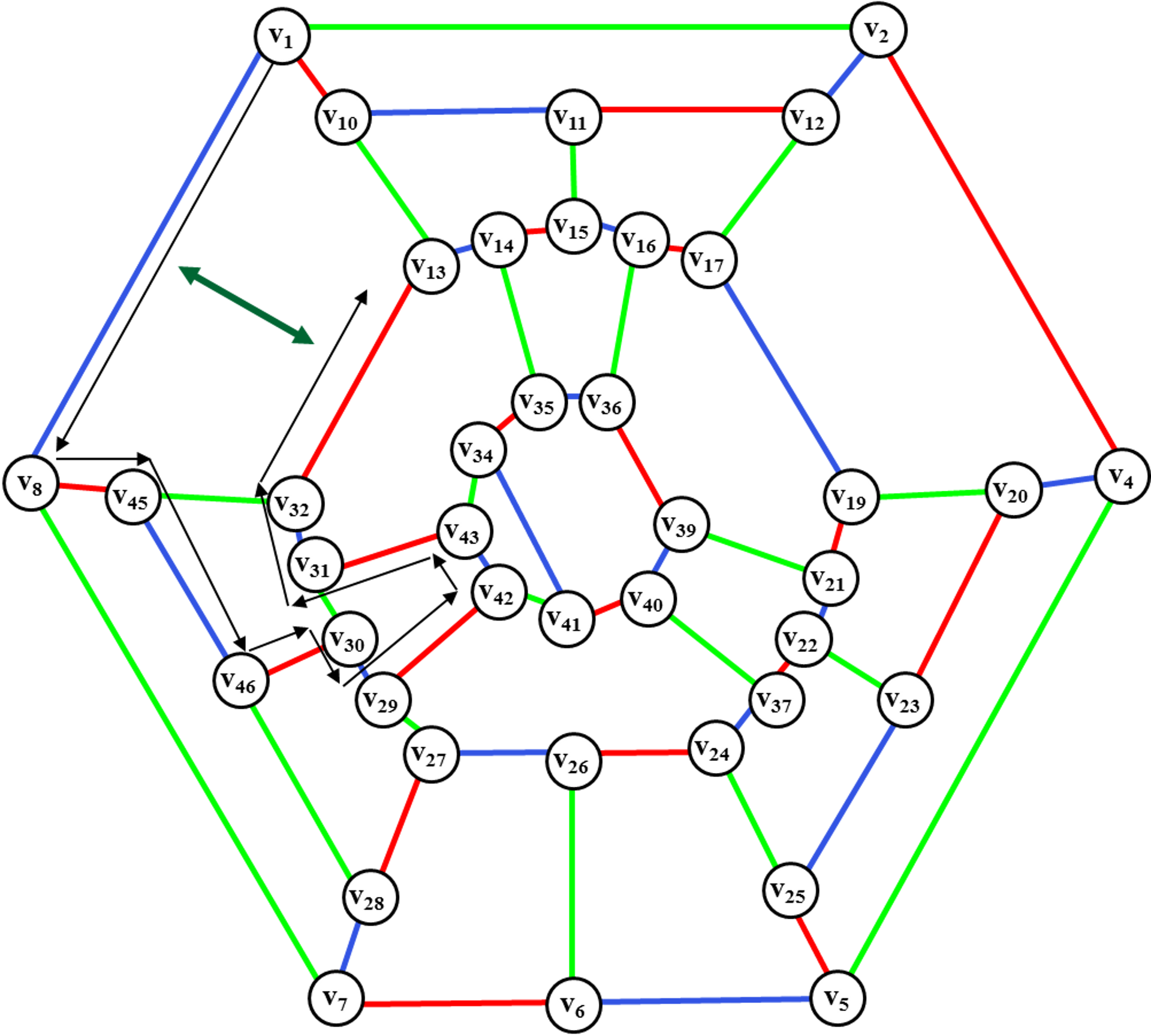
Рис. 38. Поиск
цветного диска для введения ребра (v9,v33).
Осуществляем поиск диска для введения ребра (v9, v33).
Это диск <v17, v19,v21, v22,v37, v24,v26, v27,v28, v7,v6, v5,v25, v23,v20, v4,v2, v12,v11, v10,v1, v9,v8, v45,v46, v30,v29, v42,v43, v31,v32,v33, v13,v14, v15,v16>.
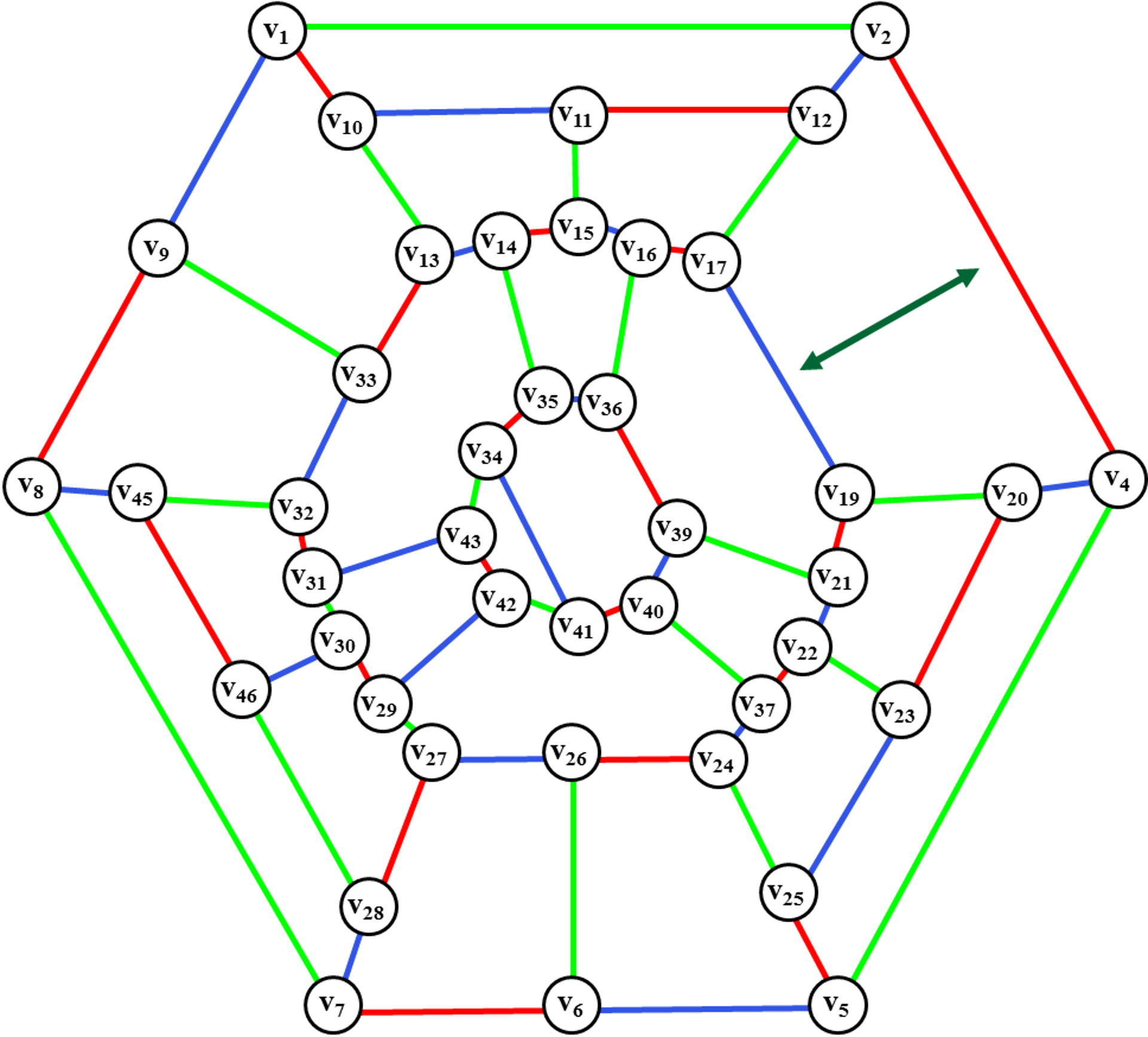
Рис. 39. Введение
ребра (v9, v33)
и перекраска ребер цветного диска.
Введение ребра (v9,v33) и перекраска ребер цветного диска.
Определение диска для введения ребра (v3,v18).
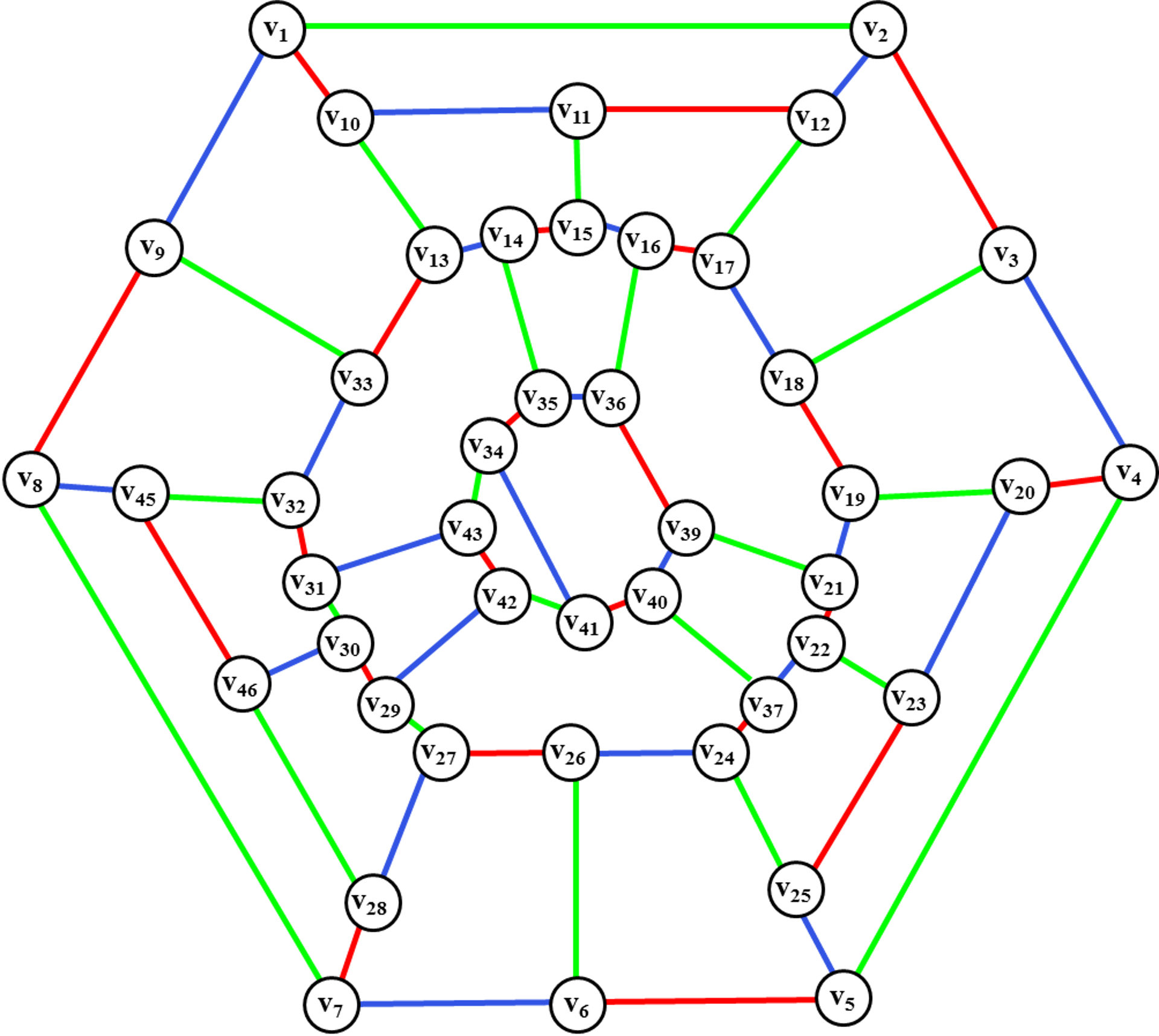
Рис. 40. Введение
ребра (v3, v18)
и перекраска ребер цветного диска.
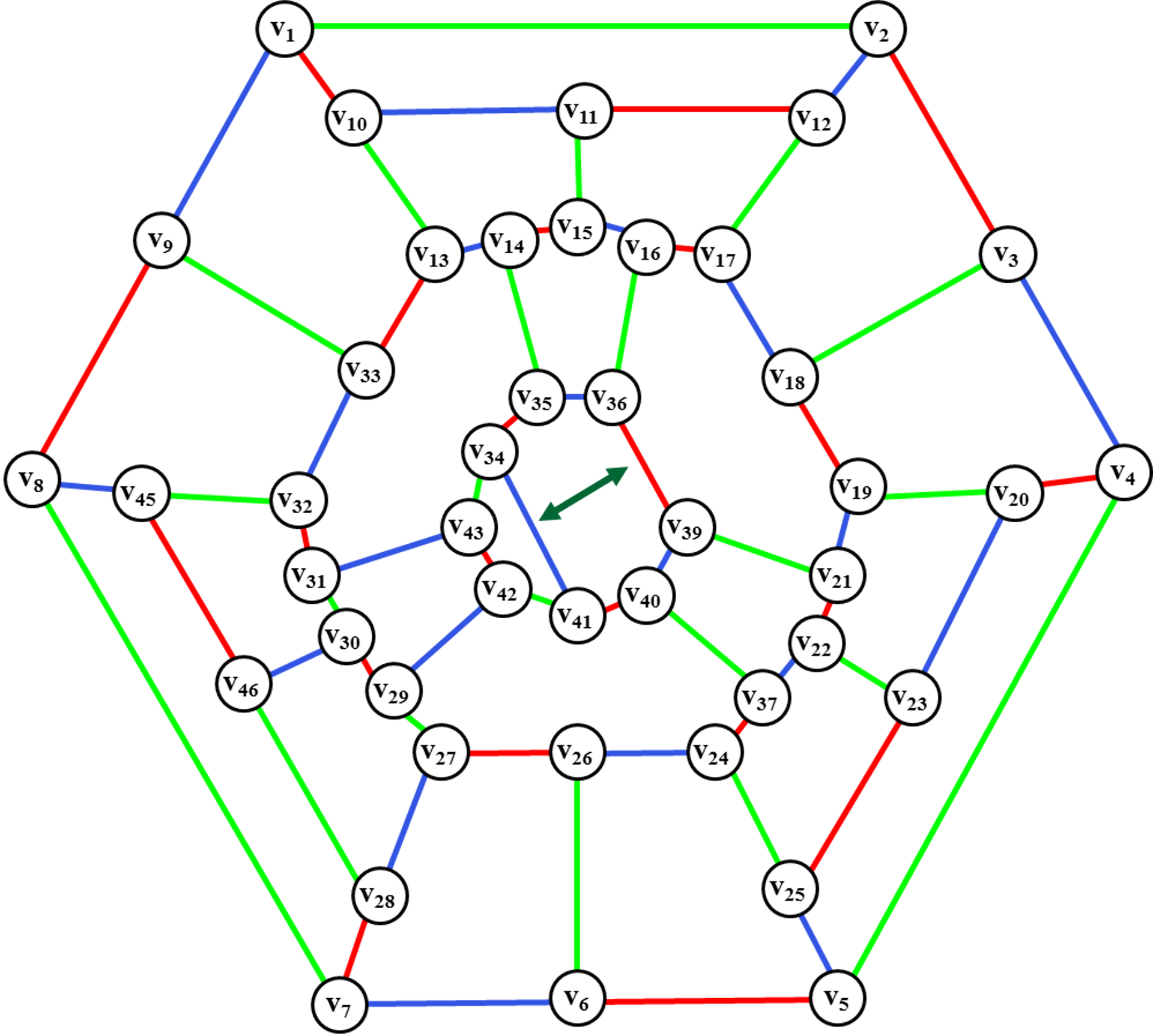
Рис. 41. Определение
местоположения для введения ребра (v38,v44).
Нахождение цветного диска <v34,v35, v36,v39, v40,v41> для введения ребра (v38, v44).
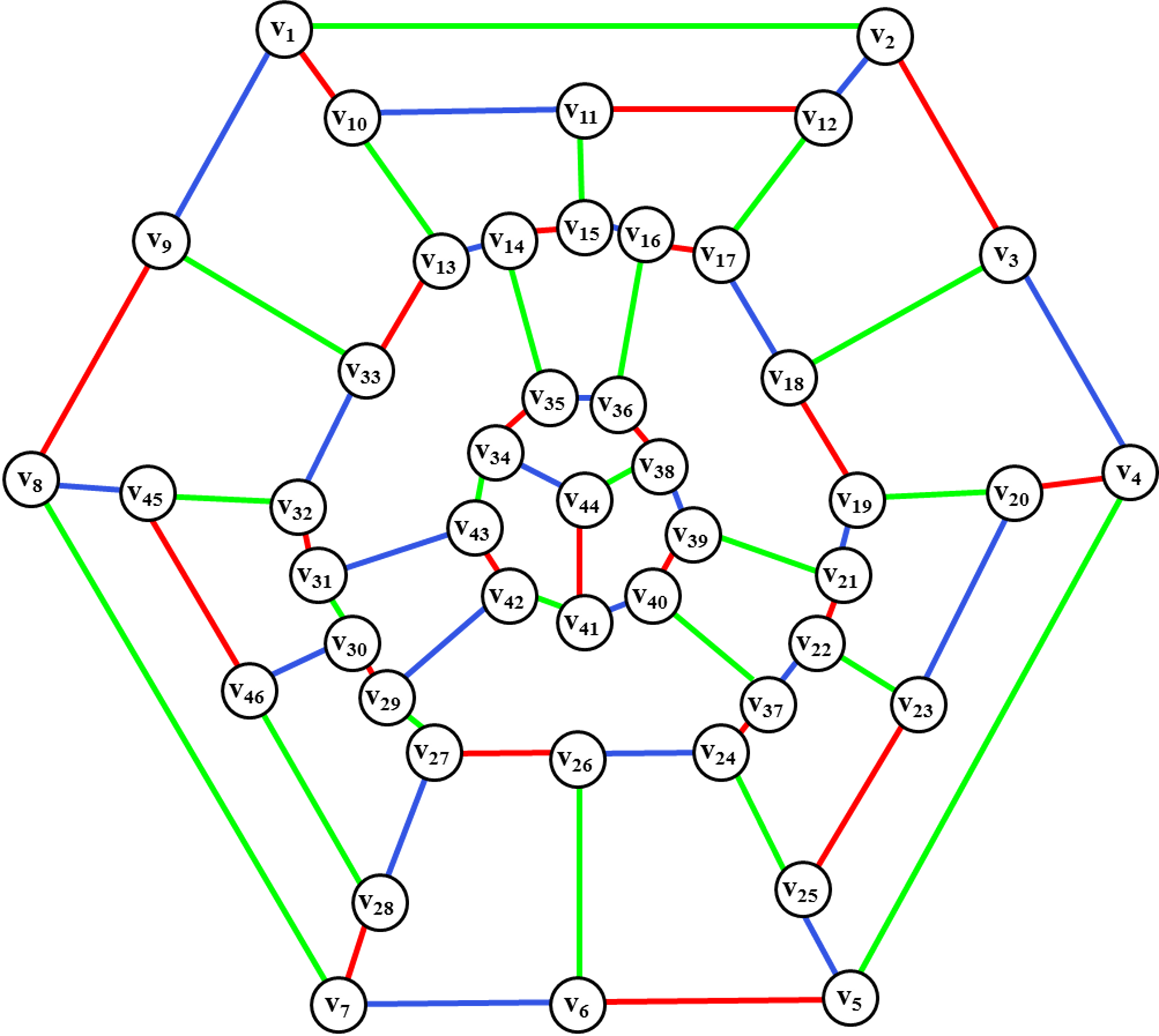
Рис. 42.
Окончательная раскраска кубического негамильтонового графа G46.
Пример 4. Раскрасим кубический негамильтонов граф G42.
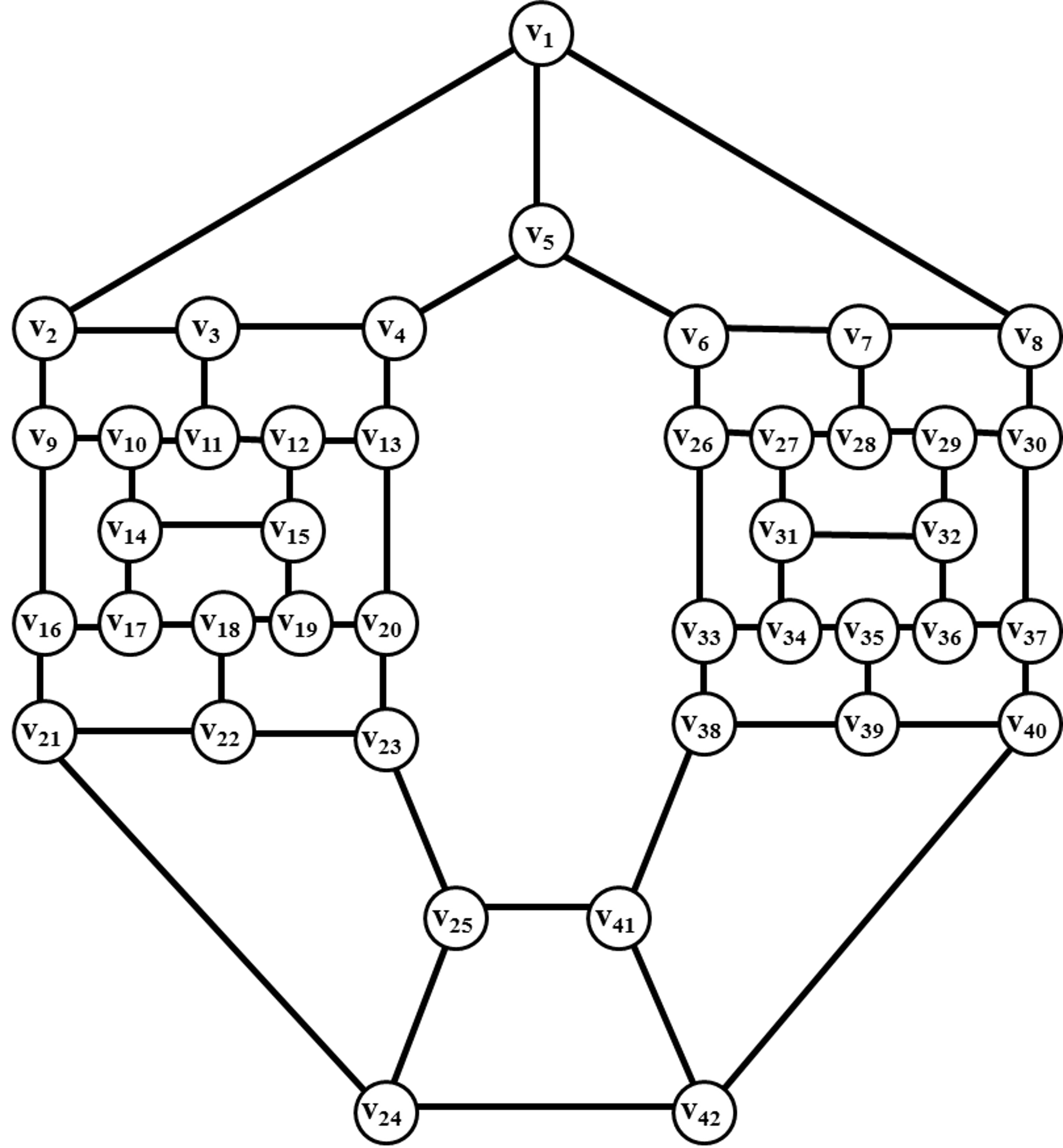
Рис. 43. Кубический
негамильтонов граф G42.
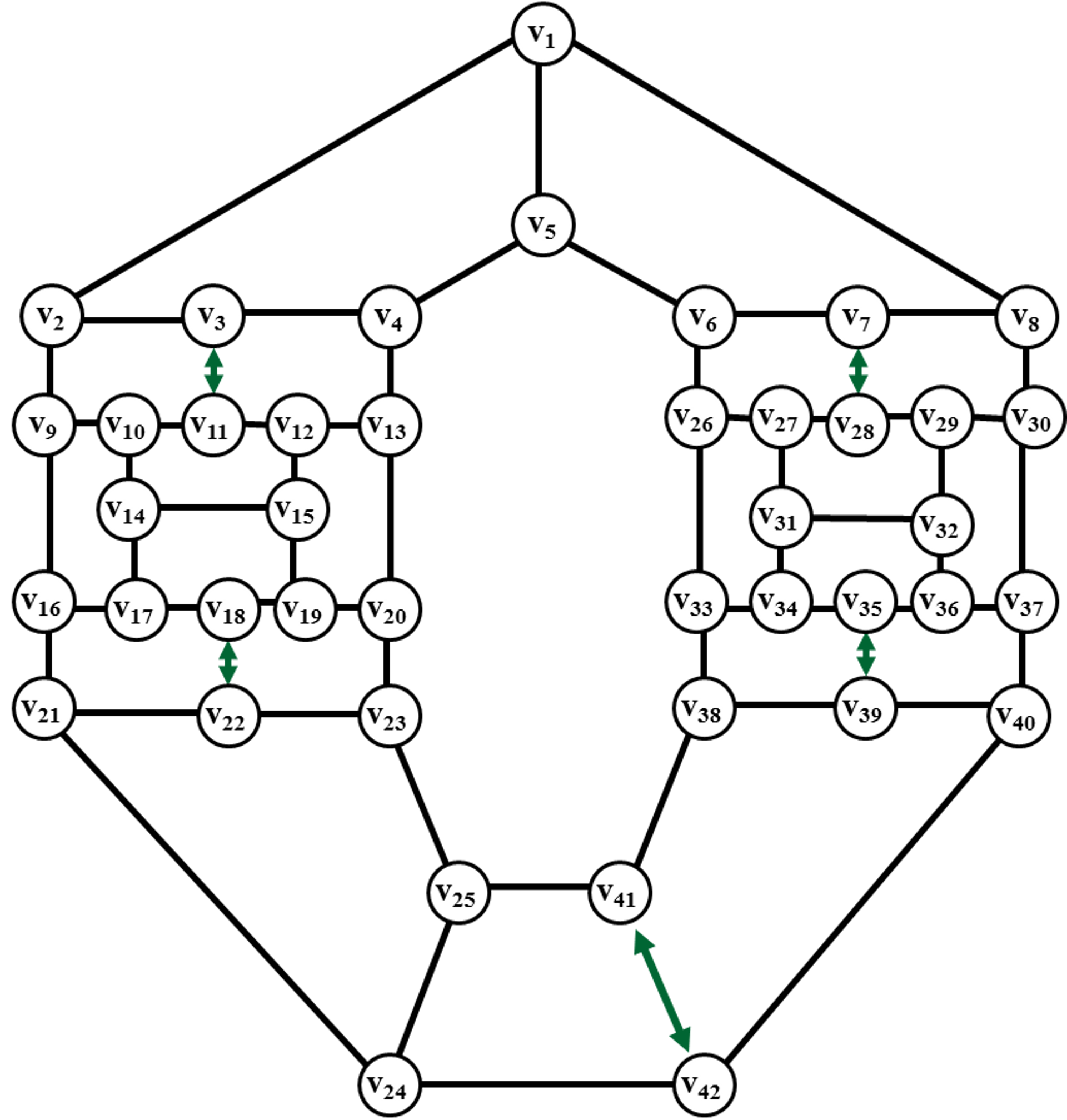
Рис. 44. Удаление
ребер для получения дисков четной длины.
Удаляем из графа ребра (v3,v11),(v18,v22),(v7,v28),(v35,v39),(v41,v42) с целью получения дисков четной длины.
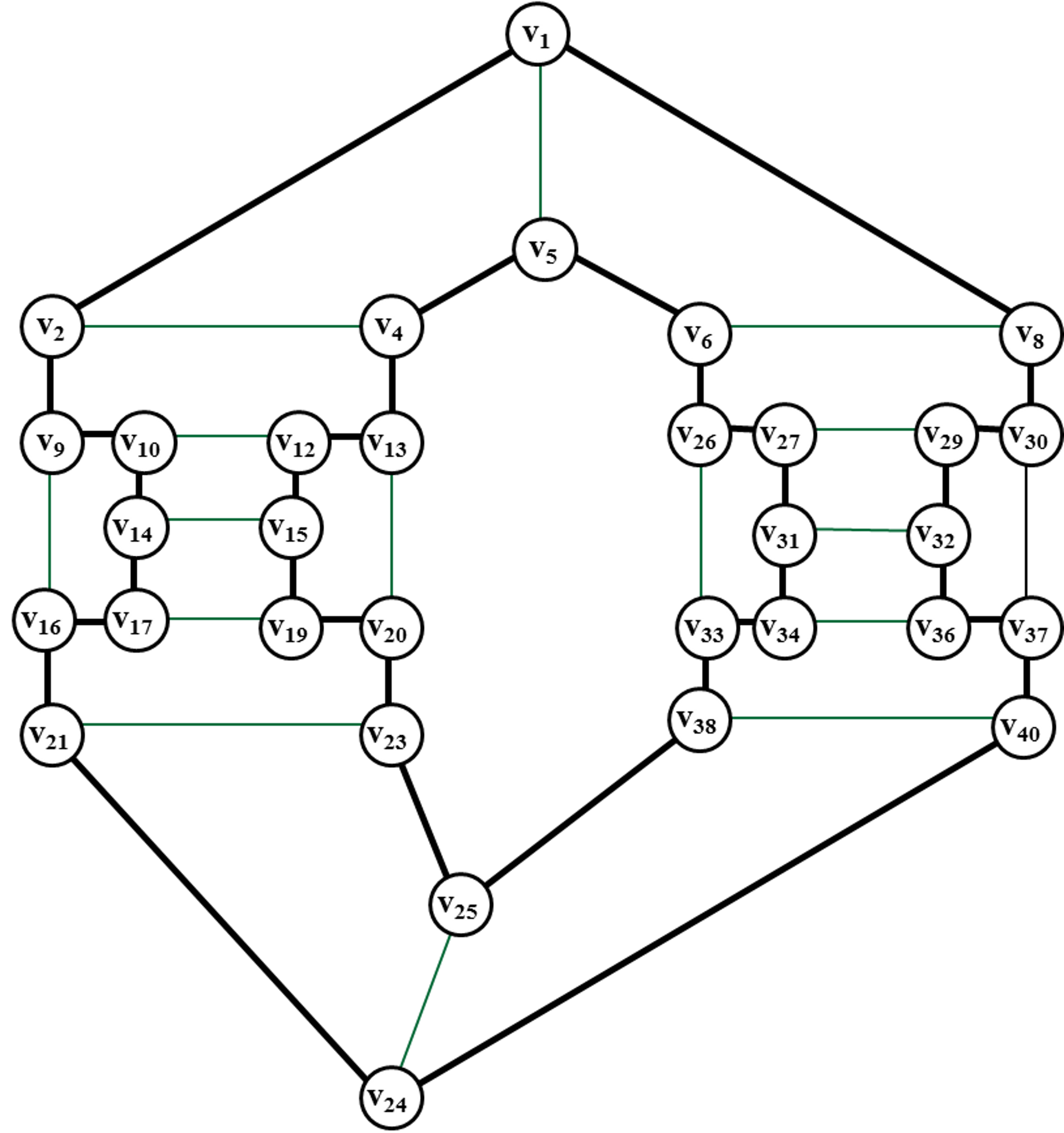
Рис. 45. Построение
дисков четной длины.
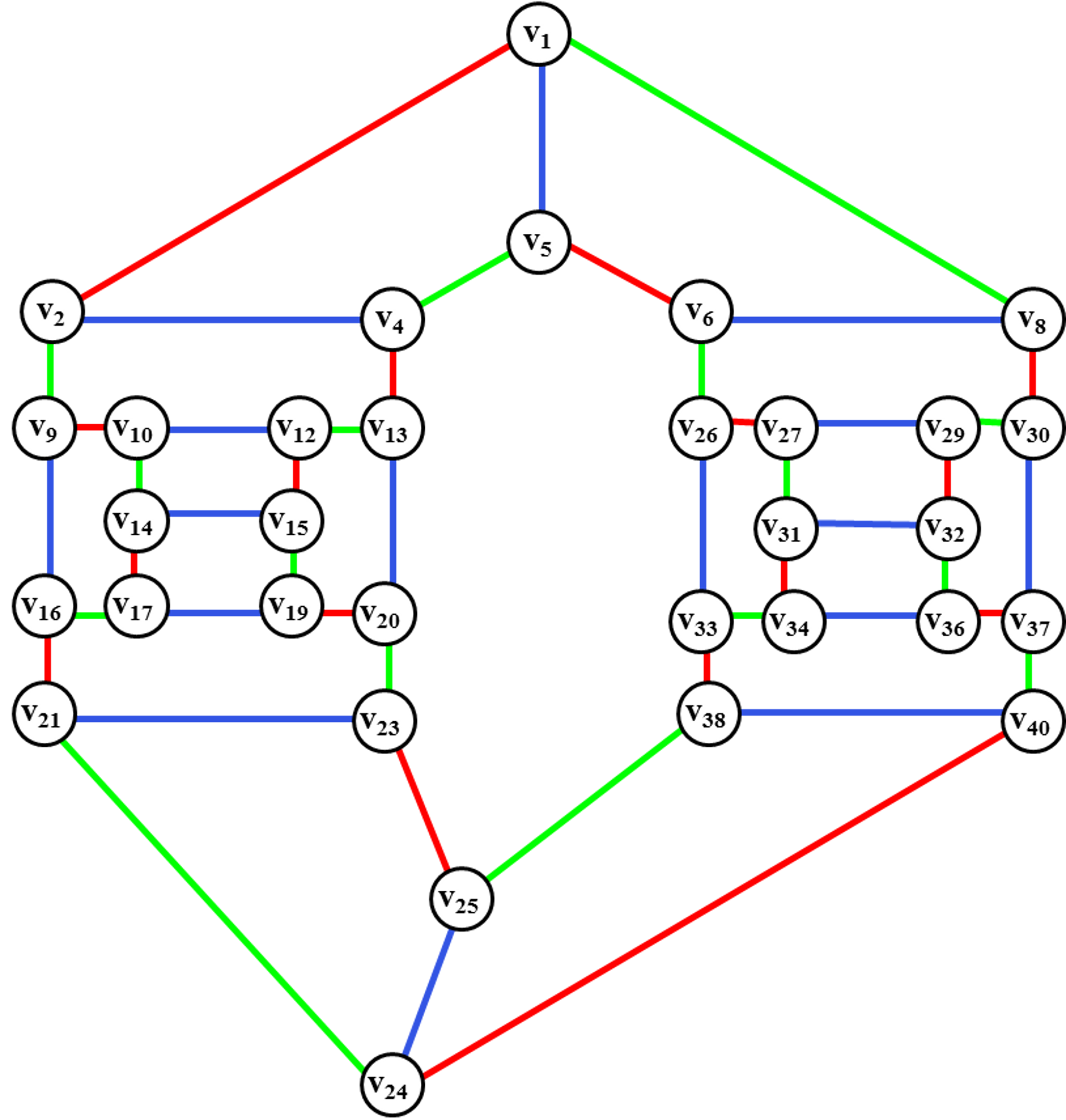
Рис. 46. Раскраска
дисков четной длины (синий цвет).
Производим раскраску дисков четной длины в синий цвет и
производим раскраска соответствующего 1-фактора также в синий цвет.
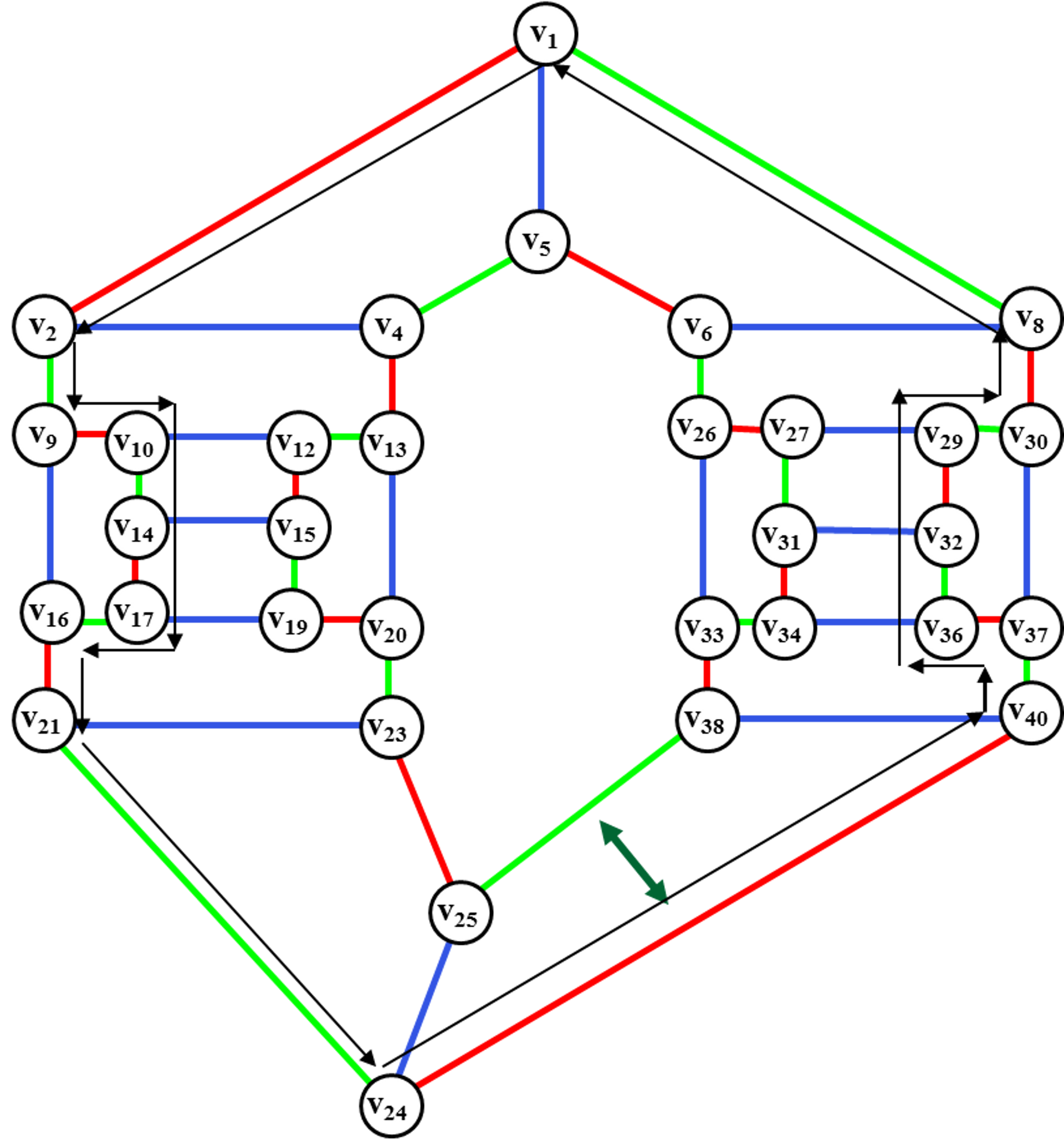
Рис. 47. Ротация
цветного диска для введения ребра (v41,v42).
Осуществляем ротацию цветного диска <v21,v16, v17,v14, v10,v9, v2,v1, v8,v30, v29,v32, v36,v37, v40,v24> для введения ребра (v41, v42).
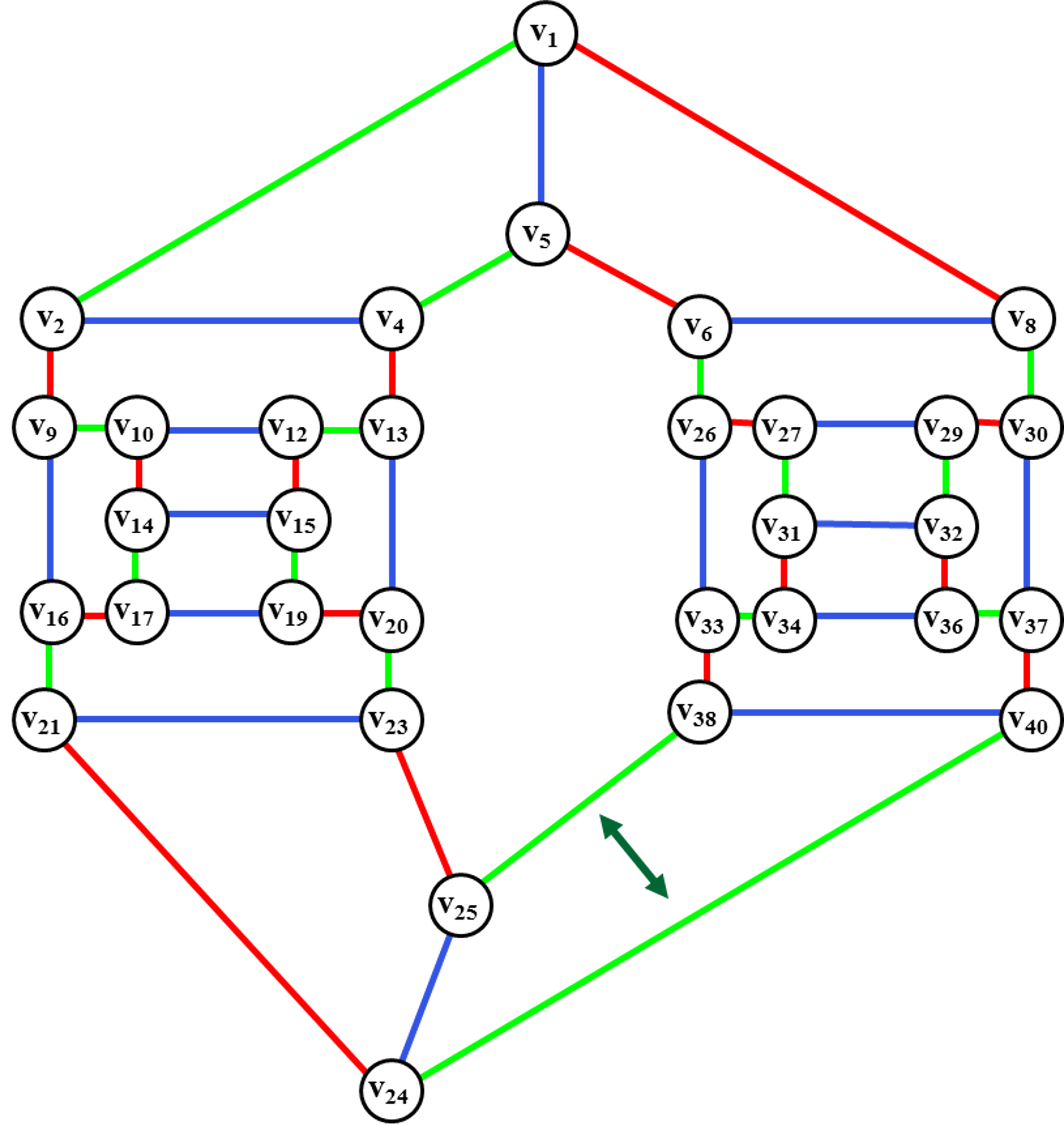
Рис. 48. Перекраска
ребер в процессе ротации цветного диска.
После проведения ротации, определяем цветной диск <v25, v38,v40, v24>для
проведения ребра (v41,v42).
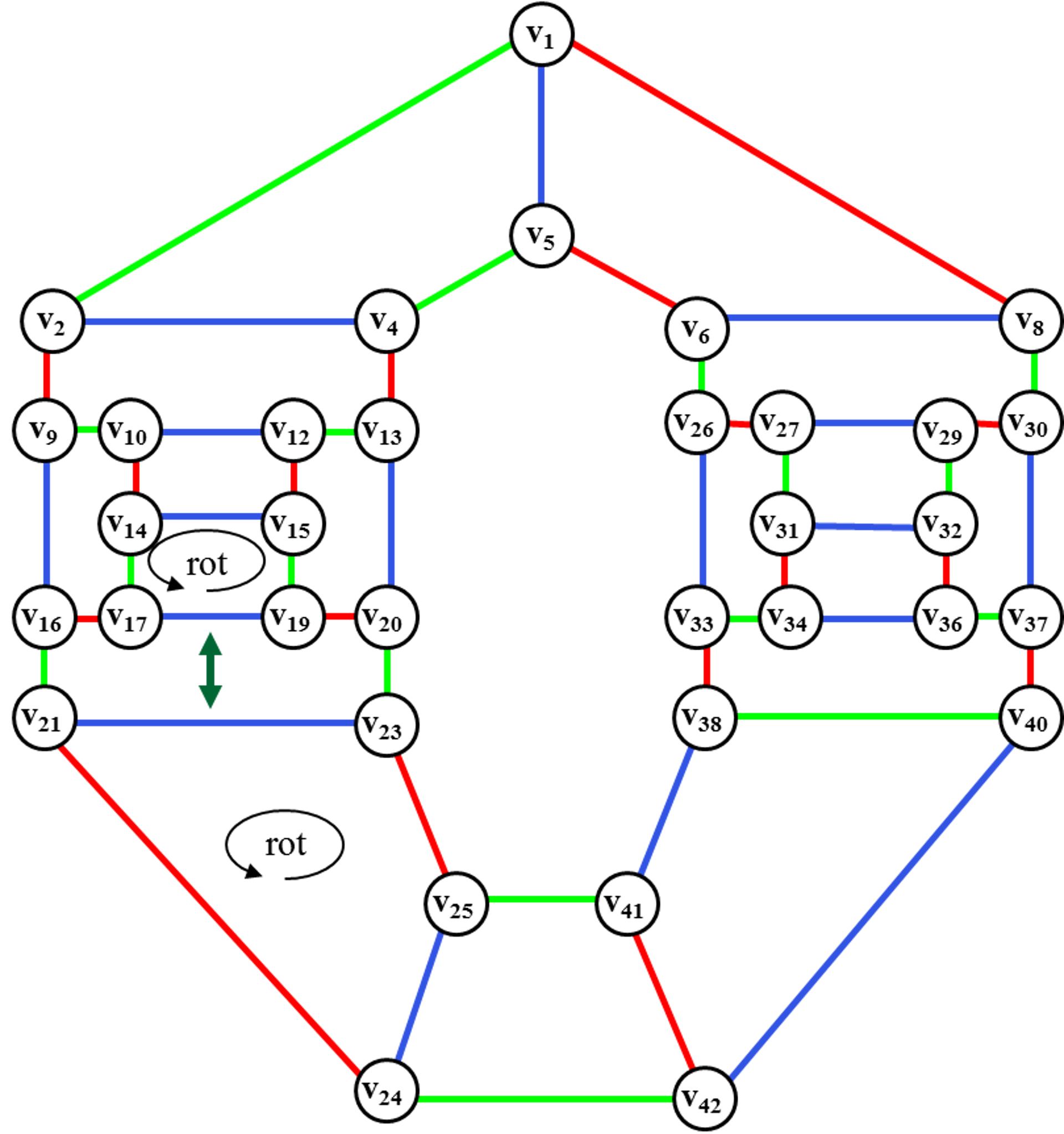
Рис. 49. Введение
ребра (v41, v42)
и перекраска ребер цветного диска.
После введения ребра (v41,v42) осуществляем ротацию цветных дисков <v21, v23,v25, v24>
и <v14, v15,v19, v17>
для введения ребра (х18,х22).
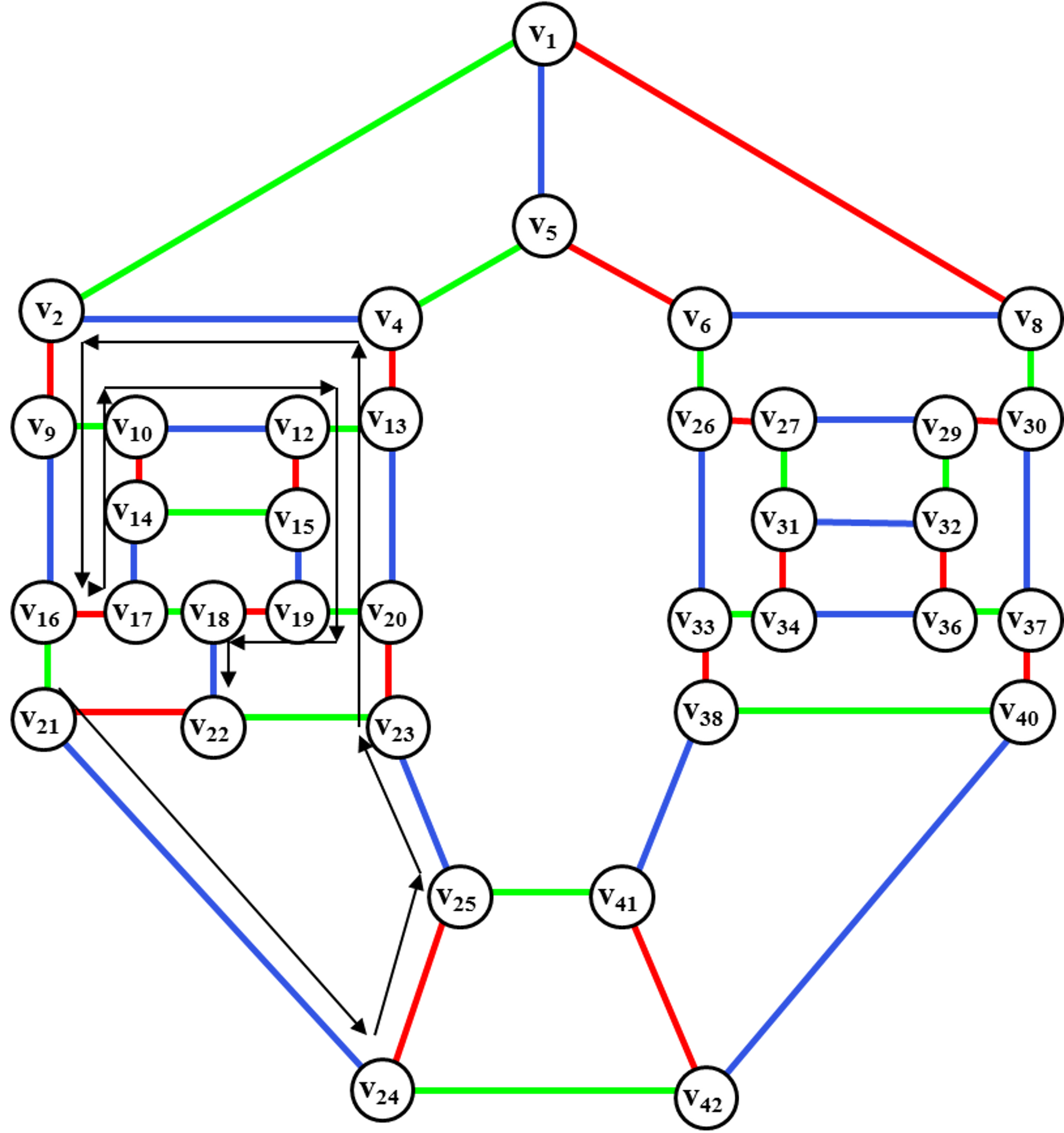
Рис. 50. Раскраска
ребер цветного диска после введения ребра (v18,v22).
После введения ребра (v18,v22) перекрашиваем ребра цветного диска <v16, v17,v18, v19,v20, v23,v22, v21>.
Далее производим ротацию диска <v21,v24, v25,v23, v20,v13, v4,v2, v9,v16, v17,v14, v10,v12, v15,v19, v18,v22> для введения ребра (v3, v11).
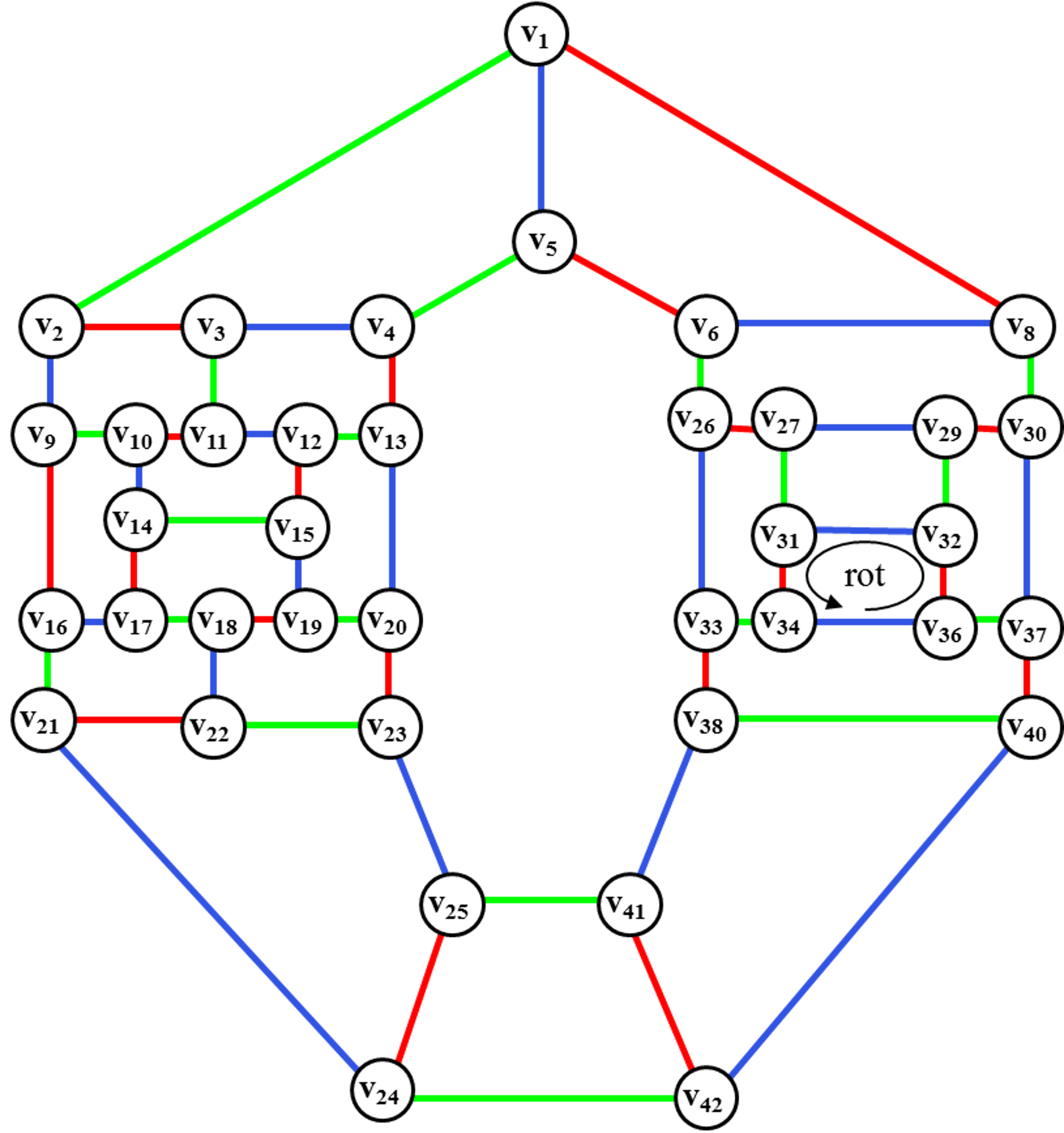
Рис. 51. Введение
ребра (v3, v11)
и перекраска ребер в цветном диске.
Для введения ребра (v35,v39) производим ротацию цветного диска <v31, v32,v36, v34>.
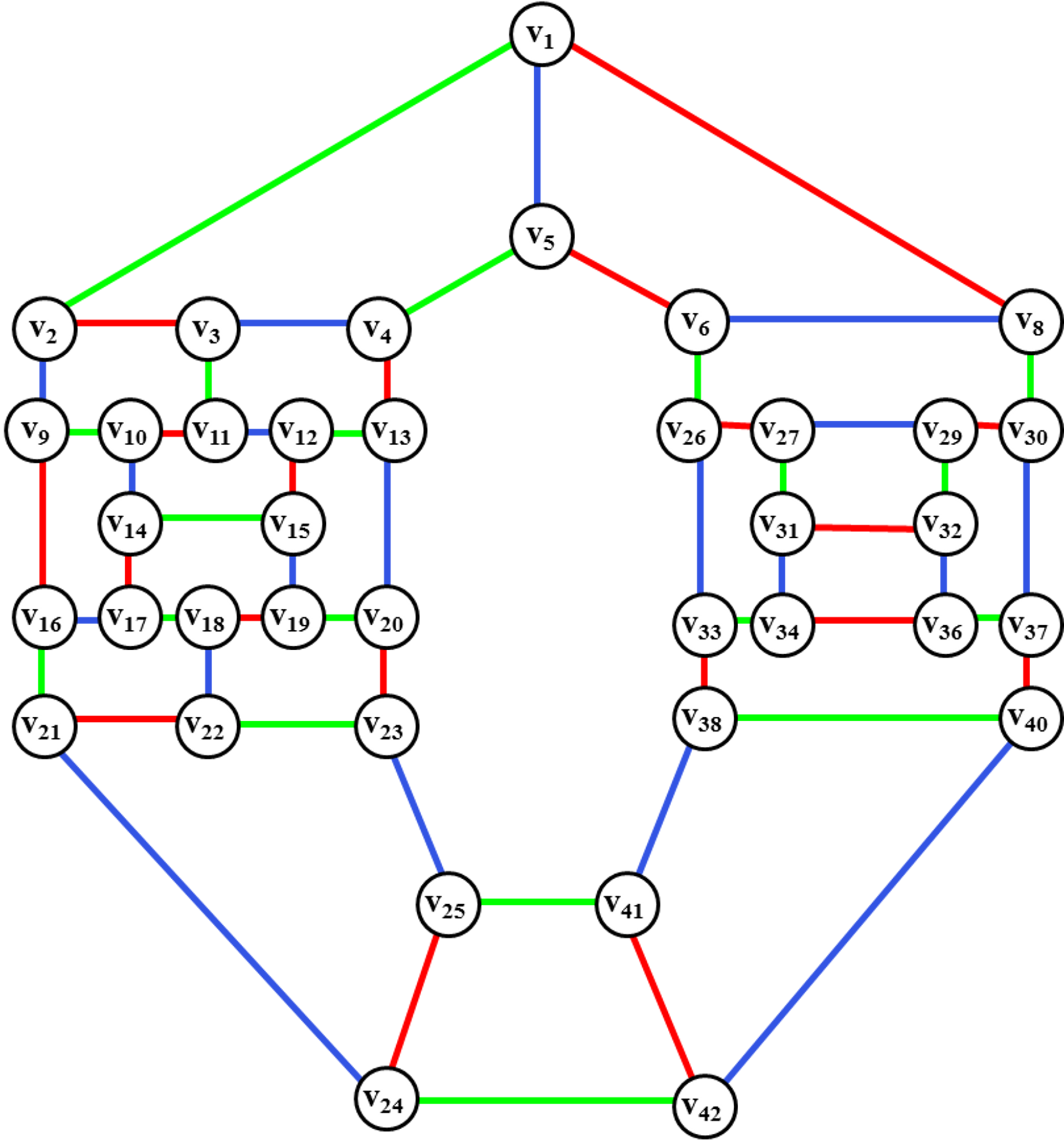
Рис. 52. Перекраска
ребер после операции ротации цветного диска.
Производим перекраску ребер цветного диска <v31, v32,v36, v34>.
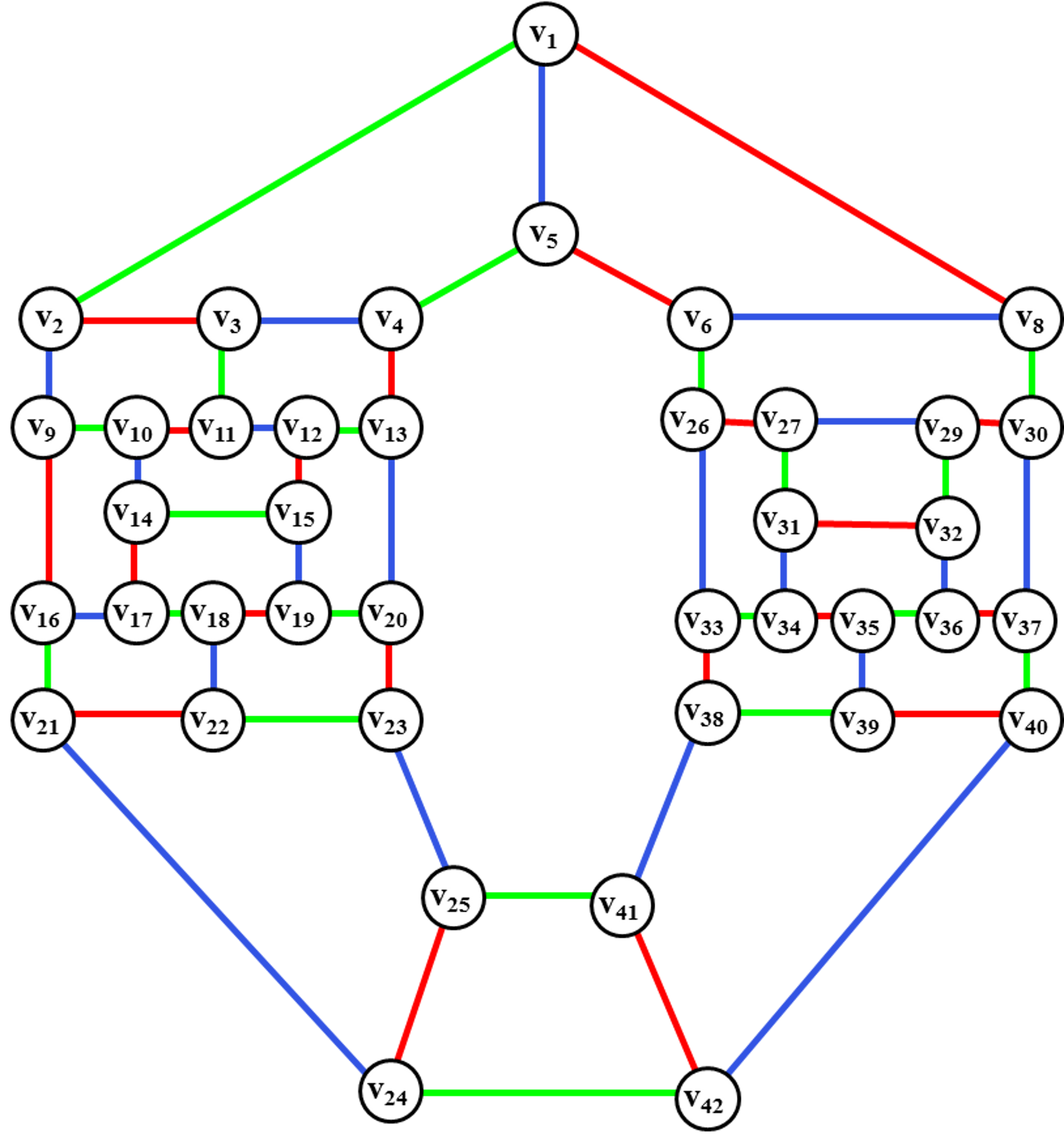
Рис. 53. Введение
ребра (v35, v39)
и перекраска ребер цветного диска.
Вводим ребро (v35,v39) и перекрашиваем ребра цветного диска <v33, v34,v35, v36,v37, v40,v39, v38>
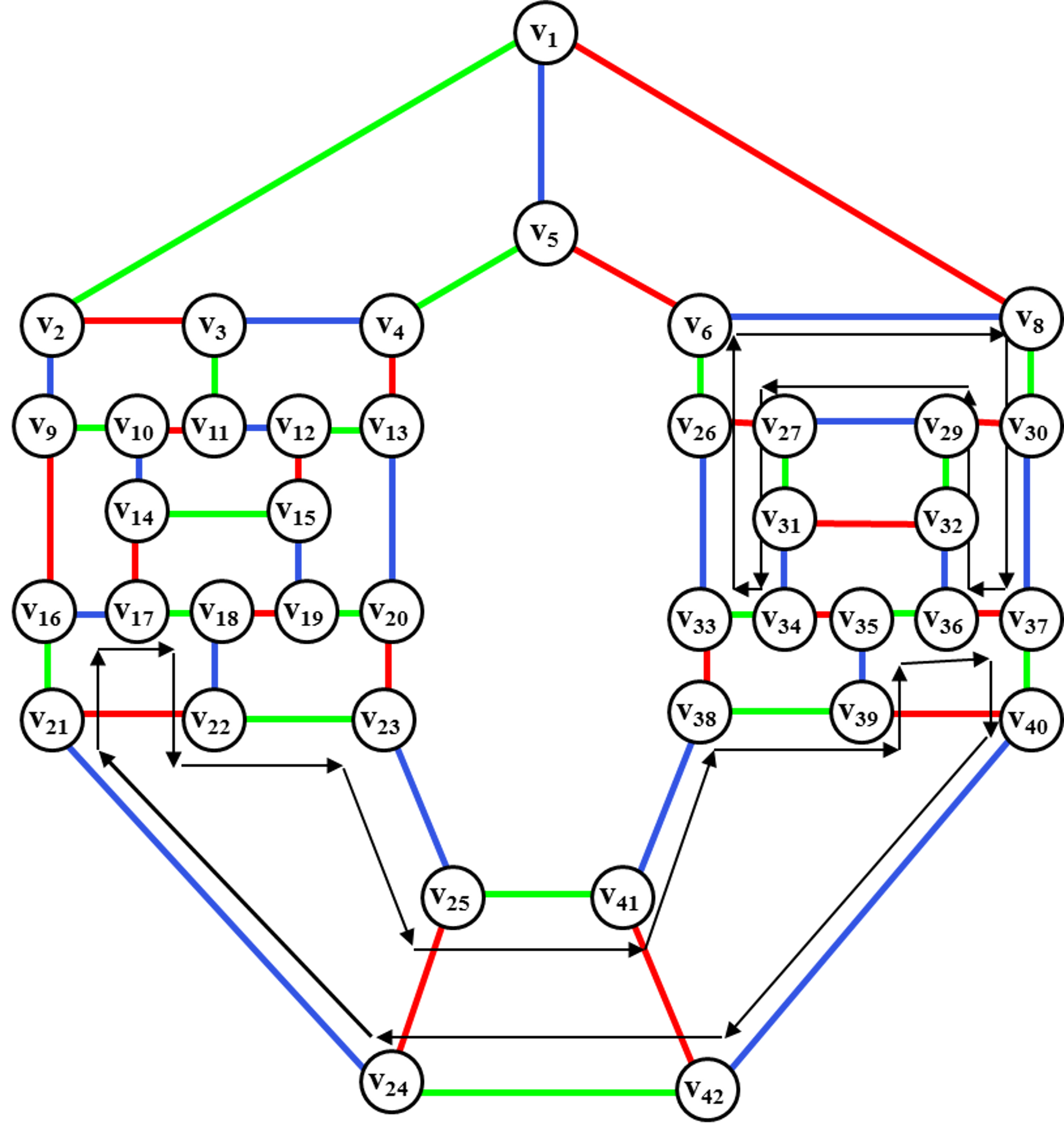
Рис. 54. Определение
цветного диска для введения ребра (v7,v28).
Осуществляем ротацию диска <v6,v8, v30,v37, v40,v42, v24,v21, v16,v17, v18,v22, v23,v25, v41,v38, v39,v35, v36,v32, v29,v27, v31,v34, v33,v26> для введения ребра (v7, v28).
Введение ребра (v7,v28) и окончательная раскраска
негамильтонового графа G42:
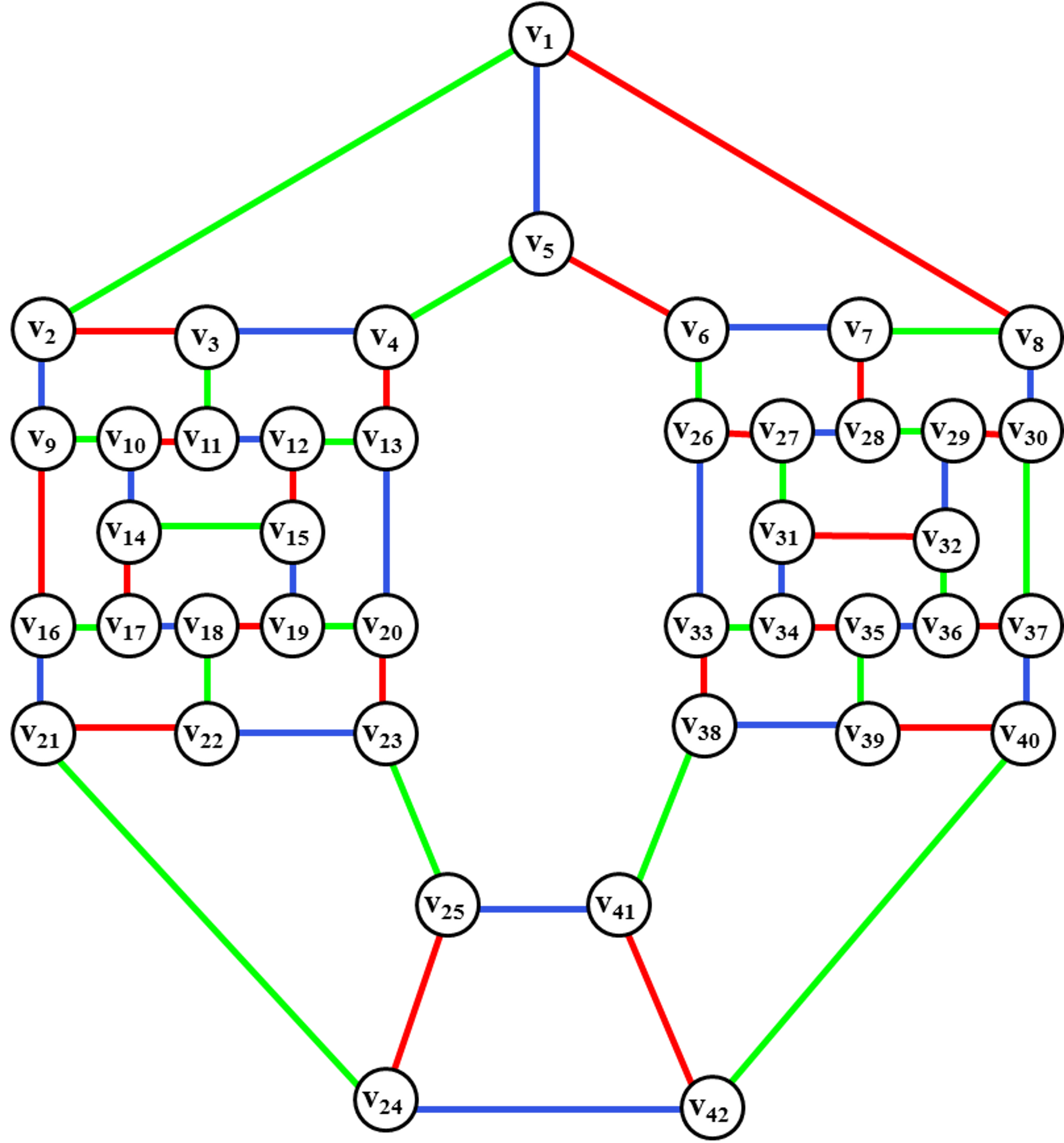
Рис. 55.
Окончательная раскраска негамильтонового графа G42.
шаг 0. [Инициализация]. Удаляем ребра из графа для
получения цветных дисков.
шаг 1. [Раскраска выбранных дисков]. Раскрашиваем
ребра выбранных дисков двумя цветами. Ребра цветного 1-фактора раскрашиваем
третьим цветом.
шаг 2. [Поиск цветного диска для сцепленных ребер]. Выбираем
вводимое ребро. Визуально осуществляем поиск цветного диска для сцепленных
ребер выбранного вводимого ребра. Если такого цикла не найдено, идем на шаг 3.
Иначе на шаг 4.
шаг 3. [Осуществляем ротацию цветных дисков]. Осуществляем
ротацию цветных дисков для получения цветного диска, проходящего по сцепленным
ребрам.
шаг 4. [Проверка подключения ребра]. Проверяем
подключение ребер. Если не все ребра подключены, то идем на шаг 2. Иначе конец
работы алгоритма.
В данной работе показано, что раскраска ребер и граней в
плоском кубическом графе без мостов осуществляется по законам преобразования
группы Клейна четвертого порядка. На основании этого подхода представлено
дедуктивное доказательство теоремы о четырех красках. Доказательство основано
на свойствах планарных графов учитывающих тесную связь между раскраской ребер
плоского кубического графа и раскраской его граней.
Для проведения вычислительного процесса раскраски и
перекраски ребер плоского кубического графа в три цвета введена операция
ротации цветных дисков. Вычислительную сложность алгоритма можно определить в
зависимости от количества удаленных ребер графа как О(m).
1.
K. Appel. The solution of the four-color-map problem // SciAm, Oct.
1977. P. 108–121.
2.
K. Appel, W. Haken. Every Planar Map Is Four Colorable // Contemporary
Mathematics. Providence (R.I.): Amer. Math Soc., 1989. Vol. 98. 308 р.
3.
В.В. Родионов. Методы четырехцветной раскраски вершин плоских графов /
В.В. Родионов - М.: КомКнига, 2005. – 48с.
4.
Y. Horibe, J. Yang, Y.-H. Cho et al. Color
Theorems, Chiral Domain Topology, and Magnetic Properties of FexTaS2 // J. Am.
Chem. Soc., 2014, 136 (23), pp 8368–8373.
5.
С.В. Курапов, М.В. Давидовский. Топологический подход к проведению
соединений в плоских конструктивах // Компоненты и технологии. 2015. № 11. С.
127–130;
6.
Ф. Харари. Теория графов. – Пер. с англ. Козырева В.П. / под ред.
Гаврилова В.Г. / Ф. Харари – М.: Мир. – 1973. – 300 с.;
7.
P.G. Tait. Remarks on the Colourings of Maps // Proc. R. Soc. Edinburgh
10: 729, 1880.
8.
W.T. Tutte. Non-Hamiltonian Planar Maps // Graph Theory and Computing,
ed. R. Read. Academic Press, New York, 1972, pp. 295–301.
9.
W.T. Tutte. On Hamiltonian Circuit // J. London Math. Soc. 21 (1946)
98–101.
10.
Н.З. Шор, Г.А. Донец. Алгебраический подход к проблеме раскраски плоских
графов / Г.А. Донец, Н.З. Шор - Київ: Наук.думка. - 1982. - 144с.
11.
И. Гроссман. Группы и их графы / Гроссман, И., Магнус В. – М.: Мир,
1971, - 238с.
12.
А.А. Зыков. Основы теории графов. / Зыков А.А. - М.: Наука, ГРФМЛ, 1987,
- 384с.
13.
М. Свами. Графы, сети и алгоритмы. М.: Мир. – 1984. – 455 с.;
14.
Ф. Харари. Теория графов. – Пер. с англ. Козырева В.П. / под ред.
Гаврилова В.Г. / Ф. Харари – М.: Мир. – 1973. – 300 с.;
15.
С. Мак Лейн. Комбинаторное условие для плоских графов / С. Мак-Лейн // В
кн.: Кибернетический сборник. Новая серия. – 1970. Вып. 7. – С.133–144.;
16.
T. Kavitha et. al. Cycle bases in graphs: characterization, algorithms,
complexity, and applications // Computer Science Review, 3 (2009), 199-243.
17.
Э. Рейнгольд. Комбинаторные алгоритмы, теория и практика. / Э.
Рейнгольд, Ю. Нивергельт, Н. Део - М.: Мир.- 1980. – 480 с;
18.
В.Г. Визинг. Об оценке хроматического класса р-графа // сб. Дискретный
анализ. – Новосибирск: Институт математики СО АН СССР, 1964. – Т.
3. – С. 25–30.
19.
В.Г. Визинг. Критические графы с данным хроматическим классом // сб.
Дискретный анализ. – Новосибирск: Институт математики СО АН СССР, 1965. –
Т. 5. – С. 9–17.
20.
С.В. Курапов, М.В. Давидовский. Раскраска плоских графов. Теория,
методы, алгоритмы. / Издательский Дом: LAP LAMBERT Academic Publishing, 2015,
142 c. IBSN 3659811246
Visual algorithm for coloring planar graphs
Authors: S.V. Kurapov1,A, M.V. Davidovsky2,A, A.V. Tolok3,B
A Zaporozhye National University, Ukraine
B Moscow State Technological University «STANKIN», Russia
1 ORCID: 0000-0003-4563-7227, lilili5050@rambler.ru
2 ORCID: 0000-0002-9472-3351, m.davidovsky@gmail.com
3 ORCID: 0000-0002-7257-9029, a.tolok@stankin.ru
Abstract
This article addresses a plane graph coloring problem. The authors propose a new visual algorithm for coloring planar graphs and present a deductive proof of the four-color theorem which is based on the properties of the Klein four-group. It is shown that an arbitrary colored cubic graph has three colored 2-factors and the addition of colors is done according to the laws of the Klein four-group transformation. The properties of colored plane cubic graphs are considered. Two theorems about the existence of a colored disk passing through linked edges and about edge coloring of a plane cubic graph are formulated and proved in the article. Moreover, it is shown that the four-color theorem can be obtained as a consequence of these proved theorems. In order to allow edge recoloring in a colored plane cubic graph the authors introduce a new operation – the rotation of a colored disk. The article provides examples of solving the problem of planar graphs coloring.
Keywords: graph, graph coloring, maximal planar graph, isometric cycles, Klein four-group, graph factors.
1.
K. Appel. The solution of the four-color-map problem // SciAm, Oct.
1977. P. 108–121.
2.
K. Appel, W. Haken. Every Planar Map Is Four Colorable // Contemporary
Mathematics. Providence (R.I.): Amer. Math Soc., 1989. Vol. 98. 308 р.
3.
V.V. Rodionov. Metody chetyrekhtsvetnoi raskraski vershin ploskikh
grafov. – M.: KomKniga, 2005. – 48s.
4.
Y. Horibe, J. Yang, Y.-H. Cho et al. Color
Theorems, Chiral Domain Topology, and Magnetic Properties of FexTaS2 // J. Am.
Chem. Soc., 2014, 136 (23), pp 8368–8373.
5.
S.V. Kurapov, M.V. Davidovskii. Topologicheskij podhod
k provedeniyu soedinenij v ploskih konstruktivah // Komponenty i tekhnologii.
2015. № 11. S. 127–130;
6.
F. Harary. Graph Theory, Reading: Addison-Wesley. – 1969.
7.
P.G. Tait. Remarks on the Colourings of Maps // Proc. R. Soc. Edinburgh
10: 729, 1880.
8.
W.T. Tutte. Non-Hamiltonian Planar Maps // Graph Theory and Computing,
ed. R. Read. Academic Press, New York, 1972, pp. 295–301.
9.
W.T. Tutte. On Hamiltonian Circuit // J. London Math. Soc. 21 (1946)
98–101.
10.
N. Z. Shor, G. A. Donets. Algebraic Approach to
the Plane Graph Coloring. Naukova Dumka, 1982, English translation published by
Springer-Verlag, Berlin, 1985.
11.
I. Grossman. Gruppy i ikh grafy / Grossman, I., Magnus, V. – M.: Mir,
1971, - 238s.
12.
A.A. Zykov. Osnovy teorii grafov. / Zykov A.A. - M.: Nauka, 1987, -
384s.
13.
M.N. S. Swamy, K. Thulasiraman. Graphs,
networks, and algorithms. – J. Wiley & Sons, 1981.
14.
F. Harary. Graph Theory, Reading: Addison-Wesley. – 1969.
15.
S. Mac Lane. A combinatorial condition for planar graphs // Fund. Math.,
28. – 1937. – P. 22–32.
16.
T. Kavitha et. al. Cycle bases in graphs: characterization, algorithms,
complexity, and applications // Computer Science Review, 3 (2009), 199-243.
17.
E.M. Reingold, J. Nievergelt, N. Deo. Combinatorial
Algorithms: Theory and Practice. Englewood Cliffs: Prentice-Hall, 1977.
18.
V.G. Vizing. On an estimate of the chromatic class of a p-graph //
Diskret. Analiz., 3: 25–30.
19.
V.G. Vizing. Critical graphs with given chromatic class // Metody
Diskret. Analiz., 5: 9–17.
20.
S.V. Kurapov, M.V. Davidovsky. Raskraska
ploskikh grafov. Teoriia, metody, algoritmy. LAP LAMBERT Academic Publishing,
2015, 142 c. IBSN 3659811246