Введение

Методы численного моделирования находят все большее применение в современных исследованиях гидрофизических процессов, включая турбулентные течения. Существует два основных подхода к моделированию турбулентных пульсаций: непосредственное воспроизведение пространственно временных флуктуаций течений на основе разрешающих методов (англ. SRS – Scale Resolve Simulation) [1] и приближенное моделирование этих же флуктуаций на основе корреляционных теорий и решений усредненных по Рейнольдсу уравнений Навье-Стокса (англ. RANS - Reynolds-Averaged Navier-Stokes) [2]. В рамках первого подхода могут быть использованы различные модели турбулентности DNS (Direct Numerical Simulation), LES (Large Eddy Simulation), ZLES (Zonal Large Eddy Simulation), WMLES (Wall-modeled Large Eddy Simulation), DES (Detached Eddy Simulation), SAS (Scale Adaptive Simulation) [3]. Часто для преодоления сложностей использования SRS методов, связанных с трудоемкостью вычислений вблизи границ твердых тел, используют гибридные методы. Например, методы, основывающиеся на совмещении RANS и LES подходов. Классическим примером такой гибридизации является DES модель турбулентности [4]-[6].

Расчеты различными численными схемами демонстрируют, что ведущую роль в формировании гидродинамического течения играют процессы взаимодействия турбулентных вихрей и пограничного слоя над твердыми границами. Численные модели должны точно воспроизводить нестационарные процессы отрыва и присоединения пограничного слоя. Течения с подобной сложной структурой (содержащей области отрыва, вихревые структуры различного масштаба, а также пограничные слои) зачастую образуются за телами с плохо обтекаемыми формами (препятствия, выемки с резкими углами). В качестве классического примера здесь можно привести прямоугольное препятствие. Необходимо отметить, что именно для подобного типа течений возникают трудности с выбором численного метода, адекватно моделирующего данное течение, а также выбором типа и размера сетки, используемой для численного счета. При этом в процессе выбора количества ячеек сетки зачастую приходится искать компромисс между качеством воспроизведения картины течения и адекватным временем проведения счета. В связи с этим, в большинстве случаев для удовлетворительного описания характеристик течений требуется предварительная верификация используемых численных подходов на основе сопоставления со специально выполненными лабораторными экспериментами.

Наиболее репрезентативным является метод верификации численных расчетов на основе сравнения общих картин течений содержащих качественную (изображения) и количественную информацию (поля скорости). Проблему получения пространственной картины течений позволяют решить лазерно-оптические методы, основанные на визуализации течений. Наиболее современный среди них - метод анемометрии по изображениям частиц Particle Image Velocimetry (PIV). PIV метод основан на использовании лазерной подсветки для визуализации частиц-трассеров (добавленных в жидкость или газ для маркировки течения) и съемки получаемых изображений на цифровые видеокамеры [7], [8]. Преимуществом метода PIV по сравнению с традиционными контактными способами измерения является то, что он обеспечивает хорошее пространственное разрешение в больших областях и не вносит возмущений в поток.

Существует достаточно большое количество работ, посвященных чисто экспериментальным исследованиям обтекания тел различной формы (в том числе плохо обтекаемых), течений в полостях и вблизи твердых поверхностей, выполненных в широком диапазоне значений чисел Рейнольдса [9]-[13]. В них в основном используются различные модификации PIV-методов. Помимо экспериментальных исследований особенностей турбулентного обтекания тел различной геометрии, отдельно неоднократно выполнялось численное моделирование таких потоков при помощи DNS, LES и DES моделей [5], [14-20]. Следует отметить, что параметры координатных сеток, общие времена измерений (расчетов) и их шаг зачастую сильно отличаются в экспериментальных и численных исследованиях. Это затрудняет сравнение результатов, полученных в разных работах. К настоящему времени существует очень небольшое количество работ, в которых одновременно с численными расчетами специально выполнялся эксперимент для их верификации [21-23]. Так, в работе [21] проводилось численное моделирование обтекания прямоугольного препятствия, с контролем расчетов при помощи метода PIV, однако данные результаты были получены для потоков c низкими значениями чисел Рейнольдса 269 – 475, когда потоки были ламинарными. В работах [22], [23] числа Рейнольдса достигали 10000, но исследования выполнялись для обтекания цилиндров.

Настоящая работа призвана восполнить обозначенные выше пробелы. В ней предлагается пошаговый комплексный подход верификации численных расчетов, проводимых различными схемами на основе сопоставления с результатами лабораторного эксперимента. Первая часть статьи посвящена описанию методики проведения экспериментов и использованию PIV-методов для качественной визуализации картины течения и количественных оценок (среднее поле скорости). Во второй части описаны численные методы и особенности их использования для моделирования исследуемого течения. При этом рассматривается несколько схем и выбирается наилучшая с точки зрения сопоставления с результатами эксперимента.

2. Описание эксперимента и проводимых измерений.

Эксперименты проводились на замкнутой аэродинамической трубе ИПФ РАН. Следуя классической компоновке на ней перед рабочим участком расположена расширяюще-сужающая секция, в которой расположен набор сеток и хонейкомбов. Рабочий участок представляет собой прямоугольную секцию с квадратным поперечным сечением со стороной 320 мм и длиной рабочего участка 1100 мм. Характерной особенностью стенда являются низкий уровень интенсивности турбулентности на входе рабочего участка ~1%. На трубе предусмотрена плавная регулировка скорости воздушного потока на входе в рабочий участок от 0 до 17 м/с.

В качестве объекта обтекания было выбрано прямоугольное препятствие. Размеры составляют 497×315×47 мм. Поперечный размер практически равен ширине рабочего участка, что обеспечивает двумерный характер течения в трубе.

Все эксперименты проводились при одной скорости воздушного потока – 8 м/с. Число Рейнольдса, рассчитанное для выбранного модельного объекта при выбранной скорости потока, с учетом кинематической вязкости воздуха 1.5е-5м2/с составляет ~5e4.

Схема расположения объекта экспериментов, показана на Рис. 1. Для формирования плоскопараллельного потока перед препятствием, оно было помещено на специальную поверхность с хорошо обтекаемой передней кромкой.

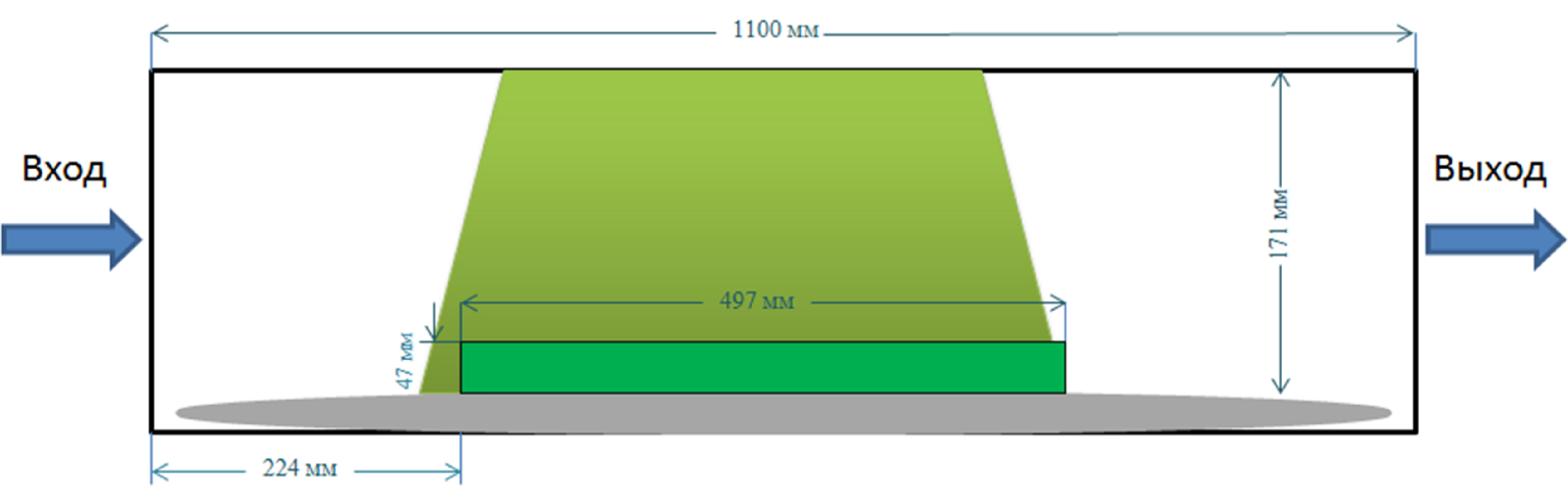
Рис. 1 – Схема расположения препятствия в канале на подстилающей поверхности (столике) с хорошо обтекаемыми передней и задней кромками со схемой подсветки для проведения измерений общей картины обтекания.

2.1. Измерения общих картин и полей скорости течений с помощью методов основанных на визуализации.

Общая схема проведения измерений аналогична работе [24]. Расположение приборов относительно рабочей секции продемонстрировано на Рис. 2. Для визуализации течения использовались твердые микрочастицы полиамида (10 мкм). Инжекция в поток не влияла на течение в рабочей секции и осуществлялась с помощью специально разработанного устройства [25], расположенного перед расширяющее-сужающей секцией. Движение частиц в плоскости вдоль канала подсвечивалось с помощью вертикального лазерного ножа (источник твердотельный лазер видимого диапазона (532 нм, 1.5 Вт)). Ширина лазерного ножа регулировалась с помощью системы цилиндрических линз. Вид сбоку снимался на высокоскоростную камеру NAC HX-3 Memrecam.

Рис. 2 – Общая схема рабочей части аэродинамической трубы с установленным препятствием оборудованием для проведения PIV-измерений.

 

Вначале были получены видеоизображения качественной картины всего течения. Для этого необходимо было реализовать максимальный размер снимаемой области, захватив в кадр весь объект. Общая схема расположения плоскости наблюдения (подсветки) в этом случае изображена на Рис. 1. Результат визуализации представлен на Рис. 3.

Кадры видеоизображений (см. Рис. 3) продемонстрировали наличие подпорного вихря, зоны экранирования (до 1/3 длины объекта) и сложную динамику образующихся за ней вихрей разного масштаба. При течении воздуха происходит срыв вихревой пелены с передней кромки объекта. Сносимая вниз по течению основным потоком вихревая пелена формирует застойную зону и вследствие неустойчивости распадается на крупные вихри. Ниже по потоку эти вихри распадаются под действием инерционных сил на хаотичные мелкомасштабные структуры, а поток снова прижимается к поверхности объекта, замыкая застойную зону в передней части тела.

  

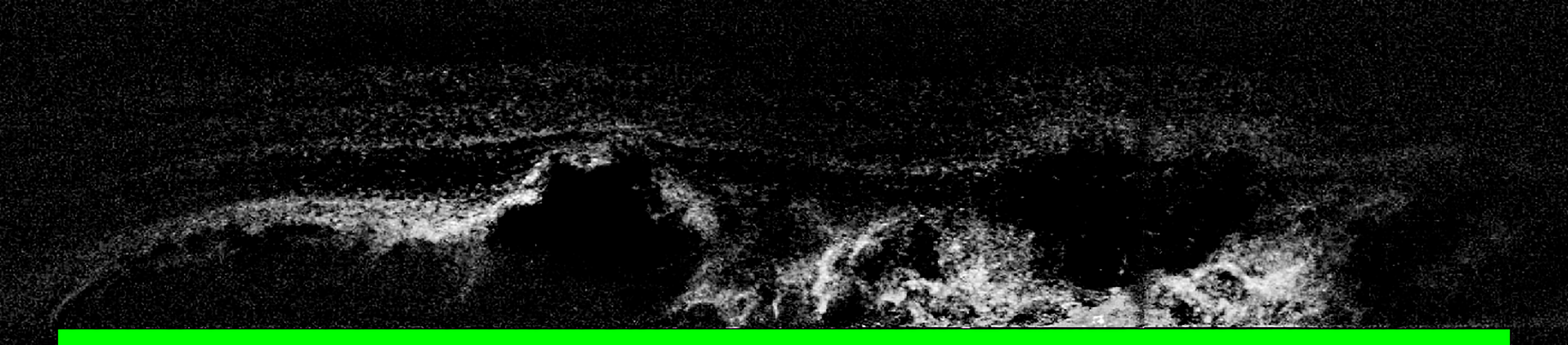
(а)                                                                                                                        (б)

Рис. 3 – (а) пример мгновенной картины качественной визуализации течения (размер 2560×472 пикс, разрешение 0.25 пикс/мм, скорость съемки 2000 кадров/сек, время выдержки одного кадра 500 мкс); (б) пример качественной визуализации подпорного вихря, образующегося перед передним уступом препятствия (размер – 384×944 пикс, разрешение – 0.166 пикс/мм, время выдержки одного кадра 1.25 мс).

 

Для получения количественной картины обтекания было решено применить классическую для PIV-метода кросскорреляционную обработку изображения. Однако пространственного разрешения полученных картин явно не хватало для определения полей скорости на малых, сравнимых с размерами наблюдавшихся вихрей, масштабах. Поэтому размер области съемки и соответственно области засветки был уменьшен, а чтобы получить полное среднее поле скорости, было принято решение выполнить измерения в нескольких сечениях. Девять сечений расположены равномерно, первое над передним краем, последнее над задним, расстояние между областями составляло 62.5 мм (см. Рис. 4). Они полностью перекрывают область наблюдения для предыдущего случая. При этом попарное перекрытие областей в горизонтальном направлении на верхней границе объекта составляло 30 мм. Разрешение уменьшено почти в 1.5 раза и составило 0.166 пикc/мм. Скорость съемки 8000 кадров/сек. Время выдержки одного кадра 20 мкс. Последовательно в каждом из сечений были измерены средние поля скорости. Перед проведением кросскорреляционной обработки для каждой реализации вычитался фон. За фоновое изображение принималось изображение, на котором интенсивность изображения пикселей равна минимальному значению в выборке (реализации). Это позволило убрать с изображений засветы от области попадания ножа на поверхность, что особенно важно для съемки над краем препятствия, где от крыла возникал интенсивный блик. При обработке видеоизображений использовался двушаговый адаптивный алгоритм поиска смещения при кросскорреляционном анализе, когда размер окна поиска уменьшался с первоначальных 64×64 пикс до 32×32 пикс (по аналогии с исследованием [26]). Перекрытие окон составляло 50%. Таким образом, конечный шаг сетки при определении поля скорости составлял около 2.5 мм.

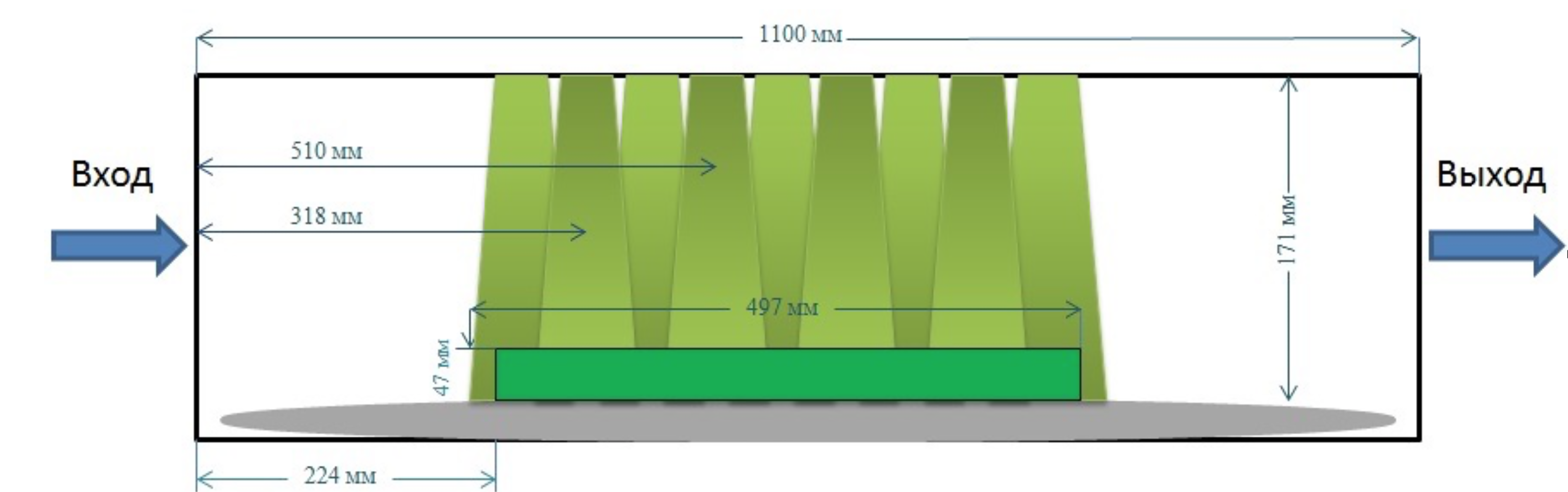
Рис.4 – Схема подсветки секторами для нахождения общего поля скорости.

 

Пример среднего поля скорости, полученного в одном сечении (первом) на передней кромке препятствия, показан на Рис. 5. Полученные поля скорости во всех сечениях сшивались (усреднялись в областях перекрытия) для получения полного среднего поля скорости.

Рис. 5 – Изображение передней кромки тела с наложенным полем скорости воздушного потока, измеренного PIV-методом (размер – 384×944 пикс, разрешение – 0.166 пикс/мм).

 

Результат измерения среднего составного поля скорости представлен на Рис. 6. В результате обработки получены данные об амплитудах и направлениях скорости в потоке. Несмотря на наличие в среднем составном поле скорости пустых областей (низкая плотность засева приводила к ошибкам), на нем, в отличие от мгновенных изображений (см. Рис. 3), можно четко выделить границы области экранирования потока. Максимальные ошибки PIV-измерений в точке составляют 15 см/с, а средние для значений на профиле скорости (рис. 8) около 2 см/с.

 

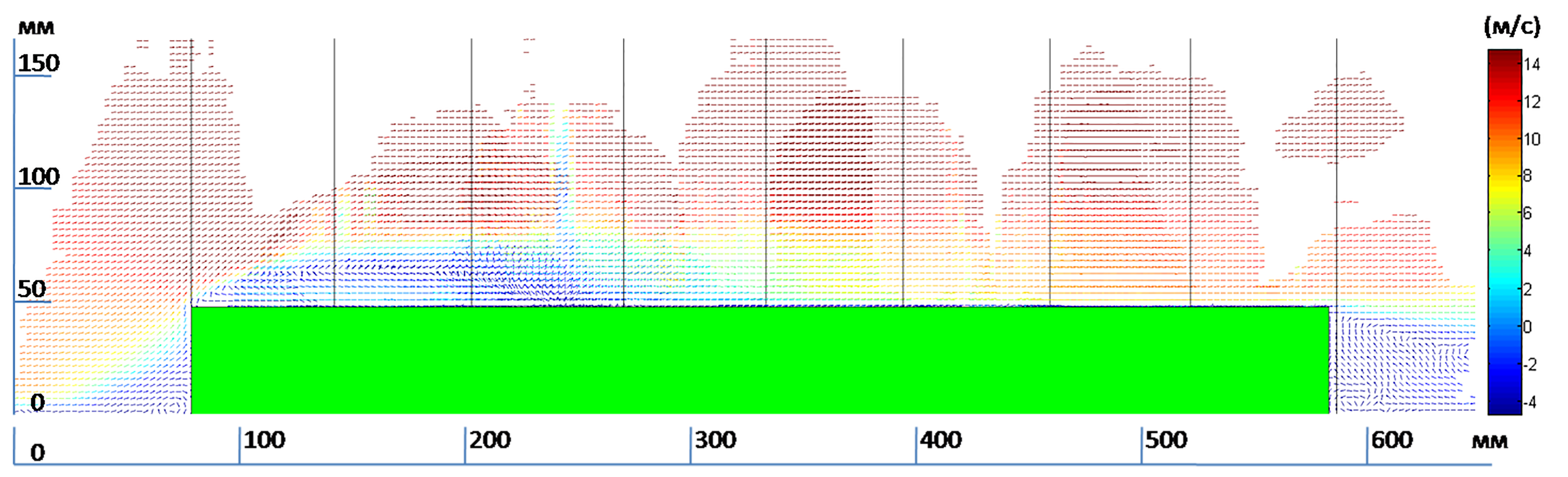
Рис. 6 – Среднее векторное поле горизонтальной компоненты скорости (составное) по результатам измерений PIV-методами. Цветом показана амплитуда скорости.

3. Численное моделирование гидродинамических неоднородностей при обтекании тел

Целями исследований, описанных в данном разделе, являлась разработка оптимальной численной модели для воспроизведения наблюдаемой в эксперименте картины течений.

Корректное моделирование локально нестационарных течений исследуемого типа в современной вычислительной гидродинамике достигается путем использования специальных гибридных моделей турбулентности, одной из которых является DES модель. Смысл ее заключается в соединении вихреразрешающих моделей и методов усреднения пульсаций таким образом, что течение на удалении от обтекаемой твердой стенки моделируется LES моделью, а в области пограничного слоя (включая область с сильной анизотропией сетки) активируется RANS модель.

В рамках данной модели осуществляется интегрирование уравнений Навье-Стокса совместно с уравнением несжимаемости и уравнениями переноса кинетической энергии турбулентности k и ее диссипации ε относительно шести неизвестных величин: трех компонент скорости, давления, а так же величин k и ε.

Исходя из того, что DES модель может быть использована только при решении задачи в трехмерной постановке в ПО ANSYS СFX была построена трехмерная модель области обтекания, геометрия которой получена вытяжкой двумерной сетки вдоль поперечной оси.

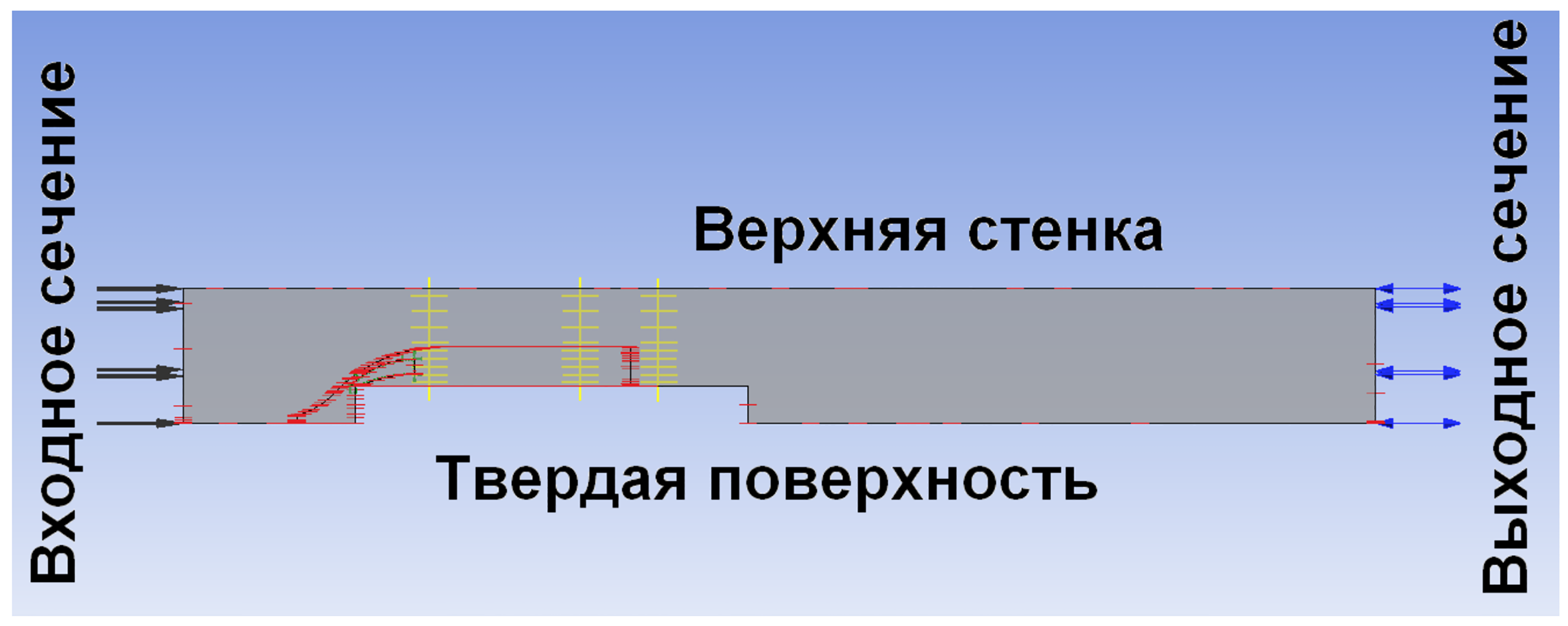
Рис. 7 - Вид сбоку на геометрию расчетной области

Для показанной на Рис. 7 модели были сформулированы следующие граничные условия: для торцевых поверхностей - условие симметрии; на входном сечении была задана нормальная скорость потока 8 м/c, на выходном сечении - нулевое давление; верхняя и нижняя стенки аэродинамической трубы - поверхности без прилипания, поверхность препятствия - поверхность с прилипанием.

Вычисления осуществлялись с применением центрально-разностной пространственной схемы и неявного алгоритма временной дискретизации второго порядка. Временной шаг интегрирования был выбран равным величине 0,1 мс. Это позволило обеспечить хорошую сходимость расчетов (не более трех итераций временной шаг).

Изначально исходная трехмерная модель не учитывала вязкого прилипания жидкости к нижней поверхности трубы перед уступом. Это было сделано для упрощения построения автоматической расчетной сетки. Однако результаты расчетов продемонстрировали, что рассчитанные количественные характеристики вихреобразования при таком упрощении, значительно отличаются от экспериментальных вблизи области формирования вихревой пелены (граница области экранирования). Анализ результатов показал, что причина различий заключается в неправильном формировании положения вихревой пелены (границе области экранирования). Такой вывод можно сделать, исходя из графиков усредненного профиля скорости в первом сечении (Рис. 8 а). На Рис. 8 красная кривая характеризует экспериментальное распределение скорости, а синяя кривая соответствует расчету исходной модели. Причина такого поведения усредненного течения заключалась в неправильном моделировании потока непосредственно перед уступом из-за пренебрежения вязким прилипанием к нижней стенке трубы.

 

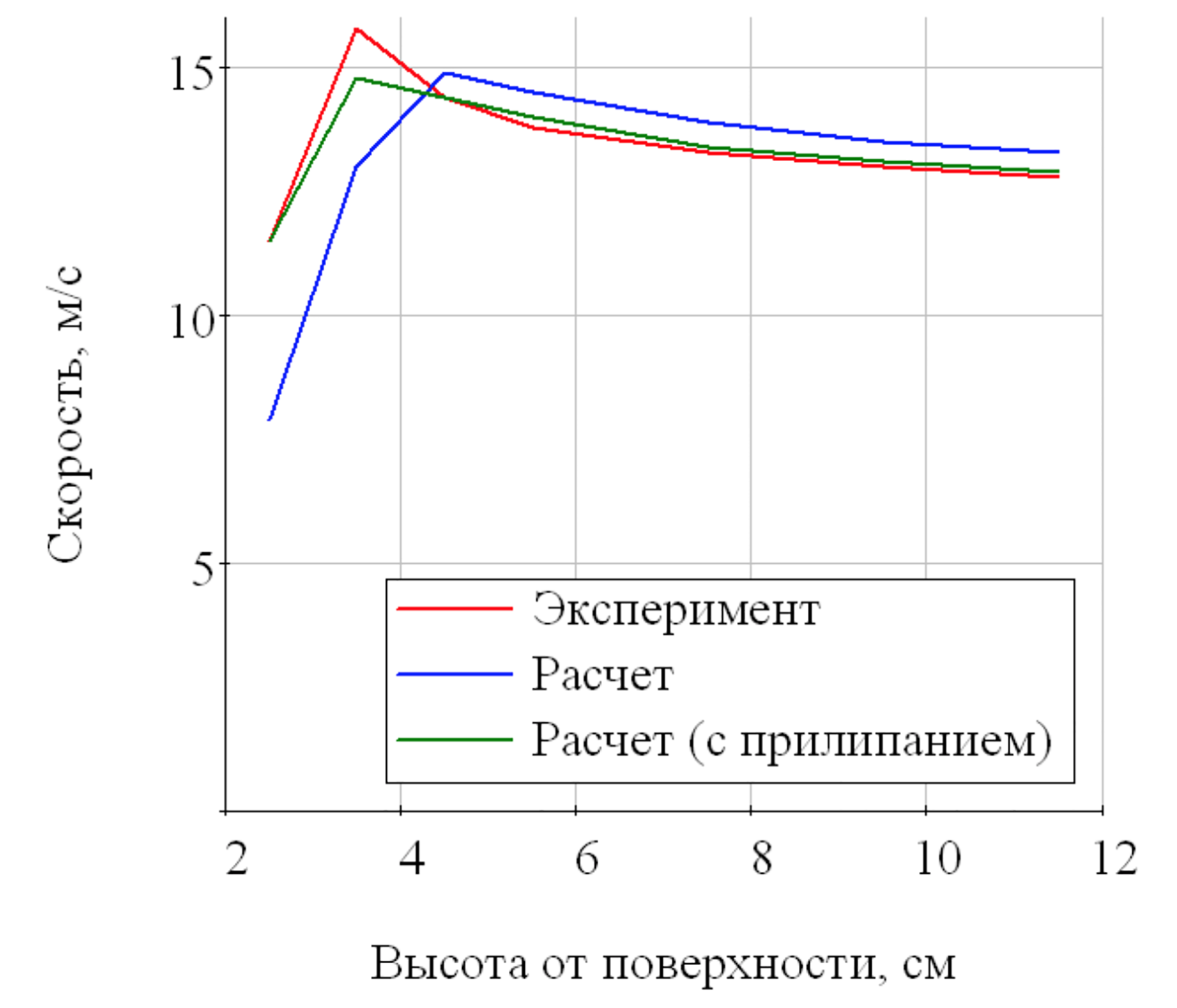
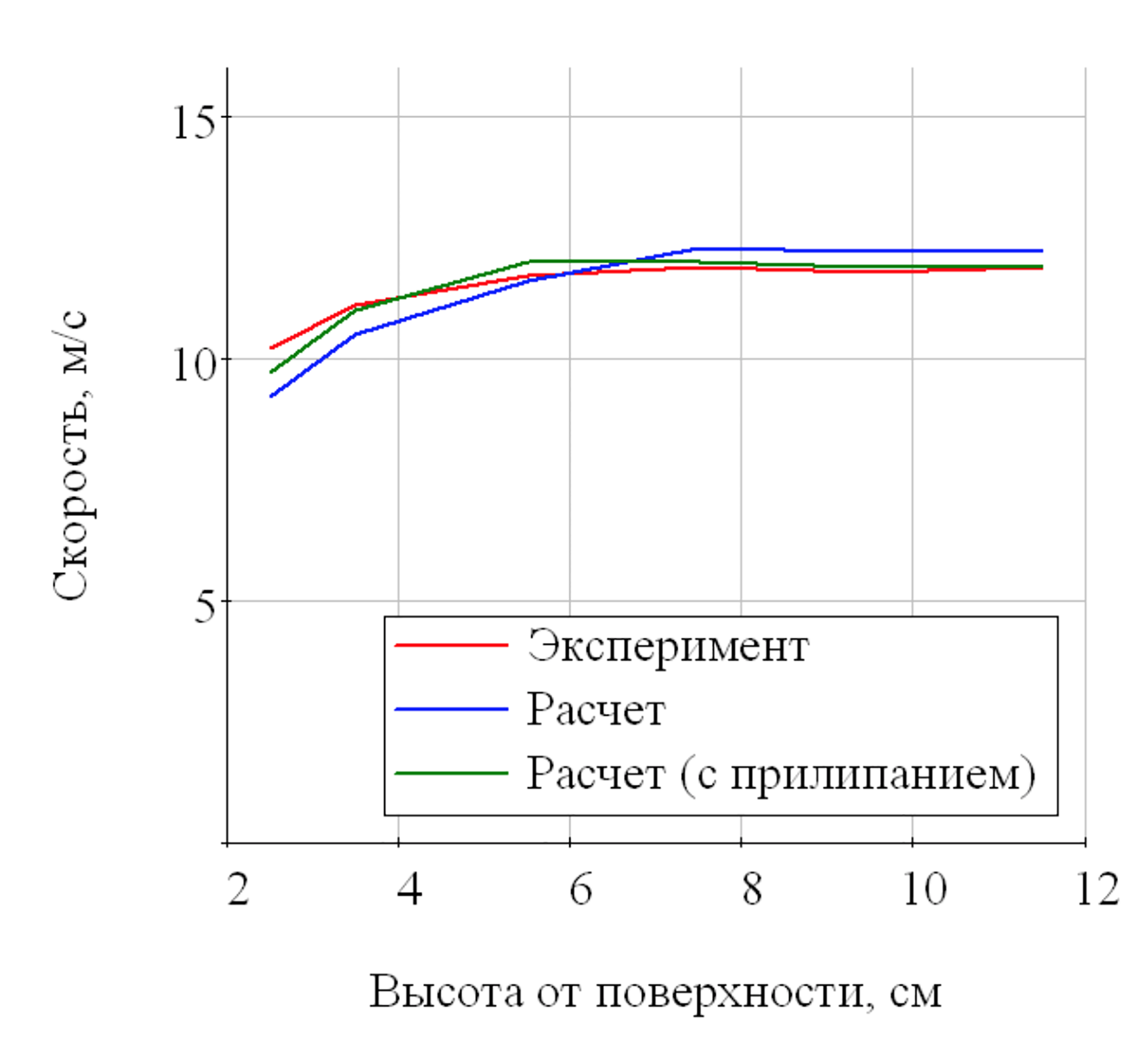
(а)                                                                                                        (б)

Рис. 8 – усредненные во времени профили скорости, построенные по значениям скорости в контрольных точках на первой контрольной линии (а) и второй контрольной линии (б).

 

Из Рис. 8 видно, что учет прилипания (зеленая кривая) приводит к значительному снижению положения пелены, и ее приближению в расчете к экспериментальному положению.

Таким образом, можно сделать вывод о том, что моделирование динамики пограничного слоя, не только в области интенсивного вихреобразования, но и вверх по потоку, является важной частью общего процесса моделирования высокочастотных вихревых процессов.

Схематичное изображение сетки итоговой численной модели (вблизи передней границы), учитывающей формирование пограничного слоя перед уступом, представлена на Рис. 9. Данная модель состоит из 6 млн. ячеек, сгущающихся вблизи верхней передней кромки.

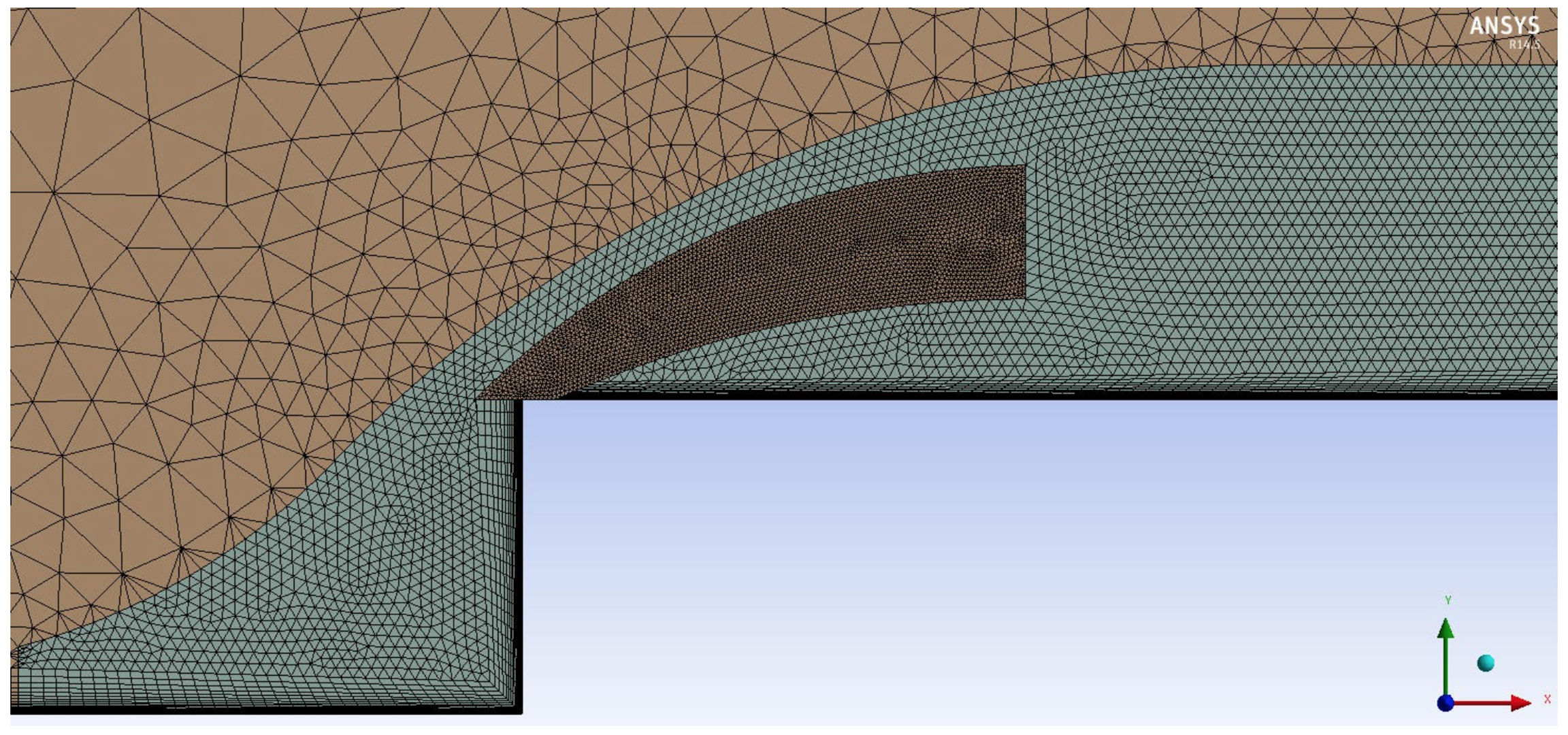
Рис. 9 – Структура ячеек итоговой трехмерной численной модели (на переднем крае).

 

Использованием более густой сетки вблизи верхней передней кромки выполнено для того, чтобы обеспечить корректное моделирование высоких градиентов скорости в сходящей с кромки вихревой пелене и как следствие правильно описать процессы потери ее устойчивости. Как показали расчеты, эволюция вихреобразования в данном случае выглядит следующим образом. Вблизи обтекаемой передней кромки (Рис. 10, 11) вихревая пелена является тонкой квазидвумерной структурой, которая быстро теряет устойчивость ("разваливается" на отдельные трубчатые вихри) при удалении вниз по потоку. Затем данные дискретные вихри уже вследствие неоднородного поля скоростей теряют устойчивость в направлении поперек потока и сворачиваются в характерные подковообразные структуры. 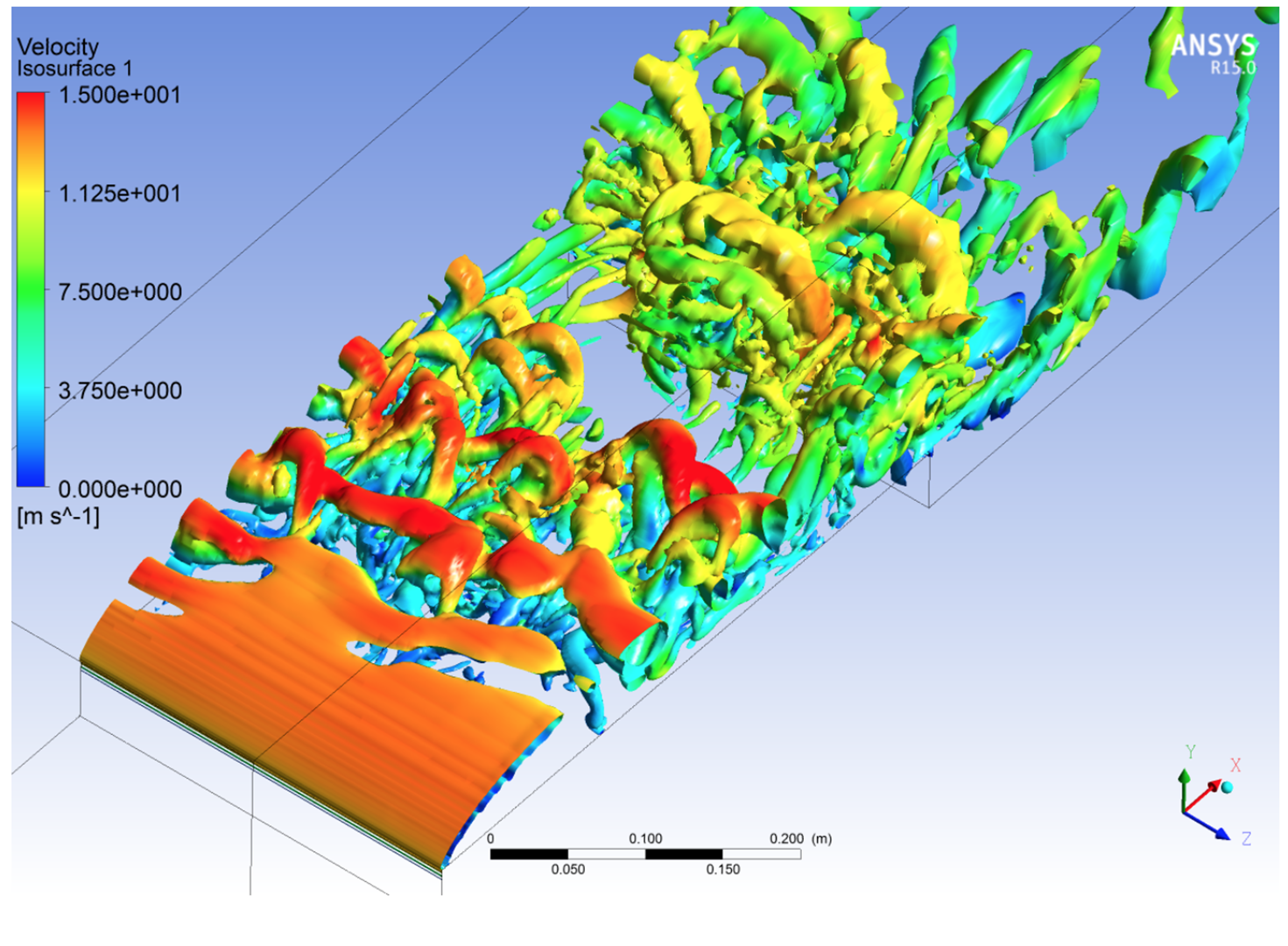Эти изначально весьма упорядоченные подковообразные вихри переносятся вниз по потоку, эволюционируя в хаотичные структуры разного пространственного масштаба. Общая картина течения, полученная в численном эксперименте, весьма близка к наблюдаемой в эксперименте.

 

Рис. 10 – Структура турбулентного потока при обтекании модельного препятствия (изолинии скорости).

 

(а)

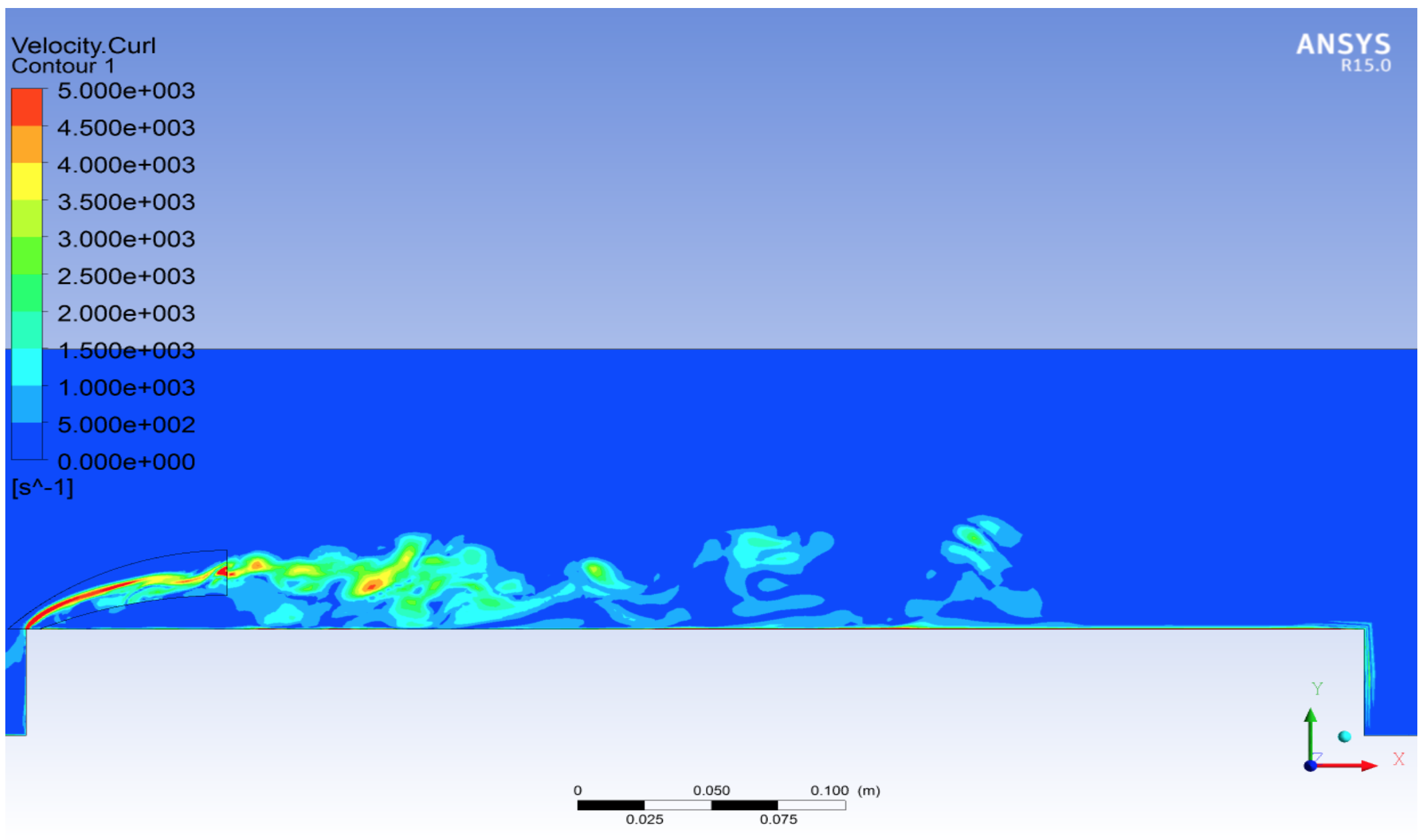
(б)

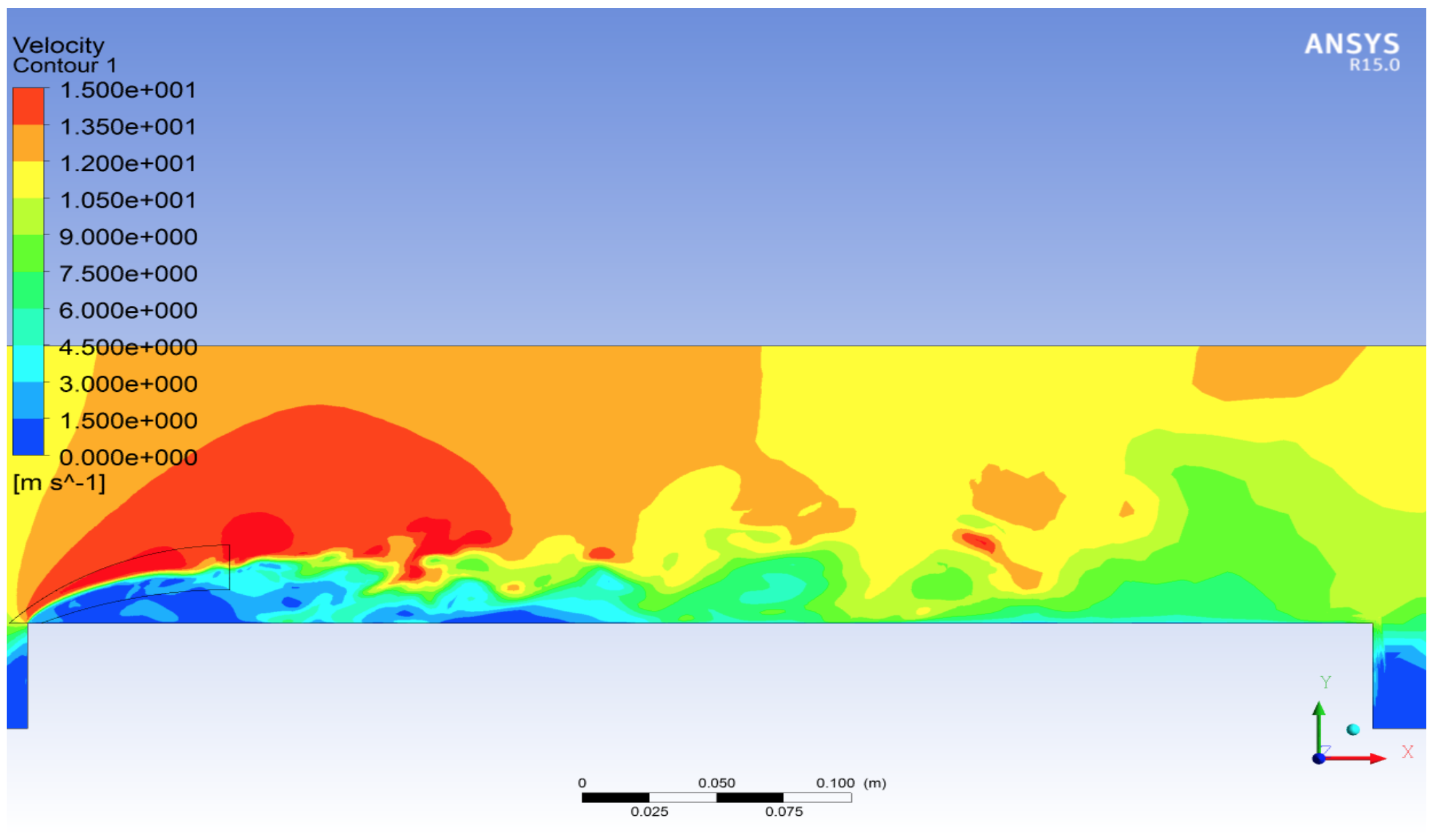
Рис.11 – Распределение модуля скорости (а) и интенсивность завихренности (б) в центральном продольном сечении модели (мгновенные картины).

Размеры призматических ячеек в измельченной области в данном случае составили 0.7 мм, за областью 2.5 мм (аналогично шагу координатной сетки в эксперименте для последующего сравнения). Время расчета на сервере производительностью 0.3 ТФпс итоговой численной модели, с сеткой, показанной на Рис. 9, с учетом необходимости накопления достаточной статистической информации (длина расчетной реализации 4 с) при временном шаге 0.1 мс (частота дискретизации 10 кГц), составило около месяца. Были выполнены попытки уменьшить это время, за счет уменьшения количества ячеек. Однако, как показали дополнительные расчеты, отказ от более мелкой ячейки вблизи передней кромки приводит к увеличению расстояния от кромки до места разрушения вихревой пелены (рис. 12 а) с последующим укрупнением вихревых структур. Если же при этом еще увеличить размер ячейки за областью до 3 мм, то структура течения становится квазистационарной (рис. 12 б).

 

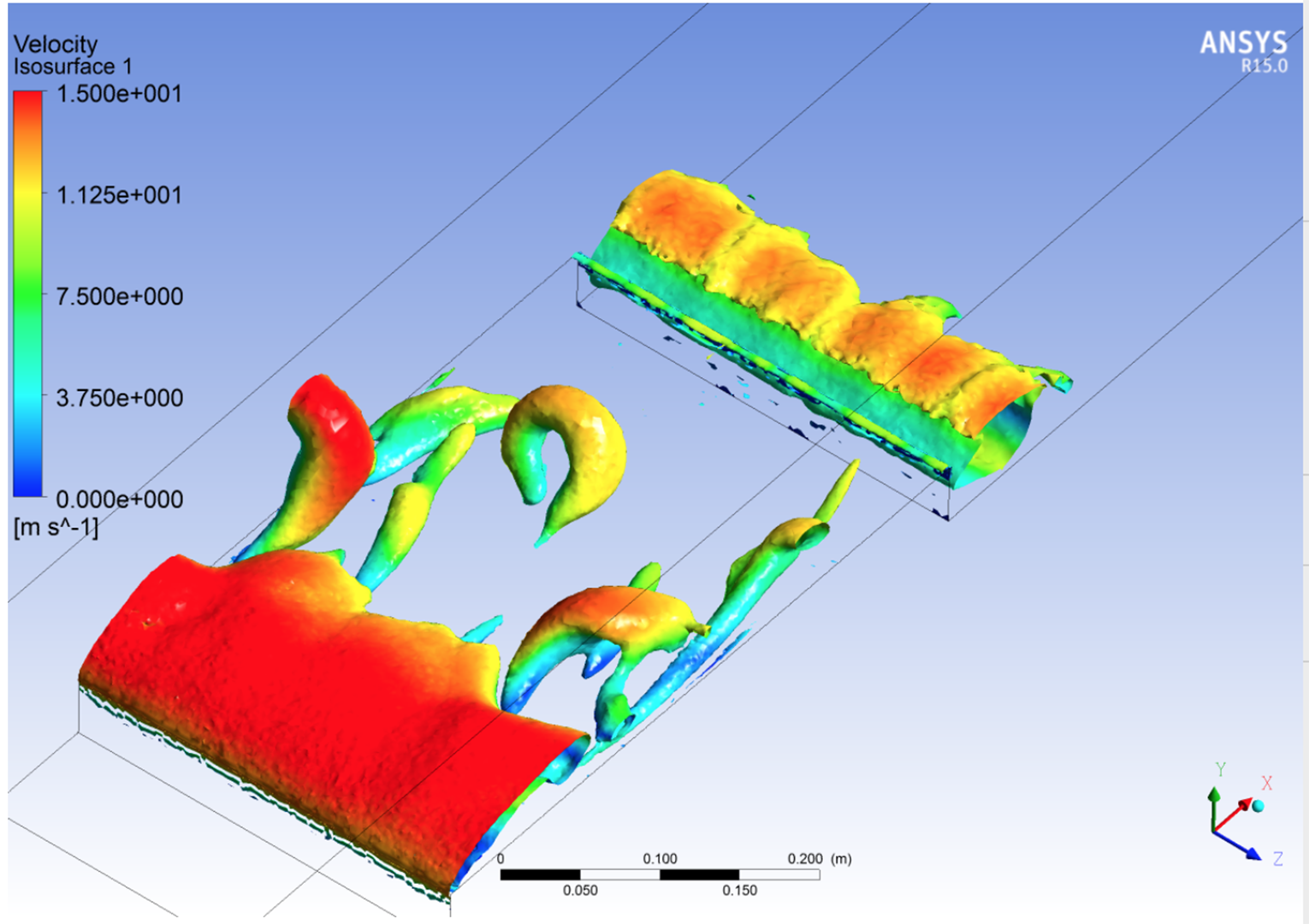
(а)                                                                                                                        (б)

Рис. 12 – Искажение картины вихреобразования при использовании грубых сеток с размером ячеек 2.5мм (а) и 3мм (б).

Заключение

В ходе демонстрационных экспериментов по исследованию структуры воздушного потока над прямоугольным препятствием реализован подход, в результате которого с помощью метода PIV исследуется общая картина течения воздуха над препятствием и его флуктуационные характеристики. В результате исследований, проведенных на базе метода PIV, было установлено, что воздушный поток может быть подразделен на области с характерными качественными особенностями: область начала формирования отрыва, область максимального вертикального масштаба отрыва и область присоединения потока. Исследования показали, что огромную роль в формировании картины гидродинамического течения играют процессы взаимодействия турбулентных вихрей и пограничного слоя. Результаты верификации, полученные в настоящей работе, показали, что исследуемые физические процессы обтекания модельных объектов могут быть смоделированы в трехмерной постановке наилучшим образом с использованием DES модели турбулентности с применением схемы центрального численного дифференцирования.

Работа по численному моделированию выполнены при поддержке проекта Российского Фонда Фундаментальных исследований №18-48-520023 р_а, экспериментальные исследования выполнены при поддержке проекта Российского Научного Фонда №18-19-00473.

Список литературы

[1] Menter F.R. Best Practice: Scale-Resolving Simulations in ANSYS CFD, ANSYS Germany GmbH, 2012. 70 p.

[2] Флетчер К. Вычислительные методы в динамике жидкостей. М. Мир, 1991. в 2-х т.

[3] Celik I. B. RANS/LES/DES/DNS: The Future Prospects of Turbulence Modeling  // J. Fluids Eng. 2003. V. 127(5), P. 829-830.

[4] Spalart P. R. Strategies for turbulence modelling and simulations // International Journal of Heat and Fluid Flow. 2000. V. 21, No. 3. P. 252–263.

[5] Spalart P. R., Deck S., Shur M. L., Squires K. D., Strelets M. Kh., Travin A. A new version of detached-eddy simulation, resistant to ambiguous grid densities // Theoretical Computational Fluid Dynamics. 2006. V. 20. P. 181–195.

[6] Travin A., Shur M., Strelets M., Spalart P. Detached-Eddy Simulations Past a Circular Cylinder // Flow, Turbulence and Combustion. 1999. V. 63. No. 1-4. P. 293–313

[7] Adrian R.J. Particle-imaging techniques for experimental fluid mechanics // Annu. Rev. FluidMech. 1991.V. 23. P. 261– 304

[8] Adrian R.J. Twenty years of particle image velocimetry // Experiments in Fluids. 2005.V. 39. P.159–69

[9] Shah M. K. and Tachie M. F. PIV investigation of flow over a transverse square rib in pressure gradients // Journal of Turbulence. V. 10. P. 1–22, 2009.

[10] Liu Y. Z., Ke F., Sung H. J. Unsteady separated and reattaching turbulent flow over a two-dimensional square rib // Journal of Fluids and Structures. 2008. V. 24. No. 3.  P. 366–381.

[11] Sherry M., Jacono D. L., Sheridan J. An experimental investigation of the recirculation zone formed downstream of a forward facing step // Journal of Wind Engineering & Industrial Aerodynamics. 2010. V. 98 No. 12. P. 888-894.

[12] Chun S., Liu Y. Z., Sung H. J. Wall pressure fluctuations of a turbulent separated and reattaching flow affected by an unsteady wake // Experiments in Fluids. 2004. V. 37. P. 531–546.

[13] Panigrahi P. K., Schroeder A., Kompenhans J. Turbulent structures and budgets behind permeable ribs // Experimental Thermal and Fluid Science. 2008. V. 32. No. 4. P. 1011–1033.

[14] Shur M.L., Spalart P.R., Strelets M.K. and Travin A.K. A hybrid RANS-LES approach with delayed-DES and wall-modeled LES capabilities // International Journal of Heat and Fluid Flow. 2008.V. 29. P. 1638-1649.

[15] Egorov Y., Menter F.R. and Cokljat D. Scale-Adaptive Simulation Method for Unsteady Flow Predictions. Part 2: Application to Aerodynamic Flows // Journal Flow Turbulence and Combustion.  2010. V. 85, No. 1. P. 139-165.

[16] Vogiatzis I. I., Denizopoulou A. C., Ntinas G. K., Fragos V. P. Simulation Analysis of Air Flow and Turbulence Statistics in a Rib Grid Roughened Duct // The Scientific World Journal. 2014. V. 2014. P. 1-10.

[17] Hwang R. R., Chow Y. C, Peng Y. F. Numerical study of turbulent flow over two-dimensional surface-mounted ribs in a channel // International Journal for Numerical Methods in Fluids. 1999.V. 31. No. 4. P. 767–785.

[18] Panigrahi P. K., Acharya S. Excited turbulent flow behind a square rib // Journal of Fluids and Structures. 2005. V. 20. No. 2. P. 235–253.

[19] Breuer M.,  Jovicic N.,  Mazev K. Comparison of  DES, RANS and LES for the separated flow around a plate at high incidence // International Journal for Numerical Methods in Fluids. 2003. V. 41. P. 357-388.

[20] Franke J., Frank W. Large eddy simulation of the flow past a circular cylinder at ReD=3900 // J. Wind. Eng. Ind. Aerod. 2002. V. 90. P. 1191-1206.

[21] Barbosa-Saldaña J.G., Morales-Contreras O.A., Jiménez-Bernal J.A., Gutiérrez-Torres C.C., Moreno Pacheco L.A. Numerical and experimental results for flow through a forward facing step channel //  IJRRAS. 2013. V. 15, Issue 2, P. 177-189.

[22] Dong B.S., Karniadakis G. E., Ekmekci A., Rockwell D. A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake // J. Fluid Mech. 2006. V. 569. P. 185–207.

[23] Parnaudeau P., Carlier J., Heitz D., Lamballais E. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900 // Physics of Fluids. 2008. V. 20. 085101. P. 1-14.

[24] Сергеев Д.А. Измерительный комплекс для исследования течений жидкости методом Particle Image Velocimetry (PIV) на основе твердотельного лазера с диодной накачкой // Приборы и техника эксперимента. 2009. № 3. С.138-144.

[25] Устройство для ввода частиц в потоки газа в аэродинамических каналах: пат. 134542 Рос. Федерация / Сергеев Д.А.; заявитель и патентообладатель Институт прикладной физики РАН.  –  № 2009126001/13; заявл. 05.06.13; опубл. 20.11.2013.

[26] Troitskaya Yu., Sergeev D., Ermakova O., Balandina G. Statistical parameters of the air turbulent boundary layer over steep water waves measured by the PIV-technique// Journal Phys. Oceanogr. 2011. V. 41. P.1421-1454.

[27] Снегирёв А.Ю. Выскопроизводительные вычисления в технической физике. Численное моделирование турбулентных течений. Санкт-Петербург, Издательство Политехнического университета, 2009. 143с.

---

Visualization tools for the numerical modeling in the reference experiment on the flow over a rectangular obstacle

Authors: D.A. Sergeev¹, O.S. Ermakova², A.S. Suvorov³, Y.I. Troitskaya⁴, A.A. Kandaurov⁵, A.I. Konkov⁶

Institute of Applied Physics RAS, Nizhny Novgorod

¹ ORCID: 0000-0003-4910-3935

² ORCID: 0000-0003-0687-4000, ermakova@hydro.appl.sci-nnov.ru

³ ORCID: 0000-0003-2277-7497

⁴ ORCID: 0000-0002-3818-9211

⁵ ORCID: 0000-0002-0014-8887

⁶ ORCID: 0000-0001-8822-8277

 

Abstract

A number of demonstration experiments on the study of the structure of the air flow over a rectangular obstacle, based on a combined approach using PIV method to restore the overall picture of an air flow over an obstacle, and its verification on the basis of numerical calculations. As a result of research carried out on the basis of PIV method, it was found that the air flow can be conditionally divided into regions, reflecting qualitatively its typical features: the origin of the formation of the separation, the separation region of maximum vertical scale and flow joining region. A step by step verification of the results of numerical simulations with the ANSYS FLUENT application based on the results of experimental measurements of the spectral characteristics of turbulent fluctuations were carried out. A selection of the optimal numerical scheme for reproducing the experimentally observed flow patterns included calculations based on SAS (Scale Adaptive Simulation) turbulence model and DES turbulence model, with the central scheme of numerical differentiation. Using SAS turbulence model has led to a distortion of the qualitative picture of flow, namely to the emergence of a false separation of the boundary layer, the characteristic frequencies in the spectrum of velocity fluctuations were much too high. Presumably the correct calculations made in the framework of SAS turbulence model are impossible due to the use of a highly anisotropic (elongated in the direction perpendicular to the main flow) computational grid. Comparison of numerical calculations with experimental results have shown that the physical process of the flow over an obstacle can be optimally modeled in a three-dimensional formulation using DES turbulence model with the scheme of central numerical differentiation.

 

Keywords: turbulence, air boundary layer, flow separation, turbulent flow, numerical simulation of turbulence.

References

               

[1] Menter F.R. Best Practice: Scale-Resolving Simulations in ANSYS CFD, ANSYS Germany GmbH, 2012. 70 p.

[2] Fletcher, C. Computational Techniques for Fluid Dynamics // Springer-Verlag Berlin Heidelberg, 1991, 494 p.

[3] Celik I. B. RANS/LES/DES/DNS: The Future Prospects of Turbulence Modeling  // J. Fluids Eng. 2003. V. 127(5), P. 829-830.

[4] Spalart P. R. Strategies for turbulence modelling and simulations // International Journal of Heat and Fluid Flow. 2000. V. 21, No. 3. P. 252–263.

[5] Spalart P. R., Deck S., Shur M. L., Squires K. D., Strelets M. Kh., Travin A. A new version of detached-eddy simulation, resistant to ambiguous grid densities // Theoretical Computational Fluid Dynamics. 2006. V. 20. P. 181–195.

[6] Travin A., Shur M., Strelets M., Spalart P. Detached-Eddy Simulations Past a Circular Cylinder // Flow, Turbulence and Combustion. 1999. V. 63. No. 1-4. P. 293–313

[7] Adrian R.J. Particle-imaging techniques for experimental fluid mechanics // Annu. Rev. FluidMech. 1991.V. 23. P. 261– 304

[8] Adrian R.J. Twenty years of particle image velocimetry // Experiments in Fluids. 2005.V. 39. P.159–69

[9] Shah M. K. and Tachie M. F. PIV investigation of flow over a transverse square rib in pressure gradients // Journal of Turbulence. V. 10. P. 1–22, 2009.

[10] Liu Y. Z., Ke F., Sung H. J. Unsteady separated and reattaching turbulent flow over a two-dimensional square rib // Journal of Fluids and Structures. 2008. V. 24. No. 3.  P. 366–381.

[11] Sherry M., Jacono D. L., Sheridan J. An experimental investigation of the recirculation zone formed downstream of a forward facing step // Journal of Wind Engineering & Industrial Aerodynamics. 2010. V. 98 No. 12. P. 888-894.

[12] Chun S., Liu Y. Z., Sung H. J. Wall pressure fluctuations of a turbulent separated and reattaching flow affected by an unsteady wake // Experiments in Fluids. 2004. V. 37. P. 531–546.

[13] Panigrahi P. K., Schroeder A., Kompenhans J. Turbulent structures and budgets behind permeable ribs // Experimental Thermal and Fluid Science. 2008. V. 32. No. 4. P. 1011–1033.

[14] Shur M.L., Spalart P.R., Strelets M.K. and Travin A.K. A hybrid RANS-LES approach with delayed-DES and wall-modeled LES capabilities // International Journal of Heat and Fluid Flow. 2008.V. 29. P. 1638-1649.

[15] Egorov Y., Menter F.R. and Cokljat D. Scale-Adaptive Simulation Method for Unsteady Flow Predictions. Part 2: Application to Aerodynamic Flows // Journal Flow Turbulence and Combustion.  2010. V. 85, No. 1. P. 139-165.

[16] Vogiatzis I. I., Denizopoulou A. C., Ntinas G. K., Fragos V. P. Simulation Analysis of Air Flow and Turbulence Statistics in a Rib Grid Roughened Duct // The Scientific World Journal. 2014. V. 2014. P. 1-10.

[17] Hwang R. R., Chow Y. C, Peng Y. F. Numerical study of turbulent flow over two-dimensional surface-mounted ribs in a channel // International Journal for Numerical Methods in Fluids. 1999.V. 31. No. 4. P. 767–785.

[18] Panigrahi P. K., Acharya S. Excited turbulent flow behind a square rib // Journal of Fluids and Structures. 2005. V. 20. No. 2. P. 235–253.

[19] Breuer M.,  Jovicic N.,  Mazev K. Comparison of  DES, RANS and LES for the separated flow around a plate at high incidence // International Journal for Numerical Methods in Fluids. 2003. V. 41. P. 357-388.

[20] Franke J., Frank W. Large eddy simulation of the flow past a circular cylinder at ReD=3900 // J. Wind. Eng. Ind. Aerod. 2002. V. 90. P. 1191-1206.

[21] Barbosa-Saldaña J.G., Morales-Contreras O.A., Jiménez-Bernal J.A., Gutiérrez-Torres C.C., Moreno Pacheco L.A. Numerical and experimental results for flow through a forward facing step channel //  IJRRAS. 2013. V. 15, Issue 2, P. 177-189.

[22] Dong B.S., Karniadakis G. E., Ekmekci A., Rockwell D. A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake // J. Fluid Mech. 2006. V. 569. P. 185–207.

[23] Parnaudeau P., Carlier J., Heitz D., Lamballais E. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900 // Physics of Fluids. 2008. V. 20. 085101. P. 1-14.

[24] Sergeev D.A. A measuring system for studying liquid flows by the Particle Image Velocimetry method based on a diode-pumped solid-state laser // Instruments and Experimental Techniques. 2009. № 3. P.438-444.

[25] Device for gas flow particle injection in wind ducts: patent no. 134542, Russian Federation / Sergeev D.А.; the applicant and the patentee Institute of Applied Physics RAS  –  № 2009126001/13; stated. 05.06.13; publ. 20.11.2013.

[26] Troitskaya Yu., Sergeev D., Ermakova O., Balandina G. Statistical parameters of the air turbulent boundary layer over steep water waves measured by the PIV-technique// Journal Phys. Oceanogr. 2011. V. 41. P.1421-1454.

[27] Snegirev А. Computer-intensive simulations in technical physics. Modeling and simulations of turbulent flows St. Petersburg State Polytechnical University, 2009. ISBN: 978-5-7422-2317-7, 143 p.