КОНЦЕПЦИЯ И ОПЫТ РАЗРАБОТКИ ПРОГРАММЫ ОПЕРАТИВНОЙ ВИЗУАЛИЗАЦИИ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ ДИНАМИЧЕСКИХ СИСТЕМ «СИНУС-Д»

С.В. Ктитров

Национальный исследовательский ядерный университет «МИФИ», Москва

Оглавление

1. Введение

2. Выбор класса исследуемых систем

3. Задание уравнений и функций

4. Особенности реализации моделирования систем

5. Графическое представление результатов моделирования

6. Переносимость и многоплатформенность

7. Заключение

Список литературы

Аннотация

Описывается программа «СИНУС-Д», предназначенная для оперативной визуализации результатов численного моделирования нелинейных динамических систем. Программа ориентирована прежде всего на решение задач анализа и синтеза нелинейных дискретно-непрерывных систем автоматического управления, включая системы с запаздыванием, что определяет класс решаемых уравнений. Программа позволяет строить численные решения нелинейных дифференциальных и разностных уравнений с правыми частями произвольной структуры, которые задаются текстовыми строками. Имена переменных могут включать символы различных алфавитов, включая греческие, что приближает запись уравнений к принятой в предметной области. В программе реализованы многие типовые нелинейные элементы, включая двузначные нелинейности, а также случайные величины, экстраполятор, чистое запаздывание. Рассматриваются особенности использованных алгоритмов, в том числе построение интерпретатора правых частей и вычислительной подсистемы программы.

Подробно описывается графическая подсистема, позволяющая оперативно представить результаты моделирования. Среди множества её возможностей можно отметить точное определение координат, управление свойствами кривых и координатной сетки. Приводятся примеры её использования для визуализации и сравнительного анализа переходных процессов и фазовых портретов.

Рассматриваются возможности программы по гармоническому анализу процессов. С помощью программы можно исследовать точность представления сигнала частичной суммой ряда Фурье и вклад отдельных гармоник в формирование сигнала.

Концепция построения программы включает её компактность и возможность использования на различных программных платформах. Программа реализована для Microsoft Windows, Apple OS X и Linux, использует общий для всех платформ текстовый формат файлов и не требует предварительной установки.

Предлагается подход к созданию подобных программ, основанный на сочетании встроенного синтаксического анализатора уравнений, предварительно реализованного набора типовых нелинейных элементов и интуитивно понятного интерфейса.

Ключевые слова: численное решение, дифференциальные уравнения, разностные уравнения, моделирование, динамическая система, система с запаздыванием, нелинейность

1. Введение

Повышение требований к точности описания динамических систем приводит к необходимости использования в их моделях нелинейных уравнений, что, в свою очередь, затрудняет, а чаще всего, делает невозможным получение аналитического описания процессов в исследуемой системе. В этом случае используется решение с применением численных методов при различных начальных условиях, или моделирование системы. Одним из наиболее эффективных, быстрых и наглядных способов исследования численного решения является анализ графического представления или отдельного решения, или семейства, в том числе в параметрической форме фазового портрета.

В настоящее время имеется значительное число программных средств, позволяющих получать численное решение систем и отображать его в форме графиков. Среди них следует отметить пакеты Mathematica [1], Maple [2], Matlab/Simulink[3], их бесплатные аналоги Maxima[4], Octave[5], Freemat[6]. Указанные программные пакеты обладают широким спектром функциональных возможностей для численного моделирования, однако при их применении возникают следующие трудности:

· в связи с широкими возможностями размер пакета большой и требует предварительной установки на компьютер;

· для описания действий используется специальный язык программирования, что, как правило, повышает гибкость, но требует изучения;

· необходимость реализовывать ряд нелинейных элементов (например, люфт), обращаться явно к процедурам делает исследование менее наглядным, приближая процедуру описания и исследования системы к разработке программы моделирования на языке высокого уровня.

В статье рассматривается разработанная автором специализированная программа «СИНУС-Д», предназначенная для моделирования нелинейных динамических систем и технические и проектные решения, принятые при её создании. При её разработке была поставлена цель получить компактное программное средство, обеспечивающее оперативное получение численного решения сложных нелинейных динамических систем в графической форме при максимальном сохранении наглядности представления как исходных данных, так и результатов. Такой подход облегчает использование программы как студенту при выполнении лабораторных работ, так и инженеру, разработчику, исследователю, экономя его время.

2. Выбор класса исследуемых систем

Программа «СИНУС-Д» разработана как инструмент для исследования и первичного проектирования сложных систем автоматического управления, что и определило класс уравнений, решение которых требуется построить. Применение цифровой техники в составе систем управления приводит к необходимости учёта эффектов квантования сигнала. Таким образом, система должна рассматриваться как дискретно-непрерывная. В общем виде непрерывная нелинейная система автоматического управления с сосредоточенными параметрами может быть описана системой обыкновенных дифференциальных уравнений (ОДУ) [7]:

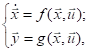(1.1)

где – переменные состояния, – выходные переменные, – вектор задающего воздействия (управляющих переменных). В (1.1) подразумевается, что все переменные отнесены к одному моменту времени : , , . Наличие чистого запаздывания по одной или нескольким переменным, то есть использование в уравнениях переменных, зависящих от предшествующих моментов времени, приводит к системе вида

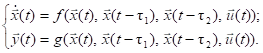(1.2)

Следует отметить, что с введением запаздывающих переменных (1.2) становится системой функционально-дифференциальных уравнений. От использования уравнений в частных производных было решено отказаться, так как их решение требует применения существенно других методов. С другой стороны, ряд явлений и процессов, обычно описываемых уравнениями с распределёнными параметрами, могут быть приближенно описаны системой вида (1.2) [8]. Например, учёт запаздывания позволяет моделировать ненулевое время распространения сигнала.

Для описания дискретной подсистемы используются разностные уравнения. Её представление в пространстве состояний имеет вид [9]:

(1.3)

где – номер шага, соответствующий времени , – такт дискретизации системы.

Уравнениями выхода в (1.1)-(1.3) являются алгебраические уравнения, и, в отличие от дифференциальных и разностных, не предполагают наличия начальных условий. Также они востребованы при задании подвыражений с целью упрощения записи системы.

Если в модели допустить любое сочетание типов и количества уравнений, то оставив в ней лишь алгебраические уравнения, можно задать функциональную зависимость. Примером из области теории автоматического управления могут служить частотные характеристики системы. Для их построения требуются операции над комплексными числами. Чтобы избежать необходимости подготовительных ручных расчетов (выделения действительной и мнимой частей), в программе предусмотрен специальный тип алгебраических уравнений, в которых операции производятся над комплексными числами. Переменная также может быть задана как решение нелинейного алгебраического уравнения, для чего предусмотрен тип уравнения «неявная функция». Наконец, для записи повторяющихся выражений, зависящих от параметра, предусмотрена возможность задать функциональное выражение – функцию одного аргумента.

3. Задание уравнений и функций

Часто используемая матричная форма записи линейных систем удобна при аналитическом описании и анализе, но задание сильно разреженной матрицы утомительно и не наглядно. Кроме того, такая форма требует определения структуры нелинейной части, что ограничивает класс моделируемых систем. В программе принята запись правой части «в строку» в естественной математической форме, что, хотя и потребовало разработки синтаксического анализатора, но одновременно позволило не только легко модифицировать правую часть, но так же легко изменять ее структуру, используя нелинейные функции и произведения переменных состояния. Уравнения в программе задаются в строку в форме:

«переменная» = «вычисляемое значение правой части» ; «начальные условия»,

причём дополнительного описания переменной не требуется (рис.1). Для ускорения ввода и сокращения числа опечаток можно использовать панель быстрого ввода, содержащую набор операций и функций, как встроенных, так и определённых пользователем (рис.2).

Пользователь имеет возможность использовать символы различных алфавитов, включая греческий и кириллический для именования переменных, что позволяет задавать их в общепринятых обозначениях и не требует переименования переменных при их задании в программе.

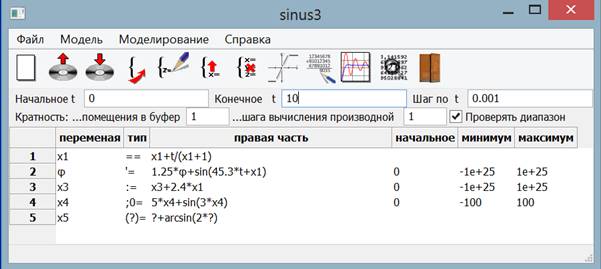
Рис. 1. Задание системы уравнений, включающее уравнения разных типов. В модель включены: алгебраическое, дифференциальное, разностное уравнение, неявная функция и функциональное выражение

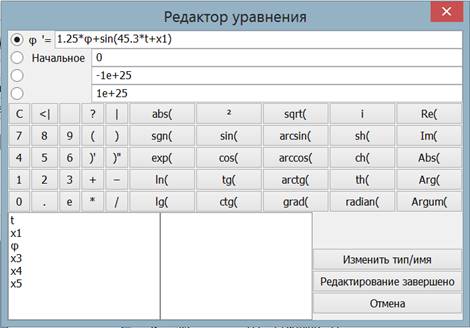
Рис. 2. Редактор уравнения для быстрого набора правой части

Для расширения класса исследуемых нелинейных систем реализован широкий набор типовых нелинейных элементов. Такие элементы, как правило, имеют один или несколько параметров. Чтобы не загромождать правую часть уравнений, пользователь должен присвоить уникальное имя каждой используемой им нелинейности с определённым набором параметров. Например, в набор включена кусочно-линейная функция с разрывами в узлах. Сопоставляя идентификатору функции, например F2, набор узлов и значений функции в них, включая пределы слева и справа, пользователь далее использует имя F2 как обычную функцию без параметров: x1+F2(u)+… Реализованы специальные элементы, обеспечивающие реализацию так называемых двузначных функций (функций, значение которых зависит от знака первой производной аргумента), функции-диапазоны, позволяющие сформировать произвольную кусочно-нелинейную функцию, описываемую на каждом участке отдельным выражением, генераторы псевдослучайных последовательностей и др. (рис.3).

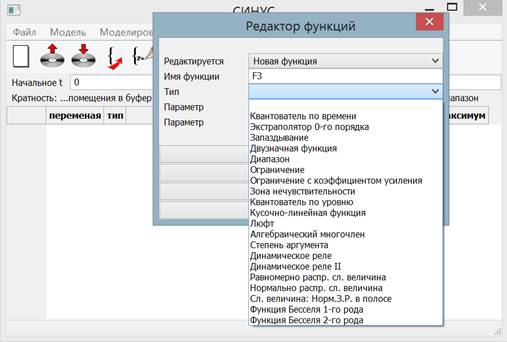
Рис. 3. Задание функций с параметрами

Описанный способ задания используется для элементов типа запаздывание, квантователь по времени и экстраполятор нулевого порядка, что позволяет в рамках одной системы избежать ограничений, накладываемых единым тактом дискретизации или единым запаздыванием.

4. Особенности реализации моделирования систем

Исследование динамики системы предполагает получение описания процессов системы во времени, причём время является единым для (1.1) и (1.3). Для реализации модельного времени предусмотрена выделенная переменная, обозначенная символом , изменяемая с постоянным шагом, называемым шагом моделирования. Использование методов решения с переменным шагом признано нецелесообразным, так как предполагается исследование систем с разрывной правой частью и дискретно-непрерывных систем

Для решения системы обыкновенных дифференциальных уравнений используется явный метод Рунге-Кутты 4-го порядка [10]. Для выполнения шага метода требуется четыре обращения к правой части системы дифференциальных уравнений. В то же время в полной моделируемой системе могут присутствовать уравнения других типов. Разностные уравнения должны быть вычислены один раз за такт, алгебраические же исследователь может захотеть использовать как средство вычисления подвыражений правой части дифференциальных или разностных уравнений, или, напротив, в качестве уравнения выхода, что требует их вычисления уже после всех промежуточных шагов метода Рунге-Кутты. Рассмотрим, как в программе разрешено это противоречие.

Алгебраические уравнения (точнее говоря, выражения, или формулы) вычисляются последовательно в порядке их описания, причем значение переменной, вычисленное в предшествующем выражении немедленно доступно для использования в последующих выражениях и правых частях дифференциальных уравнений. Это сделано для соблюдения следующего принципа (назовем его принципом подстановки): подстановка правой части алгебраического выражения вместо переменной, определяемой выражением, не изменяет результат. Для соблюдения этого принципа формировать последовательность алгебраических выражений следует без использования в их правых частях переменных, алгебраические выражения для которых описаны ниже. Если этого избежать не удается, используется значение переменной с предыдущей итерации.

Порядок записи дифференциальных уравнений несущественен: переход на следующий шаг осуществляется одновременно для всех переменных состояния, объединенных в вектор.

Рассмотрим выполнение принципа подстановки при использовании переменных, задаваемых алгебраическими выражениями, в правой части дифференциальных уравнений. Алгебраические выражения вычисляются каждый раз перед вычислением правой части дифференциальных уравнений. С другой стороны, выражения для выходных переменных предполагают алгебраические преобразования уже после перехода на следующий шаг. Чтобы удовлетворить этому требованию, не нарушая принцип подстановки, в программе при переходе к следующему шагу по времени значения правых частей уравнений вычисляются в порядке, указанном в таблице 1. Цифрами обозначен порядок вычислений выражений при выполнении одного шага интегрирования, – шаг моделирования по времени. Результат вычислений алгебраических выражений с использованием значений переменных дифференциальных уравнений, полученных как результат перехода на k+1-й шаг, может также рассматриваться как подготовка информации для правых частей дифференциальных уравнений для выполнения следующего шага, что учитывается в схеме вычислений. Для сохранения схемы алгебраические выражения применяются и к начальным условиям перед выполнением первого шага.

Таблица 1. Порядок вычислений алгебраических и дифференциальных уравнений при выполнении k-го шага метода Рунге-Кутты

Значение модельного времени	Алгебраические уравнения	Дифференциальные уравнения
	8 (k-1 шаг)	1
	2	3
	4	5
	6	7
	8	1 (k+1 шаг)

Для корректного моделирования дискретно-непрерывной системы необходимо, чтобы такт дискретизации был бы существенно больше шага моделирования, но при этом кратен ему. Это означает, что переход к следующему значению, определяемому разностными уравнениями, должен производиться существенно реже, чем для дифференциальных уравнений. Чтобы реализовать возможность моделирования систем, содержащих одновременно несколько квантователей по времени с различными тактами дискретизации, предлагается использовать элемент типа «экстраполятор», подавая на его вход правую часть уравнения. Данный элемент вычисляет свой аргумент только в моменты времени, соответствующие следующему такту.

Переход от к сопровождается проверкой на выход переменной из допустимого диапазона. Минимальное и максимальное значения для каждой переменной могут быть заданы не только числом, но и алгебраическим выражением, включающим другие переменные системы. При выходе переменной из заданного диапазона моделирование прекращается. Эта возможность программы позволяет моделировать системы методом припасовывания или моделировать системы с переменной структурой.

Значения всех вычисленных переменных и соответствующее им модельное время сохраняются во внутреннем массиве. Если размерность системы достаточно большая, а шаг моделирования мал, размер буферной памяти может оказаться недостаточным. Малый шаг, как правило, используется для обеспечения устойчивости численного метода, а отображение результатов планируется с более крупным шагом, поэтому с использованием параметра «кратность запоминания» можно сохранять значения переменных, пропуская часть шагов. По такому же принципу регулируется шаг вычисления производных от выражений, которые могут вычисляться методом простой разности в правых частях уравнений.

Уравнения типа «неявная функция» на каждом шаге по времени решаются методом золотого сечения, с помощью которого минимизируется невязка. В качестве начального условия берётся или начальное условие, которое задаёт пользователь наряду с диапазоном допустимых значений, или ее величина на предыдущей итерации.

Правые части уравнений, как указывалось в п.3, пользователь может ввести либо в форме текстовой строки, либо сформировать ее с использованием панели быстрого ввода. Перед началом моделирования производится синтаксический анализ уравнений, формируется древовидная структура объектов – элементарных операций и функций, связанных в соответствии с заданным выражением. Например, для вычисления правой части дифференциального уравнения вида

x3’=1/T1*(F(u+x1+x2)-x3),

где u, T1 – переменные алгебраических уравнений, F – заданная пользователем нелинейность, будет построена структура, представленная на рис. 4.

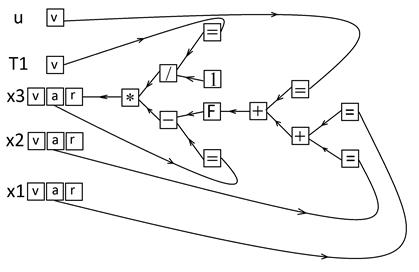
Рис. 4. Пример вычисления правой части дифференциального уравнения

Выражения вычисляются рекурсивно по построенному дереву, вызывая элементарные операции через указатели на функции. Каждой операции, указанной в прямоугольнике, соответствует вызов функции. Символом «=» обозначена операция копирования значения. Для каждой переменной, соответствующей дифференциальному уравнению, используется три типа ячеек для хранения значений. Тип «v» соответствует вычисленному значению на k-м шаге – результату моделирования, тип «a» – аргумент правой части, который используется для вычисления промежуточных шагов в методе Рунге-Кутты, тип «r» – значение правой части на промежуточном шаге. Разделение ячеек типов «a» и «r» обеспечивает использование значений вектора переменных состояния, соответствующих одному времени. Через F обозначена нелинейность, заданная пользователем. Наряду с типом функции, хранится набор параметров, связанный с данным идентификатором, используемый для вычисления значения. Построение дерева в памяти позволяет считать, что в программе осуществляется предварительная компиляция кода, причём реализованная средствами языка высокого уровня без использования особенностей архитектуры целевой ЭВМ. Сравнение быстродействия программы «СИНУС-Д» и компилированного с оптимизацией кода показывает отставание всего в 2-5 раз в зависимости от выражений в правой части. Следует учитывать, что в процессе моделирования программно отслеживаются исключительные ситуации, такие как деление на ноль, аргументы функций вне области определения, выход переменной за заданный диапазон.

Полученные численные результаты пользователь может просмотреть в форме таблицы и при необходимости записать в файл (рис.5).

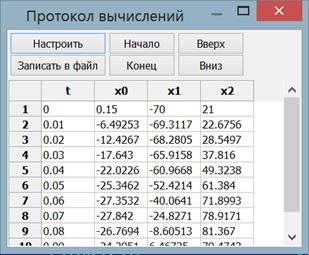
Рис. 5. Просмотр численных результатов моделирования

5. Графическое представление результатов моделирования

Наиболее эффективным способом анализа результатов численного моделирования динамических систем является графическое представление результатов. Реализованы следующие возможности отображения:

- многооконный режим, позволяющий представлять данные в различных системах координат;

- возможность отображения нескольких графиков в одной системе координат (рис.6);

- возможность укрупнения фрагментов построенных графиков;

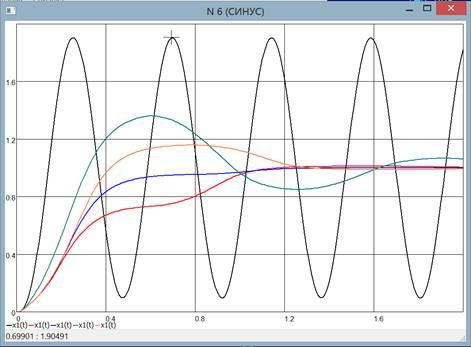
Рис. 5. Отображение нескольких графиков при выборе параметра корректирующего устройства при подавлении автоколебаний. Координаты курсора позволяют определить амплитуду автоколебаний

- определение точных значений координат под курсором (рис. 6);

- цветовое выделение графиков и осей координат;

- автоматическое определение диапазона отображения;

- автоматическое определение цены деления координатной сетки для получения круглых значений;

- использование сдвига делений координатной сетки для более удобной маркировки делений;

- сохранение изображений в различных растровых (bmp, jpg, png, tiff) и векторных форматах (ps, svg);

- удаление построенных графиков, перенос их между окнами;

- изменение толщины линий для отрисовки графиков.

Реализована возможность сохранения графика в файл в форме текстовой таблицы значений и загрузки его из файла. Принятый формат позволяет загружать зависимости, в том числе сгенерированные в других программах и использовать «СИНУС-Д» как средство просмотра графиков. Для этого предусмотрены опции, подавляющие вывод основного окна для задания модели – на экране представлено только окно с графиком.

Программа предоставляет возможность построить зависимость произвольной вычисленной переменной от любой другой (рис. 7), что даёт возможность строить отдельные фазовые траектории (рис.8), а с учётом возможности совмещать множество графиков в одних системах координат – и фазовые портреты (рис.9).

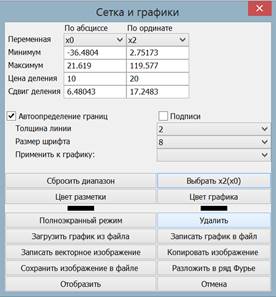
Рис. 7. Диалог описания свойств графика

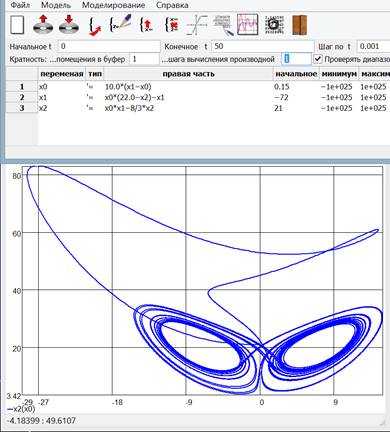
Рис. 8. Фазовая траектория – странный аттрактор Лоренца

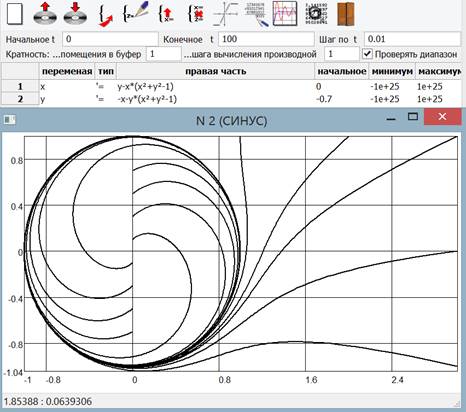
Рис. 9. Фазовый портрет – предельный цикл в нелинейной системе

Как можно видеть на рис. 7, предоставляются средства частотного анализа полученного процесса – пользователь может разложить полученную зависимость в ряд Фурье с использованием заданного числа гармоник, а затем наложить полученную частичную сумму ряда на график. Максимальное число гармоник, предлагаемых для разложения, ограничено теоремой Котельникова, а отрезок разложения автоматически вычисляется исходя из периодичности функции, но может быть задан пользователем вручную. На рис. 10 приведена иллюстрация явления Гиббса с использованием 1,3, 5, 7 и 25 гармоник. Параметры гармоник представлены в формате амплитуда/фаза. Пользователь может изменить произвольный параметр, построить график такой функции, оценить вклад той или иной гармоники в сигнал.

10а

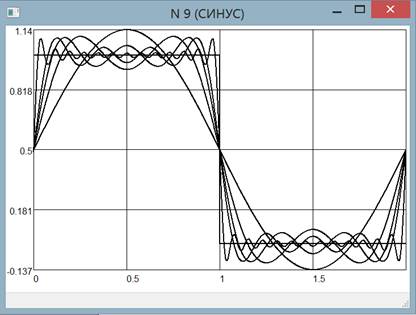
Рис. 10. Демонстрация явление Гиббса

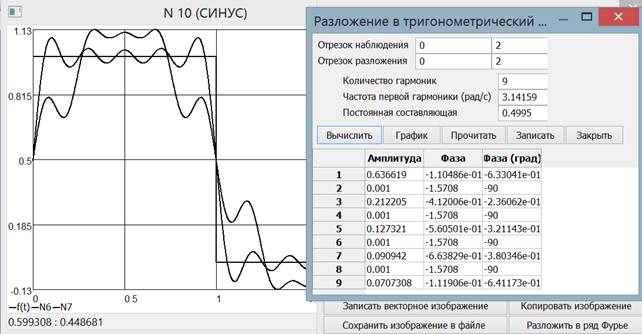
Рис. 11. Сравнение разложения в ряд Фурье до 9-й гармоники с разложением, в котором отсутствуют 3 и 5 гармоники

6. Переносимость и многоплатформенность

Графический интерфейс программы разработан с использованием библиотеки wxWidgets, что обеспечило возможность ее реализации для основных операционных систем: Microsoft Windows, Apple OS X и Linux. Программа выполнена монолитной с использованием статической компоновки требуемых библиотек, поэтому ей не требуется специальная процедура установки – для переноса на другой компьютер достаточно копирования. Применение средства динамической компрессии выполняемого файла обеспечивает ее размер около 1 Мб. Файлы программы имеют единый формат и используют кодировку UTF-8. Компактный размер, многоплатформенность, готовность к использованию позволяют постоянно иметь программу на переносном носителе в качестве инструмента оперативного моделирования и визуализации процессов.

7. Заключение

Программа моделирования нелинейных динамических систем «СИНУС-Д» предоставляет широкие возможности для графического анализа процессов в таких системах. Ориентированная прежде всего на моделирование дискретно-непрерывных систем автоматического управления, программа может служить графическим инструментом для построения сложных нелинейных, в том числе комплекснозначных функций, и, даже средством решения систем нелинейных алгебраических уравнений.

Разработанная программа отличается чрезвычайной компактностью, не требует установки и может быть использована в качестве легко доступного средства для решения сложных задач. Для начала работы с программой не требуется специального обучения или изучения языков программирования, что подтверждается многолетним опытом использования в качестве основы для лабораторного практикума.

При разработке программы был решен ряд задач в области проектирования как вычислительного ядра, так и построения графического интерфейса. Опыт создания данной программы может быть использован в дальнейшем при разработке других программ для оперативной визуализации результатов численных экспериментов.

Список литературы

1. www.wolfram.com

2. www.maplesoft.com

3. www.mathworks.com

4. maxima.sourceforge.net

5. www.gnu.org/software/octave

6. freemat.sourceforge.net

7. Zadeh L, Desoer Ch. Linear System Theory. The State Space Approach. McGraw-Hill New York /Пер. С англ. Заде Л., Дезоер Ч. Теория линейных систем. Метод пространства состояний. М.:Наука, 1970.

8. Hale J. Theory of Functional Differential Equations. Springer-Verlag. NewYork Heidelberg Berlin 1977. / Пер. с англ. Хейл Дж. Теория функционально-дифференциальных уравнений. М.: Мир, 1984.

9. Kuo B. Digital Control Systems. Holt, Rinehart and Winston Inc.1980. /Пер. с англ. Куо Б. Теория и проектирование цифровых систем управления. М.:Машиностроение, 1986.

10. Butcher J.C. Numerical Methods for Ordinary Differential Equations. John Wiley&Sons,Ltd, 2003.

CONCEPTION AND DEVELOPMENT EXPERIENCE OF "SINUS-D" SOFTWARE FOR RAPID VISUALIZATION OF DYNAMIC SYSTEMS SIMULATION

S.V. Ktitrov

National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Russian Federation

SVKtitrov@mephi.ru

Abstract

"SINUS-D" is software designed for rapid visualization of numerical simulation of nonlinear dynamic systems. The primary area of using the software is analysis and synthesis of nonlinear discrete-continuous automatic control systems including systems with delay. It determines the class of equations to be solved. The software builds the numerical solution of nonlinear differential and difference equations of arbitrary structure specified by text strings. Variable names can contain characters of various alphabets including Greek which makes the equation written similar to its representation in the subject area. Many typical nonlinear elements including two-valued non-linearities, random variables, extrapolator, pure delay are implemented. This article is focused on details of the software design and implemented algorithms including the design of the expression interpreter and a computing subsystem.

The graphics subsystem is described in detail. It is designed to present the simulation results operatively. A lot of possibilities of graphic canvas include precise coordinate detection, the adjustment of the plot and the coordinate grid properties and others. Examples of its use for the visualization and comparative analysis of transient processes and phase portraits are presented.

The means implemented for the harmonic analysis of processes are presented. That helps to research the approximation quality by the partial sums of the Fourier series and the contribution of individual harmonics to the waveform shaping.

The conception of the software design includes its compactness and the possibility of using various software platforms. The software is single file compiled for Microsoft Windows, Apple OS X and Linux. It uses the common text file format for all platforms. Installation is not required.

The suggested approach to development of the similar programs is based on a combination of a built-in equation parser along with previously implemented set of typical nonlinear elements and intuitive interface.

Keywords: numerical solution, differential equations, difference equations, simulation, dynamic system, delayed system, nonlinear element

References