ВИЗУАЛИЗАЦИЯ И АНАЛИЗ АЛГОРИТМА ТОЧНОГО РЕШЕНИЯ ЗАДАЧИ О РЮКЗАКЕ, ОСНОВАННОГО НА ИСПОЛЬЗОВАНИИ КОНСТРУКТИВНОГО ПЕРЕБОРА
М.А. Куприяшин, Г.И. Борзунов
Национальный исследовательский ядерный университет «МИФИ», Россия
kmickle@yandex.ru; parproc@gmail.com
Содержание
2. Визуализация вычислительной сложности проверки векторов укладок
3. Анализ баланса вычислительной нагрузки средствами визуализации
Аннотация
Проведён анализ процедуры анализа векторов укладки при реализации параллельного алгоритма решения задачи о рюкзаке методом прямого перебора. Экспериментально получены графики зависимости трудоёмкости проверки векторов укладок для различных размерностей элементов рюкзака. Построены и проанализированы диаграммы распределения вычислительной нагрузки при использовании равных отрезков лексикографической последовательности векторов.
Ключевые слова: задача о рюкзаке, прямой перебор, параллельные вычисления
1. Введение
В настоящее время повысился интерес к новым рюкзачным системам шифрования, которые устойчивы к ранее разработанным атакам [1-3]. Как следствие, повышается значение алгоритма точного решения задачи о рюкзаке, основанного на использовании конструктивного перечисления, для анализа стойкости рюкзачным системам шифрования. Возможности использования этого алгоритма могут быть значительно расширены за счёт применения современных достижений в области распределённых вычислений[4]. Вместе с тем необходимо учитывать, что эффективность распределенных вычислений в определяющей степени зависит от равномерности распределения вычислительной нагрузки между используемыми процессорами (вычислительными узлами) [5]. Данная работа посвящена визуализации и анализу баланса вычислительной нагрузки при использовании распределенных вычислений для реализации указанного алгоритма.
Задача о рюкзаке — сложная задача оптимизации, в общем
случае являющаяся NP-полной и имеющая экспоненциальную временную сложность [6].
Пусть задан вектор ![]() , где
, где ![]() — натуральные числа. Каждый
элемент
— натуральные числа. Каждый
элемент ![]() выражает вес предмета с номером
выражает вес предмета с номером ![]() . Будем
называть вектор
. Будем
называть вектор ![]() рюкзачным вектором. Каждый предмет может либо
входить, либо не входить в состав рюкзака. Вектор
рюкзачным вектором. Каждый предмет может либо
входить, либо не входить в состав рюкзака. Вектор![]() , где
, где ![]() , причём
, причём ![]() предмет
с номером
предмет
с номером ![]() входит в рюкзак, назовём вектором укладки
рюкзака. Величина
входит в рюкзак, назовём вектором укладки
рюкзака. Величина ![]() — вес укладки
— вес укладки ![]() . Значение
. Значение ![]() —
размерность задачи. Формулировка задачи: найти укладки, вес которых в точности
равен заданному значению, либо доказать, что такой укладки не существуют.
—
размерность задачи. Формулировка задачи: найти укладки, вес которых в точности
равен заданному значению, либо доказать, что такой укладки не существуют.
Самым простым в реализации и требующим наименьших затрат
по памяти является алгоритм конструктивного перечисления всех векторов
укладок рюкзака с целью нахождения укладки, вес которой равен заданному
значению. При этом векторы укладок генерируются в лексикографическом порядке.
Но, так как существует ![]() различных вариантов векторов укладки рюкзака
размерности
различных вариантов векторов укладки рюкзака
размерности ![]() ,
временная сложность этого алгоритма ограничивает его применение на практике.
,
временная сложность этого алгоритма ограничивает его применение на практике.
Разработка параллельного алгоритма полного перебора векторов укладок и использование распределённых вычислений позволяет существенно сократить время решения рассматриваемой задачи. Если считать базовой операцию вычисления веса одной укладки и принять её в качестве условной единицей вычислительных затрат, то легко достижимо равномерное распределение вычислительной нагрузки для любого количества вычислительных узлов (m).
Естественным порядком конструктивного перечисления векторов
является лексикографический порядок. Он позволяет легко пересчитывать
порядковый номер вектора в его двоичное представление и обратно. Таким образом,
при распределении вычислительной нагрузки, главному процессору достаточно
указать рабочим процессорам номера начального и конечного вектора. При этом
временная сложность последовательного алгоритма составляет в условных единицах
![]() , а временная
сложность каждой из параллельных ветвей, выполняемых на одном из m
процессоров (вычислительных узлов) равна
, а временная
сложность каждой из параллельных ветвей, выполняемых на одном из m
процессоров (вычислительных узлов) равна ![]() . Тогда коэффициент ускорения параллельного
алгоритма оказывается равным
. Тогда коэффициент ускорения параллельного
алгоритма оказывается равным ![]() , а коэффициент его эффективности - равным
, а коэффициент его эффективности - равным ![]() . Из этих оценок
следует, что при
. Из этих оценок
следует, что при ![]() достигается
практически идеально равномерное распределение вычислительной нагрузки между
процессорами. Опыт анализа параллельных комбинаторных алгоритмов показывает:
выбор базовых операций в значительной степени влияет на равномерность
распределения вычислительной нагрузки[5], и потому требует дополнительного
экспериментального исследования. Ниже приводятся результаты такого
исследования при помощи средств визуализации.
достигается
практически идеально равномерное распределение вычислительной нагрузки между
процессорами. Опыт анализа параллельных комбинаторных алгоритмов показывает:
выбор базовых операций в значительной степени влияет на равномерность
распределения вычислительной нагрузки[5], и потому требует дополнительного
экспериментального исследования. Ниже приводятся результаты такого
исследования при помощи средств визуализации.
2. Визуализация вычислительной сложности проверки векторов укладок
Есть основания предполагать, что время проверки одной укладки зависит от свойств вектора укладки и, как следствие, не является постоянным. При этом приведённые выше аналитические оценки временной сложности параллельного алгоритма требуют коррекции. Рассмотрим подробнее операцию вычисления веса укладки. На входе имеется вектор укладки в двоичном представлении, а также рюкзачный вектор. Для того, чтобы вычислить вес укладки, можно воспользоваться одной из следующих вычислительных схем.
Во-первых, можно последовательно оценить значения ![]() и,
если они ненулевые, добавить соответствующее значение
и,
если они ненулевые, добавить соответствующее значение ![]() к промежуточному
значению веса укладки. Таким образом, для задачи размерности
к промежуточному
значению веса укладки. Таким образом, для задачи размерности ![]() необходимо
выполнить
необходимо
выполнить ![]() сравнений и от
сравнений и от ![]() до
до ![]() сложений.
Далее будем обозначать эту схему как IF-ADD.
сложений.
Далее будем обозначать эту схему как IF-ADD.
Во-вторых, можно непосредственно вычислить ![]() . Это
потребует
. Это
потребует ![]() операций сложения и
операций сложения и ![]() операций умножения.
Далее будем обозначать такую вычислительную схему как MUL-ADD.
операций умножения.
Далее будем обозначать такую вычислительную схему как MUL-ADD.
Ниже приводится описание этих двух вычислительных схем с использованием псевдокода:
// TASK_SIZE — размерность задачи ![]() ;
;
// *a[] — элементы рюкзачного вектора;
// p_list — поэлементный массив векторов укладок;
// cursor — смещение текущего элемента относительно начала p_list;
// *weight — переменная, хранящая текущий вес укладки;
// y — итератор
*weight = 0;
for (int y = 0; y < TASK_SIZE; y++)
if (p_list[cursor++]) *weight += (*a[y]); // Подход IF-ADD
// ИЛИ
*weight += (p_list[cursor++])*(*a[y]); // Подход MUL-ADD
if (*weight == *w) /* Действия по обработке решения */;
Для выявления наиболее эффективной вычислительной схемы веса укладки был проведён вычислительный эксперимент, в холе которого с использованием каждого из двух указанных выше алгоритмов вычислялись веса укладок векторов, содержащих от одной до 15 единичных координат. В каждой точке по числу единичных координат вычисления повторялись для 320000 векторов, генерация которых выполнялась с использование функций , осуществляющих циклический лексикографический перебор всех векторов и возвращающих те, в которых число единичных координат соответствует заданному. В результате были получены зависимости среднего времени вычисления веса укладки от количества единичных координат. График этой зависимости приводится на Рис. 1.
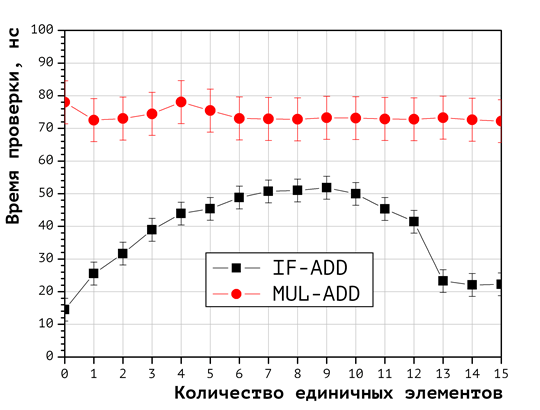
Рис. 1. Сравнение эффективности подходов MUL-ADD и IF-ADD
Здесь и далее в качестве погрешности для каждой кривой на графике приводится максимальное достигнутое значение среднеквадратической погрешности. Анализ графика показывает, что реализации подходов IF-ADD и MUL-ADD всюду статистически различимы, при этом эффективность IF-ADD стабильно выше. Это является основанием для применения подхода IF-ADD в ходе дальнейшего исследования.
Данный и последующие вычислительные эксперименты проводились
на тестовом стенде следующей конфигурации: процессор Intel Core 2 Quad Q9505; 4
ядра с тактовой частотой 2,83МГц, оперативной памятью объёмом 8ГБ (![]() ) с установленной
интегрированной средой разработки Microsoft Visual Studio 2013 Express. Для
сборки исходных кодов использовался компилятор Microsoft Visual C++ версии 12.
Стенд функционирует под управлением 64-разрядной операционной системы Windows 7
Enterprise с установленным пакетом обновлений Service Pack 1.
) с установленной
интегрированной средой разработки Microsoft Visual Studio 2013 Express. Для
сборки исходных кодов использовался компилятор Microsoft Visual C++ версии 12.
Стенд функционирует под управлением 64-разрядной операционной системы Windows 7
Enterprise с установленным пакетом обновлений Service Pack 1.
Этот и все дальнейшие практические эксперименты проводятся с целью исследования конкретных элементарных операций. Соответственно, в ходе экспериментов не применяются программные и аппаратные средства организации распределённых вычислений, а прогнозы по быстродействию параллельного алгоритма являются расчётными значениями, полученными без учёта коммуникационных затрат в распределённой вычислительной системе. Точность этих результатов приемлема в силу того, что в решаемой задаче очень слабо выражены взаимосвязи между процессорами по данным — синхронизация требуется только при первоначальном распределении нагрузки.
Рассмотренный выше псевдокод применим только в том случае, если разрядность отдельных элементов рюкзачного вектора и их суммы не превышает разрядности регистров процессора. В противном случае, реализация операции сложения требует существенно больше времени, так как числа требуется складывать по частям, с учётом возможного переноса разрядов. Далее по тексту для обозначения случая превышения данными разрядности регистров используется термин «длинная арифметика». Операции сложения и сравнения в этом случае реализуются следующим образом:
// ELEMENT_SIZE — длина элемента рюкзака (количество ячеек памяти, необходимое для хранения каждого элемента рюкзачного вектора)
// __INT64_HI_DIGIT — Битовая маска, соответствующая старшему биту 64-разрядного целого беззнакового числа
// __INT64_LO_DIGIT — Битовая маска, соответствующая 63 младшим битам 64-разрядного целого беззнакового числа
// add_tmp — буфер для хранения суммы пар ячеек памяти
#define __INT64_HI_DIGIT 0x8000000000000000
#define __INT64_LO_DIGIT 0x7FFFFFFFFFFFFFFF
// Сложение (результат записывается на место первого операнда)
_inline LargeAdd(unsigned __int64* a, unsigned __int64* b)
{
unsigned __int64 add_tmp;
for (int z = 0; z < ELEMENT_SIZE; z++)
{
add_tmp = a[z] + b[z];
if (add_tmp&__INT64_HI_DIGIT)
{
a[z + 1]++;
a[z] = add_tmp&__INT64_LO_DIGIT;
}
else a[z] = add_tmp;
}
}
// Сравнение
_inline LargeCmp(unsigned __int64* a, unsigned __int64* b)
{
for (int z = 0; z < ELEMENT_SIZE; z++)
if (a[z] != b[z]) return 0;
return 1;
}
Для исследования влияния перехода к длинной арифметики на время проверки очередной укладки рюкзака был проведён вычислительный эксперимент, в котором использовались элементы рюкзака, требующие для своего хранения 1, 2, 4, 8 ячеек памяти (что соответствует 64, 128, 256 и 512 битам памяти соответственно). Результаты этого эксперимента приводятся в виде графика на Рис. 2.
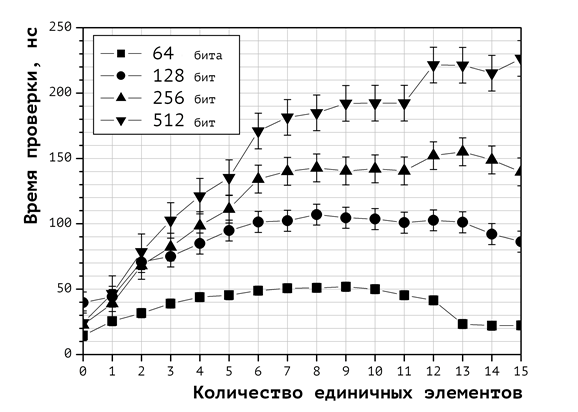
Рис. 2. Влияние размерности элементов рюкзачного вектора на сложность проверки укладок
На графике, приведенном на Рис. 2, отчётливо видна зависимость: с увеличением размерности элементов рюкзака время проверки укладок растет быстрее при увеличении числа единиц в векторах укладок. Это связано с тем, что время на сложения веса предмета с промежуточным значением веса укладки возрастает с ростом размерности операндов. Если для арифметики в пределах разрядности регистров процессора разница во времени вычисления веса укладок для векторов укладок с малым числом единичных координат и для векторов укладок с большим числом единичных координат несущественна, то для чисел с разрядностью 512 бит имеет место разница приблизительно в 10 раз.
Отметим, что наличие в рюкзаке элементов большой разрядности является обычным явлением в криптографических задачах. В частности, для сверхрастущих рюкзаков разрядность элементов в битах, как правило, велика, и гарантированно не меньше числа элементов в рюкзаке.
3. Анализ баланса вычислительной нагрузки средствами визуализации
Пусть последовательность векторов укладок при
лексикографическом перечислении разбивается на подряд идущие
подпоследовательности равной длины. Далее на Рис. 3 приводятся экспериментально
полученные данные для размерности ![]() . Всё множество возможных укладок делилось на 2,
4, 8 равных частей для 2, 4 и 8 процессоров соответственно
. Всё множество возможных укладок делилось на 2,
4, 8 равных частей для 2, 4 и 8 процессоров соответственно ![]() .
.
Экспериментально полученный вид распределения векторов укладок с фиксированным числом единичных координат по процессорам представлен на Рис. 3 (для двух процессоров), Рис. 4 (для четырёх) и Рис. 5 (для восьми). Цвета фигур соответствуют номерам процессоров (чем меньше номер процессора, тем ближе к началу расположен обрабатываемый им фрагмент лексикографической последовательности). Красный цвет соответствует первому процессору, зелёный — второму, и т.д. Темно-синий соответствует восьмому процессору. Для получения этих диаграмм, сначала была построена диаграмма распределения векторов по количеству единичных координат: чем левее точка на диаграмме, тем меньше единичных координат в векторе, чем правее — тем больше. Высота диаграммы для фиксированного количества единичных элементов есть количество векторов с таким количеством единичных элементов. Далее, построено разбиение полученной диаграммы на непересекающиеся фигуры таким образом, что вектора, относящиеся к одной и той же фигуре, попадают на один и тот же процессор. Площади фигур равны и отражают общее количество векторов, обрабатываемых соответствующими процессорами. Площадь всех диаграммы равна общему количеству векторов.
Как было показано ранее, время проверки одного вектора укладки зависит от количества единичных координат в этом векторе. Применительно к диаграммам на Рис 3-5 это означает, что вычислительная нагрузка для каждого процессора зависит не только от площади фигуры (количества векторов), но и от её смещения по горизонтальной оси (доли единичных координат в этих векторах). То есть, если фигура, соответствующая процессору, смещена вправо, то этот процессор обрабатывает больше единичных координат и, соответственно, вычислительная нагрузка на него больше.
По диаграммам Рис. 3-5 видно, что полученные фигуры обладают заметным смещением. Это свидетельствует о том, что для данного варианта распределения вычислительная нагрузка распределяется по процессорам неравномерно.
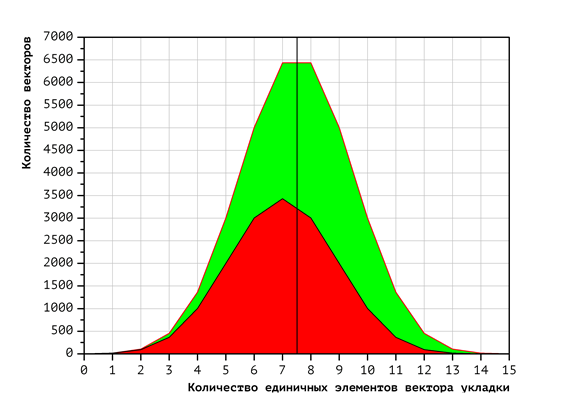
Рис. 3. Распределение векторов укладок в зависимости от числа единичных координат при использовании 2 процессоров
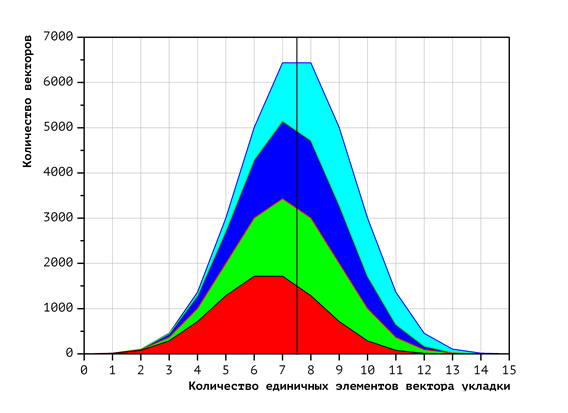
Рис. 4. Распределение векторов укладок в зависимости от числа единичных координат при использовании 4 процессоров
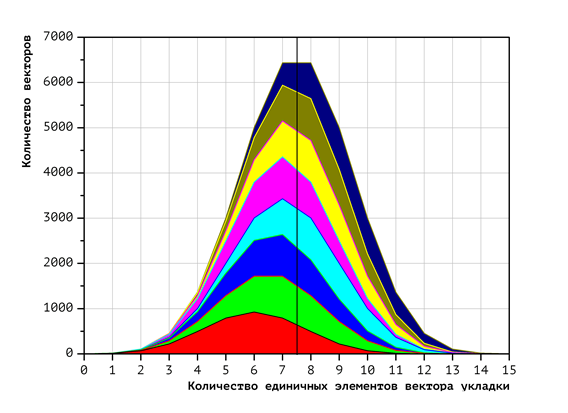
Рис. 5. Распределение векторов укладок в зависимости от числа единичных координат при использовании 8 процессоров
Вспомогательные диаграммы на Рис. 6-8 отражают соответствующие различия в количестве единичных и нулевых координат, обрабатываемых каждым процессором. Номера столбцов соответствуют номерам процессоров, а величина столбцов показывает отклонение содержания единичных и нулевых координат от равновесного. Так, согласно диаграмме на Рис. 8, первый из восьми процессоров (на диаграмме Рис. 5 ему соответствует красная фигура) при указанном способе распределения получает вектора, содержащие в сумме 60% нулевых и 40% единичных координат (что соответствует первому столбцу «-10%»). Восьмой процессор, напротив, получает 60% «единиц» и 40% «нулей». Это иллюстрирует дисбаланс вычислительной нагрузки.
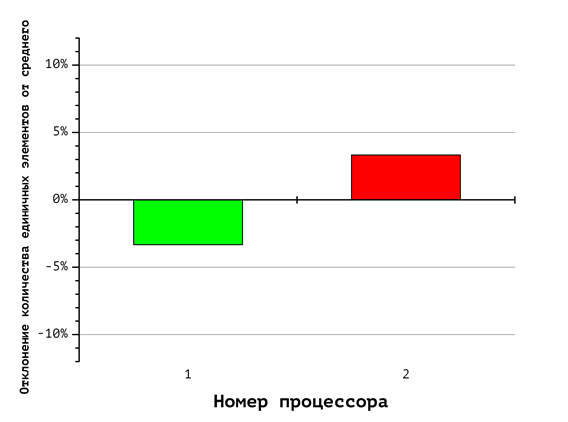
Рис. 6. Отклонение количества единичных векторов от среднего значения при использовании 2 процессоров
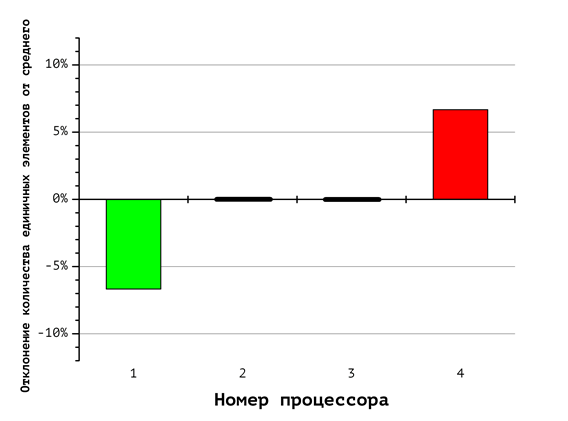
Рис. 7. Отклонение количества единичных векторов от среднего значения при использовании 4 процессоров
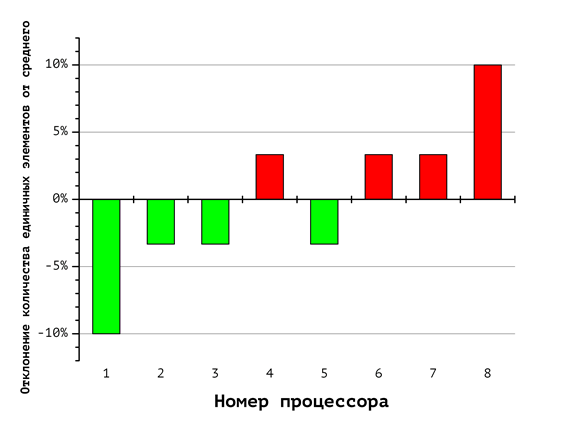
Рис. 8. Отклонение количества единичных векторов от среднего значения при использовании 8 процессоров
Таким образом, визуализация распределения векторов укладок при разделении их лексикографической последовательности по процессорам показала, что процессоры с бо́льшим номером получают большее количество «тяжёлых» (содержащих больше единиц, чем нулей) векторов, с меньшими номерами — «лёгких» (содержащих больше нулей и меньше единиц). Это выражается в смещении соответствующих фигур на диаграммах рис. 3-5 вправо (более «тяжёлые» вектора) и влево (более «лёгкие»).
При рассмотрении разбиения лексикографической последовательности на ещё более мелкие части неоднородности не сглаживаются. Чтобы проиллюстрировать этот факт, разобьём каждую из подзадач (блоков) для случая с 8 процессорами ещё на 16 подзадач (подблоков) и представим результат в виде пространственной диаграммы. Цвет блока соответствует номеру процессора. По вертикальной оси отмечена доля единичных элементов в векторах каждого подблока. По горизонтальной оси откладывается номер подблока. Чем меньше номер — тем ближе подблок к началу блока. Полученная диаграмма представлена на Рис. 9.
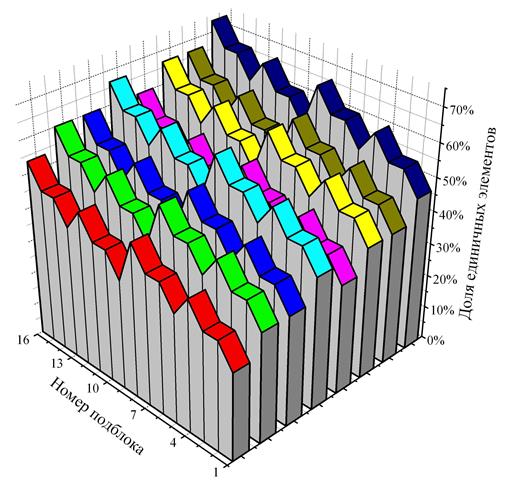
Рис. 9. Вариация сложности подблоков в подзадачах
Трёхмерное представление сложности подблоков позволяет
одновременно оценить как перепады сложности внутри подзадач-блоков, так и
сопоставить сложность различных блоков. Также трёхмерное представление
позволяет проиллюстрировать регулярные структуры, возникающие внутри каждого
блока за счёт того, что количество блоков равно ![]() . Отчётливо видно, что структура
блоков схожа, но средняя доля единичных элементов в них непостоянна. При этом,
блок с большим номером не обязательно имеет более высокую сложность. Например,
блок процессора 5 (пурпурный) содержит меньше единичных элементов, чем блок
процессора 4 (голубой). Это также хорошо заметно на Рис. 8.
. Отчётливо видно, что структура
блоков схожа, но средняя доля единичных элементов в них непостоянна. При этом,
блок с большим номером не обязательно имеет более высокую сложность. Например,
блок процессора 5 (пурпурный) содержит меньше единичных элементов, чем блок
процессора 4 (голубой). Это также хорошо заметно на Рис. 8.
В случае с длинной арифметикой это существенно сказывается на балансе вычислительной нагрузки. Отклонение вычислительной нагрузки процессоров в каждом из этих случаев (выраженное отношением суммарного числа единичных к суммарному числу нулевых компонент всех векторов укладки) можно оценить по диаграммам отклонения количества единичных векторов от среднего значения, изображенных на рис. 6-8. Например, первый процессор из восьми (рис. 8) получает набор векторов укладок, содержащий 40% единиц и 60% нулей, в то время как восьмой процессор должен обработать набор векторов укладок, содержащий 60% единиц и 40% нулей.
С учётом исследования случаев длинной арифметики, можно отметить, что распределение равных отрезков лексикографической последовательности векторов между процессорами не гарантирует равномерного распределения нагрузки.
На основе оценок скорости проверки векторов укладки и равномерности распределения единичных и нулевых координат векторов укладок между процессорами можно оценить значение коэффициента эффективности параллельных вычислений.
Будем считать за единицу вычислительной нагрузки трудоёмкость
операции проверки вектора с нулевыми координатами. Также будем считать, что
трудоёмкость проверки вектора линейно возрастает при увеличении числа единичных
координат. По графику на Рис. 2 определим время проверки единичного вектора в выбранных единицах:![]() .
Получается, что трудоёмкость проверки одной вершины линейно возрастает от
.
Получается, что трудоёмкость проверки одной вершины линейно возрастает от ![]() до
до ![]() при росте числа единичных
координат от 0 до 15. Зная это, можно оценить вычислительную нагрузку каждого
из процессоров. Это, в свою очередь, позволяет вычислить показатели ускорения и
эффективности параллельного алгоритма.
при росте числа единичных
координат от 0 до 15. Зная это, можно оценить вычислительную нагрузку каждого
из процессоров. Это, в свою очередь, позволяет вычислить показатели ускорения и
эффективности параллельного алгоритма.
Полученные описанным способом предварительные оценки эффективности отображены на диаграмме на Рис. 10. Каждый цвет соответствует определённому размеру элементов рюкзачного вектора. Отметим, что в идеальном случае величина средней эффективности должна быть равна 1 независимо от количества процессоров.
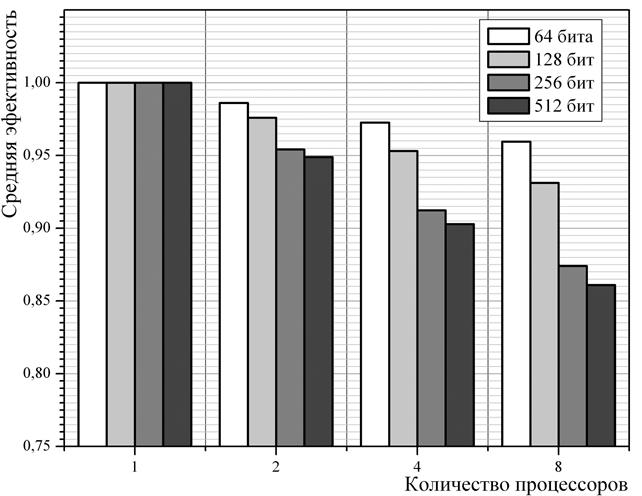
Рис. 10. Распределение векторов укладок по процессорам
На Рис. 10 отчётливо видно, что эффективность параллельных вычислений существенно снижается как при увеличении числа процессоров, так и по мере роста размерности элементов рюкзачного вектора. Если вычисления производятся на 8 процессорах, а элементы рюкзачного вектора имеют размерность 512 бит (8 ячеек памяти) — средняя эффективность вычислений падает до 0,86.
Подчеркнём существенное значение выявленного дисбаланса при помощи моделирования процесса решения задачи о рюкзаке. Рассмотрим задачу размерности 15 с размером элементов 128 бит. Для начала, воспользуемся данными эксперимента (Рис. 2), чтобы определить время обработки единичного и нулевого элемента вектора укладки. Положим время проверки нулевого элемента 25нс (левый край графика на Рис. 2) и время проверки нулевого элемента 90нс (правый край). Далее, на основе структуры блоков (Рис. 9) вычислим среднюю производительность каждого процессора в каждом подблоке, исчисляемую количеством векторов, обрабатываемых в единицу времени. Путём численного интегрирования вычисленной производительности и сравнения значения интеграла с размером блока (количеством векторов в подзадаче), определим долю проверенных векторов в процентном исчислении. Выполняя эту процедуру для дискретных моментов времени (с шагом 25мкс), можно проследить динамику исполнения параллельной программы.
Результаты моделирования приведены на Рис. 11 в формате GIF.
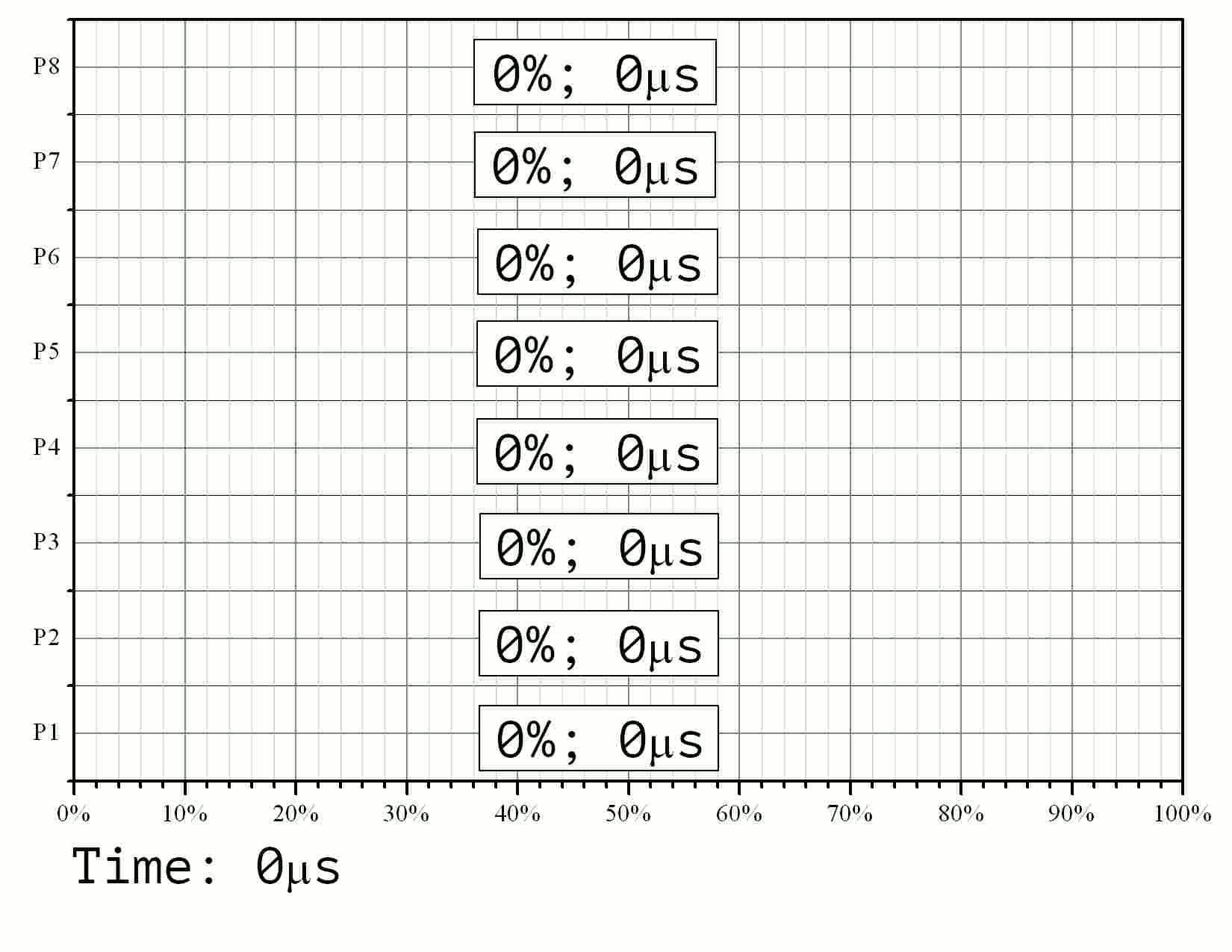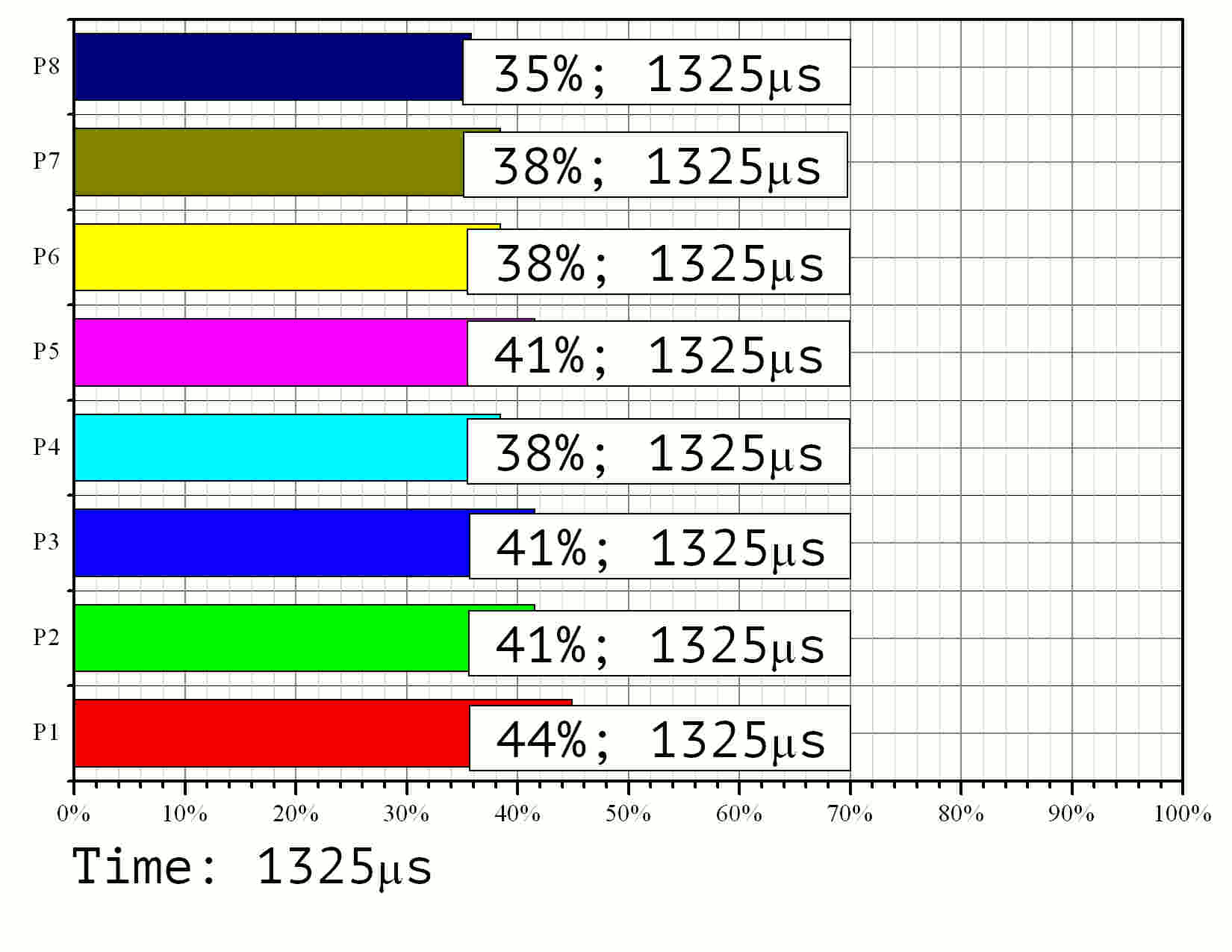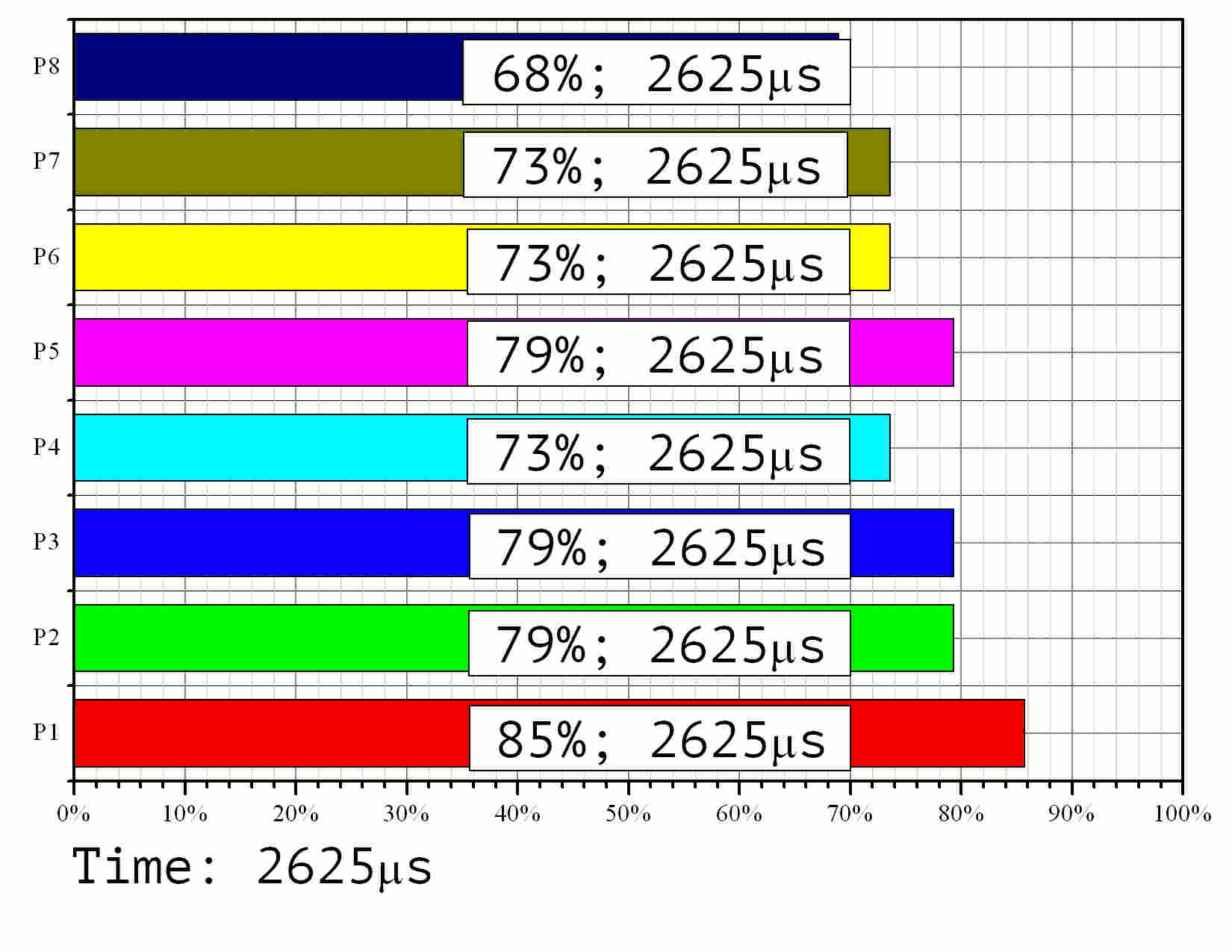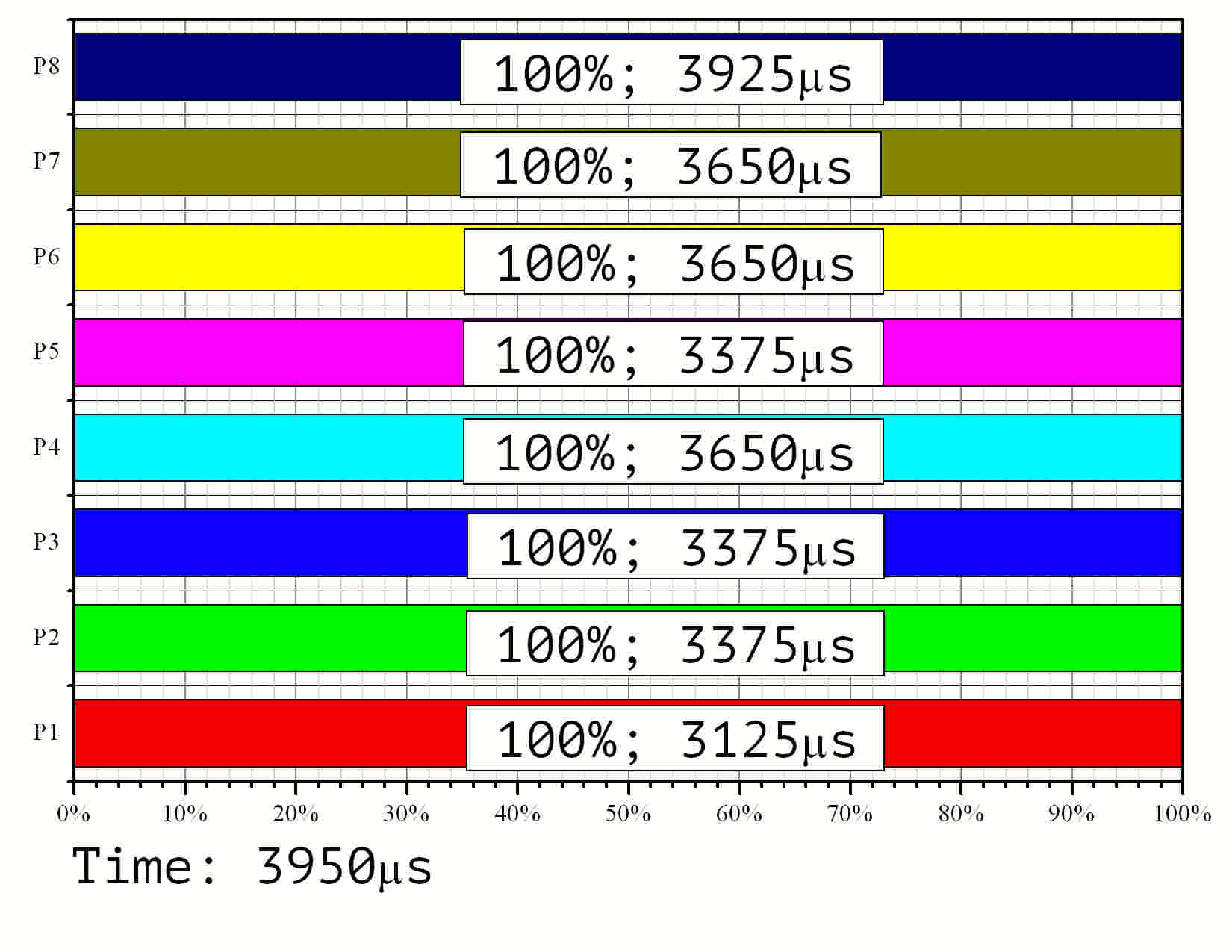
Рис. 11. Моделирование процесса выполнения параллельного алгоритма на 8 процессорах для задачи размерности 15 со 128-битными элементами
По времени выполнения видно, что наименее нагруженный
процессор работает лишь ![]() от общего времени выполнения задачи. Это
соответствует значению эффективности
от общего времени выполнения задачи. Это
соответствует значению эффективности ![]() . Среди остальных 8 процессоров три работали с
эффективностью
. Среди остальных 8 процессоров три работали с
эффективностью ![]() ,
ещё три с эффективностью
,
ещё три с эффективностью ![]() . Ускорение оказалось равным
. Ускорение оказалось равным ![]() вместо теоретически
достижимого
вместо теоретически
достижимого ![]() .
Соответственно, средняя эффективность составила
.
Соответственно, средняя эффективность составила ![]() . Согласно графику на Рис. 9, эта
величина должна составлять порядка
. Согласно графику на Рис. 9, эта
величина должна составлять порядка ![]() . Разница обусловлена неточным выбором время
обработки нулевого элемента, которое трудно однозначно определить по графику на
Рис. 2.
. Разница обусловлена неточным выбором время
обработки нулевого элемента, которое трудно однозначно определить по графику на
Рис. 2.
4. Заключение
Использованные в работе средства визуализации наглядно и достоверно показали, что разделение лексикографической последовательности на равные отрезки вызывает существенный дисбаланс вычислительной нагрузки. Соответственно, для обеспечения эффективной реализации алгоритма точного решения задачи о рюкзаке, основанного на использовании конструктивного перебора, необходима разработка особого метода распределения нагрузки, учитывающего выявленные особенности.
Список литературы.
- Осипян В.О. Разработка математических моделей систем передачи и защиты информации. 2007.
- Kate A., Goldberg I. Generalizing cryptosystems based on the subset sum problem. International Journal of Information Security, 2011, vol. 10, no. 3, pp. 189–199.
- Куприяшин М.А., Борзунов Г. И. Анализ состояния работ, направленных на повышение стойкости шифросистем на основе задачи о рюкзаке. Безопасность информационных технологий, 2013, №1, с. 111-112.
- Гергель В.П. Теория и практика параллельных вычислений. ИНТУИТ, Бином. Лаборатория знаний, 2007.
- Борзунов Г.И., Петрова Т. В., Сучкова Е. А. Повышение эффективности масштабирования набора задач при поиске экстремальных разбиений. Безопасность информационных технологий, 2011, № 3, 116–120с.
- Karp R.M. Reducibility Among Combinatorial Problems The IBM Research Symposia Series, под ред. R.E. Miller, J.W. Thatcher, J.D. Bohlinger. Springer US, 1972, с. 85–103.
VISUALIZATION AND ANALYSIS OF THE EXACT ALGORITHM FOR KNAPSACK PROBLEM BASED ON EXHAUSTIVE SEARCH
M.A. Kupriyashin, G.I. Borzunov
National Research Nuclear University “MEPhI”, Russia
kmickle@yandex.ru; parproc@gmail.com
Annotation
Knapsack packing vector testing procedures for the parallel exhaustive search algorithm have been analyzed. Graphs of computational complexity to test a single knapsack vector have been obtained via experiment for different values of knapsack element sizes. Diagrams of load balancing have been obtained and analyzed for the case when lexicographic sequence is split into equal-length segments.
Keywords: knapsack problem, exhaustive search, parallel computing
References
- Osipyan V.O. Razrabotka matematicheskih modelej sistem peredachi i zashhity informacii [Developing mathematical models of information security and transfer], 2007. [In Russian]
- Kate A., Goldberg I. Generalizing cryptosystems based on the subset sum problem. International Journal of Information Security, 2011, vol. 10, no. 3, pp. 189–199.
- Kupriyashin M.A., Borzunov G.I. Analiz sostojanija rabot, napravlennyh na povyshenie stojkosti shifrosistem na osnove zadachi o rjukzake [Analysis of papers on knapsack ciphersystems security enhancement]. Bezopasnost Informatsionnykh Tekhnology, 2013, no 1, pp. 111-112. [In Russian]
- Gergel V.P. Teorija i praktika parallel'nyh vychislenij [Theory and practice of parallel computing]. INTUIT, Binom. Laboratoriya Znaniy, 2007. [In Russian]
- Borzunov G.I., Petrova T.V., Suchkova E.A. Povyshenie jeffektivnosti masshtabirovanija nabora zadach pri poiske jekstremal'nyh razbienij [Task set scaling efficiency enchancement in extremal partitions search]. Bezopasnost Informatsionnykh Tekhnology, 2011, no. 3, pp. 116–120. [In Russian]
- Karp R.M. Reducibility Among Combinatorial Problems The IBM Research Symposia Series. ed. R.E. Miller, J.W. Thatcher, J.D. Bohlinger. Springer US, 1972. pp. 85–103.