МАТЕМАТИЧЕСКОЕ
МОДЕЛИРОВАНИЕ И ВИЗУАЛИЗАЦИЯ
ТЕЧЕНИЙ ЖИДКОСТИ В ГРУЗОВОЙ ЕМКОСТИ ГАЗОВОЗА
ПРИ ЕГО СОУДАРЕНИИ С ЛЕДОВЫМ ПРЕПЯТСТВИЕМ
Т. Елизарова1, Д. Сабурин2
1 Институт прикладной математики им. М.В. Келдыша РАН, Москва, Россия
2 Московский государственный университет им. М.В. Ломоносова, Москва, Россия
telizar@mail.ru, asoulofan@gmail.com
Оглавление
4. Результаты численного моделирования
4.1. Сила инерции вдоль
направления движения судна
4.2. Сила инерции под углом к направлению движения судна
Аннотация
В данной работе рассматривается проблема движения жидкости в баках современных ледоколов-газовозах, которые используются для транспортировки сжиженного газа в арктических условиях, при столкновении с ледовым препятствием.
Численное моделирование данной проблемы производится в рамках приближения мелкой воды. Расчеты выполнены для 10% заполнения бака с учетом формы его дна для случая направления скорости судна вдоль плоскости симметрии бака и под углом к ней. Проведена визуализация полученных нестационарных движений свободной поверхности и линий тока для оценок распределения нагрузки на стенки бака.
Для моделирования применяется алгоритм регуляризованных уравнений мелкой воды. Для их численного решения используется явная по времени разностная схема с аппроксимацией всех пространственных производных центральными разностями. Устойчивость численного алгоритма обеспечивается слагаемыми с коэффициентом τ, величина которого связывается с шагами пространственной сетки.
Шаг по времени выбирается в соответствии с условием Куранта. Предварительная настройка параметров разностного алгоритма была выполнена при численном моделировании данной задачи в одномерном приближении, когда решение рассчитывалось только в плоскости симметрии резервуара без учета формы дна.
В результате работы была проведена визуализация полученных нестационарных движений свободной поверхности и линий тока, а также были получены кривые распределения нагрузки на стенки бака и экспериментальные оценки для максимальной нагрузки на стенки бака. Адекватность работы метода была подтверждена соответствием полученных данных результатам выполненных ранее расчетов на основе более полной модели процесса с использованием трехмерных нестационарных уравнений Навье-Стокса.
Таким образом, в работе изложены результаты использования нового подхода для описания течений жидкостей в баке грузового судна при его взаимодействии с ледовым препятствием. В качестве математической модели используется приближение мелкой воды, численное решение основано на регуляризованном виде исходных уравнений. Трудоемкость такого численного алгоритма не велика и позволяет решать поставленную задачу с достаточной точностью даже на персональном компьютере. Алгоритм позволяют рассчитывать колебания жидкости на больших временах при разнообразных вариантах движения судна, в том числе его колебаниях на волнах. Представление результатов в виде фильмов дает возможность наглядно и оперативно анализировать распределение нагрузок на стенки бака.
Транспортировка сжиженных газов морским способом является в настоящее время одним из самых экономичных способов его доставки потребителям. Для этого применяются специальные топливные танки или баки, расположенные на судах-газовозах (см. Рис. 1 и 2). Большинство месторождений находится за полярным кругом или в непосредственной близости от него, поэтому суда-газовозы, работающие в арктических условиях, должны быть также и ледоколами. При столкновении судна со льдиной топливо в баке приходит в движение, которое может вызвать не только повреждения, но и разрушение стенки бака. Это явление требует наглядное представление. Только детальная визуализация этого трехмерного нестационарного процесса обеспечивает его понимание и адекватную трактовку. Только детальная визуализация позволит учесть все особенности данного явления и предотвратить неприятные последствия. Поэтому своевременной и важной является задача расчета колебаний жидкости в топливных танках газовоза, их качественное описание и количественный расчет, его визуальный анализ и определение предельных нагрузок на стенки бака, вызванных сложными маневрами судна,[1,2,3].

Рис. 1. Транспортировка газа морским способом

Рис. 2. Внутренний вид топливного танка
Данная задача может быть решена как экспериментально, с помощью модуляции столкновения жидкости (воды) со стенкой в специальном резервуаре, так и теоретически - численно в рамках трехмерных уравнений Навье-Стокса, дополненных условиями описания свободной поверхности жидкости и моделью турбулентности. У каждого подхода есть свои плюсы и минусы - так, теоретический подход намного дешевле по сравнению с экспериментальным, с другой стороны, он требует использования современных интеллектуальных технологий и менее нагляден. Расчет одного варианта - первых 20 секунд столкновения - требует около 12 часов работы соответствующей программы на суперкомпьютере. Согласно условиям технической безопасности, учитывающим конструкцию баков и толщину его стенок, транспортировка сжиженных газов допустима при заполнении бака меньше 15% и при его заполнении больше 75%. В первом случае помимо полных уравнений Навье-Стокса расчет возможен и с помощью двумерных уравнений мелкой воды [4]. Последнее позволяет существенно сократить времена счета, которые в этом случае составляют менее часа на персональном компьютере.
В данной работе рамках приближения мелкой воды проведено численное моделирование колебаний топлива в танке ледохода при его остановке после столкновения со льдиной. Расчеты выполнены для 10% заполнения бака с учетом формы его дна для случая направления скорости судна вдоль плоскости симметрии бака и под углом к ней. Получены картины течения и их детальный анализ с использованием программ визуализации нестационарного движения свободной поверхности и соответствующего вихревого движения жидкости. На основе данных этого анализа вычислены распределения нагрузки на стенки бака и определены их максимальные значения. Рассмотрены варианты симметричного и несимметричного взаимодействия с ледовым покрытием.
Расчетной областью является
емкость танка со следующими размерами: длина - 33.6 м, ширина - 29.8 м, высота - 23 м. Внешний вид емкости показан на Рис.2. Выберем неинерциальную
систему координат, связанную с самим баком. В этой системе направим ось Х вдоль
движения судна, ось Z - противоположно ускорению свободного падения ![]() , и ось Y - перпендикулярно
осям Х и Z На Рис.3 изображен поперечный срез емкости танка. В нижней части
функция рельефа дна выглядит следующим образом:
, и ось Y - перпендикулярно
осям Х и Z На Рис.3 изображен поперечный срез емкости танка. В нижней части
функция рельефа дна выглядит следующим образом:
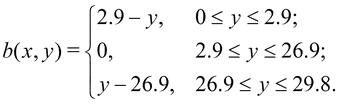 (1)
(1)
Размеры приведены в метрах.
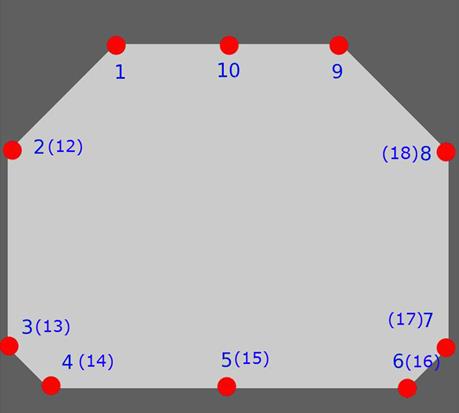
Рис. 3. Вертикальное сечение танка и обозначение реперных точек
Обозначим момент столкновения
судна со льдиной ![]() .
Изменения во времени скорости движения судна-газовоза при его соударении с
ледовым препятствием описываются полиномами шестой степени. Для начальной
скорости движения судна в 8 узлов этот полином имеет вид
.
Изменения во времени скорости движения судна-газовоза при его соударении с
ледовым препятствием описываются полиномами шестой степени. Для начальной
скорости движения судна в 8 узлов этот полином имеет вид
![]() (2)
(2)
для начальной скорости движения судна в 6 узлов
![]() (3)
(3)
для начальной скорости судна в 4 узла
![]() (4)
(4)
Один морской узел = 0.514 м/сек. В приведенных выше формулах размерность скорости - метры в секунду. В дальнейшем все величины даны в системе СИ. Графики скоростей приведены на Рис.4. Из графиков наглядно видно, что для всех трех вариантов остановка судна происходит за время порядка 1 сек.
Поведение жидкости в баке при
внезапном торможении судна будем рассматривать в неинерциальной системе
координат с помощью введения внешней силы ![]() , которая вычисляется на основе приведенного
выше известного закона изменения скорости , или :
, которая вычисляется на основе приведенного
выше известного закона изменения скорости , или :
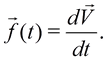 (5)
(5)
Данная задача может быть решена в рамках уравнений гидродинамики вязкой несжимаемой жидкости, записанных в приближении мелкой воды. В декартовой системе координат уравнения мелкой воды имеют следущий вид:
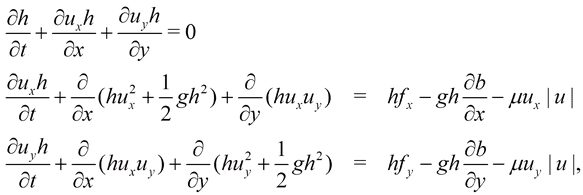 (6)
(6)
где
![]() - высота
жидкости над уровнем дна,
- высота
жидкости над уровнем дна, ![]() и
и ![]() - компоненты скорости течения,
- компоненты скорости течения, ![]() и
и ![]() - составляющие внешней силы,
- составляющие внешней силы, ![]() - рельеф дна,
- рельеф дна, ![]() - ускорение силы тяжести,
- ускорение силы тяжести, ![]() - коэффициент трения,
задаваемый из эмпирических соображений. Схема течения и обозначения приведены
на Рис.4.
- коэффициент трения,
задаваемый из эмпирических соображений. Схема течения и обозначения приведены
на Рис.4.
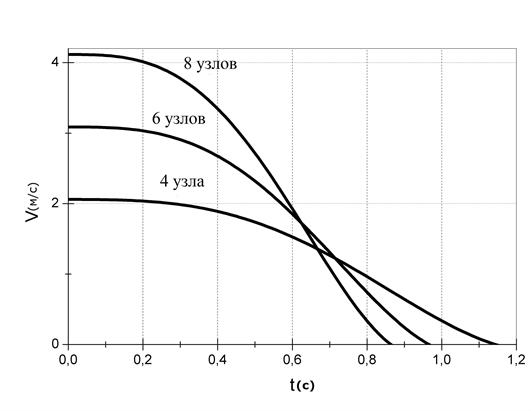
Рис. 4. Законы торможения судна-газовоза
при
его соударении с ледовым препятствием
В начальный момент времени t=0 полагаем уровень жидкости ![]() м, что соответствует 10%
заполнению бака. Считаем, что в начальный момент времени жидкость в баке
покоится.
м, что соответствует 10%
заполнению бака. Считаем, что в начальный момент времени жидкость в баке
покоится.
В качестве граничных условий
используем условия непротекания со скольжением для скорости и отражения для
величины ![]() :
:
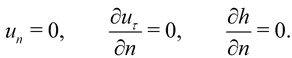
Здесь обозначено ![]() - направление,
перпендикулярное к границе области,
- направление,
перпендикулярное к границе области, ![]() - направление по касательной к границе
области.
- направление по касательной к границе
области.
При колебаниях жидкости в баке могут образовываться зоны течения, в которых высота жидкости обращается в ноль -- так называемые зоны сухого дна. Для описания течения с учетом таких зон с подвижной границей используется специальный алгоритм, позволяющий отслеживать границу с областями сухого дна.
С практической точки зрения
интерес представляет величина нагрузки на стенки бака при остановке судна.
Давление в баке ![]() вычисляется
как
вычисляется
как ![]() , где
, где ![]() = 700 кг/м3 --
плотность жидкости,
= 700 кг/м3 --
плотность жидкости, ![]() атмосферное
давление, включая давление паров жидкости.
атмосферное
давление, включая давление паров жидкости.
Для численного решения уравнений мелкой воды будем использовать регуляризованный вид этих уравнений, который получается путем усреднения уравнений мелкой воды по некоторому малому промежутку времени [5]. Система регуляризованных уравнений мелкой воды (РУМВ) имеет вид:
Лагаем
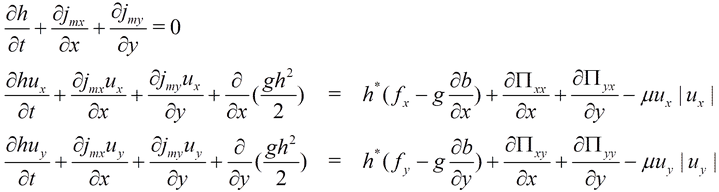 (7)
(7)
где использованы обозначения
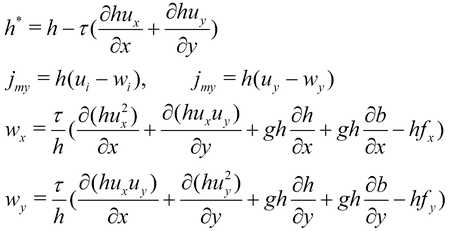 (8)
(8)
 (9)
(9)
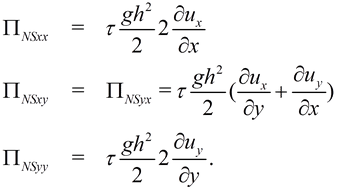
При ![]() = 0 система уравнений - переходит в систему уравнений
мелкой воды
= 0 система уравнений - переходит в систему уравнений
мелкой воды
При проведении численных расчетов
слагаемые с коэффициентом ![]() рассматриваются как регуляризирующие добавки,
обеспечивающие точность и устойчивость численного решения. Примеры применения
указанного алгоритма к широкому кругу течений в приближении мелкой воды
изложены, например, в [5,6,7,8].
рассматриваются как регуляризирующие добавки,
обеспечивающие точность и устойчивость численного решения. Примеры применения
указанного алгоритма к широкому кругу течений в приближении мелкой воды
изложены, например, в [5,6,7,8].
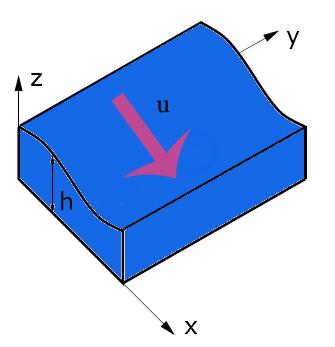
Рис. 5. Переменные уравнений мелкой воды
Для численного решения
регуляризованных уравнений мелкой воды будем использовать явную по времени
разностную схему с аппроксимацией всех пространственных производных
центральными разностями, e.g., [9]. Значения искомых переменных ![]() и
и ![]() отнесены к узлам пространственной
сетки. Устойчивость численного алгоритма обеспечивается слагаемыми с
коэффициентом
отнесены к узлам пространственной
сетки. Устойчивость численного алгоритма обеспечивается слагаемыми с
коэффициентом ![]() ,
величина которого связывается с шагами пространственной сетки
,
величина которого связывается с шагами пространственной сетки ![]() и
и ![]() и вычисляется в виде
и вычисляется в виде
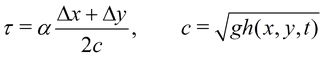 (10)
(10)
где
c - скорость распространения малых возмущений, рассчитанная в приближении
модели мелкой воды, ![]() численный
коэффициент, выбираемый из условий точности и устойчивости счета. Шаг по
времени выбирается в соответствии с условием Куранта, которое для данной задачи
имеет вид
численный
коэффициент, выбираемый из условий точности и устойчивости счета. Шаг по
времени выбирается в соответствии с условием Куранта, которое для данной задачи
имеет вид
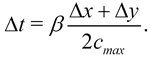 (11)
(11)
Здесь
число Куранта 0 < ![]() <
1 зависит от величины параметра регуляризации
<
1 зависит от величины параметра регуляризации ![]() в виде
в виде ![]() и подбирается в процессе вычислений для
обеспечения монотонности численного решения. В расчетах использовались
равномерные пространственные сетки.
и подбирается в процессе вычислений для
обеспечения монотонности численного решения. В расчетах использовались
равномерные пространственные сетки.
Важной особенностью задачи
является существование подвижной границы между областью, занятой жидкостью, и
зонами сухого дна, конфигурация которых меняется во времени. Последнее
усложняет вычислительный процесс и делает его менее устойчивым. Численный
алгоритм для расчета движения зоны сухого дна для регуляризованных уравнений
мелкой воды был предложен в [6] и имеет следующий вид: если в процессе расчета
оказывается, что ![]() ,
то полагаем
,
то полагаем ![]() и
и ![]() . Величина параметра
отсечения
. Величина параметра
отсечения ![]() связывается
с величиной наклона дна соотношением
связывается
с величиной наклона дна соотношением
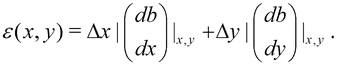 (12)
(12)
Аппроксимация условия для двумерных уравнений строится следующим образом:
![]() (13)
(13)
где
![]() .
.
Значение коэффициента ![]() и, соответственно,
предельного уровня отсечки
и, соответственно,
предельного уровня отсечки ![]() , подбирается в процессе вычислений из
соображений разумной точности описания зон сухого дна.
, подбирается в процессе вычислений из
соображений разумной точности описания зон сухого дна.
Разностный алгоритм решения
задачи включает в себя несколько настраиваемых параметров - это размер шагов по
пространству ![]() и
и ![]() , шаг по времени
, шаг по времени ![]() , который определяется
числом Куранта
, который определяется
числом Куранта ![]() ,
параметр регуляризации
,
параметр регуляризации ![]() ,
и величины для расчета движения границы области сухого дна - параметр отсечения
,
и величины для расчета движения границы области сухого дна - параметр отсечения
![]() или коэффициент
или коэффициент ![]() , связанный с наклоном дна.
Все эти величины определяют точность и трудоемкость численного решения.
, связанный с наклоном дна.
Все эти величины определяют точность и трудоемкость численного решения.
Оптимальное значение пространственного шага обусловлено выбором между быстротой решения, его точностью и устойчивостью расчета, поскольку уменьшение шага по пространству требует пропорционального уменьшения шага по времени.
Предварительная настройка
параметров разностного алгоритма была выполнена при численном моделировании
данной задачи в одномерном приближении, когда решение рассчитывалось только в
плоскости симметрии резервуара без учета наклона дна [8]. Для двумерного
расчета потребовалась дополнительная калибровка полученных ранее значений с
учетом наклона дна бака, то есть величин ![]() и
и ![]() .
.
Дополнительная сложность задачи
заключается в том, что в начальный момент времени из-за наклона нижней части
стенок бака в ![]() части
расчетной области имеется зона сухого дна. При численном решении задачи этот
факт вызывает сильные нефизичные осцилляции решения в начальные моменты времени
вблизи границы сухого дна. Для исключения этого численного эффекта в начальный
момент времени удобно положить, что в указанных областях высота уровня жидкости
имеет малое, но не нулевое значение
части
расчетной области имеется зона сухого дна. При численном решении задачи этот
факт вызывает сильные нефизичные осцилляции решения в начальные моменты времени
вблизи границы сухого дна. Для исключения этого численного эффекта в начальный
момент времени удобно положить, что в указанных областях высота уровня жидкости
имеет малое, но не нулевое значение ![]() = 0.0001 м. При дальнейшем уменьшении
= 0.0001 м. При дальнейшем уменьшении ![]() погрешность решения
практически не изменяется, в то время как устойчивость алгоритма, то есть шаг
по времени, уменьшается.
погрешность решения
практически не изменяется, в то время как устойчивость алгоритма, то есть шаг
по времени, уменьшается.
Таким образом оптимальными параметрами решения задачи является следующий набор величин:
• Равномерная
пространственная сетка с шагами: ![]() м;
м;
• Параметр регуляризации: ![]() ;
;
• Шаг по времени: 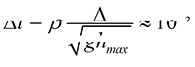 c,
что соответствует числу Куранта
c,
что соответствует числу Куранта ![]() ;
;
• Параметры сухого дна: ![]() =
0.0001 м,
=
0.0001 м, ![]() .
.
В этом случае вычислительная погрешность решения составляет 0.08 м.
Указанные параметры расчета
соответствуют числу Куранта ![]() = 0.01. Выбор столь малого числа Куранта
= 0.01. Выбор столь малого числа Куранта ![]() , и, соответственно, малого
шага по времени, обусловлен жесткими разрывами, возникающими в задаче в
начальные моменты времени. Для ускорения расчета шаг по времени может быть
сделан переменным, в зависимости
, и, соответственно, малого
шага по времени, обусловлен жесткими разрывами, возникающими в задаче в
начальные моменты времени. Для ускорения расчета шаг по времени может быть
сделан переменным, в зависимости ![]() , что позволяет существенно увеличить его на
больших временах расчета, когда начальные градиенты решения достаточно
сгладились.
, что позволяет существенно увеличить его на
больших временах расчета, когда начальные градиенты решения достаточно
сгладились.
Величина коэффициента трения
составляет ![]() =
0.001. Исключение силы трения
=
0.001. Исключение силы трения ![]() = 0 мало меняет результаты численного
расчета, что свидетельствует о слабом влиянии силы трения в данной задаче.
= 0 мало меняет результаты численного
расчета, что свидетельствует о слабом влиянии силы трения в данной задаче.
4. Результаты численного моделирования
Представление результатов
моделирования, в соответствии с расставленными выше акцентами, будет проходить
в два этапа. На первом этапе будет представлена качественная визуализация
поведения жидкости в баке. Она осуществляется с помощью графического
отображения поверхности жидкости ![]() и ее линий тока в расчетной области в
последовательные моменты времени, начиная с момента столкновения судна с
ледовым препятствием (t=0c.). Такая картина позволяет не только получить общую
картину динамики процесса, но и выявить все его особенности. На втором этапе
приводятся количественные графики для величин нагрузок на стенки бака. С их
помощью описывается зависимость давления в конкретной точке бака от времени, а
также определяются основные характеристики процесса: величина максимального
давления
и ее линий тока в расчетной области в
последовательные моменты времени, начиная с момента столкновения судна с
ледовым препятствием (t=0c.). Такая картина позволяет не только получить общую
картину динамики процесса, но и выявить все его особенности. На втором этапе
приводятся количественные графики для величин нагрузок на стенки бака. С их
помощью описывается зависимость давления в конкретной точке бака от времени, а
также определяются основные характеристики процесса: величина максимального
давления ![]() , период
колебаний Т и др.
, период
колебаний Т и др.
4.1. Сила инерции вдоль направления движения судна
Предполагаем, что перед
столкновением скорость судна направлена вдоль оси ![]() , то есть в плоскости симметрии вдоль
продольной оси судна, и скорость судна перед соударением составляет 8 узлов.
, то есть в плоскости симметрии вдоль
продольной оси судна, и скорость судна перед соударением составляет 8 узлов.
Общая картина течения и его особенности отражены на Рис. 6 и 7. Рисунки показывают характерный заброс жидкости вверх по передней стенке бака в начальные моменты времени и постепенное понижение этого максимума. Отразившись от передней стенки, волна, практически не теряя энергии, накатывает на противоположную, происходит аналогичный заброс жидкости вверх и последующее снижение уровня максимума. Таким образом, мы наблюдаем периодическое колебательное движение. C течением времени амплитуда колебаний жидкости в баке уменьшается, колебания приобретают гармонический вид, который соответствует распространению гравитационных волн в жидкости [4]., Постепенно колебания полностью затухают [8]. Виден также существенно двумерный характер течения вне плоскости симметрии, формирование и эволюция вихревых зон и линий растекания. Эти вихревые зоны образуются в результате жесткого торможения судна, а также из-за наличия сложной геометрии стенок бака и не плоского профиля его дна.
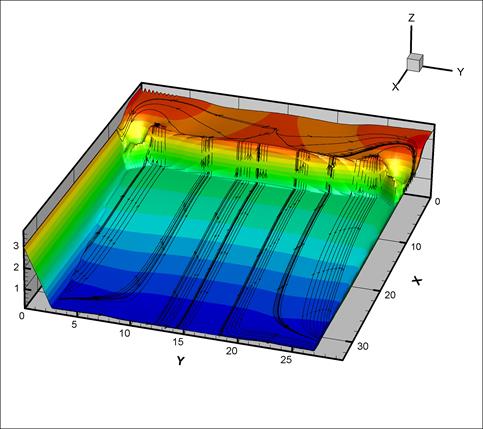
Рис. 6. Линии тока и поверхность
жидкости
при столкновении вдоль оси ОХ, t=1.5c
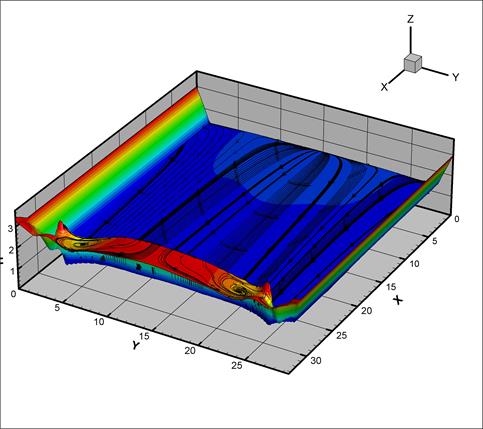
Рис. 7. Линии тока и поверхность
жижкости
при столкновении вдоль оси ОХ, t=8c
Графики для величин нагрузок на стенки бака для характерных реперных точек, расположенных в плоскости симметрии, приведены на Рис.8 для двумерных уравнений мелкой воды, на Рис.9 для трехмерных осредненных уравнений Навье-Стокса [3] и на Рис.10 для решения этой задачи в плоскости симметрии на основе одномерных уравнений мелкой воды [8]. Из графиков видно, что решения, рассчитанные в трех указанных постановках, в Одномерные колебанияплоскости симметрии (точки 5 и 15) очень близко совпадают между собой не только по значению максимального пика давления, но и по времени его появления, а также по времени появления второго и третьего пиков, и их высоты. Сравнение решения задач в рамках двумерных уравнений мелкой воды и трехмерных уравнений Навье-Стокса вне плоскости симметрии (точки 4 и 14) также показывает, что полученные течения практически идентичны. Исключение составляет небольшие отличия поведения решения на границе в реперных точках 3 и 7 (см. Рис.3), где расположена граница жидкости с областью сухого дна (здесь не приведены). Замеченные различия согласуются с общей картиной движения топлива, и тем самым не представляют особого практического интереса, так как в этих зонах не наблюдаются существенные нагрузки на стенки.
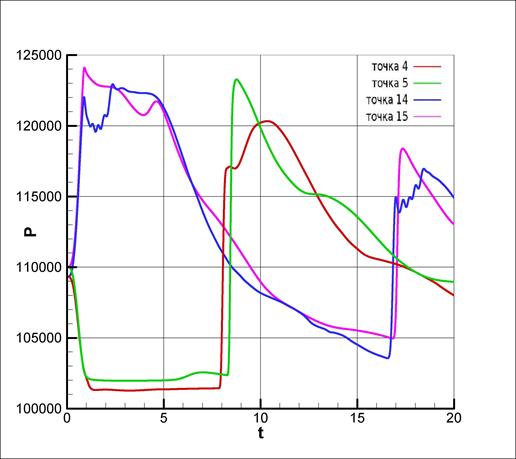
Рис.8. Эволюция давления. Двумерные уравнения мелкой воды
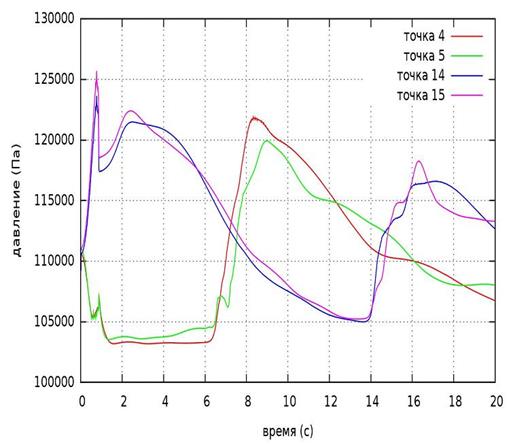
Рис. 9. Эволюция давления. Трехмерные уравнения Навье-Стокса
Далее в таблице приведены максимальные значения давлений на стенку бака, полученные с помощью трех указанных подходов, обозначенных как 3Д Навье-Стокс, 1Д РУМВ и 2Д РУМВ для трех значений начальной скорости судна:
|
|
8 узлов |
6 узлов |
4 узла |
|
3Д Навье-Стокс |
125 кПа |
121 кПа |
117 кПа |
|
1Д РУМВ |
125.8 кПа |
121,5 кПа |
116,6 кПа |
|
2Д РУМВ |
124.2 кПа |
120 кПа |
116,2 кПа |
Таблица показывает, что все полученные значения пиковых нагрузок на стенки бака оказываются весьма близкими.
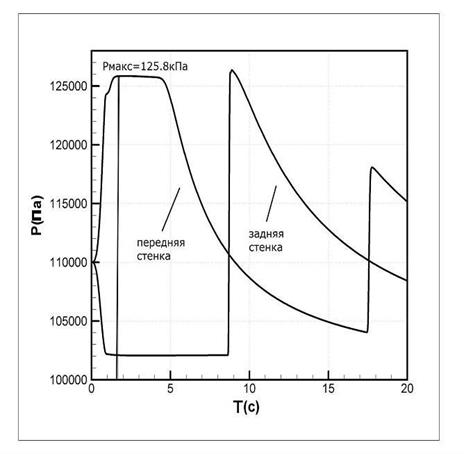
Рис. 10. Эволюция давления. Одномерные
уравнения
мелкой воды, расчет в плоскости симметрии
Таким образом, мы получили подтверждения адекватности решения задачи о колебаниях топлива на основе решения полных уравнений Навье-Стокса и в рамках приближения мелкой воды. Хорошее соответствие данных, полученных в рамках разных математических моделей и различной алгоритмической реализации для трех значений начальной скорости судна подтверждает правильность результатов математического моделирования поставленной задачи.
4.2. Сила инерции под углом к направлению движения судна
Важным практическим случаем
столкновений является вариант столкновения с льдиной, происходящее под небольшим
углом к продольной оси судна. Такой вид остановки судна является частным
случаем двойного столкновения с ледовым препятствием, при котором корабль,
ударяясь об одну льдину, затем сталкивается уже под некоторым ненулевым углом с
другим препятствием. Здесь мы не будем рассматривать конкретный случай двойного
столкновения, а рассмотрим его модельный вариант, для чего направим скорость ![]() под некоторым углом к оси судна
ОХ, что приводит к появлению отличной от нуля компоненты силы инерции
под некоторым углом к оси судна
ОХ, что приводит к появлению отличной от нуля компоненты силы инерции ![]() . Далее приведен расчет для
столкновения под углом 20 градусов.
. Далее приведен расчет для
столкновения под углом 20 градусов.
Общая картина течения и его особенности отражены на Рис.11 и 12.
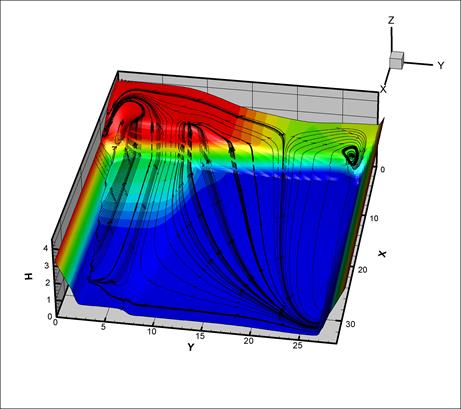
Рис. 11. Линии тока и поверхность жидкости
при
столкновении под углом к оси ОХ, t=1,5c
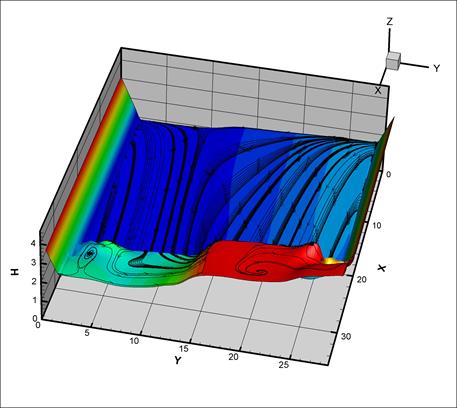
Рис. 12. Линии тока и поверхность
жидкости при
столкновении под углом к оси ОХ, t=8c
Отметим, что и в таком случае
движение топлива получается колебательным, поэтому мы не будем повторять
описание общей картины течения, которое было дано для предыдущего случая, а
сразу перейдем к обсуждению его особенностей. Данное течение является
существенно двумерным и несимметричным. Наличие ненулевой компоненты силы
инерции ![]() приводит
к кардинальной перестройке течения и перераспределению нагрузок на стенки бака
по сравнению со случаем симметричного течения. При этом наблюдаются колебания
жидкости, которые являются результатом нелинейного взаимодействия колебаний
вдоль осей ОХ и ОY. В частности, максимальные значения уровня в начальные
моменты времени сосредоточены только в левой нижней части плоскости XY, а
наибольшие значения достигаются в точке 4. Интересен и другой факт - так как
размеры резервуара по осям
приводит
к кардинальной перестройке течения и перераспределению нагрузок на стенки бака
по сравнению со случаем симметричного течения. При этом наблюдаются колебания
жидкости, которые являются результатом нелинейного взаимодействия колебаний
вдоль осей ОХ и ОY. В частности, максимальные значения уровня в начальные
моменты времени сосредоточены только в левой нижней части плоскости XY, а
наибольшие значения достигаются в точке 4. Интересен и другой факт - так как
размеры резервуара по осям ![]() и
и ![]() близки, т.е.
близки, т.е. ![]() , то следующий максимум уровня жидкости
возникает на противоположной стенке бака в точке 16. Между этими двумя пиками
уровня жидкости движение представляет собой два поперечных колебания, которые
сосуществуют практически независимо друг от друга.
, то следующий максимум уровня жидкости
возникает на противоположной стенке бака в точке 16. Между этими двумя пиками
уровня жидкости движение представляет собой два поперечных колебания, которые
сосуществуют практически независимо друг от друга.
Графики нагрузок на стенки бака в этих точках, а также для сравненияв точке 5 приведены на Рис.13. Отметим, что по сравнению с вариантом симметричного течения, здесь образуется более высокое максимальное давление на стенку - 127.5 кПа.
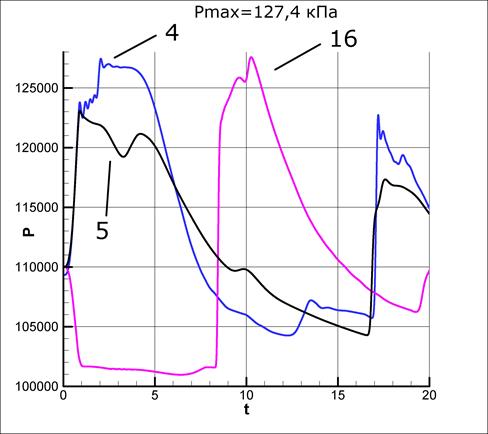
Рис. 13. Зависимость давления сжиженного
газа на стенку при
столкновении под углом в реперных точках 4, 5, 16
В дополнение к приведенным рисункам (№ 6,7,11,12) представлены анимации (фильмы), изображающие в 3Д проекции эволюцию уровня жидкости и линий тока вплоть до момента времени t = 40cек. Кроме того, для обоих вариантов течения представлены анимации, на которых показаны двумерные распределения высоты уровня жидкости и мгновенные распределения линий тока. Такое представление результатов в виде фильмов дает возможность наглядно и оперативно анализировать распределение нагрузок на стенки бака.
Таким образом в работе изложены результаты использования комплекса программ для описания течений жидкостей в баке грузового судна при его взаимодействии с ледовым препятствием. В качестве математической модели используется приближение мелкой воды, численное решение основано на регуляризованном виде исходных уравнений.
Адекватность работы метода подтверждается соответствием полученных данных результатам выполненных ранее расчетов на основе более полной модели процесса с использованием трехмерных нестационарных уравнений Навье-Стокса осредненных по Рейнольдсу, в которые включен блок расчета свободной поверхности жидкости.
Трудоемкость численного алгоритма не велика и позволяет решать поставленную задачу с достаточной точностью даже на персональном компьютере. Алгоритм позволяют рассчитывать колебания жидкости на больших временах при разнообразных вариантах движения судна, в том числе его колебаниях на волнах.
Работа поддержана грантом РФФИ 13-01-00703.
1. Гурьев Ю.В., Ткаченко И.В., Якушенко Е.И. Компьютерные технологии в корабельной гидродинамике: состояние и перспективы // Фундаментальная и прикладная гидрофизика,. Сб. научн. трудов. Т 4, № 3, 2011, с. 8-21.
2. Сафрай А.С., Ткаченко И.В. Численное моделирование гравитационных течений жидкости в наклонных каналах // Изв. РАН, Механика жидкости и газа. 2009. № 1. № 3, с. 8-21.
3. Дукарский А.О., Кисилев Д.Б., Ткаченко И.В., Тряскин В.Н., Тряскин Н.В., Якимов В.В. Математическое моделирование колебаний жидкости в грузовых емкостях газовозов при соударении с ледовым препятствием // Морские интеллектуальные технологии. 2011. № 4. с. 69-75.
4. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. Наука, М., 1986.
5. Булатов О.В., Елизарова Т.Г. Регуляризованные уравнения мелкой воды и эффективный метод численного моделирования течений в неглубоких водоемах // Ж. вычисл. матем. и матем. физ., 2011, т.51, № 1, с.170--184.
6. Bulatov O.V., Elizarova T.G. Regularized shallow water equations in numerical modeling of tsunami propagation and runup. Joint Conference Proceedings, 9th International Conference on Urban Earthquake Engineering/ 4th Asia Conference on Earthquake Engineering, March 6-8, 2012, Tokyo Institute of Technology, Tokyo, Japan. pp 2017-2025
7. Елизарова Т.Г., Истомина М.А., Шелковников Н.К. Численное моделирование формирования уединенной волны в кольцевом аэрогидроканале. Математическое моделирование, 2012, том 24, № 4, с.107-116
8. Елизарова Т.Г., Сабурин Д.А. Численное моделирование колебаний жидкости в топливных баках. Математическое моделирование, 2013, том 25, № 3, с.75-88.
9. Елизарова Т.Г. Квазигазодинамические уравнения и методы расчета вязких течений. Москва, Научный мир, 2007 -- 351 с.
MATHEMATICAL
MODELING AND VISUALIZATION
OF THE SLOSHING IN THE ICE-BREAKER’S TANK AFTER
IMPACT INTERACTION WITH ICE BARRIER
T. Elizarova1, D. Saburin2
1 Keldysh Institute for Applied Mathematics RAS, Moscow, Russian Federation
2 Lomonosov Moscow State University, Moscow, Russian Federation
telizar@mail.ru, asoulofan@gmail.com
Abstract
The problem of the sloshing in the modern ice-breaker’s tankers used for transporting the liquefied gas in arctic conditions after impact interaction with ice barrier is considered.
Mathematical modeling is produced using regularized shallow water equations. The calculations is made for 10-percent tanker fill with bottom shape taken into account in case of vessel velocity directed along the plane of symmetry of the tank and with angle to it. The received non-stationary motions of the free surface and stream lines were visualized for pressure distribution on the tank wall.
The regularized shallow water equations algorithm is used for the modeling. The explicit finite-difference scheme with approximation of the spatial derivatives by central differences is used for the numerical solution. The stability of the numerical algorithm is provided by components with factor τ, which value is linked with the spatial grid step. The time step was chosen in accordance of Courant condition. The preliminary numerical algorithm’s factors adjustment was made during the numerical modeling of this problem in one-dimensional approximation, where the solution was calculated only in the plane of symmetry of the tank ignoring the bottom shape.
As the result of this modeling, the visualizations of received non-stationary motions of the free surface and stream lines and experimental estimations of maximum pressure values on the tank wall were obtained. The adequacy of this method was proved by full consistency of this calculations to the previous calculations based on more complete model of the process using three-dimensional nonstationary Navier-Stokes equations accomplished by surface motion.
Thus, the results of the new approach for describing sloshing in modern ice-breaker’s tankers after impact interaction with ice barrier are presented in this article. The shallow water approximation is used as a mathematical model here; the numerical solution is based on the regularized form of the initial equations. The complexity of such a numerical algorithm is not great and it allows to solve the problem under consideration using ordinary personal computer. Algorithm allows to calculate the sloshing during large times in a variety of variants of vessel movement, including the sloshing on waves. The result presentation in the form of short movies gives an ability to clearly and quickly analyze the pressure distribution on the tank wall.
References
1. Yu. V. Gur’ev, I. V. Tkachenko, and E. I. Yakushenko. Kompyuternye tekhnologii v korabelnoy gidrodinamike: sostoyanie i perspektivy [Computer technology in naval hydrodynamics: status and prospects]. Fundam. Appl. Hydrophys., vol. 4, № 3, 2011, pp. 8–21.
2. A. S. Safrai and I. V. Tkachenko. [Numerical simulation of gravitational fluid flows in inclined channels]. Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza, № 1, 2009, pp. 27–38.
3. A. O. Dukarskii, D. B. Kisilev, I. V. Tkachenko, V. N. Tryaskin, N. V. Tryaskin, and V. V. Yakimov. Matematicheskoe modelirovanie kolebaniy zhidkosti v gruzovykh emkostyakh gazovozov pri soudarenii s ledovym prepyatstviem [Mathematical modeling of fluid oscillations in the LNG cargo tanks in a collision with an ice barrier]. Morskie intellektualnye tekhnologii, 2011. № 4. pp. 69-75.
4. L.D. Landau, and E. M. Lifshits. Fluid Mechanics. Butterworth[1]Heinemann, Oxford, 1987.
5. O. V. Bulatov and T. G. Elizarova. Regulyarizovannye uravneniya melkoy vody i ffektivnyy metod chislennogo modelirovaniya techeniy v neglubokikh vodoemakh [Regularized shallow water equations and efficient method for the numerical simulation of flows in shallow water]. Zh. vychisl. matem. i matem. fiz., vol. 51, № 1, 2011, pp. 170--184.
6. O. V. Bulatov and T. G. Elizarova. Regularized shallow water equations in numerical modeling of tsunami propagation and runup. Joint Conference Proceedings, 9th International Conference on Urban Earthquake Engineering, 4th Asia Conference on Earthquake Engineering, Tokyo Inst. Technol, Tokyo, 2012, pp. 2017–2025
7. T. G. Elizarova, M. A. Istomina, and N. K. Shelkovnikov. Chislennoe modelirovanie formirovaniya uedinennoy volny v koltsevom aerogidrokanale [Numerical simulation of the formation of a solitary wave in the annular aerial hydraulic canals]. Matematicheskoe modelirovanie [Math. Models Comput. Simul.], vol. 24, № 4, 2012, pp.107–116.
8. T. G. Elizarova, D.S. Saburin. Chislennoe modelirovanie kolebaniy zhidkosti v toplivnykh bakakh [Numerical Simulation of Fluid Oscillations in Fuel Tanks], Matematicheskoe modelirovanie [Mathematical Modeling], vol. 25, № 3, 2013, pp. 75–88.
9. T. G. Elizarova, Quasi-Gas Dynamic Equations. Springer, IBSN 978-3-642-0029-5, 2009.