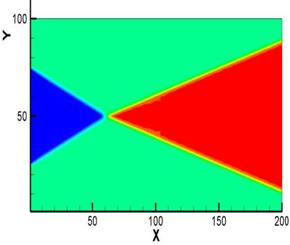
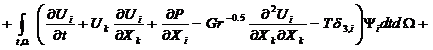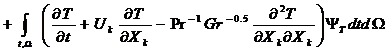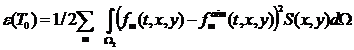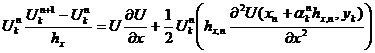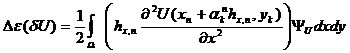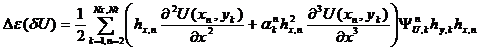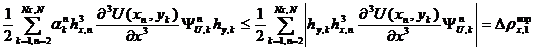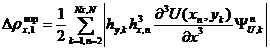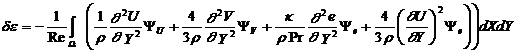За последнее десятилетие произошло интенсивное развитие методов и подходов научной визуализации, основанных на дополнительном анализе данных. Следуя условной классификации, приведенной в [1], будем называть эту группу методов и подходов – методы анализа данных. Общее свойство данной группы методов – достижение новых результатов с помощью препроцессингового, параллельного расчету, или дополнительного анализа основного поля данных. Процесс анализа данных, как правило, предполагает применение мощного математического аппарата, разработанного в других областях знания.
Общую концепцию визуального представления для данной группы методов можно сформулировать так: мы получаем основное поле данных, применяем к нему для анализа и обработки некий математический аппарат, получаем новую информацию, и затем применяем средства визуализации к полученной новой информации и к основному полю данных. Таким образом, методы анализа данных основаны на синтезе методов визуального представления и математического аппарата из разных областей.
Подобная концепция имеет самые разнообразные формы и методы применения и позволяет получать новые результаты в самых разных направлениях. Примерами могут служить такие направления как:
- локализация структур в поле течения с помощью вейвлет-анализа [2] ;
- статистическая обработка основного поля данных с целью выявления областей резких градиентов [3];
- визуализация решений оптимизационных задач как многомерных данных [4];
- применение сопряженных уравнений для создания полностью управляемой и физически точной визуализации распространения жидкостей и газов [5].
К этой же группе методов можно отнести материалы и результаты, представленные в данной работе. Данная работа посвящена различным аспектам трактовки и использования визуального представления сопряженных параметров при решении сопряженных уравнений.
Сопряженные уравнения в настоящее время широко применяются при решении оптимизационных и обратных задач в самых разных областях приложения вычислительной математики. Использование сопряженных уравнений позволяет определять чувствительность искомых функционалов в различных задачах к различного рода возмущениям. Развернутая теория сопряженных уравнений и различных способов их применения в практических расчетах представлена в работах [6,7]. В задачах вычислительной механики жидкости и газа сопряженные уравнения применяются при решении задач, связанных с необходимостью идентификации и управления изучаемым течением. Также теория сопряженных уравнений может быть применена в задачах верификации и валидации численных результатов и математических моделей в целом.
При решении задач идентификации и управления течением жидкости, сформулированных в оптимизационной постановке, единственным практически доступным способом определения чувствительности целевого функционала к управляющим параметрам является решение сопряженных уравнений [6,8,9]. Эти уравнения описывают поля сопряженных параметров, являющихся некоторыми аналогами (дуальными величинами согласно принципу двойственности) параметров течения. Сопряженные параметры в определенном смысле описывают распространение информации при решении обратных задач в оптимизационной постановке. Сопряженные параметры зависят от вида прямой задачи (уравнений и соответствующего поля течения) и целевой функции. В зависимости от вида управляющих параметров, градиент целевого функционала зависит от различных функций от сопряженных параметров. Сопряженные параметры позволяют отслеживать распространение информации в обратных задачах и получать сложные информационные связи, не совпадающие с имеющимися в реальных физических процессах и соответствующие постановкам обратных (некорректно поставленных) задач.
Однако до сравнительно недавнего времени при решении подобных задач обычно ограничивались визуальным представлением поля основных газодинамических параметров, согласно устоявшимся представлениям и методам визуализации газодинамических процессов. Визуальное представление поля сопряженных параметров не было широко распространено из-за непрозрачности их физического смысла и отсутствия соответствующих интуитивных представлений.
Ранее сопряженные параметры использовались для расчета вариации некоторых функционалов наблюдения при изменении источников и назывались функция ценности информации [6] или ценность (importance) [9]. В обратных задачах конвекции они, как правило, использовались чисто формально либо для расчета градиента (внутри алгоритма) либо для постановки необходимого условия оптимальности [8-10].
В работе [11] было предложено при решении сопряженных задач получать новую дополнительную информацию из визуального представления сопряженных параметров. В задачах управления течением, идентификации течения сопряженные параметры используются для расчета градиента целевого функционала. Визуализация сопряженных параметров в подобных задачах может быть использована для поиска зон наиболее эффективного контроля или для выбора зон измерения.
За последнее десятилетие в вычислительной математике и математическом моделировании сложилась новая самостоятельная дисциплина – верификация и валидация (Verification&Validation –V&V). Основная цель данной дисциплины – обеспечить уверенность исследователя и пользователя во всей цепочке исследования: физическая модель – математическая модель – численный алгоритм – программная реализация алгоритма – организация расчета – обработка и представление результатов. Установление новых стандартов надежности программ и результатов расчетов привело к формализации понятий верификации (подтверждения правильности численной модели) и валидации (подтверждения соответствия физической модели задаче реального мира) в вычислительной аэрогазодинамике [12-14]. В рамках V&V стандартные методы, включающие асимптотическую сходимость по сетке и проверку на тестовых задачах, дополняются методами, основанными на апостериорной оценке численной погрешности расчета [15-17], оценке погрешности выбора модели [18], В подобных задачах визуализация играет ключевую роль, например, при адаптации сетки [16] или анализе оптимального расположения датчиков [19].
Как отмечается в работе [20], именно синтез математического аппарата с инструментами визуализации позволяет создавать надежные и востребованные средства V&V.
Использование поля сопряженных параметров в работе [15] позволяет рассчитать и визуализировать вклады ошибки исходных данных, ошибки физической модели и погрешности дискретизации в погрешность целевого функционала. Это может использоваться для уменьшения погрешности и для получения решения с необходимой гарантированной точностью.
Данная работа является логическим продолжением работ [11,15], обобщая и развивая полученные в них результаты в области задач идентификации и управления течением. Одновременно особое внимание уделяется аспектам применения сопряженных уравнений и визуального представления сопряженных параметров в качестве инструментов V&V.
2. Упрощенная формальная схема алгоритма
Данная работа посвящена анализу применения сопряженных уравнений и визуального представления сопряженных параметров в задачах идентификации и управления течением, верификации и валидации расчетов. Одной из важных компонент анализа является использование градиента некоторого функционала по отношению к набору управляющих параметров или набор этих управляющих параметров, полученный при минимизации функционала. Рассмотрим упрощенную формальную схему алгоритма. Пусть основная (прямая) задача имеет вид
|
|
(1) |
,с граничными условиями
|
|
(2) |
Здесь 
нелинейный
дифференциальный оператор (
), 
- набор физических
переменных (плотность, компоненты скорости и т.д.) (
). 
- некоторые управляющие
параметры (источники, локальная погрешность аппроксимации, члены, ответственные
за малые физические эффекты) (
, 
). Операторы 
дифференцируемы по Фреше,
соответствующие производные 
,
. Используем также краткие
обозначения: 
и
,
.
Рассмотрим также дифференцируемый
по Фреше целевой функционал 
. Кроме его величины, существенный
практический интерес представляют также его чувствительность к вариации
управляющих параметров (для краткости далее опустим граничные члены).
Соответствующие градиенты выражаются через сопряженные переменные
. Для их
определения введем Лагранжиан
|
|
(3) |
.
Вариация Лагранжиана имеет вид
|
|
(4) |
Можно показать, что вариация целевого функционала равна вариации Лагранжиана на решении прямой задачи (1,2) и задачи в возмущениях:
|
|
(5) |
|
|
(6) |
Удобно использовать
производные Гато (производные вдоль направления 
) вместо вариаций
функционала
|
|
(7) |
и производную Гато оператора вместо уравнений для возмущений
|
|
(8) |
Оператор Гато прямой задачи обозначается как касательная линейная задача и имеет вид:
|
|
(9) |
,с граничными условиями
|
|
(10) |
.
Эта форма удобнее, чем (5-6), так как не включает предположений о малости возмущений.
Производная Гато целевого функционала является линейным
непрерывным функционалом и может быть представлена как внутреннее произведение
в 
|
|
(11) |
Соответственно, производная Гато Лагранжиана имеет вид:
|
|
(12) |
.
Используя тождество
Лагранжа 
реализованное
интегрированием по частям можно преобразовать (12)
|
|
(13) |
Производная Лагранжиана по управляющим параметрам
|
|
(14) |
Она выполняется на сопряженных уравнениях
|
|
(15) |
Вариация Лагранжиана под действием возмущения 
|
|
(16) |
В результате
мы получаем исключительно ценное выражение, позволяющее определять вариацию
целевого функционала и представление его градиента в 
. Градиент целевого
функционала, а также результаты поиска оптимального решения 
, обычно
получаемого градиентным методом 
, особо информативны при
визуализации и будут рассмотрены в дальнейшем на нескольких частных примерах.
Мы обсудим визуализацию градиента целевого функционала в том случае, когда
управляющими параметрами являются: погрешность аппроксимации, отличия в
используемой модели (вязкие источники). Рассмотрим также задачи оптимального
управления. Форма уравнений (15) и градиента (16) достаточно универсальна, в
данной работе представлены результаты как для управления с помощью источников,
так с помощью граничных условий. Вариация сопряженных уравнений для всех
вариантов минимальна.
3. Задачи идентификации и управления течением
Рассмотрим применение подобного подхода на примере достаточно простой задачи конвекции в параллелепипеде.
Для этого случая проводится решение обратных задач для трехмерного ламинарного течения газа, описываемого уравнениями Навье-Стокса в приближении Буссинеска [21,22]:
|
|
|
|
(17) |
|
|
|
|
Задача идентификации течения: определить распределение температуры на границе Tw(X,Y,0) (или тепловой источник Q(X,Y,Z)), используя в качестве исходных данных измерения компонент скорости fexp(Xm,Ym,Zm).
Задача управления течением: определить распределение температуры на границе Tw(X,Y,0) (или источники тепла Q(X,Y,Z)), которое позволяет создать необходимое поле скоростей fexp(Xm,Ym,Zm).
Для решения этих задач необходимо минимизировать целевой функционал
|
|
(18) |
невязку между расчетными и целевыми (экспериментальными) величинами fexp(Xm,Ym,Zm). Для этого используем градиент функционала. Так как число управляющих параметров может быть очень велико (порядка числа узлов в поле), то, единственным быстрым способом расчета градиента (не зависящим от числа управляющих параметров) является решение сопряженной задачи [7,8,22]. К тому же, одно и то же поле сопряженных параметров может быть использовано для большого набора управляющих параметров (как граничных, так и объемных). Для формулирования сопряженной задачи объединим целевой функционал и слабую постановку прямой задачи в Лагранжиан.
|
|
|
|
|
(19) |
+
|
|
Будем считать, что сопряженные величины (множители Лагранжа) Yp,Yi,YTÎH1,2(W), (Yi=Yu,Yv,Yw,), H1,2(W) - Гильбертово пространство функций, имеющих суммируемые обобщенные производные первого по времени и второго по пространству порядка.
Сопряженная система
Сопряженная система, как правило, формулируется, как условие, при котором приращение Лагранжиана выражается через вариацию управляющих параметров так, чтобы, остальные члены первого порядка были равны нолю. Это дает возможность получить градиент невязки и, соответственно, необходимое условие минимума.
|
|
|
|
|
|
(20) |
|
|
Начальные и граничные условия
|
|
В отличие от прямой задачи начальные условия соответствуют концу временного интервала, и эволюция течения по времени идет вспять.
Если мы управляем течением с помощью температуры
стенки 
, то на решении этой системы
вариация невязки записывается в виде:
|
|
(21) |
отсюда определяем градиент невязки через градиент сопряженной температуры:
|
|
(22) |
Если
мы управляем течением с помощью распределенных источников тепла 
, то
|
|
(23) |
Градиент функционала указывает на направление продвижения к минимуму, там, где он мал по амплитуде, там влияние управления на целевой функционал мало, и наоборот.
Численные эксперименты
Поле течения рассчитывается с помощью конечно-разностной аппроксимации уравнений Навье-Стокса первого порядка точности по времени и второго по пространственным координатам.
При решении сопряженной задачи используется тот же конечно-разностный алгоритм, что и для решения прямой задачи, но установление по времени проводится в обратном направлении, начиная с t=T. Параметры течения, входящие в коэффициенты берутся из решения прямой задачи.
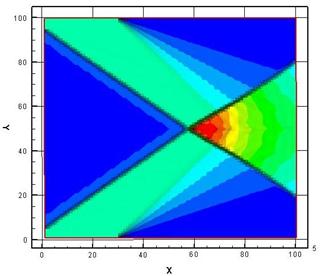
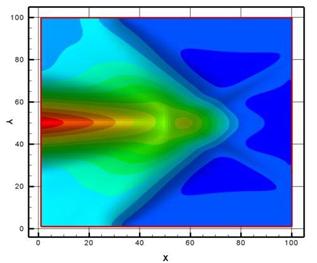
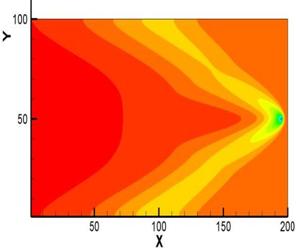
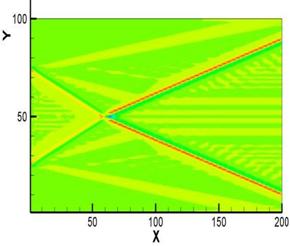
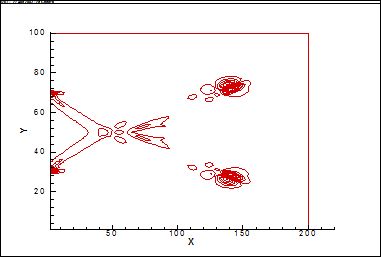
В качестве целевой функции рассмотрено распределение одной из компонент скорости W(X,Y,Z), полученное предварительным расчетом при нагреве нижней границы. Полученное в расчете поле течения представлено на рисунках 1,2. На рис.1 представлено поле вертикальной компоненты W от источника тепла на нижней границе. На рис.2 представлено поле температуры от источника тепла на нижней границе.
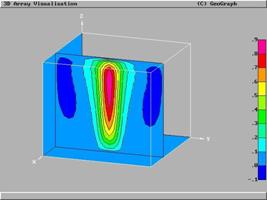
Рис. 1 Поле вертикальной компоненты W от источника тепла на нижней границе
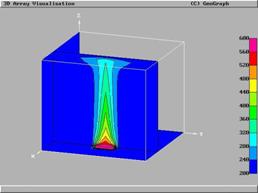
Рис. 2 Поле температуры от источника тепла на нижней границе
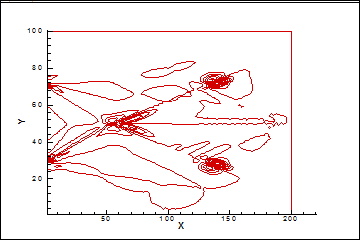
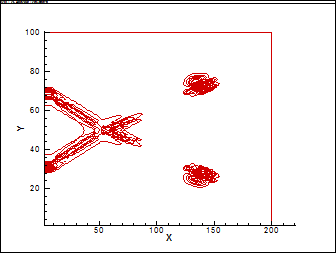
Рассчитано соответствующее поле сопряженных параметров, на рис. 3 представлена весовая функция для управления источниками тепла, на рис. 4 для управления температурой.
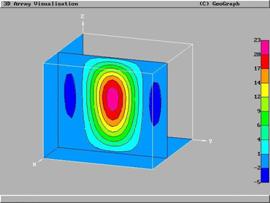
Рис. 3 Поле сопряженного параметра (на однородном поле), градиент для источника тепла
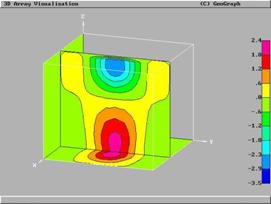
Рис. 4 Поле градиента сопряженного параметра (на однородном поле), градиент для температуры.
Поле сопряженных параметров использовано для определения температуры стенки по измерениям скорости с помощью метода наискорейшего спуска. Результат расчета температуры стенки представлен на рис. 5, истинное распределение – на рис. 6.
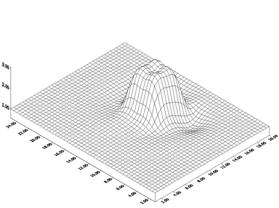
Рис. 5 Температура стенки, полученная расчетом
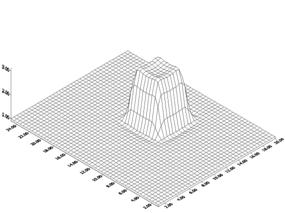
Рис. 6 Искомое распределение температуры стенки
Рис. 7 демонстрирует возможность сравнения двух точек измерения с координатами (0.6,0.2,0.8) и (0.6,0.6,0.8) с точки зрения их влияния на сопряженное поле, измерения во второй точке существенно информативней, так как она находится в восходящей части факела.
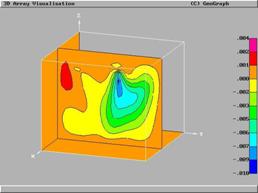
Рис. 7 Поле сопряженного параметра (на неоднородном поле) для двух точек измерения
Данный расчет представляет собой попытку качественного анализа с использованием сопряженных параметров для одной обратной задачи конвекции (трактуемой как задача управления или идентификации). Какую новую информацию мы получаем в данном случае на простом примере от использования визуального представления поля сопряженных параметров, не ограничиваясь визуализацией лишь стандартных газодинамических величин? Во-первых, рисунки 3 и 4 позволяют определить относительную эффективность управления в данной точке. Во-вторых, рисунок 7 позволяет нам судить о ценности измерений в конкретной точке.
Корректность определения сопряженных параметров подтверждается непосредственным решением обратной задачи (рисунки 5,6).
Таким образом, результаты расчетов данного примера иллюстрируют нам, как визуальное представление поля сопряженных параметров позволяет найти зоны для наиболее эффективного управления течением и для проведения измерений.
Далее рассмотрим задачу управления переходом между регулярным и маховским режимами взаимодействия ударных волн на примере уравнений Эйлера. Известно, что при пересечении косых скачков уплотнения существует диапазон чисел Маха и углов наклона скачков, в котором могут одновременно существовать как режим регулярного взаимодействия ударных волн, так и маховская конфигурация. Наличие двух устойчивых режимов течения, существующих в одних и тех же условиях, делает управление данным течением особенно перспективным, так как позволяет сосредоточиться на переходе к желаемому режиму течения, не заботясь о его поддержании в дальнейшем. В данном разделе на примере уравнений Эйлера проиллюстрирована возможность управления переходом от регулярного режима к маховскому за счет распределенного по пространству теплового импульса, приложенного в начальный момент времени. Чувствительность параметров течения (градиент некоторого функционала невязки между параметрами текущего и целевого поля) к начальному возмущению температуры рассчитывалась с помощью решения сопряженных уравнений. Необходимое для перехода возмущение находилось итерациями с использованием градиентных методов оптимизации.
Рассматривается модель взаимодействия двух плоскопараллельных сверхзвуковых потоков воздуха, образующихся при обтекании симметричных клиньев.
В качестве математической модели используются двумерные нестационарные уравнения Эйлера. На входной границе задаются условия втекания, соответствующие пересекающимся скачкам уплотнения. На боковых границах задаем условия втекания, соответствующие пересекающимся скачкам уплотнения и течению за веером волн разрежения, имитирующему обратный разворот потока на нижней по течению кромке клиньев. В данном течении веер волн разрежения выполняет существенную роль. В его отсутствие на маховском режиме скачок уплотнения прижимается к левой границе. Веер волн разрежения обеспечивает разгон течения в “жидком сопле Лаваля” до сверхзвуковых скоростей, что существенно облегчает постановку граничных условий на правой (выходной) границе. На выходной границе задаем условия вытекания. Структура течения на обоих режимах представлена на Рис. 8-9.
В качестве целевого функционала рассмотрена
невязка между текущим и желаемым распределениями параметров течения. Расчеты
проводятся в области неединственности по 
,
где одновременно возможны две структуры течения.
В качестве
управляющих параметров использованы возмущения начального распределения
параметров течения 
. Предполагается, что в момент 
на течение
подействовал некоторый тепловой импульс, изменивший 
, но оставивший
неизменными поля скоростей и плотности. В ходе дальнейшей временной эволюции
течение некоторым образом перестраивается. В рассматриваемой задаче нужно
определить пространственное распределение возмущения начальной температуры , которое минимизирует
невязку
|
|
(24) |
между расчетными 
и целевыми 
значениями
параметров течения.
Здесь 
-область нагрева (в данных расчетах
совпадает со всем полем), 
-область наблюдения за параметрами
течения, 
в
и 
- вне .
Для рассмотренной задачи имеется существенное отличие от обычных постановок обратных задач. Эволюция по пространству способна через некоторое время стереть вклад начальной температуры или начального импульса тепла. Если управляющий импульс не перевел течение в другое устойчивое состояние, через некоторое время он будет забыт.
В соответствии с уравнением
(16) при управлении с помощью граничных (в нашем случае начальных)
условий 
.
Чувствительность функционала к управляющим
параметрам (начальному полю температуры) рассчитывается с помощью решения
системы сопряженных уравнений, полученных стандартным образом и имеющих
в нашем случае форму:
|
|
(25) |
|
|
(26) |
|
|
(27) |
.|
начальные условия Граничные: |
(28) |
.Здесь 
- сопряженные
переменные.
Решение сопряженной системы позволяет определить градиент целевого функционала по отношению к возмущению начальной температуры в виде:
|
|
(29) |
При поиске
оптимального импульса нагрева использованы метод сопряженных градиентов и
наискорейшего спуска. Начиная с начального распределения определялось возмущенное
поле температуры итерациями вида 
(в случае наискорейшего спуска).
Каждая итерация соответствует решению одной прямой и одной сопряженной задач.
Численные эксперименты
При
тестировании прямой задачи получены неединственные решения для чисел Маха 
и углов
отклонения потока 
. Уравнения Эйлера решались
методом второго порядка точности MUSCL [23], задача Римана решалась методом HLLC
[24]. В основной части расчетов использовался метод четвертого порядка
точности по пространству [25] с расчетом задачи Римана по [24].
С помощью решения обратной задачи проведен поиск возмущения начальной температуры, переводящего решение с одной ветви на другую. Сопряженные уравнения решались с использованием метода [26]. Целевой функционал формировался как невязка плотности в текущем и в целевом состояниях.
|
|
|
|
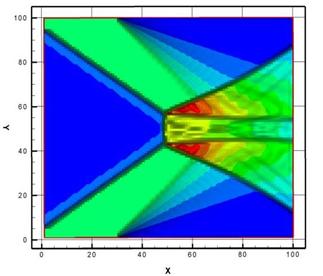
Рис. 8. Изолинии плотности (регулярный режим) |
Рис. 9. Изолинии плотности (маховский режим) |
|
|
|
|
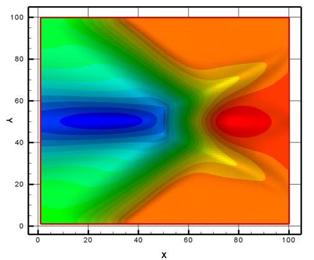
Рис. 10. Сопряженная плотность (регулярный режим) |
Рис. 11. . Сопряженная плотность (маховский режим) |
|
|
|
|
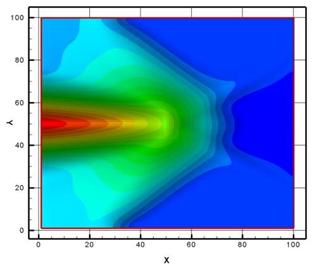
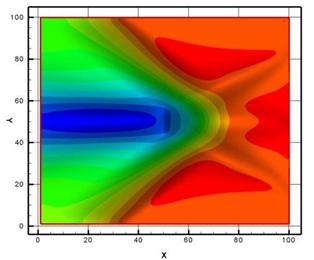
Рис. 12. Сопряженная энергия (регулярный режим) |
Рис. 13. Сопряженная энергия (маховский режим) |
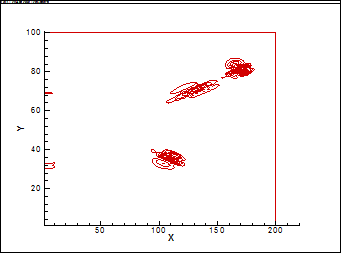
На рис. 8 представлены изолинии плотности на регулярном режиме, на рис. 9 изолинии на маховском режиме (М=3.45). Рисунки 10 и 11 представляют изолинии сопряженной плотности для регулярного и маховского режимов соответственно. Аналогичным образом представлены изолинии сопряженной энергии для обоих режимов на рисунках 12 и 13.
Рассмотрим, каким образом визуальные представления сопряженных полей позволяют нам получить в данной задаче ключевую информацию, необходимую для управления переходом между режимами.
При управлении с помощью распределенного источника нагрева сопряженная энергия соответствует градиенту целевого функционала. Она определяет как знак возмущения, так и его относительную величину и содержит основную информацию как необходимую для качественного понимания процесса (в каких зонах целесообразно воздействовать, в каких не имеет смысла, знак воздействия), так и для реализации итерационного цикла решения обратной задачи. При управлении с помощью вдува (источника массы) сопряженная плотность будет соответствовать градиенту. При более сложных управлениях (например, динамических) градиенту соответствует некоторая комбинация сопряженных параметров и параметров течения. В любом случае, вся необходимая для оптимизации информация содержится в поле сопряженных переменных.
Таким образом, рисунки 12 и 13 показывают направление (в пространстве управлений - вариаций температуры), вдоль которого надо двигаться, чтобы перейти от регулярного к маховскому режиму (рис. 12) и наоборот (рис. 13). Сопряженная плотность в данной постановке имеет скорее вспомогательный характер. Тем не менее, визуальное представление сопряженной плотности позволяет качественно судить о зонах, в которых образуется ценная информация (зонах значительного расхождения текущего и целевого поля) и о переносе этой информации по расчетному полю. В тех зонах, где сопряженная плотность близка к нулю, управление (а возможно и наблюдение) малоэффективно.
На рис. 14 представлено поле возмущения начальной температуры, осуществляющее переход из регулярного режима в маховский (невозмущенному полю температуры соответствует единица). Возмущения начальной температуры в основном положительны (соответствуют нагреву). При использовании только положительной части этого возмущения (проекции полученного возмущения на множество воздействий, соответствующих выделению энергии) позволяет добиться желаемого перехода.
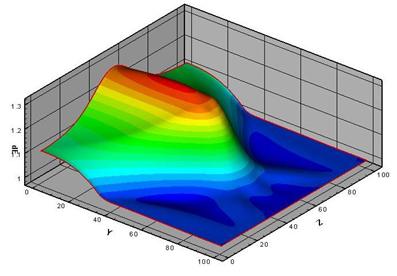
Рис. 14. Возмущения начальной температуры при переходе от регулярного к маховскому режиму.
4. Задачи верификации и валидации
Данный раздел ставит своей целью показать возможность применения сопряженных уравнений к оценке погрешности расчета (верификация) и погрешности физической модели (валидация). С применением сопряженных уравнений проводится оценка и прямая визуализация погрешности для различных случаев. Визуальное представление позволяет определить местоположение необходимых сеточных сгущений с целью уменьшения погрешности, а также непосредственно показать погрешность, вносимую влиянием тех или иных членов системы уравнений математической модели.
Верификация
Рассмотрим существенные новые элементы верификации, а именно апостериорную оценку погрешности расчета (учитывающую регулярность данного решения и не содержащую неопределенных констант).
Апостериорная оценка погрешности расчета
Начнем с апостериорной оценки погрешности в ее варианте для конечно-разностных схем [15-17].
|
(30) |
.(управлений на границе нет).
Пусть численное решение получено некоторым конечно-разностным методом
|
(31) |
.
В результате решения получим
сеточную функцию
. Предположим существование функции
совпадающей с сеточной в узлах. Конечные разности в 
разложим в ряд Тейлора, что дает дифференциальное
приближение схемы [27].
|
(32) |
.
Здесь 
ошибка аппроксимации, содержащая
члены ряда Тейлора и служащая возмущающим источником 
. Соответствующее
уравнение
|
(33) |
,
Согласно (16)
|
|
(34) |
Сопряженные уравнения:
|
(35) |
В качестве примера рассмотрим расчет и визуализацию погрешности на примере двумерного сверхзвукового вязкого течения, рис. 15.
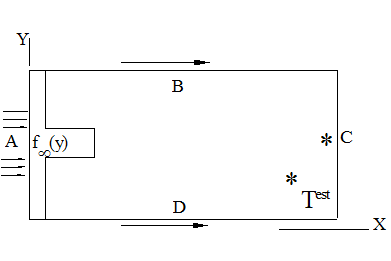
Рис. 15
Используем недивергентную конечно-разностную аппроксимацию параболизированных уравнений Навье-Стокса. Расчет проводится маршевым методом вдоль X.
|
|
(36) |
|
|
(37) |
|
|
(38) |
|
|
(39) |
На входной границе (A (X=0), Рис.15):
на боковых границах B, D (Y=0,
Y=1) выполнены условия
В качестве целевого функционала, погрешность которого мы будем рассчитывать, выберем температуру или плотность потока в некоторой точке.
Обозначим 
как 
.
|
|
(40) |
Нам нужно рассчитать градиент целевого функционала по отношению к погрешности исходных данных, погрешности модели и погрешности численной аппроксимации.
Соответствующие сопряженные переменные рассчитываются с помощью следующей системы уравнений.
|
|
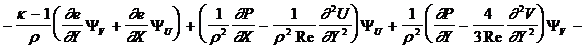
(41) |
Источник в уравнении для 
соответствует
расположению оцениваемой точки.
|
|
(42) |
|
|
( 43 ) |
|
|
(44) |
Величины 
являются
сопряженными аналогами плотности, компонент скорости и энергии.
|
Начальные условия C (X=Xmax): |
(45) |
Выражение для соответствует расположению
оцениваемой точки на границе Xmax.
|
Граничные условия B,D (Y=0; Y=1): |
(46) |
Сопряженная задача решается в обратном направлении по X. При решении сопряженной задачи используется тот же конечно-разностный алгоритм, что и для решения прямой задачи. Параметры течения, входящие в коэффициенты, берутся из решения прямой задачи.
Погрешность дискретизации в каждой расчетной точке можно представить в качестве ряда Тейлора, соответственно конечно-разностное представление задачи оказывается эквивалентно исходной форме задачи (в виде ЧДУ) с дополнительными источниковыми членами.
Здесь использована разностная схема первого порядка точности, позволяющая получить наименее громоздкие выражения для оценок ошибки и достаточно большую погрешность аппроксимации в сравнении с другими источниками ошибки (такими, как разрядность компьютера).
Для оценки точности конечно-разностного решения рассмотрен подход, основанный на использовании оценки погрешности с помощью ряда Тейлора в форме Лагранжа и сопряженных уравнений в непрерывной постановке.
Вариация целевого функционала в зависимости от ошибки дискретизации имеет вид:
|
|
(47) |
В качестве примера приведем оценку
погрешности аппроксимации производных вдоль маршевой координаты. Для ее оценки разложим разностные
выражения в окрестности 
, используя ряд Тейлора в форме Лагранжа.
|
|
(48) |
Соответствующая компонента погрешности целевого функционала
имеет вид
|
|
(49) |
Ее дискретную форму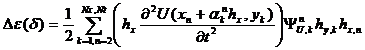 
в первом порядке точности 
можно
представить как
|
|
(50) |
Первая часть этой суммы может быть использована для уточнения функционала, она является аналогом систематической ошибки в лабораторном эксперименте.
|
Уточнение
функционала |
(51) |
Неустранимая погрешность создается
второй частью 
. Она является аналогом случайной ошибки в лабораторном
эксперименте. Для нее можно получить верхнюю оценку ошибки функционала (после
уточнения):
|
|
(52) |
|
Верхняя
оценка ошибки функционала |
(53) |
Соотношения (51) и (53) позволяют получить следующую оценку погрешности численного решения
Рассматриваемый подход позволяет определить устранимую (систематическую) погрешность расчета и верхнюю оценку случайной ошибки. В этом смысле он эквивалентен лабораторному эксперименту.
В качестве
иллюстрации рассчитана погрешность плотности за скачками уплотнения (по линии
симметрии течения на границе вытекания). Соответствующее поле плотности
представлено на рис. 16. Поле сопряженной плотности изображено на рис. 17. Вторая
производная плотности представлена на рис. 18, на равномерной сетке это поле
соответствует полю максимальных локальных погрешностей аппроксимации в
уравнении неразрывности. Пространственная плотность систематической погрешности
(51)
представлена на рис. 19, а плотность неустранимой погрешности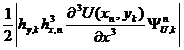 
(53) на рис. 20,21.
|
|
|
|
Рис. 16. Плотность |
Рис. 17. Сопряженная плотность
|
|
|
|
|
Рис. 18. Вторая производная плотности |
Рис. 19. Плотность устранимой погрешности (51) |
Следует отметить, что стандартные методы повышения точности, основанные на сгущении сетки в областях больших градиентов, приведут к сгущению сетки в соответствии с рис. 16, в то время как зоны реальной погрешности расчета соответствуют рис. 20 и 21 (для разных точек оценки, k=50, k=70).
|
|
|
|
Рис. 20. Плотность неустранимой погрешности, оценивается плотность течения в точке k=50 |
Рис. 21. Плотность неустранимой погрешности, оценивается плотность течения в точке k=70 |
Таким образом, зоны максимального вклада ошибки дискретизации в погрешность искомой величины и, соответственно, зоны сгущения сетки существенно зависят не только от поля течения, но и от выбора оцениваемого параметра, поэтому не могут быть определены без решения сопряженной задачи.
Следует
отметить, что при наличии значительного числа ценных функционалов 
, и разных
наборов параметров, содержащих ошибку 
, возникает необходимость решения 
практически
совпадающих задач. Это обстоятельство делает данный подход к определению
погрешности перспективным для реализации параллельных вычислений с точки зрения
концепции многозадачного параллелизма.
Валидация
Еще одним источником погрешности расчета является отклонение используемой физической модели от точной. Доказательство соответствия этих моделей является предметом валидации.
В том случае, когда отклонение сводится к наличию или отсутствию в системе уравнений некоторых членов, не приводящих к радикальной перестройке течения, использование сопряженных уравнений позволяет количественно определить вносимую ими погрешность. Ее малая величина может являться обоснованием верности применяемой физической модели и, соответственно, существенным элементом валидации. В качестве примера рассмотрим влияние вязких членов в уравнениях (41-44) на оцениваемую величину. Пусть возмущенные величины описываются параболизованными уравнениями Навье-Стокса
,
а невозмущенные -уравнениями Эйлера
Вариация целевого функционала (плотности в некоторой точке) принимает вид
Влияние вязкости на целевой функционал имеет вид
|
|
(54) |
При этом соответствующие сопряженные уравнения в отличие от системы (41-44) не содержат вязких членов. Пространственная плотность вклада вязких членов в погрешность расчета целевого функционала представлена на рис. 22.
|
|
|
Рис. 22. Плотность погрешности, вызванной влиянием вязких членов |
Таким образом, сопряженные параметры дают возможность оценки влияния вариации физической модели на целевой функционал. Рис. 22 показывает те зоны, в которых влияние рассматриваемой вариации наиболее велико. В рамках рассматриваемой относительно простой задачи эти зоны интуитивно понятны и без данной визуализации - они соответствуют пересечению скачков уплотнения и характеристик, приходящих в точку измерения. В более реалистичных задачах такого сорта интуитивные оценки затруднены или невозможны, поэтому поля сопряженных параметров могут служить весьма важной эвристической информацией. Визуальное представление этих полей позволяет определять в расчетной области зоны наибольшего влияния вариации физической модели.
Представленный в настоящей работе подход, согласно классификации [1], несомненно, относится к методам анализа данных, так как основан на синтезе математического аппарата теории сопряженных операторов и уравнений и методов визуального представления. Применение данного подхода позволяет решать широкий спектр обратных задач вычислительной механики жидкости и газа, в том числе задачи идентификации течения и управления течением. Непосредственное визуальное представление градиента целевого функционала и связанных с ним полей сопряженных параметров позволяет получать новую информацию, являющуюся ключевой для рассматриваемой конкретной задачи. Визуализация градиента целевого функционала и сопряженных параметров позволяет выйти за рамки привычных визуальных представлений газодинамических величин и процессов в вычислительной механике жидкости и газа, значительно расширяя возможности анализа данных для исследователя.
В задачах управления течением, идентификации течения (определения начальных или граничных условий, коэффициентов) поле управляющих параметров и градиент целевого функционала используются для поиска зон наиболее эффективного контроля или для выбора зон измерения.
Особо следует отметить перспективность рассмотренного в данной работе подхода для практического решения актуальных задач верификации и валидации (V&V).
Визуализация поля градиента целевого функционала и связанных с ним полей сопряженных параметров позволяет не только качественно и количественно оценить вклад погрешности аппроксимации, но и выработать рекомендации по выбору расчетных сеток и необходимого числа итераций. Это обстоятельство делает рассматриваемый подход перспективным инструментом для верификации алгоритмов и результатов расчетов.
В задачах валидации применение данного подхода к изучению влияния членов уравнений, описывающих малые (отбрасываемые) эффекты на градиент целевого функционала также предоставляет количественную и качественную информацию, которая может быть визуально представлена.
Важным фактором является то, что задачи, решаемые с помощью подобного подхода, при наличии значительного числа ценных функционалов, и разных наборов управляющих параметров, либо параметров, содержащих ошибку, приводят к необходимости решения большого количества практически совпадающих однотипных задач с различными наборами данных. Это обстоятельство делает рассматриваемый в данной работе подход перспективным с точки зрения многозадачного параллелизма для применения параллельных вычислений.
- Бондарев А.Е., Галактионов В.А., Чечеткин В.М. Научная визуализация в задачах вычислительной механики жидкости и газа / научный электронный журнал «Научная визуализация», Национальный Исследовательский Ядерный Университет "МИФИ" , М., 2010, Т.2, N 4, C.1-26. URL: http://sv-journal.com/2010-4/01.php?lang=ru
- Афендиков А.Л., Луцкий А.Е., Плёнкин А.В. Вейвлетный анализ локализованных структур в идеальной и вязкой моделях / Математическое моделирование, 2011, т.23, N 1, С.41-50.
- Mogilenskikh D.V. Nonlinear Color Interpretation of Physical Processes // Proc. 10th International Conference on Computer Graphics & Vision GRAPHICON'2000, Moscow, 2000, p.202-211.
- Бондарев А.Е. Оптимизационный анализ нестационарных пространственно-временных структур с применением методов визуализации / научный электронный журнал «Научная визуализация», Национальный Исследовательский Ядерный Университет "МИФИ" , М., 2011, Т.3, N 2, C.1-11. URL: http://sv-journal.com/2011-2/01.php?lang=ru
- McNamara A., Treuille A., Popovic Z. , Stam J. Fluid control using the adjoint method. ACM Transactions on Graphics (SIGGRAPH 2004), 23(3), August 2004.
- Марчук Г.И. Сопряженные уравнения и анализ сложных систем, М., Наука, 1992, 336 с.
- Марчук Г.И. Сопряженные уравнения и их применения / Труды Института математики и механики УрО РАН, 2006, т.12, N 1, С.184-195.
- Pironneau O. On Optimum Design in Fluid Mechanics / J. Fluid Mech., v. 64, N 1. 1974. pp. 97-110.
- Льюинс Дж. Ценность. Сопряженная функция, Атомиздат, 1972
- Huang J., Modi V. Optimum Design of Minimum Drag Bodies in Incompressible Laminar Fow Using a Control Theory Approach / Inverse Problems in Engineering, vol. 1, 1994, pp. 1-25.
- Алексеев А.К., Бондарев А.Е., Молотилин Ю.А.. О визуализации сопряженных полей при идентификации и управлении трехмерным течением вязкой жидкости // «Применение методов научной визуализации в прикладных задачах», Сб. науч. тр., Москва, МГУ, 2000, с.8-18.
- Guide for verification and validation of computational fluid dynamic simulations / AIAA Guide, AIAA G-077-1998.
- Roache P. J., Verification and Validation in Computational Science and Engineering. Hermosa Publishers, Albuquerque, New Mexico, 1998.
- Oberkampf W. L., Blottner F. G., Issues in Computational Fluid Dynamics Code Verification and Validation / AIAA Journal, v.36, N 5, 1998, pp.687–695.
- Алексеев А.К., Бондарев А.Е. Визуализация переноса погрешности при расчете поля течения // «Научная визуализация в прикладных задачах», Сб. науч. тр., Москва, МГУ, 2003, с.4-13.
- Venditti D., Darmofal D. Grid Adaptation for Functional Outputs: Application to Two-Dimensional Inviscid Flow / J. Comput. Phys., 176 (2002), pp.40-69.
- Алексеев А.К. Апостериорная оценка погрешности конечно-разностного решения с помощью сопряженных уравнений и дифференциального представления / ЖВМ и МФ, т. 45, N7, с. 1213-1225, 2005.
- Braack M., Ern A. A Posteriori Control of Modeling Errors and Discretization Errors / Multiscale Model. Simul., V. 1, N. 2, , 2003, pp. 221–238.
- Alekseev A., Navon M. Criteria of optimality for sensors’ location based on adjoint transformation of observation data interpolation error / Int. J. Numer. Meth. Fluids, V. 62, Issue 1, 2010, pp. 74-89.
- Kirby R. M., Silva C. T. The Need for VerifiableVisualization // IEEE Computer Graphics and Applications, Volume 28, Number 5, 2008, pp.78-83.
- Alekseev A.K., Bondarev A.E., Molotilin Y.A. On Inverse Problems for 3D Time-Dependent Free Convection Heat Transfer // Proc. National Heat Transfer Conference, Oregon, USA, Vol.10, 1995, pp.112-122.
- Алексеев А.К. К управлению свободно-конвективным теплообменом с помощью температуры стенки // Тепломассообмен, ММФ-2000, т. 1, Конвект. тепломассообмен, Минск, 2000, стр. 59-66
- van Leer B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method / J. Comput. Phys., 32 (1979), 101–136
- Toro E. F. Riemann Solvers and Numerical Methods for Fluid Dynamics, Berlin: Springer Verlag, 2006
- Yamamoto S., Daiguji H. Higher-order-accurate upwind schemes for solving the compressible Euler and Navier-Stokes equations / Computers and Fluids, 22, 1993. pp.259-270
- Toro E., Siviglia A. PRICE: Primitive centred schemes for hyperbolic system of equations / Int. Journal for Numerical Methods in Fluids, 42, 2003, pp. 1263–1291
- Шокин Ю.И., Яненко Н.Н. Метод дифференциального приближения, Наука, 1985.