ВИЗУАЛИЗАЦИЯ ПРОЦЕССА ОПТИМИЗАЦИИ ПАРАМЕТРОВ КРИТЕРИАЛЬНОЙ ФУНКЦИИ ОШИБОК В ЗАДАЧЕ МЕДИЦИНСКОЙ ДИАГНОСТИКИ

И.Д. Колесин¹, О.А. Трояножко¹, П.П. Сиващенко²

¹Санкт-Петербургский государственный университет (СПбГУ), Санкт-Петербург, Россия

²Военно-медицинская академия имени С.М. Кирова МО РФ (ВМедА), Санкт-Петербург, Россия

kolesin_id@mail.ru, med_otpor@mail.ru, pavel-siv@yandex.ru

Содержание

1. Введение

2. Цель исследования

3. Задача поиска минимума с применением визуального метода

4. Материалы и методы исследования

5. Программное обеспечение

6. Результаты исследования и их обсуждение

7. Сравнение результатов

8. Заключение

Список литературы

Аннотация

Работа посвящена решению задачи анализа многомерных данных визуальным методом. С помощью хорошо зарекомендовавших себя методов визуальной аналитики предпринят подход к оптимизации функции ошибок в задаче диагностики. Используемый визуальный метод позволяет отображать функцию ошибок и проводить анализ её поведения в пространствах размерности 2D и 3D, решая задачу поиска оптимальной классификации двух множеств. Метод визуализации позволил выявить ряд характеристик поведения функции ошибок, полученных авторами как обобщение практических результатов при обработке медицинских баз данных. В качестве примера одного эффективного применения метода визуализации проведена оптимизация диагностики больных раком молочной железы. На этапе диагностики была исследована возможность оптимизации путем предварительного выяснения особенностей строения многомерных образований в пространстве параметров линейной дискриминантной функции. В качестве критерия оценки точности используется дискретная функция ошибок, регистрирующая число неверно распознанных объектов. Некоторые использующиеся ныне методы классификации слабо приспособлены для поиска минимума в задачах медицинской диагностики и являются затратными по времени и ресурсам. Другие дают значительную вероятность ошибок, что недопустимо при постановке диагноза в особо ответственной сфере принятия решений. Поэтому авторами проведено исследование в этой области и предложен простой и визуально понятный метод для выяснения особенностей строения функции ошибок. Использован визуальный метод исследования, состоящий в алгоритме построения поверхностей равного уровня и использовании их для движения к минимуму. В итоге было показано, что достаточно надежную диагностику можно провести, если применить метод визуализации дискретной функции ошибок при спуске по экстремали к минимуму. С помощью визуального метода было разработано программное обеспечение, в результате применения которого доброкачественную опухоль с точностью 94,73% удалось отделить от злокачественной по двум диагностическим показателям.

Ключевые слова: анализ данных, научная визуализация, классификация объектов, оптимизация.

1. Введение

Одна из важнейших задач врача заключается в постановке правильного диагноза. В свою очередь, постановка правильного диагноза зачастую сводится к отнесению пациента к группе "болен" или "здоров". При этом врачи должны стремиться к постановке правильного диагноза по минимальному числу информативных признаков той или иной болезни с максимальной точностью. Решение подобных задач получило название классификации.

Для решения подобного класса задач разработаны разнообразные методы и подходы. Так, для решения задач идентификации, ранжирования диагностических показателей и прогнозирования используется математический аппарат распознавания образов [1,2,3] и др. При классификации объектов на два множества возникает задача отыскания дискриминантной функции с наименьшей ошибкой классификации. Ряд приемов решения этой задачи сводится к построению гиперплоскости , разделяющей два множества с наименьшим числом неверно распознанных объектов. К числу таких приемов относятся кластерные алгоритмы, деревья решений, алгоритмы Фишера, Хо–Кашьяпа [4] со множеством их модификаций [5,6,7] и пр. Центральным моментом дискриминантного анализа является предложение функционала, позволяющего оценивать качество классификации. Одно из направлений развития методов классификации – введение "суррогатных" непрерывных функционалов, подробно описанных в [8,9]. Они исключают скачкообразные изменения дискретной функции ошибок. Такой функционал должен быть неотрицателен и обращаться в ноль, когда все точки классифицированы правильно, а также он должен быть непрерывен и обладать достаточно хорошими (с точки зрения поиска минимума) аналитическими свойствами. Следует отметить, что помимо минимизации непосредственно "суррогатных" функционалов, на практике главным образом реализуется идея использования суррогатных функционалов для построения различных направлений наискорейшего спуска, а минимизируется при этом сам исходный натуральный функционал – количество неверно определенных объектов.

Однако и дискретные функции могут быть полезны, если использовать их для выявления особенностей строения многомерного пространства параметров дискриминантной функции. Это особенно важно, если речь идет о выявлении одного минимума в массе локальных. В отличие от использования "суррогатных" непрерывных функций, в данной работе вводится дискретная функция ошибок и строится последовательность конечных полусеток, позволяющих искать локальные минимумы функции ошибок.

2. Цель исследования

В соответствии с основной задачей научной визуализации – сделать невидимое видимым, тремя основными направлениями являются представление как реальных очень маленьких, больших, так и абстрактных объектов, невидимых в силу своей нематериальной природы [10]. Исследуемым объектом в нашем случае является функция многих переменных, а именно, дискретная функция ошибок.

Приведем пример использования визуализации дискретной функции ошибок в недавнем прошлом. В 1990-х годах военно-воздушные силы США спонсировали разработку сканирующих оптических микроскопов ближнего поля. В ходе своих исследований физик Lorant Muth продемонстрировал, в частности, весьма любопытное применение визуального анализа дискретной функции ошибок при вычислении разности фаз между содержащими и не содержащими ошибки моделируемыми полями в ближнем поле индукции [11]. Из последних работ за 2016г. в области распознавания образов можно отметить оригинальную идею визуализации процесса формирования обучающей выборки (а также определения ее объема), необходимой в проектировании искусственных нейронных сетей [12].

В нашей работе представлен визуальный анализ дискретной функции ошибок в приложении к задаче классификации объектов с помощью разделяющей гиперплоскости. Развивается подход, основанный на переносе поиска минимума в координатное пространство весовых коэффициентов линейной дискриминантной функции. Заметим, что подобная задача не является аналогом часто возникающей задачи о чувствительности дискриминантной функции к малым изменениям ее коэффициентов, т.к. предметом анализа является не дискриминантная функция, а функция ошибок [13].

Для получения начальной информации о местонахождении минимума достаточно построить семейство поверхностей равного уровня, либо даже одну, чтобы ограничить область, содержащую минимум. Эта визуально интерпретируемая информация может стать полезной при отыскании минимума. Однако дискретный характер функции ошибок придает такому подходу ряд специфических особенностей. Цель статьи – выявить эти особенности и предложить эффективные модификации алгоритма, апробируя их на базах данных по онкологии.

Практический интерес решения задачи классификации состоит в постановке точных медицинских диагнозов. Поэтому прикладной математик сталкивается с задачей поиска оптимального решения – разделения двух и более множеств гиперплоскостью. Если осуществлять поиск минимума, например, простым перебором, то реализация алгоритма приведет к генерации порядка миллиарда шагов с соответствующими значениями на выходе. Поэтому наше научное любопытство было вполне удовлетворено созданием дополнительного визуального трехмерного представления общего вида области минимума, а особенно ее внутренней части – сердцевины. Для этого мы создали программные модули, позволяющие визуально представить поведение функции ошибок, при этом дающие наглядное представление о внешней и внутренней структуре. Разработанные программные модули позволяют выявить область минимума и визуально исследовать ее в разных ракурсах, вращая на 360 градусов.

3. Задача поиска минимума с применением визуального метода

Анализ научных публикаций показал, что средства визуализации незаслуженно игнорируются при построении разделяющей гиперплоскости на этапе оптимизации коэффициентов дискретной функции ошибок при классификации медицинских баз данных. В связи с недостатком информации по данному вопросу, а также отсутствием аналитического вида функции ошибок, актуальной задачей представляется применение визуального метода, чтобы сделать поиск минимума более прозрачным. В нашей статье мы делаем акценты на некоторые аспекты поведения функции ошибок в 2D и 3D, визуально анализируя следующее:

1. отображение области допустимых значений коэффициентов функции ошибок в области минимума;

2. исследование чувствительности функции ошибок к изменению коэффициентов разделяющей гиперплоскости;

3. анализ того, с каким шагом происходит улучшение качества классификации и от чего зависит шаг для каждой медицинской базы;

4. анализ того, на какую величину можно менять коэффициенты, оставаясь на максимально качественном уровне классификации;

5. особенности поведения функций ошибок вблизи минимума в частности, около "проблемных" областей, которые необходимо исследовать более тщательно, уменьшая шаг и увеличивая, таким образом, количество точек для более качественного анализа;

6. использование понятия "плато", выход на которое гарантирует максимальное постоянное значение функций ошибок, т.е. наихудшее качество классификации;

7. использование понятия "сердцевины", нахождение которой гарантирует минимальное значение функций ошибок;

8. выявление общих особенностей поведения функций ошибок для различных баз данных.

Поставим задачу поиска минимума, разработав алгоритм движения к минимуму при помощи визуального анализа.

Пусть в пространстве показателей заданы два множества объектов: и , из которых соотносятся с объектами класса , а – с объектами класса . Пусть построена начальная гиперплоскость

разделяющая и с ошибкой . Необходимо уточнить, что понимается под .

Напомним, что врачами используются различные критерии качества классификации:

1. Чувствительность – это относительная частота отнесения истинно больного к группе больных;

2. Специфичность – это относительная частота отнесения истинно здорового к группе здоровых;

3. Безошибочность – это относительная частота принятия безошибочных решений, как по отношению к истинно больным, так и истинно здоровым;

4. Ложноотрицательный ответ (ошибка первого рода) – это относительная частота отнесения истинно больного к группе здоровых;

5. Ложноположительный ответ (ошибка второго рода) – это относительная частота отнесения истинно здорового к группе больных.

Коллегиально было принято решение рассматривать безошибочность как критерий качества классификации. В соответствии с этим, представляет собой отношение числа неверно распознанных объектов к общему числу объектов :

Будем менять коэффициенты (тем самым поворачивать гиперплоскость), минимизируя число неверно распознанных объектов. Для этого введем функцию ошибок:

где – число неверно распознанных объектов на -м шаге приближений к минимуму функции . Требуется построить последовательность векторов такую, что

Перейдем от пространства измеряемых показателей к пространству весовых коэффициентов линейной дискриминантной функции и будем отмечать каждый новый набор ее коэффициентов точкой и значением . Соединяя точки с одинаковым значением , получим в двумерном случае линию равного уровня , а в многомерном – поверхность. Требуется построить семейство поверхностей равного уровня , различающихся на величину , (либо , – целое), где – минимальная ошибка, обусловленная дискретностью функции и числом объектов :

Переход к визуальной картине выполняется следующим образом. В случае, когда разделяющая гиперплоскость строится в пространстве двух параметров, например, , то по оси абсцисс откладываются значения параметра , по оси ординат – значения параметра , значения функции ошибок – по оси . Визуально мы увидим объемную геометрическую фигуру (см. "овраг" на Рис. 1) в системе координат [14]. Можно заметить, что функция ошибок в пространстве двух параметров по своему строению оказалась схожей с функциями Букина, являющимися крайне сложными для отыскания глобального минимума любыми методами оптимизации [15]. Функции Букина являются почти фрактальными, с острыми неровными краями в окрестности их точек минимума.

В случае, когда разделяющая гиперплоскость строится в пространстве не двух, а трех параметров , то визуально мы уже увидим объемные геометрические фигуры, напоминающие по форме "кристаллы", в системе координат . Причем дискретная функция ошибок представлена как семейство вложенных друг в друга поверхностей равного уровня, где каждый уровень соответствует своему значению функции ошибок .

В пространствах размерности визуальное представление о поведении дискретной функции ошибок можно получить путем построения "срезов". "Срезом" (сечением, профилем) называем двумерную фигуру, полученную фиксированием одного из параметров при n=3, двух при n=4 и т.д. Тем же образом можно сводить многомерные фигуры к трехмерным, имея в виду, что трехмерные фигуры содержат больше информации, чем двумерные. "Срезы" могут быть представлены как графически на плоскости, так и в табличном виде, где каждой паре параметров соответствует свое значение функции ошибок, выраженным в процентах (Таблица 1).

4. Материалы и методы исследования

Работоспособность метода визуализации процесса классификации исследовалась на медицинских базах данных с различными патологиями. В данной работе ограничимся рассмотрением примеров двух баз данных по онкологии. Первая база данных рака молочной железы РМЖ-569 из Висконсинского университета США содержит информацию о 569 пациентах, имеющих опухоль, и о 30 диагностических показателях [16]. Гистохимия пунктатов опухоли молочной железы выполнена с помощью тонкоигольной аспирационной пункции. По результатам анализа характеристик ядер клеток проводилось разделение по двум группам: доброкачественная опухоль (357 пациентов) и злокачественная (212 пациентов). Оцифрованные снимки представлены тремя подгруппами показателей, характеризующими снимки ядер:

1 – размером, выраженным радиусом и площадью;

2 – формой, выраженной гладкостью, степенью вогнутости, плотностью, долей вогнутых участков контура, симметрией и фрактальностью;

3 – текстурой, полученной разницей интенсивности черно-белой шкалы в компонентах пикселя [17]. Заметим, что ранжирование в биомедицинских базах данных – определение набора информативных показателей – методом фильтрации является нетривиальной задачей и требует применения серьезных математических подходов, описанных, например, в [18,19].

Механизм отбора наиболее информативных показателей описан в статье [20], где показателем значимости признака служит площадь пересечения функций плотности распределения. Этот показатель соответствует коэффициенту перекрытия. По определению E.L. Bradley [21], коэффициент перекрытия равен площади перекрытия функций плотности распределения. В таком подходе является мерой сходства между двумя распределениями и варьируется от 0 до 1. Применение коэффициента перекрытия основывается на существовании зависимости площади перекрытия от диагностической ценности (информативности) показателя: чем меньше площадь перекрытия функций плотности распределения, тем более информативен диагностический показатель.

Нами также предварительно было проведено ранжирование исходных диагностических показателей, т.е. упорядочивание по степени уменьшения информативности. В итоге были выделены два наиболее информативных диагностических показателя: наибольший периметр и наибольшая доля вогнутых участков контура ядер клеток .

Вторая база данных РМЖ-253 из того же университета содержит информацию о 253 пациентах по 39 показателям [22]. Пациенты перенесли операцию по удалению опухоли молочной железы, причем 140 из них далее подверглись химио- или гормональной терапии. Разделение проводилось по двум группам: прожила более 5 лет после операции (61 пациент) и менее 5 лет (79 пациентов). Также было проведено ранжирование исходных диагностических показателей и выделены два наиболее информативных: фрактальный размер и наихудший фрактальный размер ядер клеток .

В качестве метода поиска минимума функции выбран метод покоординатного спуска, позволяющий войти в область фактического нахождения минимума. Для движения в этой области к точке минимума избран метод градиента. Начальная точка находится методом минимизации средне-квадратической ошибки, что аналогично первому шагу известной процедуры Хо-Кашьяпа.

Определение 1. Под размытым многомерным образованием в пространстве параметров линейной дискриминантной функции понимается объект, выделяемый последовательностью поверхностей равного уровня таких, что , при , где – начальная ошибка.

Определение 2. Под экстремальной областью размытого многомерного образования понимается множество точек локального минимума дискретной функции .

Определение 3. Под экстремалью размытого многомерного образования понимается линия, соединяющая множество точек с наименьшими значениями дискретной функции в каждом сечении размытого образования.

В двумерном случае при размытое образование соотносится с "оврагом", а экстремальная область – с его "дном". Движение по "дну" позволяет выявить минимум. Если эксперименты с поиском минимума обнаруживают неровность дна, обусловленную характером функции , то возникает необходимость в разработке специальных приемов поиска минимума. При этом, экстремаль может быть неровной, если значение минимума от профиля к профилю изменяется. В зависимости от характера изменения различаем возрастающую экстремаль, ниспадающую и особую (состоящую из единственной точки). Особая экстремаль, состоящая из точек (дно оврага с малыми "покачиваниями" гиперплоскости), требует отдельного рассмотрения.

Отметим следующую особенность поведения дискретной функции . При "соприкосновении" разделяющей плоскости с очередным объектом наблюдается скачок функции на величину . Движение в пространстве параметров связано в этом случае с последовательностью таких скачков. Движение по заданной поверхности представляет траекторию в пространстве параметров , вдоль которой функция не меняет своей величины. В отличие от такого движения, малое "покачивание" плоскости в окрестности также может обеспечивать . Однако движение по заданной поверхности предполагает наличие дискретной последовательности точек . Семейство таких поверхностей, вложенных одна в другую, иллюстрирует наличие минимума функции .

5. Программное обеспечение

Программное обеспечение находится в стадии разработки. Приведем краткое описание уже разработанного программного обеспечения. Платформа: серверная часть – ОС Windows, клиентская часть – любая, поддерживающая работу с MS Office. Основные возможности для пользователя: пользователь может загрузить базу данных из Excel, далее база данных анализируется, пользователю выводится результат анализа: наиболее значимые признаки для разделения на две группы (больных/здоровых), возможность согласно полученному анализу классифицировать новых пациентов, сохранять результаты анализа. Интерфейс отвечает основным возможностям – просматривать загруженную базу данных, выводить результаты анализа, визуально контролировать оптимизацию классификации. Более детально интерфейс программного обеспечения представлен в [23].

6. Результаты исследования и их обсуждение

Описанные в предыдущем разделе методы научной визуализации мы применили к базе РМЖ-569. Напомним, в качестве критериальной была использована дискретная функция ошибок, регистрирующая количество неверно диагностированных пациентов. Для наглядности визуального представления функции ошибок (Рис. 1), заданной таблично (Таблица 1), мы оперировали выделенными ранее в результате ранжирования двумя диагностическими показателями: и .

Приведем результат графического построения поверхностей равного уровня. На рис.1 представлен рельеф функции ошибок в графическом виде. По осям – два меняющихся весовых коэффициента ,; по оси – соответствующее значение в процентах; цветом обозначены разные срезы оврага. Т.е. мы наблюдаем размытое многомерное образование с несколькими параллельными срезами и локальными минимумами (экстремалями), обозначенными точками на самом дне.

В результате исследования линий уровня было выявлено, что "дно оврага" изобилует локальными минимумами. При выходе из дна оврага на "берега" линии уровня резко увеличивают свои значения, т.к. количество ошибок увеличивается. При движении вдоль оврага линии уровня плавно увеличивают свои значения, т.е. количество ошибок увеличивается не так быстро. Наглядно показано, что минимум отыскивается на дне оврага среди локальных за конечное число итераций.

В экспериментах на всех тестированных базах данных экстремальная область визуально напоминает длинный овраг с берегами – "плато" и вытянутым неровным дном. Минимум функции ошибок во всех случаях был найден на одном из срезов размытых многомерных образований вблизи начального приближения на дне оврага среди "ложбин". Также были найдены общие закономерности геометрических характеристик размытых многомерных образований, которые могли бы подсказать, где искать экстремаль. В результате проведенных экспериментов обнаружено сходство видов размытых многомерных образований для баз данных по онкологии, классифицирующих пациентов на разные подгруппы. Ниже мы привели подробные результаты численного эксперимента для базы РМЖ-569, а для базы РМЖ-253 конечный результат представлен видео-роликами и таблицей с динамикой изменений значений функции ошибок.

cuts_253_visualization__21112016

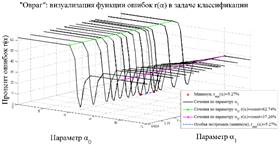
Рис. 1. Вид на "овраг": визуализация функции ошибок для базы данных РМЖ-569 слева и для базы данных РМЖ-253 справа

Ниже в табличном виде представлен рельеф функции ошибок в численном виде. По горизонтали и вертикали – два меняющихся весовых коэффициента или срезы по ; в ячейках – соответсвующее значение функции ошибок в процентах. Цвет, по аналогии с физическими картами местности, визуализирует динамику изменения значений функции ошибок по аналогии с "перепадами высот": от минимального (оптимального), обозначенного красным до максимального, обозначенного зеленым, находящимся на "плато".

Таблица 1. Динамика изменений значений функции ошибок, выраженными в процентах, для базы РМЖ-569 слева и для базы данных РМЖ-253 справа

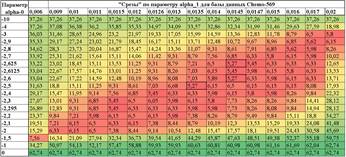
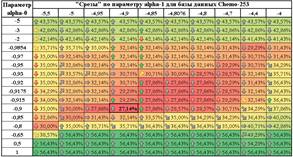
Из таблицы рельефа функции ошибок видно, что дно оврага находится в точке (-2,5;0,0135;6,8168), что является минимумом функции ошибок со значением 5,27% при оптимальной гиперплоскости ; при этом мы зафиксировали параметр , а первые два меняли. Неровности дна обусловлены погрешностью вычисления , равной , (соответствующей погрешности в одного пациента). Дно оврага вытянуто. От точки минимума функция ошибок возрастает по "берегам" (по параметру ). Причем функция возрастает быстрее на левой стороне оврага и выходит на "плато" на постоянном значении количества ошибок . Справа функция возрастает медленнее и выходит на "плато" на постоянном значении количества ошибок .

Проследим численно за скачкообразными изменениями дискретной функции ошибок. Видна следующая особенность поведения дискретной функции : при "соприкосновении" разделяющей плоскости с очередным объектом наблюдается скачок функции на величину , – количество пациентов в каждой базе. В рассмотренном случае количество пациентов . Соответственно, шаг для рассматриваемой базы обратно пропорционален количеству объектов: . Движение в пространстве параметров связано в этом случае с последовательностью таких скачков. Причем чем ближе мы приближаемся к искомому минимуму "сердцевине", тем мельче становится шаг для каждого коэффициента. И наоборот, чем дальше удаляемся от оптимума, тем более вариабельны коэффициенты.

По аналогии, рассмотрим результат графического построения поверхностей равного уровня в координатном пространстве . Визуально – это три "кристалла", вложенные друг в друга (рис. 2). Данные три поверхности с постоянным уровнем ошибок представлены, соответственно, значениями , и наименьшим . Графическое построение выполнено в Matlab с использованием метода линейных оболочек. "Кристаллы" имеют вершины и грани, что происходит при построении по малому, но достаточному для визуального анализа количеству точек. При многократном увеличении количества точек грани "кристаллов" закономерно сгладятся, но суть вложенности и наличия "сердцевины" не изменится. Внешняя поверхность с функцией ошибок – это "кристалл" с самой большой площадью поверхности, отображенной зеленым цветом. Область, содержащая минимум – "сердцевина" – с наименьшей площадью поверхности, отображена красным цветом. Она спрятана внутри внешних слоев, что и является естественным поведением настоящего оптимума. При этом толщина слоя между соседними поверхностями равного уровня показывает, насколько чувствительна функция ошибок к изменению коэффициентов разделяющей гиперплоскости: чем толще слой, тем более свободны в изменении коэффициенты при постоянном значении функции ошибок. Чем тоньше слой, тем более чувствительна функция ошибок к малейшим изменениям коэффициентов.

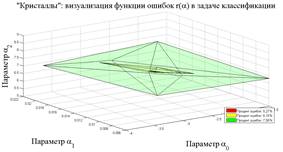
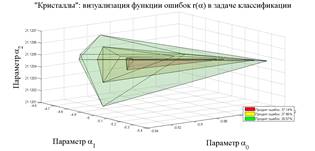
egg_569_21112016 egg_253_21112016

Рис. 2. Размытое многомерное образование для базы данных РМЖ-569 слева и для базы данных РМЖ-253 справа

В соответствии с предложенным определением 1, мы получили объект, выделенный последовательностью поверхностей равного уровня таких, что , где – начальная ошибка. В соответствии с определением 2, экстремальной областью размытого многомерного образования является множество точек локального минимума дискретной функции . Заметим, что данная наименьшая величина ошибки была получена как при применении дискретной функции ошибок, так и при "суррогатной" непрерывной функции. Получив визуальное представление поведения дискретной функции ошибок в 2D или в 3D вблизи "сердцевины", можно делать выводы о корректности работы алгоритма построения оптимальной разделяющей гиперплоскости, степени вариабельности ее коэффициентов и о качестве классификации. В итоге доброкачественную опухоль с точностью 94,73% удалось отделить от злокачественной, используя лишь два диагностических показателя. Это хороший результат, учитывая, что точность диагностики по всем показателям составила 96,5%. Таким образом, предложенный способ построения оптимальной гиперплоскости свидетельствует об уместности использования метода визуализации.

Заметим, что метод визуализации дискретной функции ошибок и его интерпретация на данный момент опробованы лишь на медицинских базах данных. Но предложенный метод визуализации в задачах классификации также может быть использован и при анализе баз данных из других сфер – важно лишь учесть их особенности. Очевидно, что при обработке баз данных при поиске, например, нефтегазовых месторождений или при спутниковой диагностике потенциального урожая зерновых возникнут свои специфичные лишь для данной области нюансы. Подведем краткие итоги выполненного исследования.

1. При помощи визуального представления стало возможным отображение области допустимых значений коэффициентов функции ошибок в области минимума. Визуально легко понять, при каких параметрах функция ошибок возрастает и, следовательно, падает качество классификации.

2. Визуальное исследование показывает, насколько чувствительна функция ошибок к изменению коэффициентов разделяющей гиперплоскости. Например, в самой "сердцевине" счет идет на тысячные. При попытке немного поменять хоть один коэффициент, функция ошибок сразу дает скачок и переходит на качественно худший уровень – на соседнюю поверхность равного уровня. Интересно поведение функции ошибок: чтобы находиться в самой "сердцевине", у коэффициентов есть минимальная свобода на отклонение. В то время как на внешних уровнях коэффициенты могут вести себя гораздо свободнее, при этом не меняя значение функции ошибок.

3. Визуально на графиках и на цветовой шкале можно проанализировать то, с каким шагом происходит улучшение качества классификации и от чего зависит шаг для каждой медицинской базы. На линиях (поверхностях) равного уровня при приближении к оптимуму динамика изменения коэффициентов разделяющей гиперплоскости меняется в сторону меньшей вариабельности.

4. Визуально ясно следующее: чтобы оставаться на максимально качественном уровне классификации близ "сердцевины", коэффициенты нужно менять с наименьшим шагом.

5. Визуально понятны особенности поведения функций ошибок вблизи минимума: в частности, около "проблемных" областей, которые необходимо исследовать более тщательно, уменьшая шаг и увеличивая, таким образом, количество точек для более качественного анализа.

6. Общей характеристикой поведения функции ошибок является выход на "плато", при котором достигается максимальное постоянное значение функций ошибок, т.е. наихудшее качество классификации – визуально это можно проследить на овраге, а численно – в таблице с цветовой шкалой.

7. Соответственно, спускаясь вниз между двумя берегами – "плато", мы достигаем "дна", где гарантировано минимальное значение функций ошибок. Заметим, что "дно", как правило, находится немного выше нулевой отметки по оси z вследствие неотделимости классов. По этой же причине "сердцевина" будет стремиться сжаться в точку, но на практике этого не происходит.

8. В итоге, работая в пространстве параметров линейной дискриминантной функции, мы исследовали геометрические особенности строения многомерных образований, характерных для различных баз данных. Были выявлены некоторые общие закономерности поведения поверхностей равного уровня. Если в двумерном случае размытое образование соотносится с "оврагом", а экстремальная область – с его "дном", то в трехмерном случае размытое образование соотносится с линейными оболочками – вложенными "кристаллами", а экстремальная область – с его "сердцевиной". По аналогии с двумерным случаем движение к "сердцевине" внутреннего "кристалла" позволяет выявить минимум.

7. Сравнение результатов

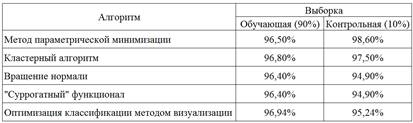
Сравним результаты применения метода научной визуализации по точности классификации с другими методами, результаты работы которых доступны для тестируемой базы данных РМЖ-569. В таблице 2 представлены только наилучшие результаты, полученные, например, методом параметрической минимизации [24], кластерным алгоритмом [25], построением гиперплоскости с помощью вращения нормали [26], применением "суррогатных" функционалов [27].

Таблица 2. Классификация на обучающей выборке (90%) и контрольной (10%)

Заметим, что в предложенном алгоритме мы использовали простой визуальный способ выбора оптимальной гиперплоскости. Он основан на визуальном изучении многомерных образований в экстремальной области около "сердцевины". При этом достигнутое качество классификации оказалось сопоставимым с качеством классификации, полученным другими методами. Мы получили хороший результат классификации при невысокой степени сложности обработки баз данных. Более того, предложенный алгоритм намного проще и нагляднее описывает происходящие процессы при подходе к "сердцевине", необходимой для построения оптимальной разделяющей гиперплоскости.

Результаты классификации с помощью оптимизации гиперплоскости оказались сопоставимы с результатами, полученными другими более сложными алгоритмами. В итоге 96,94% правильно определенных пациентов для обучающего множества и 95,24% – для контрольного множества (Таблица 2). Отметим, что степень сложности предложенного алгоритма намного ниже, чем его аналогов. Это может быть простым и удобным решением для постановки эксперсс-диагноза по малому набору диагностических показателей (например, для принятия оперативного решения при большом одномоментном поступлении пациентов и др.).

Достоинством описанного метода визуализации процесса поиска минимума дискретной функции ошибок является прозрачность процедуры. Предложенный метод визуализации применим для анализа баз данных, и может быть добавлен в общую "копилку" полезных вариантов. Это особенно важно, т.к. в поведении функции ошибок не просматривается каких-то скрытых сложных фигур. Визуально наличие "сердцевины" внутри семейства вложенных объемных образований удобно анализировать.

8. Заключение

Проделанная работа показала возможность использования метода визуальной аналитики для решения задачи оптимизации параметров функции ошибок в приложении к медицинской диагностике. В более общем случае визуальный метод позволяет решать задачи оптимальной классификации двух множеств. В итоге было разработано программное обеспечение, с помощью которого удалось отделить доброкачественную опухоль от злокачественной с точностью 94,73%, используя для этого два диагностических показателя. В перспективе планируется усовершенствование предложенного метода визуализации, а также его настройка на применение в разных прикладных областях. Преимуществом описанного метода визуализации является несложность его программирования при разработке приложений для устройств, поддерживающих работу на таких платформах как Windows и Android.

Список литературы

1. Журавлев Ю.И., Рязанов В.В., Сенько О.В. Распознавание. Математические методы. Программная система. Практические применения. М.: Фазис, 2006. 176 с.

2. Vapnik, V. Estimation of Dependences Based on Empirical Data. Springer, New York, 2006. 505 pp. http://dx.doi.org/10.1007/0-387-34239-7

3. Bradley P.S., Fayyad U.M., Mangasarian O.L. Mathematical Programming for Data Mining: Formulations and Challenges. Informs J. Comput., 1998. pp. 217-238. http://dx.doi.org/10.1287/ijoc.11.3.217

4. Ho Y.-C., Kashyap R. An algorithm for linear inequalities and its applications. IEEE Trans. Elec.Comp. 1965. Vol. 14. pp. 683–688.

5. Friedrichs C.I. Evolutionary tuning of multiple SVM parameters 12th European Symposium on Artificial Neural Networks (ESANN), 2004. pp. 519-524. http://dx.doi.org/10.1016/j.neucom.2004.11.022

6. Leski J. An ε–margin nonlinear classifier based on if–then rules IEEE Transactions on Systems, Man and Cybernetics. 2004. Vol. 34. pp. 68-76.

7. Leski J. Ho-Kashyap classifier with generalization control. Pattern Recognition Letters. 2003. Vol. 24. pp. 2281-2290.

8. Григорьева К.В. Суррогатные функционалы в задачах диагностики. Вестник Санкт-Петербургского университета. Прикладная математика. Информатика. Процессы управления. 2009. Том 1. c. 33-43.

9. Demyanov, V.F. Mathematical diagnostics via nonsmooth analysis. Optimization Methods and Software, 2005. Vol. 20. pp.197–218. http://dx.doi.org/10.1080/10556780512331318236

10. М.Н. Стриханов, Н.Н. Дегтяренко, В.В. Пилюгин, Е.Е. Маликова, Н.А. Матвеева, В.Д. Аджиев, А.А. Пасько. Опыт компьютерной визуализации наноструктур в НИЯУ МИФИ. Научная визуализация. 2009. Т. 1. С. 1-18. Url: http://sv-journal.org/2009-1/01.php?lang=ru

11. Muth L.A. Probe-Position Error Correction in Planar Near Field Measurements at 60 GHz: Experimental Verification. Journal of Research of the National Institute of Standards and Technology, Volume 97, Number 2, 1992 273-297.

12. Mikhailov A.S., Staroverov B.A. Visualization of training sample creation process for artificial neural network, Scientific Visualization, 2014, 8, P.85-97, URL: http://sv-journal.org/2016-2/07.php?lang=ru.

13. Муравьева, О.В. Исследование параметрической устойчивости решений систем линейных неравенств и построение разделяющей гиперплоскости. Дискретный анализ и исследование операций. – 2014. – Том3. – С. 53-63.

14. Калиткин, Н.Н. Численные методы. М.: Наука, 1978. 512 с.

15. Bukin A.D. New Minimization Strategy for Non-Smooth Functions. Novosibirsk, 1997. 24 p.

16. Bache K., Lichman M. UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science, 2013. URL: http://archive.ics.uci.edu/ml.

17. Wolberg W.H. Computerized Diagnosis of Breast Fine-Needle Aspirates. The Breast J. 1997. Vol. 3. pp. 77–80.

18. Zhang Y., Dong Z., Phillips P., Wang S. Detection of subjects and brain regions related to Alzheimer's disease using 3D MRI scans based on eigenbrain and machine learning. Frontiers in Computational Neuroscience. 2015. Vol. 9. http://dx.doi.org/10.3389/fncom.2015.00066

19. Phuong T.M., Lin Z. et Altman R.B. Choosing SNPs using feature selection. Journal of Bioinformatics and Computational Biology, 2005. pp. 301-309. http://dx.doi.org/10.1109/CSB.2005.22

20. Трояножко О.А., Колесин И.Д. Анализ влияния выбора вида распределения на точность ранжирования диагностических показателей. Научно-технический вестник Поволжья. 2013. Том6. С. 457–461.

21. Bradley E.L. Overlapping Coefficient. Encyclopedia of statis-tical Sciences: S. Kotz and N.L. Johnson (Eds.), Wiley: New York, 1985. vol. 6. pp. 546-547.

22. Wisconsin Prognostic Breast Cancer Chemotherapy Database. Computer Science Dept., University of Wisconsin, Madison, 1999. URL: ftp://ftp.cs.wisc.edu/math-prog/cpo-dataset/machine-learn/cancer/WPBCC/.

23. Трояножко О.А., Колесин И.Д. Двухэтапная экспертная система диагностики заболеваний. Журнал "Известия Юго-Западного государственного университета" Серия Управление, вычис-лительная техника, информатика. Медицинское приборостроение. 2017. №1(22) С. 82-88.

24. Mangasarian O.L. Misclassification minimization. Journal of Global Optimization 5, 1994, pp. 309-323. http://dx.doi.org/10.1007/BF01096681

25. Bagirov A.M., Rubinov A.M., Soukhorukova N.V. and Yearwood J. Unsupervised and supervised Data Classification Via onsmooth and Global Optimization. Top, Volume 11, Number 1. June 2003. Sociedad de Estadistica e Investigacion Operativa, Madrid, Spain, pp. 1-93.

26. Демьянов В.Ф., Демьянова В.В., Кокорина А.В. Прогнозирование эффективности химиотерапии при лечении онкологических заболеваний. Вестник Санкт-Петербургского университета, Прикладная математика. 2006. Том 4. c. 30-36.

27. Григорьева, К.В. Аппроксимация критериального функционала в задачах математической диагностики, диссертация, дис. канд. физ.-мат. наук. 2006. СПб. 191 c.

VISUALIZATION OF CRITERIAL FUNCTION PARAMETERS OPTIMISATION PROCESS IN MEDICAL DIAGNOSIS PROBLEM

I.D. Kolesin¹, O.A. Troyanozhko¹, P.P. Sivashhenko²

¹Saint-Petersburg State University (SPbSU), Russian Federation

²Military medical academy of S.M. Kirov (VMedA), Russian Federation

kolesin_id@mail.ru, med_otpor@mail.ru, pavel-siv@yandex.ru

Abstract

This article is dedicated to the scientific visualization method for the task of big data analysis. With the help of well proved methods of visual analytics the approach undertaken was directed at the criterial function optimization in medical diagnostics problems. The visual method being used makes it possible to represent error function and analyze its behavior in 2D and 3D, solving the problem of optimal classification of two sets. The visualization method made it possible to reveal a variety of error function characteristics which were obtained by authors as by a practical results generalization while processing medical data bases. An example of the effective use of visualization method is the application to optimize the diagnostics of breast cancer patients. At the stage of diagnostics, the possibility of optimizing by pre-determination the structural characteristics of the multidimensional structures in the parameter space of the linear discriminant function was investigated. As the criterion function, a discrete error function was used that registers the number of incorrectly recognized objects. Some currently used classification techniques are poorly adapted to find the minimum of medical diagnostics problems and are time- and resource-consuming. Others give a significant probability of error, that is unacceptable in the diagnostics of a particularly responsible decision-making area. Therefore, the authors proposed a simple and visually intuitive method to determine the structural characteristics of the error function. We used a visual method of investigation consisting of the algorithm of constructing the equal level surfaces and used them to go down to a minimum. As a result, it was shown that a sufficiently reliable diagnosis can be made, if we apply the method for visualizing the discrete error function when running on extremal to a minimum. With the help of a visualization method the software has been developed, as a result of which we get an accuracy of 94.73% when a benign tumour was separated from a malignant tumour using two diagnostic features.

Keywords: data analysis, scientific visualization, objects classification, optimization.

References

1. Zhuravlev Yu.I., Ryazanov V.V., Senko O.V. Recognition. Mathematical methods. Program system. Practical applications. Fazis, 2006. 176 p.

2. Vapnik, V. Estimation of Dependences Based on Empirical Data. Springer, New York, 2006. 505 pp. http://dx.doi.org/10.1007/0-387-34239-7

3. Bradley P.S., Fayyad U.M., Mangasarian O.L. Mathematical Programming for Data Mining: Formulations and Challenges. Informs J. Comput., 1998. pp. 217-238. http://dx.doi.org/10.1287/ijoc.11.3.217

4. Ho Y.-C., Kashyap R. An algorithm for linear inequalities and its applications. IEEE Trans. Elec.Comp. 1965. Vol. 14. pp. 683–688.

5. Friedrichs C.I. Evolutionary tuning of multiple SVM parameters 12th European Symposium on Artificial Neural Networks (ESANN), 2004. pp. 519-524. http://dx.doi.org/10.1016/j.neucom.2004.11.022

6. Leski J. An ε–margin nonlinear classifier based on if–then rules IEEE Transactions on Systems, Man and Cybernetics. 2004. Vol. 34. pp. 68-76.

7. Leski J. Ho-Kashyap classifier with generalization control. Pattern Recognition Letters. 2003. Vol. 24. pp. 2281-2290.

8. Grigorieva К.V. Surrogate functionals in problems of diagnostics. Vestnik of St. Petersburg State University. Applied Mathematics. Informatics. Processes of Control. 2009. Vol. 1. pp. 33-43.

9. Demyanov V.F. Mathematical diagnostics via nonsmooth analysis. Optimization Methods and Software, 2005. Vol. 20. pp.197–218. http://dx.doi.org/10.1080/10556780512331318236

10. M.N. Strihanov, N.N. Degtyarenko, V.V. Pilyugin, E.E. Malikova, N.A. Matveeva, V.D. Adzhiev, A.A. Pas'ko. Experience in computer visualization of nanostructures in NIYaU MEPhI. Scientific Visualization. 2009. V. 1. pp. 1-18. Url: http://sv-journal.org/2009-1/01.php?lang=en

13. Murav'eva О.V. Studying the stability of solutions to systems of linear inequalities and constructing separating hyperplanes. Journal of Applied and Industrial Mathematics. 2014. V. 3. pp. 53-63.

14. Kalitkin N.N. Numerical methods. Nauka, 1978. 512 p.

15. Bukin, A.D. New Minimization Strategy for Non-Smooth Functions. Novosibirsk, 1997. 24 p.

16. Bache K., Lichman M. UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science, 2013. URL: http://archive.ics.uci.edu/ml.

17. Wolberg W.H. Computerized Diagnosis of Breast Fine-Needle Aspirates. The Breast J. 1997. Vol. 3. pp. 77–80.

19. Phuong T.M., Lin Z. et Altman R.B. Choosing SNPs using feature selection. Journal of Bioinformatics and Computational Biology, 2005. pp. 301-309. http://dx.doi.org/10.1109/CSB.2005.22

20. Troyanozhko О.А., Kolesin I.D. Analysis of influence of probability distribution type on accuracy of diagnostic features ranking. Scinentific and Technical Volga Region Bulletin. 2013. Vol. 6. pp. 457-461.

21. Bradley E.L. Overlapping Coefficient. Encyclopedia of statis-tical Sciences: S. Kotz and N.L. Johnson (Eds.), Wiley: New York, 1985. vol. 6. pp. 546-547.

23. Troyanozhko О.А., Kolesin I.D. Two-Stage Medical Expert System. Izvestiya Yugo-Zapadnogo gosudarstvennogo universiteta. Seriya: Upravlenie, vychislitel'naya tekhnika, informatika. Medicinskoe priborostroenie. 2017. №1(22) pp. 82-88.

24. Mangasarian O.L. Misclassification minimization. Journal of Global Optimization 5, 1994, pp. 309-323. http://dx.doi.org/10.1007/BF01096681

26. Demyanov V.F., Demyanova V.V., Kokorina A.V. On prognosing the efficiency of chemotherapy in the treatment of oncological patients. Vestnik of St. Petersburg State University, Applied Mathematics. 2006. Vol. 4. pp. 30-36.

27. Grigorieva, K.V. Approximation of a criterial functional in problems of mathematical diagnostics. M.Sc. dissertation. 2006. SPb. p. 191.