КОМПЬЮТЕРНАЯ ВИЗУАЛИЗАЦИЯ ИНДИКАТРИС РАССЕЯНИЯ РЭЛЕЯ В ДИНАМИКЕ

М.В. Сапронов, Н.М. Скорнякова

Национальный исследовательский университет «МЭИ», Россия

E-mail: nmskorn@mail.ru

 

Содержание

1. Введение

2. Расчет безразмерных комплексных амплитудных функций рассеяния

3. Компьютерная визуализация индикатрис рассеяния

4. Заключение

Благодарности

Список литературы

 

Аннотация

Исследована зависимость индикатрис рассеяния электромагнитных волн на сферических однородных и изотропных частицах от параметров центров рассеяния методами компьютерного моделирования. Составлен алгоритм расчета двухмерных и трехмерных индикатрис рассеяния на основе теории Ми. Визуализирована динамика индикатрис рассеяния плоско поляризованного излучения при изменении радиуса частиц и их показателя преломления.

 

Ключевые слова: рассеяние ми, компьютерная визуализация, компьютерное 2d- и 3d-моделирование, рассеяние рэлея

 

1. Введение

 

Рассеяние и поглощение света – фундаментальные процессы взаимодействия излучения с веществом, которые лежат в основе всех оптических явлений. Проблема строгого расчета рассеяния света на атомах, молекулах и других неоднородностях приобрела актуальность в середине XIX в., но значительный прорыв в расчете рассеяния произошел лишь в 1908 г., когда Г. Ми получил строгие выражения для расчета безразмерных комплексных амплитудных функций рассеяния света на сферических изотропных частицах произвольного размера, не обладающими выраженным поглощением [1]. Теория расчета рассеяния Ми обобщила существующие в то время методы расчета индикатрис рассеяния света на малых по отношению к длине волны частицах (приближение Рэлея), на частицах больших размеров, соизмеримых с длиной волны, (приближение Рэлея – Ганса) и на больших частицах (приближение больших частиц) [2]. Несмотря на то, что теория Ми разработана для упругого рассеяния света на сферических частицах, она с высокой точностью описывала экспериментальные результаты, что, несомненно, оказало влияние на развитие оптических методов диагностики фазовых неоднородностей в оптически прозрачных средах.

Эффект упругого рассеяния света диэлектрическим частицами лежит в основе таких методов диагностики как, например, методы лазерной доплеровской анемометрии [3, 4] и анемометрии по изображению частиц (PIV) [5], которые позволяют восстанавливать поля скоростей и визуализировать потоки жидкости и газа. Одним из преимуществ этих методов является относительная простота практического применения, но они обладают и серьезными недостатками. Чаще всего исследуемый поток засеивается рассеивающими центрами искусственно, что иногда недопустимо изменяет параметры потока, кроме того, движение частиц внутри среды отличается от движения самой среды, что также негативно влияет на точность измерений. Избавиться от указанных недостатков возможно, если использовать в качестве рассеивателей частицы исследуемой среды – молекулы и атомы вещества.

Кроме диагностики потоков в последние годы развиваются методы определения размеров наночастиц на основе результатов измерения параметров рассеянного ими излучения [6, 7]. 

Ввод частиц в поток продиктован недостаточной для регистрации мощностью сигнального излучения, поэтому чаще всего на используемых рассеивающих центрах рассеяние соответствует приближению Рэлея–Ганса или приближению больших частиц, рассеяние света на молекулах или атомах соответствует приближению Рэлея, теоретическое и экспериментальное исследование которого еще полностью не закончено и становится все более актуальным в наши дни. Физики первой половины XX в. не исследовали вопрос рассеяния Рэлея, поскольку не было возможности прямого экспериментального подтверждения правильности теоретического расчета. Тогда этот тип рассеяния исследовался лишь в прикладных науках, а интерес проявлялся в основном к численным результатам [1]. К середине XX в. таких результатов накопилось достаточно много, и на их основе в 1957 г. голландский физик Г. ван де Хюльст изложил физические основы рассеяния света на частицах малых по отношению к длине волны в монографии «Рассеяние света малыми частицами».

Современный уровень развития вычислительной техники, мощных когерентных источников и высокочувствительных приемников излучения создает возможность экспериментального исследования Рэлеевского рассеяния и вновь открывает широкое поле для научной деятельности.

Необходимым этапом каждого экспериментального исследования является разработка экспериментального макета установки и подбор ее параметров, в частности, для исследования рассеяния света необходимо знать, каким образом исследуемый тип рассеивающих центров влияет на характеристики рассеянного излучения, чтобы правильно выбрать подходящий источник зондирующего излучения и приемник излучения, несущего информацию о среде. Зависимость интенсивности рассеяния от направления наблюдения называется индикатрисой и является наиболее информативной энергетической характеристикой рассеяния.

Моделирование 2D- и 3D-индикатрис рассеяния по формулам Ми позволяет сделать оценку параметров экспериментальной установки для регистрации упруго рассеянного света, исследовать зависимость свойств детектируемого излучения от таких параметров рассеивающих центров, как характерный размер, оптическая плотность и поглощение. Кроме того, 3D-модели индикатрис помогают визуализировать и более полно понять физическую природу рассеяния.

В следующих главах при моделировании индикатрис акцент будет сделан на Рэлеевский характер рассеяния, поскольку в будущем авторы планируют подготовку электронно-оптического комплекса диагностики температурных полей в пламени, разогретых газах и плазме.

 

2. Расчет безразмерных комплексных амплитудных функций рассеяния

 

Размеры используемых на практике рассеивающих центров гораздо меньше, чем размер фронта зондирующей волны, поэтому можно считать, что на отдельный рассеиватель падает плоская волна. Для расчета индикатрис рассеяния необходимо определить направление падения зондирующей волны, плоскость наблюдения и ориентацию вектора напряженности электрического поля. На рис. 1 изображена схема единичного акта рассеяния плоской линейно поляризованной волны. Для определенности введена трехмерная система декартовых координат (x, y, z). Зондирующее излучение распространяется в направлении оси y и поляризовано в плоскости y0z. Определение интенсивности рассеянного излучения проводится в точке M, удаленной от центра рассеяния на расстояние R.

Плоскость P, образованная точкой наблюдения М и волновым вектором зондирующего излучения k, называется плоскостью рассеяния. Волновой вектор kS рассеянного излучения лежит в плоскости P и направлен под углом θ к вектору k.

Для энергетического расчета рассеяния необходимо разложить вектор напряженности электрического поля E на две компоненты, одна из которых  ортогональна плоскости падения, а другая  – параллельна. Тогда вектор Джонса для падающей волны может быть представлен выражением (1)

 

,

(1)

 

где  и  – комплексные амплитуды компонент  и  вектора E.

 

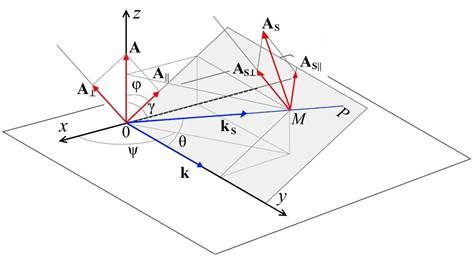
Схема рассеяния 1

Рис. 1. Схема рассеяния плоской линейно поляризованной волны

 

Электрический вектор рассеянной волны ES в точке наблюдения M на достаточно большом расстоянии R от центра рассеяния (R >> r2 / λ, r – радиус частицы, λ – длина волны излучения) можно представить следующим вектором Джонса (2)

 

,

(2)

 

где  ,  и ,  – имеют тот же смысл, что и в выражении (1), но отнесены к рассеянной волне.

Соотношения между комплексными амплитудами компонент рассеянного поля и комплексными амплитудами компонент падающего поля в линейном приближении можно представить в виде (3)

 

 

,

(3)

 

где [S] – матрица рассеяния, которая в системе отсчета, связанной с плоскостью раcсеяния, имеет диагональный вид (4)

 

,

(4)

 

 и  – безразмерные комплексные амплитудные функции рассеяния для составляющих, перпендикулярной и параллельной плоскости рассеяния. Общие выражения для  и в виде рядов (5) были получены Ми (G. Mie) в 1908 г.:

 

;

(5)

 

.

 

Формулы для расчетов n-ых коэффициентов Ми an и bn, а также выраженных через полиномы Лежандра и их производные коэффициентов πn и τn, приведены в монографии [8]. Амплитудные функции рассеяния  и зависят лишь от трех параметров:
m – комплексного показателя преломления частицы относительно окружающей ее среды (m = m1 / m2, где m1 – показатель преломления частицы, m2 – показатель преломления среды), x = kr – относительного размера частицы радиуса r (k = 2π / λ = 2πm2 / λ0), угла рассеяния θ между волновыми векторами падающей и рассеянной волн. Предполагается, что среда, в которой распространяется излучение, прозрачна, следовательно, m2 – действительная величина.

Векторы Джонса комплексных амплитуд падающей и рассеянной волн удобно представлять в нормированном виде

 

,   ,

(6)

 

где , .

Углы φ и φS определяются соотношениями

 

,   .

(7)

 

Как было упомянуто выше, рассеяние принято описывать безразмерными функциями, показывающими относительное угловое распределение интенсивности рассеянного света [9], – индикатрисами (8)  или  в обычном или логарифмическом масштабах соответственно:

 

  и  .

(8)

 

Поскольку формулы Ми (5) включают сумму бесконечного ряда, то редко представляется возможным получить аналитическое выражение, описывающее индикатрисы рассеяния. Поэтому сумму ряда ищут, используя рекурсию и ограничившись конечным числом членов при достижении заданной точность ε. Для построения алгоритмов рекурсии используются рекуррентные формулы расчета коэффициентов an, bn, πn и τn [8].

Для численного расчета угловых коэффициентов πn и τn, входящих в (5) используются соотношения:

 

,

(6)

 

,

 

где

,   ,   ,

 

, , .

 

Формулы для расчета коэффициентов Ми an и bn выглядят следующим образом:

 

,

(7)

 

,

 

где  – множители, которые определяются через функции Бесселя комплексного аргумента [8],  – круговые функции, которые в данном случае имеют действительный аргумент и совпадают с функциями Рикатти – Бесселя [8].

 

3. Компьютерная визуализация индикатрис рассеяния

 

Для визуализации трехмерных индикатрис рассеяния необходимо охватить весь диапазон возможных направлений наблюдения, и, следовательно, использовать трехмерную систему координат, которая не может быть связана с плоскостью рассеяния P, ведь сама эта плоскость, определяемая точкой наблюдения М и вектором k, будет вращаться вокруг оси, содержащей вектор k, с перемещением точки M в пространстве. Весьма удобной для представления индикатрис является сферическая система координат (ξ, ψ, γ) или (Υ, ψ, γ), где широта ψ – угол, отсчитываемый от оси x в плоскости x0z, долгота γ – угол, отсчитываемый от оси z, а ξ и Υ – значение индикатрисы в заданном углами ψ, γ направлении в обычном и логарифмическом масштабах соответственно.

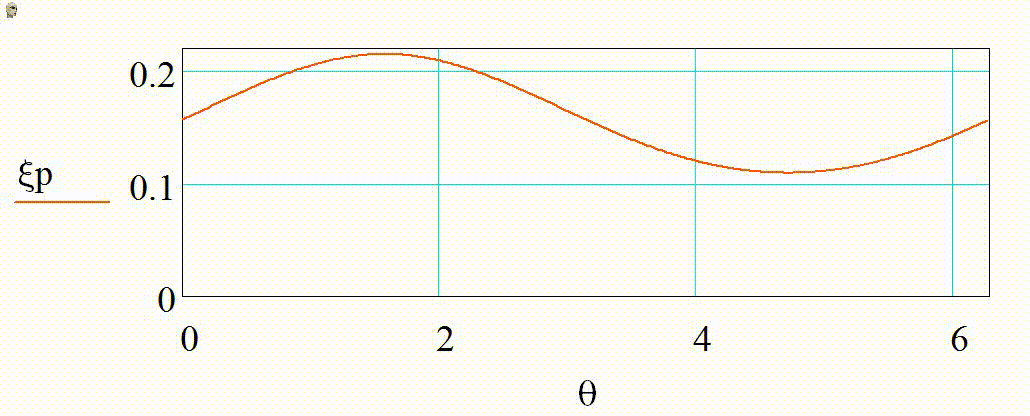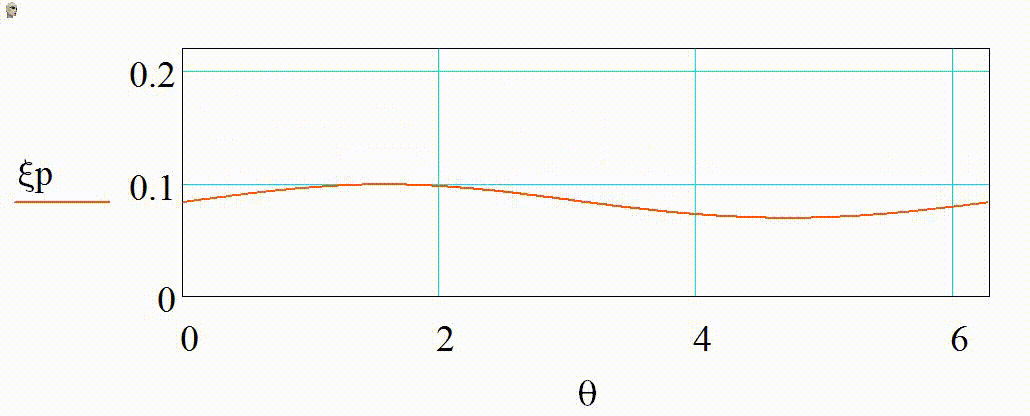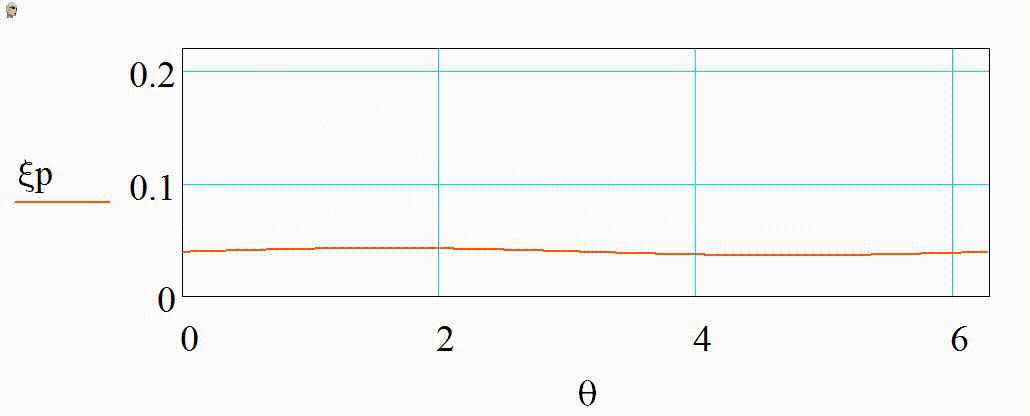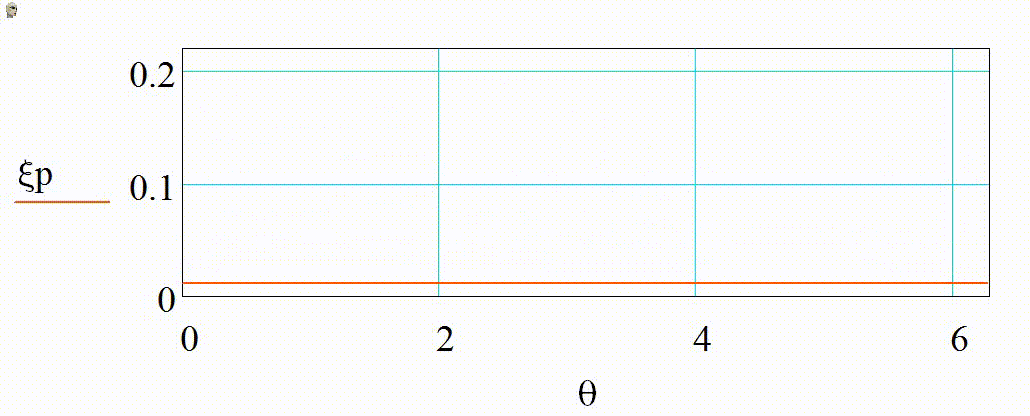
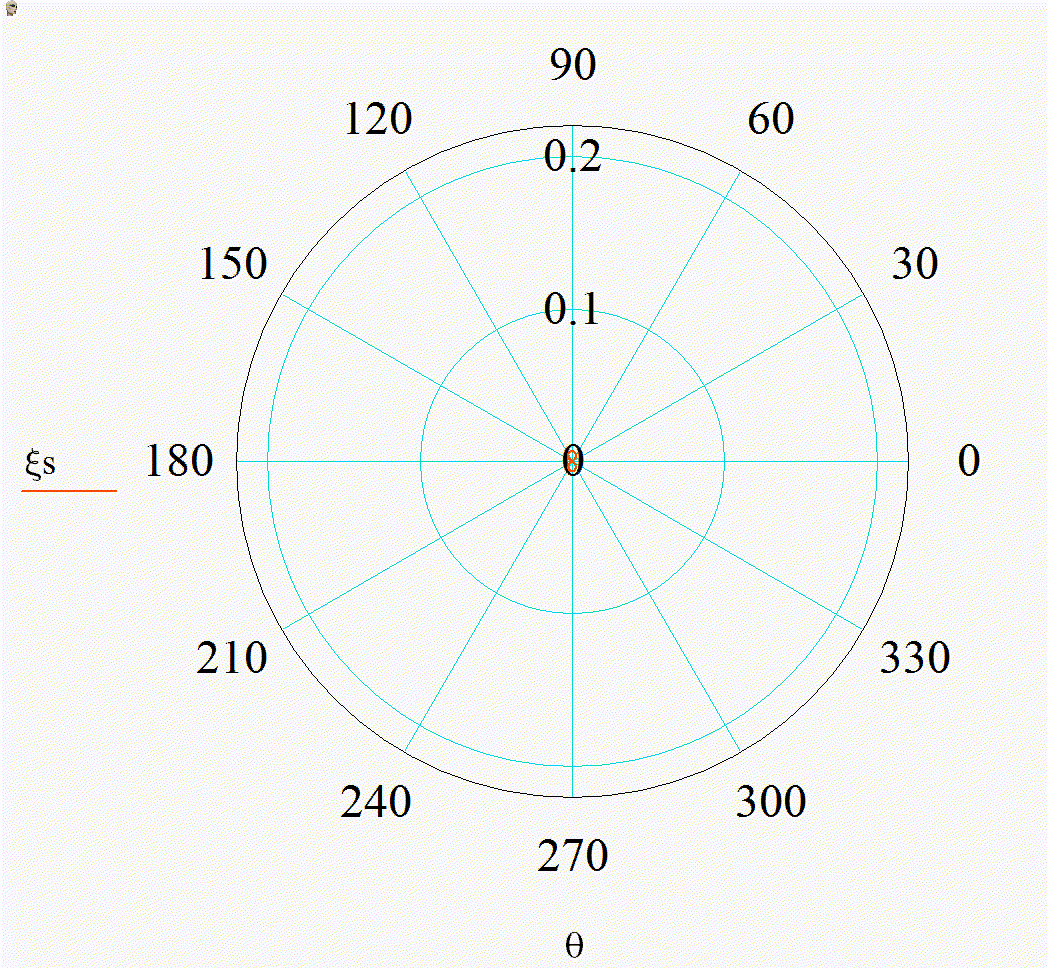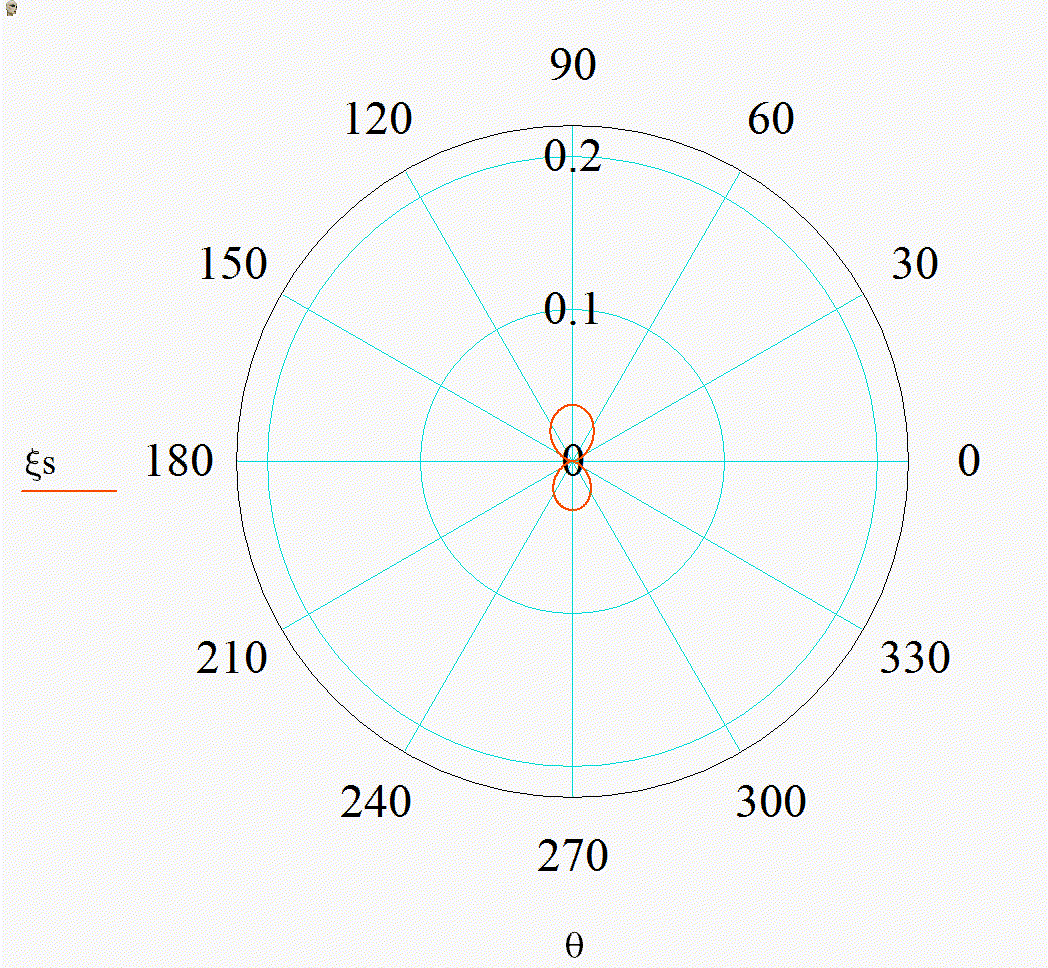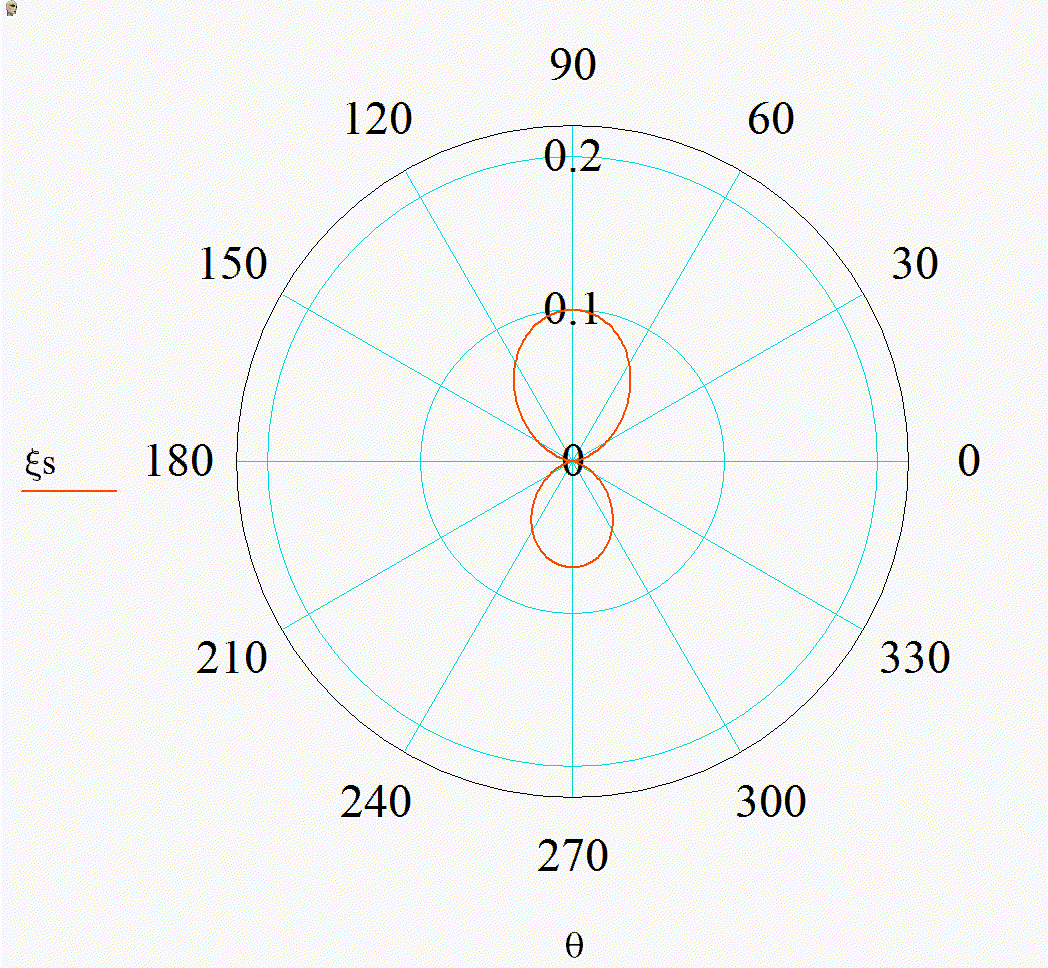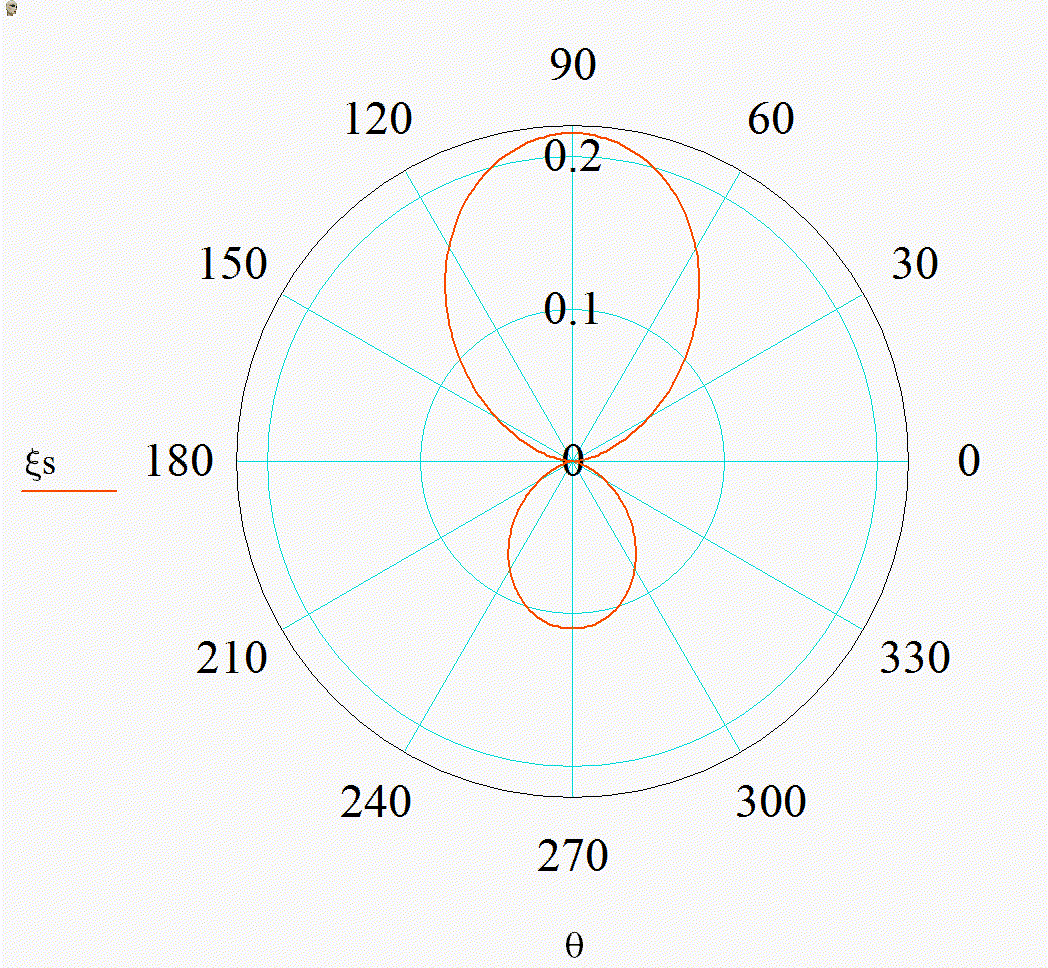
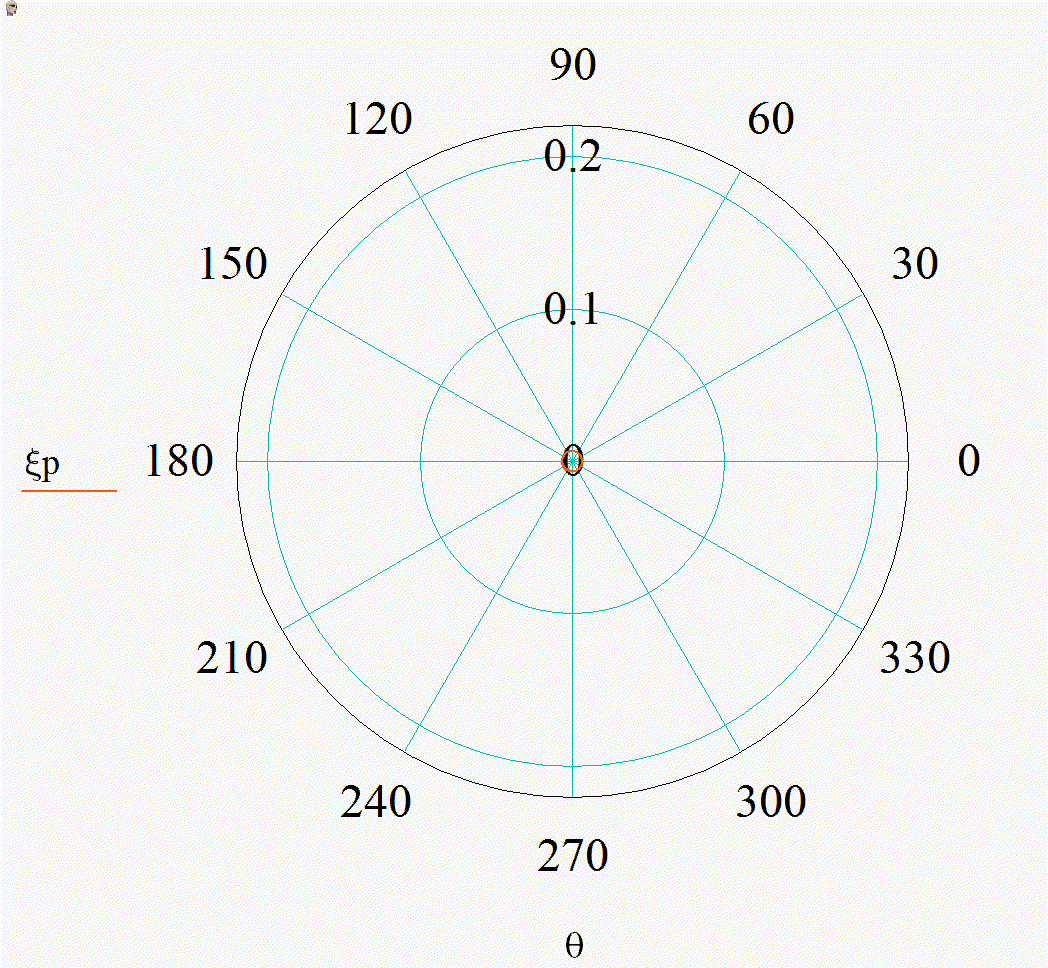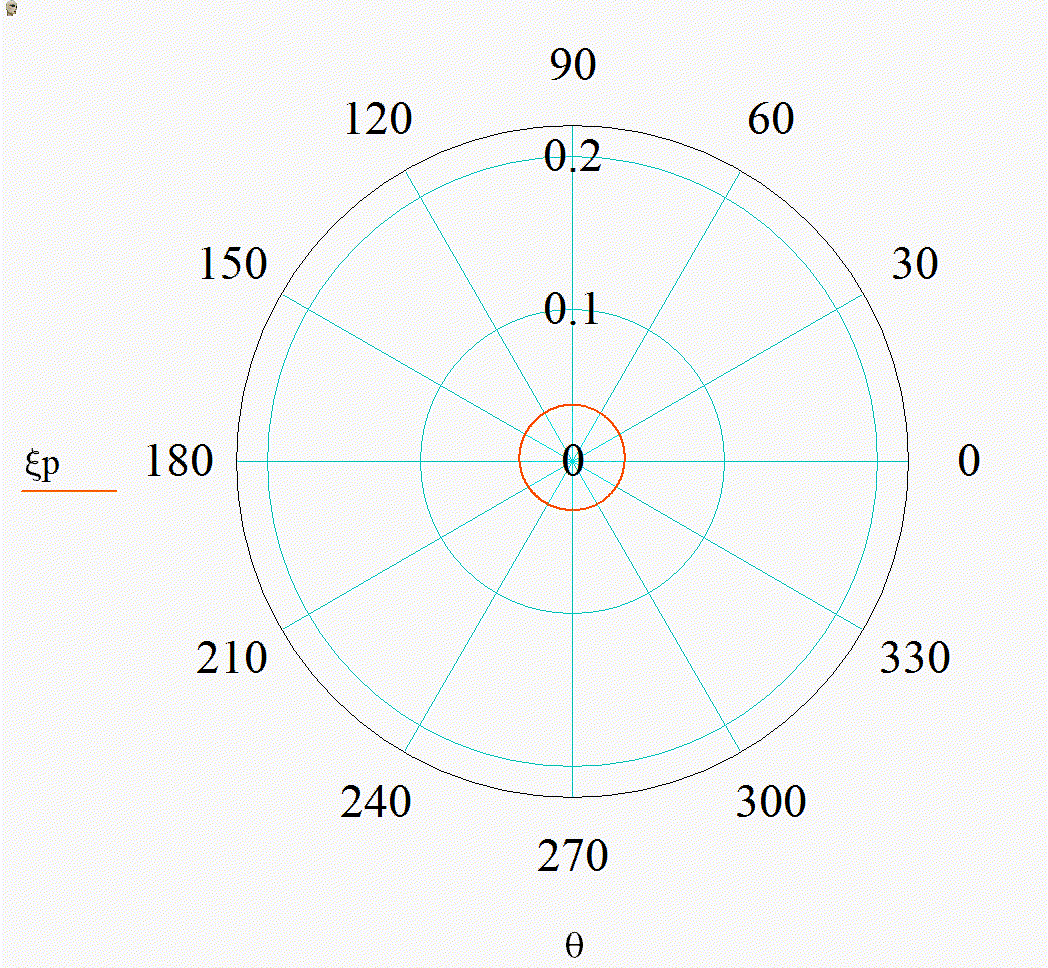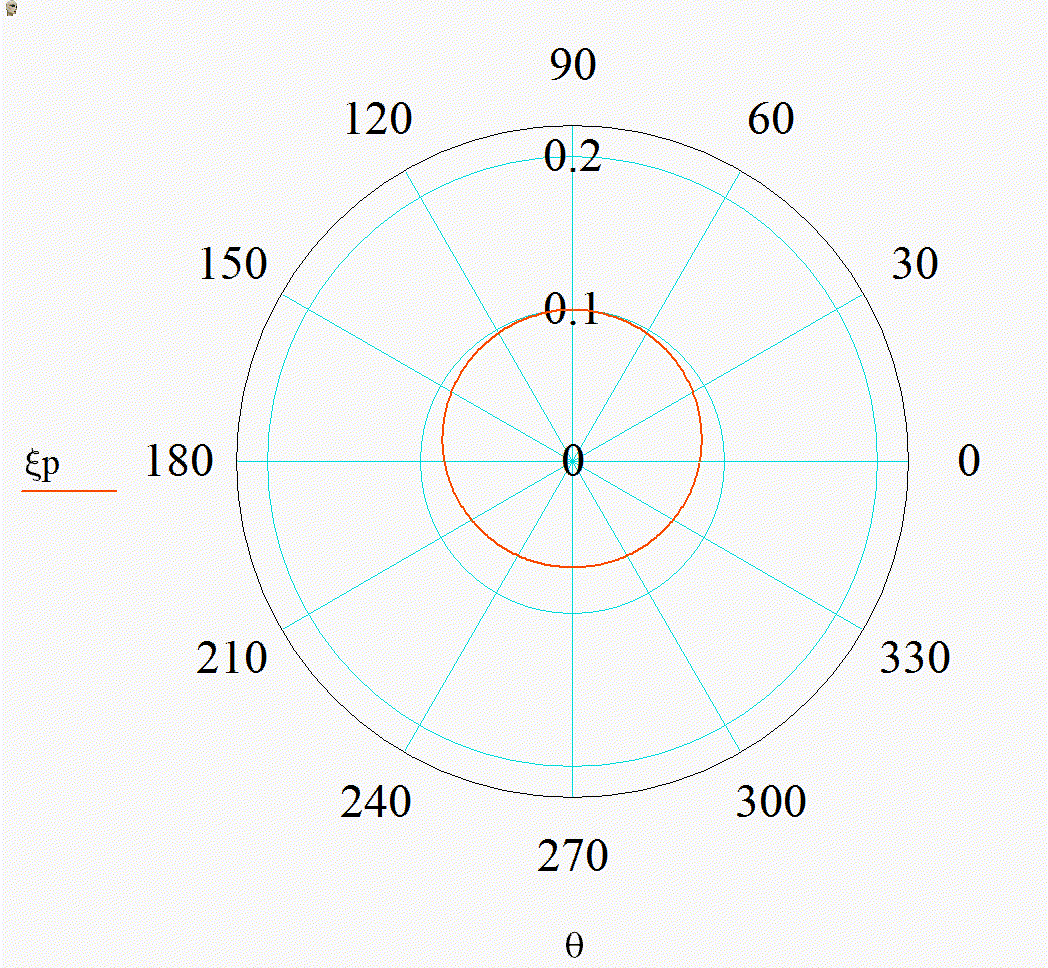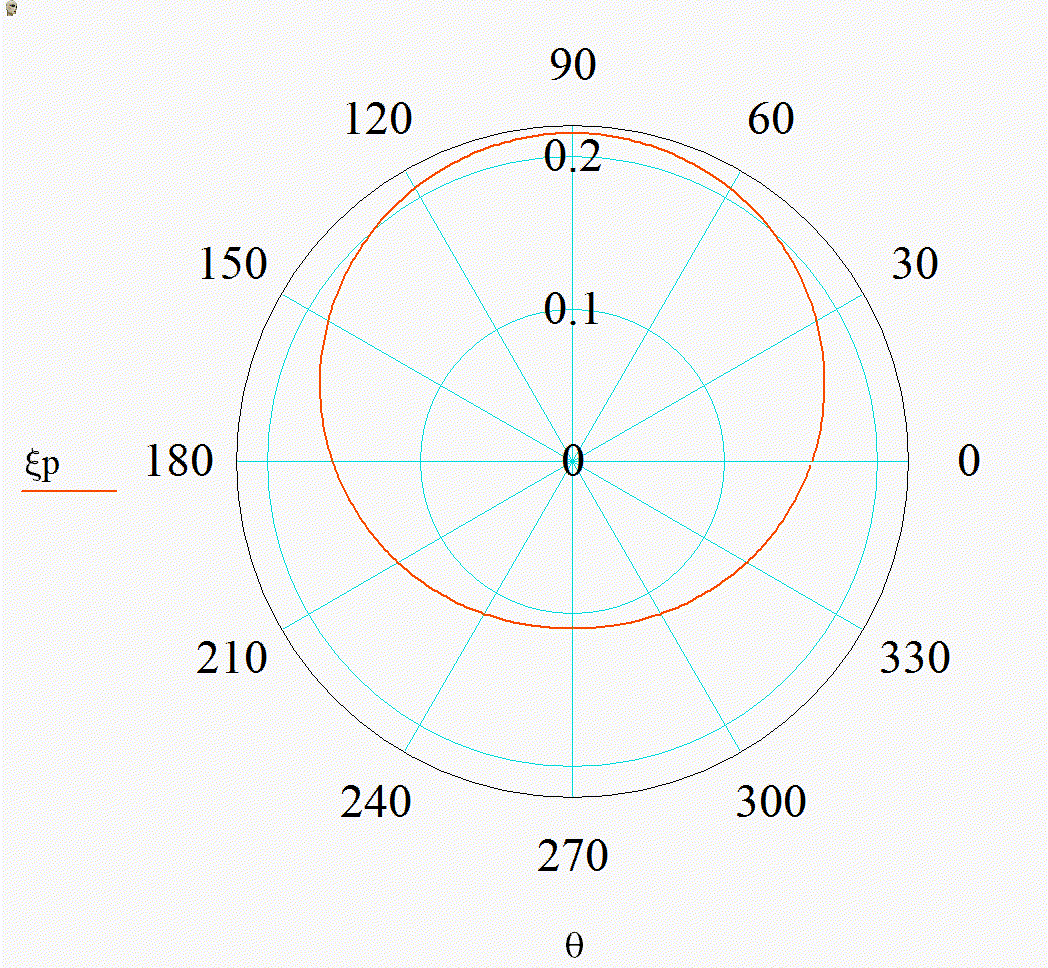
На анимации 1 представлены 2D-индикатрисы рассеяния линейно-поляризованного излучения с длиной волны λ = 355 нм на диэлектрических частицах с показателем преломления m = 1,4 при изменении их радиуса r в диапазоне от 3 до 15 нм в плоскости поляризации (а), (в) и ортогональной ей (б), (г) в декартовой и полярной системах координат.

Значение длины волны света λ = 355 нм выбрано для моделирования по двум основным причинам. Во-первых, известно, что при Рэлеевском характере рассеяния интенсивность рассеянного излучения I на частице постоянного размера будет тем выше, чем короче длина волны у падающего излучения, причем . Во-вторых, как было отмечено, в будущем авторами планируется исследование рассеяния в плазме и в пламени с использованием импульсного лазера на кристалле YAG:Nd с большой энергией в импульсе совместно с нелинейными кристаллами, которые могут использоваться для генерации первых 4-х гармоник лазерного излучения. С учетом чувствительности предполагаемой к использованию системы регистрации рассеянного излучения, состоящей из усилителя фотонов и фотокамеры, оптимально использовать 3-ью гармонику лазера, длина волны которой λ = 355 нм. Показатель преломления выбран безотносительно к какому-либо конкретному типу рассеивателей, но принадлежит диапазону показателей преломления предполагаемых для исследования частиц, среди которых есть как молекулы и атомы газов, например, Ar и CO2, так и твердые частицы, например, углеродная сажа.

 

1

 

1

а)

б)

1

 

1

в)

г)

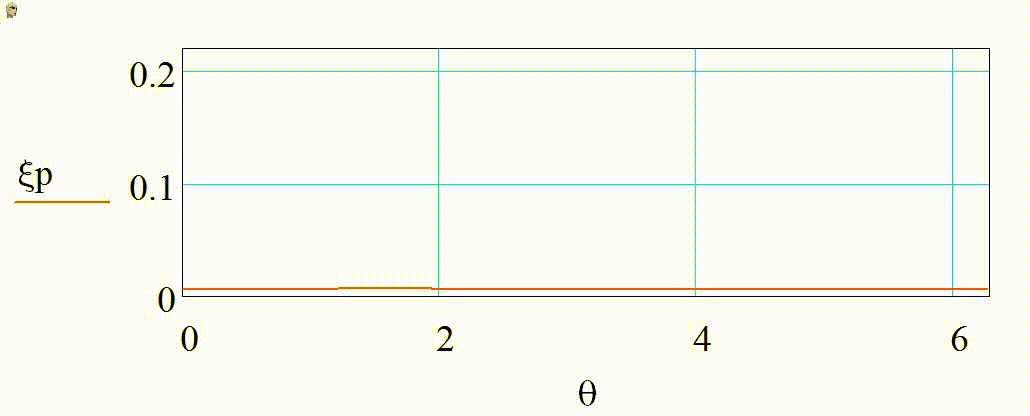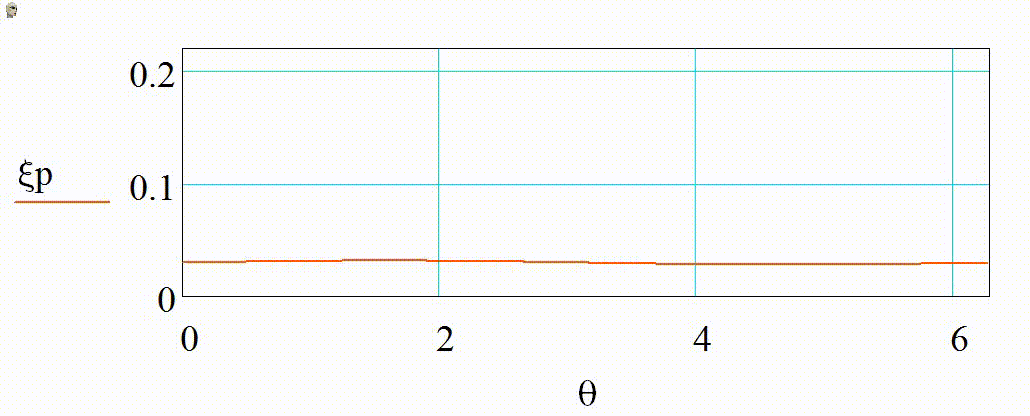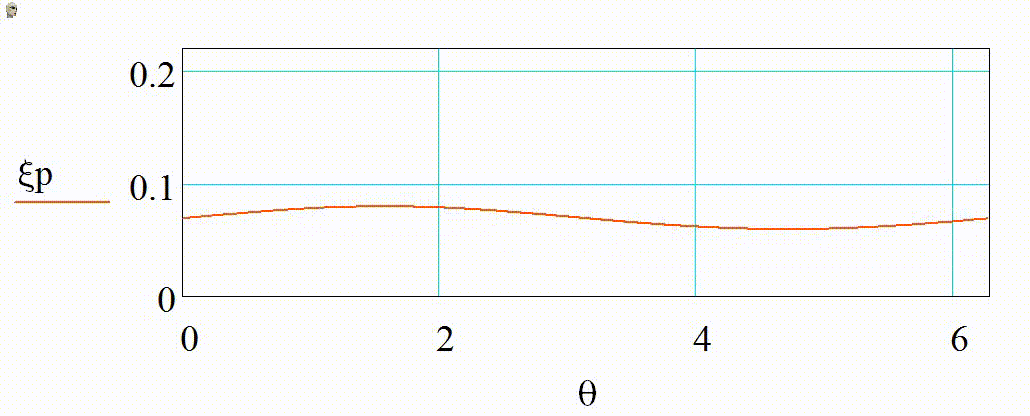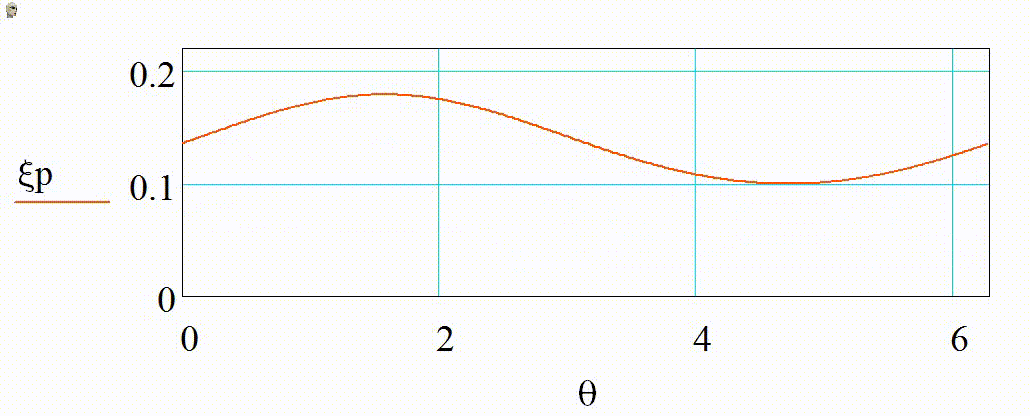
Анимация 1. Динамика 2D-индикатрис рассеяния при изменении r от 3 до 15 нм (λ = 355 нм, m = 1,4):

а) в плоскости поляризации в декартовых координатах, б) в плоскости, ортогональной поляризации в декартовых координатах, в) в плоскости поляризации в полярных координатах, г) в плоскости, ортогональной поляризации в полярных координатах

 

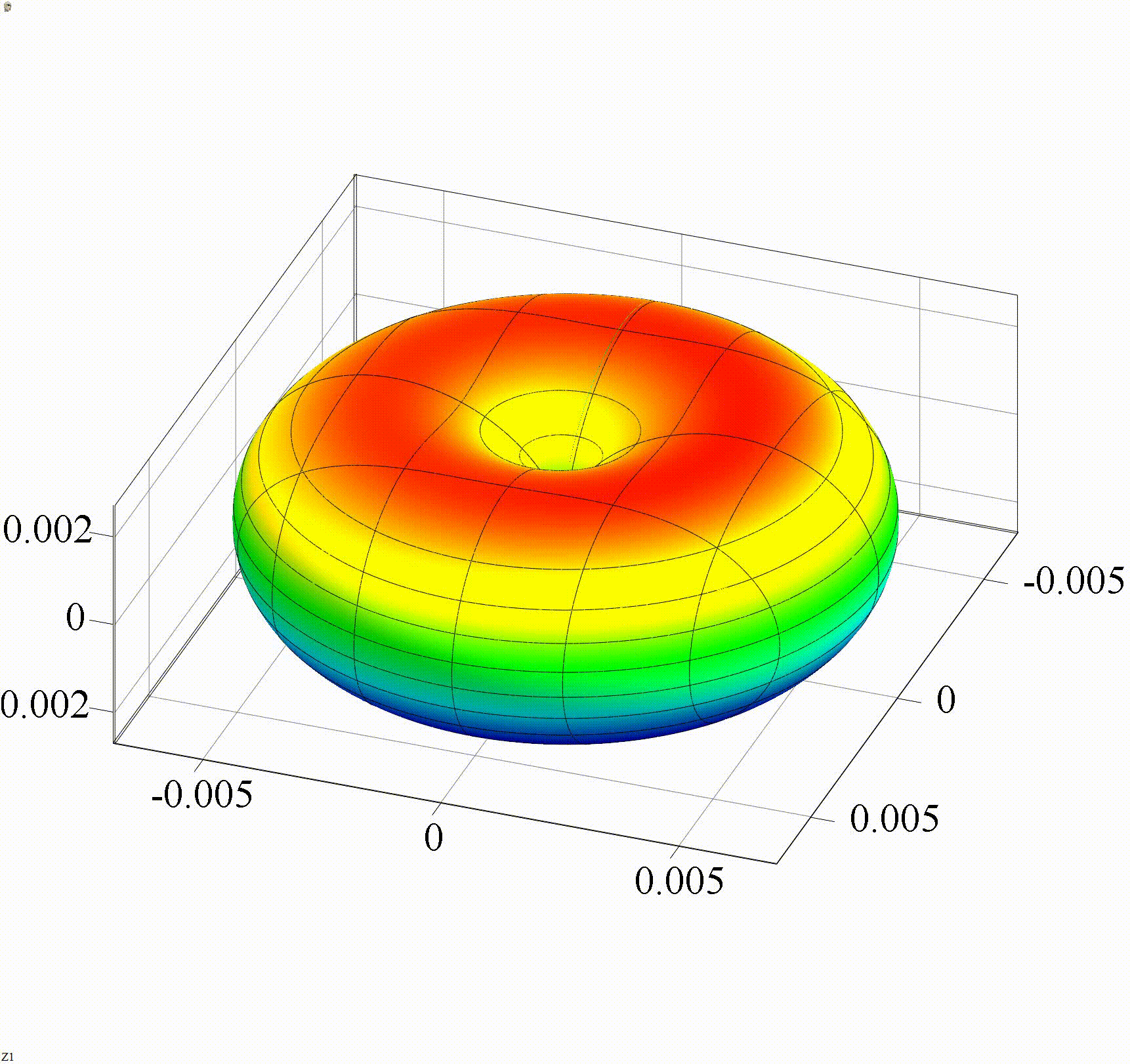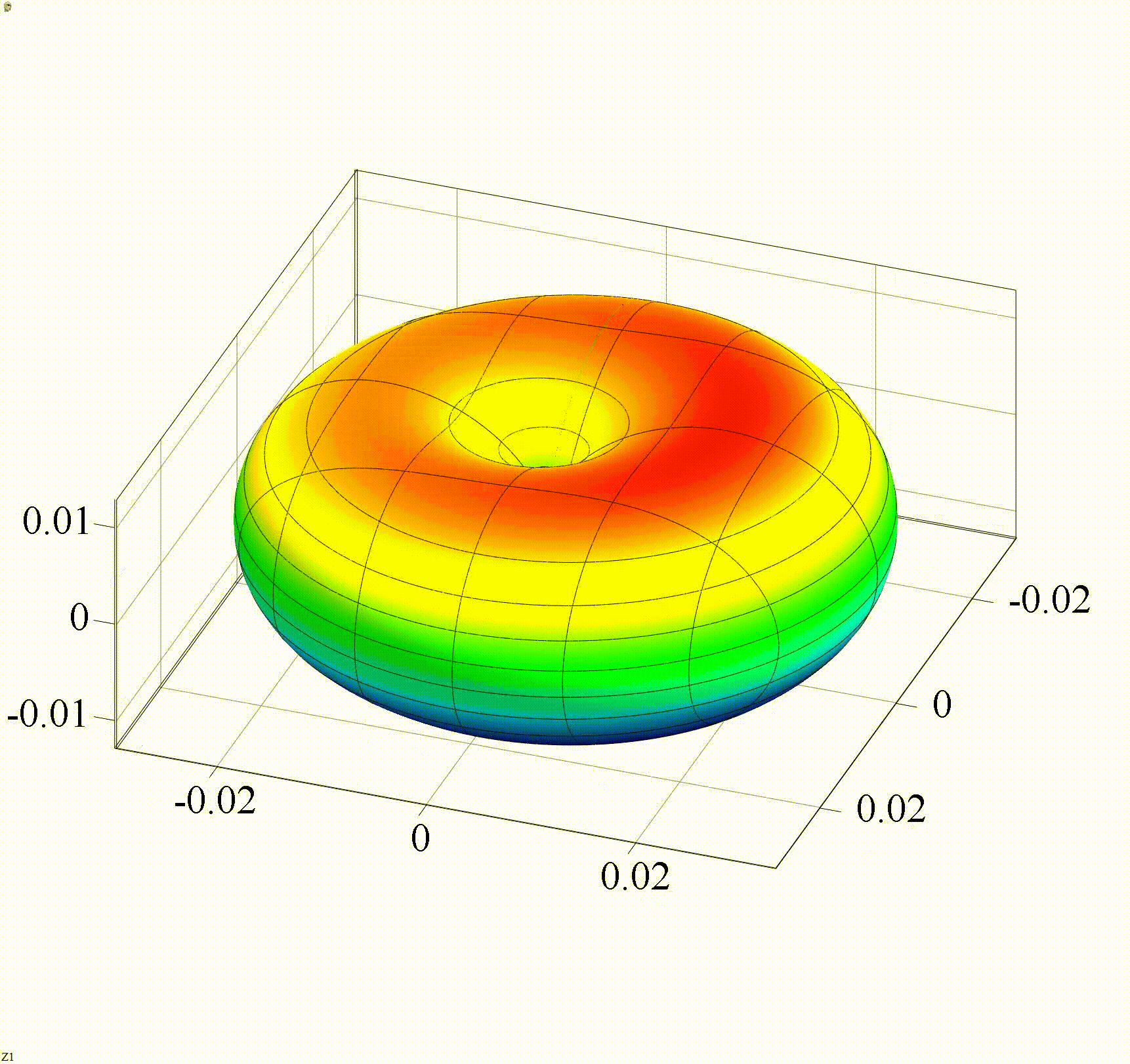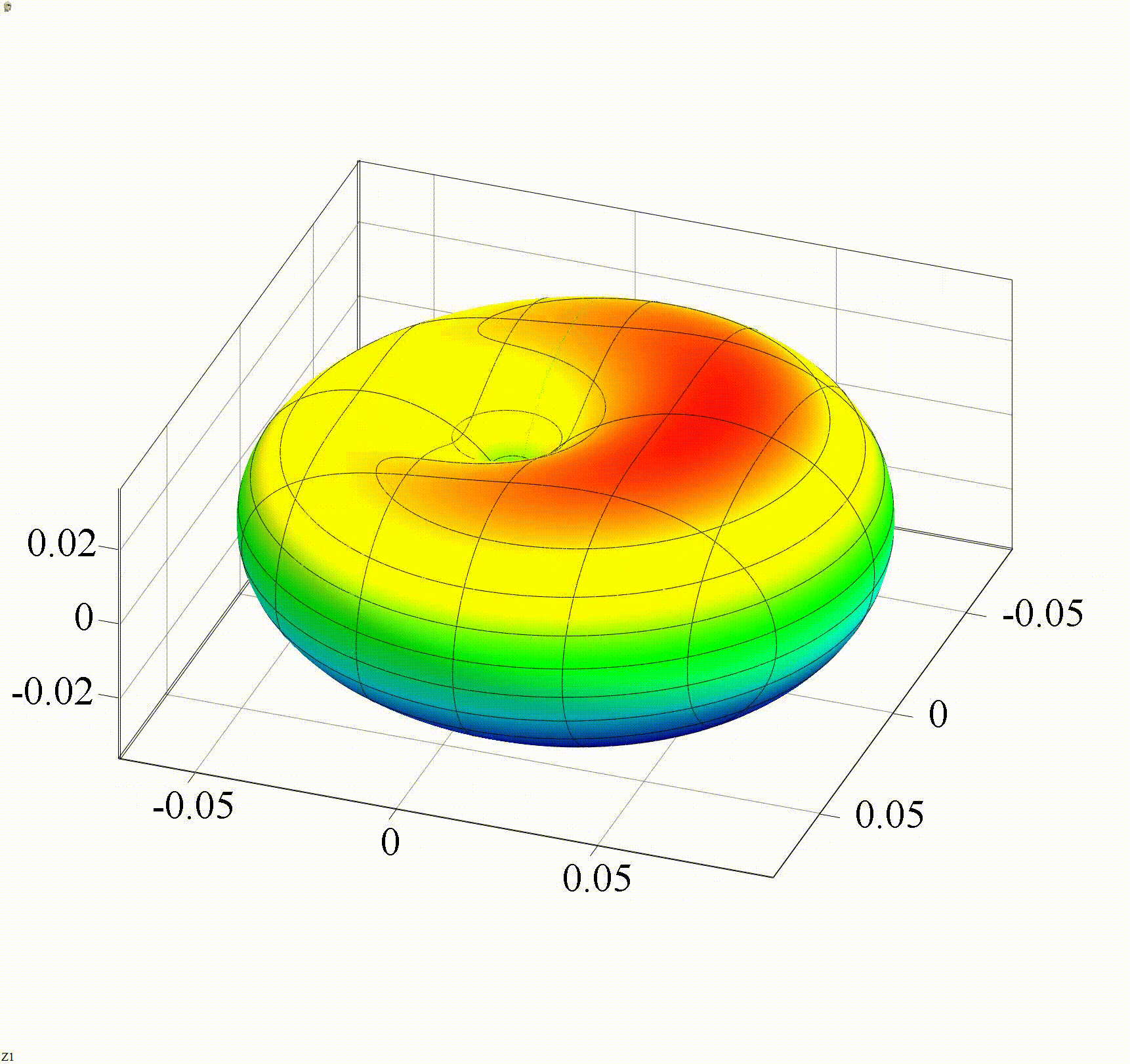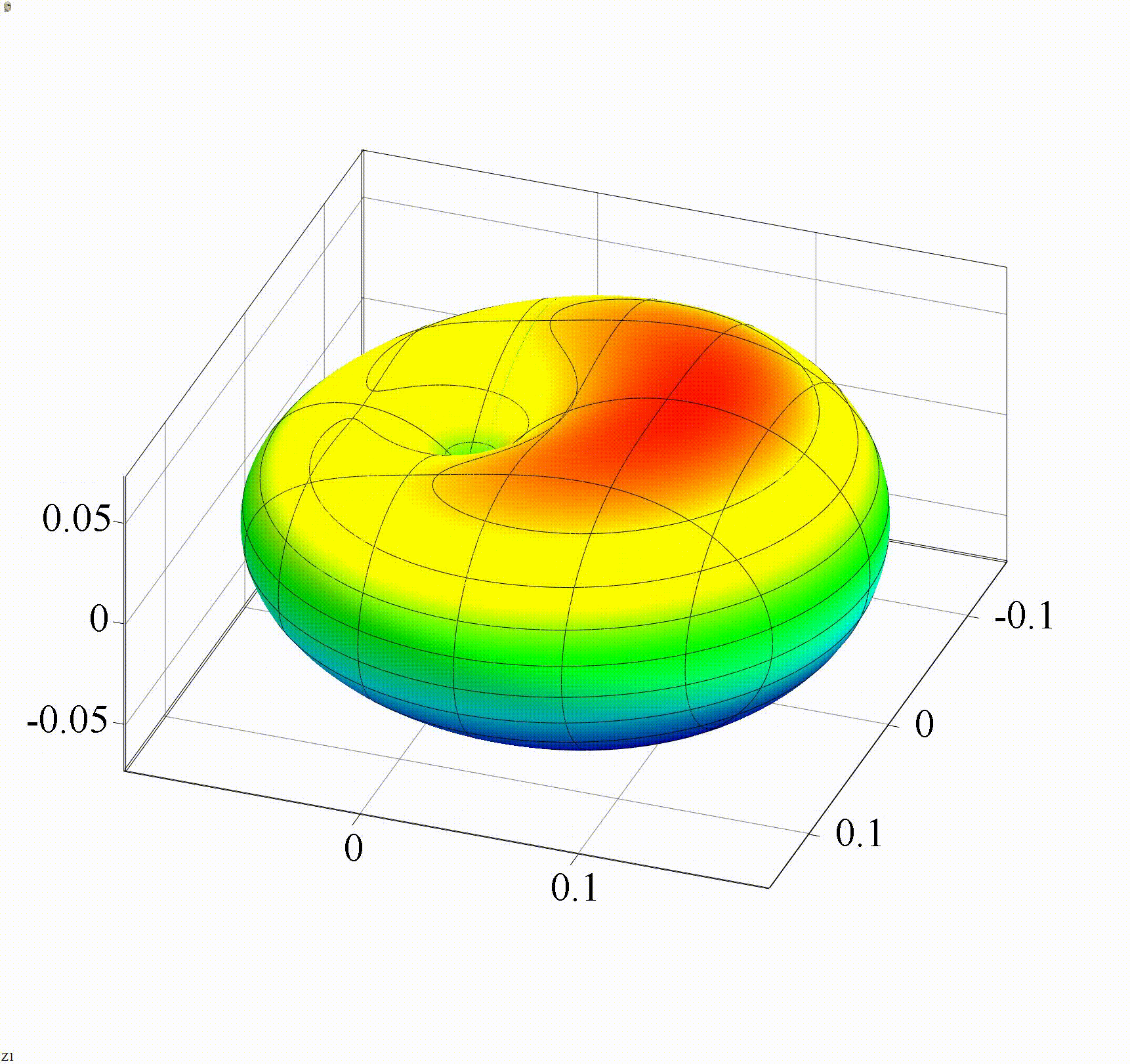
На анимации 2 представлена 3D-индикатриса рассеяния линейно-поляризованного излучения с длиной волны λ = 355 нм на диэлектрических частицах с показателем преломления m = 1,4 при изменении их радиуса r в диапазоне от 3 до 15 нм в сетке с постоянным масштабом (а) и с переменным масштабом (б).

 

2

 

а)

2

 

б)

Анимация 2. Динамика 3D-индикатрисы рассеяния при изменении r от 3 до 15 нм (λ = 355 нм, m = 1,4):

а) в сетке с постоянным масштабом, б) в сетке с переменным масштабом

 

Два способа задания сетки обоснованы тем, что анимация 2а наглядно отражает изменение средней интенсивности рассеянного излучения, а анимация 2б показывает изменение характера распределения интенсивности по направлениям рассеяния.

В представленном случае на анимациях 1 и 2 в индикатрисе отсутствуют интерференционные лепестки, что говорит о Рэлеевском характере рассеяния. Динамика индикатрисы демонстрирует две характерные особенности. Средняя интенсивность рассеянного излучения нелинейно возрастает с увеличением размера частицы (шаг изменения размера постоянен на каждой анимации). Выбранный диапазон радиусов хорошо демонстрирует предел применимости Рэлеевского рассеяния, ведь если для r = 3 нм интенсивности рассеянного излучения вперед и рассеянного излучения назад еще слабо отличаются по величине, то при r = 15 нм рассеяние вперед значительно преобладает.

На анимации 3 представлены 2D-индикатрисы рассеяния линейно-поляризованного излучения с длиной волны λ = 355 нм на диэлектрических частицах с показателем преломления m = 1,4 при изменении их радиуса r в диапазоне от 30 до 100 нм в плоскости поляризации (а) и ортогональной ей (б) в полярной системе координат. В отличие от случая, продемонстрированного на анимации 1, здесь используется логарифмическая индикатриса , потому что при выбранном диапазоне радиусов рассеяние вперед сильно доминирует над обратным.

 

2

3

а)

б)

Анимация 3. Динамика 2D-индикатрис рассеяния в логарифмическом масштабе при изменении r от 30 до 100 нм (λ = 355 нм, m = 1,4): а) в плоскости поляризации в полярных координатах, б) в плоскости, ортогональной поляризации в полярных координатах

 

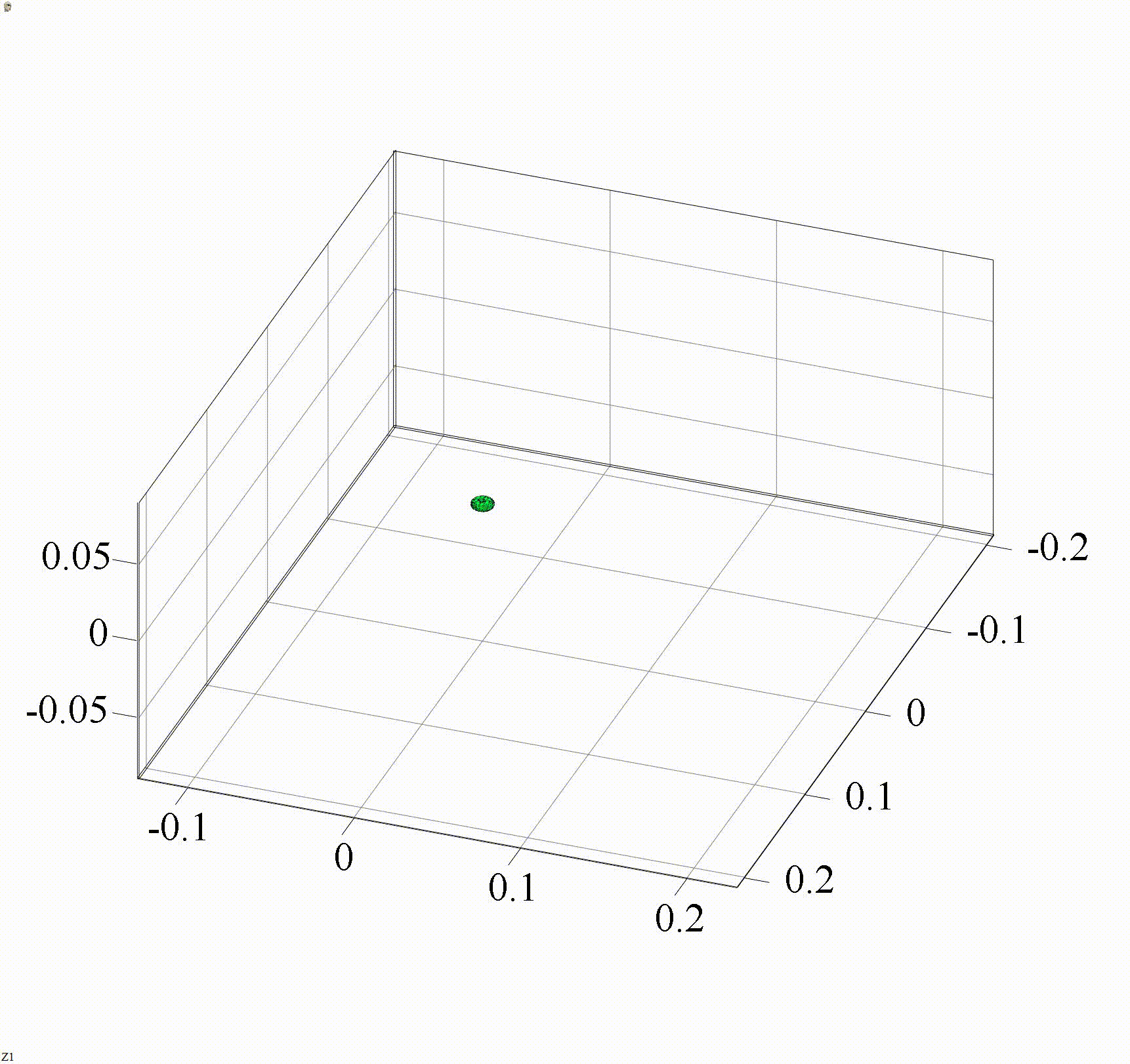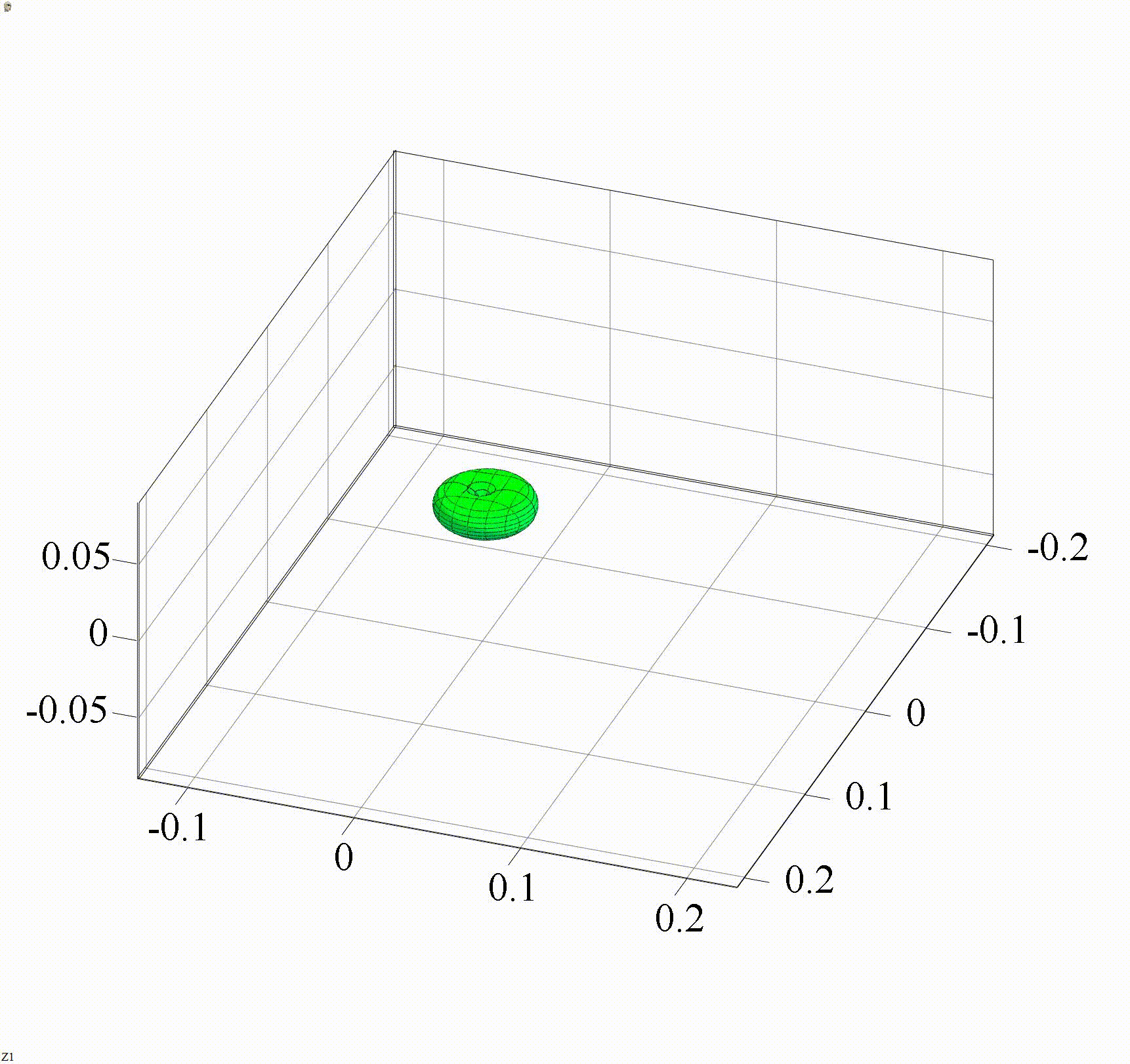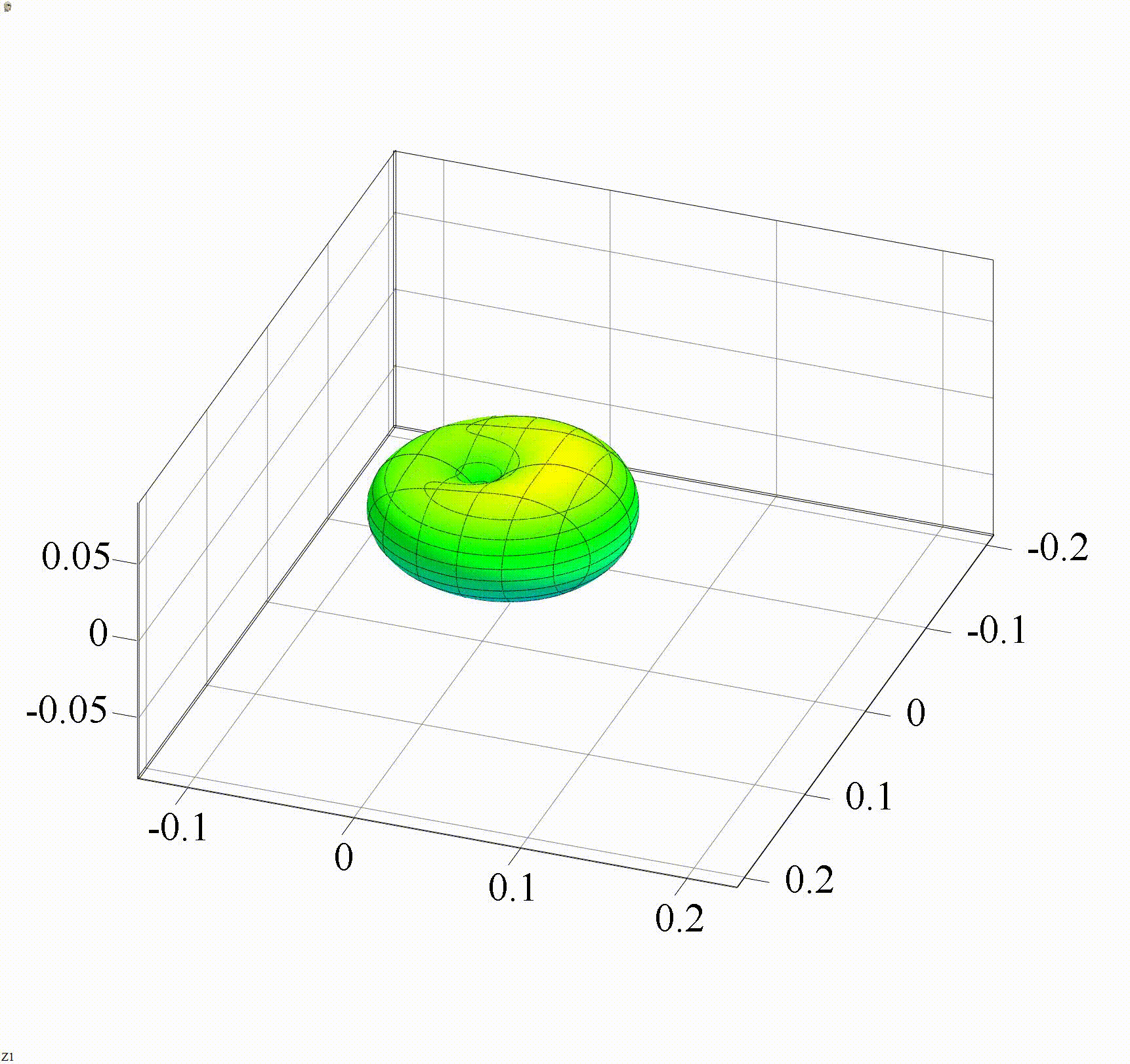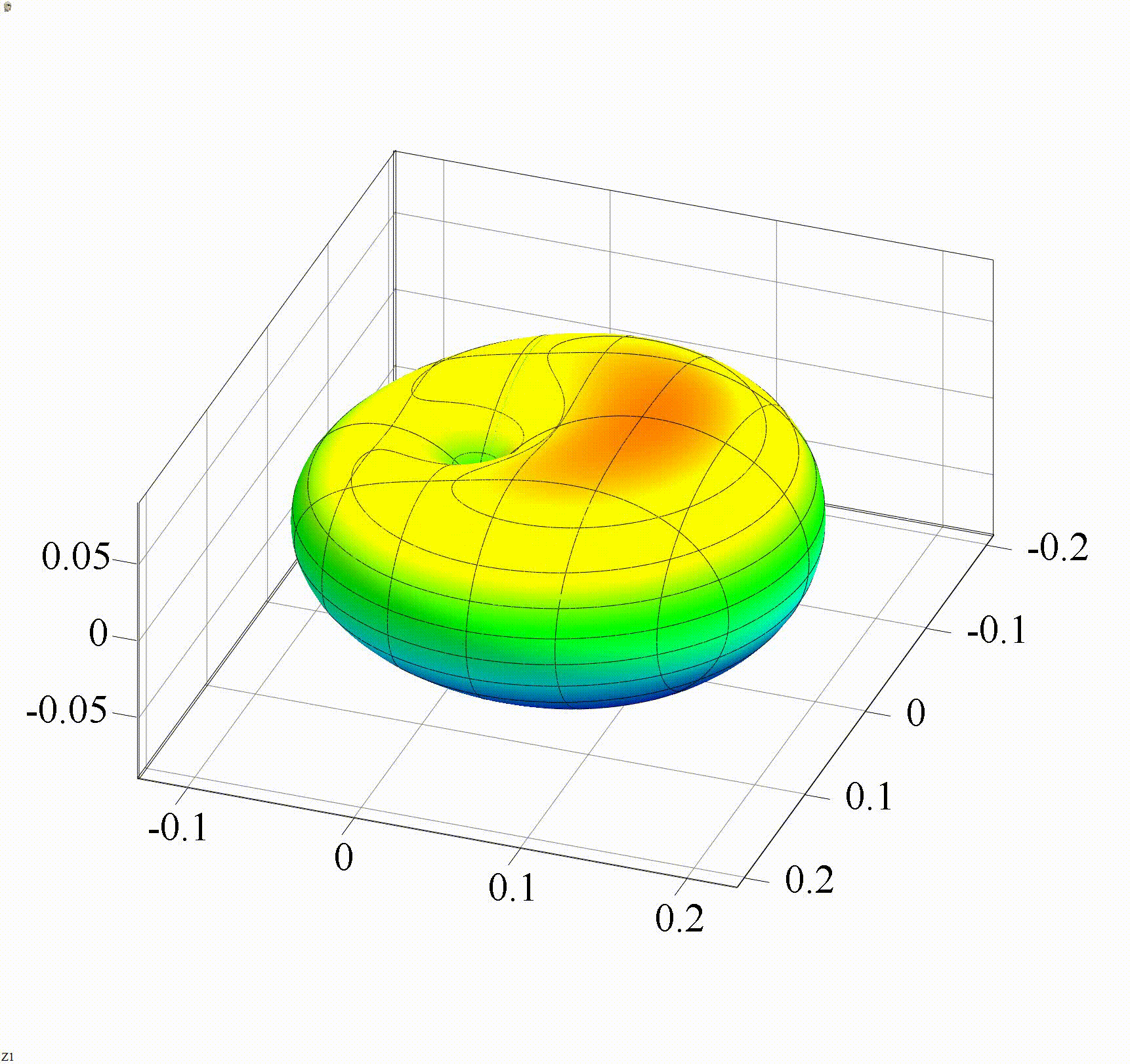
На анимации 4 представлены 3D-индикатрисы рассеяния в логарифмическом масштабе линейно-поляризованного излучения с длиной волны λ = 355 нм на диэлектрических частицах с показателем преломления m = 1,4 при изменении их радиуса r в диапазоне от 30 до 100 нм.

В диапазоне размеров частиц на анимациях 3, 4 начинают проявляться интерференционные эффекты – возникновение локальных максимумов и минимумов в индикатрисе рассеяния. Количество «лепестков» невелико, качественно можно утверждать, что интегральная величина рассеянного излучения осциллирует, но вместе с тем, ее среднее значение за каждое колебание увеличивается вместе с числом «лепестков». Такой характер рассеяния соответствует приближению Рэлея-Ганса.

 

3d-1

 

Анимация 4. Динамика 3D-индикатрисы в логарифмическом масштабе рассеяния при изменении r от 30 до 100 нм (λ = 355 нм, m = 1,4)

 

4. Заключение

 

В ходе компьютерного моделирования индикатрис рассеяния плоской линейно поляризованной волны на сферических диэлектрических частицах был разработан алгоритм расчета значений безразмерных комплексных амплитудных функций рассеяния в направлении, заданном углами ψ, γ. Разработана программа в среде MathCAD 14, которая позволяет строить двухмерные и трехмерные индикатрисы рассеяния и визуализировать их изменение в динамике при изменении радиуса и показателя преломления рассеивающих центров или длины волны падающего излучения.

Результаты работы программы дают наглядное представление о рассеянии света и помогают понять характер изменения индикатрисы рассеяния с варьированием каждого из параметров, влияющих на ее форму.

Ограничение приведенных результатов в перспективе их практического применения заключается в отличии формы реальных рассеивателей от сферической. Несмотря на это, компьютерное моделирование рассеяния света на основе теории Ми позволяет выбрать подходящее соотношение параметров частиц и зондирующего пучка света, оценить преобладающее направление рассеяния и величину интенсивности рассеянного излучения. Это дает возможность подбора условий проведения исследований и оптимальных параметров приемной оптической системы для корректного экспериментального исследования рассеяния.

 

Благодарности

 

Работа выполнялась при поддержке Министерства образования и науки РФ (проект 3.8009.2017/БЧ).

 

Список литературы

 

1. Ван де Хюлст Г. Рассеяние света малыми частицами / Пер. с англ.: Под ред. В.В. Соболева. М.: Изд-во иностр. лит-ры, 1961. 536 с.

2. Mie G. Beitra .ge zur Optik tru ber Medien speziell kolloidaler Goldlo sungen (contributions to the optics of diffuse media, especially colloid metal solutions). Ann. Phys., 1908. 25:377 – 445.

3. Ринкевичюс Б.C. Лазерная диагностика потоков. М.: Изд-во МЭИ, 1990.

4. Дубнищев Ю.Н., Ринкевичюс Б.С. Методы лазерной доплеровской анемометрии. М.: Наука, 1982. 303 с.

5. Raffel M., Willert C.E., Kompenhans J. Particle image velocimetry. A practical guide. Corrected 3rd printing. Springer, Germany, Berlin. 2013.

6. Зобов К.В. Особенности измерения размеров частиц в гидрозолях нанопорошка диоксида кремния оптическими методами. Вестн. Новосиб. гос. ун-та. Серия: Физика. 2016. Т.11. №4. С. 68 – 77.

7. Голубенко Ю.В. и .др. Применимость метода динамического рассеяния света для анализа диапазона размеров наночастиц золота и меди, полученных при помощи лазерной абляции твердых тел в жидкости. Наука и Образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2014. № 10. С. 15 – 28.

8. Дейрменджан Д. Рассеяние электромагнитного излучения сферическими полидисперсными частицами / Пер.с англ.: Под ред. К.Н. Кондратьева. М.: Мир, 1971. 165 с.

9. Смирнов В.И., Янина Г.М. Расчет и проектирование лазерных анемометров. М.: Моск. энерг. ин-т., 1996. – 84 с.



COMPUTER VISUALIZATION OF RAYLEIGH SCATTERING INDICATRIX IN DYNAMIC

M.V. Sapronov, N.M. Skornyakova

National Research University "MPEI"., Russian Federation

E-mail: nmskorn@mail.ru

 

Abstract

The dependence scattering indicatrix of electromagnetic waves on spherical homogeneous and isotropic particles on the parameters of the scattering centers by computer simulation methods is studied. An algorithm is developed for calculating two-dimensional and three-dimensional scattering indicatrix based on the Mie theory. The dynamics scattering indicatrix of plane-polarized radiation is visualized with a change in the radius of the particles.

 

Keywords: scattering g. mie, computer visualization, computer 2d- and 3d- modeling

 

References

 

1. H. C. van de Hulst. Light scattering by small particles. New York, Dover Publications, Inc., 1957, 470 p.

2. G. Mie. Contributions to the optics of turbid media, particularly colloidal metal solutions. Annalen der Physik, 1908, No.25, pp.377 – 445.

3. Rinkevichyus B. S. Laser diagnostics of flows. Moscow, MPEI, 1990, 288 p.

4. Dubnishchev Yu.N., Rinkevichyus B.S. Methods of laser Doppler anemometry. Moscow, Nauka, 1982, 303 p.

5. Raffel M., Willert C.E., Kompenhans J. Particle image velocimetry. A practical guide. Corrected 3rd printing. Berlin, Springer, 2013, 448 p.

6. Zobov K.V., Syzrantsev V.V., Bardakhanov S.P. Features of particle size measurements in the nanosilica hydrosol by the optical methods // Siberian physical journal, 2016, vol.11, No.4, pp. 68 – 77.

7. Golubenko Yu.V., Savkin A.N., Sidorovnina T.Iu., Timoshenko V.A. Validity of Dynamic Light Scattering Method to Analyze a Range of Gold and Copper Nanoparticle Sizes Attained by Solids Laser Ablation in Liquid. Science and Education of the Bauman MSTU, 2014, No.10, pp.15 – 28.

8. D. Deirmendjian. Electromagnetic scattering on spherical polydispersions . New York, American Elsevier Publishing Company INC., 1969, 165 p.

9. Smirnov V.I., Yanina G.M. Calculation and design of laser anemometers. Moscow, MPEI, 1984, 83 p.
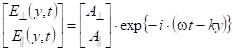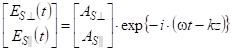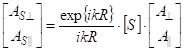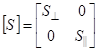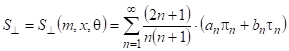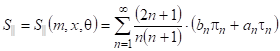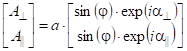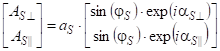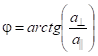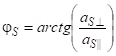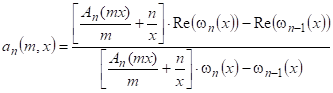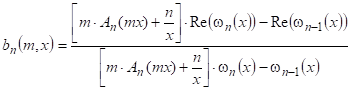