ВИЗУАЛИЗАЦИЯ ТЕКСТУРЫ СВЕРХГЛАДКИХ ПОВЕРХНОСТЕЙ С ПРИМЕНЕНИЕМ МЕТОДА ФЛИККЕР-ШУМОВОЙ СПЕКТРОСКОПИИ

Н.И. Каргин¹, А.С. Гусев¹, С.М. Рындя¹, А.Д. Бакун¹, А.Е. Иешкин², А.А. Акованцева³, П.И. Мисуркин⁴, С.Г. Лакеев⁵, И. Матющенко¹, С.Ф. Тимашев^1,5

¹Национальный исследовательский ядерный университет «МИФИ», Москва

²Московский государственный университет имени М.В. Ломоносова, Москва

³Институт фотонных технологий ФНИЦ «Кристаллография и фотоника РАН», Москва

⁴Институт химической физики им. Н.Н. Семенова РАН, г. Москва

⁵Научно-исследовательский физико-химический институт им. Л.Я. Карпова, г. Москва

Содержание

1. Введение

2. Постановка проблемы

3. Основные ФШС соотношения для извлечения информации, содержащейся в АСМ сканах

4. Экспериментальные данные

5. Заключение

Литература

Аннтотация

В данной статье предложен метод параметризации особенностей нанорельефа сверхгладких поверхностей, используемых в микро- и наноэлектронике в качестве материалов-подложек, а также в качестве светоотражательных элементов технических устройств. Метод основан на использовании фликкер-шумовой спектроскопии (ФШС) как общего феноменологического подхода к извлечению информации из хаотических временных или пространственных сигналов. Согласно ФШС, информация о текстуре поверхности содержится в корреляционных связях составляющих исследуемых сигналов в разных диапазонах пространственных частот – низкочастотных (резонансных) и высокочастотных, представляемых последовательностью нерегулярностей разных типов (всплески, скачки, разрывы производных) на всех уровнях пространственной иерархии структуры исследуемых систем. В качестве модельных объектов, топология поверхности которых исследовалась методом атомно-силовой микроскопии, использовались образцы ситалла до и после ионно-кластерной обработки. Обработка оптической стеклокерамики газовыми кластерными ионами осуществлялась с целью уменьшения шероховатости поверхности. В ходе выполнения исследований установлено, что ионно-кластерная обработка при выбранных режимах воздействия, приводит, во-первых, к сглаживанию дефектов поверхности экспериментальных образцов, мерой которого может служить изменение вводимых 3D параметров поверхности, характеризующих нерегулярности рельефа, и, во-вторых, к «планаризации» поверхности, мерой которой являются величины среднеквадратичных отклонений ФШС параметров.

Ключевые слова: филиккер-шумовая спектроскопия, атомно-силовая микроскопия, параметризация текстуры поверхности, ситалл, ионно-кластерная обработка

1. Введение

Современные методы научной визуализации поверхности различных объектов в материаловедении, биологии, медицине и других областях науки и техники предполагают получение массивов первичных оцифрованных данных и последующее использование методов анализа, позволяющих извлечь из первичных данных адекватную информацию об особенностях структурной организации поверхности, об изменениях текстуры поверхности при различных сторонних воздействиях на исследуемые системы. Обычно интерес представляют твердофазные открытые системы, поверхность которых под воздействием сторонних факторов претерпевает сложные перестройки текстуры и характеризуется пространственной перемежаемостью (intermittency) [1], чему способствуют нелинейные взаимосвязи между фрагментами рассматриваемых систем при неизбежных диссипативных процессах и инерции. Соответствующий характер рельефа поверхности в разных диапазонах пространственных частот представляется последовательностью нерегулярностей двух типов: относительно умеренных по величине скачков, свойственных т.н. «ламинарным фазам», и более значимых по величине и более локализованных в пространстве всплесков. Перемежаемый характер текстуры поверхностей свойственен как разнообразным природным объектам, так и формирующимся при различных обработках поверхностям различных материалов для систем микроэлектроники и техники.

В данной статье будут обсуждаться конкретные проблемы формирования сверхгладких поверхностей, рельеф которых характеризуется перепадами высот на уровне нм и долей нм, что является одной из ключевых проблем при создании подложек для последующей эпитаксии функциональных слоев при изготовлении элементов микро- и наноэлектроники, для напыления покрытий светоотражательных систем различных технических устройств и т.д. При этом поверхность формируемых на подложках функциональных слоев малых, нанометровых или субмикронных толщин в значительной мере отражает (воспроизводит) особенности структуры поверхности подложки, что обусловливает необходимость, особенно если речь идет о создании технологии, осуществления метрологического контроля основных 3D параметров рельефа поверхности.

2. Постановка проблемы

Как известно, главной особенностью технологического процесса получения сверхгладких поверхностей полупроводников и диэлектриков является многостадийность процессов шлифования и полирования с постепенным доведением уровня «шероховатости» до минимума. Реализующиеся при этом сложные, в общем случае, нелинейные взаимодействия микро- и нанофрагментов различных абразивов с полируемой поверхностью обусловливают динамику формирования поверхности как последовательность необратимых изменений состояний системы на каждом уровне пространственно-временной иерархии (на всех проявляющих себя в анализируемом процессе пространственно-временных масштабах) в режиме перемежаемости. Это означает, что на формирующихся сверхгладких поверхностях на общем «гладком» фоне должны с неизбежностью проявляться достаточно резкие нерегулярности рельефа – «наноострия» и «наноступени». Насколько наличие таких нерегулярностей рельефа оказывается функционально значимым (критическим) в каждом конкретном случае, будет зависеть от специфики создаваемого изделия и плотности указанных нерегулярностей на создаваемой поверхности. Но в любом случае методология анализа АСМ изображений сверхгладких поверхностей наряду со стандартными характеристиками должна предусматривать выявление и такого типа нерегулярностей.

В отличие от традиционных линейных параметров, определяемых по ГОСТ 2789-73 «Шероховатость поверхности. Параметры и характеристики» (R_a – среднеарифметическое отклонение профиля, R_z – высота неровностей профиля по 10 точкам, R_max – наибольшая высота профиля), такие возможности заложены в общем феноменологическом подходе к решению комплекса проблем параметризации динамики сложных систем, в том числе, формирующихся сложных структур поверхности в нанометровом диапазоне – фликкер-шумовой спектроскопии (ФШС) [2 - 5]. Согласно ФШС, информация о текстуре поверхности содержится в корреляционных связях составляющих исследуемых сигналов в разных диапазонах пространственных частот – низкочастотных (резонансных) и высокочастотных, представляемых последовательностью нерегулярностей разных типов (всплески, скачки, разрывы производных) на всех уровнях пространственной иерархии структуры исследуемых систем. При этом для получения метрологически значимой информации о структуре таких поверхностей на нанометровых масштабах, содержащейся в АСМ изображениях поверхности, формируемых в большой совокупности оцифрованных профилей рельефа, необходимо адекватным образом «отстроиться» от неизбежно присутствующих помех – низкочастотных составляющих рельефа, пространственные частоты которых менее f_x ~ (100 нм)^-1. Ниже будут изложены основные принципы такой операции, а также представлена методология введения всей совокупности 3D параметров поверхности в нанометровом диапазоне (раздел 2), использование которой будет продемонстрировано на примере одной из известных подложек – ситалла (раздел 3).

3. Основные ФШС соотношения для извлечения информации, содержащейся в АСМ сканах

Современные методы сканирующей зондовой микроскопии, прежде всего, атомно-силовой микроскопии (АСМ), позволяют предоставлять топографию флуктуирующих рельефов поверхности в виде трехмерных массивов оцифрованных профилей h(x; y), где x и y – координаты поверхности [6 - 8]. Исходная информация о рельефе поверхности регистрируется при перемещении чувствительного элемента (зонда) приборов вдоль координаты x каждого из N сканов (обычно N = 512 или 1024) на интервале 0 ≤ x ≤ L (L – характерный размер окна цифруемого изображения) с шагом Δl = L/N для всей совокупности сканов, каждому из которых соответствует фиксированное значение координаты по оси y, нормальной к оси x.

Согласно ФШС методологии, основная информация, содержащаяся в зависимостях высот h(x) каждого профиля рельефа поверхности от текущей координаты x, связывается с корреляционой зависимостью значений h(x) и последующих значений h(x + Δ), Δ > 0, высот профиля. По этой причине локальные значения h(x) можно интерпретировать как динамические переменные исследуемой системы и привязывать параметры поверхности при анализе каждого из профилей рельефа к базовому для статистической физики образу автокорреляционной функции:

, (1)

где Δ – параметр пространственного сдвига, а угловые скобки означают усреднение по интервалу L – Δ:

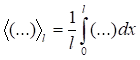. (1а)

Процедура усреднения по интервалу L означает, что все характеристики, которые можно будет извлечь при анализе зависимостей ψ(Δ), следует рассматривать как средние по указанному интервалу. При этом необходимо иметь в виду, что в общем случае каждый профиль рельефа поверхности представляет собой последовательность хаотических значений высот h(x) в виде нерегулярностей–скачков и всплесков на фоне изменяющихся на относительно больших расстояниях огибающих – резонансных (регулярных) составляющих. ФШС методология состоит в определении и извлечении информации, относящейся к обсуждаемым взаимосвязям последующих значений динамических переменных с предыдущими, а также содержащейся в совокупности резонансных пространственных частот и неспецифических хаотических, более высокочастотных составляющих исследуемых сигналов.

Для выявления информации, заключенной в ψ(Δ), удобно анализировать некоторые преобразования (проекции) этой функции: неполное косинус-преобразование S(f_x) автокоррелятора (спектр мощности):

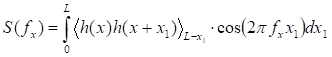(2)

(здесь полагаем <h(x)> = 0; f_x – пространственная частота), а также разностный момент второго порядка F⁽²⁾(Δ) (переходная структурная функция Колмогорова):

. (3)

При этом зависимости, характеризующие хаотические составляющие F_c⁽²⁾(Δ) зависимости F⁽²⁾(Δ), формируются исключительно нерегулярностями-скачками динамической переменной на каждом уровне иерархии системы, а в формирование хаотических составляющих S_c(f_x) зависимостей S(f_x) вносят вклад не только нерегулярности-скачки, но и более резко изменяющиеся нерегулярности-всплески. Информационные «паспортные» характеристики анализируемых поверхностей, характеризующие хаотические составляющие F_c⁽²⁾(Δ) и S_c(f_x), извлекаются из сопоставления расчетных и полученных на основе экспериментальных данных зависимостей S(f_x) и F⁽²⁾(Δ) и имеют смысл длин корреляции и параметров, определяющих темпы ослабления (корреляционных связей) на этих длинах корреляции для нерегулярностей различного типа. Учитывая интервалы усреднения в зависимостях (2) и (3), для обеспечения статистической достоверности вводимых параметров будем ограничивать величины f_x и Δ сверху: 0 ≤ Δ ≤ ¼L; 1/L ≤ f_x ≤ ¼f_d, где f_d – пространственная частота дискретизации при получении АСМ изображения. Вводится также понятие «стационарной структуры» как характеризующейся одной и той же совокупностью параметров на каждом пространственном уровне иерархической организации (на разных масштабах). Тем самым в ФШС, в отличие от геометрического, масштабного самоподобия (скейлинга) теории фракталов и мультифракталов, вводится динамическое самоподобие по уровням иерархии, по сути многопараметрическое, поскольку каждая из зависимостей S(f_x) и F⁽²⁾(Δ) в общем случае может быть охарактеризована совокупностью двух и более параметров.

Выпишем интерполяционные выражения для хаотических составляющих структурной функции 2-го порядка F_c⁽²⁾(Δ) и спектра мощности S_c(f_x), проявляющихся в чистом виде при отсутствии низкочастотных составляющих в профиле рельефа поверхности. Будем полагать, что в последовательности скачков и всплесков рельефа проявляется лишь один характерный масштаб. Тогда:

(4)

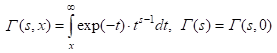Здесь G(s) и G(s, x) – соответственно гамма-функция и неполная гамма-функция (x ³ 0 и s > 0); s – среднеквадратичное отклонение значения измеряемой динамической переменной от среднего значения (размерность [h]); H₁ – константа Херста, характеризующая скорость, с которой динамическая переменная теряет память о своей величине на пространственных интервалах, меньших длины корреляции L₁. В этом случае, L₁ может интерпретироваться как характерное расстояние, на котором формируется дисперсия измеряемых высот профиля рельефа. В качестве реперного значения для величины H₁ может рассматриваться H₁ = 0.5. При таком значении H₁ характер потери коррелированности (памяти) в фиксируемых значениях h при каждом последующем смещении зонда в среднем по скану соответствует потере памяти при диффузионном фиковском процессе. При H₁ < 0.5 степень коррелированности уменьшается медленнее, при H₁ > 0.5 – быстрее, нежели при фиковской диффузии.

Интерполяционная зависимость для суммарного хаотического вклада в спектр S_c(f_x) автокоррелятора представляется в виде:

. (5)

Здесь S_с(0) , L₀ и n₀ – феноменологические параметры, которые вводятся для описания спектров мощности при обработке экспериментально получаемых пространственных рядов. Удобство такого представления обусловлено тем, что в высокочастотной области вклады в спектр мощности от хаотической составляющей сигнала, формируемой нерегулярностями-всплесками и нерегулярностями-скачками, могут быть сопоставимы. Именно поэтому в качестве меры хаотической составляющей сигнала в области высоких пространственных частот выбирается параметр S_c(L₀^{– 1}).

Как отмечалось выше, проблема параметризации профилей рельефа поверхности в сложных хаотических структурах состоит в извлечении из пространственных серий h(x) всей возможной совокупности параметров, относящихся не только к хаотической компоненте, но и к совокупности специфических низкочастотных огибающих, резонансных составляющих, изменяющихся на больших пространственных масштабах. В дальнейшем будем представлять профиль высот h(x), соответствующий каждому скану, в виде линейной суперпозиции высокочастотной хаотической компоненты h_c(x) и медленно изменяющейся резонансной компоненты h_r(x):

. (6)

В этом случае функции автокоррелятора и спектра мощности можно представить в виде:

. (7)

При этом естественно полагать, что резонансные составляющие h_r(x), соответствующие указанному диапазону частот, можно рассматривать как совокупность гармоник, формирующую стационарный профиль высот.

С учетом сказанного, определяем резонансную составляющую рассматриваемого автокоррелятора ψ_r(∆) с использованием неполного обратного косинус-преобразования от резонансного вклада S_r(f_x):

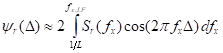, (8)

где интервал интегрирования [1/L, f_x,LF] определяет область «резонансных» частот. Основной вклад в (8) формирует область частот, f_x,LF £ (0.1-0.2)f_d, и формальное увеличение верхнего предела в (7) до значения f_x,max = 0.5 f_d практически не влияет на зависимость ψ_r(∆). На основе (7) находим резонансную составляющую F_r⁽²⁾( ∆), учитывая стационарный характер h_r(x) профиля:

. (9)

Тогда хаотическую составляющую F_c⁽²⁾(∆) разностного момента 2-го порядка, для которой справедливо интерполяционное выражение (4), можно представить в виде:

. (10)

На основе (4) - (10) удается последовательно разрешить проблему разделения вкладов резонансных и хаотических составляющих с полной параметризацией исследуемых профилей высот. Из сопоставления экспериментальных (3) и расчетных зависимостей (7) с использованием метода наименьших квадратов находятся параметры σ, L₁ и H₁, характеризующие вклад в структурную функцию, определяемый нерегулярностями-скачками. При этом параметр H₁, равно как и параметры σ и L₁, выбираются из условия наилучшего согласования расчетной зависимости F⁽²⁾(Δ) с экспериментальной во всем рассматриваемом интервале Δ. Тем самым вводимый параметр H₁ несколько отличается по смыслу от параметра Херста, вводимого обычно для описания зависимостей F⁽²⁾(Δ) при малых Δ. Следует подчеркнуть также, что введенный параметр σ является мерой нерегулярностей-скачков исследуемого профиля и характеризует среднеквадратичное отклонение высот профиля от базового профиля, формируемого совокупностью низкочастотных резонансных составляющих хаотических зависимостей h(x). Следует отметить, что поскольку в ФШС методологии рассматривается многопараметрическое самоподобие фиксируемых динамических переменных (высот профилей рельефа, в рассматриваемом случае) по уровням иерархии, то на все феноменологические параметры, включая H₁ и n, не накладывается ограничений, имеющих место в теории фракталов, когда 0 ≤ H₁ ≤ 1 и n ≤ 3.

Два основных параметра:

1. Параметр σ, нм, являющийся мерой нерегулярностей-скачков исследуемого профиля и характеризующий среднеквадратичное отклонение высот профиля от базового профиля, формируемого совокупностью низкочастотных резонансных составляющих хаотических зависимостей h(x); этот параметр определяется как фактор «ступенчатости» хаотической составляющей высот профиля.

2. Параметр S_c(L₀^–1), (нм)²мкм, являющийся мерой «высокочастотных» нерегулярностей исследуемого профиля, наиболее резко изменяющихся на масштабах 1-100 нм особенностей рельефа; этот параметр определяется как фактор «острийности» структуры поверхности.

Дополнительные 3D параметры поверхности, которые связываются с нерегулярностями-скачками (параметры L₁, H₁) и нерегулярностями-всплесками (параметры L₀ и n₀) рельефа поверхности в нанометровом диапазоне.

3. Параметр L₁ – характерное расстояние, на котором формируется дисперсия измеряемых высот профиля рельефа.

4. Параметр H₁ – константа Херста, характеризующая скорость, с которой динамическая переменная теряет «память» о своей величине на пространственных интервалах, меньших длины корреляции L₁.

5. Параметр L₀ – характерное расстояние, на котором теряются корреляционные связи в последовательности нерегулярностей-всплесков (соответствующая длина корреляции).

6. Параметр n₀, или фликкер-шумовой показатель, характеризует меру потери таких корреляций (падает с ростом n₀).

4. Экспериментальные данные

Возможности ФШС подхода в определении параметров «сверхгладких» поверхностей ниже продемонстрированы при АСМ исследовании образцов из литиевого алюмосиликатного ситалла СО-115М, которые предназначены для изготовления элементов прецизионной отражающей оптики. При этом следует иметь в виду, что каждая из исследуемых подложек была предварительно подвергнута механо-химической обработке, на финишной стадии которой использован абразив с размерами зерен 0.1 ¸ 0.4 mm. Полированная поверхность такой стеклокерамики включает дефекты разного происхождения, характеризующиеся разными пространственными масштабами:

- следы механо-химического воздействия в виде анизотропных линейно структурированных особенностей, оставшиеся после абразивного полирования;

- уединенные выступы (впадины) при локальных нарушениях однородности;

- остаточный хаотический рельеф;

- наночастицы, соответствующие оказавшимся на поверхности участкам кристаллитов b-эвкриптита LiO₂×Al₂O₃×2SiO₂.

Для удаления (сглаживания) перечисленных дефектов поверхности в работе применялся метод ионно-кластерной обработки [9 - 12]. Использование пучков ускоренных кластерных ионов в качестве дополнения или замещения стандартной технологии химико-механической планаризации позволяет избавиться от основного ее недостатка – формирования остаточного рельефа с размахом высот порядка 1 нм. К достоинствам метода также следует отнести меньшую трудоемкость и хорошую совместимость с планарной технологией изготовления полупроводниковых приборов и интегральных микросхем.

Обработка экспериментальных образцов осуществлялась с помощью установки «nAccel 100» (Exogenesis), в которой газовые кластеры образуются при адиабатическом расширении рабочего газа (аргона) в вакуум через сверхзвуковое сопло с диаметром критического сечения 50 мкм. Сформированные кластеры ионизировались электронным ударом и ускорялись разностью потенциалов 10 – 30 кВ. Затем пучок ускоренных кластерных ионов попадал в камеру образца, где происходило его взаимодействие с обрабатываемой поверхностью. Плотность тока в центре пучка при ускоряющем напряжении 30 кВ составляла 2 мкА/см², профиль распределения тока гауссов с полушириной около 12 мм. В ходе экспериментов давление остаточных газов в камере образца не превышало 4×10^-2 Па. Сепарация ионизированных частиц по массам не осуществлялась. Типичная схема установки для получения газовых кластерных ионов приведена на рисунке 1.

Отличительной особенностью применяемого ускорителя является возможность обработки поверхности пучком ускоренных нейтральных атомов [13]. Для этого перед камерой образца располагается электростатический конденсатор, отклоняющий заряженные частицы, содержащиеся в пучке. На мишень попадает только пучок ускоренных нейтральных атомов, образовавшийся при частичном разрушении кластерных ионов в результате столкновений с молекулами остаточных газов. В этом случае отсутствие корреляции между ударами отдельных атомов исключает возбуждение ударных волн и образование «кратеров» на поверхности. Обработка стеклокерамики пучком ускоренных атомов привела в поставленных экспериментах к наилучшим результатам.

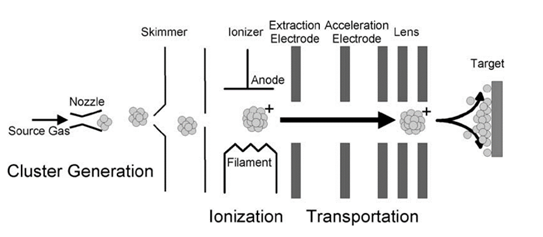
Рис. 1. Схема получения газовых кластерных ионов [14]

Для получения АСМ-изображений образцов исходного ситалла и образцов ситалла, прошедших ионно-кластерную обработку, использовали сканирующий зондовый микроскоп Asylum Research MFP-3D StandAlone (США). В процессе съема топографии исследуемых объектов были использованы кремниевые кантилеверы Asyelec01 (длина балки 240 мкм с коэффициентом жесткости 2,2 Н/м, резонансная частота находилась в пределах 45÷95 кГц, радиус кривизны острия кантилеверов составлял менее 30 нм). Сканирование с получением 1024 растров, формирующих изображение, проводили полуконтактным методом на воздухе при постоянной амплитуде (топография) при температуре окружающей среды в диапазоне 22-25^оС и относительной влажности воздуха порядка 50 – 56%.

АСМ изображения поверхности образцов ситалла (исходного и прошедшего ионно-кластерную обработку) записывались в окнах 10×10 мкм², 5×5 мкм² и 3×3 мкм², по три изображения в каждом формате. Примеры полученных АСМ изображений поверхности ситалла (размер скана 10×10 мкм) приведены на рис. 2а (исходный образец ситалла) и 3а (образец, прошедший ионно-кластерную обработку). Для определения локальных 3D параметров поверхности образцов ситалла по оцифрованным АСМ изображениям использовались методики, аттестованные ФГУП «Уральский научно-исследовательский институт метрологии» (свидетельства об аттестации методики (метода) измерений №№ 223.0263/01.00258/2010 - 223.0267/01.00258/2010). Согласно этим методикам, совокупность 1024 растров изображения сначала разбивается на m = 256 субгрупп с равным количеством растров N = 4: с 1-го по 4-й, с 5-го по 8-й, …, с 1021 по 1024, и для каждой из субгрупп рассчитывается усредненный профиль h_i(x) (i = 1, 2, 3, ... , 256). Здесь индекс i указывает на субгруппу растров, отсчитываемых от нижнего (или левого) края изображения, если растры формируются вдоль оси x (или y). Каждый усредненный профиль h_i(x) определяется совокупностью 3D параметров P_k = {σ, L₀, L₁, H₁, n₀, S_c(L₀^–1)}_k, (k = 1, 2, ..., m) в нанометровом диапазоне. Затем совокупность P_k разбивается на К = 8 групп по R = 32 элемента в каждой группе{P_k}, и для каждой такой группы вычисляются средние значения параметров, а на их основе – усредненные 3D параметры всей поверхности, оцифрованное изображение которой анализировалось.

Совокупность ФШС параметров поверхности образцов ситалла, 3-х исходных и 3-х прошедших ионно-кластерную обработку, соответственно, полученных на основе ФШС анализа изображений поверхности в окнах 10×10 мкм², 5×5 мкм² и 3×3 мкм², а также усредненных параметров поверхности по проанализированным трем фрагментам поверхности для каждого из указанных окон, представлена в Таблицах 1 и 2. Примеры ФШС зависимостей, на основе которых определялись ФШС параметры, приводимые в Таблицах 1 и 2, представлены на рис. 2 б-е и рис. 3 б-е.

Таблица 1. ФШС параметры для отдельных участков исходной поверхности ситалла, полученные при анализе АСМ изображений в окнах 10×10 мкм², 5×5 мкм² и 3×3 мкм².

Образец	<h>, нм	σ, нм	S_c(L₀^-1), (нм)³	H₁	L₁, мкм	L₀, мкм	n₀
10×10 мкм²
P92_13_0000	3.56	0.43	0.77	1.18	0.143	0.140	2.9
P92_13_0004	6.84	0.63	0.70	1.41	0.131	0.090	3.2
P92_13_0007	7.18	0.71	1.72	1.39	0.110	0.083	3.4
среднее	5.86	0.59	1.06	1.33	0.128	0.104	3.2
ср.кв.откл.	2.00	0.15	0.57	0.12	0.017	0.031	0.22
5×5 мкм²
P92_13_0002	2.58	0.36	0.45	1.11	0.103	0.091	2.83
P92_13_0005	3.82	0.45	0.28	1.25	0.067	0.056	3.08
P92_13_0008	3.46	0.40	0.29	1.27	0.070	0.065	3.02
среднее	3.29	0.40	0.34	1.21	0.080	0.071	2.97
ср.кв.откл.	0.64	0.04	0.09	0.09	0.020	0.019	0.13
3×3 мкм²
P92_13_0003	1.85	0.31	0.29	0.95	0.077	0.070	2.71
P92_13_0006	2.95	0.39	0.24	1.22	0.054	0.049	2.93
P92_13_0009	2.17	0.32	0.21	0.99	0.060	0.050	2.82
P92_13_0010	2.08	0.31	0.23	0.93	0.059	0.051	2.74
среднее	2.26	0.33	0.24	1.02	0.061	0.055	2.80
ср.кв.откл.	0.48	0.04	0.04	0.14	0.010	0.010	0.10

Таблица 2. ФШС параметры для отдельных участков поверхности ситалла после ионно-кластерной обработки, полученные при анализе АСМ изображений в окнах 10×10 мкм², 5×5 мкм² и 3×3 мкм².

Образец	<h>, нм	σ, нм	S_c(L₀^-1), (нм)³	H₁	L₁, мкм	L₀, мкм	n₀
10×10 мкм²
P92_13_0000m	1.52	0.30	0.69	0.90	0.217	0.190	2.72
P92_13_0003m	1.77	0.33	0.98	0.92	0.207	0.188	2.67
P92_13_0006m	1.68	0.30	0.73	0.96	0.174	0.155	2.74
среднее	1.65	0.31	0.80	0.93	0.199	0.178	2.71
ср.кв.откл.	0.13	0.02	0.16	0.03	0.023	0.020	0.02
5×5 мкм²
P92_13_0001m	1.52	0.28	0.50	0.794	0.164	0.128	2.58
P92_13_0004m	2.56	0.28	0.37	0.958	0.105	0.101	2.74
P92_13_0007m	1.47	0.26	0.41	0.837	0.127	0.110	2.59
среднее	1.85	0.27	0.43	0.863	0.132	0.113	2.64
ср.кв.откл.	0.62	0.01	0.07	0.085	0.030	0.014	0.08
3×3 мкм²
P92_13_0002m	1.43	0.27	0.44	0.81	0.125	0.104	2.54
P92_13_0005m	1.41	0.25	0.29	0.89	0.090	0.086	2.61
P92_13_0008m	1.35	0.24	0.21	0.86	0.092	0.076	2.62
среднее	1.40	0.25	0.31	0.85	0.102	0.089	2.59
ср.кв.откл.	0.04	0.02	0.12	0.04	0.019	0.014	0.04

$Описание: C:\Users\Asylum User\Documents\Asylum Research Data\160930\MEPhI_P92_13_0004_10x10mkm.jpg$

Рис. 2. АСМ изображение и 3D параметры фрагмента поверхности MEPhI_P92_13_00:

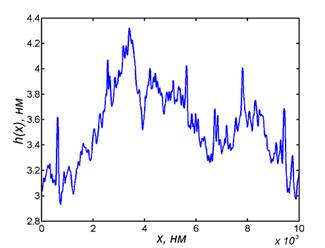
а) АСМ изображение фрагмента (размер 10×10 мкм²);

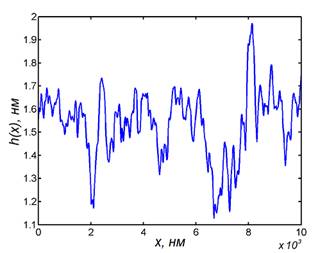
б) усреднённая зависимость высот h₃(x) профиля рельефа;

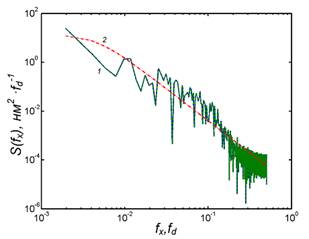
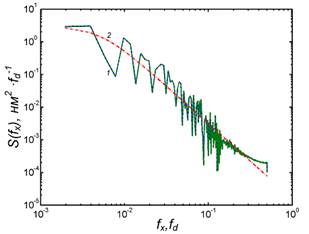
в) модуль спектра S(f), соответственно, общий и хаотическая его составляющая, рассчитанные для высот h₃(x) профиля рельефа: 1 – «экспериментальная» зависимость; 2 – интерполяционная зависимость (5) для хаотической составляющей, построенная при значениях параметров: S_с(L₀^-1) = 0.109 (нм)²∙ 1.06 (нм)³, L₀ = 35.6 0.35 мкм, n₀ = 2.6;

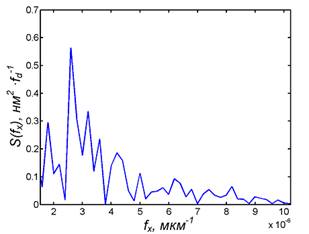
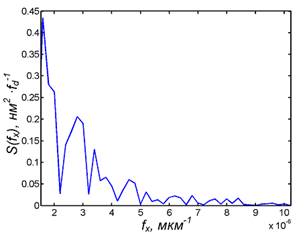
г) модуль регулярной части спектра S(f) в области низких пространственных частот для высот h₃(x) профиля рельефа;

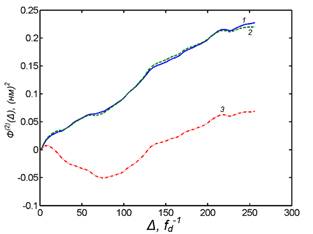
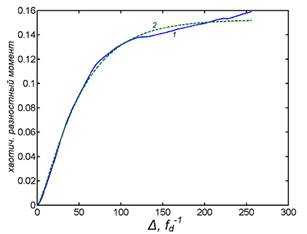
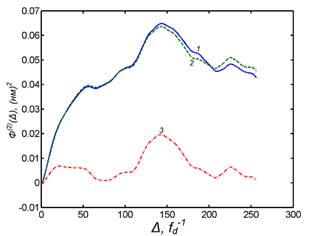
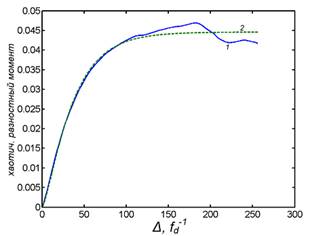
д и е) структурные функции для высот h₃(x) профиля рельефа F⁽²⁾(Δ), соответственно, полная и хаотическая составляющая, рассчитанная по интерполяционному соотношению (4): 1 – «экспериментальная» зависимость; 2 – расчетная зависимость при σ = 0.28 нм; H₁ = 0.71; L₁ = 48.3 0.47 мкм; 3 – вклад специфических частот.

$Описание: C:\Users\Asylum User\Documents\Asylum Research Data\161007\MEPhI_P92_13_0003_10x10mkm.jpg$

Рис 3 – АСМ изображение и 3D параметры фрагмента поверхности MEPhI_P92_13_13_8min_15keV:

а) АСМ изображение фрагмента (размер 10×10 мкм²);

б) усреднённая зависимость высот h₅(x) профиля рельефа изображения;

в – е) все обозначения такие же, как на рис. 2. Зависимости построены при следующих наборах параметров: S_с(L₀^-1) 0.42 нм³, L₀ 0.31 мкм, n₀ = 2.3; σ = 0.15 нм; H₁ = 0.74; L₁ 0.32 мкм.

Как следует из сопоставления ФШС параметров, представленных в Таблицах 1 и 2, обработка при выбранном режиме воздействия на исходный образец существенно изменяет топографию его поверхности, заметно сглаживая неоднородности рельефа. Действительно, средние перепады <h> фиксируемых глубин рельефа при окнах изображения 3×3 мкм² и 10×10 мкм², составляющие у исходного образца 2,26 и 5,86 нм, у образца после обработки равны 1,40 и 1,65 нм. Заметно изменились и два основных ФШС параметра – σ и S_c(L₀^–1), значения которых в окне 10×10 мкм², составляющие у исходного образца 0,59 нм и 1,06 (нм)³, уменьшились после обработки кластерными ионами до 0,31 нм и 0,80 (нм)³, соответственно. Важно указать и на величины среднеквадратичных отклонений ФШС параметров. Эти отклонения характеризуют, фактически, степень «гетерогенности» или меру нарушения «планарности» рельефа. Для параметров σ и S_c(L₀^-1) в окне 10×10 мкм² относительные величины δ среднеквадратичных отклонений по отношению к средним значениям составляли для исходных образцов 25% и 54%, тогда как после обработки величины δ составили 6% и 20%, соответственно. Таким образом, обработка поверхности ситалла кластернами ионами аргона действительно приводит «планаризации» исходной поверхности.

5. Заключение

Основная цель данного исследования состояла в разрешении чисто методической задачи – представлении возможностей метода ионно-кластерной обработки как финишного этапа приготовления сверхгладких поверхностей материалов-подложек, которые обычно используются при формировании на их основе функциональных элементов для оптоэлектроники и отражательных устройств. А также в представлении метода ФШС для обеспечения соответствующего контроля осуществляемой «планаризации» поверхности. Как показывает опыт авторов [15], для обеспечения стандартизации поверхности реальных изделий с характерной площадью ~ 1 см² по контролю 3D параметров рельефа обычно требуется анализ около 10 АСМ изображений для определенного окна (обычно со стороной от 2-х до 15 мкм) из-за неизбежной гетерогенности формируемых рельефов поверхностей перед их финишной обработкой. Представленные в Таблице 2 данные, фактически, демонстрируют это обстоятельство. В рассмотренных случаях это выявилось при анализе АСМ изображения образца ситалла P92_13_0002m после ионно-кластерной обработки в окне 3 × 3 мкм². Здесь следует иметь в виду, что фиксируемые методом АСМ участки поверхности исходного образца ситалла и этого же образца, прошедшего ионно-кластерную обработку, геометрически разнесены. И как следует из полученного для образца P92_13_0002m значения фактора острийности S_c(L₀^-1), этот фрагмент заметно отличался по указанному параметру от большинства других фрагментов исходной поверхности, а процедура сглаживания при выбранной длительности оказалась для него недостаточной. Указанное отличие проявилось в том, что относительная величина среднеквадратичного отклонения для этого параметра превысила соответствующую величину (17%) для исходного образца и составила после обработки 39%. Очевидно, фиксация таких отклонений более вероятна, когда число анализируемых фрагментов будет более 3-х, как это имело место в данной работе.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ (уникальный идентификатор прикладных научных исследований RFMEFI57814X0064). При проведении исследований использовалось оборудование Центра коллективного пользования «Материаловедение и металлургия» НИТУ МИСиС и ЦКП «Гетероструктурная СВЧ-электроника и физика широкозонных полупроводников» НИЯУ МИФИ. Образцы стеклокерамики для исследований были безвозмездно предоставлены АО «НИИ «Полюс» им. М.Ф. Стельмаха».

Литература

1. Тимашев С.Ф. Фликкер-шумовая спектроскопия: информация в хаотических сигналах. С. Ф. Тимашев. - М.: Физматлит, 2007. - 248 с.

2. Mirsaidov U., Timashev S.F., Polyakov Yu.S., Misurkin P.I., Polyakov S.V., Musaev I. Analytical method for parameterizing the random profile components of nanosurfaces imaged by atomic force microscopy Analyst. 2011. Vol. 136. N 3. P. 570 – 576; (http://dx.doi.org/10.1039/C0AN00498G).

3. Timashev S.F., Polyakov Yu.S., Lakeev S.G., Misurkin P.I., and Danilov A.I. Fundamentals of Fluctuation Metrology. Russian Journal of Physical Chemistry A, 2010, Vol. 84, No. 10, pp. 1807–1825 (http://dx.doi.org/10.1134/S0036024410100183).

4. Kuznetsov, Y.I., Vershok, D.B., Timashev, S.F., Solov'eva, A.B., Misurkin, P.I., Timofeeva, V.A., Lakeev, S.G. Features of formation of magnetite coatings on low-carbon steel in hot nitrate solutions Russian Journal of Electrochemistry, 2010, Vol. 46, No. 10, pp. 1155–1166 (http://dx.doi.org/10.1134/S1023193510100113).

5. Timashev S. F., Polyakov Yu. S. Review of flicker noise spectroscopy in electrochemistry. Fluctuation and Noise Letters. 2007. Vol. 7. N 2. P. R15 - R47; (http://dx.doi.org/10.1142/S0219477507003829, http://arxiv.org/abs/0812.0030).

6. Binning G., Quate C. F., Gerber Ch. Atomic force microscope. Phys. Rev. Lett., 1986. Vol. 56. P. 930 – 933.

7. Magonov S.N., Whangbo M.-H. Surface analysis with STM and AFM: experimental and theoretical aspects of image analysis. WeinHeim – New York – Basel – Cambridge – Tokyo: VHC, 1996. – 318 p.

8. Быков В.А. Приборы и методы сканирующей зондовой микроскопии для исследования и модификации поверхностей: дисс. ... докт. техн. наук. – М., 2000. – 393 с.

9. Insepov Z. Cluster Ion-Solid Interactions: Theory, Simulation, and Experiment. CRC Press, Taylor&Francis Group, Boca Raton, FL, USA, 2016. – 272 p. – ISBN-10: 1439875421

10. Yamada I., Historical milestones and future prospects of cluster ion beam technology, Applied Surface Science, Volume 310, 15 August 2014, Pages 77-88, ISSN 0169-4332, http://dx.doi.org/10.1016/j.apsusc.2014.03.147. (http://www.sciencedirect.com/science/article/pii/S0169433214006989).

11. Popok V.N., Energetic cluster ion beams: Modification of surfaces and shallow layers, Materials Science and Engineering: R: Reports, Volume 72, Issues 7–8, 22 August 2011, Pages 137-157, ISSN 0927-796X, http://dx.doi.org/10.1016/j.mser.2011.03.001. (http://www.sciencedirect.com/science /article/pii/ S0927796X11000131).

12. Yamada I., Matsuo J., Insepov Z., Aoki T., Seki T., Toyoda N., Nano-processing with gas cluster ion beams, Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, Volumes 164 – 165, April 2000, Pages 944-959, ISSN 0168-583X, http://dx.doi.org/10.1016/S0168-583X(99)01163-5. (http://www.sciencedirect.com/science/article/pii/S0168583X99011635).

13. Kirkpatrick A., Kirkpatrick S., Walsh M., Chau S., Mack M., Harrison S., Svrluga R., Khoury J., Investigation of accelerated neutral atom beams created from gas cluster ion beams, Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, Volume 307, 15 July 2013, Pages 281-289, ISSN 0168-583X, http://dx.doi.org/10.1016/j.nimb.2012.11.084. (http://www.sciencedirect.com/ science/article/pii/S0168583X13001304).

14. Seki T., Matsuo J., Takaoka G.H., Yamada I., Generation of the large current cluster ion beam, Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, Volume 206, May 2003, Pages 902-906, ISSN 0168-583X, http://dx.doi.org/10.1016/S0168-583X(03)00896-6. (http://www.sciencedirect.com/science/article/pii/S0168583X03008966).

15. Тимашев С.Ф., Лакеев С.Г., Мисуркин П.И., Поляков Ю.С., Тимашев П.С., Томашпольский Ю.Я., Садовская Н.В., Тереньтьев Г.И., Медведевских С.В., Соловьева А.Б., Каргин Н.И., Воронцов П.С., Рындя С.М., Тимофеева В.А. Параметризация структуры хаотических поверхностей в нанометровом диапазоне по данным атомно-силовой микроскопии // Заводская лаборатория. Диагностика материалов. 2013. Т. 79. № 3. С. 26 – 38. (http://zldm.ru/upload/iblock/50a/1028686120137903026.pdf).

VISUALIZATION OF SUPERSMOOTH SURFACES TEXTURE BY THE METHOD OF FLICKER-NOISE SPECTROSCOPY

N.I. Kargin¹, A.S. Gusev¹, S.M. Ryndya¹, A.D. Bakun¹, A.E. Ieshkin², A.A. Akovantseva³, P.I. Misurkin⁴, S.G. Lakeev⁵, I. Matushchenko¹, S.F. Timashev^1,5

¹National Research Nuclear University MEPhI, Moscow

²Lomonosov Moscow State University, Moscow

³Institute of Photonic Technologies, Research Center of Crystallography and Photonics RAS, Moscow

⁴N.N. Semenov Institute of Chemical Physics RAS, Moscow

⁵Karpov Institute of Physical Chemistry, Moscow

Abstract

A method of parameterization of supersmooth surfaces used in micro- and nanoelectronics as substrates, as well as light-reflecting elements of technical devices is proposed. The method is based on the flicker-noise spectroscopy (FNS) as the general phenomenological approach to extracting information from the chaotic temporal or spatial signals. According to FNS, the information about surface texture is contained in correlation components of the signals in different ranges of spatial frequencies - low frequency (resonance) and high-frequency, representing a sequence of different types of irregularities (spike-, jump-like, derivative discontinuities) at all levels of the hierarchy of the spatial structure of the studied systems. As the model objects, the topology of the surface of which was investigated by atomic force microscopy, the glass-ceramic samples were used before and after the ion-cluster treatment. Processing of optical glass ceramics by gas cluster ions was carried out in order to reduce the surface roughness. During the research it was determined that the ion-cluster processing at selected exposure modes leads, firstly, to the smoothing of surface defects of experimental samples as measure of which can serve the values of FNS parameters σ and S_c(L₀^-1), and, secondly, to its "planarization" as measure of which can serve the value of root-mean-square deviation.

Keywords: flicker-noise spectroscopy, atomic force microscopy, surface texture parameterization, glass ceramics, gas cluster ions treatment.

References

1. Timashev S.F. Flicker-noise spectroscopy: information in chaotic signals. Fizmatlit, 2007. 248 p.

6. Binning G., Quate C. F., Gerber Ch. Atomic force microscope. Phys. Rev. Lett., 1986. Vol. 56. P. 930 – 933.

7. Magonov S.N., Whangbo M.-H. Surface analysis with STM and AFM: experimental and theoretical aspects of image analysis. VHC, 1996. 318 p.

8. Bykov V.A. Instruments and methods of scanning probe microscopy for the study and modification of surfaces: diss. ... Doct. Tech. Sciences. - M., 2000. - 393 p.

9. Insepov Z. Cluster Ion-Solid Interactions: Theory, Simulation, and Experiment. CRC Press, Taylor&Francis Group, Boca Raton, FL, USA, 2016. – 272 p. – ISBN-10: 1439875421

15. Timashev S.F., Lakeev S.G., Misurkin P.I., Polyakov Yu.S., Timashev P.S., Tomashpolsky Yu.Ya., Sadovskaya N.V., Terentyev G.I., Medvedevkovsky S.V., Solovieva A.B., Kargin N.I., Vorontsov P.S., Ryndya S.M., Timofeeva V.A. Parametrization of the structure of chaotic surfaces in the nanometer range from atomic force microscopy data. Zavodskaya Laboratoriya. Diagnostika materialov. 2013. V.79. №3. P. 26 - 38. (http://zldm.ru/upload/iblock/50a/1028686120137903026.pdf).