РАЗРАБОТКА ПРОГРАММНОГО КОМПЛЕКСА ВОССТАНОВЛЕНИЯ И ВИЗУАЛИЗАЦИИ 3D-МОДЕЛЕЙ ПО НАБОРУ ПРИБЛИЖЕННЫХ ОРТОГОНАЛЬНЫХ ПРОЕКЦИЙ

В.Ф. Барабанов, А.М. Нужный, С.Л. Подвальный, В.В. Сафронов

Воронежский государственный технический университет, Россия

bvf@list.ru, nam14@mail.ru, spodvalny@yandex.ru, safronov.vitaliy@mail.ru

Содержание

1. Введение

2. Формализация процесса восстановления 3D-модели по набору приближенных ортогональных проекций

3. Описание программного комплекса восстановления пространственных моделей по набору ортогональных проекций

4. Последовательность действий по восстановлению 3D-моделей в разработанном программном комплексе

Список литературы

Аннотация

Данная статья посвящена задаче восстановления пространственной графической модели по набору ортогональных проекций, которые могут иметь погрешности построения. Актуальность проблемы обусловлена наличием в проектных организациях значительных объемов проектно-конструкторской документации на разработанные ранее изделия, в которой графическая часть представлена ортогональными проекциями изделий, а 3D-модели отсутствуют. Размещение и повторное использование такой документации в корпоративных электронных архивах оказывается весьма затруднительным, так как для этих манипуляций требуется наличие 3D-модели изделия.

В статье выполнена формализация процесса восстановления трехмерной модели по набору ортогональных проекций, имеющих погрешности построения, описан программный комплекс, реализованный на основе приведенной математической модели. Особенностью этого программного комплекса является его универсальность с точки зрения используемых для визуализации моделей графических систем. В заключительной части статьи приведена последовательность действий по восстановлению 3D-модели по набору ортогональных проекций, используемая в разработанном программном комплексе.

Ключевые слова: ортогональные проекции, восстановление трехмерных моделей, 3D-визуализация, графическая система.

1. Введение

Несмотря на то, что в сфере проектирования и конструирования переход от двумерных графических систем к трехмерным является давно свершившимся фактом, задача восстановления трехмерной модели (3D-модели) по набору ортогональных проекций не теряет актуальности. Это объясняется следующими факторами.

Многие российские предприятия, занимающиеся проектной деятельностью на протяжении длительного промежутка времени, имеют значительные архивы проектно-конструкторской документации (ПКД), в которой используются элементы графических баз данных (ГБД), выполненные в виде ортогональных проекций. Отсутствие трехмерных моделей исключает возможность использования этих наработок в современных системах 3D-моделирования, так как эти системы, как правило, не обладают средствами для восстановления трехмерных моделей по ортогональным проекциям.

По этой же причине затруднено включение такой ПКД в состав современных корпоративных электронных архивов, осуществляющих хранение конструкторских документов и данных в составе электронной структуры изделия, формируемой на основе трехмерной модели [1].

При этом создание 3D-моделей для ранее разработанных изделий «с нуля» является настолько трудоемким, что зачастую признается нецелесообразным. По этой причине значительные объемы ПКД не вносятся в корпоративные электронные архивы и, при возникновении необходимости повторного использования изделий или их деталей, воссоздаются фрагментарно.

Исходя из вышесказанного и в связи с тем, что в настоящее время отсутствуют универсальные программные средства для восстановления трёхмерной модели по набору ортогональных проекций, вопрос разработки такого инструментария является весьма актуальным.

2. Формализация процесса восстановления 3D-модели по набору приближенных ортогональных проекций

Первые попытки решения задачи восстановления пространственного объекта по чертежам проекций относятся к 60-м годам ХХ века. Подходы, предложенные советскими учеными B.C. Полозовым, И.И. Котовым, Л.В. Широковой [2], охватывающие проблему в целом и предлагающие общее решение на основе эвристик, получили развитие как в России, так и за рубежом. Базовые работы, посвященные решению этой задачи, принадлежат авторам M. Idesawa, G. Markowsky, A. Wesley и пр. [3]. Интересные современные подходы предложены в трудах L. Governi, R. Furferi [4].

Недостатком этих работ является то, что алгоритмы восстановления оперируют идеальными, лишенными ошибок ортогональными проекциями. На практике электронные ортогональные проекции могут содержать ошибки построения, исключающие использование перечисленных алгоритмов [5].

Среди наиболее распространенных ошибок, характерных для таких проекций, можно выделить следующие: наличие разрывности в «замкнутых контурах»; нарушение масштабного соотношения между видами проекций; ошибки размещения графических примитивов основного и вспомогательного контуров, размеров и текстовых примитивов по слоям чертежа; ошибки взаимного расположения видов на чертеже и соответствия их сторонам трехмерного объекта.

Поэтому процедура восстановления пространственных графических моделей по чертежам ортогональных проекций должна позволять учитывать неточность их построения.

При формализации процедуры восстановления 3D-моделей будем использовать следующие понятия:

1. Грань – сегмент поверхности, образовывающий границу между внутренней областью тела и наружным пространством. При наличии криволинейных поверхностей производится их разделение на плоские сегменты (грани) с использованием вспомогательных ребер.

2. Ребро – линия пересечения двух граней. Ребра, добавленные для разбиения криволинейных поверхностей на плоские грани, называются вспомогательными.

3. Вершина – точка пересечения трех или более ребер. Отличают точки пересечения  вспомогательных граней  (вспомогательные вершины) и точки пересечения основных граней.

С учетом введенных понятий трехмерная модель V может быть представлена следующим образом:

      V=S_XYZ ={P_XYZ,L_XYZ,I_PL},                                                                                   (1)

где S_xyz – множество граней, ограниченных наборами ребер I_PL, причем, если точку обзора поместить с внешней стороны грани, то элемент I_PL будет классифицироваться как наружная граница грани, будучи рассмотренный в направлении против часовой стрелки, или как внутренняя граница – будучи рассмотренный по часовой стрелке; L_XYZ – множество ребер трехмерной модели, представляющих собой совокупность отображений свойств графических примитивов (отрезок, дуга, окружность и т.д.) и их конечных точек, представленных множеством вершин P_XYZ, заданных координатами (рисунок 1).

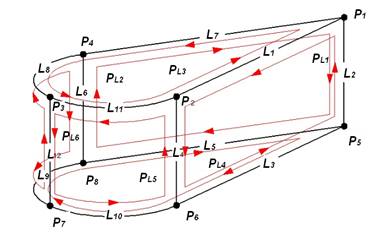
Рис. 1. Элементы представления трехмерной фигуры

Как следует из рисунка, множество вершин состоит из элементов {P₁, P₂, P₄, P₅, P₆, P₈}, а элементы {P₃, P₇} принадлежат множеству вспомогательных вершин. Множество ребер содержит элементы {L₁, … L₁₁}, а ребро L₁₂ принадлежит множеству вспомогательных ребер. Множество граней состоит из элементов {P_L1, … P_L6}

Процесс формирования описаний ортогональных проекций на основе предложенной модели можно представить как функцию трансформации Ψ, схематически представленную на рисунке 2.

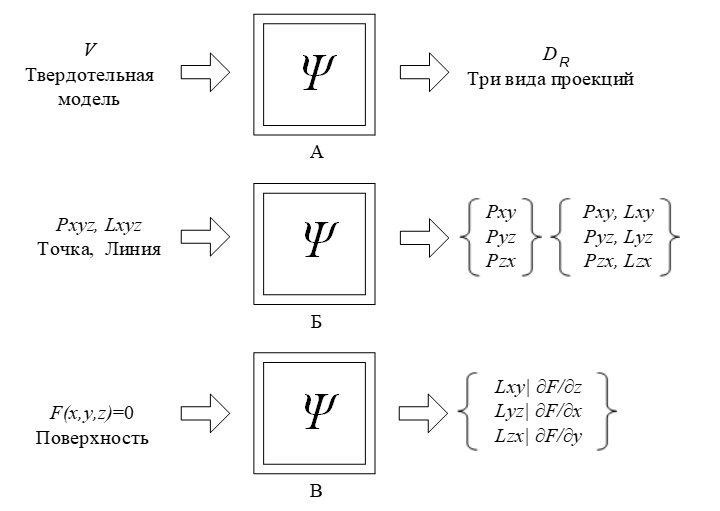
Рис. 2. Процесс формирования ортогональных проекций

Математическая запись видов проекций D_R выражается формулой 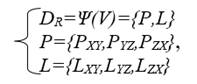(2):

           (2)

где L_XY, L_ZX, L_YZ – множества линий каждого из планов трех видов; P_XY, P_ZX, P_YZ – множества точек вершин каждого из планов.

Как следует из рисунка 2, наборы вершин трех видов формируются не только из конечных и начальных точек ребер модели с помощью операции, показанной на рисунке 2 (Б), но также возникают как результат пересечения сегментов линий (рис. 2 (В)). Сегменты линий, также, могут формироваться не только из исходных ребер модели, но и образовываться точками, полученными в результате разбиения линии на сегменты другой линией в точке их соприкосновения.

С другой стороны, имеются группы точек и линий, перекрывающихся на одном из видов проекций и вырождающихся в одну точку или линию.

Этот факт исключает точное соответствие между трехмерной графической моделью и видами на чертеже на уровне точек и линий и приводит к появлению проблемы ложных геометрических элементов (псевдофигур), рассмотренной ниже.

Процедура формирования описания трехмерной модели по трем видам ортогональных проекций может быть представлена как противоположная трансформации Ψ, рассмотренной выше.

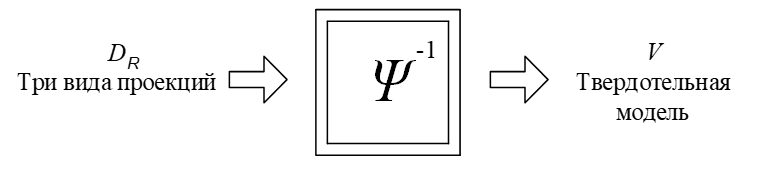
Рис. 3.  Формирование трехмерной модели по набору ортогональных проекций

Поскольку в нашей модели рассматриваются изображения проекций с возможной погрешностью построения (обозначим их как D_R'), для устранения ошибок введем функцию приведения проекций к эталонному виду, что позволяет представить трансформацию двумерных изображений в 3D-модель в виде преобразования Ψ^-1, состоящего из пяти операций:

V=Ψ^-1(D_R')=Ψ_PL[Ψ_GH{Ψ_LN(Ψ_ER(D_R'))U Ψ_PN(Ψ_ER(D_R'))],                  (3)

где Ψ_ER – операция устранения погрешностей построения; Ψ_PN – трансформация точек в трехмерное пространство; Ψ_LN – трансформация линий в трехмерное пространство; Ψ_GH – операция исключения псевдофигур из пространственной модели; Ψ_PL – операция построения граней.

Схематично формула 3 изображена на рисунке 4.

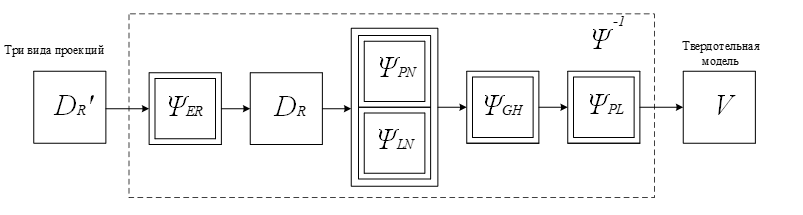
Рис. 4. Схема представления процесса восстановления 3D-модели по ортогональным проекциям

Применение операции устранения погрешностей Ψ_ER к элементам множества неточных ортогональных проекций D_R'= {P’, L'} может быть описано следующим образом:

 P=Ψ_ER(D_R')={P_XY' Δ ((K_CH∩P_XY') U K_COR)} U

{P_YZ'Δ ((K_CH∩P_YZ') U K_COR)} U {P_XZ'Δ((K_CH∩P_XZ') U K_COR)};                               (4)

L=Ψ_ER(D_R')={L_XY'Δ ((K_CH∩L_XY') U K_COR)} U

{L_YZ'Δ ((K_CH∩L_YZ') U K_COR)} U {L_XZ'Δ((K_CH∩L_XZ') U K_COR)},                                (5)

где K_CH –  множество корректируемых видов погрешностей построения; K_COR – множество откорректированных значений величин относительно протокола контроля; P_XY', P_ZX', P_YZ' – множества вершин видов проекций с возможной погрешностью построения; L_XY', L_ZX', L_YZ' – множества линий видов проекций с возможной погрешностью построения.

Трансформация точек Ψ_PN в трехмерное пространство выражается формулой:

Pxyz'=Ψ_PN (D_R) =P_XY∩ P_YZ∩ P_ZX,              (6)

где P_XYZ' – множество так называемых вершин связи, включающее в себя вершины трехмерной модели и псевдовершины; P_XY, P_YZ, P_ZX – множества точек, соответствующих каждому из видов ортогональных проекций.

Трансформация в трехмерное пространство линий Ψ_LN выражается формулой:

L_XYZ'=Ψ_LN (D_R) = (L_XY∩ L_YZ∩ L_ZX)U(L_XY∩ L_YZ∩

                                       P_ZX)U(L_XY∩ P_YZ∩ L_ZX)U(P_XY∩ L_YZ∩ L_ZX),                   (7)

где L_XYZ' – множество ребер связи, включающее в себя ребра трехмерной модели и псевдоребра;

L_XY, L_YZ, L_ZX – множества линий, соответствующих каждому из видов ортогональных проекций.

Преобразование Ψ_GH является функцией исключения псевдофигур из пространственной модели и выражается формулой (8):

{P_ХYZ,L_ХYZ}=Ψ_GH[{P_ХYZ',L_XYZ'}]= {P_ХYZ',L_XYZ'}-{P_GHUL_GH}∩{P_ХYZ',L_ХYZ'},          (8)

где {P_ХYZ,L_ХYZ} – множество связанных вершин и ребер, полученных после исключения всех псевдофигур из трехмерного объекта;  P_GH и L_GH – множества условий, описывающих псевдовершины и псевдоребра соответственно.

Преобразование Ψ_PL, отвечающее за построение граней, выражается формулой (9):

V=S_XYZ=Ψ_PL[{P_XYZ,L_XYZ}]=K_PL∩{P_XYZ, L_XYZ},                 (9)

где K_PL – множество условий для формирования граней твердого тела.

В состав множества K_PL могут быть включены следующие условия:

· грань, содержащая n вершин, получается, как пересечение n ребер;

· ребро является границей двух граней и проходит в противоположных направлениях в списках их границ;

· граница грани является замкнутым контуром.

Перечень критериев для определения псевдофигур включает в себя следующие:

· изолированная вершина является псевдовершиной;

· вершина, являющаяся точкой пересечения менее чем трех ребер – псевдовершина;

· ребро, начинающееся или заканчивающееся псевдовершиной, является псевдоребром;

· точка внутри ребра является псевдовершиной;

· вершина, являющаяся точкой пересечения трех или более ребер, два из которых имеют одинаковое направление обхода для смежных граней – псевдовершина, а ребра, имеющие одинаковое направление обхода – псевдоребра;

· удаление псевдоребер и исследование соседних вершин приводит к обнаружению новых псевдофигур.

Описанные выше критерии применяются при анализе вершин и позволяют обнаружить и удалить псевдофигуры до построения граней.

Разработанное математическое обеспечение используется в специализированной части универсального интерактивного программного комплекса восстановления пространственных моделей.

3. Описание программного комплекса восстановления пространственных моделей по набору ортогональных проекций

Разработанный программный комплекс обеспечивает выполнение следующих функций:

· возможность интеграции с различными графическими системами, применяемыми в качестве инструмента визуализации;

· возможность комплексного контроля и коррекции чертежей;

· возможность взаимодействия с ГБД и получения доступа к объектной модели хранимых в базе чертежей;

· восстановление 3D-модели объекта по набору ортогональных проекций.

С учетом вышеперечисленных функций разработана структура программного комплекса, приведенная на рисунке 5.

Отличительной особенностью комплекса является возможность применения в качестве графического ядра и средства визуализации широкого перечня программных систем геометрического моделирования, таких как AutoCAD, ProgeCAD, Autodesk Inventor.

Взаимодействие элементов программного комплекса с системами компьютерной графики осуществляется посредством динамически подключаемых библиотек (англ. DLL – Dynamic Link Library), которые предоставляют универсальный механизм процедур и функций и могут разрабатываться для любых графических систем, обладающих соответствующим API (англ. Application Programming Interface). Среда взаимодействия с графическими системами построена таким образом, что в исполняемом коде содержатся лишь названия процедур и функций для обработки графических данных. Функции обработки графических данных расположены в файлах DLL-библиотек, являющихся уникальными для каждой графической системы [6].

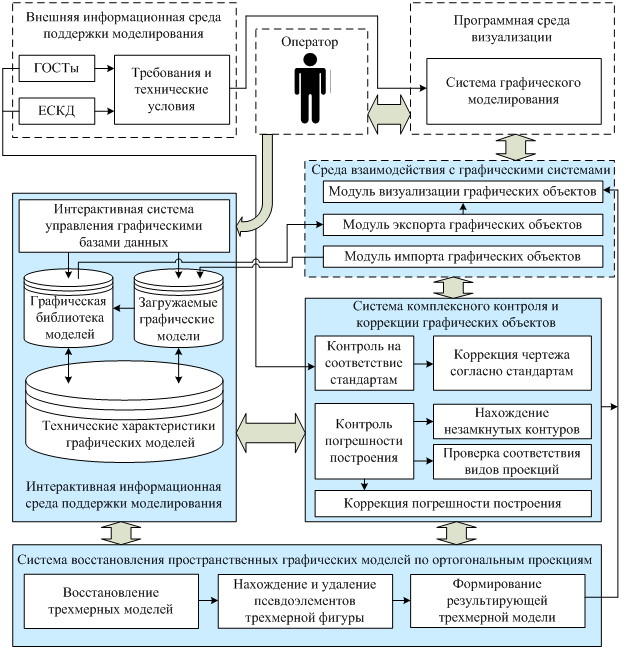
Рис. 5. Структура универсального программного комплекса восстановления 3D-моделей по ортогональным проекциям

В данной работе остановимся подробно на рассмотрении подсистемы комплексного контроля и коррекции графических объектов (рисунок 6), являющейся основной особенностью разработанного программного комплекса.

В состав системы входят взаимосвязанные модули контроля и коррекции графических данных. Настраиваемый перечень контролируемых параметров хранится в одном из компонентов внешней информационной среды программного комплекса. На начальном этапе работы эти сведения используются для выполнения комплексного контроля графических данных с последующим формированием протокола.

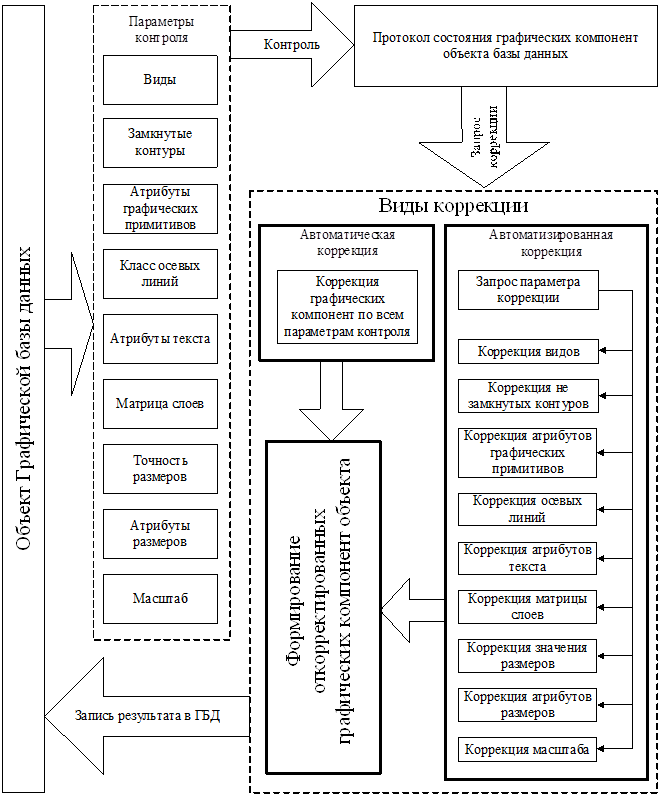
Рис.6. Структурная схема подсистемы контроля и корректировки проекций в разработанном программном комплексе

Контроль чертежей проекций осуществляется в автоматическом режиме. Информация обо всех выявленных ошибках заносится в протокол, который изучается пользователем для принятия решения о необходимости и способе корректировки.

В автоматическом режиме выполняются такие корректировки, как устранение незамкнутых контуров, распределение видов проекций, набор процедур форматирования графических примитивов по образцу (корректировка атрибутов текста, формирование перечня слоев, размещение примитивов по слоям, и т.д.). Затем производится повторный контроль и определяется эффективность корректировки, на основании чего принимается решение о необходимости повторной корректировки данных в автоматизированном режиме. После того, как результаты корректировки признаются удовлетворительными, исправленный набор проекций сохраняется в ГБД и передается в систему восстановления модели (рисунок 7).

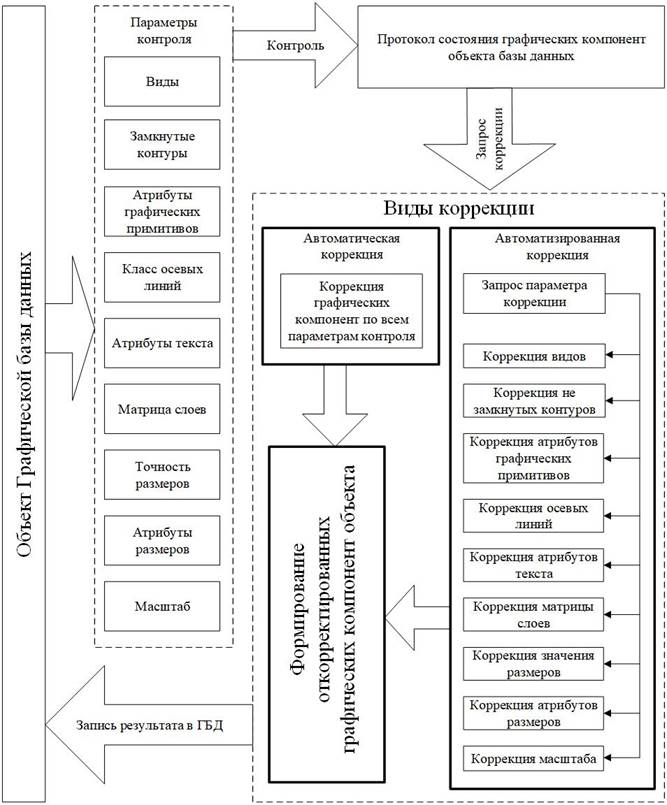
Рис. 7. Схема контроля и корректировки проекций в разработанном программном комплексе

На рисунке 8 приведена схема организации человеко-машинного интерфейса, отображающая модульность структуры программного комплекса.

Интегрирующим звеном комплекса является система управления ГБД, отличающаяся возможностью манипулирования широким набором классов графических данных и библиотек и обеспечивающая многовариантный поиск по информационным полям.  Система управления ГБД разработана на основе клиент-серверной СУБД MySQL и взаимодействует с ней через интерфейс динамически подключаемых библиотек.

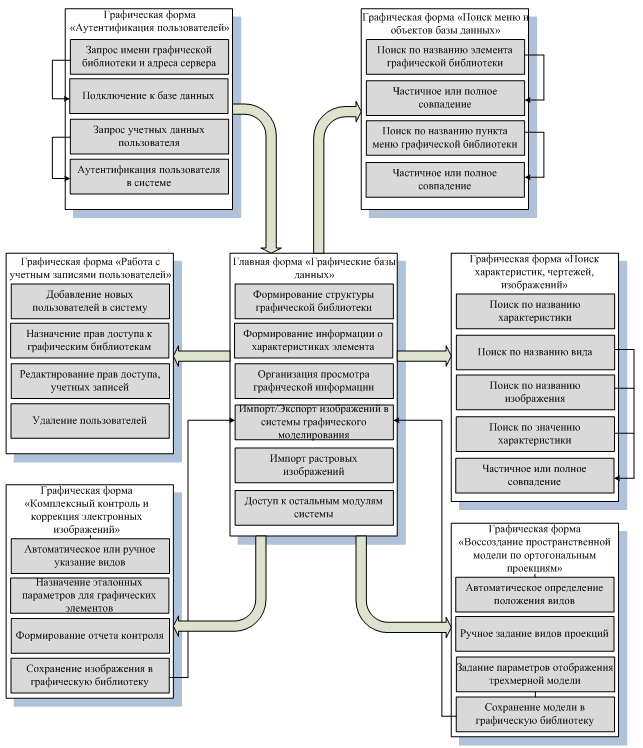
Рис. 8. Схема организации человеко-машинного интерфейса в разработанном программном комплексе

Состав разработанного программного комплекса не ограничивается вышеперечисленными подсистемами и, в зависимости от решаемой задачи, может расширяться.

4. Последовательность действий по восстановлению 3D-моделей в разработанном программном комплексе

Процедура восстановления 3D-модели по набору ортогональных проекций включает следующие шаги.

Шаг 1. Загрузка из ГБД набора ортогональных проекций для восстановления 3D-модели (рисунок 9).

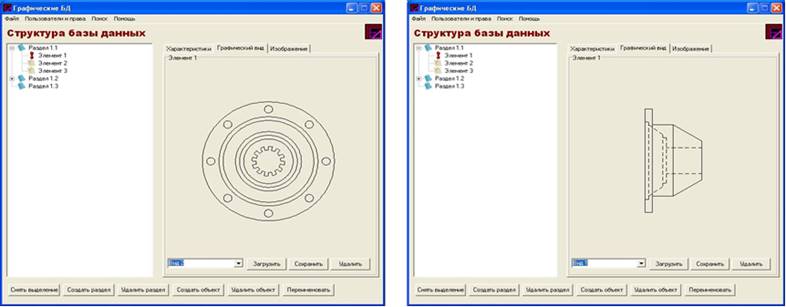
Рис. 9. Окно экспорта и предварительного просмотра графических данных

Шаг 2. Загрузка проекций в рабочее пространство (рисунок 10 а).

Шаг 3. Анализ проекций, формирование и визуализация протокола контроля (рисунок 10 б).

Шаг 4. Изучение протокола, выполнение коррекции и сохранение результатов.

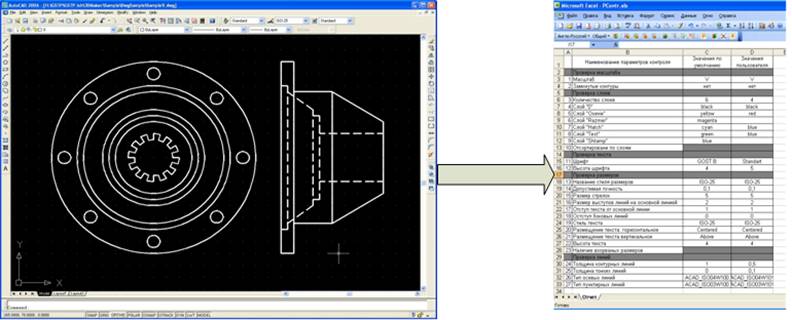
а                                                                                  б

Рис. 10. Экспорт и контроль видов ортогональных проекций

Шаг 5. Итерационный контроль и корректировка проекций до получения безошибочного протокола контроля. Передача управления подсистеме восстановления пространственных моделей.

Шаг 6. Восстановление пространственных моделей по откорректированным чертежам ортогональных проекций, формирование и визуализация 3D-модели (рисунок 11).

Шаг 7. Сохранение итоговой трехмерной модели в графическую базу данных.

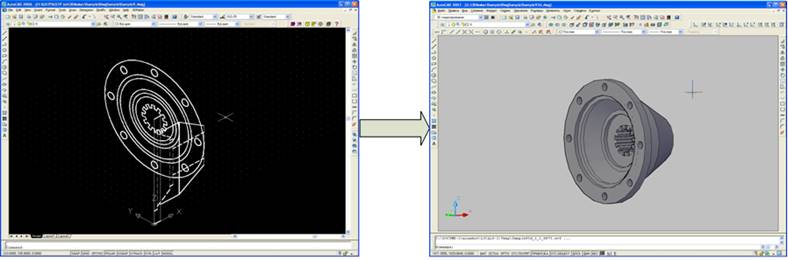
Рис. 11. Визуализация процесса восстановления 3D-модели по набору ортогональных проекций

Разработанный программный комплекс предназначен для эффективного решения задач контроля и корректировки ортогональных проекций с последующим восстановлением пространственных моделей.

Список литературы

1. Нужный А.М., Барабанов А.В., Сафронов В.В. Средства управления электронным архивом на базе системы 1С:PDM. Актуальные направления научных исследований XXI века: теория и практика. 2015. Т. 3. № 5-1 (16-1). С. 173–177.
2. Котов И.И., Полозов В.С., Широкова Л.В. Алгоритмы машинной графики. Москва: Машиностроение. 1977. 231 с.
3. Никаноров А.А. Алгоритмы восстановления 3D объектов по 2D проекциям. Современная техника и технологии. 2014. № 7 [Электронный ресурс]. URL: http://technology.snauka.ru/2014/07/4177
4. Governi L., Furferi R., Palai M., Volpe Y. 3D geometry reconstruction from orthographic views: A method based on 3D image processing and data flitting. Computers in industry. 2013. № 64. P. 1290–1300.
5. Минаков С.А., Барабанов А.В., Кенин С.Л. Комбинирование современных подходов восстановления трехмерных объектов по графическим проекциям. Вестник Воронежского государственного технического университета. 2010. Т. 6. № 9. С. 142–144.
6. Барабанов В.Ф., Нужный А.М., Минаков С.А. Разработка универсальной графической автоматизированной информационной системы. Информационные технологии моделирования и управления: научно-технический журнал. Воронеж: Научная книга. 2008. Вып. 2(45). С. 225–229.

---

DEVELOPMENT OF THE SOFTWARE TO RECONSTRUCT AND VISUALIZE 3D MODELS BY THE SET OF APPROXIMATE ORTHOGRAPHIC PROJECTIONS

V.F. Barabanov, A.M. Nuzhnyy, S.L. Podvalniy, V.V. Safronov

Voronezh State Technical University, Russian Federation

bvf@list.ru, nam14@mail.ru, spodvalny@yandex.ru, safronov.vitaliy@mail.ru

Abstract

The article considers the problem of reconstructing 3D models from orthographic 2D projections, which contain errors.

There is a lot of archival project documentation in the form of orthographic projections. To use this documentation in modern CAD systems it is necessary to restore the 3D models from orthographic 2D projections. Therefore, this problem is urgent.

Formalized process of 3D models reconstruction is described, as well as universal software system based on this mathematical model.

In the final part of the article step-by-step description of the 3D model reconstruction technique is provided.

Keywords: orthographic projections, reconstruction of 3D models, 3D visualization, CAD.

References

1. Нужный А.М., Барабанов А.В., Сафронов В.В. Средства управления электронным архивом на базе системы 1С:PDM [Controls electronic archive on the basis of system 1C:PDM] The Urgent directions of scientific research of the 21st century: theory and practice, vol. 3, no. 5-1 (16-1). pp. 173–177.
2. Котов И.И., Полозов В.С., Широкова Л.В. Алгоритмы машинной графики [Algorithms of machine graphics]. Mechanical engineering. 1977. 231 p.
3. Никаноров А.А. Алгоритмы восстановления 3D объектов по 2D проекциям [Algorithms of restoration of 3D objects on 2D views]. The Modern technique and technologies. 2014. No. 7. URL: http://technology.snauka.ru/2014/07/4177
4. Governi L., Furferi R., Palai M., Volpe Y. 3D geometry reconstruction from orthographic views: A method based on 3D image processing and data flitting. Computers in industry. 2013. № 64. P. 1290–1300.
5. Минаков С.А., Барабанов А.В., Кенин С.Л. Комбинирование современных подходов восстановления трехмерных объектов по графическим проекциям [Combination of the modern approaches of restoration of three-dimensional objects on graphic projections]. The Bulletin of the Voronezh state technical university. 2010. Vol. 6. No. 9. Pp. 142–144.
6. Барабанов В.Ф., Нужный А.М., Минаков С.А. Разработка универсальной графической автоматизированной информационной системы [Development of the universal graphic automated information system]. Information technologies of simulation and control: scientific and technical journal, Voronezh: Scientific book, vol. 2(45). Pp. 225–229.