В работе рассмотрены вопросы, связанные с представлением и описанием динамики гладкой поверхности с краем при заданном поле скорости. Используется неявное представление поверхности с помощью метода «ближайшей точки», который основан на задании поверхности как множества проекций точек пространства из некоторой окрестности поверхности на саму поверхность. Для сеточного представления вмещающей поверхность области и аппроксимации оператора проектирования используются неструктурированные трехмерные сетки, не адаптированные к геометрии поверхности.

В работе рассмотрены вопросы расчета эволюции поверхности при ее движении в заданном поле скорости, вычисление локальных базисов поверхности в ее внутренних точках и на крае, а также интегрирование и дифференцирование функций, заданных на поверхности. Приводится подробное описание соответствующих алгоритмов, а также результаты их тестирования. Кратко описано программное обеспечение, используемое для визуализации данных расчетов. Рассмотренный в работе способ представления данных моделирования не только позволяет эфективно использовать его в вычислительных алгоритмах, но и удобен для визуального представления, позволяющего лучше понять динамику процесса развития трещины.

Работа выполнена при финансовой поддержке Российского научного фонда, проект 15-11-00021.

Ключевые слова: эволюция поверхности, метод «ближайшей точки», неструктурированные сетки.

1. Введение

Необходимость моделирования динамики поверхности с краем в заданном поле скорости возникает в различных задачах математического моделирования и компьютерной графики. Полученные в рамках настоящей работы результаты были получены в ходе разработки комплекса вычислительных алгоритмов для задачи моделирования динамики крупномасштабной трещины гидроразрыва пласта.

Гидравлический разрыв пласта (гидроразрыв пласта, ГРП) является одним из самых распространенных методов увеличения нефтеотдачи, используемым при промышленной разработке нефтегазовых месторождений. Сущность технологии ГРП заключается в закачке в нефтеносный пласт специальной жидкости с целью создания искусственной (техногенной) трещины длиной м, высотой м и средним раскрытием мм). В результате создается соединенный со скважиной искусственный канал и большую площадь притока, который имеет высокую (на порядки превышающую пластовую) проницаемость. Это обеспечивает значительное увеличение притока пластового флюида к скважине. Инженерные аспекты технологии рассматриваются, например, в [1, 2].

Физико–математическое описание динамики трещины ГРП в ходе ее развития сводится к решению сложной связанной задачи, включающей в себя следующие системы уравнений:

• система уравнений пороупругости, описывающие эволюцию напряженно–деформированного состояния пласта и полей давления флюида в нем в ходе развития трещины;

• уравнения течения жидкости в трещине;

• механические условия развития трещины, определяющие направление ее развития в каждой точке ее фронта;

• заданные на боковых поверхностях трещины динамические условия согласования между полями давления в трещине и в пласте, а также кинематические условия, связывающие раскрытие трещины и перемещение точек пласта.

При таком описании геометрическая модель трещины представляет собой гладкую поверхность с подвижным краем. Разработка эффективных и надежных численных методов решения этой задачи включает в себя создание способа представления срединной поверхности трещины в дискретной задаче с учетом того, что:

• изменение геометрии срединной поверхности трещины в ходе ее эволюции априорно не известно и определяется последовательно в ходе решения полной связанной задачи;

• на срединной поверхности трещины решается уравнение смазочного слоя, описывающее течение флюида в трещине и, косвенно, динамику эволюции трещины;

• полная задача является сопряженной и необходимо такое представление геометрии трещины, которое бы позволило удобно переносит информацию о полях, заданных на трещине, в трехмерную область.

Для описания геометрии поверхности с подвижным краем в известно достаточно много подходов, включая полигональные модели, параметрическое представление, представление в виде множества точек, неявное представление через поверхности уровня заданных в пространстве функций и др. Все они достаточно эффективны в том случае, если конечной задачей является лишь описание динамики изменения геометрии поверхности, как, например, в ряде задач компьютерной графики. Однако не все они подходят для решения сформулированной выше задачи моделирования ГРП.

Среди известных методов в качестве наиболее предпочтительного был выбран метод проекции ближайшей точки. Мотивацией служит прежде всего то, что в рамках этого подхода известны и достаточно хорошо разработанные методы решения дифференциальных уравнений на поверхностях, см. [3, 4, 5, 6], а сам метод представления поверхности хорошо адаптирован для использования совместно с методом X-FEM для расчета напряженно–деформированного состояния среды в окрестности трещины.

Однако большинство работ, посвященных этому методу, связаны с его применением к анализу стационарных поверхностей или динамических поверхностей, но без края. В настоящей работы предложен эффективный метод расчета эволюции поверхностей с подвижным краем, рассмотрены вопросы представления, интегрирования и дифференцирования функций, заданных на этой поверхности, а так же методы расчета ее локальных геометрических свойств, в частности, построения ортогональных базисов во внутренних и граничных точках поверхности.

Отметим так же, что в большинстве работ по моделированию развития трещин с помощью обобщенного метода конечных элементов ([7, 8, 9]) геометрическая модель трещины строится с использованием метода поверхностей уровня (level set method, см. [10, 11]). Поверхность с краем задается при этом парой определенных в пространстве скалярных функций , так, что

(1)

где — время. Другими словами, в фиксированный момент времени поверхность задается как часть поверхности уровня ноль функции , ограниченная изоповерхностью функции . Для проведения расчетов удобно, чтобы функции , являлись знаковыми расстояниями, определенными в некоторой небольшой окрестности поверхности . При этом движение края поверхности задается полем скоростей , описывающим эволюцию функций , . Для пересчета функций , применяются уравнения типа Гамильтона–Якоби. Основным недостатком такого метода является сложность реализации: например, для описания эволюции поверхности требуется согласованное решение десяти различных уравнений типа Гамильтона–Якоби относительно функций и , обеспечивающих, помимо прочего, сохранение ортогональности их градиентов, свойств знаковых расстояний и т.д. [7, 8, 9].

Альтернативный подход, отчасти близкий использованному в настоящей работе, описан в работе [12]. В нем поверхность задается с помощью так называемых «векторных поверхностей уровня» («vector level sets»), представляющих собой пару функций, первая из которых является оператором проектирования точки на поверхность в смысле ближайшего расстояния, а вторая определяет ориентацию поверхности. Вместе с тем в описанном подходе используется полигональное представление поверхности и ее, которое используется для построения проекторов. В ходе эволюции поверхности сначала обновляется ее полигональное представление, которое затем используется для построения проекторов и функций уровня.

В отличие от этого подхода в настоящей работе не используется полигональное представление поверхности, а значения операторов проектирования в ходе ее эволюции вычисляются непосредственно. При этом сама поверхность и задающие ее поверхности уровня, при необходимости, могут быть восстановлены локально. В этом смысле предложенный в настоящей рабе подход на основе метода проекции ближайшей точки (ПБТ), является более гибким и, по своей сути, близок к методам представления поверхностей как «облака точек» («point cloud surfaces», см., например, [15]).

Несмотря на то, что представленные в работе алгоритмы разрабатывались для решения конкретной прикладной задачи, они являются универсальными и могут быть использованы для решения широкого круга задач, связанными с расчетом и визуализацией динамики поверхностей с краем.

Для визуализации реультатов моделирования в работе используется разработанная в ИПМ им. М.В. Келдыша РАН программа FrontView, основное назначение которой - . «быстрая» визуализация данных большого объема, заданных на днамических поверхностях, которые описываются неструктурированными треугольными сетками.

Описанная выше прикладная задача об эволюции трещины ГРП пласта приводит к необходимости рассмотрения сложной связанной (сопряженной) пространственно-трехмерной системы уравнений в частных производных. Рассматриваемые поля являются как трехмерными, так и двумерными, заданными на срединной поверхности трещины. Помимо этого, решением задачи является непосредственно эволюция трещины, которая в рамках рассмотренной постановки описывается как гладкая поверхность с краем. Распределение свойств вмещающей трещину среды, вообще говоря, является трехмерным. В силу этого полноценный качественный и количественный анализ результатов моделирования принципиально невозможен без эффективных средств визуализации. Набор готовых средств для визуализации и анализа результатов моделирования, пригодных, без дополнительной адаптации, для анализа эволюции поверхностей с краем, является ограниченным. По этой причине рассмотренные в настоящей работе подходы для описания эволюции поверхности с краем имеют самостоятельный интерес в контексте задач представления и визуализации данных моделирования.

2. Метод ПБТ

Рассмотрим основные понятия метода ближайшей точки. Строгое математическое обоснование этого метода приведено в [13].

Рассмотрим гладкую поверхность с краем, вложенную в трехмерное пространство . Термин «гладкая» здесь и далее будем понимать как то, что множество является образом гладкого отображения ограниченной замкнутой подобласти двумерной плоскости в трехмерное пространство . При этом будем считать, что используемые отображения имеют любое требуемое число производных. Также будем считать, что поверхность целиком расположена внутри пространственной области .

Пусть для произвольной , является ближайшей к ней точкой на поверхности :

Здесь и далее используются еквклидовы нормы.

Точку будем называть проекцией точки на поверхность в смысле наименьшего расстояния, а соответствующий оператор проектирования будем обозначать ,

Оператор является векторнозначным; он отображает область на поверхность , рассматриваемую как подмножество в . В случае, если поверхность и ее край являются гладкими, а область — «достаточно маленькая», то оператор однозначно определен, т.е. каждая точка области однозначно проектируется в единственную точку на поверхности.

Если для поверхности можно задать функцию знакового расстояния (то есть — ориентированная поверхность без края), то для оператора справедливо представление:

Можно показать, что проектор однозначно описывает поверхность как множество своих неподвижных точек:

Отметим, что такой способ описания является достаточно общим. Он позволяет описывать геометрию поверхности с краем и без края, неориентируемые многообразия или многообразия коразмерности больше единицы, (то есть кривые (коразмерность ) и точки (коразмерность ), а так же объединение объектов разной коразмерности.

В дальнейшем нам понадобится различать точки области , которые проектируются во внутренние точки поверхности или на ее край . Для этого рассмотрим вспомогательный оператор , который определим как [4]:

(2)

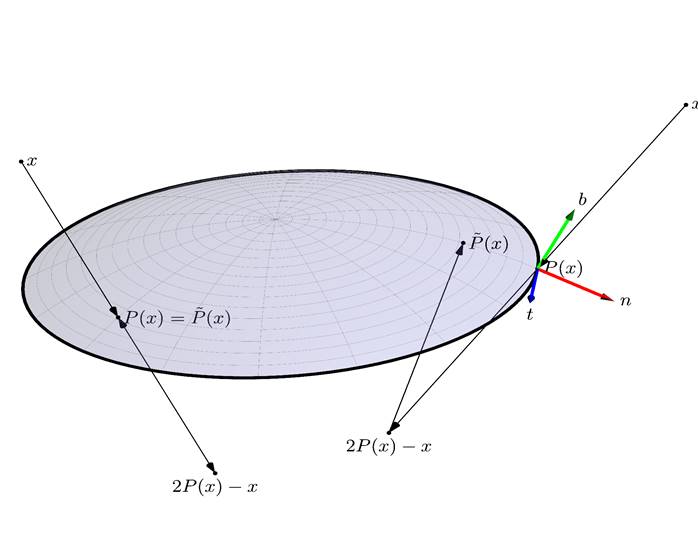
Рис. 1. К определению оператор и .

Из простых геометрических соображений (см. рисунок 1) следует, что для точек , проекции которых принадлежат краю поверхности, справедливо соотношение

(3)

а для точек, проекции которых принадлежат внутренним точкам , значения проекторов и совпадают:

(4)

Вместе с описанным выше способом описания поверхности в дальнейшем нам понадобится способ представления функций, заданных на этой поверхности. В силу того, что никаких локальных координат на поверхности не вводится, удобно использовать «неявный» способ их представления. А именно, функцию на поверхности будем задавать как след на ней функции, заданной в области .

Удовлетворяющее последнему свойству продолжение функции, заданной на поверхности, в область может быть построено различными способами. Удобным и используемом в дальнейшем способом является ее продолжение с помощью оператора . А именно, для произвольной функции , заданной на поверхности, ее продолжение в определим как:

Таким образом построенное продолжение постоянно вдоль отрезков, соединяющих точку области и ее проекцию. Этот факт позволяет удобным способом вычислять производные функции на поверхности, а так же дифференциальные операторы более высокого порядка (см. ниже в этом разделе).

Отметим, что для произвольной функции в , постоянной в направлении нормали к справедливо [13]:

где — поверхностный градиент (см. [14]). Аналогично, для произвольного гладкого векторного поля в , касательного к поверхности :

Тогда, в силу свойств проектора и оператора продолжения имеем:

В силу того, что восполнение постоянно вдоль направлений, нормальных к поверхности, векторное поле является касательным к . Отсюда следует, что

где — оператор Бельтрами–Лапласа («поверхностный» оператор Лапласа, [14] ). Аналогичные продолжения можно построить и для более сложных эллиптических операторов дивергентного типа, см. [3, 13].

3. Модель эволюции поверхности

Выше были изложены основные идеи метода ближайшей точки применительно к стационарной поверхности. Рассмотрим теперь постановку задачи об эволюции поверхности.

Пусть — время. Обозначим через рассматриваемую поверхность в момент времени . Будем считать, что при выполняется условие . Другими словами, семейство поверхностей, соответствующих бо́льшим моментам времени содержится внутри поверхности, соответствующей любому большему моменту времени. Или, что то же самое, поверхность может эволюционировать только за счет движения ее края. Такая ситуация соответствует специфики решаемой задачи, а именно развитию срединной поверхности трещины в ходе роста последней.

Будем считать, что:

• в каждый момент времени в рассматриваемом интервале поверхность целиком содержится внутри области ;

• эволюция поверхности является «гладкой», то есть поверхность в каждый момент времени может быть гладко и взаимно-однозначно отображена на, например, диск единичного радиуса в . В частности, в ходе эволюции у не должны появляться самопересечения и т.д.

В этом случае семейство поверхностей может быть представлено как объединение начальной поверхности и следа «движения» ее криволинейного края:

где — подвижный край поверхности в момент времени .

В дальнейшем будем считать, что в каждый момент времени на линии задано векторное поле скорости , , описывающее ее эволюцию. Таким образом, движение точки границы описывается уравнением

(5)

Будем считать, что поле скорости является гладкой функцией точки в каждый фиксированный момент времени и для каждой фиксированной (лагранжевой) точки границы является гладкой функцией времени.

В каждый момент времени будем описывать поверхность с помощью оператора проекции ближайшей точки. Построение алгоритма вычисления этого оператора (точнее, его аппроксимаций) в каждый момент времени при его известном значении в предыдущие моменты времени и заданной скорости будет рассмотрено ниже.

4. Дискретная модель поверхности

Пусть в области , содержащей поверхность , задана расчетная сетка, ячейки которой являются тетраэдрами. Полученную триангуляцию будем считать регулярной (т.е. пересечение двух различных тетраэдров может являться пустым множеством, узлом сетки, ее ребром или грань). Соответствующую дискретную область обозначим как . Предполагается, что сетка является достаточно мелкой так, что характерный шаг сетки много меньше радиусов главных кривизн поверхности и радиуса кривизны ее края.

Множество узлов сетки обозначим как , , — число узлов сетки. Отнесем к каждому узлу сетки базисную функцию . В простейшем случае могут быть использованы непрерывные кусочно-линейные базисные функции, для которых , где — символ Кронекера, а внутри ячеек сетки продолжены линейно.

В дискретном случае оператор проектирования задается своими значениями в узлах сетки. Для вычисления оператора проектирования в произвольной точке области используется ранее введенная система базисных функций. Если — произвольная точка области , — тетраэдр, в котором она расположена, — ее барицентрические координаты относительно вершин тетраэдра . Тогда проекцией точки считается точка

Построенные аппроксимации проектора позволяют естественным образом построить аппроксимации проектора в соответствии с (2).

Пусть, далее, — множество всех узлов сетки. Определим его подмножества , , , соответствующие узлам, которые проектируются во внутренние точки поверхности и на ее край, соответственно:

(6)

где — малый вещественный параметр, который является параметром алгоритма.

Очевидно, что в ходе эволюции поверхности множество может только увеличиваться (по включению). Другими словами, при имеем:

Это позволяет, в частности, при движении поверхности, на каждом очередном временном шаге дискретизации обновлять информацию только для узлов из множества .

5. Алгоритм расчета эволюции поверхности

В настоящем разделе рассматривается алгоритм пересчета дискретизации проектора в ходе эволюции поверхности.

Общая идея алгоритма имеет следующий вид: сначала вычисляются, по известной информации, координаты точек проекций узлов сетки из множества . Далее эти точки смещаются в заданном направлении в соответствии с заданной скоростью движения края и заданной величиной шага по времени. Полученные точки принадлежат новому положению фронта, однако вектор, соединяющий исходный узел пространственной сетки и новое положение точки края не является вектором проекции ближайшей точки. Поэтому аппроксимации проектора корректируются.

Далее будем считать, что поверхность эволюционирует на интервале времени . Введем на этом интервале расчетную сетку с шагами , ,

где — число узлов сетки.

В начальный момент времени аппроксимация проектора считается известной. Также будем считать, что в течении интервала времени поверхность остается внутри сеточной области .

Полный алгоритм построения дискретного оператора в момент времени при заданных параметрах метода и известной аппроксимации представлен на схеме алгоритма 1.

Входными данным алгоритма являются дискретизация проектора в момент времени и множества и . В результате своей работы алгоритм возвращает значения те же переменных в момент времени .

Параметрами метода являются величины , и . Параметр определяет обусловленность проекции точки на отрезок и точность вычисления проекции,

где определяет радиус шара, в котором производится поиск точек на шаге 6 алгоритма 1. Считается, что — достаточно велик по сравнению с шагом сетки, но не превышает максимального расстояния от точки до ее проекции на край,

В общем случае достаточно положить . Параметр определяет пороговое значение, которое используется для того, чтобы определить принадлежит ли проекция краю поверхности или множеству ее внутренних точек. При вычислении значения (см. этап 5 алгоритма), должно использовать то же значение параметра , что и в (6).

1.	Входные данные: дискретное представление поверхности в момент времени : множества , , аппроксимации проектора , шаг , параметры алгоритма: , , , ..
2.	Положить
3.	Вычислить новые положения всех проекций на край в соотвествии с аппроксимацией (5):
4.	forall // Для всех узлов, проектирующихся на край
5.		Определить ближайший к узел из :
6.		Определить (под)множество , такое что:
7.		if // Точка является проекцией на край поверхности.
8.			Положить
9.		else // Точка не является проекцией на край поверхности.
10.			Найти среди точек в такую, что длина отрезка минимальна:
11.			Положить
12.		end if
		// Определить проекцию точки на отрезок :
13.		Положить
14.		if // Точка проектируется на поверхность.
15.			Положить
16.		else if // Точка проектируется на край.
17.			Положить
18.		else if // Точка проектируется на поверхность.
19.			Положить
20.		end if
21.	end forall
22.	Выходные данные: дискретное представление поверхности в момент времени : множества , , аппроксимации проектора .

Алгоритм 1. Расчет эволюции проектора .

6. Интегрирование по поверхности

Рассмотрим вопросы интегрирования функций на поверхностях, заданных проектором «ближайшей точки». Конкретно, речь пойдет о вычислении интегралов вида:

или, в частном случае, о вычислении площади рассматриваемой поверхности с краем:

Рассмотрим сразу дискретный случай. Как и ранее, будем считать, что поверхность расположена внутри некоторой сеточной области . Пусть — ее граница, образованная объединением треугольных граней :

где — число граней. При известном разбиении области множество граней легко может быть определено как множество граней, инцидентных одному и только одну тетраэдру триангуляции.

Представим в виде объединения трех попарно непересекающихся множеств:

где состоит из граней, все узлы которых проектируются на фронт (то есть являются элементами множества ), а и — множество остальных граней, причем все грани из множества и лежат по одну сторону от поверхности.

Заметим теперь, что:

• все узлы граней из проектируются на край поверхности. Площади треугольников, вершины которых являются проекциями вершин треугольников из пренебрежимо малы при стремении шага сетки к нулю;

• оператор проектирования (как континуальный, так и дискретный), ограниченный на множества является сюрьекцией (отображением «на») на поверхность ;

• в случае, если прямая, проходящая через произвольную точку на поверхности и ориентированная единичной нормалью к ней, пересекает границы множества по одному разу, то треугольные сетки, заданные на порождают треугольные сетки на поверхности . Узлы этих сеток образованы проекциями вершин треугольников из , при этом два узла этой сетки считаются связанными ребром, если им связаны соответствующие узлы в .

Для вычисления интегралов от функций, заданных на поверхности, будем, фактически, использовать эти сетки, при этом для вычисления приближенного значения интеграла по одному треугольнику будем использовать одноточечную квадратурную формулу.

При этом не возникает необходимости в явном представлении в алгоритме описанных выше сеток на поверхности — суммирование по треугольникам такой сетки можно проводить в цикле по всем треугольникам, образующим множество . При это вклад от треугольников, принадлежащих множеству будет исчезающе мал при , а вклад от поверхностей будет (асимптотически) удваиваться.

Далее, в том случае, если прямая проходящая через произвольную точку на поверхности и ориентированная единичной нормалью к ней пересекает границы множества более одного раза, проекции сеток уже не будут образовывать корректную сетку на в силу того, что проекции отдельных треугольников могут иметь непустое пересечение. В этом случае приведенную выше схема вычислений должна быть скорректирована. А именно, необходимо учитывать взаимную ориентацию внешней нормали к грани и направления проектирования, например, ее центра.

Так, рассмотрим некоторую грань (треугольник) , образованную узлами сетки , и . Соответственно, четвертый узел тетраэдра будем обозначать . Тогда нормаль к грани определяется выражением:

где «» обозначает векторное произведение в . Направление нормали можно определить по взаимной ориентации рассчитанной нормали и вектора, соединяющего центр грани и его проекцию. А именно, вектор нормали будет являться вектором внешней нормали, если величина

В дальнейшем будем считать, что это условие выполняется.

Таким образом, приходим к следующему выражению для вычисления интеграл по поверхности:

где — какое-либо продолжение функции с поверхности в область . Если , то имеем:

и выражение для приближенного вычисления интеграла соответственно упрощается.

Множитель «2» перед интегралом возникает за счет того, что, фактически, интеграл вычисляется дважды — при обходе треугольников из и .

7. Расчет локальных базисов на поверхности и ее крае

В контексте рассматриваемой прикладной задачи, а именно задаче моделирования эволюции крупномасштабной трещины ГРП, возникает необходимость вычисления на крае и поверхности и его окрестности локальных векторных базисов. В частности, это требуется при применении расширенного метода конечных элементов (X-FEM) для расчета напряженного–деформированного состояния во вмещающей трещину среде. В настоящем разделе рассмотрен этот и смежные вопросы.

Введем еще один оператор проектирования , представляющий собой оператор проектирования в смысл кратчайшего расстояния на край поверхности:

Оператор корректно (в смысле единственности проекции) определен в некоторой достаточно малой окрестности края поверхности . Соответствующую окрестность будем обозначать как .

Будем считать, что (а) и (б) область содержит все точки области , которые проектируются на край поверхности в смысле критериев (3) и (4). Далее, пусть — подобласть областей и состоящая из точек, которые проектируются на край поверхности, см. рисунок 2.

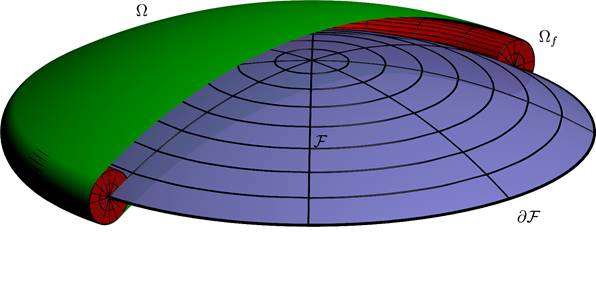
Рис. 2: Области , и

Отсюда следует, что:

• в подобласти определены все три оператора , и ;

• образы операторов и , действующих на области , совпадают между собой и с множеством точек края поверхности.

Если обозначить через множество точек множества , проектирующихся на край поверхности, то множество может быть выбрано в виде:

то есть получено «зеркальным» отражением множества относительно края поверхности. Этот же алгоритм может быть применен и для построения области в дискретной постановке.

Рассмотрим теперь вопрос о построении локальных базисов на поверхности и ее крае.

Во всех точках проекций узлов сетки из множества вектор единичной нормали к поверхности может быть определен как:

(7)

при этом направления векторов для всех узлов сетки, лежащих «по одну сторону» от поверхности , совпадают. В том случае, если поверхность «слабо искривлена», то есть ее радиус кривизны существенно больше диаметра самой поверхности, ориентация поверхности может быть однозначно задана выбором (не зависящего от точки поверхности и области ) вектора . В этом случае для узла сетки , положение узла и ориентация нормали может быть определена путем вычисления знака скалярного произведения .

Тогда во всех узлах из множества может быть восстановлено значение аппроксимации функции знакового расстояния до поверхности:

В произвольной точке области, проектирующейся на поверхность (но не на ее край), вектор единичной нормали в точке проекции и значение функции знакового расстояния могут быть восстановлены интероляцией. Если — барицентрические координаты точки относительно тетраэдра, в котором она расположена, то имеем:

где определены согласно (7). Рассмотрим теперь аналогичные вопросы для точек, проекция которых попадает на край поверхности.

Пусть — вектор в точке края поверхности, который является нормальным к ее краю и лежит в касательной плоскости поверхности. Для произвольной точки области («трубчатой» окрестности края поверхности) определим аппроксимацию вектора в точке проекции как:

Очевидно, что этот вектор аппроксимирует точное значение вектора нормали с точность . Если «диаметр» трубчатой окрестности линейно уменьшается с уменьшением шага расчетной сетки (например, «диаметр» окрестности ограничен фиксированным числом шагов сетки), то

Далее, аппроксимация вектора , касательного к краю поверхности в точке , может быть вычислен как:

Наконец, вектор , который является нормалью и к поверхности, и к ее краю, может быть определен как:

Приведенные выше построения иллюстрирует рисунок 1.

Таким образом, в каждой точке проекции может быть построен локальный ортогональный базис векторов. Ориентация этого базиса может быть определена, если известен не зависящий от точки поверхности «глобальный» вектор , задающий ориентацию поверхности, см. выше.

Введенный базис позволяет ввести в каждом «сечении» трубчатой окрестности локальные декартовы и полярные координаты по правилу:

где функция определена всюду кроме точки , в соответствии с:

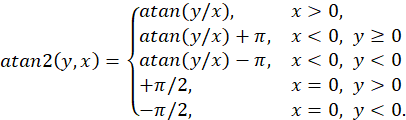
и возвращает значение полярного угла вектора в базисе

Функции, задающие поверхность и ее край как множества меры ноль (см. (1)) могут быть восстановлены как:

Наконец, как в окрестности точек на как поверхности, так и на ее крае, возможно локально восстановить непосредственно поверхность. Для этого можно воспользоваться методами, развитыми в связи с представлением поверхностей как множества принадлежащих им точек («point cloud surfaces»), см., например, [15].

8. Тестирование алгоритмов

Разработанные алгоритма расчета эволюции поверхности с краем и интегрирования заданных на ней функций были программно реализованы на языке С++ и Python для ОС GNU Linux. Ниже кратко приведены результаты тестирования реализаций этих алгоритмов. Для визуализации результатов расчетов исполльзовадась пограмма FrontView, краткое описание которой приведено в соответствующем разделе.

8.1. Диск в однородном поле скоростей

В качестве первого теста рассмотри задачу о развитии плоской поверхности, которая представляет собой след движущегося поступательно и с постоянной скоростью диска радиуса . В начальный момент времени поверхность задается как половина такого диска, расположенная области . Расчетная область имеет вид параллелепипеда со сторонами, параллельными осям координат. Плоскость диска горизонтальна, его центр в начальный момент времени совпадает с центром боковой грани расчетной области. Заданное на крае диска поле скоростей считается постоянным и однородным во всех точках края, , . Тогда в момент времени центра диска расположен в точке . Поверхность образуется как след от движения диска в расчетной области.

Непосредственными вычислениями можно получить следующее аналитическое выражение для проектора :

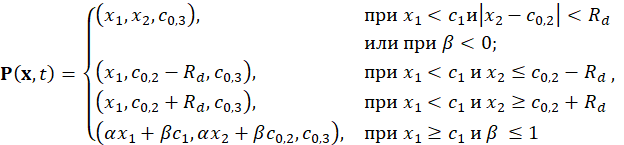
где , , , , — декартовы координаты в области.

Зависимость площади трещины от времени имеет вид:

8.2. Диск в вихревом поле скоростей

В качестве второго теста рассмотрим аналогичную задачу, в которой, однако, поверхность не является плоской. Как и ранее, будем считать, что в начальный момент времени поверхность представляет собой половину диска, однако, теперь, расположенную на поверхности цилиндра заданного радиуса. в ходе эволюции поверхность остается на цилиндре, «наматываясь» на него вдоль сечения, плоскость которого перпендикулярна оси цилиндра. Ось цилиндра параллельна координатной оси . Поле скорости является вихревым с осью, параллельной оси . Считается, что ось вихря находится на правой границе расчетной области и проходит через точку . Тогда поле скоростей имеет вид:

где — такое расстояние от точки пространства до оси вихря, на котором модуль скорости равняется .

Пусть — радиус цилиндра, которому принадлежит поверхность. На поверхности цилиндра введем угловую координату . Тогда координаты точек на поверхности цилиндра будут иметь вид:

Если в начальный момент времени центр диска по оcи имеет координату , то уравнение края поверхности можно записать в параметрическом виде как:

где — параметр. В этом случае условие проекции на край (т.е. условие минимума расстояния от точки пространства до края) можно записать в виде:

Отсюда получается следующее уравнение относительно значения , соотвтсвующего проекции заданной точки пространства на криволинейный край поверхности:

В расчетах, при построении точного решения, это уравнение решается методом Ньютона.

Аналитическое решение для проектора имеет вид:

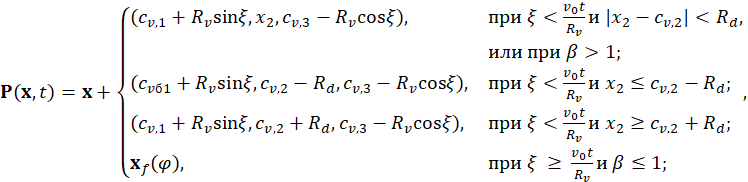
где .

Для площади поверхности справедливо выражение:

8.3. Результаты тестирования

В процессе тестирования изучалась зависимость средней ошибки определения проекции в конце расчета, при заданном :

где суммирование ведется по всем узлам расчетной сетки и ошибки определения площади:

от характерного шага сетки .

Отметим, что алгоритм расчета эволюции поверхности никак не использует информацию о структуре сетки, для его работы необходима информация лишь о координатах ее узлов. В то же время, информация о структуре сетки необходима для вычисления интегралов от функций, заданных на поверхности.

Для расчета использовалась сетка из тетраэдров в характерным шагом , не адаптированная к геометрии поверхности. Параметры тестов имели значения , для случая диска в однородном поле скоростей и , , для случая диска в вихревом поле скорости.

Во всех расчетах временной шаг и время моделирования , .

На рисунках 3 приведены этапы эволюции поверхности для теста «диск в однородном поле скоростей», в котором рассматривается эволюция плоской поверхности, которая представляет собой след движущегося поступательно и с постоянной скоростью диска заданного радиуса. Детали теста описаны в разделе 8.1.

На рисунке 4 представлены анимации, соответствуюшие тесту «диск в вихревом поле скорости». Начальная конфигурация поверхности - диск на поверхности цилиндра. Поле скоростей является осесимметричным с осью вращения, совпадающей с осью цилиндра. Детальное описание теста приведено в разделе 8.2. На левой анимации показана эволюция непосредственно поверхности. Цветом показана величина ошибки сеточной аппроксимации поверхности. Справа представлена анимация эволюция границы неструктурированной тетраэдрической сетки, вмещающей поверхность с краем. Показанная в анимации сетка используется для представления поверхности с использованием метода проекции ближайшей точки. По мере эволюции поверхности тетраэдрическая сетка достраивается соответствующим образом. Детальное описание теста приведено в разделе 8.2. статьи. Цветом показан уровень ошибки сеточной аппроксимации поверхности.

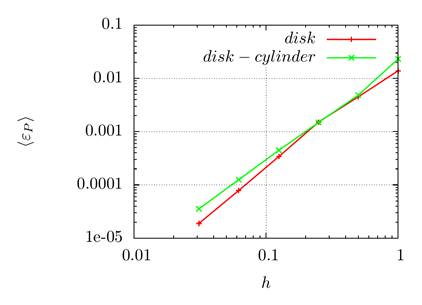
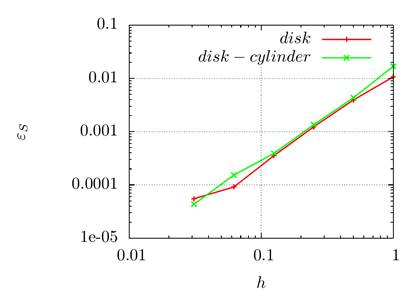
Графики на рисунке 5 показывают зависимость ошибки вычисления проектора и площади поверхности в ходе ее эволюции от шага сетки. Видно, что построенный алгоритм имеет порядок сходимости по , близкий ко второму.

Рис. 3. Эволюция диска в однородном поле скоростей при , , цветом показан уровень ошибки проекции в интервале

Рис. 4. Эволюция диска в вихревом поле скоростей при , , цветом показан уровень ошибки проекции в интервале


(а)	(б)

Рис. 5. Зависимость ошибок и от параметра для двух тестовых постановок — диска в однородном поле скоростей (кривые «disk») и диска в вихревом поле скоростей (кривые «disk-cylinder»)

9. Визуализатор FrontView

Для визуализации результатов применялось приложение FrontView, изначально разработанное в ИПМ им. М.В. Келдыша РАН С.А. Хилковым (МФТИ) в процессе решения задачи о сейсмической миграции до суммирования в асимптотическом приближении. Основное назначение этой программы – быстрая визуализация больших объемов данных, заданных на динамических поверхностях, представляемых в виде неструктурированных треугольных сеток.

Приложение FrontView разработано под OS Linux на языках C++ и Python с использованием библиотек OpenGL (www.opengl.com) и glm (http://glm.g-truc.net). Для отображения приложение FrontView использует собственный бинарный формат данных, для организации записи данных пользователю предоставляется заголовочный файл на C++.

Для визуализации полей, зависящих от времени, данные записываются в единый файл покадрово, кадры расположены в файле последовательно. Каждый кадр содержит мгновенное значение визуализируемых полей. Данные, отнесенные к различным моментам времени могут быть заданы на различных сетках. Данные, соответствующие одному кадру включают в себя треугольную неструктурированную сетку в 3D пространстве - координаты вершин список троек индексов, задающих треугольные ячейки сетки. С каждой ячейкой и каждой вершиной сетки может ассоциироваться дополнительная информация - произвольное (но одинаковое для всех ячеек) число значений в формате float4. Таким образом формат данных позволяет сохранять на сетке различные скалярные и векторные поля.

При работе с приложением FrontView пользователь имеет возможность переходить между кадрами, выбирать углы обзора и масштабирование, задействовать плоскости отсечения, сохранять построенное изображение в различных растровых графических форматах. При отображении используется четыре массива данных выбираемых пользователем - три массива отображаются как координаты вершин треугольников (по умолчанию это действительно координаты вершин исходной сетки), четвертый массив данных отображается цветом. Такой подход позволяет эффективно визуализировать различные проекции сложных многомерных функций. В рассмотренной в настоящей статье задаче в качестве координат выбирались как координаты вершин исходной сетки, так и их проекции на аппроксимируемую поверхность. Цветом, как правило, показывалось значение ошибки.

Интерфейс приложения FrontView состоит из окна, в котором происходит визуализация, и интерфейса командной строки. Переход между кадрами, изменение углов обзора и масштабирования возможны как при помощи манипулятора «мышь», так и при помощи «горячих клавиш». Интерфейс командной строки использует синтаксис языка Python, вызывая функцию «exec» для разбора команд пользователя. Это позволяет гибко настраивать параметры визуализации, создавать свои сценарии обработки данных и выполнять пакетную обработку (например, используя циклы и другие управляющие конструкции языка Python).

10. Заключение

В работе были рассмотрены вопросы, связанные с представлением и расчетом динамики поверхностей с краем. Для представления поверхности использован метод «ближайшей точки». Рассмотрены вопросы представления функций на таких поверхностях и вычисления их дифференциальных характеристик. Предложены новый алгоритм расчета эволюции поверхностей по заданному полю скорости и алгоритм интегрирования функций, заданных на поверхности. По сравнению с традиционно используемыми для таких задач методами, основанными на представлении поверхности как множества уровня ноль заданной функции, построенный алгоритм не требует решения уравнений типа Гамильтона–Якоби и оказывается значительно проще в реализации на неструктурированных сетках. Результаты численных расчетов продемонстрировали достаточную для приложений точность и эффективность предложенных алгоритмов. Приведено описание программы FrontView, которая была использована для визуального представления данных расчетов. Рассмотренный в работе способ представления данных моделирования не только позволяет эффективно использовать его в вычислительных алгоритмах, но и удобен для визуального представления, позволяющего лучше понять динамику процесса развития трещины.

Список литературы

1. Экономидес М., Олини Р., Валько П. Унифицированный дизайн гидроразрыва пласта. От теории к практике. Институт компьютерных исследований, 2007. 236 С.

2. Салимов В.Г., Ибрагимов Н.Г., Насыбуллин А.В., Салимов О.В. Гидравлический разрыв карбонатных пластов. Нефтяное хозяйство, 2013. 471 С.

3. Ruuth S.J., Merriman B.M. A simple embedding method for solving partial differential equations on surfaces. J. Comput. Phys., 227 (2008), pp. 1943–1961.

4. Macdonald C.B., Brandman J., Ruuth S.J. Solving eigenvalue problems on curved surfaces using the Closest Point Method. J. Comput. Phys., 230 (2011), pp. 7944–7956.

5. Macdonald C.B., Ruuth S.J. Level set equations on surfaces via the Closest Point Method. J. Sci. Comput., 35 (2008), pp. 219–240.

6. Macdonald C.B., Ruuth S.J. The implicit Closest Point Method for the numerical solution of partial differential equations on surfaces. SIAM J. Sci. Comput., 31 (2009), pp. 4330–4350.

7. Stolarska M., Chopp D., Moes N., Belytschko T. Modelling crack growth by level sets in the extended finite element method. Int. J. Numer. Meth. Engng. 2001; 51:943–960.

8. Moes, N., Gravouil, A., Belytschko, T. Non-planar 3D crack growth by the extended fiite element and level sets—Part I: Mechanical model. Int. J. Numer. Meth. Engng 2002; 53:2549–2568 (DOI: 10.1002/nme.429)

9. Gravouil, A., Moës, N., Belytschko, T. Non-planar 3D crack growth by the extended finite element and level sets—Part II: Level set update. Int. J. Numer. Meth. Engng. V. 53, 2002. pp. 2569–2586. DOI: 10.1002/nme.430.

10. Osher, S. J., Fedkiw, R.P. Level Set Methods and Dynamic Implicit Surfaces. Springer-Verlag. ISBN 0-387-95482-1. 2002.

11. Sethian, J. A. Level Set Methods and Fast Marching Methods : Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science. Cambridge University Press. ISBN 0-521-64557-3. 1999.

12. Ventura G., Budyn, E., Belytschko T. Vector level sets for description of propagating cracks in finite elements. Int. J. Numer. Meth. Engng 2003; 58:1571–1592 (DOI: 10.1002/nme.829).

13. März T., Macdonald C.B. Calculus on surfaces with general closest point functions. SIAM J. Numer. Anal., Vol. 50, No. 6, pp. 3303–3328.

14. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия: методы и приложения, Наука, 1986. 760 С.

15. Berger M., Tagliasacchi A., Seversky L., Alliez, P., Levine, J., Sharf, A., Silva, C. State of the Art in Surface Reconstruction from Point Clouds. EUROGRAPHICS 2014 / S. Lefebvre and M. Spagnuolo. STAR –– State of The Art Report, 2014.

SIMULATION AND VISUALIZATION OF THE DYNAMICS OF A SURFACE WITH A MOVABLE BOUNDARY ON A STATIONARY UNSTRUCTURED MESH

A.V. Ivanov, E.B. Savenkov

Keldysh Institute of Applied Mathematics, Russian Academy of Sciences

aivanov@keldysh.ru, e.savenkov@gmail.com

Abstract

The paper deals with the problems concerning the representation and description of the dynamics of a smooth surface with a boundary at a given velocity field. An implicit representation of the surface is used with the help of the "closest point" method based on specifying a surface as a set of projections of points of space from some neighborhood of the surface onto the surface itself. Non-structured three-dimensional meshes that are not adapted to the surface geometry are used for the mesh representation of the domain containing the surface and for approximating the projection operator.

The problems of simulation of a surface during its motion in a given velocity field, computation the surface local bases at its interior points and at the boundary, and integration and differentiation of the functions defined on the surface are considered. A detailed description of the corresponding algorithms and the results of their testing are presented. The software used to visualize the calculation data is briefly described. The method of representation of data of modeling considered in this work not only makes it possible to use it effectively in computational algorithms, but it is also convenient for visual representation, which enables to understand better the dynamics of the process of crack development.

Keywords: surface evolution, the closest point method, unstructured meshes.

References

1. Ekonomides M., Olini R., and Val’ko P. Unifitsirovannyi dizain gidrorazryva plasta. Ot teorii k practike [Unified Design of Hydraulic Fracturing. From Theory to Practice]. Institute of Computer Science, 2007, p.236.

2. Salimov V.G., Ibragimov N.G., Nasybullin A.V., and Salimov O.V. Gidravlicheskii razryv karbonatnyh plastov [Hydraulic Fracturing of Carbonaceous Formations]. Neftyanoe Hozyaistvo, 2013, p. 471.