SIMULATION AND VISUALIZATION OF THE DYNAMICS OF A SURFACE WITH A MOVABLE BOUNDARY ON A STATIONARY UNSTRUCTURED MESH
A.V. Ivanov, E.B. Savenkov
Keldysh Institute of Applied Mathematics, Russian Academy of Sciences
aivanov@keldysh.ru, e.savenkov@gmail.com
Contents
4. Discrete Model of the Surface
5. Algorithm for Calculating the Surface Evolution
6. Integration over the Surface
7. Calculation of Local Bases on a Surface and its Boundary
8.1. Disc in the uniform velocity field
8.2. Disk in the vortex velocity field
Abstract
The paper deals with the problems concerning the representation and description of the dynamics of a smooth surface with a boundary at a given velocity field. An implicit representation of the surface is used with the help of the "closest point" method based on specifying a surface as a set of projections of points of space from some neighborhood of the surface onto the surface itself. Non-structured three-dimensional meshes that are not adapted to the surface geometry are used for the mesh representation of the domain containing the surface and for approximating the projection operator.
The problems of simulation of a surface during its motion in a given velocity field, computation the surface local bases at its interior points and at the boundary, and integration and differentiation of the functions defined on the surface are considered. A detailed description of the corresponding algorithms and the results of their testing are presented. The software used to visualize the calculation data is briefly described. The method of representation of data of modeling considered in this work not only makes it possible to use it effectively in computational algorithms, but it is also convenient for visual representation, which enables to understand better the dynamics of the process of crack development.
Keywords: surface evolution, the closest point method, unstructured meshes.
1. Introduction
The necessity of modelling of the dynamics of the surface with a boundary in a given velocity field arises in various problems of mathematical modelling and the computer graphics. The results of this study have been obtained in the course of developing the complex of computational algorithms for the problem of simulatio the dynamics of a large-scale hydraulic fracture of a oil ot gas reservoir.
The hydraulic fracturing is one of the most commonly used methods increasing oil recovery applied in the development of oil and gas fields. The essence of the fracturing technology consists in pumping a special liquid nto the oil reservoir to create an artificial crack with a length of ~100 m, height of ~10 m, and an average opening of ~5--10 mm. As a result, an artificial channel is created that is connected with a well and has a large inflow area and a high permeability (by orders of magnitude greater than the one of the oil reservoir). This provides a significant increase in the inflow of the formation fluid to the well. Engineering aspects of the technology are considered, for example, in [1, 2].
Physical and mathematical description of the crack dynamics in the course of its development in hydraulic fracturing consists in solving a complex interrelated problem including the following equation systems:
· a system of poroelasticity equations describing the evolution of stress-strain state of the formation and the fluid pressure fields in it during the development of the crack;
· equations of fluid flow in the crack;
· mechanical conditions for the development of the crack determining the direction of its development at each point of its front;
· dynamic interface conditions between the pressure field in the crack and in the formation defined on the lateral surfaces of the crack as well as kinematic conditions connecting the crack opening and the diaplacement of the formation.
In such a description, the geometrical model of the crack is a smooth surface with a movable boundary. The development of effective and reliable numerical methods for solving this problems includes the creation of a method for representing the median surface of the crack in a discrete problem taking into account the following:
· the change in the geometry of the median surface of the crack during its evolution is a priori unknown and is determined successively in the course of solving the complete interrelated problem;
· on the median surface of the crack, the equation of the lubricating layer describing the fluid flow in the crack and, indirectly, the crack evolution dynamics is solved;
· the complete problem is conjugate, so it is necessary to have a representation of the geometry of the crack which would make it possible to transfer the information about the fields given at the crack to a three-dimensional region.
To describe the geometry of a surface with a moving boundary, many approaches are known, including polygonal models, a parametric representation, a point cloud representation, an implicit representation through a level set approach, etc. All of them are quite efficient in the case when the final task consists only in describing the dynamics of the change in the geometry of the surface, like in a number of computer graphics problems. However, not all of them can be used to solve the above formulated problem of hydraulic fracturing simulation.
Among the known methods, the closest-point projection method was chosen as the most preferable. The motivation of this choice is primarily that there are known and well developed methods for solving differential equations on surfaces within the framework of this approach (see [3, 4, 5, 6]), and the surface representation method itself is well adapted for using it in conjunction with the X-FEM method to calculate the stress-strain state of the medium in the vicinity of the crack.
However, most of the works devoted to this method are associated with its application to the analysis of stationary surfaces or dynamic surfaces, but without a boundary. In this paper we propose an effective method for calculating the evolution of surfaces with a moving boundary; we consider the problems of representation, integration, and differentiation of functions defined on this surface, as well as the methods for calculating its local geometric properties, in particular, the construction of orthogonal bases at interior and boundary points of the surface.
It should be also noted that in most works on modeling the development of cracks with the help of the extended finite element method [7, 8, 9], the geometrical model of the crack is constructed using the level set method (see [10, 11]). Then, the surface with the boundary is given by a pair of scalar functions φ (x, t), ψ (x, t) defined in space such that
![]() (1)
(1)
where t is time.
In other words, at a fixed time t, the surface is defined as
a part of the level surface of the zero function ![]() bounded
by the isosurface of the function
bounded
by the isosurface of the function ![]() . To
carry out the calculations, it is convenient for the functions
. To
carry out the calculations, it is convenient for the functions ![]() ,
, ![]() to be the sign
distances defined in some small neighborhood Ω of the surface F. The
motion of the boundary of the surface is given by the velocity field
to be the sign
distances defined in some small neighborhood Ω of the surface F. The
motion of the boundary of the surface is given by the velocity field ![]() describing the evolution of the functions
describing the evolution of the functions ![]() ,
, ![]() . For the
recalculation of the functions
. For the
recalculation of the functions ![]() ,
, ![]() , the
equations of Hamilton-Jacobi type are applied. The main disadvantage of this
method is the complexity of its implementation: for example, to describe the
evolution of a surface, an agreed solution of ten different Hamilton-Jacobi
equations is required with respect to the functions
, the
equations of Hamilton-Jacobi type are applied. The main disadvantage of this
method is the complexity of its implementation: for example, to describe the
evolution of a surface, an agreed solution of ten different Hamilton-Jacobi
equations is required with respect to the functions ![]() and
and ![]() , ensuring, among
other things, the orthogonality of their gradients, the properties of sign
distances, etc. [7, 8, 9].
, ensuring, among
other things, the orthogonality of their gradients, the properties of sign
distances, etc. [7, 8, 9].
An alternative approach, somewhat similar to that used in this work, is described in [12]. The surface in this approach is defined by means of so-called "vector level sets", representing a pair of functions, the first of which is the operator projecting a point onto the surface in the sense of the nearest distance, and the second one determines the orientation of the surface. At the same time, the described approach uses a polygonal representation of the surface which is used for constructing the projection operators. During the evolution of the surface, its polygonal representation is updated first, and then, it is used to construct the projection operators and level functions.
In contrast to this approach, the present paper does not use the polygonal representation of the surface, and the values of projection operators in the course of its evolution are calculated directly. In this case, the surface itself and the level surfaces defining it can be reconstructed locally, if necessary. In this sense, the approach proposed in this paper and based on the closest- point projection method (CPPM) is more flexible and, in effect, it is close to the methods of representing surfaces as "point cloud surfaces" (see, for example, [ 15]).
Despite the fact that the algorithms presented in the paper were developed for solving a specific applied problem, they are universal and can be used to solve a wide range of problems related to the calculation and visualization of the dynamics of surfaces with a boundary.
In order to visualize the simulation results, the computer code FrontView developed at KIAM RAS is used in the work. Its main purpose is. "fast" visualization of large-volume data set on dynamic surfaces, which are described by unstructured triangular meshes.
The above described applied problem of evolution of the formation crack requires considering a complex coupled three-dimensional system of partial differential equations. The unknown fields are three-dimensional or two-dimensional, defined on the median surface of the fracture. The solution of the problem is also the evolution of the fracture itself, which is described as a smooth surface with a boundary in the considered problem statement. In general, the distribution of the properties of the medium containing the crack is three-dimensional. Therefore, a complete qualitative and quantitative analysis of the results of modeling is impossible without effective means of visualization. A set of existing means for visualization and analysis of modeling results, which would be suitable without additional adaptation to analysing the evolution of surfaces with a boundary is limited. For this reason, the approaches considered in this paper for describing the evolution of a surface with a boundary are of interest in itself in the context of problems of representation and visualization of modeling data.
2. CPP Method
Let us consider the basic concepts of the closest point method. A rigorous mathematical justification of this method is given in [13].
Let us consider a smooth surface ![]() with a
boundary embedded in the three-dimensional space
with a
boundary embedded in the three-dimensional space ![]() . Here
and in what follows, the term "smooth" will mean that the set
. Here
and in what follows, the term "smooth" will mean that the set ![]() is an
image of a smooth mapping of a bounded closed subdomain of the two-dimensional
plane
is an
image of a smooth mapping of a bounded closed subdomain of the two-dimensional
plane ![]() into
the three-dimensional space
into
the three-dimensional space ![]() . We
will assume that the used mappings have any required number of derivatives. We
also assume that the surface F is entirely located inside the spatial domain
. We
will assume that the used mappings have any required number of derivatives. We
also assume that the surface F is entirely located inside the spatial domain ![]() .
.
Let us suppose that for an arbitrary ![]() ,
, ![]() is the
closest point to it on the surface
is the
closest point to it on the surface ![]() :
:
![]()
Here and below, the Euclidean norms are used.
The point ![]() will
be called the projection of the point
will
be called the projection of the point ![]() onto
the surface
onto
the surface ![]() in
the sense of the shortest distance; the corresponding projection operator will
be denoted by
in
the sense of the shortest distance; the corresponding projection operator will
be denoted by ![]() ,
,
![]()
The operator ![]() is
vector-valued; it maps the domain
is
vector-valued; it maps the domain ![]() onto
the surface
onto
the surface ![]() considered
as a subset of
considered
as a subset of ![]() . In
the case that the surface and its boundary are smooth and the domain
. In
the case that the surface and its boundary are smooth and the domain ![]() is
"sufficiently small", the operator
is
"sufficiently small", the operator ![]() is
uniquely defined, i.e., each point of
is
uniquely defined, i.e., each point of ![]() is
uniquely projected onto a single point on the surface.
is
uniquely projected onto a single point on the surface.
If for the surface ![]() we
can define the signed distance function
we
can define the signed distance function ![]() (i.e.,
(i.e.,
![]() is an
oriented surface without a boundary), then for the operator
is an
oriented surface without a boundary), then for the operator ![]() the
following representation holds:
the
following representation holds:
![]()
It can be shown that the projections operator ![]() uniquely
describes the surface
uniquely
describes the surface ![]() as a
set of its fixed points:
as a
set of its fixed points:
![]()
It should be noted that this method of description is quite general. It allows one to describe the geometry of a surface with a boundary and without a boundary, nonorientable manifolds or manifolds of codimension greater than one (i.e., curves (codimension is equal to 2) and points (codimension is equal to 3), and also the union of objects of different codimension.
Further, it will be necessary to distinguish the points of ![]() that
are projected into the interior points of
that
are projected into the interior points of ![]() or
onto its boundary
or
onto its boundary ![]() . With
this purpose, let us consider the auxiliary operator
. With
this purpose, let us consider the auxiliary operator ![]() which
we define as [4]:
which
we define as [4]:
![]() (2)
(2)
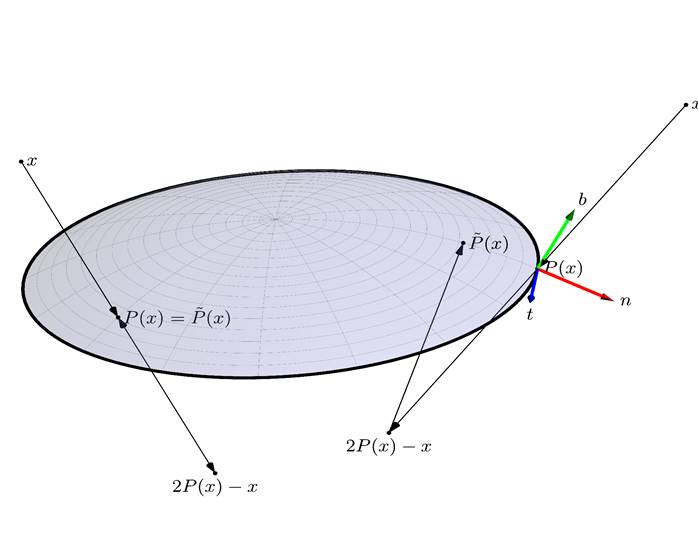
Fig. 1. Definition of operators ![]() and
and ![]() .
.
It follows from the geometrical consideration (see Fig. 1)
that for the points ![]() whose
projections belong to the boundary of the surface,
whose
projections belong to the boundary of the surface,
![]() (3)
(3)
while for the points whose projections belong to the
interior points of ![]() , the
values of the projectors
, the
values of the projectors ![]() and
and ![]() coincide:
coincide:
![]() (4)
(4)
Together with the above presented method of describing the
surface ![]() , we
will need a way of representation of the functions defined on this surface. Due
to the fact that there are no local coordinates on the surface
, we
will need a way of representation of the functions defined on this surface. Due
to the fact that there are no local coordinates on the surface ![]() , it
is convenient to use the "implicit" way of their representation.
Namely, a function on the surface will be defined as a trace on it of a
function defined in the domain
, it
is convenient to use the "implicit" way of their representation.
Namely, a function on the surface will be defined as a trace on it of a
function defined in the domain ![]() .
.
The extension of the function given on the surface to the
domain ![]() can
be constructed in various ways. A convenient and subsequently used method is
its extension with the help of the operator
can
be constructed in various ways. A convenient and subsequently used method is
its extension with the help of the operator ![]() .
Namely, for an arbitrary function u given on the surface, its continuation
.
Namely, for an arbitrary function u given on the surface, its continuation ![]() in
in ![]() is
defined as:
is
defined as:
![]()
Thus, the constructed continuation is constant along the
segments connecting a point of ![]() and
its projection. This fact allows us to calculate the derivatives of a function
on the surface in a convenient way, as well as differential operators of higher
order (see below in this section).
and
its projection. This fact allows us to calculate the derivatives of a function
on the surface in a convenient way, as well as differential operators of higher
order (see below in this section).
It should be noted that for an arbitrary function ![]() in
in ![]() that
is constant in the direction of the normal to
that
is constant in the direction of the normal to ![]() , we
have [13]:
, we
have [13]:
![]()
where ![]() is
the surface gradient (see [14]). Similarly, for an arbitrary smooth vector
field
is
the surface gradient (see [14]). Similarly, for an arbitrary smooth vector
field ![]() in
in ![]() tangent
to the surface
tangent
to the surface ![]() :
:
![]()
Then, by virtue of the properties of the projector ![]() and
the extension operator
and
the extension operator ![]() , we
have:
, we
have:
![]()
Since the completion of ![]() is
constant along directions normal to the surface, the vector field
is
constant along directions normal to the surface, the vector field ![]() is
tangent to
is
tangent to ![]() . This
implies that
. This
implies that
![]()
where ![]() is
the Beltrami-Laplace operator (the "surface" Laplace operator, [14]).
Analogous extensions can also be constructed for more complicated elliptic
operators of divergent type, see [3, 13].
is
the Beltrami-Laplace operator (the "surface" Laplace operator, [14]).
Analogous extensions can also be constructed for more complicated elliptic
operators of divergent type, see [3, 13].
3. Model of Surface Evolution
Above, we outlined the basic ideas of the closest point method with respect to a stationary surface. Let us formulate the problem of the surface evolution.
Let us designate time by t; the surface under
consideration at time t by ![]() . We
assume that for
. We
assume that for![]() , the
condition
, the
condition ![]() is
satisfied. In other words, the family of surfaces corresponding to greater
moments of time is contained within the surface corresponding to any greater
moment of time. Or, which is the same, the surface can evolve only by moving
its boundary. This situation corresponds to the specifics of the problem being
solved, namely, the development of the median surface of the crack during the
growth of the latter.
is
satisfied. In other words, the family of surfaces corresponding to greater
moments of time is contained within the surface corresponding to any greater
moment of time. Or, which is the same, the surface can evolve only by moving
its boundary. This situation corresponds to the specifics of the problem being
solved, namely, the development of the median surface of the crack during the
growth of the latter.
We will assume that:
• at each moment t within the interval under
consideration, the surface ![]() is
entirely contained inside the domain
is
entirely contained inside the domain ![]() ;
;
• the evolution of the surface ![]() is
"smooth", i.e, the surface at each moment of time can be smoothly and
mutually unambiguously mapped onto, for example, a disc of unit radius in
is
"smooth", i.e, the surface at each moment of time can be smoothly and
mutually unambiguously mapped onto, for example, a disc of unit radius in ![]() . In
particular, in the course of evolution, self-intersections should not appear in
. In
particular, in the course of evolution, self-intersections should not appear in
![]() , etc.
, etc.
In this case, the family of surfaces ![]() can
be represented as a union of the initial surface
can
be represented as a union of the initial surface ![]() and
the trace of the "motion" of its curvilinear boundary:
and
the trace of the "motion" of its curvilinear boundary:
![]()
where ![]() is the
movable boundary of the surface
is the
movable boundary of the surface ![]() at
time
at
time ![]() .
.
In what follows, we assume that a vector velocity ![]() ,
, ![]() is
defined on the line
is
defined on the line ![]() describing
its evolution at each moment of time. Thus, the motion of a point of the
boundary is described by equation
describing
its evolution at each moment of time. Thus, the motion of a point of the
boundary is described by equation
![]() (5)
(5)
We assume that the velocity field ![]() is a
smooth function of the point
is a
smooth function of the point ![]() at
each fixed time t and for each fixed (Lagrangian) point of the boundary is a
smooth function of time.
at
each fixed time t and for each fixed (Lagrangian) point of the boundary is a
smooth function of time.
At each moment of time, we will describe the surface ![]() with
the help of the projection operator of the closest point. The construction of
an algorithm for computing this operator (more precisely, its approximations)
at each moment of time with its known value at the previous moments of time and
a given velocity
with
the help of the projection operator of the closest point. The construction of
an algorithm for computing this operator (more precisely, its approximations)
at each moment of time with its known value at the previous moments of time and
a given velocity ![]() will
be considered below.
will
be considered below.
4. Discrete Model of the Surface
Suppose that in a domain ![]() containing
a surface
containing
a surface ![]() , a
computational mesh composed of tetrahedral cells is defined. The resulting
triangulation will be considered regular (i.e., the intersection of two
different tetrahedra can be an empty set, a mesh node, its boundary, or its
face). We denote the corresponding discrete domain by
, a
computational mesh composed of tetrahedral cells is defined. The resulting
triangulation will be considered regular (i.e., the intersection of two
different tetrahedra can be an empty set, a mesh node, its boundary, or its
face). We denote the corresponding discrete domain by ![]() . It
is assumed that the mesh is sufficiently fine so that the characteristic mesh
step
. It
is assumed that the mesh is sufficiently fine so that the characteristic mesh
step ![]() is much smaller than the radii of the
principal curvatures of the surface and the radius of the curvature of its
boundary.
is much smaller than the radii of the
principal curvatures of the surface and the radius of the curvature of its
boundary.
Let us denote the set of mesh nodes by ![]() ,
, ![]() , and
, and ![]() is the number of mesh
nodes. We assign a basic function
is the number of mesh
nodes. We assign a basic function ![]() to
each node of the mesh. In the simplest case, continuous piecewise-linear basis
functions can be used for which
to
each node of the mesh. In the simplest case, continuous piecewise-linear basis
functions can be used for which ![]() ,
where
,
where ![]() is
the Kronecker symbol, and the cells of the mesh
is
the Kronecker symbol, and the cells of the mesh ![]() are
continued linearly.
are
continued linearly.
In the discrete case, the projection operator ![]() is
given by its values
is
given by its values ![]() at
the mesh nodes. To calculate the projection operator
at
the mesh nodes. To calculate the projection operator ![]() at an
arbitrary point in the domain, the above introduced system of basis functions
is used. If
at an
arbitrary point in the domain, the above introduced system of basis functions
is used. If ![]() is an
arbitrary point of the domain
is an
arbitrary point of the domain ![]() ,
, ![]() is the tetrahedron in
which it is located,
is the tetrahedron in
which it is located, ![]() is
its barycentric coordinates with respect to the vertices of the tetrahedron
is
its barycentric coordinates with respect to the vertices of the tetrahedron ![]() , then the projection
of the point
, then the projection
of the point ![]() is the
point
is the
point
![]()
The constructed approximations of the projector ![]() allow
us to construct in a natural way the approximations of the projection
allow
us to construct in a natural way the approximations of the projection ![]() in accordance
with (2).
in accordance
with (2).
Now, let ![]() be the
set of all nodes of the mesh. Define its subsets
be the
set of all nodes of the mesh. Define its subsets ![]() ,
, ![]() ,
, ![]() ,
corresponding to the nodes projected into the interior points of the surface
and its boundary, respectively:
,
corresponding to the nodes projected into the interior points of the surface
and its boundary, respectively:
![]() (6)
(6)
where ![]() is a
small real parameter of the algorithm
is a
small real parameter of the algorithm
Obviously, in the course of the surface evolution, the set ![]() can
only increase (by inclusion). In other words, for
can
only increase (by inclusion). In other words, for ![]() we
have:
we
have:
![]()
This allows, in particular, as the surface moves, to update
information at each next time step of the discrete sampling only for the nodes
from the set ![]() .
.
5. Algorithm for Calculating the Surface Evolution
In this section, we consider the algorithm for recalculating
the discrete sampling of the projector ![]() in
the course of the surface evolution.
in
the course of the surface evolution.
The general idea of the algorithm is as follows: first,
according to the known information, the coordinates of the projection points of
the mesh nodes from the set ![]() are
calculated. Then, these points are shifted in a given direction in accordance
with a given boundary speed and a given time step value. The resulting points
belong to the new position of the front, but the vector connecting the original
node of the spatial mesh and the new position of the boundary point is not the
projection vector of the closest point. Therefore, the approximations of the
projector are corrected.
are
calculated. Then, these points are shifted in a given direction in accordance
with a given boundary speed and a given time step value. The resulting points
belong to the new position of the front, but the vector connecting the original
node of the spatial mesh and the new position of the boundary point is not the
projection vector of the closest point. Therefore, the approximations of the
projector are corrected.
Then, we will assume that the surface evolves on the time
interval ![]() . We
introduce on this interval a computational mesh with steps
. We
introduce on this interval a computational mesh with steps ![]() ,
, ![]() ,
,
![]()
where ![]() is
the number of mesh nodes.
is
the number of mesh nodes.
At the initial time ![]() , the
approximation of the projector
, the
approximation of the projector ![]() is
assumed to be known. We also assume that during the time interval
is
assumed to be known. We also assume that during the time interval ![]() , the
surface remains inside the mesh domain
, the
surface remains inside the mesh domain ![]() .
.
The complete algorithm for constructing the discrete
operator ![]() at
time
at
time ![]() for
given parameters of the method and the known approximation
for
given parameters of the method and the known approximation ![]() is
presented in the scheme of Algorithm 1.
is
presented in the scheme of Algorithm 1.
The input data of the algorithm are the discrete sampling ![]() of
the projector at a time
of
the projector at a time ![]() and
the sets
and
the sets ![]() and
and ![]() . As a
result of application of the algorithm, the values of input data are replaced
by the corresponding values of output data at time
. As a
result of application of the algorithm, the values of input data are replaced
by the corresponding values of output data at time ![]() .
.
The parameters of the method are the values ![]() ,
, ![]() , and
, and ![]() . The
parameter
. The
parameter ![]() determines
the conditionality of the projection of a point on the segment and the accuracy
of the projection computation,
determines
the conditionality of the projection of a point on the segment and the accuracy
of the projection computation,
![]()
where ![]() determines
the radius of the sphere bounding the region in which the points are searched
for in step 6 of algorithm 1. It is assumed that
determines
the radius of the sphere bounding the region in which the points are searched
for in step 6 of algorithm 1. It is assumed that ![]() is
sufficiently large as compared with the mesh spacing, but does not exceed the
maximum distance from the point to its projection onto the boundary,
is
sufficiently large as compared with the mesh spacing, but does not exceed the
maximum distance from the point to its projection onto the boundary,
![]()
In the general case, it suffices to put ![]() . The
parameter
. The
parameter ![]() defines
the threshold value that is used to determine whether the projection belongs to
the boundary of the surface or to the set of its interior points. When
calculating the value of
defines
the threshold value that is used to determine whether the projection belongs to
the boundary of the surface or to the set of its interior points. When
calculating the value of ![]() (see
step 5 of the algorithm), the same value of the parameter
(see
step 5 of the algorithm), the same value of the parameter ![]() as that in (6) should
be used.
as that in (6) should
be used.
|
1. |
Input Data: Discrete
representation of the surface at time |
|||
|
2. |
Set |
|||
|
3. |
Calculate the new positions of all projections onto the boundary in accordance with approximation (5):
|
|||
|
4. |
Forall |
|||
|
5. |
|
Determine the closest to
|
||
|
6. |
|
Define (sub)set
|
||
|
7. |
|
if |
||
|
8. |
|
Set |
||
|
9. |
|
else // Point |
||
|
10. |
|
Find such a point among the points in
|
||
|
11. |
|
Set |
||
|
12. |
|
end if |
||
|
|
|
// Determine the projection of the
point |
||
|
13. |
|
Set |
||
|
14. |
|
if |
||
|
15. |
|
Set |
||
|
16. |
|
else if |
||
|
17. |
|
Set |
||
|
18. |
|
else if |
||
|
19. |
|
Set |
||
|
20. |
|
end if |
||
|
21. |
end forall |
|||
|
22. |
Output data: a discrete
representation of the surface at |
|||
|
|
|
|
||
|
Algorithm 1. Calculation of the evolution of the projector |
||||
6. Integration over the Surface
Let us consider the problem of integrating functions on the surfaces given by the "closest point" projector. Specifically, we will deal with the calculation of integrals of the form:
![]()
or, in a particular case, with the calculation of the area of the surface under consideration with a boundary:
![]()
Let us consider the discrete case. We assume, like it was
made above, that the surface is located inside some mesh domain ![]() . Let
. Let ![]() be
its boundary formed by the union of triangular faces
be
its boundary formed by the union of triangular faces ![]() :
:
![]()
where ![]() is the
number of faces. With a known partition of the domain
is the
number of faces. With a known partition of the domain ![]() , the
set of faces
, the
set of faces ![]() can
be easily defined as the set of faces incident to one and only one tetrahedron
of the triangulation.
can
be easily defined as the set of faces incident to one and only one tetrahedron
of the triangulation.
Let us represent ![]() in
the form of a union of three pairwise disjoint sets:
in
the form of a union of three pairwise disjoint sets:
![]()
where ![]() consists
of faces, all nodes of which are projected onto the front (i.e., they are
elements of the set
consists
of faces, all nodes of which are projected onto the front (i.e., they are
elements of the set ![]() );
); ![]() and
and ![]() are
the sets of other faces; all the faces of the sets
are
the sets of other faces; all the faces of the sets ![]() and
and ![]() lie
on the same side of the surface.
lie
on the same side of the surface.
We note that:
• all nodes of the faces from ![]() are
projected onto the boundary of the surface. The areas of triangles whose
vertices are the projections of the vertices of triangles from
are
projected onto the boundary of the surface. The areas of triangles whose
vertices are the projections of the vertices of triangles from ![]() are
negligible when the mesh spacing
are
negligible when the mesh spacing ![]() tends
to zero;
tends
to zero;
• the projection operator (both continuous and discrete)
bounded on the set ![]() is a
surjection (mapping "onto") onto the surface
is a
surjection (mapping "onto") onto the surface ![]() ;
;
• In the case when a straight line passing through an
arbitrary point on the surface and oriented by a unit normal to it intersects
the boundaries of the set ![]() one
at a time, then triangular meshes defined on
one
at a time, then triangular meshes defined on ![]() generate
triangular meshes on the surface
generate
triangular meshes on the surface ![]() . The
nodes of these meshes are formed by the projections Vertices of triangles from
. The
nodes of these meshes are formed by the projections Vertices of triangles from ![]() ,
while two nodes of this mesh are considered to be connected by a boundary if
the corresponding nodes in
,
while two nodes of this mesh are considered to be connected by a boundary if
the corresponding nodes in ![]() are
connected to it.
are
connected to it.
To calculate the integrals of the functions defined on the surface, we will, in fact, use these meshes; in order to calculate the approximate value of the integral over a single triangle we will use the single-point quadrature formula.
In this case, there is no need to represent explicitly in
the algorithm the described above meshes on the surface ![]() ,
since summation over triangles of such a mesh can be carried out in a cycle
over all triangles forming the set
,
since summation over triangles of such a mesh can be carried out in a cycle
over all triangles forming the set ![]() . The
contribution from the triangles belonging to the set
. The
contribution from the triangles belonging to the set ![]() will
be vanishingly small at
will
be vanishingly small at ![]() ,
while the contribution from the surfaces
,
while the contribution from the surfaces ![]() will
be (asymptotically) doubled.
will
be (asymptotically) doubled.
Next, if a straight line passing through an arbitrary point
on the surface and oriented by the unit normal to it intersects the boundaries
of the set ![]() more
than once, the projections of the meshes
more
than once, the projections of the meshes ![]() will
no longer form a correct mesh on
will
no longer form a correct mesh on ![]() ,
since the projections of the individual triangles can have a non-empty
intersection. In this case, the above presented calculation scheme must be
corrected. Namely, it is necessary to take into account the mutual orientation
of the outer normal to the face and the directions of the projection, for
example, of its center.
,
since the projections of the individual triangles can have a non-empty
intersection. In this case, the above presented calculation scheme must be
corrected. Namely, it is necessary to take into account the mutual orientation
of the outer normal to the face and the directions of the projection, for
example, of its center.
Thus, let us consider some face (triangle) ![]() ,
formed by mesh nodes
,
formed by mesh nodes ![]() ,
, ![]() , and
, and ![]() .
Correspondingly, the fourth node of the tetrahedron will be denoted by
.
Correspondingly, the fourth node of the tetrahedron will be denoted by ![]() . Then
the normal to the face is given by the following expression:
. Then
the normal to the face is given by the following expression:
![]()
where the sign «![]() »
denotes the vector product in
»
denotes the vector product in ![]() . The
direction of the normal can be determined from the mutual orientation of the
calculated normal and the vector connecting the center of the face and its
projection. Namely, the normal vector
. The
direction of the normal can be determined from the mutual orientation of the
calculated normal and the vector connecting the center of the face and its
projection. Namely, the normal vector ![]() will
be the outer normal vector if
will
be the outer normal vector if
![]()
In what follows, we will consider that this condition is satisfied.
Therefore, we come to the following expression for computing the surface integral:
![]()
where ![]() is
some extension of the function g from the surface to the domain
is
some extension of the function g from the surface to the domain ![]() . If
. If ![]() , then
we have:
, then
we have:
![]()
and the expression for the approximate calculation of the integral is simplified.
The factor «2» before the integral arises from the fact that
the integral is calculated twice by traversing triangles from ![]() and
from
and
from ![]() .
.
7. Calculation of Local Bases on a Surface and its Boundary
In the context of the considered applied problem, namely, the problem of modeling the evolution of a large-scale crack of hydraulic fracturing, it becomes necessary to calculate local vector bases at the boundary and on the surface and its neighborhood. In particular, this is required when using the extended finite element method (X-FEM) to calculate the stress-strain state in the host medium. This section considers this and allied problems.
Let us introduce another projection operator ![]() ,
which is a projection operator in the sense of the shortest distance to the
boundary of the surface:
,
which is a projection operator in the sense of the shortest distance to the
boundary of the surface:
![]()
The operator ![]() is
well-defined (in the sense of the uniqueness of the projection) in some sufficiently
small neighborhood of the boundary
is
well-defined (in the sense of the uniqueness of the projection) in some sufficiently
small neighborhood of the boundary ![]() of
the surface
of
the surface ![]() . We
denote the corresponding neighborhood by
. We
denote the corresponding neighborhood by ![]() .
.
We assume that (a) ![]() and
(b) the domain
and
(b) the domain ![]() contains
all the points of
contains
all the points of ![]() that
are projected onto the boundary of the surface in the sense of criteria (3) and
(4). Next, let
that
are projected onto the boundary of the surface in the sense of criteria (3) and
(4). Next, let ![]() be
the subdomain of
be
the subdomain of ![]() and
and ![]() domains
consisting of the points that are projected onto the boundary of the surface
(see Fig. 2).
domains
consisting of the points that are projected onto the boundary of the surface
(see Fig. 2).
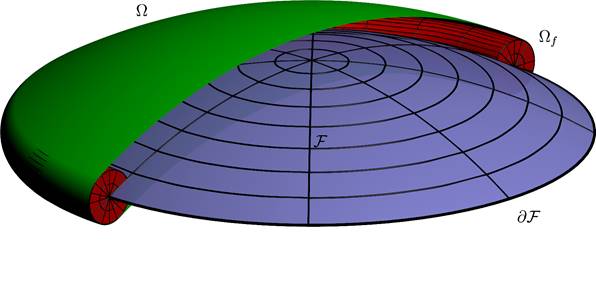
Fig. 2: Domains ![]() ,
, ![]() , and
, and ![]()
It follows from this that:
• In the subdomain ![]() all
three operators
all
three operators ![]() ,
, ![]() and
and ![]() are
defined;
are
defined;
• The images of the operators ![]() and
and ![]() acting
on the domain
acting
on the domain ![]() coincide
with each other and with the set of points of the boundary
coincide
with each other and with the set of points of the boundary ![]() of
the surface.
of
the surface.
If we denote the set of points of the set ![]() projected
onto the boundary of the surface
projected
onto the boundary of the surface ![]() , then
the set
, then
the set ![]() can
be chosen in the form:
can
be chosen in the form:
![]()
i.e, this set is obtained by "mirror" reflection
of the set ![]() with
respect to the surface boundary. The same algorithm can also be used to
construct the domain
with
respect to the surface boundary. The same algorithm can also be used to
construct the domain ![]() in the
discrete problem statement.
in the
discrete problem statement.
Let us consider the problem of constructing the local bases on the surface and its boundary.
At all points of the projections ![]() of
the mesh nodes from the set
of
the mesh nodes from the set ![]() , the
vector of the unit normal to the surface can be defined as:
, the
vector of the unit normal to the surface can be defined as:
![]() . (7)
. (7)
The directions of the vectors ![]() for
all the nodes of the mesh lying "on the same side" from the surface
for
all the nodes of the mesh lying "on the same side" from the surface ![]() coincide
with each other. In the case when the surface is "slightly curved",
i.e., its radius of curvature is considerably larger than the diameter of the
surface itself, the orientation of the surface can be uniquely determined by
the choice (not depending on the point of the surface and the domain
coincide
with each other. In the case when the surface is "slightly curved",
i.e., its radius of curvature is considerably larger than the diameter of the
surface itself, the orientation of the surface can be uniquely determined by
the choice (not depending on the point of the surface and the domain ![]() ) of
the vector
) of
the vector ![]() . In
this case, for the mesh node
. In
this case, for the mesh node ![]() ,
, ![]() , the
position of the node and the normal orientation
, the
position of the node and the normal orientation ![]() can
be determined by computing the sign of the scalar product
can
be determined by computing the sign of the scalar product ![]() .
.
Thefore, at all nodes of the set ![]() , the
value of the approximation of the function
, the
value of the approximation of the function ![]() of the
sign distance to the surface can be restored:
of the
sign distance to the surface can be restored:
![]()
At an arbitrary point of the domain projected onto the
surface (but not at its boundary), the vector of the unit normal at the
projection point and the value of the sign-distance function can be restored by
interpolation. If ![]() are
the barycentric coordinates of the point
are
the barycentric coordinates of the point ![]() with
respect to the tetrahedron in which it is located, then we have:
with
respect to the tetrahedron in which it is located, then we have:
![]()
where ![]() are
defined according to (7). Let us consider similar questions for the points
whose projection lies at the boundary
are
defined according to (7). Let us consider similar questions for the points
whose projection lies at the boundary ![]() of
the surface.
of
the surface.
Let ![]() be a
vector at the point of the boundary of the surface that is normal to its
boundary and lies on the tangent plane of the surface. For an arbitrary point
be a
vector at the point of the boundary of the surface that is normal to its
boundary and lies on the tangent plane of the surface. For an arbitrary point ![]() of the
domain
of the
domain ![]() (the
"tubular" neighborhood of the surface boundary), we define the
approximation of the vector n at the projection point
(the
"tubular" neighborhood of the surface boundary), we define the
approximation of the vector n at the projection point ![]() as:
as:
![]()
It is obviously that this vector approximates the exact
value of the normal vector ![]() with
an accuracy
with
an accuracy ![]() . If
the "diameter" of the tubular domain
. If
the "diameter" of the tubular domain ![]() decreases
linearly with computational mesh convergence (for example, the
"diameter" of the domain is limited by a fixed number of elements of
the mesh, then
decreases
linearly with computational mesh convergence (for example, the
"diameter" of the domain is limited by a fixed number of elements of
the mesh, then
![]()
The approximation of the vector ![]() tangent
to the boundary of the surface at the point
tangent
to the boundary of the surface at the point ![]() can
be calculated as:
can
be calculated as:
![]()
Finally, the vector ![]() ,
which is the normal to both the surface and its boundary, can be defined as:
,
which is the normal to both the surface and its boundary, can be defined as:
![]()
The constructions presented above are illustrated in Fig. 1.
Thus, at each projection point, a local orthogonal basis of
vectors can be constructed. The orientation of this basis can be determined if
we know a "global" vector ![]() which
specifies the orientation of the surface (see above) and does not depend on the
point of the surface.
which
specifies the orientation of the surface (see above) and does not depend on the
point of the surface.
Such a basis allows us to introduce the local Cartesian and
polar coordinates in each "section" of the tubular domain ![]() according
to the rule:
according
to the rule:
![]()
![]()
![]()
where the function ![]() is
defined everywhere except for the point
is
defined everywhere except for the point ![]() ,
, ![]() in
accordance with:
in
accordance with:
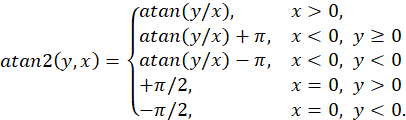
and returns the value of the polar angle of the vector ![]() in the
basis
in the
basis ![]() .
.
The functions that define the surface and its boundary as null set (see (1)) can be reconstructed as:
![]()
Finally, it is possible to make a local reconstruction of the surface directly in the neighborhood of points on both the surface and its endge. To do this, one can use the methods developed when dealing with the representation of surfaces as a set of points belonging to them ("point cloud surfaces"), see, for example, [15].
8. Testing of algorithms
The developed algorithms for calculating the evolution of a surface with a boundary and integrating the functions defined on it were programmed in C ++ and Python for the GNU Linux OS. Below, the results of testing the implementations of these algorithms are presented. To visualize the results of calculations, the FrontView program was used. Its brief description is given in the corresponding section.
8.1. Disc in the uniform velocity field
As a first test, let us consider the problem of development
of a plane surface, which is a trace of a disk of radius ![]() moving
in a translation motion with a constant velocity. At the initial time, the
surface is defined as a half of such a disk located in the region
moving
in a translation motion with a constant velocity. At the initial time, the
surface is defined as a half of such a disk located in the region ![]() . The
computational domain has the form of a parallelepiped with sides parallel to
the coordinate axes. The disk plane is horizontal, its center
. The
computational domain has the form of a parallelepiped with sides parallel to
the coordinate axes. The disk plane is horizontal, its center ![]() at the
initial moment of time coincides with the center of the lateral face of the
computational domain. The velocity field specified at the boundary of the disk
is assumed to be constant and homogeneous at all points of the boundary,
at the
initial moment of time coincides with the center of the lateral face of the
computational domain. The velocity field specified at the boundary of the disk
is assumed to be constant and homogeneous at all points of the boundary, ![]() ,
, ![]() .
Then, at time t, the center of the disk is located at the point
.
Then, at time t, the center of the disk is located at the point ![]() . The
surface is formed as a trace from the motion of the disk in the computational
domain.
. The
surface is formed as a trace from the motion of the disk in the computational
domain.
Direct calculations yield the following analytic expression for the projector P:
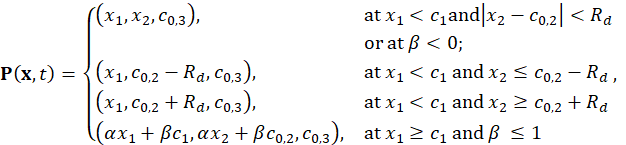
where ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are
the Cartesian coordinates of the domain.
are
the Cartesian coordinates of the domain.
The time dependence of the crack area has the form:
![]()
8.2. Disk in the vortex velocity field
As a second test, let us consider a similar problem, in
which, however, the surface is not flat. Like it was made above, we assume that
at the initial moment of time, the surface is a half of a disk, however, now
located on the surface of a cylinder with a given radius. In the course of
evolution, the surface remains on the cylinder, "wound" on it along
the section, the plane of which is perpendicular to the axis of the cylinder.
The axis of the cylinder is parallel to the coordinate axis ![]() . The
velocity field is vortex with an axis parallel to the axis
. The
velocity field is vortex with an axis parallel to the axis ![]() . It
is assumed that the vortex axis is on the right boundary of the computational
domain and passes through the point
. It
is assumed that the vortex axis is on the right boundary of the computational
domain and passes through the point ![]() . Then
the velocity field has the form:
. Then
the velocity field has the form:
![]()
where ![]() is
the distance from the point of space to the axis of the vortex, at which the
velocity modulus is
is
the distance from the point of space to the axis of the vortex, at which the
velocity modulus is ![]() .
.
Let ![]() be
the radius of the cylinder to which the surface belongs. We introduce the
angular coordinate
be
the radius of the cylinder to which the surface belongs. We introduce the
angular coordinate ![]() on the surface of the cylinder. Then,
the coordinates of the points
on the surface of the cylinder. Then,
the coordinates of the points ![]() on
the surface of the cylinder will have the form:
on
the surface of the cylinder will have the form:
![]()
If at the initial moment of time the center of the disk
along the ![]() -axis
has the coordinate
-axis
has the coordinate ![]() , then
the equation of the surface boundary can be written in the parametric form as
follows:
, then
the equation of the surface boundary can be written in the parametric form as
follows:
![]()
where ![]() is a parameter. In this case, the
condition of projection onto the boundary (i.e., the condition of the minimum
distance from the point of space to the boundary) can be written in the form:
is a parameter. In this case, the
condition of projection onto the boundary (i.e., the condition of the minimum
distance from the point of space to the boundary) can be written in the form:
![]()
Hence, the following equation is obtained with respect to
the value of ![]() corresponding to the projection of a
given point of space onto the curvilinear boundary of the surface:
corresponding to the projection of a
given point of space onto the curvilinear boundary of the surface:
![]()
In calculations, when constructing an exact solution, this equation is solved by Newton's method.
The analytical solution for the projector ![]() is:
is:
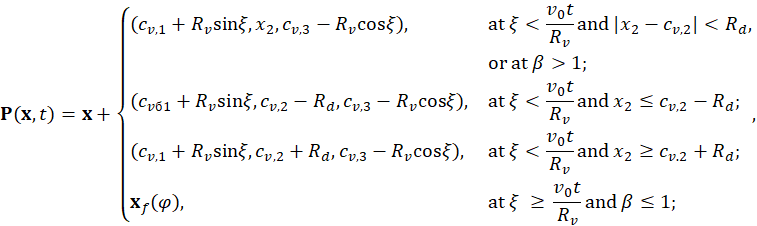
where ![]() .
.
For the surface area, the following expression holds:
![]()
8.3. Results of testing.
In the testing process, we studied the dependence of the
mean error in determining the projection ![]() at
the end of the calculation at a given
at
the end of the calculation at a given ![]()
![]()
where the summation is carried out over all nodes of the computational mesh and the error in determining the area
![]() ,
,
on the characteristic mesh spacing h.
It should be noted that the algorithm for calculating the evolution of the surface does not use any information about the mesh structure; its operation requires only information about coordinates of its nodes. At the same time, the information about the mesh structure is needed to calculate integrals of functions defined on the surface.
For the calculation, we used a mesh consisting of tetrahedra
with a characteristic spacing ![]() , not adapted to the geometry of the
surface. The test parameters had the values
, not adapted to the geometry of the
surface. The test parameters had the values ![]() ,
, ![]() for
the case of a disk in a uniform velocity field and
for
the case of a disk in a uniform velocity field and ![]() ,
, ![]() ,
, ![]() for
a disk in a vortex velocity field.
for
a disk in a vortex velocity field.
In all calculations, the time step ![]() and
the modeling time
and
the modeling time ![]() ,
, ![]() .
.
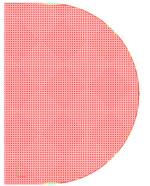
Fig. 3 shows the phases of the evolution of the surface for the test named as "a disk in a homogeneous velocity field" which considers the evolution of a plane surface, which is a trace of a disk of a given radius moving with a constant velocity. The details of the test are described in section 8.1.
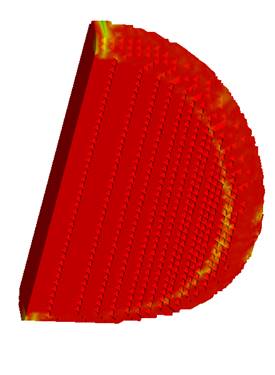
Fig. 4 demonstrates the animations corresponding to the "disk in the vortex speed field" test. The initial configuration of the surface is a disk on the surface of a cylinder. The velocity field is axisymmetric with the rotation axis coinciding with the axis of the cylinder. A detailed description of the test is given in Section 8.2. The left animation shows the evolution of the surface itself. The color indicates the error of the mesh approximation of the surface. On the right, one can see the animation of the evolution of the boundary of an unstructured tetrahedral mesh enclosing the surface with the boundary. The mesh shown in the animation is used to represent the surface by means of the closest point projection method. As the surface evolves, the tetrahedral mesh is being completed appropriately. A detailed description of the test is given in section 8.2. of the paper. The color indicates the error level of the mesh approximation of the surface.
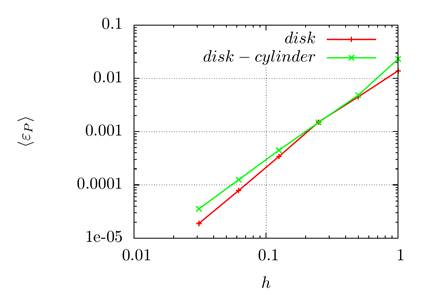
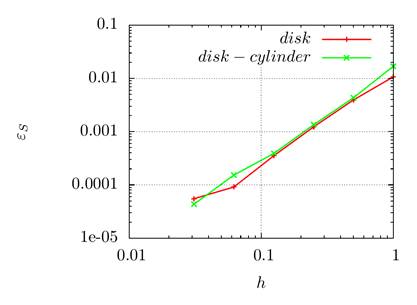
The graphs in Fig. 5 show the dependence of the calculation
error of the projector and the surface area during its evolution on the mesh
spacing. It can be seen that the constructed algorithm has the order of
convergence with respect to ![]() close to the second one.
close to the second one.
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 3. Evolution of a disk in a homogeneous velocity
field at ![]() ,
, ![]() , the
color indicates the level of the projection error
, the
color indicates the level of the projection error ![]() on
the interval
on
the interval ![]()
|
|
|
Fig. 4. Evolution of a disk in a vortex velocity field at
![]() ,
, ![]() , the
color indicates the level of the projection error
, the
color indicates the level of the projection error ![]() on
the interval
on
the interval ![]()
|
|
|
|
(à) |
(b) |
Fig. 5. Dependence of the errors ![]() and
and ![]() on
the parameter
on
the parameter ![]() for two test statements: a disc in an
uniform velocity field ("disk" curves) and a disk in a vortex
velocity field ("disk-cylinder" curves)
for two test statements: a disc in an
uniform velocity field ("disk" curves) and a disk in a vortex
velocity field ("disk-cylinder" curves)
9. Visualizer FrontView
To visualize the results, the FrontView application was used. It was originally developed in Keldysh Institute of Applied Mathematics of the Russian Academy of Sciences by S.A. Khilkov (MIPT) in the process of solving the problem of seismic migration before summation in the asymptotic approximation. The main purpose of this program is a rapid visualization of a large amount of data set on dynamic surfaces represented as unstructured triangular meshes.
The FrontView application is developed under Linux OS in C ++ and Python languages using OpenGL libraries (www.opengl.com) and glm (http://glm.g-truc.net). To visualize data, the FrontView application uses its own binary data format; to organize the data recording, the user is provided with a header file in C ++.
To visualize time-dependent fields, the data is written into a single file in a frame-by-frame manner, the frames are sequentially located in the file. Each frame contains the instantaneous value of the visualized fields. Data related to different time points can be specified on different meshes. The data corresponding to one frame includes a triangular unstructured mesh in 3D-space---the coordinates of the vertices are a list of triples of indices that define triangular cells of the mesh. Each cell and each vertex of the mesh can be associated with additional information---an arbitrary (but the same for all cells) number of values in the float4 format. In this way, the data format allows one to store various scalar and vector fields on the mesh.
When working with the FrontView application, the user can navigate between frames, select viewing angles and zooming, activate the clipping planes, save a constructed image in various raster graphic formats. When mapping, four user-selectable data arrays are used: three arrays are displayed as the coordinates of the vertices of the triangles (by default, these are the coordinates of the vertices of the initial mesh), the fourth data array is displayed in color. This approach allows an efficient visualization of various projections of complex multidimensional functions. In the problem considered in this paper, both the coordinates of the vertices of the initial mesh and their projections onto the surface to be approximated were chosen as coordinates. Color, as a rule, indicates the error value.
The FrontView application interface consists of a window, in which the visualization is carried out, and a command-line interface. The transition between frames, changing viewing angles and zooming are possible with the help of both a mouse and hotkeys. The command-line interface uses the syntax of Python, calling the exec function to parse user commands. This allows one to configure flexibly the visualization parameters, create various data processing scripts, and perform batch processing (for example, using loops and other Python control constructs).
10. Conclusions
This paper has dealt with the problems related to the representation and calculation of the dynamics of surfaces with a boundary. To represent the surface, the "closest point" method was used. The problems of representation of functions on such surfaces and calculation of their differential characteristics are considered. A new algorithm for calculating the evolution of surfaces using a given velocity field and the algorithm for integrating the functions defined on a surface are proposed. In comparison with the methods traditionally used for such problems, which are based on the representation of a surface as a zero-level set of a given function, the constructed algorithm does not require solving the equations of Hamilton-Jacobi type and proves to be much simpler in implementation on unstructured meshes. The results of numerical calculations demonstrated the appropriate accuracy and efficiency of the proposed algorithms for applications. The description of the FrontView program used to visualize the calculation data is given. The method of representation of the data of modeling considered in this work not only allows one to use it effectively in computational algorithms, but it is also convenient for the visual representation, which makes it possible to better understand the dynamics of the process of crack development.
Acknowledgements
This work was supported by the Russian Science Foundation, project no. 15-11-00021.
References
1. Ekonomides M., Olini R., and Val’ko P. Unifitsirovannyi dizain gidrorazryva plasta. Ot teorii k practike [Unified Design of Hydraulic Fracturing. From Theory to Practice]. Institute of Computer Science, 2007, p.236.
2. Salimov V.G., Ibragimov N.G., Nasybullin A.V., and Salimov O.V. Gidravlicheskii razryv karbonatnyh plastov [Hydraulic Fracturing of Carbonaceous Formations]. Neftyanoe Hozyaistvo, 2013, p. 471.
3. Ruuth S.J., Merriman B.M. A simple embedding method for solving partial differential equations on surfaces. J. Comput. Phys., 227 (2008), pp. 1943–1961.
4. Macdonald C.B., Brandman J., Ruuth S.J. Solving eigenvalue problems on curved surfaces using the Closest Point Method. J. Comput. Phys., 230 (2011), pp. 7944–7956.
5. Macdonald C.B., Ruuth S.J. Level set equations on surfaces via the Closest Point Method. J. Sci. Comput., 35 (2008), pp. 219–240.
6. Macdonald C.B., Ruuth S.J. The implicit Closest Point Method for the numerical solution of partial differential equations on surfaces. SIAM J. Sci. Comput., 31 (2009), pp. 4330–4350.
7. Stolarska M., Chopp D., Moes N., Belytschko T. Modelling crack growth by level sets in the extended finite element method. Int. J. Numer. Meth. Engng. 2001; 51:943–960.
8. Moes, N., Gravouil, A., Belytschko, T. Non-planar 3D crack growth by the extended fiite element and level sets—Part I: Mechanical model. Int. J. Numer. Meth. Engng 2002; 53:2549–2568 (DOI: 10.1002/nme.429)
9. Gravouil, A., Moës, N., Belytschko, T. Non-planar 3D crack growth by the extended finite element and level sets—Part II: Level set update. Int. J. Numer. Meth. Engng. V. 53, 2002. pp. 2569–2586. DOI: 10.1002/nme.430.
10. Osher, S. J., Fedkiw, R.P. Level Set Methods and Dynamic Implicit Surfaces. Springer-Verlag. ISBN 0-387-95482-1. 2002.
11. Sethian, J. A. Level Set Methods and Fast Marching Methods : Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science. Cambridge University Press. ISBN 0-521-64557-3. 1999.
12. Ventura G., Budyn, E., Belytschko T. Vector level sets for description of propagating cracks in finite elements. Int. J. Numer. Meth. Engng 2003; 58:1571–1592 (DOI: 10.1002/nme.829).
13. März T., Macdonald C.B. Calculus on surfaces with general closest point functions. SIAM J. Numer. Anal., Vol. 50, No. 6, pp. 3303–3328.
14. Dubrovin B.A., Novikov S.P., and Fomenko A.T. Sovremennaya geometriya: metody I prilozheniya [Modern Geometry: methods and applications]. Nauka, 1986, p. 760.
15. Berger M., Tagliasacchi A., Seversky L., Alliez, P., Levine, J., Sharf, A., Silva, C. State of the Art in Surface Reconstruction from Point Clouds. EUROGRAPHICS 2014 / S. Lefebvre and M. Spagnuolo. STAR –– State of The Art Report, 2014.