ФУНКЦИОНАЛЬНО-ВОКСЕЛЬНЫЙ МЕТОД КОМПЬЮТЕРНЫХ ВЫЧИСЛЕНИЙ

А.В. Толок, Н.Б. Толок*

Институт проблем управления им. В.А. Трапезникова РАН, Москва, Россия.

*Лаборатория компьютерной графики, лаборатория газодинамических средств автоматизации.

a.tolok@stankin.ru, nat_tolok@mail.ru

 

Содержание

1. Введение

2. Функционально-воксельное представление геометрической модели

3. Функционально-воксельная арифметика

4. Определение значения интеграла функционально-воксельным методом

5. Решение САУ функционально-воксельным методом

6. Заключение

Литература

 

Аннотация

В работе рассматривается один из подходов к применению средств воксельной визуализации для компьютерного представления алгебраической функции, заданной на некоторой области. Предлагается краткое изложение функционально-воксельного метода для компьютерных вычислений широкого класса задач, приводимых к геометрической постановке. Показан принцип построения компьютерной модели алгебраической функции набором воксельных образов. Каждый такой образ отображает один из коэффициентов локальной аппроксимирующей функции, полученной для окрестности точки на рассматриваемой области алгебраической функции. Конечный состав таких базовых воксельных образов организует воксельное компьютерное представление геометрической модели алгебраической функции, которое применимо в компьютерных вычислениях для различных математических конструкций. В качестве примера рассматриваются основные вычислительные конструкции, основанные на сложении/вычитании алгебраических функций, их умножении/делении, а также процедура взятия по модулю. Приведены примеры решения функциональных уравнений, где результатом является воксельное представление функции. Рассматривается оригинальный геометрический подход к решению систем алгебраических уравнений с применением функционально-воксельной модели. Предложено компьютерное вычисление интегральных характеристик R-функционально для описанной суперпозиции алгебраических функций как средство определения площадей или объемов геометрических объектов сложной формы. Для каждого из рассматриваемых примеров приводится обобщение решения на многомерное пространство.

 

Ключевые слова: Воксель, локальные геометрические характеристики, функционально-воксельный метод, функционально-воксельная модель, М-образ, функционально-воксельная арифметика, функционально-воксельное интегрирование.

 

1. Введение

 

Компьютерные вычисления математических конструкций зачастую представляются непростой задачей. Особенно когда речь заходит о вычислении сложных интегральных выражений, уравнений с частными производными, функциональных уравнений, систем нелинейных уравнений высоких степенных порядков и т.п. Современные компьютерные вычислительные средства в основном представлены численными методами. Визуальный метод графических построений, хоть и применим для решения широкого класса задач, и имеет превосходство перед остальными методами в своей наглядности, но сложно переносим на компьютерную платформу. К тому же недостатком графического метода, а также его визуализации, является пространственный предел, который не позволяет решать задачи, размерность которых выше четырёхмерной. В 2016 году в работе [7] формулируется компьютерный метод функционально-воксельного моделирования, основанный на принципах линейной аппроксимации области определения алгебраической функции для вычисления его локальных геометрических характеристик. При этом под термином воксель понимается цветовая характеристика, заданная целым положительным числом. В работах [1-4,6] приводятся различные приложения метода и раскрываются его возможности. Главной особенностью является его преемственность в организации компьютерного графического подхода к решению математических задач с геометрической постановкой. Отметим, что к геометрической постановке можно сводить решение достаточно широкого класса математических задач, основанных на применении алгебраических функций. Функционально-воксельное содержание предложенной компьютерной модели позволяет организовать согласованность между её тройственным компьютерным представлением: функциональное (аналитическое, символьное представление), функционально-воксельное (локальное значение алгебраической функции выражается через локальные геометрические характеристики, отображённые на воксельные структуры) и воксельное (процедура вычислений локальных характеристик строится исключительно на информации воксельных структур). Согласованность  модели обеспечивается операторами перехода из представления области алгебраической функции к воксельному пространству и обратно. В работе [7] в подробной форме излагаются все три подхода к работе моделью.

Статья посвящена способу применения компьютерных графических технологий в построении воксельных геометрических моделей для сложных алгебраических функции с приведением основных вычислительных конструкций.

 

2. Функционально-воксельное представление геометрической модели

 

Как уже отмечалось, построение функционально-воксельной модели основано на принципах линейной аппроксимации пространства функции для вычисления его локальных геометрических характеристик. В отличие от существующих подходов к линейной аппроксимации, локальные геометрические характеристики этой модели представлены компонентами нормали повышенной размерности пространства на основе утверждения: В пространстве E^m+1 гиперплоскость вида n₁x₁+ n₂x₂+…+ n_mx_m=p представима как . Например, модель для функции плоской фигуры «круг»:  Определение. Графический образ, соразмерный его прототипу и отображающий некоторое единственное свойство прототипа, называется графическим образом-моделью прототипа, или графический М-образ.

Поскольку создаваемая воксельная геометрическая модель базируется на отображении локальных геометрических характеристик, то каждый из воксельных образов модели есть графический М-образ.

 

Рис. 1. Образ поверхности

 

Представим аппроксимированную модель  некоторой функции  (рис.1) нормальным векторным полем, выраженным четырьмя скалярными полями  согласно условиям утверждения.

Установим некоторое соответствие скалярных полей , определяемых на промежутке  с их воксельным представлением (воксельным скалярным полем) , выразив через градацию интенсивности тона монохромной палитры  (рис.2):

 

Рис. 2. Воксельное отображение компонентов нормали функции косинуса

 

Характерно то, что на этом этапе прекращается компьютерная обработка функции аналитического вида и в дальнейших преобразованиях появляется возможность использовать только образные данные полученных базовых М-образов для реализации различных вычислений. Аналитическая функция может быть востребована лишь при определении максимально точных решений, а значит в достаточно редких случаях, либо для промежуточного уточнения модели при накоплении возможной погрешности от целочисленных вычислений в ходе её преобразований.

Основным достоинством такого компьютерного представления геометрической модели является её соразмерная связь с евклидовым пространством E, позволяющая работать с любой размерностью задаваемых функций.

 

3. Функционально-воксельная арифметика

 

Сумма. Сумму двух функций с одинаковой областью определения можно записать как функцию

При этом каждая из функций должна быть представлена в явном виде:

,

тогда значение суммы запишем как

Для примера рассмотрим две разнородные по своей структуре функции для суммирования:

1.    Тригонометрическая функция  вида

2.    Экспоненциальная функция  вида

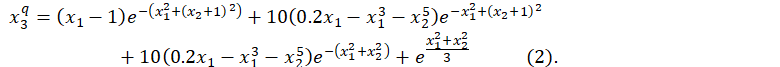
На рисунке 3 приведены воксельные представления, полученные на основе этих функций.

 

Рис. 3. Пример воксельных моделей функций () и ()

 

Примечательным является тот факт, что через воксельный образ компонента  выражается как

,

а функция любой сложности и размерности () приобретает линейный вид:

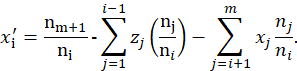
В рассматриваемом случае имеем сумму двух выражений функций () и ():

Перегруппировав уравнение, получим:

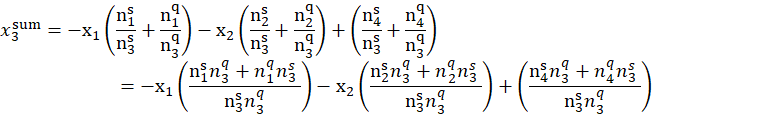
 Отсюда .

Нормируя коэффициенты имеем

На рисунке 4 представлены М-образы для суммы функций (s) и (q), полученной воксельным подходом.

 

Рис. 4. Воксельная модель суммы двух функций, полученная воксельным подходом

 

Достоверность результата проверяется построением воксельной модели арифметической суммы двух заявленных функций. При этом все четыре образа совпадают. В общем случае:

, где

 , где .

Разность. Представим разность в виде суммы с отрицательной функцией, а значит, достаточно рассмотреть способы получения конструкции .

На рисунке 5 изображена воксельная модель для функции . При рассмотрении функционально-воксельного представления получим выражение:

Рисунок 5 наглядно показывает, что М-образы ,  и  по отношению к образам ,  и  имеют инвертированный (обратный) цвет  (где  - максимальное значение палитры). -образ по отношению к М-образу  сохраняет свои цветовые значения, что подтверждается выражением (4).

 

Рис. 5. Воксельная модель функции, полученная функциональным подходом

 

Взятие по модулю. По сути, модуль предполагает изменение знака отрицательной области на противоположный, а посему, достаточно определить знак значения

чтобы получить конструкцию вида

На рисунке 6 изображена воксельная модель функции (s), взятой по модулю.

 

Рис. 6. Воксельная модель функции (s), взятой по модулю

 

Умножение. Аналогично рассмотрим арифметическую процедуру умножения функций воксельным подходом. В качестве примера оставим те же функции: (s) тригонометрическая и (q) - экспоненциальная.

Воксельный подход к представлению умножения приводит к определению нормированных коэффициентов, исходя из уравнения

Проведём упрощение формулы через переприсвоение:

Получаем следующее упрощённое выражение:

Рассмотрим отдельно каждый многочлен при аргументах :

Отсюда можно сделать вывод, что теперь

Получение компонентов приводит к нормированию коэффициентов

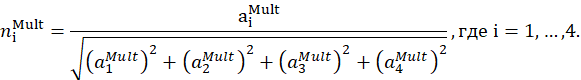
На рисунке 7 представлены М-образы для произведения функций (f) и (g), полученного воксельным подходом.

 

Рис. 7. Воксельная модель произведения двух функций, полученная воксельным подходом

 

В общем случае имеем выражение:

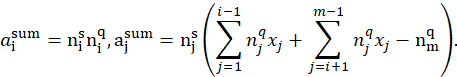
Воксельный подход функционального деления приводит к определению нормированных коэффициентов исходя из уравнения

Проведём упрощение формулы через переприсвоение:

Получаем следующее упрощённое выражение:

 

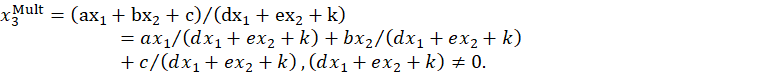
Рассмотрим отдельно каждый многочлен при аргументах :

Отсюда делается вывод, что

Получение компонентов приводит к перенормированию коэффициентов

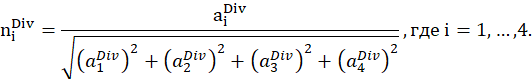
На рисунке 8 представлены М-образы воксельной модели для частного функций (f) и (g), полученного воксельным подходом.

 

Рис. 8. Воксельная модель деления двух функций, полученная воксельным подходом

 

Реализация основных арифметических процедур позволяет говорить о возможности применения воксельных моделей в решении функциональных уравнений. Например, такое уравнение как   (5) можно представить уравнением , где , а . Такие функции не только содержат достаточную компьютерную информацию для решения, но и позволяют применять такое представление функций в формулировке новых, более сложных уравнений.

На рисунке 9 демонстрируется решение уравнения (5) на основе функционального  и воксельного  подходов.

 

Рис. 9. Функционально-воксельное представление функции как решения функционального уравнения

 

4. Определение значения интеграла функционально-воксельным методом

 

В общем случае площадь положительной функциональной области вычисляется взятием двойного интеграла по границам функции

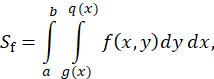
Продемонстрируем функционально-воксельный способ интегрирования функции  по аналогии с классическим способом. Преобразуем функцию  таким образом, что положительные значения обратим в единицу, а отрицательные обнулим:

Теперь можно записать, что

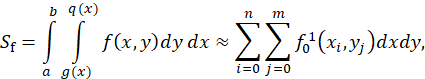
где  — двумерная целочисленная область воксельного пространства, - площадь элемента аппроксимационной сетки.

Характерен тот факт, что полученный способ определения площади для двойного интеграла легко адаптируется для получения объемов многомерных функций. Рассматривая n-мерный случай для функции вида можно записать, что

 

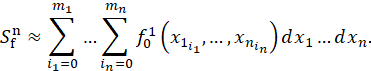
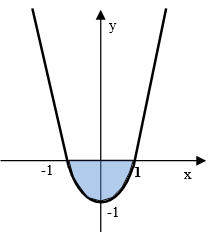
Рис. 10. Функция параболы

 

Рассмотрим простой пример определения площади параболы вида  (рис.10). Для описания сложных замкнутых областей обратимся к математическому аппарату R-функций [5]. Представим рассматриваемую функцию в предикатном виде как . Но фигура параболы не является замкнутой, и представленный вид описания не отвечает поставленному требованию задачи. Допустим, нас интересует площадь фигуры, расположенной ниже оси , т.е. в области отрицательных значений  (рис.10). Представим замкнутую область пересечением двух незамкнутых областей:  и полупространства. В результате имеем общий вид замкнутой функции-предиката , где  и .

 

Рис. 11. Отрицательная область выделена белым цветом

 

Рис. 12. Положительная область выделена белым цветом

 

Для проверки корректности полученного результата произведён расчёт площади «отрицательной» (рис.11)  и «положительной» (рис.12)  области . Учитывая, что площадь заданной области определения функции должна стремиться к 2, суммируем оба полученных значения: . Как видно из примера, в ходе расчётов потеря площади составила стотысячные доли.

 

5. Решение САУ функционально-воксельным методом

 

Рассмотрим решение примера системы элементарных линейных уравнений:

Результатом будет являться некоторая точка пересечения двух прямых, заданных уравнениями системы. Для решения системы уравнений функционально-воксельным методом достаточно преобразовать математическую запись системы уравнений в запись единого уравнения поверхности (рис.12):

При этом общий вид решения системы САУ методом ФВМ можно записать как

 

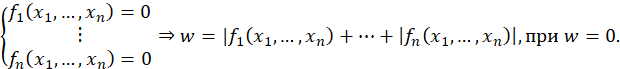
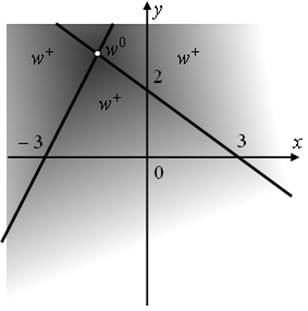
Рис. 12. Поверхность суммы модулей двух линейных функций

 

Рассмотрим случай пересечения квадратичных кривых: параболы и окружности

Для этого преобразуем систему кривых в общую поверхность

. Получаем образ, изображённый на рисунке 13, где результатом отображаются точки для значений .

 

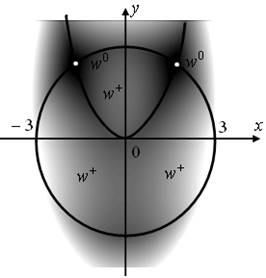
Рис. 13. Поверхность суммы модулей двух нелинейных функций

 

Можно также говорить о корректности получаемого результата при рассмотрении других разнообразных примеров двухмерных алгебраических функций различного степенного порядка, поскольку применяемое свойство нуля на границе присутствует для всех неявно заданных алгебраических функций. То же самое относится к повышению размерности пространства системы алгебраических уравнений, что позволяет отнести такой подход к разряду универсальных компьютерных способов решения таких систем.

 

6. Заключение

 

Основным достоинством функционально-воксельного метода является значительное повышение информативности компьютерной модели за счёт увеличенной размерности пространства алгебраической функции, позволяющей упростить расчёт таких условных математических конструкций, как дифференцирование и интегрирование алгебраической функции. Решать сложные системы алгебраических уравнений. Все продемонстрированные расчётные конструкции метода базируются на применении локальных геометрических характеристик (дифференциалов) и ориентированы на компьютерное моделирование сложных многомерных алгебраических функций для применения в решениях математических задач с геометрической постановкой.

 

Литература

 

1.  Васильев С.Н., Локтев М.А., Толок А.В., Толок Н.Б., Ульянов С.А. К планированию маршрутов в 3D-среде с многовариантной моделью. Труды СПИИРАН, Выпуск №2 (45). ISSN 2078-9181. Санкт-Петербург, 2016 г., С 5 - 25.

2.  Григорьев С.Н., Локтев М.А., Толок А.В. Построение воксельных моделей геометрических объектов. Прикладная информатика № 4 (46) 2013 г. С.50-55.

3.  Григорьев С.Н., Силантьев Д.А., Лоторевич Е.А., Пушкарёв С.А., Толок А.В. Автоматизация графического способа решения некоторых математических задач. Прикладная информатика № 5 (41) 2012. С.44-50.

4.  Ковалёв С.П., Толок А.В. Применение модельно-ориентированного подхода в управлении жизненным циклом технических изделий. Информационные технологии в проектировании и производстве. 2015. №2(158). С.3-9.

5.  Максименко-Шейко К.В. R-функции в математическом моделировании геометрических объектов и физических полей; Монография. - Харьков, ИПМаш НАН Украина, 2009. 306 с.

6.  Силантьев Д.А., Лоторевич Е.А., Пушкарёв С.А., Толок А.В. Воксельно-математическое моделирование при решении задач определения площади для поверхностей деталей. Информационные технологии в проектировании и производстве №3, 2013, С 29-33.

7.  Толок А.В. Функционально-воксельный метод в компьютерном моделировании / Под. ред. академика РАН С.Н. Васильева. М.:ФИЗМАТЛИТ, 2016. 112 с. ISBN 978-5-9221-1680-0.

---

FUNCTIONAL VOXEL METHOD FOR THE COMPUTER CALCULATIONS

A.V. Tolok, N.B. Tolok*

V. A. Trapeznikov Institute of Control Sciences of Russian Academy of Sciences, Moscow, Russia.

*Laboratory of the Computer Graphics, Laboratory of GasHydro-dynamic Tools for Automation.

a.tolok@stankin.ru, nat_tolok@mail.ru

 

Abstract

In this paper, one of the approaches to the voxel visualization tools’ application in the computer representation of algebraic function defined over some field is being considered. Here we offer the thumbnail summary of the functional voxel method intended for the computer solution of a wide class of mathematical problems with geometrical definition. The design principle of the computer model of algebraic function using a set of voxel images is shown. Each image reflects one of the coefficients of the local approximating function, determined for the point environment in the considered field of algebraic function. The final composition of such basic voxel images organizes voxel computer representation for the geometrical model of algebraic function which can be applied in different mathematical computer calculations. As an example, we consider the main computational constructions based on addition/subtraction of algebraic functions, their multiplication/division and taking the modulus. Given examples show the solutions of functional equations with voxel representation of a function as a result. The original geometrical approach to solve the system of algebraic equations using the functional voxel model is considered. Also, the computer calculation of integral characteristics R-functional for the described superposition of algebraic functions is proposed as a tool of square and volume definition for the surfaces and objects of irregular shape. Each example is provided with generalization of the solution for multidimensional space.

 

Keywords: Voxel, local geometrical characteristics, the functional voxel method, functional voxel model, M-image, functional voxel arithmetics, functional voxel integration

 

References

 

1.       Vasil'ev S.N., Loktev M.A., Tolok A.V., Tolok N.B., Ul'janov S.A. K planirovaniju marshrutov v 3D-srede s mnogovariantnoj model'ju [To planning routes in the 3D-environment with a multivariate model]. Proceedings SPIIRAS, Issue No. 2 (45). ISSN 2078-9181. St. Petersburg, 2016, pp. 5 - 25. [In Russian]

2.       Grigor'ev S.N., Loktev M.A., Tolok A.V. Postroenie voksel'nyh modelej geometricheskih ob#ektov [Construction of models on voxel for geometric objects]. Applied Informatics No. 4 (46), 2013. pp. 50-55. [In Russian]

3.       Grigor'ev S.N., Silant'ev D.A., Lotorevich E.A., Pushkarjov S.A., Tolok A.V. Avtomatizacija graficheskogo sposoba reshenija nekotoryh matematicheskih zadach [Automation of graphical method of solving certain mathematical problems]. Applied Informatics No. 5 (41) 2012. pp. 44-50. [In Russian]

4.       Kovaljov S.P., Tolok A.V. Primenenie model'no-orientirovannogo podhoda v upravlenii zhiznennym ciklom tehnicheskih izdelijThe use of model-based approach to manage the lifecycle of industrial products. Information technologies in the design and manufacture. 2015. No. 2(158). Pp.3-9. [In Russian]

5.       Maksimenko-Shejko K.V. R-funkcii v matematicheskom modelirovanii geometricheskih obektov i fizicheskih polej [R-function in the mathematical modeling of the geometry and physical fields]. Monograph. Kharkiv, IPMash NAS of Ukraine, 2009. 306 p.  [In Russian]

6.       Silant'ev D.A., Lotorevich E.A., Pushkarjov S.A., Tolok A.V. Voksel'no-matematicheskoe modelirovanie pri reshenii zadach opredelenija ploshhadi dlja poverhnostej detalej [Mathematical modeling on voxeles in solving problems of determining the area for surface of details] Information technologies in the design and manufacture No. 3, 2013, P. 29-33. [In Russian]

7.       Tolok A.V. Funkcional'no-voksel'nyj metod v komp'juternom modelirovanii [Functional voxel method in computer modeling / Under. Ed. academician SN Vassilyev]. FIZMATLIT, 2016. 112 p. ISBN 978-5-9221-1680-0. [In Russian]