ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ И ВИЗУАЛИЗАЦИЯ ТЕЧЕНИЙ С ГОРЕНИЕМ В ВЫСОКОСКОРОСТНОЙ КАМЕРЕ СГОРАНИЯ
И.Г. Гудич, В.Т. Жуков, К.В. Мануковский*, Н.Д. Новикова, Ю.Г. Рыков, О.Б. Феодоритова
Институт прикладной математики им. М.В. Келдыша РАН, Москва, РФ
*Институт теоретической и экспериментальной физики им. А.И. Алиханова, Москва, РФ
igudich@gmail.com, zhukov@kiam.ru, manu@itep.ru, nn@kiam.ru, rykov@keldysh.ru, feodor@kiam.ru
Содержание
2. Описание математической модели течения
3. Модифицированная вычислительная модель, реализованная в пакете OpenFOAM
4. Вычислительные эксперименты
Аннотация
В работе рассматриваются течения многокомпонентных сред с наличием турбулентных явлений и горения для численного исследования газодинамических процессов в модели прямоточного воздушно-реактивного двигателя. Для обеспечения зажигания смеси использовано кратковременное запирание канала потоком сжатого воздуха, подача которого осуществляется поперек основного потока. В результате образуется сложное почти периодическое течение газовой смеси, характеризующееся циклическим распространением волны горения на фоне основного течения с разномасштабной структурой. Вследствие этого для эффективной интерпретации полученных результатов необходимо использовать методы научной визуализации. В статье рассмотрены и визуализированы режимы течения многокомпонентной смеси без горения и с горением углеводородного топлива. Анализ и качественное понимание столь сложных физических процессов невозможны без полноценного использования средств научной визуализации.
Сходимость приближенных решений продемонстрирована серией расчетов на измельчающемся наборе сетки. В расчетах используется многопроцессорный суперкомпьютер К-100, средства для работы с графикой, а также библиотека MPI для коммуникации между различными вычислительными узлами. Для визуальной верификации использованы графические системы ParaView, Tecplot.
Ключевые слова: научная визуализация, математическое моделирование, уравнения Навье-Стокса, вязкая сжимаемая среда, турбулентные течения, процессы горения, прямоточный воздушно-реактивный двигатель, OpenFOAM
Работа выполнена при финансовой поддержке Российского научного фонда, проект № 14-21-00025.
1. Введение
Процессы, происходящие в прямоточных воздушно-реактивных двигателях на гиперзвуковых скоростях полета, представляют собой сложную комбинацию газодинамических явлений, таких как: развитие турбулентных пограничных слоев, их взаимодействие с ударными волнами и формирование псевдоскачка, комплекс физических явлений, связанных с горением топлива и ответственных за формирование и поддержание двигателем тяги, необходимой для устойчивого атмосферного полета высокоскоростного летательного аппарата. Вследствие высоких скоростей, сложной структуры происходящих процессов и вытекающей отсюда сложности постановки и высокой стоимости натурных экспериментов (продувок в аэродинамических трубах) важную роль приобретает возможность проведения предсказательных численных расчетов, включая научно-обоснованный выбор методов, алгоритмов и математических моделей.
Настоящая работа предпринята для численного анализа функционирования модельной камеры сгорания. Модельная задача предложена коллективом ЦАГИ [1]. Задача охватывает большой круг интересных математических и вычислительных вопросов и представляется крайне полезной с точки зрения изучения вычислительных возможностей различных методик, их работоспособности и гибкости. Отметим также, что она представляет не только методический, но и практический интерес, поскольку подготавливает естественный переход к трехмерным постановкам задач и расчету реальных компоновок.
Для проведения численных экспериментов в работе используется пакет OpenFOAM (версия 2.3.1) [2]. Пакет OpenFOAM представляет собой открытую объектно-ориентированную библиотеку, написанную на языке С++ и предназначенную для численного моделирования задач механики сплошной среды. Библиотека поддерживает механизмы массивного распараллеливания с помощью MPI. Элементы OpenFOAM активно используются в промышленности, в академической сфере и экспертном сообществе. Описанная в предлагаемой статье методология расчетов ранее была верифицирована и частично валидирована авторами для задач академического плана, см. [3], [4].
Открытость исходных кодов данного пакета предоставляет широкие возможности по изучению и модификации реализованных в нем математических и вычислительных моделей. К их числу относятся методы дискретизации дифференциальных уравнений в частных производных, модели турбулентности, методы решения систем дискретных уравнений и другие.
Дискретизация уравнений в OpenFOAM получается методом контрольного объема, который обеспечивает строгое соблюдение законов сохранения массы, импульса и полной энергии. Для дискретизации расчетная область разбивается на некоторое число непересекающихся контрольных объемов таким образом, что каждый узел сетки содержится в одном контрольном объеме. Дифференциальные уравнения интегрируются по каждому контрольному объему и таким образом получаются интегральные соотношения. Для вычисления интегралов используются различные полиномиальные аппроксимации, задаваемые в соответствующих параметрах OpenFOAM.
Дискретизации дифференциальных уравнений по времени основаны на явной и неявной схемах. Первые используют как противопотоковый, так и современный центрально-разностный варианты. Последние реализованы с помощью различных итерационных методов (предобусловленные методы сопряженных и бисопряженных градиентов, алгебраический многосеточный метод и т.п.).
Особенностью настоящей работы является то, что все расчеты нестационарных течений, включая расчеты с горением, верифицированы на последовательности сеток с увеличивающимся количеством расчетных ячеек. Средствами визуализации и анимации показан характер возникающих газодинамических полей, а также «сходимость» получающейся картины течений и устойчивость их основных характеристик. Дополнительно отметим, что рассчитываемые в статье течения многокомпонентных смесей реагирующих газов имеют достаточно сложную динамическую структуру, состоящую из серий ударных волн, взаимодействующих между собой и с пограничными слоями, ножек Маха, вихревых течений и специфических нестационарных волн горения.
Объективная трактовка результатов численных экспериментов и обеспечение контроля за достоверностью всех процессов невозможна без использования средств научной визуализации. На современном этапе иллюстративная функция процесса визуализации объективно добавлена аналитическими возможностями этого инструмента. Это связано в первую очередь с существенно возросшими объемами данных численного эксперимента. Важным требованием является возможность параллельной обработки данных, предоставляемая современными графическими средами. Мы в своей работе активно использовали кроссплатформенное приложение ParaView [5], предназначенное для интерактивной научной визуализации, и коммерческий пакет Tecplot [6].
2. Описание математической модели течения
Расчеты течения газа проводились на основе системы осредненных по Рейнольдсу уравнений Навье-Стокса с введением дополнительных членов и уравнений для учета эффектов турбулентности и горения (ниже по повторяющимся индексам предполагается суммирование), описание подобной модели см., например, в [7]:
.Система уравнений (1)– дополняется уравнением состояния для смеси идеальных газов
|
|
|
и калорическим уравнением состояния
|
|
|
.В системе уравнений (1)– использованы следующие обозначения:
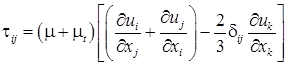
– тензор вязких напряжений, компоненты которого получены
осреднением по мелкомасштабным пульсациям; 
– вектор скорости осредненного течения; 
– плотность;
– давление;
–
температура; и 
–
массовая концентрация и молекулярный вес m-ой компоненты, 
– количество компонент
в смеси; 
–
удельная кинетическая энергия; 
и 
– молекулярная и турбулентная вязкости; 
и 
– турбулентная
кинетическая энергия и удельная скорость диссипации турбулентной энергии
соответственно.
В приведенных выше формулах использованы также следующие обозначения:
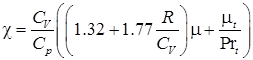
– коэффициент диффузии, в котором 
– динамическая вязкость,
зависящая от температуры по закону Сазерленда. Заметим, что коэффициент не зависит от
состава смеси и принят для всех компонент одинаковым. 
– турбулентное число Прандтля (
); 
– универсальная газовая
постоянная; 
–
удельная теплоемкость при постоянном объеме, множитель перед – модифицированная
поправка Эйкена к коэффициенту теплопроводности для смеси многоатомных газов
(учитывает поступательные и внутренние степени свободы), далее
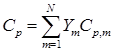
– удельная теплоемкость смеси при постоянном давлении. Для каждой компоненты смеси зависимость удельной теплоемкости от температуры задается многочленом, аппроксимирующим известные термодинамические таблицы (см. например [8]) в нужном диапазоне:
.
Наконец, 
– дополнительный член в уравнении
энтальпии для учета изменения энергии, обусловленного протеканием химических
реакций. Величина определяется по формуле
,
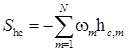где 
– скорость производства или расходования m-ой
компоненты за счет химических реакций 
, 
– энтальпия образования вещества при
стандартной температуре 
(эти же величины используются в формуле (5)).
Для описания химических реакций используется редуцированный
механизм, состоящий из одной квазиглобальной реакции горения условного
углеводородного топлива 
и элементарных обратимых реакций для восьми
химических компонент: 
. Константы скоростей химических реакций
подчиняются модифицированному закону Аррениуса 
(с зависимостью от температуры
множителя перед экспонентой). Исключение составляет глобальная брутто-реакция
окисления топлива до 
и 
. Она задается в нестандартной форме (множитель
перед экспонентой зависит от давления).
В данной работе для описания турбулентности использована SST-модель
Ментера [9], включающая два дифференциальных уравнения для транспорта удельной
кинетической энергии турбулентности и удельной скорости диссипации турбулентной
энергии .
В уравнении (2) 
представляет собой скорость генерации
турбулентной кинетической энергии, 
. Функция переключения 
имеет вид
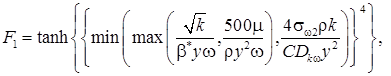
где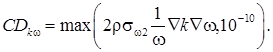 
Коэффициент турбулентной вязкости рассчитывается по формуле
,
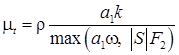где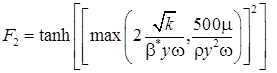 
.
В вышеприведенных формулах и в (2) 
– тензор скоростей деформации:
.
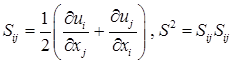Все константы 
подчиняются интерполяционной формуле 
с подстановкой
вместо 
значений:
, 
, 
, 
, 
, 
, 
, 
. Входящий в выражения для 
параметр 
задан постоянным: 
.
В настоящей работе использовались квадратичные аппроксимации для энтальпии входящих в смесь веществ. Такие аппроксимации являются частью поставленной модельной задачи и предоставлены ЦАГИ [1]. Коэффициенты квадратичной аппроксимации приведены в табл. 1.
Предлагаемая кинетическая модель представлена ниже в табл. 2, в которой указаны параметры всех реакций.
Таблица 1. Аппроксимирующие коэффициенты термодинамической
модели 
, 
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В табл. 2 использован формат представления, предложенный
нашими коллегами из ЦАГИ. Он несколько отличается от традиционного формата , включающего в
себя энергию активации, и имеет вид
.
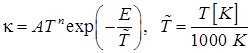Индексами “f” и “b” в табл. 2 обозначены прямая и обратная реакции соответственно.
Таблица 2. Детальная кинетическая модель, используемая в экспериментах
|
Реакция |
|
|
|
|
|
|
|
|
|
0 |
8.84 |
|
0 |
0 |
|
|
|
0 |
4.76 |
|
0 |
3.67 |
|
|
|
0 |
2.59 |
|
0 |
10.57 |
|
|
|
0 |
0.39 |
|
0 |
9.47 |
|
|
|
-2 |
61.51 |
|
-1 |
0 |
|
|
|
0 |
0 |
|
-1 |
0 |
|
|
|
-2 |
52 |
|
-1 |
0 |
|
|
|
-1 |
60.6 |
|
0 |
0 |
|
|
|
0 |
3.17 |
|
-0.79 |
15.45 |
|
|
|
0 |
0.90 |
|
-0.7 |
64.92 |
|
|
|
0.66 |
29.8 |
|
0 |
25.68 |
Скорость дополнительной прямой брутто-реакции описывается эмпирической формулой
, 
.
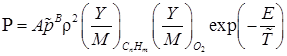Здесь – плотность смеси 
, параметры 
являются кусочно-постоянными и терпят
разрыв при некоторой заданной температуре.
Скорости прямых и обратных реакций представляются в виде
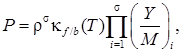
где константа реакции вычисляется по трехпараметрической
формуле Аррениуса 
; 
для бимолекулярных реакций и 
для тримолекулярных реакций.
Использованная кинетическая схема является составной частью поставленной модельной задачи.
3. Модифицированная вычислительная модель, реализованная в пакете OpenFOAM
Мы не будет описывать детально вычислительные аспекты и концепции, на которых базируется программный пакет OpenFOAM. Отошлем заинтересованного читателя к двум большим работам, опубликованным в 2014– 2015 годах, [10], [11]. Здесь ограничимся контурным описанием выбранных нами вариантов и модификаций, которые позволили, в частности, осуществить подробную визуализацию картины течения.
Открытая библиотека OpenFOAM содержит большое количество готовых решателей для описания специальных вариантов, например, стационарных и нестационарных течений, течений сжимаемого и несжимаемого газа, реагирующего газа, с возможным учетом турбулентности и т.д. Дополнительно существует возможность выбрать модель турбулентности, горения, термодинамики. Главное достоинство библиотеки – возможность использовать перегруженные операторы для самостоятельной реализации сложных физических моделей. Решатели OpenFOAM разрабатываются исследователями достаточно большого сообщества вычислителей-программистов.
OpenFOAM основывается на конечно-объемных аппроксимациях и предоставляет выбор значительного числа дискретизационных схем. Основная масса решателей базируется на алгоритме сопряжения скорости и давления SIMPLE. Существует возможность декомпозиции расчетной области на основе нескольких известных программных комплексов (METIS, Scotch и другие) и параллельного счета задач. Для решения линейных систем уравнений предоставлены некоторые варианты метода подпространств Крылова: предобусловленный метод сопряженных градиентов для симметричных матриц и предобусловленный метод бисопряженных градиентов для несимметричных матриц.
В вычислительных экспериментах, представленных в статье, использовались два решателя: сначала в модели идеального газа рассчитывалось газодинамическое течение в канале (решатель sonicFOAM), затем полученное решение использовалось в качестве начального приближения для расчета многокомпонентной реагирующей среды (решатель reactingFOAM).
В основе обоих решателей лежит один и тот же алгоритм PIMPLE,
который относится к алгоритмам SIMPLE типа и использует некоторые
дополнительные корректирующие процедуры для обеспечения сходимости на каждом
временном шаге. Для аппроксимации конвективных членов использовались схемы
второго порядка точности с лимитерами, например, для аппроксимации
«турбулентных» конвективных членов применялась NVD схема Gamma [12] с
параметром 
:
div(phi,omega) Gauss Gamma 1.0;
div(phi,k) Gauss Gamma 1.0.
Аппроксимация диффузионных членов базируется на линейной интерполяции, что соответствует второму порядку точности. Не останавливаясь на всех деталях вычислительного характера, отметим только, что для расчета поставленной задачи пришлось внести некоторые изменения и дополнения в оригинальный код, часть которых сделана на макроуровне языка OpenFOAM, другая часть на уровне языка С++.
Приведем в качестве примера модификацию, внесенную в
решатель reactingFOAM. В его оригинальном варианте в уравнении для энтальпии
реакций 
(см.
(1)) отсутствовали члены 
и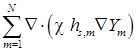 
. Для исправления этой ситуации в файл EEqn.H
были внесены изменения, выделенные ниже жирным шрифтом
{
volScalarField& he = thermo.he();
fvScalarMatrix EEqn
(
fvm::ddt(rho, he) + mvConvection->fvmDiv(phi, he)
+ fvc::ddt(rho, K) + fvc::div(phi, K)
+ (
he.name() == "e"
? fvc::div
(
fvc::absolute(phi/fvc::interpolate(rho), U),
p,
"div(phiv,p)"
)
: -dpdt
)
- fvm::laplacian(turbulence->alphaEff(), he)
reaction->Sh()
+ fvOptions(rho, he)
+ fvc::div(turbulence->muEff()*(fvc::grad(U)&U))
+ fvc::div( turbulence->muEff()*(dev2(fvc::grad(U)().T())&U))
);
if(he.name() != "e")
{
volScalarField& TCells = thermo.T();
volScalarField& pCells = thermo.p();
forAll(hsi, i)
{
forAll(TCells, celli)
{
hsi[i][celli] = thermo.composition().Hs(i,pCells[celli], TCells[celli]);
}
}
forAll(Y, i)
{
EEqn -= fvc::laplacian(turbulence->alphaEff()*hsi[i], Y[i]);
}
}
EEqn.relax();
fvOptions.constrain(EEqn);
EEqn.solve();
fvOptions.correct(he);
thermo.correct();
Info<< "min/max(T) = " << min(T).value() << ", " << max(T).value() << endl;
Дополнительно в файл createFields.H добавлено описание
PtrList<volScalarField> hsi(Y.size());
forAll(hsi,i)
{
hsi.set( i,
new volScalarField (
IOobject
(
"hsi " + Y[i].name(),
runTime.timeName(),
mesh,
IOobject::NO_READ,
IOobject::NO_WRITE
),
mesh,
dimensionedScalar("hsi"+Y[i].name(),
dimEnergy/dimMass, 0.0)
) );
}
Более низкий уровень программирования понадобился, например, для учета глобальной брутто-реакции, входящей в приведенный кинетический механизм. Дело в том, что OpenFOAM использует для конвертации формат представления CHEMKIN. Однако реакция горения условного углеводородного топлива имеет нестандартную форму и не может быть представлена в этом формате.
Рассмотренная модельная задача состоит в расчете течения реагирующего газа в канале с расширением в виде обратного уступа. В канал слева втекает сверхзвуковой поток газа, при этом предполагается, что в окрестности стенок уже сформировались соответствующие пограничные слои; в невязком ядре потока число Маха близко к значению 2.5. На стенках канала для учета прилипания потока ставится граничное условие в виде пристеночных функций. На небольшом расстоянии вверх по потоку от уступа внутрь канала подается углеводородное топливо в газовой фазе, а в некоторый момент времени в конце канала включается пневмодроссель – поток сжатого воздуха короткое время вдувается в канал перпендикулярно течению. Геометрию задачи, расположение отверстий для вдува топлива и место дросселирования можно увидеть на рис. 1.
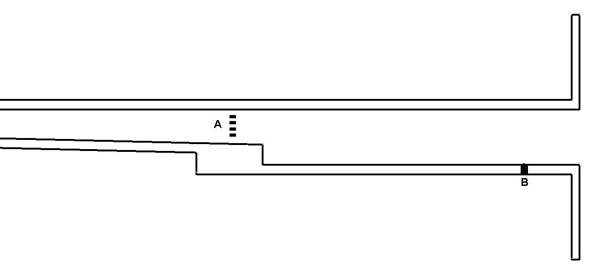
Рис. 1. Геометрия задачи: А – зона впрыска; В – область дросселирования
Расчетная область представляет собой прямоугольник, внутрь которого помещен канал с обратным уступом (см. рис. 2).
Для проведения расчетов выделено восемь граничных частей – это шесть частей прямоугольника, ограничивающих расчетную область (на рис. 2 они обозначены “inlet-1”, “inlet-2”, “inlet-3”, “outlet”, “top”, “bottom”), поверхность канала (обозначение – “body”), на которой выделен отрезок для моделирования дросселя (обозначен “throttle”).
На вход канала (граница «inlet-2») подается профилированный
поток 10-компонентного газа с массовыми концентрациями 
, 
. Профили всех величин заданы таблицами вида 
.
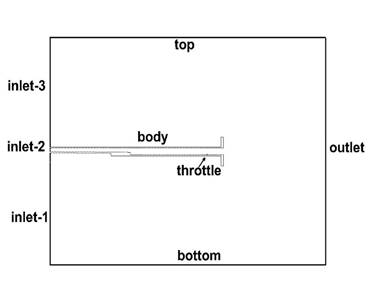
Рис. 2. Геометрия расчетной области с указанием счетных границ
На внешних границах расчетной области “outlet”, “inlet-1”, “inlet-3”,
”top”, “bottom” для всех рассчитываемых величин задается краевое условие 
. Исключение
составляют массовые концентрации смеси – на всех границах, кроме границы «outlet»,
=
=
=
=
=
=
, 
=0.0004051864, 
= 0.2345016207, 
= 0.7650931929.
На всей поверхности канала (граница “body”) задано условие
прилипания 
.
Давление, температура и массовые концентрации определяются условием 
. Граничные условия
на стенках канала для турбулентных величин , ставились при помощи аппарата пристеночных
функций.
Начальные распределения всех полей однородны: 
, 
, 
, 
, 
,
, 
, 
, 
.
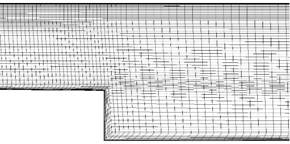
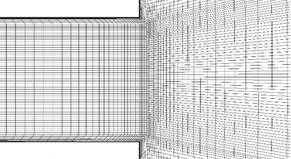
Первоначально была использована сетка, предоставленная коллегами из ЦАГИ. Это блочно-структурная сетка, содержащая 108592 расчетные ячейки, максимальный показатель анизотропии 144, на пограничный слой число приходится около 10 ячеек. Всюду ниже эту сетку именуем как grid_1x1. Ее фрагменты показаны на рис. 3.
|
|
|
|
|
|
|
|
|
Рис. 3. Блочно-структурная сетка. Фрагменты сетки на входе в воздухозаборник, в зоне расширения тракта и выходе из воздухозаборника
Моделирование впрыска топлива и включение процесса дросселирования подробно описано ниже в разделе 3.
Все расчеты по решению задач математического моделирования модельной камеры сгорания проводились на гибридном вычислительном кластере К-100 в ИПМ им. М.В. Келдыша РАН (см. [13]).
4. Вычислительные эксперименты
Для отработки методики предварим расчет полной задачи изучением нескольких подзадач. Первая подзадача воспроизводит течение газовой смеси в тракте модельной камеры сгорания, при этом на входе в тракт заданы массовые концентрации компонент, и демонстрирует влияние на картину течения впрыска холодного топлива. Вторая подзадача рассматривает картину взаимодействия течения в тракте с потоком сжатого воздуха, выдуваемого вверх, перпедикулярно стенке (дросселирование). При этом впрыск топлива не осуществляется. В обеих подзадачах газ не является реагирующим. Реакции рассматриваются только при расчетах полной задачи, когда включены уже все процессы – подача топлива и зажигание смеси после короткого периода дросселирования.
Подзадача 1. В этой подзадаче нас интересует влияние на характеристики течения впрыска холодного углеводородного топлива, осуществляемого внутрь тракта немного выше обратного уступа.
В тракте на расстоянии 0.4 от полной длины тракта от входа располагаются четыре отверстия для подачи топлива:
Параметры подаваемого топлива известны. Среди них 
– статическая
температура, 
–
кинетическая энергия вдуваемого топлива, параметры турбулентности 
, 
. Дополнительно задается
полный расход топлива 
, 
. Соответственно расход топлива через каждое
отверстие составляет 
. Полный расход массы топлива соответствует
значению интегрального коэффициента избытка воздуха 
.
Вдув топлива моделируется добавлением в уравнения системы правых частей в четырех кластерах ячеек, моделирующих отверстия вдува
,
,
,
,
.
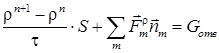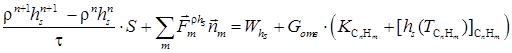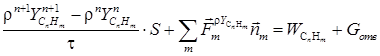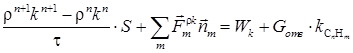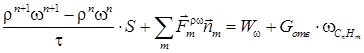Здесь S – площадь расчетной ячейки, 
– внешняя
нормаль к грани ячейки, m – индекс суммирования по всем граням,
ограничивающим ячейку, 
, 
, 
, 
, 
– потоки через грань ячейки; 
, 
, 
, 
– источниковые члены, не связанные с
впрыском топлива, см. уравнения (1–3).
В расчетах впрыск топлива осуществляется только после установления газодинамической картины течения в канале, то есть когда начинается второй этап расчета стационарной картины. Топливо подается непрерывно в течение всего второго этапа установления.
Для определения достаточного объема сетки проведем серию
расчетов на сгущающейся последовательности вложенных сеток, обозначив их ниже grid_1x1
(сетка, предложенная ЦАГИ, с числом ячеек 108592), grid_2x2, grid_4x4, grid_8x8.
Каждая из сеток получена из предыдущей удвоением числа ячеек по обоим
направлениям в прямоугольнике, целиком содержащем внутри себя тракт. Этот
прямоугольник (зона дробления) не совпадает со всей расчетной областью (см.
рис. 4). Сетка grid_4x4 состоит из ~
ячеек, а объем сетки grid_8x8 равен ~
ячеек.
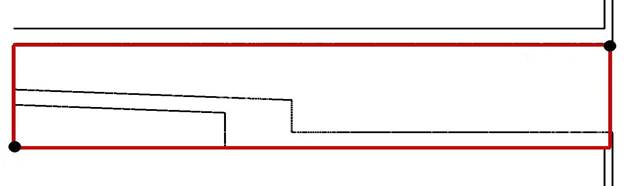
Рис. 4. Геометрия блока, в котором происходит измельчение сетки
На рис. 5 и 6 приведены профили давления 
и температуры Т для двух
сеток grid_1x1 и grid_4x4 вдоль середины тракта (рис. 5) и его верхней кромки
(рис. 6). Под серединой тракта мы понимаем линию, проходящую через середину
границы inlet_2 и параллельную горизонтальной оси 
.
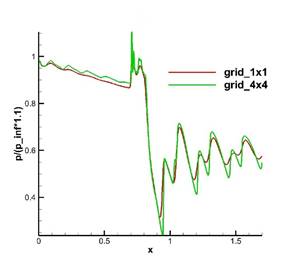
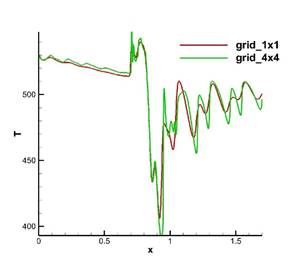
Рис. 5. Распределение нормированного давления (слева) и температуры (справа) на сетках grid_1x1 и grid_4x4 вдоль середины канала.
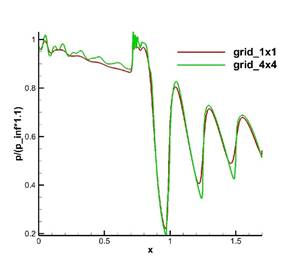
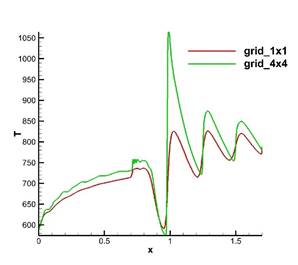
Рис. 6. Распределение нормированного давления (слева) и температуры (справа) на сетках grid_1x1 и grid_4x4 вдоль верхней кромки канала.
Проведенные расчеты позволяют сделать вывод, что сетка grid_4x4
имеет достаточное пространственное разрешение для получения достоверного
результата при решении подзадачи 1. Приведем установившиеся на этой сетке поля
нормированного давления
, температуры T и числа Маха, см. рис. 7.
|
|
|
а). давление |
|
|
|
б). температура |
|
|
|
в). число Маха |
Рис. 7. Поля давления , температуры Т и числа Маха на
сетке grid_4x4, установленные после подачи топлива
Подзадача 2. В этой подзадаче рассматривается взаимодействие течения многокомпонентного газа в исходном модельном тракте с потоком сжатого воздуха, выдуваемого вверх перпедикулярно стенке (дросселирование) в течение короткого времени. Подача углеводородного топлива отключена.
Дроссель работает в течении t=0.00832 c. Сжатый
воздух подается в щель, расположенной на расстоянии 0.14 L от конца тракта (L –
полная длина тракта). Предполагается, что число Маха равно 1 в потоке
вдуваемого воздуха. Кроме того, известны давление торможения вдуваемого воздуха
,
его температура торможения 
и состав газа в струе сжатого воздуха (массовые
доли компонент смеси):
, 
, 
, 
,
Параметры турбулентности в струе сжатого воздуха 
, 
.
В вычислительных экспериментах процедура дросселирования моделируется изменением краевых условий в предписанном участке нижней границы тракта после полного установления течения.
Используется уже описанная выше вычислительная стратегия:
сначала в модели идеального газа (
) рассчитываем газодинамическое течение в тракте
и берем полученные газодинамические поля в качестве начального приближения для
моделирования течения многокомпонентной среды. Краевые условия при переходе от
одного решателя к другому не меняются. После установления течения в тракте
включаем процедуру дросселирования, изменив краевое условие на соответствующей
части нижней стенки канала. Расчет завершается с окончанием работы дросселя.
Расчеты проводятся на серии сеток, введенных в рассмотрение
выше при описании подзадачи 1. При этом первоначально проверка сходимости
проводится в рамках модели однокомпонентного газа. На рис. 8 приведены графики
давления 
на сетках grid_1x1, grid_4x4 и grid_8x8 вдоль
верхней и нижней стенок тракта, а также середины тракта в момент окончания
работы дросселя.
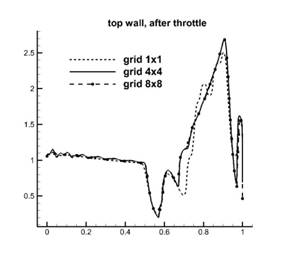
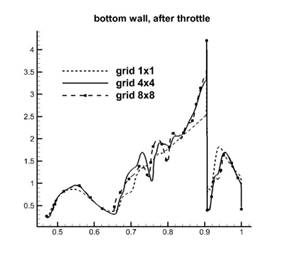
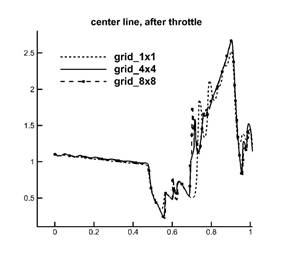
Рис. 8. Сравнение графиков давления на верхней, нижней стенках
и вдоль середины тракта на сетках – grid_1x1, grid_4x4 и grid_8x8 в модели однокомпонентного газа
Как видно из сравнения одномерных графиков результаты на сетках grid_4x4 и grid_8x8 практически совпадают. Дополним картину двумерными полями давления в канале в момент окончания работы дросселя на тех же сетках grid_1x1, grid_4x4 и grid_8x8, см. рис. 9.
Переход к все более подробным сеткам обнаруживает, что в канале вниз по потоку формируется система ударных волн, взаимодействующих как между собой, так и с пограничным слоем. Также формируется серия ножек Маха. Кроме того, в районе дросселя все более явно просматривается зона повышенного давления. Представляется, что возникшая система ударных волн может оказывать влияние на режим горения в канале, но сетка grid_4x4 уже достаточна для того, чтобы ухватить и воспроизвести особенности решения полной задачи (хотя детальную разработку этого вопроса, по-видимому, имеет смысл отложить до проведения трехмерных расчетов).
|
|
grid_1x1 |
|
|
grid_4x4 |
|
|
grid_8x8 |
Рис. 9. Нормированное поле давления, посчитанное на основе модели
однокомпонентного газа на сетках grid_1x1, grid_4x4 и grid_8x8.
Перейдем теперь к модели многокомпонентного газа и расчет проведем на сетке grid_4x4. Как можно видеть из рис. 10, многокомпонентность оказывает существенное влияние на количественную сторону течения – меняется положение скачка, зона повышенного давления формируется уже на верхней стенке канала.
|
|
|
|
Рис. 10. Поля давления на сетке grid_4x4 в модели однокомпонентного газа (верхний график) и многокомпонентного газа (нижний график).
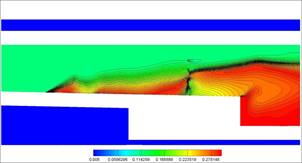
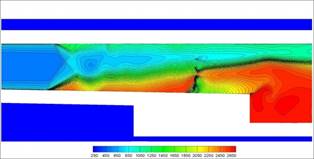
Дополним картину течения полями температуры, чисел Маха и скорости в момент окончания работы дросселя на сетке grid_4x4, см. рис. 11.
|
|
|
|
|
|
Рис. 11. Поля
температуры, числа Маха, линии тока и поле продольной компоненты скорости 
в приближении
многокомпонентного газа. Сетка grid_4x4.
Отметим, что расчеты течений однокомпонентного и
многокомпонентного газа выполнены на разных решателях (sonicFOAM и reactingFOAM
соответственно). Чтобы снять вопрос о влиянии на результаты собственно
вычислительного алгоритма и его конкретной реализации, были проведены
дополнительные расчеты: с помощью решателя reactingFOAM, предназначенным для
анализа течений многокомпонентной среды, было рассчитано течение
однокомпонентного газа с 
с сохранением начально-краевых условий и
вычислительной постановки. Результаты совпали. Таким образом, у авторов нет
оснований думать, что причина отмеченного различия в выборе решателя.
Перейдем к полной постановке задачи. Анализ распределений основных газодинамических характеристик для рассмотренного набора сеток и для расчетов двух описанных выше подзадач показывает, что сетка grid_4x4 имеет пространственное разрешение, минимально возможное (с точки зрения получения достоверного результата) для проведения полного расчета с учетом всех физических явлений – впрыска топлива, дросселирования и горения. При включении всех указанных физических процессов течение принимает ярко выраженный нестационарный характер, см. анимацию ниже на рис. 12.
Представленная анимация выполнена на основе функционала программной платформы ParaView и дает возможность увидеть и оценить качественные характеристики изучаемого физического процесса, указать точки максимального внимания для исследователя.
Рис. 12. Эволюция поля температуры
Тем не менее, при сравнении результатов расчетов для сеток grid_4x4 и grid_8x8 удается выделить инвариантные характеристики течения с горением, что говорит об устойчивости рассчитанного режима течения.
Опишем более подробно получившийся сценарий развития событий. Приведенные ниже расчеты выполнены на сетке grid_4x4. Волна сжатия, вызванная процессом дросселирования, достигает середины канала за обратным уступом и в этот момент инициирует поджиг смеси топлива с воздухом. Это происходит по истечении одной четверти от полного времени дросселирования. Поля распределений температуры и давления на момент поджига приведены на рис. 13.
|
Т |
|
|
Рис. 13. Поля температуры T и нормированного
давления в
момент поджига
Далее волна сжатия быстро распространяется вверх по потоку и поднимается выше места впрыска топлива. Горение следует за псевдоскачком. Это происходит по прошествии половины времени от полного времени работы дросселя. Газодинамическая картина на момент достижения инжекторов волной горения представлена ниже на рис. 14.
|
T |
|
|
|
M |
Рис. 14. Поле температуры
Т, давления 
и числа Маха на момент достижения волной
горения инжекторов
Проходя через инжекторы вверх по потоку, волна сжатия проталкивает влево топливо, однако оно быстро сгорает (см. рис. 15).
|
|
|
Рис. 15. Относительная концентрация 
(слева) и температура T
(справа)
Через короткий отрезок времени волна горения отступает, в то время как волна сжатия продолжает двигаться в сторону входа в тракт. Однако позднее волна горения возвращается, возникает пульсационный режим.
Ниже на рис.16 показано поведение во времени давления и температуры в трех точках (сенсорах) p1, p2, p3 (сетка grid_4x4). Красная линия, проведенная поперек канала, указывает место впрыска топлива. Время отсчитывается от момента окончания работы дросселя.
На рис. 17, 18 показано сравнение поведения во времени давления и температуры соответственно в тех же точках, рассчитанных для сеток grid_1x1, grid_4x4, grid_8x8.
Как видно из рис. 17, 18 прохождение волны горения сопровождается синхронным всплеском величин давления и температуры с примерным периодом 0.003 сек. При этом поведение и давления, и температуры существенно различаются в зависимости от расположения точки наблюдения: до или после впрыска топлива. Вниз по потоку после впрыска топлива наблюдаются четко выраженные, но относительно постепенные колебания давления, амплитуда которых со временем стабилизируется. Этот процесс происходит на фоне сильных колебаний температуры (амплитуда колебаний составляет чуть менее 15000 К). Основной процесс горения происходит в этой зоне. Вверх по потоку до впрыска топлива наблюдается достаточно резкий подъем давления с последующим спадом, причем амплитуда со временем стабилизируется до уровня колебаний в точках р2, р3. Этот процесс происходит на фоне относительно небольших (по сравнению с точками р2, р3) и довольно плавных колебаний температуры, которые, однако, возрастают со временем. Такое различие поведения температуры в точках р1 и р2, р3, по-видимому, обусловлено тем фактом, что точки р2 и р3 находятся в зоне интенсивного горения, в то время, как точка р1 находится выше зоны интенсивного горения в области, расположенной вверх по потоку от впрыска.
Рис. 17, 18 также показывают, что с увеличением размера сетки характер изменений давления и температуры в начале несколько изменяется, но затем воспроизводит ту же картину, что и на рис. 16, при этом период колебаний сохраняется. Это говорит о том, что найденный режим течения является устойчивым.
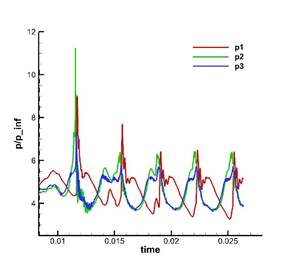
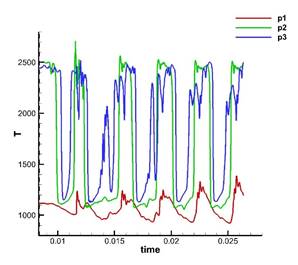
Рис. 16. Зависимость давления и температуры от времени в точках p1, p2, p3 на сетке grid_4x4.
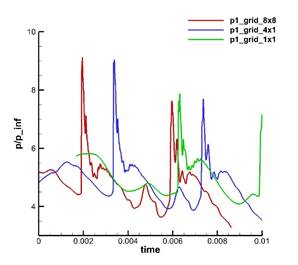
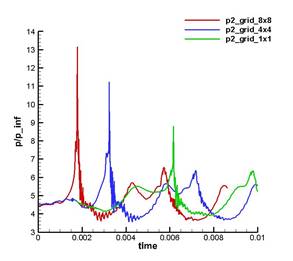
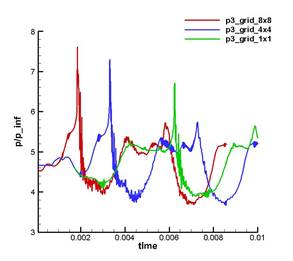
Рис. 17. Cравнение поведения во времени давления на разных сетках в точках p1, p2, p3
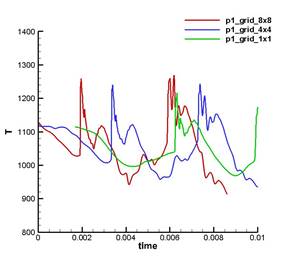
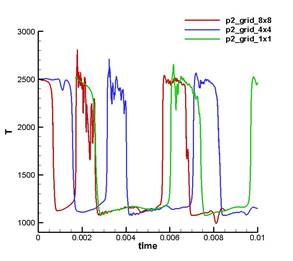
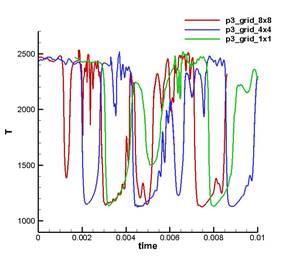
Рис. 18. Cравнение поведения во времени температуры на разных сетках в точках p1, p2, p3
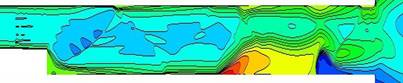
Также приведем картину поля модуля завихренности для сетки grid_8x8, time=0.0201 сек., рис. 19.
Рис. 19. Поле модуля завихренности
Из рис. 19 видно, что вниз по потоку после псевдоскачка течение довольно сильно завихрено, также в основной зоне горения присутствует сильно развитый турбулентный пограничный слой. В анимации на рис. 20 показана эволюция поля модуля завихренности со временем.
Рис. 20. Эволюция модуля завихренности со временем
В настоящей работе взаимовлияние турбулентности и горения не учитывается. Визуальный анализ статического (рис. 19) и динамического (рис. 20) режимов работы ПВРД показывают, что учет этого явления может изменить найденный режим течения. Также общий режим течения может измениться при переходе к трехмерным расчетам. Эти замечания определяют направление дальнейших усовершенствований разработанных методик расчетов. Динамический процесс, продемонстрированный на рис. 20, выполнен средствами графического комплекса Tecplot.
5. Заключение
Результаты расчетов, полученных с помощью комплекса OpenFOAM, показывают принципиальную возможность его использования для расчетов многокомпонентных реагирующих смесей.
Продемонстрирована возможность проведения верификации расчета на основе сходимости решений по набору сеток увеличивающегося объема.
Данная задача требует дальнейшего углубления расчетных исследований, поскольку можно ожидать существенного влияния на характер течения пока неучтенных в модели процессов (влияния турбулентного перемешивания на горение, обмена энергией со стенками канала и т.п.). Проведенная работа также позволяет перейти к изучению динамики многокомпонентной реагирующей среды в трехмерной постановке. Все эти аспекты предполагается отразить в последующих публикациях.
Следует заметить, что современные компьтерные технологии и системы, позволяющие работать с огромными массивами данных, выводят вопросы научной визуализации на передний план, делают практически невозможным быстрый и надежный анализ результатов численного исследования без использования графическеого контента задачи как статического, так и динамического характера, и предложенная работа подтверждает данное утверждение.
Авторы выражают благодарность В.В. Власенко за инициирование данной работы и полезные обсуждения. Авторы выражают признательность А.И. Аптекареву за полезные обсуждения и комментарии.
Список литературы
1. Власенко В.В., Ширяева А.А. Расчеты течения в модельной высокоскоростной камере сгорания с использованием различных моделей химической кинетики. Горение и взрыв. Т. 8, №1, 2015, стр.116-125.
2. OpenFOAM®. URL: http://www.openfoam.com
3. Жуков В.Т., Мануковский К.В., Новикова Н.Д., Рыков Ю.Г., Феодоритова О.Б. Исследование картины течения в модельном тракте двигателя высокоскоростного летательного аппарата. Препринты ИПМ им. М.В. Келдыша 2015. № 5. 23 с.
4. URL: http://library.keldysh.ru/preprint.asp?id=2015-5
5. Жуков В.Т., Мануковский К.В., Новикова Н.Д., Рыков Ю.Г., Феодоритова О.Б. Расчет, анализ и визуализация течения в модельном тракте двигателя высокоскоростного летательного аппарата. Научная визуализация, т. 7, № 1 (2015), 78–95.
6. ParaView. URL: http:// http://www.paraview.org/
7. Tecplot. URL: http://www.tecplot.com/
8. C. Fureby, E. Fedina, J. Tegner. A computational study of supersonic combustion behind a wedge-shaped flameholder. Shock waves, v. 24, issue 1 (2014), pp. 41-50.
9. Дзюбан А. Термодинамика в глобальной сети: текстовый поиск и базы данных. МГУ им. Ломоносова. Научный семинар лаборатории химической термодинамики. 2014.
10. URL: http://td.chem.msu.ru/uploads/files/courses/labseminar/2014/td_www.pdf
11. F.R. Menter, M. Kuntz, R. Langtry. Ten Years of Industrial Experience with the SST Turbulence Model. 2003.
12. F. Moukalled, L. Mangani, M. Darwish. The finite volume method in computational Fluid Dynamics. Springer. 2015.
13. T. Maric, J. Hopken, K. Mooney. The OpenFOAM technology primer. URL: www.sourceflux.de/book, 2014.
14. H. Jasak. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. PhD, Imperial College of Science, Technology and Medicine, 1996.
15. Гибридный вычислительный кластер K-100 URL: http://www.kiam.ru/MVS/resourses/k100.html
ON SIMULATION AND VISUALIZATION OF HIGH-VELOCITY FLOW AND COMBUSTION IN RAMJET ENGINE
I.G. Gudich, V.T. Zhukov, K.V. Manukovskii*, N.D. Novikova, Yu.G. Rykov, O.B. Feodoritova
Keldysh Institute of Applied Mathematics RAS, Moscow, Russian Federation
*Institute for Theoretical and Experimental Physics, Moscow, Russian Federation
igudich@gmail.com, zhukov@kiam.ru, manu@itep.ru, nn@kiam.ru, rykov@keldysh.ru, feodor@kiam.ru
Abstract
The flows of multicomponent media with turbulence and combustion for the numerical study of gas-dynamic processes in the model ramjet engine are considered. To provide ignition of mixture the short time channel lock by compressed air is used. The lock is performed across the main flow. As a result, a quasi-periodic flow with cyclical combustion wave propagation in the background of the complex multiscale structure flow is formed. Consequently, effective interpretation of the results involves the usage of the scientific visualization methods. In the article the flow regimes of multi-component mixture with and without combustion are considered and visualized. The verification of calculations with the help of demonstration of the convergence of approximate solutions by mesh refinement is performed. The calculations are performed on the hybrid supercomputer K-100. Graphical tools and MPI library for the internode communication are used.
Keywords: scientific visualization, mathematical modeling, Navier-Stokes equations, compressible viscous medium, turbulent flows, combustion process, ramjet/scramjet engine, OpenFOAM
References
1. Vlasenko V.V., Shiryaeva A.A. Issledovanie kartiny techenija v model'nom trakte dvigatelja vysokoskorostnogo letatel'nogo apparata [On high velocity flow in model ramjet engine using different kinetic schemes]. Combustion and Explosion. vol. 8, No. 1, 2015, p.116-125. [In Russian]
2. OpenFOAM®. URL: http://www.openfoam.com
3. Zhukov V.T., Manukovskii K.V., Novikova N.D., Rykov Yu.G., Feodoritova O.B. Issledovanie kartiny techenija v model'nom trakte dvigatelja vysokoskorostnogo letatel'nogo apparata [On high velocity flow simulation in model ramjet engine]. Keldysh Institute preprints 2015. № 5. 23 p. [In Russian]
4. URL: http://library.keldysh.ru/preprint.asp?id=2015-5
5. Zhukov V.T., Manukovskii K.V., Novikova N.D., Rykov Yu.G., Feodoritova O.B. Calculation, analysis and visualization of flow simulation in model ramjet engine on high velocity. Scientific visualization, 2015, vol. 7, No. 1, pp. 78–95. [In Russian]
6. ParaView. URL: http:// http://www.paraview.org/
7. Tecplot. URL: http://www.tecplot.com/
8. C. Fureby, E. Fedina, J. Tegner. A computational study of supersonic combustion behind a wedge-shaped flameholder. Shock waves, v. 24, issue 1 (2014), pp. 41-50.
9. Dzuban A. Termodinamika v global'noj seti: tekstovyj poisk i bazy dannyh [Thermodynamics of the global networks: text search and database]. Lomonosov Moscow State University. Scientific seminar of Chemical Thermodynamics Laboratory. 2014. [In Russian]
10. URL: http://td.chem.msu.ru/uploads/files/courses/labseminar/2014/td_www.pdf
11. F.R. Menter, M. Kuntz, R. Langtry. Ten Years of Industrial Experience with the SST Turbulence Model. 2003.
12. F. Moukalled, L. Mangani, M. Darwish. The finite volume method in computational Fluid Dynamics. Springer. 2015.
13. T. Maric, J. Hopken, K. Mooney. The OpenFOAM technology primer. URL: www.sourceflux.de/book, 2014.
14. H. Jasak. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. PhD, Imperial College of Science, Technology and Medicine, 1996.
15. Hybrid computing cluster K-100 URL: http://www.kiam.ru/MVS/resourses/k100.html
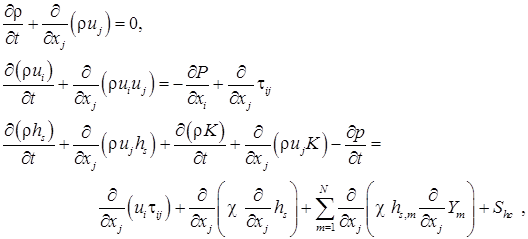
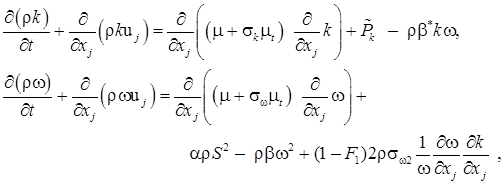
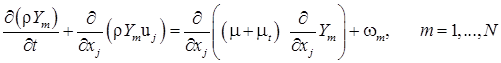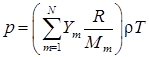
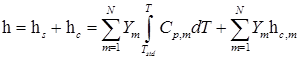