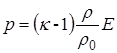В статье представлены результаты расчетного и экспериментального исследования процессов ударно-волнового нагружения прозрачных и непрозрачных твердых тел двумя методами: теоретическим - на основе численного моделирования на регулярной трехмерной сетке с использованием явного решателя в связной лагранжево-эйлеровой постановке, экспериментальным – с использованием метода теневого фотографирования.

Ключевые слова: ударно-волновое нагружение, метод численного решения, теневая фоторегистрация.

1. Введение

Изучение реакции твердых тел на ударно-волновое нагружение является важной и сложной задачей. Определение характера и времени распространения волновых возмущений позволяет дать заключение о физико-механических свойствах нагружаемого объекта, подобрать константы и провести верификацию математической модели. Для этих целей применяются различные экспериментальные методы: метод Кольского, методы с использованием манганиновых датчиков, а также методы визуализации быстропротекающих процессов.

Для визуализации ударно-волновых процессов в оптически прозрачных объектах применяются методы, основанные на зависимости показателя преломления прозрачных сред от локальной плотности среды - теневые методы. В непрозрачных телах волновой портрет на заданный момент времени содержит набор ударных волн над поверхностью противоположной нагружаемой – результат преломления волн сжатия, циркулирующих в нагруженном материале, на свободной границе с воздухом. Кроме того, выход сильной ударной волны на свободную границу может сопровождаться откольными явлениями, либо пылением (ejecta), что также визуализируется теневым методом регистрации.

Вместе с тем необходимо отметить неизменно возрастающую роль численного моделирования и средств компьютерной обработки и представления результатов в изучении быстропротекающих процессов. И сейчас чаще всего именно комплексное использование экспериментальных методов и средств получения необходимой информации о том или ином физическом процессе и численного моделирования с широкими возможностями представления полученных результатов расширяет инструментарий исследователя [1,2,3].

В настоящей работе показаны результаты применения схемы теневой фоторегистрации-прямотеневой регистрации на низкочувствительную пленку с применением взрывного источника света с отсечкой излучения за счет перемешивания [4] - развития волнового возмущения в образце из оргстекла, процессы, сопровождающие выход ударной волны на границу стальной пластины и результаты численного моделирования. Численное моделирование осуществлялось на регулярной трехмерной сетке с использованием явного решателя в связной лагранжево-эйлеровой постановке. На основе сравнения экспериментальных теневых картин распространения возмущения с расчетными данными определены упругие характеристики оргстекла.

Для представления результатов численного расчета и визуализации используются средства и возможности графического интерфейса LS-PrePos [5].

2. Визуализация процессов ударно-волнового нагружения плиты из оргстекла

2.1. Постановка эксперимента

Объектом исследования является плита из оргстекла с размерами 55x55x10 мм. Нагружение осуществлялось взрывом электродетонатора, который располагался снизу, контактируя с центром нижней грани. Объект исследования показан на рисунке 1. Принципиальная схема [4] размещения экспериментального оборудования и образца приведена на рисунке 2.

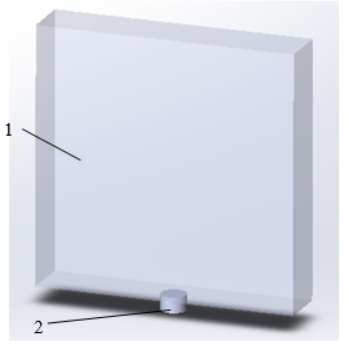
Рис. 1. Объект исследования: 1 - плита из оргстекла, 2 – электродетонатор

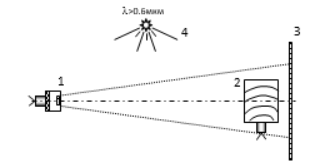
Рис. 2. Принципиальная схема размещения экспериментального оборудования: 1 - миниатюрный взрывной источник света, 2 - объект исследования, 3 - низкочувствительная фотопленка, 4 - искусственное освещение

На основе полученных в различные моменты времени фотографий можно сделать вывод о скорости, характере распространения возмущения по образцу, и подобрать физико-механические свойства математической модели.

2.2. Численное моделирование

Численный расчет ударно-волнового нагружения проводился в конечно-элементном программном комплексе ANSYS с использованием явного решателя LS-DYNA [6,7]. Решение осуществлялось произвольным Лагранжево-Эйлеровым методом (Arbitrary Lagrangian-Eulerian Formulation) [8,9] на регулярной трехмерной сетке. Использовались трехмерные восьмиузловые элементы Solid 164 с заданием формулировки Лагранжа для описания плиты из оргстекла, и формулировки Эйлера - для описания тех частей, которые ведут себя как жидкость - воздух и ВВ. Вид расчетной модели показан на рисунке 3.

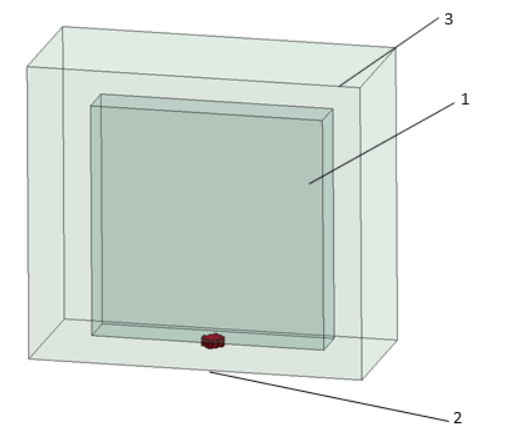
Рис. 3. Расчетная модель: 1 - пластина из оргстекла, 2 - электродетонатор (слой ВВ), 3 - объем воздуха

Конечно-элементная сетка показана на рисунке 4.

Рис. 4. Конечно-элементная сетка (объем воздуха не показан)

Размер ячейки расчетной области, занимаемой оргстеклом, составляет 0,76 мм. Количество ячеек, описывающих объем оргстекла, составляет 72576. Общее количество ячеек, принятое для описания данной задачи, составляет 268654.

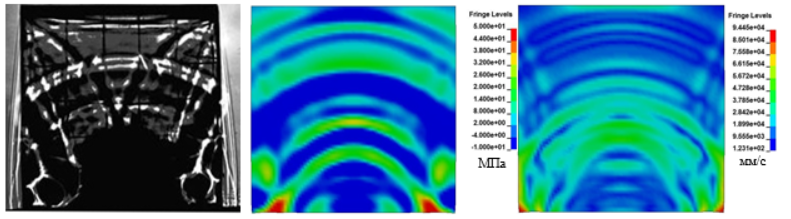
Система уравнений, описывающих течение среды [10], имеет вид


	(1)

где – плотность среды, – вектор скорости среды, – вектор скорости узлов сетки, - векторное поле массовых сил, – тензор напряжений, – тензор скоростей деформаций, – внутренняя энергия, – текущее время.

Напряженно-деформированное состояние в точке расчетной области определялось общей системой уравнений:

p = p(ρ,E),

(2)

где - тензор напряжений, - девиатор напряжений, - символ Кронекера, p - гидростатическое давление, заданное УРС.

Каждой части расчетной модели ставится в соответствие своя математическая модель материала, позволяющая адекватно описать заданное воздействие.

Плита из оргстекла описывалась упругой моделью материала в соответствии с системой уравнений

(3)

где G - модуль сдвига материала, - девиатор напряжений, p - гидростатическое давление, - девиатор деформаций, θ - объемная деформация.

Воздух в расчете подразумевался идеальной средой без учета вязкостных свойств. Напряженно-деформированное состояние определяется только гидростатическим давлением

(4)

где = 1,4 - показатель адиабаты, E – внутренняя энергия на единицу объёма, - начальная плотность.

Для задания материала ВВ использовалась специальная модель взрывчатого вещества, позволяющая моделировать детонацию и течение продуктов взрыва [6,8]. Давление в элементе ВВ в каждый момент времени определяется по формуле

(5)

где – доля выгорания взрывчатого вещества,, , ρ –плотность ВВ, D–скорость детонации, P_CJ– давление Чепмена-Жуге, t_b– время выгорания элемента, Δx – характерный размер элемента.

УРС для продуктов детонации ВВ принято в форме Джонса-Уилкинса-Ли [6,8,11]:

(6)

где - относительный объем продуктов детонации ВВ в процессе взрыва, A, B, R₁, R₂, ω - эмпирические константы, E - внутренняя энергия в единице объема.

Уравнению (1) соответствует изоэнтропа продуктов взрыва:

(7)

Упругие свойства оргстекла и плотность приведены в таблице 1.

Таблица 1. Физико-механические свойства оргстекла

Плотность, кг/м³

Модуль упругости

Коэффициент Пуассона ν

1180

7000

0,3

Плотность оргстекла принята в соответствии с [12]. Модуль упругости и коэффициент Пуассона подобраны таким образом, чтобы волновая картина численного расчета совпадала с экспериментом.

Плотность воздуха составляла кг/м³.

Параметры модели материала ВВ, принятые в соответствии с [13] приведены в таблице 2.

Таблица 2. Параметры модели материала ВВ

Плотность ВВ ρ,

Скорость детонации

D, км/с

Давление Чепмена-Жуге

P_CJ, ГПа

1717

7,98

29,5

Параметры УРС ВВ взяты в соответствии с [13] и приведены в таблице 3.

Таблица 3. Параметры уравнения состояния продуктов детонации ВВ

A, ГПа	B, ГПа	R₁	R₂	ω
524,2	7,678	4,2	1,1	0,34

2.3. Результаты численного моделирования и эксперимента

На приведенных ниже рисунках представлены картины распространения ударно-волнового возмущения по плите из оргстекла. На теневой фотографии это выражено в регистрации оптических неоднородностей при выходе возмущений на свободную поверхность и зоны потери прозрачности в объеме оргстекла. Рядом с теневыми фотографиями приведены результаты численного расчета в виде полей скорости и давления.

Чтобы выполнить сравнение результатов численного расчета с результатами эксперимента, выбиралось распределение давлений и скоростей эквивалентное распределению зон потери прозрачности оргстекла. Критерием правильности выбора параметров расчетной модели, описывающей оргстекло, было совпадение моментов времени экспериментальных картин и расчетных.

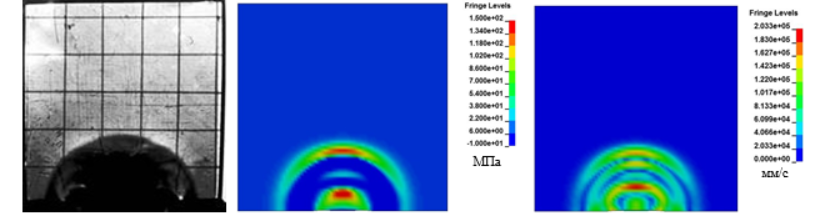
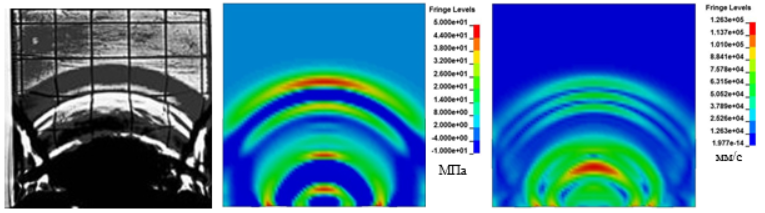
На рисунках 5-8 помимо теневых фотографий представлены картины распределения полей давления и результирующей скорости. Процесс распространения возмущения и в эксперименте и в численной реализации начинается от нижней грани образца после приложения импульсной нагрузки - взрыва капсюля-детонатора (заряда взрывчатого вещества). В процессе распространения волнового возмущения происходит многократное отражение волны от свободной нижней грани с формированием сложной картины, как показано на рисунке 5. С течением времени отражение происходит от боковых и верхней граней. Это хорошо заметно на рисунках 6-8. Качественно лучшее совпадение с экспериментом наблюдается у картин с распределением скоростей ввиду того, что затемнения на теневой картине соответствуют горбам и впадинам на поверхности плиты из оргстекла, то есть колебательному характеру распространения возмущения. А колебательный процесс в данном численном эксперименте лучше всего визуализировать, отображая скорость точек модели.


а) 6,1 мкс	б) 6,3 мкс	в) 6,3 мкс

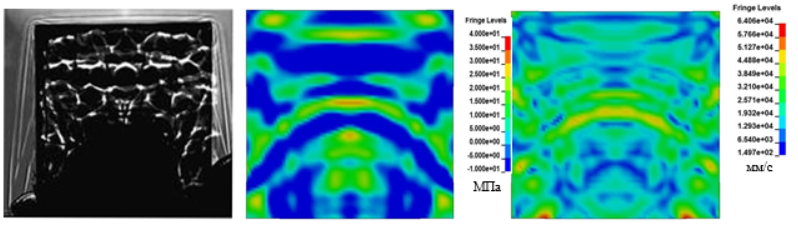
Рис. 5. а - теневая картина процесса, б - распределение давления, в - распределение результирующей скорости


а) 12 мкс	б) 12,2 мкс	в) 12,2 мкс

Рис. 6. а - теневая картина процесса, б - распределение давления, в - распределение результирующей скорости


а) 20 мкс	б) 20,2 мкс	в) 20,2 мкс

Рис. 7. а - теневая картина процесса, б - распределение давления, в - распределение результирующей скорости


а) 30 мкс	б) 30,68 мкс	в) 30,38 мкс

Рис. 8. а - теневая картина процесса, б - распределение давления, в - распределение результирующей скорости

Как видно из рисунков 5-8, максимальная погрешность временной реализации волновой картины в расчете по сравнению с экспериментом составляет не больше 3,2 %.

Об осцилляции свободной поверхности можно судить по графику изменения скорости точки, расположенной на свободной поверхности плиты. Точки, в которых определялась скорость, показаны на рисунке 9.

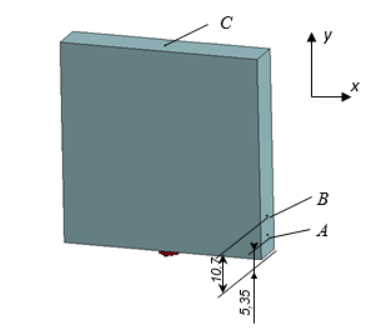
Рис. 9. Точки определения скорости

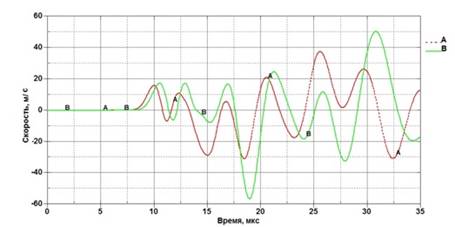
Рис. 10. Скорости точек А и В в направлении оси X (см. рис. 9)

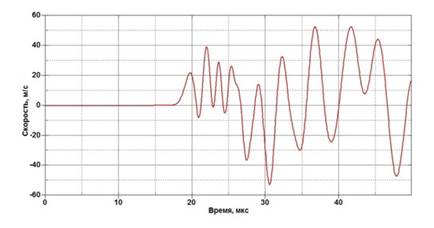
Рис. 11. Скорости точки С в направлении оси Y (см. рис. 9)

По графикам изменения скоростей точек можно сделать вывод, что на момент времени t=30 мкс боковая поверхность (где расположены точки А и В) совершила 6 осцилляций, верхняя (где расположена т. С) - 5 осцилляций. Это соответствует теневой картине.

3. Визуализация процессов ударно-волнового нагружения стальной пластины

В этом разделе приводятся результаты схемы теневой фоторегистрации - прямотеневой регистрации на низкочувствительную пленку с применением взрывного источника света, использующего сжатие в условиях остроугольной геометрии без фазового ускорения [4] - процесса ударно-волнового нагружения стальной пластины, а также результаты численного моделирования. Численное моделирование, также как и в предыдущем разделе, осуществлялось на регулярной трехмерной сетке с использованием явного решателя в связной лагранжево-эйлеровой постановке.

3.1. Постановка эксперимента

Объектом исследования является пластина из стали Ст45 с размерами 15x15x5 мм. Нагружение осуществлялось взрывом электродетонатора, который располагался снизу, контактируя с центром нижней грани. Объект исследования показан на рисунке 12.

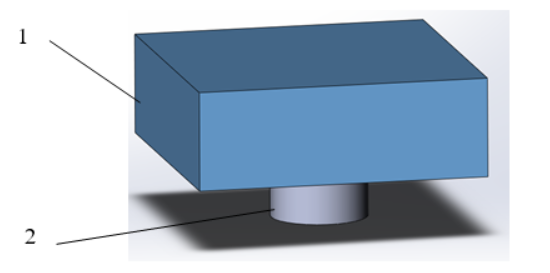
Рис. 12. Объект исследования: 1 - стальная пластина (Ст 45), 2 – электродетонатор

Принципиальная схема [4] размещения экспериментального оборудования и образца показана на рисунке 13.

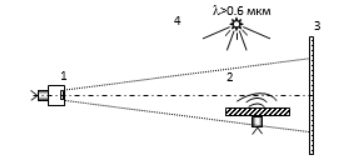
Рис. 13. Принципиальная схема размещения экспериментального оборудования: 1 - миниатюрный взрывной источник света, 2 - объект исследования, 3 - низкочувствительная фотопленка, 4 - искусственное освещение

3.2. Численное моделирование

Численный расчет ударно-волнового нагружения проводился в конечно-элементном программном комплексе ANSYS с использованием явного решателя LS-DYNA [6,7]. Решение осуществлялось произвольным Лагранжево-Эйлеровым методом (Arbitrary Lagrangian-Eulerian Formulation) [8,9] на регулярной трехмерной сетке. Использовались трехмерные восьмиузловые элементы Solid 164 с заданием формулировки Лагранжа для описания стальной пластины, и формулировки Эйлера - для описания тех частей, которые ведут себя как жидкость - воздух и ВВ. Вид расчетной модели показан на рисунке 14.

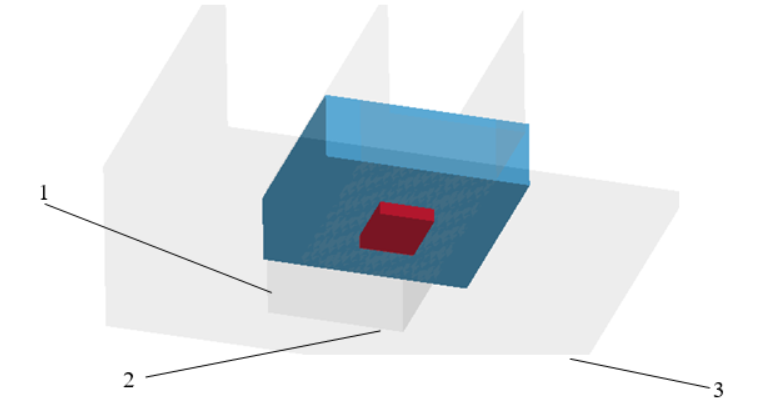
Рис. 14. Расчетная модель: 1 - стальная пластина, 2 - электродетонатор (слой ВВ), 3 - объем воздуха

Конечно-элементная сетка показана на рисунке 15.

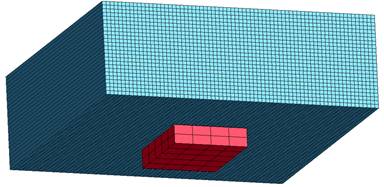
Рис. 15. Конечно-элементная сетка (объем воздуха не показан)

Размер ячейки расчетной области, занимаемой стальной пластиной, составляет 0,2 мм. Количество ячеек, описывающих объем стальной пластинки, составляет 122500. Общее количество ячеек, принятое для описания данной задачи, составляет 138276.

Система уравнений, описывающих течение среды [10], имеет вид (1).

Напряженно-деформированное состояние в точке расчетной области определялось общей системой уравнений (2).

Каждой части расчетной модели ставится в соответствие своя математическая модель материала, позволяющей адекватно описать заданное воздействие.

Пластические свойства описывались моделью Джонсона-Кука, учитывающей скоростное упрочнение и температурное разупрочнение. Выражение для напряжения текучести в рамках модели Джонсона-Кука [14,15] имеет следующий вид:

(8)

где – модуль упрочнения, – эффективная пластическая деформация, – скорость эффективной пластической деформации, 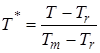, – комнатная температура; – температура плавления; – параметры.

Параметры модели Джонсона-Кука для стали Ст 45 класса прочности k56 подбирались из аппроксимации диаграмм деформирования [16,17,18]. Параметры приведены в таблице 4.

Таблица 4. Параметры модели материала Джонсона-Кука для стали класса прочности k56

Обозначение

параметра

МПа

T_r,

°С

T_m,

°С

Значение

параметра

410

280

0,0037

0,12

1530

Для определения зависимости p = p(ρ,E) для стали использовалось УРС Грюнайзена [6] вида:

(9)

де ρ₀ – начальная плотность, - относительное изменение объема, γ₀ - постоянная Грюнайзена, a - коррекция постоянной Грюнайзена, ,, – коэффициенты аналитического выражения ударной адиабаты вещества

(, D – скорость фронта ударной волны, с₀ – объемная скорость звука, u – массовая скорость вещества),

E – внутренняя энергия на единицу объёма.

Параметры УРС стали Ст45 подобраны в соответствии с экспериментальными данными по ударному сжатию [18,19] и приведены в таблице 5.

Таблица 5. Параметры УРС стали Ст45

Название

параметра

Плотность

Объемная скорость звука

Коэффициент Грюнайзена

Параметр

()

Значение

параметра

7500

3,7

2,9

1,87

Воздух в расчете подразумевался идеальной средой без учета вязкостных свойств. Состояние определяется только гидростатическим давлением

(10)

где = 1,4 - показатель адиабаты, E – внутренняя энергия на единицу объёма, - начальная плотность. Начальная плотность воздуха составляла кг/м³.

Для задания материала ВВ использовалась та же модель взрывчатого вещества, что и приведенная в разделе 2.

Параметры модели материала ВВ, принятые в соответствии с [11,13], аналогичны приведенным в таблице 1. Параметры УРС ВВ взяты в соответствии с [11,3] и аналогичны приведенным в таблице 2.

3.3. Результаты численного моделирования и эксперимента. Сравнение.

На рисунке 16 показано распределение давления в пластине на момент выхода ударной волны на свободную поверхность, полученное в численном расчете. На рисунках 17 и 18 представлены теневые картины осцилляций свободной поверхности пластины с формированием зон оптических неоднородностей в воздухе в моменты времени t = 5,3 мкс и t = 20 мкс. На теневой картине также зафиксированы процессы пылеобразования при выходе ударной волны на свободную поверхность.

На рисунке 19 приведен график изменения скорости центральной точки свободной поверхности, противоположной той, где производится нагружение.

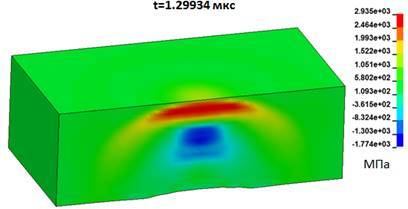
Рис. 16. Распределение давления в пластине на момент выхода ударной волны на свободную поверхность

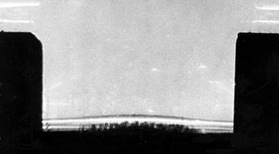
Рис. 17. Теневая картина процесса нагружения стальной пластины на момент времени t = 5,3 мкс

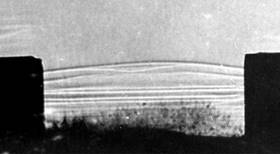
Рис. 18. Теневая картина процесса нагружения стальной пластины на момент времени t = 20 мкс

По теневой картине процесса нагружения стальной пластины (рис. 17) можно заключить, что ко времени t = 5,3 мкс ударная волна прошла минимум 5 раз по толщине пластины, так как на картине зафиксированы три линии оптической неоднородности - скачки уплотнения в воздухе, вызванные колебанием свободной поверхности пластины.

На графике изменения скорости центральной точки (рис. 19) также хорошо видны три осцилляции до момента t = 5,3 мкс.

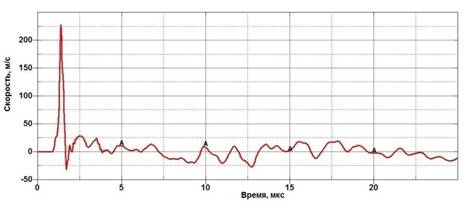
Рис. 19. График изменения скорости центральной точки

4. Заключение

1. В статье приведены теневые фотографии ударно-волнового нагружения оргстекла. Представлены результаты численного моделирования в связанной лагранжево-эйлеровой постановке, в котором оргстекло описывалось упругой моделью материала. Упругие константы модели подобраны итерационно из соответствия волновых картин в различные моменты времени экспериментальным данным, а именно: модуль упругости E=7000 МПа, коэффициент Пуассона ν =0,3. По данным экспериментов проведена верификация математической модели, которая показала хорошее соответствие расчетной модели полученным экспериментальным данным.

2. Представлены экспериментальные данные по ударно-волновому нагружению пластины из стали и результаты численного моделирования в связанной лагранжево-эйлеровой постановке. Сопоставление экспериментальных и расчетных данных позволило оценить адекватность математической модели реальным процессам.

3. Показано, что, имея результаты оптической регистрации процесса распространения ударно-волнового возмущения, не прибегая к дополнительным инструментариям, например, емкостным датчикам скорости, и используя возможности современных программных комплексов численного моделирования, можно идентифицировать некоторые константы материала экспериментального образца, а также провести верификацию математических моделей, описывающих деформирование материала образцов.

Работа проводилась при финансовой поддержке Министерства образования и науки Российской Федерации в рамках Соглашения № 14.577.21.0104 с федеральным государственным бюджетным образовательным учреждением высшего профессионального образования «Нижегородский государственный технический университет им. Р.Е. Алексеева» (уникальный идентификатор проекта RFMEFI57714X0104).

Список литературы

1. Знаменская И., Луцкий А., Ханхасаева Я., Цзинь Ц. Взаимодействие численной и экспериментальной визуализации при исследовании свойств разрядов методом анализа ударно-волновых конфигураций. Научная визуализация. Т.5, №3, с 40-51, 2013.

2. Бондарев А., Галактионов В. Современные направления развития визуализации данных в вычислительной механике жидкости и газа. Научная визуализация. Т.5, №4, с 18-30, 2013.

3. Пилюгин В., Маликова Е. Пасько А., Аджиев В. Научная визуализация как метод анализа научных данных. Научная визуализация. Т.4, №4, с 56-70, 2012.

4. Герасимов С.И., Файков Ю.И. Теневое фотографирование в расходящемся пучке света: Монография. Саров: ФГУП "РФЯЦ-ВНИИЭФ", 2010. 344 с.

5. Кравчук А.С., Чашинский А.C., Кравчук А.И. Основные элементы графического интерфейса LS-PREPOST. Электрон. текстовые дан. Минск : БГУ, 2013. 74 с.

6. Hallquist J.O. LS-DYNA: Theoretical manual. Livermore Software Technology Corporation, Livermore, 1998. 498 p.

7. Ansys, customer number 602402.

8. Souli M. "LS-Dyna Advanced Course in ALE and Fluid/Structural Coupling". Course Note for Arbitrary Lagrangian-Eulerian Formulation Technique. M. Souli. Livermore, LSTC, CA, 2000.

9. Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике. М.: Наука. Главная редакция физ.-мат. литературы, 1982. 392 с.

10. Муйземнек А.Ю., Богач А.А. Математическое моделирование процессов удара и взрыва в программе LS-DYNA. Пенза: Информационно-издательский центр ПГУ, 2005.

11. Lee E, Finger M., Collins W. JWL equation of state coefficients for high explosives. Rept-UCID-16189, Lawrence Livermore National Laboratory, 1973.

12. ГОСТ 17622-72. Стекло органическое техническое. Технические условия.

13. Орленко Л.П. Физика взрыва. Изд. 3-е, испр. В 2 т. Т.1. М.:ФИЗМАТЛИТ, 2004.

14. Johnson G.R., Cook W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. Proc. of 7th Symposium on Ballistics, Hague, Netherlands, 1983. P. 541-547

15. Ozel T., Karpat Y. Identification of constitutive material model parameters for high-strain rate metal cutting conditions using evolutionary computational algorithms. Materials and Manufacturing Processes, 2007. Vol. 22. Pp. 659-667.

16. В.Г. Сорокин и др. Стали и сплавы. Марочник: Справ. изд. М.: "Интермет Инжиниринг", 2001. 608 с.

17. Михайлов Н.Я., Учаев А.А., Хорошкина Г.П. Физико-механические свойства конструкционных материалов и некоторые современные методы их исследования: Справочное пособие. М.: ЦНИИатоминформ, 1982. 239 с.

18. Б.Л. Глушак, В.Ф. Куропатенко, С.А. Новиков. Исследование прочности материалов при динамических нагрузках. Новосибирск: "Наука". Сиб. отделение, 1992. 395с.

19. Р.Ф. Трунин, Л.Ф. Гударенко, М.В. Жерноклетов, Г.В. Симаков Экспериментальные данные по ударно-волновому сжатию и адиабатическому расширению конденсированных веществ: Научное издание - 2-е изд., перераб. и доп. Саров: ФГУП "РФЯЦ-ВНИИЭФ", 2006. 531 c.

NUMERICAL AND EXPERIMENTAL STUDY OF SHOCK-WAVE LOADING OF SOLIDS

S.I. Gerasimov^1,2,3,4, V.A. Kuzmin^3,4, V.A. Kikeev⁴ , R.V. Gerasimova^1,2

¹ Sarov Physics and Technical Institute of National Research Nuclear University «MEPhI», 607186 Nizhny Novgorod region, Russia

² National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), 115409 Moscow

³ Russian Federal Nuclear Center – All-Russia Research Institute of Experimental Physics, 607188 Sarov, Nizhny Novgorod region, Russia

⁴ Nizhny Novgorod State Technical University n.a. R.E. Alekseev, 603950 Russia

E-mail: s.i.gerasimov@mail.ru, v_a_kuzmin@mail.ru, vkikeev@mail.ru, r.v.gerasimova@mail.ru

Abstract

The article presents the results of computational and experimental studies of the processes of shock-wave loading of transparent and opaque solids using two methods: theoretical - based numerical simulation on a regular three-dimensional grid using an explicit solver in a connected Lagrangian-Eulerian formulation, experimental – using the method of shadow photography.

Keywords: shock-wave loading, method of numerical solution, the shadow photographic.

References

1. Znamenskaya I., Lutsky A., Khankhasaeva Y., Jin J. Vzaimodejstvie chislennoj i jeksperimental'noj vizualizacii pri issledovanii svojstv razrjadov metodom analiza udarno-volnovyh konfiguracij [Interaction of numerical and experimental visualization at investigation of discharge properties by means of shock wave configurations analysis]. Scientific Visualization. Vol. 5. No. 3. Pp 40-51, 2013. [In Russian]

2. Bondarev A., Galaktionov V. Sovremennye napravlenija razvitija vizualizacii dannyh v vychislitel'noj mehanike zhidkosti i gaza [State-of-the-art in data visualization for CFD problems]. Scientific Visualization. Vol. 5. No. 4. Pp. 18-30, 2013. [In Russian]

3. Pilyugin V., Malikova E., Pasko A., Adzhiev V. Nauchnaja vizualizacija kak metod analiza nauchnyh dannyh [Scientific Visualization as Method of Scientific Data Analysis]. Scientific Visualization. Vol. 4. No. 4. Pp. 56-70, 2012. [In Russian]

4. Gerasimov S.I., Phaykov Y.I. Tenevoe fotografirovanie v rashodjashhemsja puchke sveta: Monografija [Shadow photographing in a divergent light beam: Monograph]. Russian federal nuclear center all-Russian research institute of experimental physics, 2010. 344 p. [In Russian]

5. Kravchuk A.S., Chashinskij A.C., Kravchuk A.I. Osnovnye jelementy graficheskogo interfejsa LS-PREPOST. Jelektronnye tekstovye dannye [The main elements of LS-PREPOST GUI. Electronic text data]. BSU, 2013. 74 p. [In Russian]

6. Hallquist J.O. LS-DYNA: Theoretical manual. Livermore Software Technology Corporation, Livermore, 1998. 498 p.

7. Ansys, customer number 602402.

8. Souli M. LS-Dyna Advanced Course in ALE and Fluid/Structural Coupling. Course Note for Arbitrary Lagrangian-Eulerian Formulation Technique. M. Souli. Livermore, LSTC, CA, 2000.

9. Belotserkovskii O.M., Davydov Yu.M. Metod krupnyh chastic v gazovoj dinamike [Method of large particles in gas dynamics]. Nauka. 1982. 392 p. [In Russian]

10. Mujzemnek A.Ju., Bogach A.A. Matematicheskoe modelirovanie processov udara i vzryva v programme LS-DYNA [Mathematical modeling of the processes of impact and explosion in the program LS-DYNA]. Information and Publishing Center of BSU, 2005. [In Russian]

11. Lee E, Finger M., Collins W. JWL equation of state coefficients for high explosives. Rept-UCID-16189, Lawrence Livermore National Laboratory, 1973.

12. GOST 17622-72. Steklo organicheskoe tehnicheskoe. Tehnicheskie uslovija [The organic glass technical. Technical conditions]. [In Russian]

13. Orlenko L.P. Fizika vzryva [Physics of explosion]. 3-d edition. First tome. FIZMATLIT, 2004. [In Russian]

16. V.G. Sorokin et al. Stali i splavy [Steel and alloys].Intermet Inzhiniring, 2001. 608 p. [In Russian]

17. Mihajlov N.Ja., Uchaev A.A., Horoshkina G.P. Fiziko-mehanicheskie svojstva konstrukcionnyh materialov i nekotorye sovremennye metody ih issledovanija: Spravochnoe posobie [Physico-mechanical properties of structural materials and some modern methods of investigation: a reference guide]. CNIIatominform, 1982. 239 p. [In Russian]

18. B.L. Glushak, V.F. Kuropatenko, S.A. Novikov. Issledovanie prochnosti materialov pri dinamicheskih nagruzkah [The investigation of the strength of materials under dynamic loads]. Nauka. 1992. 395 p. [In Russian]

19. R.F. Trunin, L.F. Gudarenko, M.V. Zhernokletov, G.V. Simakov Jeksperimental'nye dannye po udarno-volnovomu szhatiju i adiabaticheskomu rasshireniju kondensirovannyh veshhestv: Nauchnoe izdanie [Experimental data on shock compression and adiabatic expansion of condensed materials: Scientific publication ]. 2-nd edition. FGUP "RFJaC-VNIIJeF". 2006. 531 p. [In Russian]
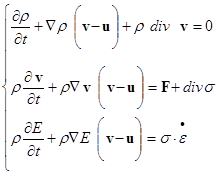
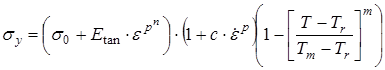
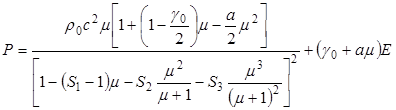