ВИЗУАЛЬНЫЙ ТЕКСТ КАК ИСТИННОСТНОЕ ПОДМНОЖЕСТВО УНИВЕРСАЛЬНОГО ПРОСТРАНСТВА
Д.В. Манаков1, В.Л. Авербух1,2, П.А. Васёв1
1 Институт математики и механики им. Н.Н. Красовского Уральского отделения РАН
2 Уральский Федеральный Университет им. Б. Н. Ельцина, Екатеринбург, Россия
manakov@imm.uran.ru ; averbukh@imm.uran.ru ; vasev@imm.uran.ru
Содержание
2. Универсальное пространство визуализации
3. Необходимые условия эффективной визуализации
Аннотация
Работа посвящена описанию формальных подходов к оценке визуального текста и эффективности визуализации. Наравне с лингвистическим подходом (построение текста по определенным правилам) рассмотрение визуального текста как истинностного подмножества универсального пространства является одним из направлений, возможность применения которого показана на примере разработки конструкторов визуализации.
Понятие визуального текста активно используется как в гуманитарных дисциплинах, так и в компьютерной визуализации. Предложено очевидное определение: визуальный текст – продукт любой системы компьютерной визуализации. Используемое в экономике определение эффективности (продуктивности) через отношение продукта к источнику продукта (ресурсам) достаточно адекватно. Формально, это скорость или полный дифференциал. Следовательно, эффективность визуализации – функция многих переменных, параметрами которой являются частные производные продукта (визуального текста) по его информативным признакам.
Необходимым условием существования производной является рассмотрение непрерывного отображения. В том числе и поэтому предлагается рассматривать метафору визуализации как непрерывное отображение, аналогично денотационной семантики, принятой в области программирования. Непрерывное отображение также можно определить через малое изменение параметров визуализации.
В математическом моделировании изучение слабо формализуемых явлений принято начинать с построения модели первого приближения. В частности, визуальный текст есть произведение логической матрицы и интеллектуального агента. Рассматривается обратная задача, поскольку интерпретация текста как подмножества универсального пространства предполагает, что визуальный текст имеет истинностное значение, а свойства интеллектуального агента в общем случае не определены.
В предлагаемую модель заложена зависимость интеллектуального агента от восприятия и понимания. Проблемы восприятия являются актуальным вопросом для компьютерной визуализации. Перспективным направлением является рассмотрение восприятия визуального текста с точки зрения теории информации. В этой связи в работе предложена метафора восхода солнца.
Ключевые слова: эффективность визуализации, универсальное пространство визуализации, визуальный текст.
1. Введение
Материалы, изложенные в данной работе, следует рассматривать в качестве постановки задач, направленных на формирование ментального пространства визуализации и требующих дальнейшей детализации. Основное внимание уделено описанию формальных подходов к оценке визуального текста и эффективности визуализации для того, чтобы в конце работы ответить на вопрос, являются ли эти понятия взаимозависимыми.
В связи с появлением большого количества разнообразных креолизованных (смешанных) текстов возникает необходимость обобщения подобных явлений. Многоязычные тексты являются не только продуктом рекламы или художественных инсталляций, но и расширенной реальности, и специальных тем, например, систем визуальной отладки параллельных программ в области компьютерной визуализации.
В данной работе визуальный текст рассматривается как универсальный (обобщенный) текст – продукт любой системы компьютерной визуализации. Под компьютерной визуализацией понимается методика перевода абстрактных представлений об объектах в визуальные образы (пространственно-временные тексты), что дает возможность исследователю наблюдать результаты компьютерного моделирования явлений и процессов. Визуализация, представляя результаты вычислений, обеспечивает интерпретацию и анализ полученных данных.
Если интерпретация изобразительных текстов возможна при наличии внешней по отношению к самому тексту информации [1], а так называемая беспредметная живопись является скорей живописью с неопределенными значениями изображений, то в области компьютерной визуализации рассматривалась бы модель с неопределенностью.
Начиная с 2012 года, проводятся Европейские семинары по проблеме воспроизводимости, верификации и валидации в визуализации [2]. Под верификацией понимается доказательство правильности, так, с точки зрения логики, визуальный текст должен иметь истинное значение. Если гуманитарно-психологическое направление ограничивается декларативным определением креолизованного текста, его анализом с помощью ай-трекинга, опросами и тестированием пользователей, то для компьютерной визуализации естественным является формализация, математизация, моделирование подобных явлений. Например, в работе [3] рассматривается множественный, в частности, бинарный вид отображения, понимаемый в обычном алгебраическом смысле: два множества (два окна), между которыми заданы некоторые отношения.
Несмотря на различный уровень формализации, можно выделить два взаимодополняющих направления, рассматриваемых, как прямая и обратная задачи. Лингвистический подход – построение текста по определенным правилам (синтаксическим, семантическим), в том числе и с точки зрения семиотики (науки о знаках), и обратный подход, когда, анализируя текст, необходимо восстановить правила или определить свойства системы визуализации. В последнем случае возможна интерпретация текста как подмножества универсального пространства.
2. Универсальное пространство визуализации
С помощью универсальных пространств можно свести изучение класса топологических пространств к изучению подпространств конкретного пространства. В области визуализации предлагается рассмотреть аналогичный подход, основанный на изучении подпространств (подмножеств) – визуальных текстов. Именно текстов, а не видов отображения или метафор визуализации, так как текст предполагает зависимость от контекста, например, от формальной модели, и от человеческого фактора, связанного с восприятием и пониманием это текста. К вопросу о доказательстве правильности или истинности текста можно подойти с точки зрения универсальной логики.
Обычное логическое пространство [4] определяется как пара LS = (V, 2V), где фиксированное непустое множество значений истинности - V рассматривается вместе с множеством своих подмножеств - 2V. Иными словами, множество истинностных значений называется логическим пространством, если на нем выделены определенные подмножества.
При рассмотрении компьютерной визуализации как самостоятельной дисциплины, необходимо построение ее ментального пространства со своей семантикой, прагматикой и базисом. Тогда любые два специалиста по визуализации смогут говорить на одном языке. Этот базис выбирается из достаточно широкой области знаний [3]. Универсальное пространство отличается от ментального пространства, не только степенью формализации, но прежде всего тем, что базисом в универсальном пространстве являются непересекающиеся истинностные подмножества (визуальные тексты). Для лингвистического подхода базис связан с когнитивной размерностью, которая определяется количеством независимых эвристик или термов.
Семантика в математическом смысле трактуется как семантическое правило (например, определение лингвистической переменной) или отображение. В качестве примера можно привести семиотическое определение метафоры визуализации, рассматриваемой как непрерывное отображение исходного множества на целевое множество [3]. В стандартное определение метафоры по Лакоффу [5] добавлено только свойство непрерывности. При рассмотрении непрерывного отображения топологический подход, основанный на построении замыкания с такими определяющими свойствами, как монотонность и существование супремума, является конструктивным. Наиболее известным примером в области программирования является денотационная семантика Скотта для l-исчисления [6]. Хотя рассмотрение подобной задачи возможно и с позиций универсальной логики и структур событий [7].
Аналогично прагматику можно рассматривать с точки зрения прагматической логики – логическая система, опирающаяся на ценности (полезность), оценки, нормы. Можно сравнить определения метафоры и инсайта [8] (озарение, понимание), являющегося целью визуализации, Инсайт – процесс установления релевантных отношений между данными и существующей областью знаний (целевой областью). Инсайт одна из абстрактных метрик, связанных с процессом познания: наряду с информационным разрывов и когнитивным расстоянием. В результате сравнения можно сделать вывод, что прагматика – это навешивание некоторой метрики на отображение. Введение к рассмотрению метрики позволяет перейти от топологии к математическому анализу, в частности к рассмотрению предела. Понятие предела целесообразно использовать при анализе больших данных, а также для определения эффективности через производную.
Эффективность визуализации можно рассматривать как одну из прагматик. Используемое в экономике определение эффективности (продуктивности) через отношение продукта к источнику продукта (ресурсам) достаточно адекватно. Формально, это скорость или полный дифференциал.
3. Необходимые условия эффективной визуализации
В [9] в рамках эмпирического подхода предлагается формализация понятий, связанных с масштабируемостью параллельных программ и рассматриваемых как функции многих переменных. “Масштабируемость – свойство параллельной программы, характеризующие зависимость изменения динамических характеристик ее работы (в частности, эффективности) от изменения параметров запуска”.
Аналогичным образом можно определить и масштабируемость визуализации, то есть необходимым условием эффективной визуализации является возможность изменения параметров программы визуализации. Многопараметрическая модель основывается на выделении свойств рассматриваемого явления или на категоризации. Формально, объекту ставится в соответствие вектор параметров. В области программирования подобный подход принято называть операционной семантикой. Возможно определение непрерывности и через малое изменение параметров. Нас, прежде всего, интересует непрерывность цикла прохождения задания и непрерывность познания, включая визуальный анализ результатов вычислений. Таким образом, для систем визуализации возможна постановка таких стандартных в математическом плане задач:
1. Определение информативных признаков, то есть, какими свойствами должна обладать система визуализации, чтобы работа с ней была эффективной;
2. Задача визуального анализа чувствительности решения в зависимости не только от параметров прикладной задачи (модели), но и от параметров параллельной программы, и от параметров визуализации.
Определим эффективность визуализации, развивая аналогичное понятие, используемое в экономике, с подстановкой определения визуального текста. Эффективность визуализации – функция многих переменных, параметрами которой являются частные производные продукта (визуального текста) по его информативным признакам. Например, одно из требований к системам визуализации - работа в режиме реального времени. В частности, необходимо обеспечить работу так, чтобы она не зависела от количества визуализируемых данных, то есть производная по количеству данных не должна превосходить константу или должна быть ограниченной. Очевидным условием существования производной является рассмотрение непрерывного отображения.
Система визуализации должна обладать свойствами, ставшими необходимыми де-факто и обеспечивающими непрерывность, в частности, через изменения параметров:
1. Он-лайн и удаленная визуализация, обеспечивающая непрерывность, в частности как зависимость объема, передаваемой информации от параметров сети [10];
2. Возможность обработки данных большого объема, в частности применяя технологию фильтрации данных [3], которая может быть реализована в следующей последовательности: кластеризация, установление частичного порядка на выделенных подмножествах и рассмотрение этих подмножеств, как истинных визуальных текстов;
3. Web-визуализация. Интернет – единое информационное пространство, фактически не ограниченное по количеству ресурсов, в том числе и по количеству пользователей. Опираясь на модель хищник – жертва можно прогнозировать экспоненциальный рост пользователей, систем визуализации использующих Web-технологии в отличие от локального применения в рамках конкретной организации.
Одним из свойств, которыми должна обладать система визуализации – прагматизм. Как уже отмечалось, эффективность можно рассматривать как одну из прагматик. Эффективность в визуализации часто имеет субъективный характер. Это объясняется тем, что в визуализации выделяются, как минимум, два действующих лица (актора): разработчик - автор визуального текста и пользователь – интерпретатор.
В деятельностном подходе один из ключевых вопросов – определение цели. В математическом моделировании целеполагание рассматривается как условие экстремальности. Очевидно, что у разработчика и пользователя цели могут не совпадать. Устранить возможное противоречие можно, разрабатывая специализированные системы визуализации. В работе [11] предлагается перейти к созданию средств визуального сопровождения процессов разработки, включая отладку и анализ программного обеспечения, основываясь на изучении конкретной деятельности программистов, работающих в рамках конкретной программно-аппаратной среды. Визуальное сопровождение можно рассматривать в рамках шаговой теории или структур событий.
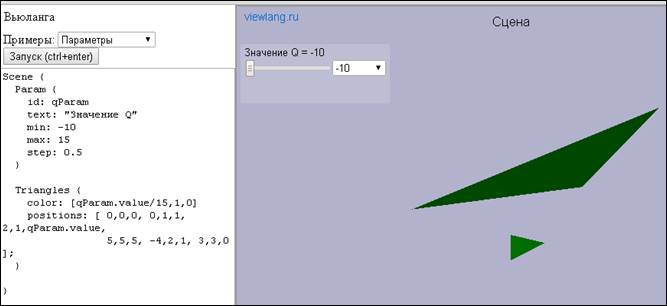
Аналогично, создание конструкторов (визуализации) можно рассматривать как достижение некоторого компромисса между универсальными и специализированными системами, например, в рамках диалоговой логики. В работе [12] предлагается декларативно-императивный подход, близкий к комбинации денотационной и операционной семантик соответственно. Конструктор Viewlang [13] (Рис. 1.) обладает всеми перечисленными свойствами, являющимися необходимые для того чтобы работа с системой визуализации была эффективной. Применение бинарного вида отображения и простых примеров, рассматриваемых в качестве базиса, обеспечивает непрерывное обучение языку: изменения текста программы в одном окне, приводит к изменению визуального представления в другом окне. Конструктор визуализации может рассматриваться как интеллектуальный агент, одной из целей которого является обучение визуальному языку с учителем - агентом.
Рис. 1. Конструктор Viewlang. Бинарный вид отображения.
В работе [14] рассматривается аналогичный (бинарный) подход, ориентированный на конечного пользователя – дизайнера (рис. 2), поэтому его можно назвать декларативно-дизайнерским. Текст программы может быть заменен любым гомеоморфным визуальным отображением (например, метафорой визуализации, используемой для статического или динамического анализа программ), или самими вычислениями (on-line визуализация), в данном случае выделен логический уровень (предметная онтология).
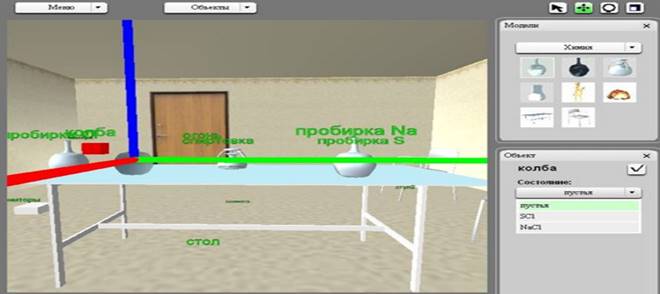
Рис. 2. Проект виртуальной химической лаборатории.
В работе [15] реализован близкий в идейном плане подход, предназначенный для имитационного моделирования: логическим уровнем, является трехмерная сцена, которая связана с параллельной программой, например, вычисляющей распространение ударной волны (on-line визуализация).
Поскольку графические библиотеки, в том числе ориентированные на Web-визуализацию, позволяют выделить интересующий объект или графический примитив, полезной с точки зрения обучения является организация обратной связи (отображение графического объекта на текст программы) [16] – см рис. 3.
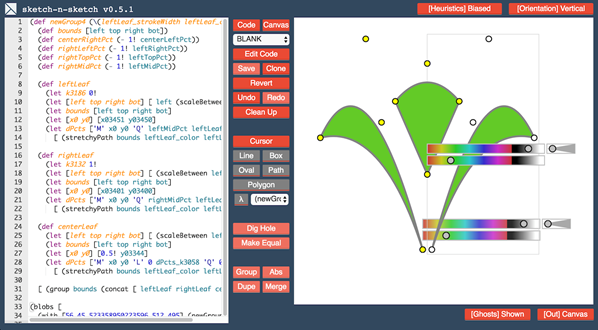
Рис. 3. Система программной манипуляции sketch-n-sketch.
Несмотря на то, что целесообразность применения бинарного вида отображения в системах и конструкторах визуализации можно обосновать с эмпирических позиций, все же формальная верификация позволяет подчеркнуть ряд важных особенностей (необходимых условий эффективной визуализации). Так в разрабатываемом конструкторе Viewlang существенной особенностью является возможность изменения параметров, что позволяет рассматривать непрерывное отображение. В приведенном примере Рис. 1. изменение слайдера связано с изменением параметра, в частности координат вершины треугольника. Многопараметрическая модель, примененная для определения необходимых условий эффективной визуализации оправданна и при рассмотрении визуального текста.
4. Визуальный текст
Определение визуального текста может основываться на категоризации, в частности на сравнении с текстом естественного языка, являющегося линейным как последовательность знаков, и многозначным по смыслу. Визуальный текст по своей природе нелинеен, и необходимо учитывать не только пространственно-временные характеристики, но и неопределенность информации.
Итак, предлагается к рассмотрению следующее определение визуального текста:
Визуальный текст (VT) есть произведение метаонтологии (MONT) и интеллектуального агента (I) со своим индивидуальным восприятием (Per) и пониманием (Cog).
VT= MONT*I(Per, Cog) (1)
Метаонтология определяет семейство математических теорий, используемых для формализации онтологий. Она обеспечивает как точную, математическую спецификацию онтологий, так и формальный анализ их свойств. В частности, она включает методы и формы представления, интеграции и слияния различных онтологий. Принятие той или иной метаонтологии непосредственно определяет состав онтологий, взаимосвязи между ними, выбор формальных моделей и языков для представления онтологий как верхнего, так и нижнего уровня [17].
Так метаонтология визуализации должна включать не только онтологию визуализации, но и специализированную онтологию предметной области (например, гидрогазодинамики или математической статистики) со своими часто пересекающимися формальными моделями. Во множестве формальных определений онтологий наиболее общими (универсальными) определениями являются, те, которые построены на моделях с неопределенностью (так в [4] онтологии разделяются на сингулярные и гранулярные). Например, в основе лингвистической онтологии лежит определение лингвистической переменной Заде. Расширение лингвистической онтологии - полностью нечеткая онтология включает I – множество индивидов (агентов) и поэтому может бать интересной для определения визуального текста. Под агентом понимают открытую, активную, целенаправленную систему, которая способна сама формировать собственное поведение в не полностью определенной среде [17]. Интеллектуальный агент – агент способный к самопознанию. В связи с этим определением представляют интерес такие направления как автономные вычисления и синергетика. Неопределенность интеллектуального агента связана с неполнотой формализации познания, поэтому I(Per,Cog) будем рассматривать как некоторую переменную - x, что приводит к наложению дополнительных требований как на метаонтологию, так и на операцию произведения в определении визуального текста.
В формуле (1) заменим метаонтологию на логическую матрицу A, например, метаонтология может рассматриваться как нечеткая когнитивная карта (частный случай нейронной сети), отслеживающая причинно-следственные связи.
VT= Ах (2)
Данная формула аналогична хорошо изученной модели первого приближения, то есть визуальный текст можно рассматривать как производную носителя языка - интеллектуального агента. Таким образом, оценка визуального текста при рассмотрении его как истинностного подмножества универсального пространства равносильна оценке эффективности визуализации, которые должны начинаться с изучения свойств интеллектуального агента. Возможно рассмотрение, как прямой задачи (по множеству визуальных текстов построить агента способного их интерпретировать, например, программу), так и обратной задачи (под конкретного агента построить систему визуализации, например, для задачи визуального сопровождения). В обоих случаях предполагается изучение свойств интеллектуального агента. Так для модели с насыщением известно, что начальные данные необходимо находить, так чтобы они были близки к равновесному состоянию, которое в визуальной форме может быть представлено логистической кривой. В то же время для модели с неопределенностью можно предположить, что равновесное состояние существует, но оно не известно. В данном случае конструктивным подходом является рассмотрение относительной эффективности или скорости сближения двух решений [3].
Важным и до конца не изученным является вопрос о том, как повлияет ввод неопределенности на доказательство непротиворечивости. Поскольку непротиворечивость знаний считаются основными критериями истины, и может рассматриваться как информативный признак системы визуализации, остановимся на этом вопросе с точки зрения различных логик:
1. В шаговой или темпоральной логике непротиворечивость сводится к проверке всех предусловий. А постусловия можно рассматривать, как отложенное исполнение. Так определенная избыточность текста программы важна в смысле предвидения, то есть включение в текст программы некоторых языковых конструкций, которые не являются необходимыми в данной версии, но возможно понадобятся на следующем шаге;
2. Для модели с неопределенностью (например, нечеткая логика) или для правдоподобных правил конструктивным подходом является рассмотрение модели с рефакторингом. В качестве такого примера приведем работу [18], в которой параметры статического анализа уточняются после проведения динамического анализа. Например, в качестве параметра может рассматриваться пороговое значение - минимальная длина графа, описывающего родителей класса, так чтобы все классы, используемые в программе, были различимы. В частности, при анализе больших данных рассмотрение предельной неопределенности является вынужденным. Аналогично, подходу, применяемому в математическом анализе, можно ввести понятие – почти всюду непротиворечивости. То есть допускаются локальные противоречия, не влияющие на значение предела. Например, в этом направлении возможно рассмотрение задачи отказоустойчивости многопроцессорной техники.
3. Возможным подходом является отказ от одного из важнейших законов Аристотелевой логики – закона непротиворечия и построения логики, свободной от этого закона. Данный подход требует построения логического пространства [4]. Вряд ли стоит отождествлять паранепротиворечивую логику с этим направлением, так как она всего лишь основывается на определение отрицания специфическим образом;
4. Алгебраическая логика вместо рассмотрения непротиворечий основывается на принципе, подобному геометрии Лобачевского - логические понятия должны быть инвариантными по отношению к группе преобразований области рассуждений (логического пространства) [5]. Например, в работе [4] вводится темпоральное нечеткое число в аффинной форме с целью обеспечения инвариантности аффинных преобразований изображений (визуальных текстов).
Важной особенностью процесса визуализации является когнитивность, которую можно рассматривать как информативный признак системы визуализации, так и как параметр интеллектуального агента (1). Конструкторы визуализации должны обеспечить создание когнитивных (наиболее полно отражающих основные свойства реальных объектов-прототипов) визуальных моделей пользователями, не имеющими высокой программистской квалификации [11]. Необходимо отметить, что понятие когнитивности является достаточно устойчивым, формализуемым и применимым для обоих типов интеллектуальных агентов и для человека и для программы.
Когнитивность - степень соответствия отображаемых объектов и процессов реальным прототипам либо общепринятым для моделируемой предметной области образам и схемам [19].
В работе [3] также предлагается рассмотреть меру «сложность интерпретации», определяемую как количество элементарных понятий-сущностей в модели визуализации. Визуализация адекватна, когда нет проблемы интерпретации. То есть сущности (визуальному объекту) однозначно соответствует понятие (ментальный объект). Очевидна постановка задачи минимума для таких абстрактных метрик, как когнитивное расстояние или информационный разрыв. Напомним, что когнитивное расстояние определяется через усилия пользователя, затраченные на интерпретацию.
Возможно и другое определение данной метрики (когнитивности), как расстояния между модельными объектами ввода и вывода и ментальными объектами. Можно провести аналогию сложности интерпретации или переопределенного когнитивного расстояния с таким понятием в области программирования как Колмогоровская или алгоритмическая сложность, определяемая, как минимальная длинна текста, реализующая данный алгоритм.
Если когнитивность можно рассматривать, как метрику, применимую для любого агента, то проблемы восприятия не формализованы должным образом. Как уже отмечалось, интерпретация визуального текста зависит от индивидуального восприятия и понимания интеллектуального агента (1), поэтому восприятие больших объемов визуальной информации представляет особый интерес.
5. Метафора восхода солнца
Визуальный анализ данных связан с восприятием и пониманием визуальной информации. Широкое распространение получили различные методики тестирования, в основе которых лежит наивный байесовский подход, пригодный для проверки адекватности модели. В тоже время, для того чтобы объяснить природу сложных явлений, необходимо разрабатывать эти математические модели.
Нами был проведен достаточно простой эксперимент по взаимной оценке информативности фотореалистического изображения с элементами динамической визуализации и стереоизображения. Предложена метафора восхода солнца – вращение точечного источника света вокруг трехмерного объекта. Практически рассматривались два объекта: 3d-сетка, узлы которой отображаются в виде тетраэдров и граница сетки (результат моделирования работы сердца – рис. 4.). Методика основана на выделение попарно ортогональных свойств: много маленьких объектов или один большой, экран или очки виртуальной реальности, применяется метафора или нет. Таким образом, анализировалось восемь изображений.

Рис. 4. Вращение источника света вокруг границы сетки. Показаны два кадра с различным положением источника.
Если на плоском экране при применении этой метафоры можно говорить о возникновение некоторого стереоэффекта, то влияние изменения освещенности на стереоизображение практически незаметно. Таким образом, можно предположить, что результирующая информативность есть сумма двух рядов, один из которых результат применения лапласиана к функции многих переменных (для построения стереоизображения и выделения границ подобный подход является стандартным), причем суммируются, те члены ряда, относительная мощность которых наибольшая. Рассматривая взвешенную сумму, которая не может быть больше суммы поглощенных и отраженных лучей, можно объяснить, почему наблюдатель воспринимает окружающий мир практически одинаково, что одним глазом, что двумя глазами или, почему один сигнал частично подавляется другим сигналом. Таким образом, на основании проведенного эксперимента и соответствующей ему полумодели можно предположить, что виртуальная реальность не является необходимым условием эффективной визуализации, но, возможно, описывающий это явление ряд быстрее сходится. Конечно, это только гипотеза уровня ментальной модели. Необходимо проведение более точных исследований, включая верификацию и валидацию визуализации совместно со специалистами нейрофизиологии и когнитивной психологии.
6. Заключение
В настоящее время отмечается интерес к формальной верификации визуализации. Наравне с лингвистическим подходом рассмотрение визуального текста как истинного подмножества универсального пространства является одним из направлений. Несмотря на высокую синонимичность формальных моделей, используемых в компьютерной визуализации, можно сделать выводы, что информативными признаками данных моделей являются:
- непрерывность,
- непротиворечивость,
- бинарность,
- масштабируемость,
- когнитивность,
- эффективность.
Визуальный текст можно рассматривать как производную носителя языка - интеллектуального агента. Следовательно, эффективность визуализации вторая производная интеллектуального агента. Таким образом, оценка эффективности визуализации и оценка визуального текста являются взаимозависимыми и должны начинаться с изучения свойств интеллектуального агента.
Проблемы восприятия не формализованы должным образом ни в области компьютерной визуализации, ни в таких науках, как нейрофизиология или психология. С целью изучения восприятия в работе предложена метафора восхода солнца. Авторы надеются, что в будущем подготовят обзор по постановкам задач, ориентированных на изучение восприятия в области компьютерной визуализации.
Список литературы
[1] Раевский Д.С. К методике интерпретации изобразительных текстов. Невербальное поле культуры. Материалы научной конференции "Невербальные коммуникации в культуре". Москва, 6-8 июня 1995 г. М. РГГУ. 1995. Стр. 144-145.
[2] The EuroRV3: EuroVis Workshop on Reproducibility, Verification, and Validation in Visualization. http://www.eurorvvv.org/.
[3] Манаков Д., Авербух В. Верификация визуализации. Научная визуализация 2016. Том 8. № 1. Стр. 58 - 94.
[4] Тарасов В.Б. Универсальная логика, грануляция информации и искусственный интеллект. http://www.raai.org/news/pii/ppt/2015/tarasov2015.ppt
[5] Lakoff G. The contemporary theory of metaphor. Metaphor and Thought. (2nd ed.). Cambridge: Cambridge University Press, 1993, pp. 202-251.
[6] Scott D.S. Data types as lattices. Proceedings of the International Summer Institute and Logic Colloquium, Kiel, in Lecture Notes in Mathematics. Springer-Verlag. 499. Pp. 579-651.
[7] Winskel G. Event structures. Invited lectures for the Advanced Course on Petri nets, September 1986. Appears as a report, of the Computer Laboratory, University of Cambridge, 1986, and in the proceedings of the school, published in Springer Lecture Notes in C.S., vol.255 (1987).
[8] North C. Toward measuring visualization insight. IEEE Computer Graphics and Applications 26 (May/June), pp. 20-23.
[9] Теплов А.М. Об одном подходе к сравнению масштабируемости параллельных программ. Вычислительные методы и программирование. 2014. Т. 15. Выпуск 4. Стр. 697-711.
[10]Бахтерев М.О., Васёв П.А., Казанцев А.Ю., Манаков Д.В. Система удалённой визуализации для инженерных и суперкомпьютерных вычислений. Вестник ЮжУрГУ, N 17 (150), 2009, серия «Математическое моделирование и программирование», Выпуск 3. Стр. 4-11.
[11]Авербух В.Л., Анненкова О.Г., Бахтерев М.О., Манаков Д.В. Анализ и оценка систем визуализации программного обеспечения параллельных вычислений. Вопросы атомной науки и техники (ВАНТ), серия Математическое моделирование физических процессов, 2015, вып.4, с. 58-70.
[12]Васёв П.А., Бахтерев М.О. Декларативно-императивный метод конструирования сцен научной визуализации. XV Международная конференция <Супервычисления и Математическое Моделирование>. Тезисы. ФГУП <РФЯЦ ВНИИЭФ>. Саров. 2014, стр. 46.
[13]Viewlang-конструктор http://viewlang.ru/code/c.html
[14]Грибова В.В., Федорищев Л.А. Визуализация виртуальных сред в облачных сервисах. Научная визуализация 2016. Кв.1. Том 8. N: 1. Стр. 133 - 145.
[15]Коршунов С.А., Павлов А.И., Николайчук О.А. Концепция программного средства визуализации результатов имитационного моделирования на основе онтологического подхода. Научная визуализация. 2016. Кв.2. Том 8. N: 2. Стр. 120 - 131.
[16]Sketch-n-sketch. https://ravichugh.github.io/sketch-n-sketch/blog/03-user-study-videos.html
[17]Тарасов В.Б., Калуцкая А.П., Святкина М.Н. Гранулярные, нечеткие и лингвистические онтологии для Обеспечения взаимопонимания между когнитивными агентами // Материалы II Междунар. науч.-техн. конф. «Открытые семантические технологии проектирования интеллектуальных систем» (OSTIS–2012). Минск: БГУИР. 2012. С. 267−278.
[18]Зубов М.В., Пустыгин А.Н., Старцев Е.В. Получение типов данных в языках с динамической типизацией для статического анализа исходного кода с помощью универсального классового представления // Вестн. Астрахан. гос. техн. ун-та. Сер. управление, вычисл. техн. информ., 2013, N 2, Стр. 66-74.
[19]Зенкин А.А. Когнитивная компьютерная графика. Под ред. Д.А. Поспелова. М.: Наука, 1991.
VISUAL TEXT AS TRUTH SUBSET OF THE UNIVERSAL SPACE
D.V. Manakov1, V.L. Averbukh1, 2, P.A. Vasev1
1Institute for Mathematics and Mechanics named by N.N. Krasovskii, Urals Branch of Russian Academy of Science, Ekaterinburg
2Urals Federal University, Ekaterinburg
Abstract
The paper considers formal approaches to evaluation of visual texts and visualization effectiveness. The consideration of the visual text as proper subset of the universal space is rather prospective approach interchangeably with linguistic approach (means to analyze the text using defined rules). Via the example of visualization builder the potentials of the formalized approach is considered. The concept of a visual text is actively used, as in the Humanities and Computer Visualization. The visual text is defined trivially as the result of any computer visualization systems.
The economy theory uses a definition of effectiveness (productivity) through the ratio of the product to the product source (resources). This definition is quite adequate. Formally, it can be considered as speed or full differential. Therefore, the effectiveness of visualization is a multivariable function. The parameters of this function are partial derivatives of visual text by its informative characteristics.
The necessary condition of derivative existence is persistence mapping. It is one of the reasons to consider visualization metaphor as persistence mapping analogous to denotational semantics using in the programming domain. Also persistence mapping may be defined throw little varying of visualization parameters. The study of poorly formalizable phenomena begins with a first approximation model. Within this framework visual texts may be set out as an intersection of a logical matrix and an intelligent agent.
Text interpretation as subsets of a universal space implies that the visual text has a true value. Properties of an intelligent agent in general are not determined. That is why an inverse problem is considered.
Problems of perception are important for computer visualization. The dependence of an intelligent agent from the perception and understanding is incorporated to the model.
Also it is interesting to consider the perception of visual texts from the point of view of information theory. In this regard, the Sunrise metaphor and its semimodel are proposed.
Keywords: visualization effectiveness, universal visualization space, visual text.
References
[1] Raevskiy D. K metodike interpretacii izobrazitel'nyh tekstov. Neverbal'noe pole kul'tury. [Toward Interpretation of pictorial texts]. Proceedings of Conference “Nonverbal Domains of Culture”, Moscow, 1995, pp. 144-145. [In Russian]
[2] The EuroRV3: EuroVis Workshop on Reproducibility, Verification, and Validation in Visualization. http://www.eurorvvv.org/
[3] Manakov D., Averbukh V. Verification of visualization Scientific Visualization. 2016. Quarter 1. Volume 8. Number 1. Pp. 58-94. [In Russian]
[4] Tarasov V.B. Universal logic, information granularity and artificial intelligence. http://www.raai.org/news/pii/ppt/2015/tarasov2015.ppt
[5] Lakoff G. The contemporary theory of metaphor. Metaphor and Thought. (2nd ed.). Cambridge: Cambridge University Press, 1993, pp. 202-251.
[6]Scott D.S. Data types as lattices. Proceedings of the International Summer Institute and Logic Colloquium, Kiel, in Lecture Notes in Mathematics. Springer-Verlag. 499. Pp. 579-651.
[7] Winskel G. Event structures. Invited lectures for the Advanced Course on Petri nets, September 1986. Appears as a report, of the Computer Laboratory, University of Cambridge, 1986, and in the proceedings of the school, published in Springer Lecture Notes in C.S., vol.255 (1987).
[8] North C. Toward measuring visualization insight. IEEE Computer Graphics and Applications 26 (May/June), pp. 20-23.
[9] Teplov A.M. Ob odnom podhode k sravneniju masshtabiruemosti parallel'nyh programm [An approach to the comparison of parallel program scalability] Numerical methods and programming. 2014. Vol. 15. Issue 4. Pp. 697-711. [In Russian]
[10] Bakhterev M.O., Vasev P.A. Kazantsev A.Yu., Manakov D.V. Sistema udaljonnoj vizualizacii dlja inzhenernyh i superkomp'juternyh vychislenij [The System of Remote Visualization for Engineering and Super Computing] Bulletin of the South Ural State University. N 17 (150), 2009, Series “Computational Mathematics and Software Engineering”. Issue 3. Pp. 4-11. [In Russian]
[11] Averbukh V., Annenkova O., Bakhterev M., Manakov D. Analiz i ocenka sistem vizualizacii programmnogo obespechenija parallel'nyh vychislenij [Analysis and Assessment of Visualization Systems Used in Software for Parallel Computations]. Voprosy Atomnoy Nauki i Tekhniki (VANT), series “Mathematical Modeling of Physical Processes”, Issue 4, 2015, pp. 58-70. [In Russian]
[12] Vasev P.A., Bakhterev M.O. Deklarativno-imperativnyj metod konstruirovanija scen nauchnoj vizualizacii [Declarative-imperative method for construction of scientific visualization scenes]. XV International Conference “Super-Computations and Computer Simulations” Sarov. 20014. P. 46. [In Russian]
[13] Viewlang-builder http://viewlang.ru/code/c.html
[14] Gribova V.V., Fedorischev L.A. Visualization of virtual environments at cloud services. Scientific Visualization. 2016. Quarter 1. Vol. 8. Number 1. Pp. 133-145. [In Russian]
[15] Korshunov S.A., Pavlov А.I., Nikolaychuk O.A. Concept of simulation visualization software based on ontology approach. Scientific Visualization. 2016. Quarter 2. Vol. 8. N 2. Pp. 120-131. [In Russian]
[16] Sketch-n-sketch. https://ravichugh.github.io/sketch-n-sketch/blog/03-user-study-videos.html
[17] Tarasov V. B., Kalutskaya A. P., Svyatkina M. N. Granuljarnye, nechetkie i lingvisticheskie ontologii dlja Obespechenija vzaimoponimanija mezhdu kognitivnymi agentami [Granular, fuzzy and linguistic ontologies to achieve understanding between cognitive agents]. Proceedings of the II Intern. Conf. “Open semantic technology of intelligent systems” (OSTIS–2012). Minsk. 2012. Pp. 267-278. [In Russian]
[18] Zubov M.V., Pustygin A.N., Startcev E.V. Poluchenie tipov dannyh v jazykah s dinamicheskoj tipizaciej dlja staticheskogo analiza ishodnogo koda s pomoshh'ju universal'nogo klassovogo predstavlenija [Obtaining of data types in languages with dynamic typing for static analysis of source code using the representation of generic classes. Bulletin of the Astrakhan]. State Tech. Univ. Ser. Management, Comp. Tech., Inform., 2013, N 2, Pp. 66-74. [In Russian]
[19] Zenkin A.A. Kognitivnaja komp'juternaja grafika [Cognitive Computer Graphics]. Nauka. 1992. [In Russian]