Статья содержит краткий исторический обзор становления методов семейства PROMETHEE. Рассматриваются классификация Б. Роя и 2 подхода к постановке ДМКЗ: подход мультиатрибутивной теории полезности и подход превосходства по рангу. Проведена формализация постановки задачи, решаемой методами семейства PROMETHEE: описаны входные, промежуточные и выходные данные ДМКЗ.

Проиллюстрирована работа с программным средством Visual PROMETHEE Academic на примере выбора автомобиля. Особое внимание уделено рассмотрению визуализации промежуточных и выходных данных при решении ДМКЗ методами PROMETHEE I и PROMETHEE II. Рассматриваются диаграммы “PROMETHEE I Partial Ranking”, “PROMETHEE II Complete Ranking”, “PROMETHEE Diamonds”, “PROMETHEE Network”, “GAIA Plane”.

В статье отмечено, что пользователь использует эти диаграммы для быстрого получения информации о результирующих выходных и промежуточных данных решения ДМКЗ, и обращается к результатам в табличной форме только при возникновении необходимости в этом.

Ключевые слова: PROMETHEE, ДМКЗ, визуализация, теория принятия решений.

1. Введение

Задачи принятия решений при многих критериях встречаются в различных областях человеческой деятельности. Разработкой методов и подходов, которые оказывают поддержку лицу, принимающему решение (ЛПР), занимается дисциплина под названием теория принятия решений, которую в англоязычной литературе принято называть multi-criteria decision analysis (MCDA) или multi-criteria decision making (MCDM). Инструменты и подходы этой дисциплины используют в самых различных отраслях: здравоохранение [1, 2], энергетика [7], окружающая среда [4], управление водными ресурсами [5], бизнес и управление финансами [6], химия, логистика, промышленное производство [8].

Данная статья освещает методы семейства PROMETHEE, поскольку они имеют широкое практическое применение в перечисленных выше областях. Кроме того, в последние годы наблюдается значительный рост публикаций, которые предлагают новые методы этого семейства, использование визуализации в рамках этих методов, их использование с методами других семейств, а также описывают приложения этих методов в различных сферах деятельности человека.

Методы семейства PROMETHEE можно охарактеризовать с помощью схемы, представленной на рис. 1:

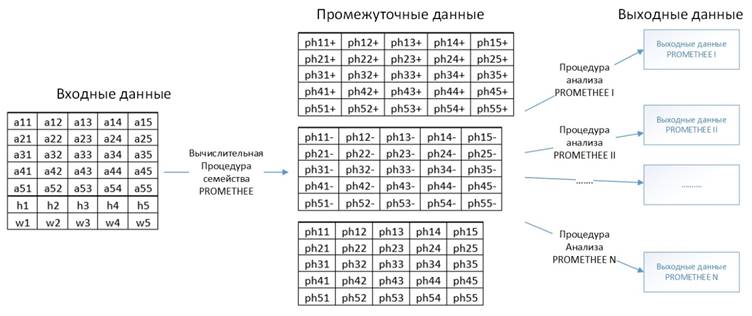
Рис. 1. Схема работы методов семейства PROMETHEE.

На этой схеме отмечено, что структура входных и промежуточных данных для всех методов этого семейства одинакова. Разные методы аналитически обрабатывают промежуточные данные по своим собственным вычислительным процедурам. Соответственно, выходные данные различаются в зависимости от используемого метода. Входные и промежуточные данные представляют собой некоторые табличные данные, выходные данные представляют собой суждения о бинарных отношениях между объектами. Более подробно исходные, промежуточные и выходные данные описаны в пункте 3.3.

Отметим, что в общем случае в процессе решения ДМКЗ, принимают участие лицо, принимающее решение (ЛПР), и аналитик. Соответственно, пользователем метода может являться как ЛПР, так и аналитик. Иногда один и тот же человек может выступать и в роли ЛПР, и в роли аналитика, одновременно.

2. Исторический обзор становления методов семейства PROMETHEE

В 1982 году Жан-Пьер Бранс (Jean-Pierre Brans) представил на конференции, проходящей в Университете Лаваля (Канада) новое семейство методов решения дискретных многокритериальных задач, под названием PROMETHEE [10]. Название PROMETHEE является аббревиатурой “Preference Ranking Organization Method for Enrichment Evaluations”, которую можно перевести на русский язык как “Метод Формирования Рангов Предпочтения для Обогащения Оценок”.

В тот момент в это семейство входило только 2 метода: метод PROMETHEE I для частичного ранжирования альтернатив и метод PROMETHEE II для полного ранжирования альтернатив. [8]

Вскоре после этого Бертранд Марешаль (Bertrand Mareschal) стал работать с Жаном-Пьером Брансом над новыми методами семейства PROMETHEE. Работа оказалась продуктивной, и в 1983 году были предложены два новых метода: метод PROMETHEE III для ранжирования с использованием интервалов и метод PROMETHEE IV для полного или частичного ранжирования альтернатив в случае, когда множество эффективных решений непрерывно. [9] В этом же году была написана первая компьютерная программа с реализацией некоторых методов семейства PROMETHEE. [11]

В методе PROMETHEE III была предпринята попытка увеличить количество отношений безразличия в итоговой матрице бинарных отношений (для более точного выявления схожих альтернатив). В методах PROMETHEE I и PROMETHEE II отношение безразличия устанавливается между двумя альтернативами только в том случае, если их потоки предпочтений строго равны. В PROMETHEE III для каждой альтернативы вычисляется не конкретное значение потока предпочтения, а интервал, в котором может находиться значение этого потока. При этом, если интервалы двух альтернатив пересекаются, то между этими альтернативами устанавливается отношение безразличия.

Важным аспектом исторического развития методов семейства PROMETHEE является появление визуализации в процессе решения ДМКЗ. В 1988 году Бранс и Марешаль разработали визуальный интерактивный модуль GAIA, который обеспечивает семейство методов PROMETHEE удобным графическим представлением. Название GAIA является аббревиатурой “Graphical Analysis for Interactive Aid”, которую можно перевести на русский язык как “Графический анализ для интерактивной поддержки принятия решений”. Так как графические представления сделали возможным оценить значения потоков предпочтения визуально, метод PROMETHEE III так и не был впоследствии реализован в программном обеспечении PROMETHEE. На сегодняшний день GAIA является одним из очень немногих эффективных описательных методов при решении дискретных многокритериальных задач.

В период с 1984 по 1989 год для многих пользователей стала доступна программа PROMCALC (для MS-DOS) с реализацией некоторых методов PROMETHEE. PROMCALC (позже PROMCALC-GAIA) стала одной из первых по-настоящему интерактивных программ с сильным акцентом на пользовательский интерфейс, графические представления и анализ чувствительности.

В 1992 году теми же авторами был представлен метод PROMETHEE V для ДМКЗ с ограничениями [13], а в 1994 году - метод PROMETHEE VI [12].

PROMETHEE I и II являются приемлемыми для выбора одной наиболее предпочтительной альтернативы из множества возможных альтернатив. Однако в некоторых случаях необходимо выделить не одну альтернативу, а целое подмножество альтернатив, учитывая набор ограничений. Метод PROMETHEE V создан как раз для решения таких классов задач.

Также был предложен метод PROMETHEE GDSS для коллективного принятия решений [14, 15] и два расширенных подхода к PROMETHEE: PROMETHEE TRI для решения проблем сортировки и PROMETHEE CLUSTER для номинальной классификации [16].

Следует отметить, что в настоящее время, разработано более десятка методов рассматриваемого семейства. Наиболее известными и освещённым методами семейства PROMETHEE являются методы PROMETHEE I и PROMETHEE II. Эти методы часто и успешно используются на практике.

3. Формальная постановка ДМКЗ

Формализация постановки ДМКЗ формировалась в течение долгого времени. Различные исследователи рассматривают ДМКЗ с разных точек зрения, поэтому формальная постановка ДМКЗ может отличаться у разных исследователей. Одной из ранних попыток формализовать МКЗ была предпринята Б. Роем.

3.1. Классификация Б. Роя

Б. Рой предлагает относить каждую ДМКЗ к одному из классов в зависимости от цели, которая преследуется в процессе решения задачи [18, 19]. Эти классы Рой назвал проблематиками.

Проблематика “альфа” включает в себя такие МКЗ, в которых нужно выбрать ровно 1 наилучший объект из конечного множества объектов. Проблематика “бета” содержит задачи, в которых каждый объект нужно отнести к одной из групп объектов (классов). Проблематика “гамма” содержит задачи, в которых требуется упорядочить объекты от лучшего к худшему. Проблематика “дельта” содержит задачи, в которых требуется описать объекты с точки зрения их эффективности по критериям.

3.2. Подходы теории полезности и превосходства по рангу

В мультиатрибутивной теории полезности формальное описание входных данных ДМКЗ задаётся моделью (А - A - E), где первая A - множество альтернатив, вторая A - множество атрибутов и E - таблица характеристик (показателей). Подход превосходства по рангу (outranking approach) использует модель (A - F - E), в этом случае A - множество альтернатив, F - упорядоченное семейство критериев (функций, определённых на A), E - таблица характеристик (показателей). В статье [17] рассмотрена модель (A - A/F - E - M), объединяющая подходы теории полезности и превосходства по рангу, а также дополняющая входные данные переменной M, которая содержит дополнительную информацию от ЛПР (например, веса критериев). Примечательно, что разные методы решения ДМКЗ требуют от ЛПР различных дополнительных сведений. В этом смысле можно сказать, что для каждого конкретного метода (семейства методов) формальная постановка ДМКЗ будет своя собственная.

3.3. Формализация постановки задачи в методах семейства PROMETHEE

Рассмотренные выше варианты постановки задачи справедливы для методов семейства PROMETHEE. Однако, как показывает практика, из-за универсальности и общности этих постановок задач, ими не всегда удобно пользоваться при описании входных данных. В данной статье предпринята попытка осуществить формализацию ДМКЗ в рамках методов семейства PROMETHEE более строго - с использованием терминов: множество, кортеж, действительное число, функция.

Пусть

- конечное множество кортежей длины :

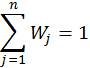
- кортеж длины :

- кортеж длины , элементами которого являются функции

Тогда входными данными ДМКЗ, решаемой семейством методов PROMETHEE будем называть кортеж .

На основе входных данных получают промежуточные данные, являющиеся общими для всех методов семейства PROMETHEE, которые можно описать в виде трёх матриц: , , .

На выходе необходимо каждый элемент множества (декартова произведения ) отнести к одному из классов (сформировать суждения об отнесении) :

· класс несравнимости (incomparability class);

· класс безразличия (indifference class);

· класс строгого предпочтения (strong preference class);

· класс строгого антипрепредпочтения (strong antipreference class).

Другими словами, требуется разбить декартово произведение на 4 непересекающихся класса. При этом некоторые классы могут быть пустыми. Сформированные суждения об отнесении элементов множества к одному из классов представляют собой выходные данные ДМКЗ, решаемой семейством методов PROMETHEE. Каждый из классов будем называть бинарным отношением на множестве .

Теперь, когда определены входные, промежуточные и выходные данные ДМКЗ, обратимся к рассмотрению вопросов визуализации в рамках методов семейства PROMETHEE.

4. Визуализация в методах PROMETHEE I и PROMETHEE II

В рамках методов данного семейства входные, промежуточные и выходные данные часто представляются в виде таблиц. При этом, таблиц может быть много. Использование визуализации позволяет быстрее анализировать данные таблицы, что упрощает для пользователя решение ДМКЗ.

Как было указано выше, наиболее известными и освещённым методами семейства PROMETHEE являются методы PROMETHEE I и PROMETHEE II. Эти методы часто и успешно используются на практике. Рассмотрим использование визуализации в этих методах.

Одной из программ для решения дискретных многокритериальных задач методами семейства PROMETHEE является программа Visual PROMETHEE Academic, разработанная совместно с создателем методов PROMETHEE I и PROMETHEE II.

4.1. Табличное представление входных данных в программе Visual PROMETHEE Academic

Проиллюстрируем работу с данным программным средством на примере выбора автомобиля.

В этой программе входные данные (структура которых, как отмечено ранее, одинакова для методов семейства PROMETHEE) представляют собой табличные данные.

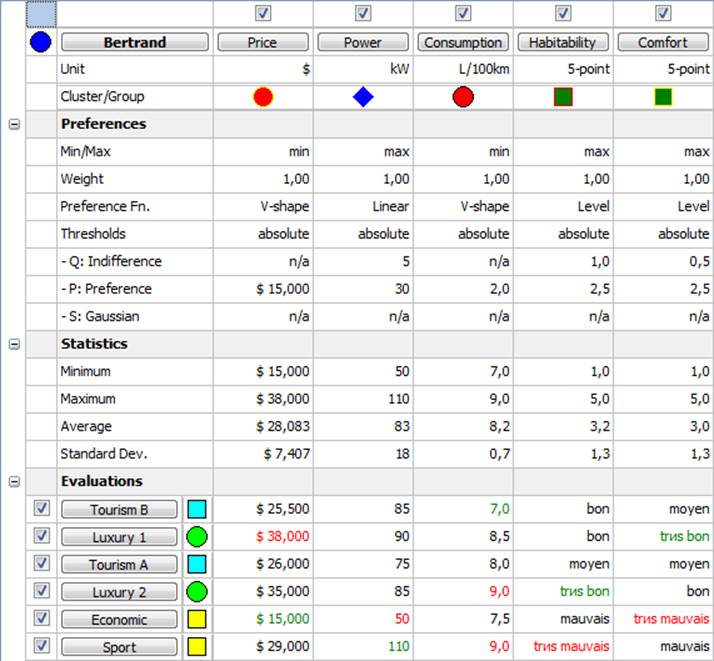
Рис. 2. Представление входных данных в программе Visual PROMETHEE Academic.

На рис. 2 представлена визуализация таких входных табличных данных о 6 автомобилях (Tourism A, Tourism B, Luxury 1, Luxury 2, Sport, Economic), по 5 критериям (Price, Power, Consumption, Habitability, Comfort). Данная визуализация полезна для контроля задания входных данных.

4.2. Табличное представление выходных данных

Пользователь стремится получить информацию о том, как упорядочены альтернативы по предпочтению. Для этого используется табличное представление (рис. 3):

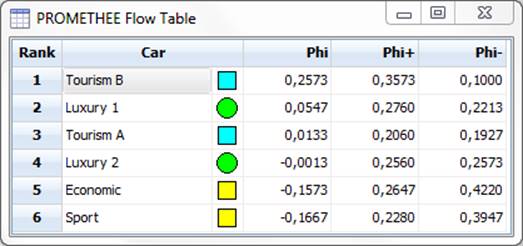
Рис. 3. Табличное представление выходных данных в программе Visual PROMETHEE Academic.

Таблица содержит результаты работы сразу двух методов: PROMETHEE I и PROMETHEE II. Работая с таблицей, аналитик способен делать выводы о том, какое отношение установлено между любыми двумя альтернативами. Метод PROMETHEE I устанавливает между альтернативами один из 4 видов отношений: безразличия, несравнимости, строгого предпочтения и строгого антипредпочтения. Метод PROMETHEE II — один из 3 видов отношений: безразличия, строгого предпочтения и строгого антипредпочтения. Аналитик пользуется следующими правилами:

1) Если для двух альтернатив B и C выполняется

то B ~ C (читается так: “B и C безразличны”). То есть между альтернативами B и C устанавливается отношение безразличия, а кортеж (B, C) относится к классу безразличия.

2) Если для двух альтернатив B и С выполняется

то B > C (читается так: “B строго предпочтительнее C”). То есть между альтернативами B и C устанавливается отношение строгого предпочтения, а кортеж (B, C) относится к классу строгого предпочтения.

3) Если между альтернативами B и C установлено отношение строгого предпочтения: B > C, то между альтернативами C и B автоматически устанавливается отношение строгого антипредпочтения: С < B (читается так: “С менее предпочтительно, чем B”). Другими словами, если кортеж (B, C) является элементом класса строгого предпочтения, то кортеж (C, B) является элементом класса строгого антипредпочтения.

4) Во всех остальных случаях устанавливается отношение несравнимости: B N C (читается так: “B и С несравнимы”).

Выходные данные (суждения) решения ДМКЗ методами PROMETHEE I и PROMETHEE II можно представить в виде матрицы бинарных отношений (табл. 1 и 2). Такие матрицы читаются по строкам. Например, во второй строке таблицы 1, отражающей результаты метода PROMETHEE I записано следующее:

Luxury 1 < Tourism B

Luxury 1 ~ Luxury 1

Luxury 1 N Tourism A

Luxury 1 > Luxury 2

Luxury 1 > Economic

Luxury 1 > Sport

Таблица 1.

	Tourism B	Luxury 1	Tourism A	Luxury 2	Economic	Sport
Tourism B	~	>	>	>	>	>
Luxury 1	<	~	N	>	>	>
Tourism A	<	N	~	N	N	N
Luxury 2	<	<	N	~	N	>
Economic	<	<	N	N	~	N
Sport	<	<	N	<	N	~

Таблица 2.

	Tourism B	Luxury 1	Tourism A	Luxury 2	Economic	Sport
Tourism B	~	>	>	>	>	>
Luxury 1	<	~	>	>	>	>
Tourism A	<	<	~	>	>	>
Luxury 2	<	<	<	~	>	>
Economic	<	<	<	<	~	>
Sport	<	<	<	<	<	~

Те же суждения можно получить, работая с графическими представлениями промежуточных и выходных данных решения ДМКЗ. Для этого используют следующие диаграммы:

· PROMETHEE I Partial Ranking;

· PROMETHEE II Complete Ranking;

· PROMETHEE Diamonds;

· PROMETHEE Network.

Рассмотрим каждую из них подробно.

4.3. Диаграмма “PROMETHEE I Partial Ranking”

На этой диаграмме, изображённой на рис. 4, представлена визуализация промежуточных данных, используемая для решения ДМКЗ методом PROMETHEE I. Каждая альтернатива изображена в виде отрезка. Концы этого отрезка расположены на левой и правой осях. Левая ось направлена вверх и отражает значения Phi+ для каждой конкретной альтернативы. Правая ось параллельна левой, направлена вниз и отражает значения Phi- для каждой конкретной альтернативы. Соединив точки, соответствующие одной и той же альтернативе (на левой и правой осях) получаются отрезки.

Цвета отрезков отражают принадлежность альтернативы к той или иной группе. Эту принадлежность в программе Visual PROMETHEE Academic определяет пользователь ещё до запуска самой вычислительной процедуры. В данном примере пользователь задал три группы альтернатив.

Первая группа альтернатив - Tourism cars. В эту группу входят альтернативы Tourism A и Tourism B. Отрезки, соответствующие этим альтернативам окрашены в бирюзовый цвет.

Вторая группа альтернатив - Luxury cars. В эту группу входят Luxury 1 и Luxury 2. Отрезки, соответствующие этим альтернативам, окрашены в зелёный цвет.

И, наконец, третья группа альтернатив - это none. В эту группу входят альтернативы Sport и Economic. Отрезки, соответствующие этим альтернативам, окрашены в жёлтый цвет.

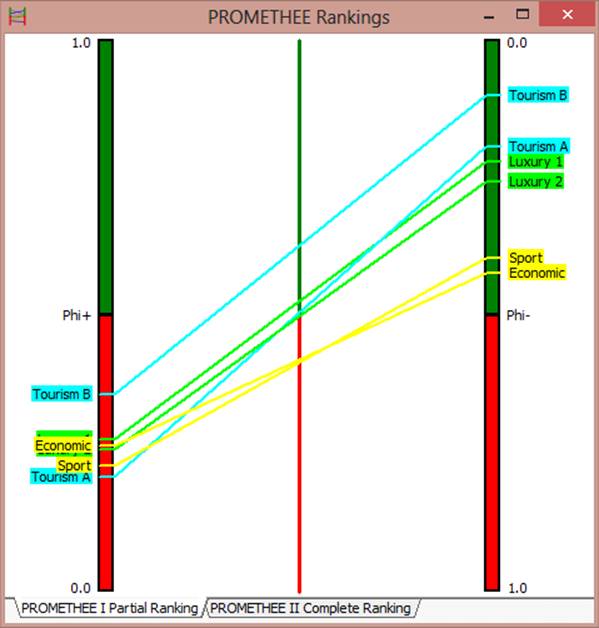
Рис. 4. Диаграмма “PROMETHEE I Partial Ranking”.

Покажем на примере, каким образом пользователь (аналитик или ЛПР) работает с этой диаграммой. Возьмём 2 альтернативы: Tourism A и Tourism B. Отрезок, соответствующий альтернативе Tourism B расположен выше отрезка Tourism A и не имеет с ним общих внутренних точек. Этот геометрический предикат интерпретируется следующим образом: между альтернативами Tourism B и Tourism A установлено отношение строгого предпочтения, то есть

Tourism B > Tourism A

Tourism A < Tourism B

Теперь возьмём другую пару альтернатив: Tourism A и Luxury 1. Отрезки, соответствующие этим альтернативам, имеют одну общую внутреннюю точку. Это означает, что между альтернативами установлено отношение несравнимости, то есть

Tourism A N Luxury 1

Luxury 1 N Tourism A

Если бы на диаграмме имелись отрезки, которые целиком бы совпадали, то между соответствующими им альтернативами было бы установлено отношение безразличия (~).

Если бы 2 отрезка имели общую конечную точку (справа или слева), но один из них лежал бы выше другого, то альтернатива, соответствующая отрезку, который расположен выше, считалась бы более предпочтительной.

Табличное представление результатов решения ДМКЗ методом PROMETHEE I с помощью матрицы бинарных отношений в предыдущем разделе (табл. 1) и графическое представление в текущем разделе (рис. 4), содержат в себе одну и ту же информацию, которая представлена в разной форме. Из-за погрешностей картинки или неудобного выбора цветовой гаммы, у пользователя могут возникнуть трудности при построении геометрических предикатов. Но графическое представление всё же является более удобным для пользователя, так как позволяет ему быстрее анализировать результаты решения ДМКЗ методами семейства PROMETHEE. То есть достоинством данной и всех последующих визуализаций является высокая скорость формирования суждений об альтернативах.

Если же пользователь всё-таки затрудняется построить геометрический предикат (например, в случае, когда Phi+ и Phi- одной альтернативы очень незначительно отличаются от Phi+ и Phi- другой альтернативы, и из-за погрешностей изображения не понятно, пересекаются эти отрезки, совпадают, или один из них целиком лежит выше другого), то можно обратиться к традиционному табличному представлению промежуточных данных, в котором Phi+ и Phi- для каждой альтернативы записаны с высокой точностью.

Таким образом, пользователь использует как графические, так и табличные представления при получении результатов решения ДМКЗ.

4.4. Диаграмма “PROMETHEE II Complete Ranking”

На следующей диаграмме, изображённой на рис. 5, представлена визуализация промежуточных данных, используемая для решения ДМКЗ методом PROMETHEE II. На ней имеется лишь одна ось - ось значений Phi. Число Phi вычисляется для каждой альтернативы как разность между Phi+ и Phi-. Альтернативам теперь ставятся в соответствие не отрезки, а точки. Причём рядом с каждой точкой стоят название и значение Phi альтернативы. Это обеспечивает такую же высокую точность, которую обеспечивает табличное представление.

Напомним, что метод PROMETHEE II не устанавливает между альтернативами отношение несравнимости. Он устанавливает только отношения безразличия, строгого предпочтения и строгого антипредпочтения между двумя любыми альтернативами.

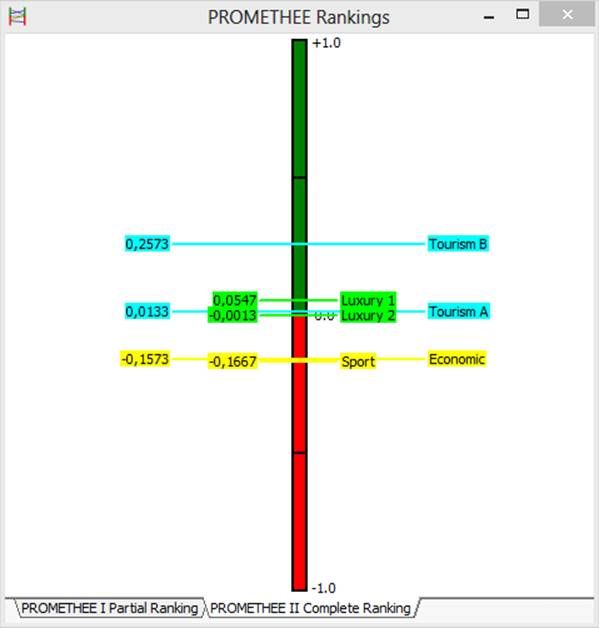
Рис. 5. Диаграмма “PROMETHEE II Complete Ranking”.

Если 2 точки на оси Phi совпадают, то между соответствующими этим точкам альтернативами устанавливается отношение безразличия.

Если одна из точек выше, то соответствующая ей альтернатива считается более предпочтительной. В данном примере, точка, соответствующая альтернативе Tourism B располагается выше точки Luxury 1. Это означает, что между альтернативами Tourism B и Luxury 1 установлено отношение строгого предпочтения:

Tourism B > Luxury 1

Luxury 1 < Tourism B

4.5. Диаграмма “PROMETHEE Diamonds”

На следующей диаграмме, изображённой на рис. 6, представлена визуализация промежуточных данных, используемая для решения ДМКЗ методами PROMETHEE I и PROMETHEE II.

На данной диаграмме изображены 2 оси, перпендикулярные друг другу.

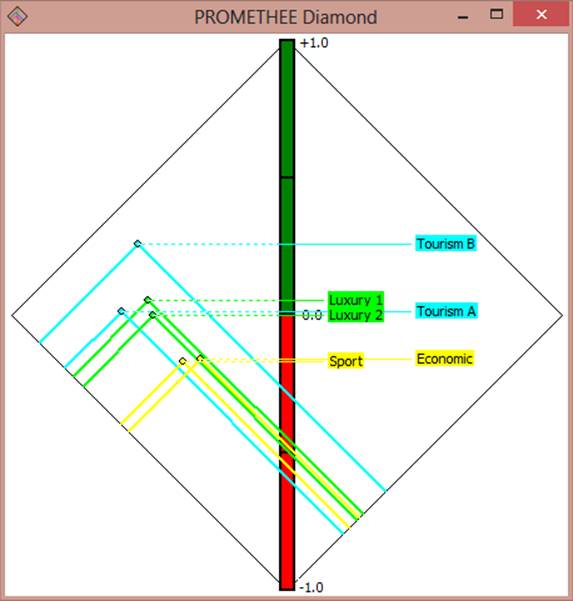
Рис. 6. Диаграмма “PROMETHEE Diamonds”.

На рис. 6 оси просматриваются плохо, поэтому авторы статьи выделили их явно на рис. 7 и 8.

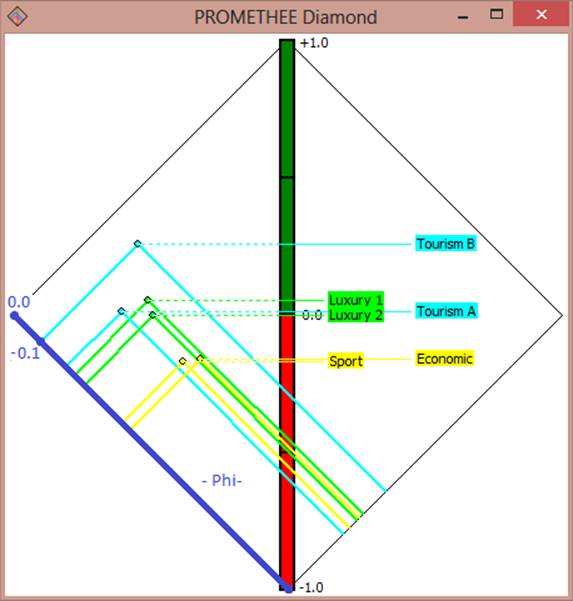
Рис. 7. Ось “- Phi-” на диаграмме “PROMETHEE Diamonds”.

Фиолетовым цветом на рис. 7 выделена ось, которую можно назвать “Phi-”, умноженное на “-1”. (На рисунке обозначено короче: “- Phi-”.) На этой оси авторами фиолетовым цветом отмечены для наглядности 2 значения: “0.0” и “-0.1”.

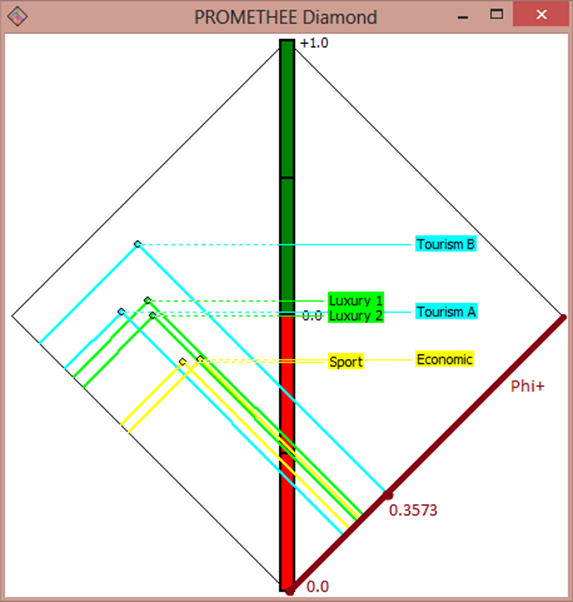
Рис. 8. Ось “Phi+” на диаграмме “PROMETHEE Diamonds”.

На рис. 8 авторами выделена бордовым цветом ось “Phi+” с отмеченными на ней значениями “0.0” и “0.3573”.

На этой диаграмме всем альтернативам ставятся в соответствие прямоугольники с общей вершиной внизу. Вторая вершина определяется значениями “Phi+” и “Phi-” для каждой альтернативы. По этим двум вершинам строится прямоугольник со сторонами, параллельными осям.

Диаграмма отражает результаты работы обоих методов: и PROMETHEE I, и PROMETHEE II.

Рассмотрим построение и интерпретацию геометрических предикатов, касающихся результатов решения ДМКЗ методом PROMETHEE I.

Если прямоугольники, соответствующие 2 альтернативам, совпадают, то между этими альтернативами устанавливается отношение безразличия.

Вершина прямоугольника Luxury 1 является внутренней точкой прямоугольника, соответствующего альтернативе Tourism B. Это означает, что альтернатива Luxury 1 менее предпочтительна альтернативы Tourism B. То есть между этими двумя альтернативами установлено отношение строгого антипредпочтения:

Luxury 1 < Tourism B

Tourism B > Luxury 1

Прямоугольники, соответствующие альтернативам Luxury 1 и Tourism A пересекаются и имеют общую “одинокую” (или дискретную) точку. Это означает, что между альтернативами Luxury 1 и Tourism A установлено отношение несравнимости:

Luxury 1 N Tourism A

Tourism A N Luxury 1

Заметим теперь, что на диаграмме присутствует вертикальный столбец (ось), на который спроецированы точки прямоугольников.

Если проекции двух точек прямоугольников совпадают, то между соответствующими им альтернативами устанавливается отношение безразличия.

Проекция точки прямоугольника, соответствующего альтернативе Tourism B расположена выше проекции точки прямоугольника, соответствующего альтернативе Luxury 1. Это означает, что между этими альтернативами методом PROMETHEE II установлено отношение строгого предпочтения:

Tourism B > Luxury 1

Luxury 1 < Tourism B

Так как метод PROMETHEE II не устанавливает между альтернативами отношение несравнимости, то не существует и геометрического предиката, который можно было бы интерпретировать как наличие отношения несравнимости между двумя альтернативами.

4.6. Диаграмма “PROMETHEE Network”

На данной диаграмме, изображённой на рис. 9, в виде графа графически отображены результирующие выходные данные — суждения, полученные с помощью метода PROMETHEE I.

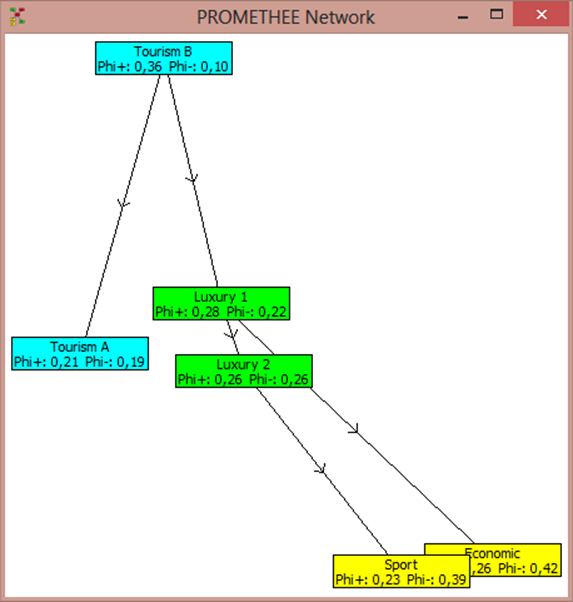
Рис. 9. Диаграмма “PROMETHEE Network”.

Альтернативы отражены в виде прямоугольников (вершин графа), содержащих название альтернативы и соответствующие ей значения Phi+ и Phi-.

Прямоугольники, соответствующие альтернативам Tourism B и Tourism A соединены стрелкой. Причём стрелка идёт от прямоугольника, соответствующему альтернативе Tourism B к прямоугольнику, соответствующему альтернативе Tourism A. Это означает, что между альтернативами Tourism B и Tourism A установлено отношение строгого предпочтения:

Tourism B > Tourism A

Tourism A < Tourism B

Прямоугольники, соответствующие альтернативам Economic и Sport не соединены стрелкой. Это означает, что между ними установлено отношение несравнимости:

Economic N Sport

Sport N Economic.

4.7. Диаграмма “Плоскость GAIA”

Самым известным способом визуализации в семействе методов PROMETHEE является “Плоскость GAIA”.

Каждая альтернатива описывается кортежем действительных чисел. Вычислительные процедуры методов семейства PROMETHEE преобразуют кортежи в кортежи . Далее каждому такому кортежу ставится в соответствие точка n-мерного Евклидова пространства.

Как правило, в ДМКЗ , поэтому используется снижение размерности с помощью метода главных компонент. Размерность пространства снижается с до 2. При этом, разумеется, сохраняется только часть информации.

На плоскость проецируются не только точки n-мерного пространства, но и оси , а так же вектор - веса критериев, которые задаются пользователем). Проекцию вектора на плоскость принято обозначать буквой , а проекции осей буквами соответственно.

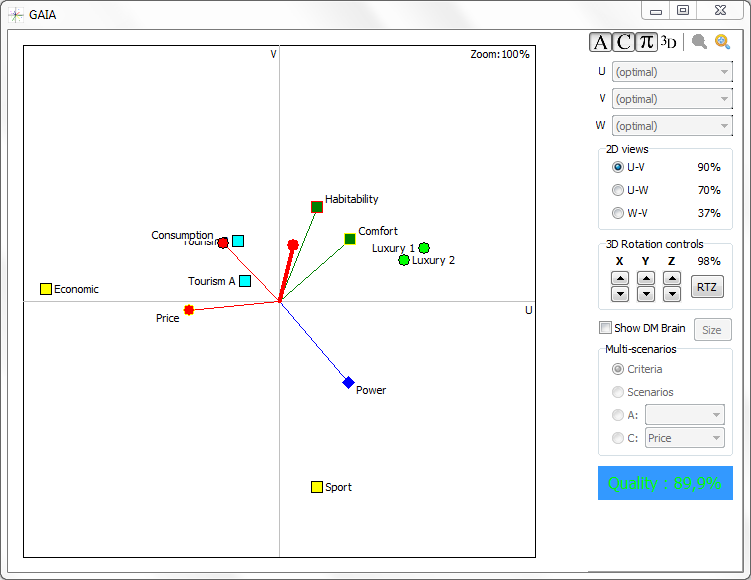
Рис. 10. Диаграмма “Плоскость GAIA”.

На следующей диаграмме, изображённой на рис. 10, представлена визуализация промежуточных данных, используемая для решения ДМКЗ методом PROMETHEE II.

Плоскость GAIA позволяет пользователю проводить анализ на конфликтность критериев значительно быстрее, чем при работе с таблицами. Кроме этого, пользователь значительно быстрее может выделить схожие альтернативы, работая с визуальным представлением данных на плоскости GAIA.

Информация о конфликтующих критериях и схожих альтернативах способна помочь пользователю в процессе решения ДМКЗ.

Стоит отметить, что из-за потерь информации при снижении размерности пространства, необходимо с осторожностью пользоваться этим способом визуализации.

5. Заключение

В данной статье были даны краткий исторический обзор становления семейства методов PROMETHEE, а также обзор различных способов визуализации, которые используются в этом семействе.

В статье отмечено, что пользователь использует изображения для быстрого получения информации о результирующих выходных и промежуточных данных решения ДМКЗ, и обращается к результатам в табличной форме только при возникновении необходимости в этом.

Улучшение способов визуализации видится авторам статьи в использовании 3-х мерной пространственной сцены в GAIA, то есть в переходе от n-мерного пространства к 3-х мерному. При этом сохраняется большая часть информации, чем во время перехода к 2-мерному пространству.

Использование традиционного графического табличного представления входных данных целесообразно дополнить и другими способами визуализации с применением более сложных графических интерпретаций. Это позволит аналитику сократить количество альтернатив ещё до использования вычислительных процедур методов семейства PROMETHEE и ускорить дальнейшее решение ДМКЗ за счёт меньшего числа альтернатив.

Список литературы

1. Diaby V., Campbell K., Goeree R. Multi-criteria decision analysis (MCDA) in health care: A bibliometric analysis. Operations Research for Health Care. 2013. 2(1-2). pp.20-24.

2. Adunlin G., Diaby V., Montero A., Xiao H. Multi-Criteria Decision Analysis In Oncology: An Overview. Value in Health. 2014. Vol. 17. No. 3, p. 184.

3. Shmelev S., van den Bergh J. Optimal diversity of renewable energy alternatives under multiple criteria: An application to the UK. Renewable and Sustainable Energy Reviews. 2016. Vol. 60. pp.679-691.

4. Felice F., Petrillo A. Multicriteria approach for process modelling in strategic environmental management planning. IJSPM. 2013. Vol. 8. No. 1. pp. 6.

5. Jaiswal R., Ghosh N., Galkate R., Thomas T. Multi Criteria Decision Analysis (MCDA) for Watershed Prioritization. Aquatic Procedia. 2015. No. 4. pp.1553-1560.

6. De Felice F., Campagiorni F., Petrillo A. Economic and Environmental Evaluation Via an Integrated Method based on LCA and MCDA. Procedia - Social and Behavioral Sciences. 2013. Vol. 99. pp.1-10.

7. Neves L., Dias L., Antunes C., Martins, A. Structuring an MCDA model using SSM: A case study in energy efficiency. European Journal of Operational Research. 2009. Vol. 199. No. 3. pp.834-845.

8. Behzadian M., Kazemzadeh R., Albadvi A., Aghdasi M. PROMETHEE: A comprehensive literature review on methodologies and applications. European Journal of Operational Research. 2010. Vol. 200. No. 1. pp.198-215.

9. Brans J.P., Mareschal B., Vincke Ph. PROMETHEE: a new family of outranking methods in multicriteria analysis. Operational Research, IFORS 84. 1984. Pp. 477–490

10. Brans J., Mareschal B. PROMETHEE methods. Multiple Criteria Decision Analysis: State of the Art Surveys. 2005. Pp. 163-196

11. Promethee-gaia.net. The PROMETHEE-GAIA FAQ. [online] Available at: http://www.promethee-gaia.net/faq-pro/index.php [Accessed 6.05.2016].

12. Brans J., Mareschal B. The PROMETHEE VI procedure: how to differentiate hard from soft multicriteria problems. Journal of Decision Systems. 1995. Vol. 4. No. 3. pp.213-223.

13. Brans J., Mareschal B. Promethee V: Mcdm Problems With Segmentation Constraints. INFOR: Information Systems and Operational Research. 1992. Vol. 30. No. 2. pp.85-96.

14. Macharis C., Brans J., Mareschal B. The GDSS PROMETHEE procedure. Journal of Decision Systems. 1998. Vol. 7. No. 4. pp.283–307.

15. Macharis C., Mareschal B., Waaub J., Milan L. PROMETHEE-GDSS revisited: applications so far and new developments. IJMCDM. 2015. 5(1/2). p.129.

16. Figueira J., Greco S., Ehrgott M. Multiple criteria decision analysis. 2005. New York: Springer.

17. Guitouni A., Martel J. Tentative guidelines to help choosing an appropriate MCDA method. European Journal of Operational Research. 1998. Vol. 109. No. 2. pp.501-521.

18. Zopounidis C., Doumpos M. Multi-criteria decision aid in financial decision making: methodologies and literature review. Journal of Multi-Criteria Decision Analysis. 2002. Vol. 11. No. 4-5. pp.167-186.

19. Roy B. Multicriteria methodology for decision aiding. 1996. Dordrecht, Netherlands: Kluwer Academic Publishers.

USING VISUALIZATION IN SOLVING DISCRETE MCDA-PROBLEM BY METHODS OF PROMETHEE FAMILY

A.Yu. Yakovlichev, I.E. Milman, V.V. Pilyugin.

National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Russian Federation.

DrewYak7@ya.ru, igalush@gmail.com, VVPilyugin@mephi.ru

Abstract

This article contains a short historical review of the establishment of methods PROMETHEE family. We consider the classification of B. Roy and 2 approach to the formulation of the discrete MCDA-problem: the approach of multi-attribute utility theory and outranking approach. Spend formalization formulation of the problem to be solved by the methods of PROMETHEE family: describes the input, intermediate and output data the discrete MCDA-problem.

Shown working with a software tool Visual PROMETHEE Academic on the example of car selection. Particular attention is paid to visualization intermediate and output data for solving discrete MCDA-problems by PROMETHEE I and PROMETHEE II. We consider the diagram "PROMETHEE I Partial Ranking", "PROMETHEE II Complete Ranking", "PROMETHEE Diamonds", "PROMETHEE Network", "GAIA Plane".

The article mentioned that a user uses these diagrams for rapid information on the resulting output data and intermediate discrete MCDA-problem solutions, and refers to the results in tabular form only when the need arises.

Keywords: MCDA-problem, PROMETHEE, visualization, decision theory.

References