ПРИМЕНЕНИЕ АЛГОРИТМА ВИОЛЫ-ДЖОНСА, ПРЕОБРАЗОВАНИЯ ХАФА И ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ ДЛЯ РАСПОЗНАВАНИЯ СИМВОЛЬНОЙ ИНФОРМАЦИИ НА СЛОЖНОМ ФОНЕ

А.А. Друки, П.А. Каковкин, Д.С. Чернета

Национальный исследовательский Томский политехнический университет, Россия

druki2008@yandex.ru, nitrokot@mail.ru, Dimano1993@rambler.ru

Оглавление

1. Введение

2. Алгоритм детектирования области расположения символов на изображении

3. Алгоритм нормализации изображения и выделение отдельных символов

4. Алгоритм распознавания символов

5. Сравнение результатов тестирования разработанных алгоритмов с существующими аналогами

6. Заключение

Список литературы

Аннотация

Работа посвящена разработке алгоритмов и программных средств, позволяющих повысить эффективность распознавания символов на сложном фоне, подверженных шумовым, аффинным и проекционным искажениям. В работе предлагается подход к решению задачи распознавания символов, включающий в себя три основных этапа: детектирование области расположения символов на изображении; нормализация изображения и выделение отдельных символов; распознавание символов. Для детектирования области расположения символов на изображениях со сложным фоном предложена реализация алгоритма Виолы-Джонса. Нормализация изображения включает в себя выделение границ, преобразование Хафа, поиск замкнутых контуров, выравнивание изображения. С помощью преобразования Хафа выполняется поиск горизонтальных граней строки символов на изображении. С помощью операции поиска замкнутых контуров выполняется обнаружение области расположения отдельных символов на изображении. Для распознавания символов предложена конфигурация сверточной нейронной сети. Представлены результаты тестирования эффективности разработанных алгоритмов и их сравнение с существующими аналогами. На основе предложенного подхода разработана программная система, которая предназначена для распознавания государственных регистрационных знаков транспортных средств на изображениях и по результатам тестирования показала высокую эффективность распознавания символов на сложном фоне.

Ключевые слова: Обработка изображений, алгоритм Виолы-Джонса, преобразование Хафа, искусственные нейронные сети, распознавание символов.

1. Введение

Задача обработки и анализа изображений является относительно новой и получила свое развитие во второй половине ХХ века, параллельно с развитием компьютерных технологий [1, 2]. Среди особо важных и интересных задач в данной предметной области можно выделить задачу распознавания объектов на изображениях со сложным (неоднородным по цвету и фактуре) фоном, что имеет большую значимость в таких областях как государственная оборона, обеспечение правопорядка, предотвращение несанкционированного доступа к секретным объектам и объектам военного назначения [2].

За последние годы был представлен ряд методов и алгоритмов, применяемых на различных стадиях процесса распознавания символов на изображениях. Однако применение данных методов недостаточно эффективно в реальных условиях, которые характеризуются наличием сложного фона на изображениях, различной степенью освещенности, наличием шумов, аффинными и проекционными искажениями объектов, возникающими из-за изменения углов регистрации. Эффективность работы большинства алгоритмов становится ниже технологически приемлемого уровня при наличии искажений подобного рода. Все это требует применения различных алгоритмов предварительной обработки, что в свою очередь усложняет процесс распознавания, делает его более громоздким, увеличивает объем и время вычислительного процесса. Таким образом, данная задача до сих пор не решена в полном объеме и является актуальной на сегодняшний день.

В процессе исследования было выявлено, что одним из наиболее актуальных и интенсивно развивающихся направлений данной предметной области является распознавание автомобильных номерных знаков (государственных регистрационных знаков транспортных средств). Поэтому было принято решение осуществлять реализацию и тестирование алгоритмов на примере распознавания символов на автомобильных номерных знаках при наличии сложного фона на изображениях.

Процесс распознавания символов на изображениях со сложным фоном можно разделить на следующие этапы [3]:

1. Детектирование области расположения символов на изображении.

2. Нормализация изображения и выделение отдельных символов.

3. Распознавание символов.

Целью работы является разработка алгоритмов и программных средств, позволяющих повысить эффективность распознавания символов на сложном фоне.

Для достижения поставленных целей необходимо решение следующих задач:

1. Разработать алгоритм, обеспечивающий детектирование области расположения символов на изображении.

2. Реализовать алгоритм, обеспечивающий нормализацию изображений и выделение отдельных символов.

3. Разработать алгоритм, обеспечивающий распознавание символов.

2. Алгоритм детектирования области расположения символов на изображении

Общий смысл процесса детектирования объектов на изображениях заключается в отнесении входных изображений к одному из двух классов: имеющие и не имеющие в обрабатываемой области объекты, соответствующие заданным критериям

На сегодняшний день существует множество алгоритмов, применяемых для решения этой задачи. Среди наиболее популярных и эффективных алгоритмов можно выделить гистограммный анализ цветовых компонент изображения [4], алгоритмы с использованием искусственных нейронных сетей [5], метод главных компонент [6], дескрипторы локальных особенностей изображения (SURF [7], SIFT [8], HOG [9], FAST [10]), алгоритм Виолы-Джонса [11].

Одним из наиболее эффективных подходов для решения данной задачи является алгоритм Виолы-Джонса, предложенный в 2001 г. исследователями P. Viola и M. Jones [11]. Для классификации объектов на изображении в данном алгоритме используются признаки Хаара, которые представляют собой прямоугольные области, состоящие из нескольких смежных частей (рис. 1).

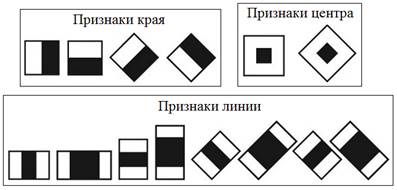
Рис. 1. Признаки Хаара.

Данный алгоритм имеет каскадную структуру, состоящую из классификаторов. Каждый уровень этого каскада представляет собой классификатор, называемый ансамблем, который состоит из нескольких признаков Хаара. Выполняется последовательное сканирование изображения окном заданного размера, и анализируемая область изображения проверяется каждым из классификаторов на соответствие искомому образу. Если на каком-либо уровне определяется, что исследуемая область не содержит признаки искомого объекта, то процедура заканчивается и данная область помечается как ложная. Таким образом, каскадный классификатор отбрасывает из рассмотрения ложные области изображения. В итоге остаются только области, имеющие наибольшую вероятность содержания искомого объекта [12].

Ансамбли первых уровней состоят из малого количества классификаторов. С увеличением порядкового номера уровня увеличивается количество классификаторов, содержащихся в нем. Ансамбли последних уровней могут содержать десятки и сотни классификаторов, для более тщательного анализа областей изображения.

Значение признака для исследуемой области изображения вычисляется путем суммирования интенсивностей пикселей в черных и белых областях признаков Хаара, затем вычисляется разность между суммами и сравнивается с заданным порогом:

где L – сумма значений пикселей, соответствующих белым областям; D – сумма значений пикселей, соответствующих черным областям.

Для сокращения числа операций при вычислении признаков в данном алгоритме используется интегральное представление изображения [13]. Данный подход предполагает представление исходного изображения в виде матрицы, в которой значение каждой ячейки является суммой интенсивностей всех пикселей, находящихся выше и левее данной ячейки:

где – яркость пикселя изображения, x, y – порядковые номера пикселя.

Таким образом, матрица состоит из элементов, каждый из которых состоит из суммы значений пикселей прямоугольной области от (0, 0) до (x, y). Расчет интегральной матрицы выполняется за один проход по всем пикселям изображения:

Обучение алгоритма Виолы-Джонса осуществляется на основе бустинга (англ. adaptive boosting – адаптивное улучшение), где классификаторы, представляющие собой всевозможные признаки Хаара, комбинируются таким образом, чтобы получить более сложный классификатор. Из всего множества признаков выбираются те, которые наиболее оптимально подходят для обнаружения искомого объекта [13].

Для обучения алгоритма была сформирована база данных из 5000 изображений сегментированных автомобильных номерных знаков (размер 28x52 пикселей), соответствующих ГОСТ Р 50577 – 93, группе 1, типу 1 (рис. 2 (а)). Основная часть изображений была получена из источников [14], [15]. Остальная часть изображений была сформирована самостоятельно.

Изображения автомобильных номерных знаков представлены при различных углах отклонения относительно регистрирующего устройства. Для обеспечения высокой степени инвариантности алгоритма к различным искажениям, к некоторым изображениям из обучающего набора применялось изменение освещения, контраста и размытие.

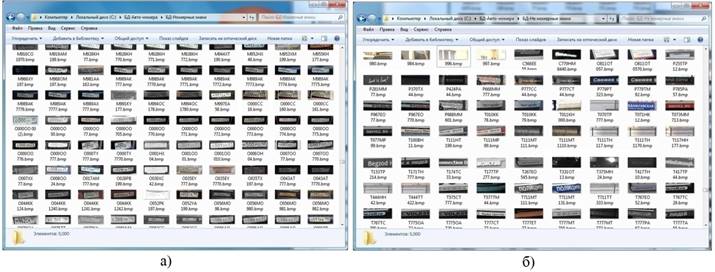
Рис. 2. Изображения из обучающей выборки: а) изображения сегментированных автомобильных номерных знаков; б) фоновые изображения.

Также для обучения была сформирована база из 6000 фоновых изображений, не содержащих образы автомобильных номерных знаков (рис. 2 (б)). Для обеспечения эффективного процесса обучения данная база содержит множество ложных образов, имеющих визуальные признаки, схожие с автомобильными номерными знаками.

Обучение классификатора осуществлялось с помощью модуля обучения алгоритма Виолы-Джонса в библиотеке OpenCV (opencv_traincascade.exe). Время обучения алгоритма составило 32,4 часа.

Тестирование классификатора производилось на 2000 изображений транспортных средств со сложной фоновой структурой. Точность классификации при тестировании составила 98.21 %.

После того как искомый объект на изображении найден, данная область изображения сегментируется для последующей обработки. Однако сложность заключается в том, что автомобильный номерной знак, может быть расположен под неизвестным углом на изображении, что может внести определенные трудности в процесс распознавания символов на данном номерном знаке (рис. 3). В связи с этим, требуется применять алгоритмы нормализации изображения.

Рис. 3. Выделение автомобильного номерного знака.

3. Алгоритм нормализации изображения и выделение отдельных символов

С целью минимизации влияния на результат распознавания шумов и фона предлагается применять выделение контуров на изображении (англ. Edge detection) оператором Собеля [16] (рис. 4) (б).

При анализе различных алгоритмов было принято решение определять угол отклонения автомобильного номерного знака на основе горизонтальных граней пластины номерного знака. Данный подход предполагает, что на полученном сегментированном изображении горизонтальные грани пластины номерного знака представляют собой линии максимальной длины. Поэтому все найденные линии, длина которых превышает заданный порог, принимаются за горизонтальные грани пластины номерного знака. Поиск прямых линий на изображении выполняется с помощью преобразования Хафа (англ. Hough transform) [16, 17] (рис. 4 (в)).

Рис. 4. Нормализация изображения: а) исходное сегментированное изображение; б) результат выделения контуров; в) результат преобразования Хафа; г) выравнивание изображения.

Из всех найденных линий выбираются линии с максимальной длинной относительно ширины изображения. Данные линии предположительно будут являться горизонтальными гранями пластины номерного знака. После нахождения горизонтальных граней пластины номерного знака, изображение выравнивается путем поворота в горизонтальную плоскость и выполняется обрезка лишних областей (рис. 4 (г)).

На следующем этапе необходимо выделить области расположения символов на изображении для их последующего распознавания. Для этого выполняется поиск замкнутых контуров. Найденные замкнутые контуры на изображении выделяются прямоугольными областями для последующей сегментации [16] (рис. 5).

Однако на изображении могут присутствовать ложные объекты, представляющие собой замкнутые контуры. Для этого выполняется проверка обнаруженных областей на соответствие следующему условию: , где h – высота области расположения символа, hmax – высота изображения. При выполнении данного условия рассматриваемая область считается ложной.

Рис. 5. Выделение областей расположения символов: а) выделение замкнутых контуров на изображении; б) исключение ложных областей.

Таким образом, находятся области прямоугольной формы, которые соответствуют границам символов, что делает возможным дальнейшее их распознавание. Полученные области изображения масштабируются к размеру 29х29 пикселей и подаются на вход алгоритму распознавания. Данный размер масштабирования соответсвует размеру изображений символов из обучающей выборки, а также размеру входного слоя сверточной нейронной сети.

4. Алгоритм распознавания символов

После этапа выделения отдельных символов, следует последний этап – распознавание символов. Основные сложности данного этапа заключаются в том, что символы на изображении могут быть подвержены шумовым, аффинным и проекционным искажениям.

При анализе различных алгоритмов, применяемых для решения данной задачи, было принято решение использовать сверточные нейронные сети (СНС) [18, 19], так как они обладают следующими преимуществами:

· Структура СНС хорошо подходит для обработки двумерных данных.

· Наслаивающиеся друг на друга локальные рецептивные поля нейронов (области входных сигналов нейронов) обеспечивают взаимосвязь пространственно-зависимых областей изображения.

· Повышенная устойчивость к аффинным и проекционным искажениям входных данных, шумам, изменению масштаба [19].

Исходя из перечисленных преимуществ, для распознавания символов на автомобильных номерных знаках, была разработана СНС, представленная на рис. 6.

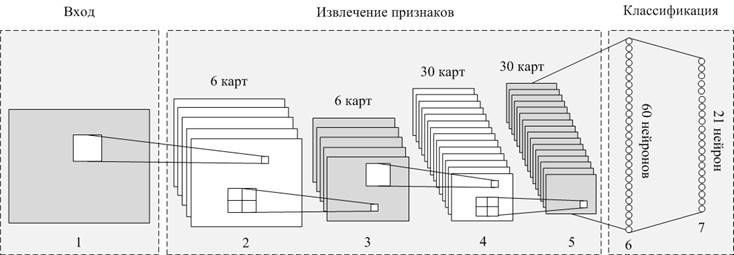
Рис. 6. Структура СНС. C1, C2 – сверточные слои; P1, P2 – подвыборочные слои; N1, N2 – слои из обычных нейронов.

Разработанная СНС состоит из двух типов слоев: сверточные и подвыборочные. Каждый слой состоит из набора карт признаков, которые в свою очередь состоят из нейронов.

Входной слой размером 29x29 нейронов служит для подачи входного образа в нейронную сеть.

Второй слой C1 является слоем свертки и состоит из 6 сверточных карт признаков размером 26х26 нейронов. Данный размер карт обеспечивает достаточное наложение рецептивных полей друг на друга. Каждая карта данного слоя имеет собственную матрицу синаптических коэффициентов и нейронное смещение. Рецептивные поля нейронов частично пересекаются и имеют размер 4x4 нейрона. Данный размер рецептивных полей подобран экспериментально. Каждой карте признаков соответствует весовых коэффициентов и нейронное смещение. Таким образом, данный слой содержит 4056 нейронов и 102 весовых коэффициента.

Размер карт признаков сверточного слоя определяется следующими формулами:

, ,

где , – параметры высоты и ширины карты признаков сверточного слоя; , – параметры высоты и ширины карты предыдущего слоя; M, N – параметры высоты и ширины локального рецептивного поля.

Функционирование нейрона сверточного слоя определяется следующей формулой:

где, – нейрон сверточного слоя, q-ой карты признаков; – нейронное смещение q-ой карты; N, M – ширина и высота локального рецептивного поля; – выходные значения нейронов предыдущего слоя; – синаптические коэффициенты.

Третий слой P1 является слоем подвыборки и обеспечивает повышенную устойчивость нейронной сети к изменению масштаба входного изображения. Количество карт признаков слоя подвыборки как правило такое же, как и в предыдущем слое, но их размер в два раза меньше. Это объясняется тем, что локальные рецептивные поля в слоях подвыборки не пересекаются и имеют фиксированный размер 2х2 нейрона. Данный слой состоит из 6 карт признаков размером 13×13 нейронов. Каждая карта признаков данного слоя связана только с одной соответствующей ей картой предыдущего слоя, имеет один синаптический коэффициент и нейронное смещение. Таким образом, данный слой содержит 1014 нейронов и всего 12 синаптических весовых коэффициентов.

Размер карт признаков подвыборочного слоя определяется следующими формулами:

, ,

где , – параметры высоты и ширины карты признаков подвыборочного слоя; , – параметры высоты и ширины карты предыдущего слоя; M, N – параметры высоты и ширины локального рецептивного поля.

Функционирование нейрона подвыборочного слоя определяется следующей формулой:

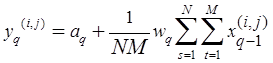где, – нейрон подвыборочного слоя, q-ой карты признаков; – нейронное смещение q-ой карты; M, N – параметры высоты и ширины локального рецептивного поля; – выходные значения нейронов предыдущего слоя; – синаптический коэффициент.

Четвертый слой C2 является слоем свертки и состоит из 30 сверточных карт признаков размером 10х10 нейронов. Рецептивные поля смежных нейронов частично пересекаются. Каждая карта признаков данного слоя имеет связи с тремя соответствующими картами предыдущего слоя. Размер локального рецептивного поля равен 4x4 нейронов. Каждой карте соответствует весовых коэффициентов и нейронное смещение. Таким образом, данный слой содержит 3000 нейронов и 510 весовых коэффициентов.

Пятый слой P2 является слоем подвыборки, состоит из 30 подвыборочных карт признаков. Размер карт признаков данного слоя в два раза меньше размера карт предыдущего слоя и равен 5х5 нейронов. Каждая карта признаков имеет связь только с одной соответствующей ей картой предыдущего слоя. Рецептивные поля смежных нейронов не пересекаются и имеют размер 2х2 нейрона. Каждой карте признаков соответствует один синаптический коэффициент и нейронное смещение. Данный слой содержит 750 нейронов и 60 синаптических весовых коэффициентов.

Первые пять слоев предназначены для извлечения признаков изображения. Следующие два слоя являются слоями классификации.

Шестой слой N1 состоит из 60 нейронов. Каждый нейрон данного слоя имеет связи со всеми нейронами двух соответствующих ему карт признаков предыдущего слоя P2. Каждый нейрон вычисляет взвешенное суммирование 50 соответствующих ему входных параметров, добавляет нейронное смещение и полученный результат передает через функцию активации. Таким образом, данный слой содержит 1530 синаптических весовых коэффициентов.

Седьмой слой N2 состоит из 21 нейрона и является выходным слоем. Роль данного слоя заключается в вычислении окончательного результата классификации. Каждый нейрон данного слоя имеет связи со всеми нейронами предыдущего слоя. Нейроны выходного слоя соответствуют 21 классу распознаваемых символов: А, В, Е, К, М, Н, О, Р, С, Т, X, У и цифры от 0 до 9 (автомобильные номерные знаки, соответствующие ГОСТ Р 50577 – 93, группе 1, типу 1). Данный слой содержит 1320 синаптических весовых коэффициентов.

На выходе каждого нейрона производится вычисление Евклидова расстояния между вектором выходных значений и параметрическим вектором:

где, х – вектор входных значений, w – параметрический вектор, y – выход сети.

СНС содержит 9742 нейронов и 3534 синаптических коэффициентов. Структура нейронной сети, количество слоев, нейронов и распределение связей подбирались экспериментальным путем.

В процессе создания обучающего и тестового наборов выполнялась задача обеспечения СНС набором изображений символов, представленных в различном стилистическом виде: символы под разными углами наклона, с искажениями, разрывами и шумовыми помехами. Согласно ГОСТ Р50577 – 93 автомобильные номерные знаки, соответствующие группе 1, типу 1, содержат следующие символы: А, В, Е, К, М, Н, О, Р, С, Т, X, У и цифры от 0 до 9.

На основании этих требований была сформирована база данных для обучения СНС, состоящая из 20000 изображений символов и содержащая 21 класс символов, используемых на автомобильных номерных знаках (рис. 7). База данных для тестирования содержит 10000 изображений.

Рис. 7. Примеры изображений символов для обучения и тестирования СНС.

Для обучения СНС применялся алгоритм обратного распространения ошибки (англ. Back propagation) [19-20]. В основе данного алгоритма лежит принцип, позволяющий вычислять вектор частных производных (градиент) функции ошибки сети. Функцией ошибки является разница между текущим выходным значением нейронной сети и желаемым, которое необходимо получить:

где – величина функции ошибки для образа k; – желаемое значение выхода нейрона j для образа k; – текущее значение выхода нейрона j для образа k.

В процессе обучения выполняется последовательная корректировка весовых коэффициентов и ошибка сети постепенно уменьшается:

где – значение ошибки нейрона j для образа k; – текущий выход нейрона j для образа k; – коэффициент скорости обучения, .

Значение ошибки для нейронов сети определяется по следующей формуле:

где – значение ошибки i-го нейрона в слое q; – значение ошибки j-го нейрона в слое q+1; – вес связи, соединяющей два нейрона; – значение производной активационной функции i-го нейрона в слое q.

Результаты обучения и тестирования:

· Ошибка обучения: .

· Количество эпох обучения: 42.

· Время обучения: 27,4 часов.

· Точность при тестировании: 98.

5. Сравнение результатов тестирования разработанных алгоритмов с существующими аналогами

Результаты работы алгоритма детектирования автомобильных номерных знаков сопоставлены с результатами работы следующих алгоритмов: ED (Edge Detection) + HT (Hough Transform); ED + BHA (Brightness Histograms Analysis) + TM (Template Method); ED + BHA + SIFT (Scale Invariant Feature Transform); ED + BHA + HOG (Histogram of Oriented Gradients); ED + BHA + SURF (Speeded Up Robust Features). Данные алгоритмы были реализованы на практике и протестированы.

Для сравнения эффективности работы различных алгоритмов, их обучение и тестирование осуществлялось на одних и тех же данных. На рис. 8 представлено сравнение результатов работы данных алгоритмов с предложенным алгоритмом детектирования.

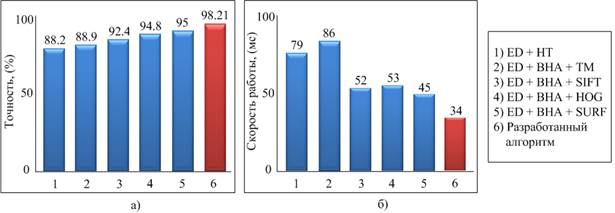
Рис. 8. Сравнение результатов работы различных алгоритмов при решении задачи детектирования автомобильных номерных знаков: а) точность классификации; б) скорость работы алгоритма.

Как видно по рис. 8 лучшие результаты точности классификации были получены с помощью разработанного алгоритма, на уровне 98,21%. Худшие результаты показали алгоритмы ED + HT, ED + BHA + TM.

По скорости работы предложенный алгоритм также показал наилучший результат, около 34 мс. Худшие результаты показали алгоритмы ED + HT, ED + BHA + TM.

Результаты работы алгоритма распознавания символов на автомобильных номерных знаках были сравнены со следующими алгоритмами: BN (Binarization) + BHA + ССA (Connected Components Analysis) + TM (Template Method); ED + BHA + ССA + KNN (K-Nearest Neighbours); ED + BHA + ССA + MA (Morphological Analysis); ED + ССA + HTM (Hierarchical Temporal Memory) [21]; BN + BHA + PCA (Principal Component Analysis) + NN (Neural Network); BN + BHA + ССA + СНС. Данные алгоритмы были реализованы на практике и протестированы.

Данные алгоритмы включают операции нормализации изображения, выделения и распознавания символов. Для сравнения эффективности работы различных алгоритмов, их обучение и тестирование осуществлялось на одних и тех же данных (изображения сегментированных автомобильных номерных знаков). На рис. 9 представлено сравнение результатов работы данных алгоритмов с предложенным алгоритмом распознавания символов. В качестве оценки точности распознавания символов используется отношение количества правильных распознаваний символов к общему числу символов на изображениях. В качестве оценки скорости работы алгоритмов представлена средняя скорость распознавания всех символов, изображенных на одном автомобильном номерном знаке совместно с этапом нормализации номерного знака.

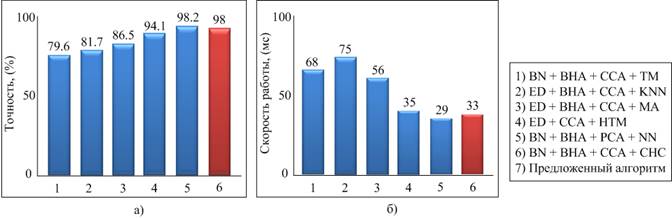
Рис. 9. Сравнение результатов работы различных алгоритмов при решении задачи распознавания символов на автомобильных номерных знаках: а) точность распознавания; б) скорость работы алгоритма.

Из данных, представленных на рис. 9, следует, что лучшие результаты точности распознавания были получены с помощью алгоритма BN + BHA + PCA + NN на уровне 98,2%. Разработанный алгоритм показал результаты точности распознавания на уровне 98%, что является вторым результатом среди сравниваемых алгоритмов.

По показателю «скорость работы алгоритма» лучшие результаты были получены с помощью алгоритма BN + BHA + PCA + NN на уровне 29 мс. Разработанный алгоритм показал результат на уровне 33 мс, что является вторым результатом среди сравниваемых алгоритмов. Худшие результаты показали алгоритмы BN + BHA + ССA + TM и ED + BHA + ССA + KNN.

На рис. 10 представлено сравнение точности распознавания разработанной программной системы с 17 существующими коммерческими программными системами, которые применяются для решения подобных задач. Методы и алгоритмы, применяемые в коммерческих системах, не публикуются.

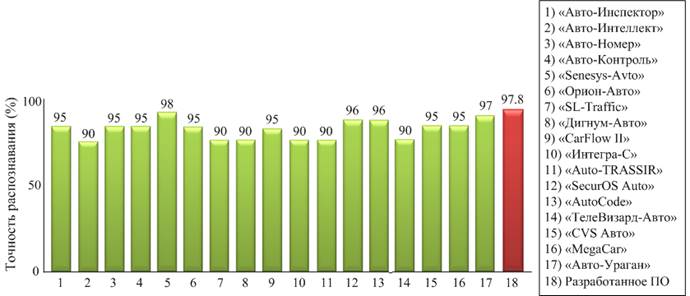
Рис. 10. Сравнение систем распознавания автомобильных номерных знаков по параметру «точность распознавания».

Из данных, представленных на рис. 10 видно, что лучший показатель точности распознавания показывает система «Senesys-Avto» на уровне 98%. Разработанная программная система показывает точность распознавания на уровне 97,8%, что является вторым результатом среди сравниваемых систем. Остальные системы показывают точность на уровне 90-97%.

6. Заключение

В результате выполнения работы получены следующие научные и практические результаты:

1. Предложена реализация алгоритма Виолы-Джонса для решения задачи детектирования области расположения символов на изображениях со сложным фоном. Алгоритм обеспечивает точность классификации на уровне 98,21%, скорость работы на уровне 34 мс и высокую устойчивость к шумовым, аффинным и проекционным искажениям входных данных.

2. Разработан алгоритм нормализации изображений символов, основанный на преобразовании Хафа и выделении замкнутых контуров на изображении. Алгоритм обеспечивает обнаружение точных границ пластины номерного знака, расположенного под различными углами наклона.

3. Разработан алгоритм распознавания символов на изображения на основе сверточной нейронной сети. Алгоритм обеспечивает точность распознавания символов на изображениях на уровне 98%, скорость работы на уровне 33 мс и высокую устойчивость к шумовым, аффинным и проекционным искажениям входных данных.

4. На основе разработанных алгоритмов была создана программная система, которая обеспечивает точность распознавания автомобильных номерных знаков, соответствующих ГОСТ Р 50577 – 93, группе 1, типу 1 на уровне 97,8%. Программная реализация алгоритмов является инициативой авторов, выполнялась с научной целью для написания научных трудов.

Список литературы

1. Анисимов Б.В., Курганов В.Д., Злобин В.К. Распознавание и цифровая обработка изображений. М.: Высшая школа. 1983. 295 с.

2. Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. М.: Наука. 1974. 416 с.

3. Елизаров А.И., Афонасенко А.В. Методика построения систем распознавания автомобильного номера. Известия томского политехнического университета. 2006. Т. 309. № 8. С. 118–122.

4. Друки А.А., Спицын В.Г. Применение сверточных нейронных сетей для выделения и распознавания автомобильных номерных знаков на изображениях со сложным фоном. Известия Томского политехнического университета. 2014. Т. 324. № 5. C. 85–91.

5. Massa F., Aubry M., Marlet R. Convolutional Neural Networks for joint object detection and pose estimation: A comparative study. Computer Vision and Pattern Recognition(CVPR). 2015. Vol. 4. Pp. 231–239.

6. Shaaban Z. An Intelligent License Plate Recognition System. International Journal of Computer Science and Network Security (IJCSNS). 2011. Vol. 11. No. 7. P. 55–61.

7. Chaturvedi A., Sethi N. Automatic License Plate Recognition System using SURF Features and RBF Neural Network. International Journal of Computer Applications. 2013. Vol. 70. No. 27. Pp. 37–41.

8. Hooi S.N., Yong H.T., Kim M.L., Hamam M., Hock W.H. Detection and Recognition of Malaysian Special License Plate Based on SIFT Features. Computer Vision and Pattern Recognition (CVPR). 2015. Pp. 321–329.

9. Yoon J., Kang B., Kim D. Car License Plate Detection under Large Variations Using Covariance and HOG Descriptors. 8th International Symposium on Visual Computing (ISVC). 2012. Pp. 636–647.

10. Rosten E., Porter R., Drummond T. FASTER and better: A machine learning approach to corner detection. Pattern Analysis and Machine Intelligence. 2010. Pp. 105–119.

11. Viola P., Jones M. Fast and Robust Classification Using Symmetric AdaBoost and a Detector Cascade. Proceedings of Neural Information Processing Systems. Vancouver, 2001. Pp. 1311–1318.

12. Viola P., Jones M.J. Robust real-time face detection. International Journal of Computer Vision. 2004. Vol. 57. No. 2. Pp. 137–145.

13. Таранян А.Р. Обучение классификатора Виолы-Джонса для локализации автомобильных номерных знаков. Молодежный научно-технический вестник. Москва: МГТУ им. Баумана. 2014. № 2. С. 5–11.

14. Изображения транспортных средств и номерных знаков. URL: https://yadi.sk/d/EAfnQ947criHW. Дата обращения: 10.12.2015.

15. Изображения транспортных средств и номерных знаков. URL: http://avto-nomer.ru. Дата обращения: 10.12.2015.

16. Гонсалес P., Вудс Р. Цифровая обработка изображений. М.: Техносфера. 2005. 1072 с.

17. Raseena A., Muhammad S. Automatic Skew Detection and Localisation of Vehicle License Plate Using Hough Transform. International Journal of Scientific & Engineering Research. 2013. Vol. 4(8). Pp. 121–128.

18. He K., Zhang X., Ren S., Sun J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI). 2015. Vol. 4. Pp. 534–542.

19. Le Cun Y., Huang F., Bottou L. Learning Methods for Generic Object Recognition with Invariance to Pose and Lighting. Proceedings of CVPR'04. Washington, DC, USA: IEEE Computer Society, 2004. Pp. 97–104.

20. Rumelhart D.E., Hinton G.E., Williams J.R. Learning Representations of Back-Propagation Errors. Nature. 1986. No. 323. Pp. 533–536.

21. Bolotova Y.A., Druki A.A., Spitsyn V.G. License plate recognition with hierarchical temporal memory model. The 9th International Forum on Strategic Technology (IFOST). Cox’s Bazar, Bangladesh. 2014. Pp. 136–139.

APPLICATION OF THE VIOLA-JONES ALGORITHM, HOUGH TRANSFORM AND ARTIFICIAL NEURAL NETWORKS FOR RECOGNITION CHARACTER INFORMATION ON A COMPLEX BACKGROUND

A.A. Druki, P.А. Kakovkin, D.S. Cherneta

National Research Tomsk Polytechnic University, Russian Federation

druki2008@yandex.ru, nitrokot@mail.ru, Dimano1993@rambler.ru

Abstract

The work is dedicated to development of algorithms to increase the efficiency of character recognition on a complex background with noise, affine and projective distortions. The paper proposes an approach to solving the problem of character recognition, which includes three main stages: detection of region character locations in the image; image normalization and selection of individual characters; character recognition. The Viola-Jones algorithm realization is proposed for detecting of the characters’ region in images with complex background. Image normalization includes the following operations: selection borders, Hough transform, closed contours search, image alignment. The search of characters string horizontal edges in the image is performed by using the Hough transform. The detection of individual characters’ regions is performed by using the closed contours search. The configuration of convolution neural network is proposed for character recognition. The testing results of the developed algorithms efficiency and their comparison with existing analogues are presented. On the basis of the approach, the software system which shows the high efficiency of character recognition on a complex background intended to recognize the car number plates in the images was developed.

Keywords: Image processing, Viola-Jones algorithm, Hough transform, artificial neural networks, character recognition.

References

1. Anisimov B.V., Kurganov V.D., Zlobin V.K. Raspoznavanie i cifrovaja obrabotka izobrazhenij [Recognition and digital image processing]. Moscow: High school, 1983. 295 p.

2. Vapnik V.N., Chervonenkis A.Ja. Teorija raspoznavanija obrazov [The theory of of pattern recognition]. Moscow: Science. 1974. 416 p.

3. Elizarov A.I., Afonasenko A.V. Metodika postroenija sistem raspoznavanija avtomobil'nogo nomera [Technique of construction license plate recognition systems]. News of Tomsk Polytechnic University, 2006, vol. 309, no. 8, pp. 118–122.

4. Druki A.A., Spicyn V.G. Primenenie svertochnyh nejronnyh setej dlja vydelenija i raspoznavanija avtomobil'nyh nomernyh znakov na izobrazhenijah so slozhnym fonom [Application of convolution neural networks for extraction and recognition of vehicle license plates in images with complex background]. News of Tomsk Polytechnic University. 2014. vol. 324. no. 5. pp. 85–91.

6. Shaaban Z. An Intelligent License Plate Recognition System. International Journal of Computer Science and Network Security (IJCSNS). 2011. Vol. 11. No. 7. P. 55–61.

7. Chaturvedi A., Sethi N. Automatic License Plate Recognition System using SURF Features and RBF Neural Network. International Journal of Computer Applications. 2013. Vol. 70. No. 27. Pp. 37–41.

9. Yoon J., Kang B., Kim D. Car License Plate Detection under Large Variations Using Covariance and HOG Descriptors. 8th International Symposium on Visual Computing (ISVC). 2012. Pp. 636–647.

10. Rosten E., Porter R., Drummond T. FASTER and better: A machine learning approach to corner detection. Pattern Analysis and Machine Intelligence. 2010. Pp. 105–119.

11. Viola P., Jones M. Fast and Robust Classification Using Symmetric AdaBoost and a Detector Cascade. Proceedings of Neural Information Processing Systems. Vancouver, 2001. Pp. 1311–1318.

12. Viola P., Jones M.J. Robust real-time face detection. International Journal of Computer Vision. 2004. Vol. 57. No. 2. Pp. 137–145.

13. Taranjan A.R. Obuchenie klassifikatora Violy-Dzhonsa dlja lokalizacii avtomobil'nyh nomernyh znakov [Education of classifier Viola-Jones for localization vehicle license plates] Youth Science and Technology Gazette. Moscow: MGTU. 2014. No. 2. Pp. 5–11.

14. Images of vehicles and license plates [website]. URL: https://yadi.sk/d/EAfnQ947criHW. Date of the application: 10.12.2015.

15. Images of vehicles and license plates [website]. URL: http://avto-nomer.ru. Date of the application: 10.12.2015.

16. Gonzalez R., Woods R. Digital image processing. Мoscow: Technosphere, 2005, 1072 p.

20. Rumelhart D.E., Hinton G.E., Williams J.R. Learning Representations of Back-Propagation Errors. Nature. 1986. No. 323. Pp. 533–536.