ВИЗУАЛИЗАЦИЯ ТЕКСТУРНЫХ ХАРАКТЕРИСТИК ИЗОБРАЖЕНИЙ НА БАЗЕ МАТРИЦЫ ХАРАЛИКА
А.К. Троицкий
Национальный исследовательский ядерный университет «МИФИ», Россия
Содержание
2. Характеристики текстурных изображений
3. Визуализация матрицы Харалика
Аннотация
В статье рассмотрен метод научной визуализации для изображений с явно выраженными текстурными характеристиками. Особенностью подобного класса изображений является то, что человеку путем непосредственного зрительного восприятия трудно дать им какие-либо объективные оценки. В качестве образцов текстурных изображений приводятся примеры из областей металлографии, медицины, деревообработки и данные аэрофотосъемки. Основной характеристикой для визуальной оценки текстурных изображений выбрана матрица Харалика. Предложены различные модификации алгоритма вычисления матрицы Харалика, позволяющие путем изменения вариантов расположения пикселов изображения, используемых при обработке, учитывать масштаб и угол поворота анализируемых текстурных изображений. Разработаны алгоритмы визуализации матрицы Харалика, позволяющие приводить ее к виду, пригодному для визуализации. Для более качественного восприятия сформированных изображений применены методы улучшения на базе гамма-коррекции. Разработан программный комплекс для визуализации текстурных характеристик изображений на базе обычной и модифицированных матриц Харалика с возможностью улучшения качества формируемых на экране монитора изображений. Проведено тестирование разработанного программного комплекса на реальных изображениях металлографического типа. Полученные результаты дают возможность предполагать, что использование приемов визуализации при анализе информации, трудновоспринимаемой человеком, будет достаточно эффективным при решении практических задач в различных областях.
Ключевые слова: научная визуализация, текстура, текстурные характеристики изображений, матрица Харалика, гамма-коррекция.
1. Введение
Обычно под научной визуализацией понимается графическое представление информации, полученной в результате теоретических или экспериментальных исследований. Суть метода научной визуализации заключается в том, что исходным анализируемым данным ставится в соответствие некоторая их статическая или динамическая графическая интерпретация, которая визуально анализируется, а результаты анализа этой графической интерпретации (графических данных) истолковываются исследователем по отношению к исходным данным [1]. Во многих случаях метод научной визуализации используют тогда, когда исходную информацию нельзя непосредственно воспроизвести, потому что ее никто никогда не видел (например, из-за очень больших или очень малых размеров). Другая ситуация – абстрактный характер отображаемой информации (например, n-мерное пространство) Существует еще один вариант, при котором человек видит исходную реальную информацию, но в силу различных причин не может дать ей какие-либо оценки. К таким типам информации относятся текстурные изображения. Поскольку многие текстурные изображения содержат информацию (текстуру), которую достаточно сложно анализировать человеку, основной задачей анализа является этап определения наличия текстур и их характеристик, которые могут быть не видны человеческим глазом. Определение наличия различных текстур на изображении также дает оценку характеристик найденных текстур, что имеет большое значение при решении задач анализа изображений. В металлографии – это определение качества металлов, при аэрофотосъемке – параметры тех или иных типов земной поверхности, в медицине – степень заболевания, в деревообрабатывающей промышленности – при оценке древесины и т. д. [2-7]. Примеры текстурных изображений приведены на следующих рисунках.
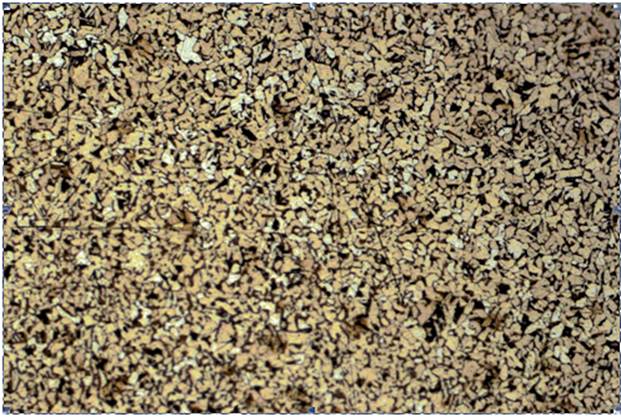
Рис. 1. Микроструктура стали при 1000-кратном увеличении.

Рис. 2. Фрагмент аэрофотоснимка горной системы.
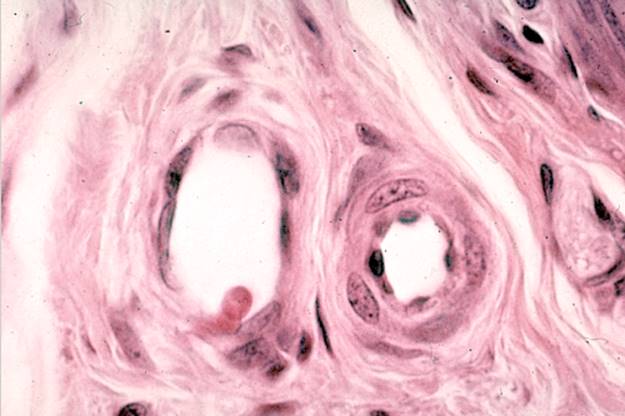
Рис. 3. Изображение гистологического препарата.

Рис. 4. Текстура древесины.
В простейшем случае текстуры можно разделить на два типа - мелкозернистые и крупнозернистые. Например, при большом количестве различимых пикселов в малой области изображения и при их случайном расположении образуется мелкозернистая текстура. В том случае, когда расположение пикселов имеет более определенный вид, а некие регулярно встречающиеся элементы изображения принимают все большие размеры, имеет место крупнозернистая текстура.
При анализе текстур изображения можно выделить следующие основные подходы:
1) Методы, основанные на вычислении матрицы Харалика [8].
2) Методы, описывающие текстуры длинами серий [7].
3) Методы, использующие измерение пространственной частоты [9].
4) Методы, основанные на вычислении количества перепадов на единицу площади изображения [5].
Для методов первого типа с ростом расстояния между оцениваемыми точками в мелкозернистых текстурах изменение распределения яркости происходит быстрее, чем крупнозернистых. Для второго серии точек в строке с постоянной яркостью на мелкозернистых текстурах короче, чем на крупнозернистых. Для методов третьего типа в крупнозернистых текстурах преобладают низкие пространственные частоты, а в мелкозернистых текстурах - высокие. Для четвертого на крупнозернистых текстурах эта величина мала, с уменьшением зернистости текстуры она возрастает.
С точки зрения визуального восприятия глазом человека текстурных изображений наиболее сложными являются те, которые обрабатываются на базе матрицы Харалика (1-й метод). На изображениях, обрабатываемых с помощью методов 2-4, человеческий глаз способен еще что-либо различить. Для мелкозернистой текстуры с расположением значений пикселов на изображении практически случайным образом человеческий глаз не в состоянии оценить видимую информацию. Это можно реализовать лишь на базе 1-го метода.
В настоящее время ведется много работ для автоматического анализа текстурных изображений. Однако все они, как правило, предназначены для работы в одной какой-либо области – медицине, металлографии, обработке аэрофотосъемки определенных типов земной поверхности и т.д. Основной проблемой является то, что учесть одновременно возможные случайные изменения масштаба, угла поворота и освещенности изображения при допустимых случайных изменениях геометрических характеристик исследуемых объектов, является весьма сложной задачей. При этом часто для анализа такого класса изображений не обязательно иметь точные значения, достаточно лишь качественной оценки результатов. Для этого нужно произвести преобразование изображения в такую форму информации, по которой принять решение можно будет по ее виду.
2. Характеристики текстурных изображений
Одной из основных характеристик изображений, содержащих пространственно-яркостную информацию, является текстура, присутствующая практически во всех изображениях. Под текстурой принято понимать наличие на изображении повторения неких базовых примитивов, имеющих различную ориентацию в пространстве и не обладающих ярко выраженными краями. Один из самых простых примеров – шахматная доска. Яркость изменяется от очень темной до очень светлой через определенные интервалы по горизонтали и по вертикали. Реальные текстуры намного сложнее: текстура может нарушаться в какой-либо части изображения, изображение может быть недостаточно четким, к тому же основные элементы текстуры практически никогда не бывают квадратами, а закономерность их повторения, как правило, носит намного более случайный характер.
Одним из основных способов описания текстуры является матрица Харалика. Она служит статистическим инструментом, предназначенным для учета случаев появления в изображении сочетаний яркостей определенной конфигурации [8]. Формируется матрица следующим образом. Пусть имеется анализируемое полутоновое черно-белое изображение произвольной размерности, причем яркость имеет 256 градаций – от 0 (черный) до 255 (белый). Матрица Харалика имеет размерность NxN, где N – число градаций яркости цвета в изображении. В нашем случае получится матрица 256х256.При построении матрицы обрабатывается каждый пиксел изображения. Сначала в формирующейся матрице Харалика фиксируется строка с индексом, равным яркости цвета пиксела анализируемого изображения. Далее рассматриваются все соседние пикселы (соседние слева, справа, сверху и снизу). Для каждого из них фиксируется столбец с индексом, равным его яркости, и к значению, стоящему на пересечении зафиксированных строки и столбца, прибавляется единица. Так и для всех соседних пикселов. Далее осуществляется переход к следующему пикселу изображения, и процедура повторяется. Таким образом, если существует N возможных градаций яркости, то матрица Харалика P будет матрицей размерности NxN и в каждой ячейке P(i,j) будет находиться «счетчик» количества значений в изображении, когда основной пиксел и пиксел, находящийся с основным в заранее определенном отношении соседства, имеют значения яркости i и j соответственно. По виду матрицы пространственной смежности можно судить о характере изображения. Так, для шахматной доски матрица Харалика будет иметь размерность 2х2 и все отличные от нуля элементы будут расположены в правом верхнем и левом нижнем углу матрицы, т.к. в данном случае темным элементам соседствуют светлые, а светлым – темные.
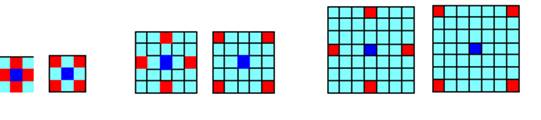
Предложенный впервые алгоритм вычисления матрицы Харалика предполагал расположение основного и смежных элементов как изображено на рис. 5 a), где центральный элемент имеет синий цвет, а смежные – красный. В дальнейшем разработчики систем обработки и распознавания текстурных изображений использовали фиксированный вариант расположения смежных элементов, пусть и не соседних, и был известен вид текстуры – мелкозернистая или крупнозернистая. Это можно объяснить тем фактом, что для автоматического анализа текстурных изображений можно было организовать одинаковый масштаб и угол поворота исследуемых изображений, а примерные параметры текстур были заранее известны. Получаемые в таких условиях матрицы Харалика легко было сравнивать между собой, для них вычислялись различные оценочные коэффициенты, которые также легко было оценивать и сравнивать между собой и т. д. Обычно такой подход используется в процессе при оценке большого количества текстурных изображений. В то же время автоматическое решение задач по оценке отдельных изображений с текстурами разного вида, с разными масштабом и углом поворота с научными целями, являлось очень сложной научно-технической задачей. Однако с появлением быстродействующих компьютеров и необходимостью визуализации различной научной информации появился смысл использовать и другие позиции соседних элементов для вычисления матрицы Харалика. В этом случае человек – оператор, анализирующий текстурные изображения с научными целями, основываясь на свой опыт путем простого перебора предложенных ему вариантов, подбирает оптимальный способ расположения соседних элементов.
Классический алгоритм вычисления матрицы Харалика можно модифицировать следующим образом. Вместо смежных с центральных элементов можно рассматривать какие-либо другие, как, например, изображено на рис. 5.
|
|
|||||
|
a) |
b) |
c) |
d) |
e) |
f) |
Рис. 5. Варианты расположения смежных элементов.
В этих случаях модифицированная матрица Харалика позволит выделить произвольные виды текстур, имеющие различный масштаб или угол поворота изображения. Можно предложить множество вариантов расположения соседних элементов и каждый из них может найти применение для решения какой-либо практической задачи.
3. Визуализация матрицы Харалика
Сформированная матрица Харалика имеет следующие характеристики:
¾ размерность матрицы 256х256 элементов (256 – стандартное число градаций яркости мониторов);
¾ диапазон изменения значений элементов матрицы от 0 до ~ (HxWх4), где H – число строк в анализируемом изображении, W – число столбцов.
Очевидно, что такую матрицу в численном виде невозможно вывести целиком на экран дисплея, чтобы оценить полностью всю информацию об изображении. Выходом из данной ситуации представляется вывод матрицы в форме изображения, т.е. изображения размерностью 256х256 пикселов, значения яркости которого будет соответствовать значениям элементов матрицы Харалика.
Проблема в данном случае будет заключаться в том, что значения яркости на экране монитора могут изменяться в диапазоне от 0 до 255, в то время, как максимальные значения элементов матрицы Харалика могут иметь величины на несколько порядков больше. Выходом в данной ситуации будет являться нормировка значений элементов матрицы Харалика таким образом, чтобы они изменялись в диапазоне от 0 до 255.Это реализуется следующим образом. Среди элементов матрицы Харалика находится такой, который имеет максимальное значение. Его величина делится на 255, в результате чего получается коэффициент нормировки К. Затем все значения элементов матрицы Харалика делятся на К. В результате получается нормированная матрица Харалика, все элементы которой изменяются в диапазоне от 0 до 255 и могут непосредственно использоваться как значения яркости пикселов изображения. Недостатком такого способа нормировки является то, что в том случае, если один элемент матрицы Харалика имеет значение намного превосходящее остальные (более чем в 255 раз, это будет в случае присутствия на изображении одной очень “мощной” текстуры), нормированная матрица будет иметь среди своих элементов лишь один, отличный от нуля. Значение его будет равно 255. Это не даст возможности обнаружить на изображении слабовыраженные текстуры. Для устранения этого недостатка необходимо использовать при нормировке подход, аналогичный степенному методу улучшения изображений (гамма-коррекция [9]). Суть его заключается в том, что при нормировке значения элементов пикселов изображения уменьшаются не путем деления или умножения на одну фиксированную величину нормировки К, а с помощью предварительного возведения значений элементов матрицы Харалика в степень больше, либо меньше единицы. Затем для вновь сформированной матрицы необходимо произвести описанную выше нормировку. Это позволяет увидеть на преобразованной и пронормированной матрице Харалика, представленной в виде изображения, присутствие слабовыраженных текстур.
В результате проведенных исследований разработан программный комплекс для визуализации текстурных характеристик на базе матрицы Харалика.
Он создан в среде программирования DELPHI. Входными данными являются цветные изображения, заданные в формате .BMP. Необходимо отметить, что в этот формат изображение должно кодироваться непосредственно после считывания изображения. Это означает, что для получения обрабатываемого изображения нельзя использовать простые цифровые фотоаппараты, потому что все они записывают снимаемые изображения в формате .JPEG. Их можно преобразовать в формат .BMP с помощью любого графического пакета. Однако качество полученного таким способом изображения будет недостаточным, чтобы анализировать его текстурные характеристики. Для подготовки изображений в такую систему нужно воспользоваться одним из двух способов. Первый – это использовать для съемки более сложные цифровые фотоаппараты, позволяющие регистрировать снимки в форматах, аналогичных или близких .BMP (например, формат. RAW). Второй – это использовать фотографии, полученные с помощью пленочного фотоаппарата, и оцифровывать их с помощью сканера непосредственно в формат .BMP.
Работа комплекса состоит из следующих этапов.
1. После запуска программы на экране монитор появляется изображение следующего вида (рис. 6):

Рис. 6. Исходное состояние программы.
Белое поле – область изображения, цветные матрицы показывают выбираемые варианты смежности пикселов, помеченные зеленым цветом указатели, позволяют выбрать вариант яркостной коррекции изображения выводимой на экран монитора матрицы Харалика.
Ниже располагаются стандартные клавиши управления LOAD, CTART, SAVE и EXIT.
2. С помощью команды LOAD из появившегося в окне списка файлов выбирается анализируемое изображение, которое появляется на экране монитора (рис. 7).

Рис. 7. Анализируемое изображение.
3. Далее с помощью 6-ти вертикальных кнопок с соответствующими пиктограммами, находящихся справа на экране монитора и показывающих возможные комбинации смежности пикселов, оператором выбирается необходимый вариант вычисления матрицы Харалика. Они дают возможность установить в программе необходимые исходные параметры. Выбор варианта зависит от вида анализируемой текстуры (мелкозернистая или крупнозернистая), а также от масштаба и угла поворота изображения. Этот выбор, как правило, основывается на опыте оператора. Кроме того, так как обработка происходит практически мгновенно, в простейшем случае оператор может просмотреть все варианты.
4. Нижние две горизонтальные кнопки с метками 1 и 2 дают возможность оператору использовать в случае необходимости улучшения изображения гамма-коррекцию при выводе его на экран монитора. Здесь возможны три варианта. Если оба поля указателей пустые, то гамма-коррекция не применяется. Если помечен указатель с номером 1, то коэффициент гамма-коррекции принимается равным 0.5. Если помечен указатель с номером 2, то коэффициент гамма - коррекции принимается равным 2.
5. По команде START производится вычисление матрицы Харалика, которая выводится на экран монитора в виде изображения. Команда SAVE позволяет сохранить в случае необходимости полученный результат в графической форме. По команде EXIT происходит выход из программы. Результат обработки приведенного на рис. 7 изображения показан на рис. 8.

Рис. 8. Визуализированная матрица Харалика.
Практическая ценность разработанной системы была продемонстрирована на следующем примере. В качестве опытных образцов использованы две фотографии, содержащие изображения структуры металлов при 1000-кратном увеличении. На одной из них изображена структура неповрежденного металла, на другой – деформированного. Простым взглядом практически невозможно обнаружить различия в изображениях. Но, рассчитав для них и визуализировав матрицы Харалика, можно без труда заметить различия и, таким образом, обнаружить дефектный металл. Изображения неповрежденного и деформированного металлов представлены на рис. 9, 10. Ниже на рис. 11, 12 размещены соответствующие им визуализированные матрицы Харалика.

Рис. 9. Неповрежденная сталь.

Рис. 10. Деформированная сталь.

Рис. 11. Визуализированная матрица Харалика для неповрежденной стали.

Рис. 12. Визуализированная матрица Харалика для деформированной стали.
На изображениях с матрицами Харалика для неповрежденной и деформированной стали хорошо видны различия. По виду исходных изображений понятно, что они не являются мелкозернистыми. Путем простого перебора было выявлено, что наиболее хорошо видны различия для этих типов текстур при 5-м варианте расположения смежных элементов и коэффициенте гамма-коррекции, равном 2, как показано на рис. 8. Следовательно, использование визуализированной матрицы Харалика позволяет проводить анализ металлографических изображений, на которых трудно найти различия в обычной форме.
4. Заключение
Применение методов научной визуализации для решения задач, в которых анализируемая информация представлена в форме, сложной для непосредственного зрительного восприятия, дает возможность легко проводить анализ исследуемых данных и принимать необходимые решения. В данной работе было показано использование приемов научной визуализации для изображений с явно выраженными текстурными характеристиками.
Предложены различные модификации алгоритмов вычисления матриц, аналогичных матрице Харалика. Разработаны алгоритмы визуализации матрицы Харалика, позволяющие реализовать нормализацию и улучшение изображений на основе гамма-коррекции.
Разработан программный комплекс для визуализации текстурных характеристик изображений на базе матрицы Харалика. Проведено тестирование разработанного программного комплекса на реальных изображениях металлографического вида. Испытания подтвердили работоспособность и практическую ценность разработанного комплекса. Полученные результаты дают возможность предполагать, что использование приемов визуализации при анализе информации, трудновоспринимаемой человеком, будет достаточно эффективным при практическом использовании в различных областях.
Список литературы
1. Стриханов М.Н., Дегтяренко Н.Н., Пилюгин В.В., Маликова Е.Е., Матвеева Н.А., Пасько А.А., Аджиев В.Д. Опыт компьютерной визуализации наноструктур в НИЯУ МИФИ. Научная визуализация. 2009. т.1. № 1. C. 1–18.
2. Перфильев Д.А. Классификация сегментов металлографических изображений деформируемых алюминиевых сплавов. Вестник Сибирской аэрокосмической академии имени академика М. Ф. Решетнева. 2006. Вып. 10. С. 16- 78.
3. Бортников А.Ю., Минакова Н.Н. Текстурно-фрактальный анализ микроскопических срезов образцов композиционных материалов, наполненных техническим углеродом. Известия Томского политехнического университета. 2006. Т. 309. № 6. С. 64-67.
4. Кирбижекова И.И., Чимитдоржиев Т.Н., Быков М.Е. Оценка ландшафтных изменений северных территорий на основе текстуры радарных изображений. Известия вузов физика. 2013. Т. 56. № 8/2. С. 196–197.
5. Мицель А.А., Колодникова Н.В., Протасов К.Т. Непараметрический алгоритм текстурного анализа аэрокосмических снимков. Известия Томского политехнического университета. 2005. Т. 308. № 1. С. 65-70.
6. Косых Н.Э., Смагин С.И., Гостюшкин В.В., Савин С.З., Литвинов К.А. Система автоматизированного компьютерного анализа медицинских изображений. Информационные технологии и вычислительные системы. № 3. 2011. С. 52-60.
7. Ковалев В.А. Анализ текстуры трехмерных медицинских изображений. Минск: Белорусская наука. 2008. 263 с.
8. Харалик Р.М. Статистический и структурный подходы к описанию текстур. ТИИЭР. 1979. Т. 67. № 5. С. 98-120.
9. Гонсалес Р., Вудс Р. Цифровая обработка изображений. Москва: Техносфера. 2005. 1072 с.
IMAGE TEXTURE CHARACTERISTICS VISUALIZATION BASED ON HARALICK MATRIX
A.K. Troitsky
National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Russian Federation
Abstract
The article considers scientific visualization method for images with obviously marked texture characteristics. Similar image type particular property is that it is very difficult for a man to give some impartial estimation for them. Metallography, medicine, wood structure and aerial photography image examples are given as texture image patterns. Haralick matrix was chosen as main characteristic for texture image visual estimation. Different algorithm calculation modifications are suggested. They allow to take into consideration the scale and the turning angle for analyzed texture images by pixel location changes. Haralick matrix visualization algorithms were developed. They allow to demonstrate the Haralick matrix at the monitor in visual form. Gamma – correction image enhancement methods are used for more high-quality visual perception of formed images. Texture image characteristic visualization program complex was developed based on simple and modified Haralick matrixes with image quality enhancement possibility. This program complex was tested for real metallography image examples. Received results give chance to assume that visualization method application by the analysis of information, which is difficult to perceive, will be very effective for practical tasks solving in various areas.
Keywords: scientific visualization, texture, image texture characteristics, Haralick matrix, Gamma – correction.
References
1. Strikhanov M.N., Degtyarenko N.N., Pilyugin V.V., Malikova E.E., Matveeva M.N., Adzhiev V.D., Pasko A.A. Computer Visualization of Nanostructures Experience at NRNU "MEPhI". Scientific Visualization, vol. 1, no. 1, 2009, pp. 1–18. [In Russian]
2. Perfilyev D. A. Klassifikatsija segmentov metallograficheskih izobrasheniy deformiruemyh aljuminievyh splavov. [Metallography Image Segment Classification of Deformed Aluminium Alloy]. Reshetnev Siberian State Aerospace University Journal. No.10, Krasnoyarsk, 2006, pp. 16- 78. [In Russian]
3. Bortnikov A.I., Minakova N.N. Teksturno-fraktalny analiz mikroskopicheskih srezov obraztsov kompozitsionnyx materialov, napolnennyh tehnicheskim uglerodom. [Texture-fractal analysis of microscopic section of composites filled with commercial carbon]. Tomsk State University Journal. 2006, vol. 309, no. 6, pp. 64-67. [In Russian]
4. Kirbizhekova I.I., Chimitdorzhiev T.V., Bikov M.E. Otsenka landshafnyh izmeneniy severnyh territoriy na osnove tekstury radarnyh izobrasheniy. [Evaluation of Landscape Change Northern Territories Based on Texture of Radar Images]. Russian Physics Journal. 2013, vol. 56, no. 8/2, pp.196-197. [In Russian]
5. Mitsel A.A., Kolodnikova N.V., Protasov K.T. Neparametricheskiy algoritm teksturnogo analiza aerokosmicheskih snimkov. [Nonparametritic Aerospace Photo Texture Analysis Algorithm]. Tomsk State University Journal. 2005, vol. 308, no. 6, pp. 66-70[In Russian]
6. Kosykih N.E., Smagin S.I., Gostyushkin V.V., Savin S.Z., Litvinov K.A. Sistema avtomatizirovannogo kompjuternogo analiza meditsinskih izobrasheniy. [Automatized Computer Medicine Image Analysis System]. Informational Technologies and Computing Systems. 2011, no 3, pp. 52-60. [In Russian]
7. Kovalev V.A. Analiz tekstury trehmernyh meditsinskih izobrasheniy. [Three-dimensional Medicine Image Texture Analysis]. Minsk: Belarusian science, 2008., 263 pp. [In Russian]
8. Haralic RM. Statisticheskiy i strukturniy podhody k opisaniyu tekstur. [Statistical and Structural Approaches to Texture]. Proceedings of the IEEE. vol.67, 1979, no. 5, pp. 98-120. [In Russian]
9. R. Gonzalez, R. Woods. Tsifrovaya obrabotka izobrasheniy. [Digital Image Processing]. Moscow: Technosphera, 2005, 1072 pp. [In Russian]