РЕШЕНИЕ ЗАДАЧ МОДЕЛИРОВАНИЯ И ВИЗУАЛИЗАЦИИ ПРОЦЕССОВ В ПЛАЗМЕ СВЧ-РАЗРЯДА

Ю.А. Лебедев, А.В. Татаринов, И.Л. Эпштейн, В.Н. Тимакин*, И.А. Ткаченко*

Институт нефтехимического синтеза им. А.В.Топчиева РАН

*Национальный исследовательский центр «Курчатовский институт»

lebedev@ips.ac.ru, atat@ips.ac.ru, epstein@ips.ac.ru, vtim@kiae.ru, tia@grid.kiae.ru

Содержание

1. Введение

2. Создание специализированной среды для вычислений и визуализации

2.1. Архитектура вычислений и визуализации

2.2. Использование созданной среды для решения поставленной задачи

2.3. Политика безопасности и условия доступа

3. Используемая для расчетов самосогласованная модель плазмы СВЧ разряда

4. Параметры расчета и визуализации

5. Результаты и обсуждение

6. Заключение

Литература

Аннотация

В статье обсуждается актуальность развития специализированных программно-аппаратных комплексов для визуализации, совершенствования алгоритмов визуального представления данных, расширения возможностей систем отображения данных. Описаны работы по созданию специализированной распределенной среды для решения поставленных задач 3D интерактивной визуализации результатов численного моделирования СВЧ разряда. Визуализация расчетной сетки позволила наглядно оценивать и вносить необходимые коррективы в построение сетки в интерактивном режиме. Реализованная распределенная архитектура вычислений и визуализации поддерживает легкую миграцию вычислительной среды между инструментальными средствами визуализации (консолидированными и клиентскими), предоставляя пользователям, возможность масштабировать общий объем данных и разрешение их визуальных отображений. Приведены результаты визуализации пространственного распределения СВЧ поля и концентрации электронов на примере самосогласованного моделирования аргоновой плазмы Бинаккеровского СВЧ разряда. Пространственная визуализация с помощью локальных сечений расчетной области позволила выявить внутреннюю структуру и особенности распределения концентрации электронов в разрядной трубке.

Ключевые слова: визуализация данных, моделирование низкотемпературной плазмы, анализ данных, научная визуализация, научные исследования, прикладная программа.

1. Введение

Современные экспериментальные методы диагностики и быстрое развитие информационных технологий позволяют в процессе исследования сложных объектов собирать и обрабатывать большие (тера- и петабайтные) объемы информации, в том числе и с применением распределенных вычислений. В последние годы наблюдается экспоненциальный рост темпов генерации данных, опережающий наши способности анализировать их как для того, чтобы использовать в научных целях, так и для того, чтобы контролировать корректность получаемых результатов в режиме реального времени. Для достижения понимания результатов обработки и моделирования больших объемов данных требуются новые подходы к анализу и визуализации, а также создание систем управления потоками заданий для выполнения задач хранения и обработки больших данных в распределенной гетерогенной компьютерной среде [1, 2]. Все это подтверждает актуальность развития специализированных программно-аппаратных комплексов для визуализации, совершенствования алгоритмов визуального представления данных, расширения возможностей систем отображения данных, в том числе, стереоскопических и систем сверхвысокого разрешения (десятки и сотни мегапикселей).

К системам обработки данных в таких условиях предъявляется особые требования:

· результатом обработки данных в таких условиях должны быть визуальные образы, которые легче воспринимаются человеческим мозгом и позволяют понять картину в целом;

· обработка научных данных и визуализация должны быть соединены в единый процесс, позволяющий на выходе получить продукт удобный для визуальной оценки получаемых результатов в интерактивном режиме;

· система обработки данных должна централизовать и консолидировать высокопроизводительные вычислительные и визуализационные ресурсы, а также давать возможность удаленно и безопасно их использовать.

Система визуализации образов может являться как выделенным программным продуктом, так и компонентом интегрированного программно-аппаратного решения, в стеке специализированного пакета обработки данных. В последнем случае, особенности структуры пакетов визуализации и требований, предъявляемых к ним (например, возможность работы в различных операционных системах, на разных аппаратных платформах; специфичные лицензионные требования), определяют в конечном счете архитектуру всего программно-аппаратного комплекса.

Технологии визуализации наиболее часто применяются в задачах численного моделирования сложных, многокомпонентных моделей, когда требуются терафлопные производительности вычислительных ресурсов [2, 3]. В силу высокой сложности исследуемых объектов построение расчетных сеток в процессе вычислений может представлять значительные трудности. Выбор размеров и структуры расчетных сеток, требуемых для решения указанных задач с приемлемой точностью, подразумевают необходимость варьировать параметры модели, анализируя результаты визуализации и корректируя параметры сетки.

Таким образом, процесс решения задачи анализа исходных данных методом научной визуализации усложняется и становится итеративным и интерактивным [1,4].То есть,для получения целевых результатов необходимо повторно выполнять алгоритм расчета и визуализации, весь или его часть, изменяя значения тех или иных параметров и проводя визуальную оценку промежуточных результатов в режиме реального времени.

Особую роль визуализация результатов моделирования приобретает в исследовании низкотемпературной плазмы. В настоящее время получили развитие самосогласованные модели, в которых решается система уравнений, описывающая электродинамику плазмы (разряды постоянного тока, НЧ, ВЧ, СВЧ и оптические разряды), кинетику процессов в ней (ионизация, возбуждение, перенос заряженных и нейтральных частиц, химические реакции, фазовые переходы, взаимодействие плазмы с твердыми телами), газодинамику плазмы, перенос тепла [5-8].

В последние годы наблюдается бурный рост работ, посвященных самосогласованному моделированию сложных газоразрядных систем в плазме [9, 10]. Это связано с двумя причинами. Во-первых, это накопление надежных баз данных о различных константах, используемых при моделировании (сечения различных процессов, коэффициенты переноса и реакций и т. д.). Во-вторых, это увеличение мощности вычислительных ресурсов, используемых для расчетов, что позволяет, как усложнить решаемые задачи и приблизить их к описанию экспериментов, так и получить результаты за разумные времена. Более того, если ранее решались нульмерные, одномерные и двухмерные задачи, то теперь, с появлением мощных вычислительных ресурсов, актуальным становится развитие трехмерных моделей.

Целью работы было создание распределенной вычислительной среды для интерактивной визуализации данных на примере численного моделирования аргоновой плазмы, генерируемой с помощью Бинаккеровского СВЧ резонатора.

Для достижения поставленной цели необходимо было решить следующие задачи.

A. Создать распределенную специализированную среду, которая должна обеспечить:

· проведение вычислений и постпроцессорной обработки данных на ресурсах высокопроизводительного кластерного комплекса;

· предоставление пользователю доступа на вычислительные узлы для управления параметрами счета, его запуском и оптимизации ресурсов, выделяемых для вычислений;

· предоставление графической консоли для удаленной интерактивной визуализации результатов моделирования;

· защищенный удаленный доступ к ресурсам кластера;

· предоставление выделенных ресурсов для удаленного рендеринга;

· отображение данных высокого разрешения.

B. Провести численное моделирование аргоновой плазмы СВЧ разряда.

C. Провести анализ результатов численного моделирования итеративно-интерактивным методом 3D визуализации.

2. Создание специализированной среды для вычислений и визуализации

2.1. Архитектура вычислений и визуализации

Для эффективного использования компьютерных ресурсов используется их кластеризация — объединение многих вычислительных узлов в связанную сеть с единой точкой входа и скрытой от пользователя внутренней архитектурой, Рис. 1.

Поскольку вычислительная среда должна позволять не только проводить вычисления, но и визуализировать результаты, в том числе в интерактивном режиме, в состав вычислительной среды необходимо было включить различные типы узлов (гетерогенный кластер).

Таким образом, создаваемая вычислительная среда, которая базировалась на гетерогенном вычислительном кластере, включала в себя:

· узлы для вычислений на CPU;

· узлы для вычислений на GPU;

· гибридные вычислительные узлы, позволяющие проводить вычисления как на CPU, так и GPU;

· визуалиционные узлы (предназначенные для работы с изображениями и анимацией) – консолидированные визуализационные ресурсы;

· система отображения высокого разрешения (видеостена);

· сервисные узлы;

· удаленную графическую станцию (клиентская часть);

· набор программ для связного и безопасного функционирования среды, численного моделирования и визуализации.

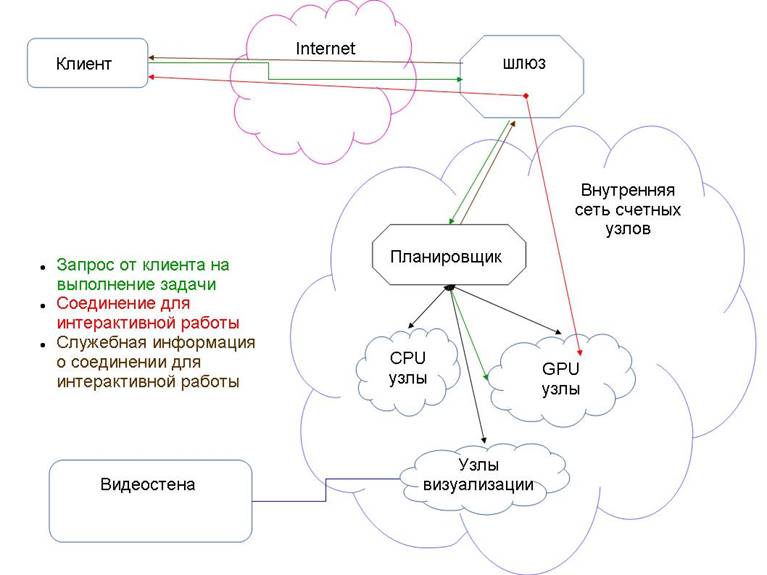
Рис. 1. Архитектура вычислительной среды.

В качестве планировщика использования ресурсов был выбран Slurm, со специально создаваемым набором скриптов для предварительной обработки запускаемых заданий. Это позволяет пользователю, в отличие от стандартных решений, подключаться непосредственно к узлу, где запущенна его вычислительно-визуализационная задача, видеть результат и, при необходимости, корректировать или варьировать параметры модели в интерактивном режиме.

Поскольку все узлы должны иметь одни и те же пользовательские данные, на узлах была настроена файловая система сетевого доступа - NFS, с источником на головном узле, куда пользователи могут копировать свои файлы для последующих расчетов.

Вычислительный модуль прикладного пакета был интегрирован в вычислительные ресурсы на кластере. В то время, как модули управления и постпроцессинга инсталлировались в соответствии с выбираемым архитектурным решением либо на удаленных ресурсах пользователя, либо на узлах специально создаваемого визуализации кластера. Таким образом, в рамках создаваемой среды было реализовано два подхода к архитектуре визуализации.

Для решения задач интерактивной визуализации на вычислительных узлах данного кластера были настроены виртуальные дисплеи, которые не были проассоцированы ни с одним реальным дисплеем, но отображение графики на нем просчитывалось при помощи видео карты, а результаты были доступны удаленному по сети клиенту путем интерактивного подключения с помощью графической консоли.

В случае необходимости вывода результатов визуализации в высоком разрешении была реализована возможность передавать видеоконтент высокого разрешения на видеостену в реальном времени. Консолидированное средство визуализации представляло из себя систему кластер визуализации - оптическая линия связи - видеостена. Видеостена расположена в конференц-зале удаленно от кластера визуализации, вычислительного кластера и хранилища данных, объединенных в единый комплекс с помощью высокоскоростной шины передачи данных Infiniband. Видеосигнал с графических карт кластера визуализации подавался по оптическим линиям на видеостену, состоящую из 12 тонкорамочных FullHD панелей. Общее разрешение составляло – 7680х3240 пикселей. Конструктивной особенностью было использование программного решения для управления стеной. Нами использовалось программное обеспечение SAGE [11]. SAGE предоставляет общую среду, которая дает возможность пользователям получать доступ, просматривать и обмениваться большими потоками разнообразных данных, в различных разрешениях и форматах, из нескольких источников, отображая их на модульные видеостены произвольного размера.

Созданная специализированная среда позволяет решать широкий спектр задач, и, при этом, оставляет возможность индивидуального подхода в каждой задаче, если это требуется. Например, чтобы запустить клиентскую часть прикладного пакета, рассчитанного на работу в операционной среде Windows, на кластере визуализации была реализована возможность запускать виртуальные машины под управлением VirtualBox, с возможностью доступа из виртуальной машины к GPU-картам узлов. Таким образом, в соответствие с одним из вариантов, рендеринг результатов мог проводиться на масштабируемых ресурсах кластера визуализации.

Другой подход учитывал специфику используемого прикладного пакета и обеспечивал возможность размещения модуля визуализации на удаленной графической станции пользователя. В данном случае реализовывалась клиент-серверная архитектура.

2.2. Использование созданной среды для решения поставленной задачи

В качестве вычислительного аппарата использовался программный пакет Comsol Multiphysics версии 3.5а (License № 1064223) [12], предназначенный для конечно-элементного анализа в различных областях физики и инженерного дела, включая рассмотрение связанных (мультифизичных) задач. Для анализа в рамках конкретной дисциплины в пакете присутствуют специализированные модули, а для расчёта связанных задач между всеми модулями обеспечивается эффективное взаимодействие.

Прямое использование данного пакета для установки на вычислительном кластере было невозможно. Необходимо было разделять его на модули: вычислительный и клиентский (управление и контроль над процессом счета, визуализация данных). Важным условием для интеграции вычислительного модуля в создаваемую среду было его выделение из программного пакета Comsol для установки на узлах кластера в операционной среде семейства Linux. Вычислительный модуль должен был устанавливаться и работать на узлах кластера без использования графического интерфейса. В качестве аппаратных ресурсов использовался один вычислительный узел SL390 (3 GPU nVidia Tesla M2050, 48Gb RAM, 2 Intel Xeon X5670). Наиболее эффективным решением с точки зрения использования программно-аппаратных средств комплекса является использование ресурсов гетерогенного кластера как для вычислений, так и для постпроцессинговой обработки (визуализации данных).

В реализованной архитектуре клиентская часть, отвечающая за управление процессом вычислений и постпроцессинг, была инсталлирована на удаленной графической станции пользователя под управлением операционной системы MS Windows, в связи с требованиями к операционной системе клиентской части и требованиями лицензионного соглашения. Таким образом, в соответствие с данной архитектурой, управление моделированием и визуализацией осуществлялось с клиентской части, установленной на графической станции пользователя удаленно от кластера вычислений, а передача данных между модулями счета и управления производилось через сетевую инфраструктуру общего доступа в интерактивном режиме.

Поскольку вычислительный модуль, выделенный из прикладного пакета, не предполагал интерактивную установку без использования графического интерфейса, на данном этапе был создан специальный скрипт для взаимодействия с программой-установщиком, позволяющий провести процедуру инсталляции в автоматическом режиме. Для подключения ресурсов графических карт на этапе запуска модуля вычислений потребовалось посредством X-сервера создать виртуальный дисплей, не имеющий подключения ни к одному физическому устройству вывода изображения, поэтому полностью исключить графические карты из работы вычислительного модуля не удалось. Для оптимизации процесса вычислений пользователь мог варьировать количество участвующих в счете ядер вычислительных узлов во время запуска вычислений.

2.3. Политика безопасности и условия доступа

Удаленный доступ к вычислительным ресурсам должен осуществляться максимально безопасно, как для пользователя, так и для вычислительного центра. Недостаточное внимание к политикам безопасности может привести к тому, что мощные вычислительные ресурсы окажутся в руках злоумышленников. Аудиту должно подвергаться также все используемое программное обеспечение.

Выделенный нами вычислительный модуль не имел достаточной защиты в рамках используемого прикладного пакета, чтобы его можно было безопасно использовать удаленно через интернет, поэтому система была защищена фаерволом (firewall) с разрешением доступа удаленного по сети клиента к вычислительной среде только с определенных IP-адресов.

Поскольку конечный пользователь может не иметь статического IP-адреса, для его безопасной работы требуется настройка дополнительного, транзитного, сервера, к которому пользователь мог бы подключаться по SSH туннелю с IP-адресом из внутрикорпоративной (приватной) сети. Далее, средствами SSH-туннелирования через транзитный сервер создается защищенный, зашифрованный канал между пользователем и модулем вычислений. Кроме того, чтобы не допустить потенциального вмешательства в работу вычислительного комплекса в случае взлома клиента, транзитный сервер настраивается таким образом, чтобы при подключении клиента в автоматическом режиме запускать вычислительный модуль на соответствующих ресурсах и останавливать его после отключения клиента. Данные действия выполняются в полностью автоматическом режиме с помощью командных и управляющих скриптов, не позволяя пользователю осуществлять какие-либо другие действия ни на транзитном узле, ни на вычислительных ресурсах.

3. Используемая для расчетов самосогласованная модель плазмы СВЧ разряда

В работе использовалась для расчетов самосогласованная модель неравновесного неоднородного СВЧ разряда. Модель основана на совместном решении уравнений Максвелла, уравнения Пуассона, уравнения Больцмана для свободных электронов плазмы и уравнений, описывающих колебательную кинетику и кинетику возбужденных и заряженных частиц плазмы. Более подробно вычислительные алгоритмы изложены в работах [5-8]. Для описания плазмы используется диффузионно-дрейфовое приближение для стационарных потоков частиц [29, 30]. Уравнения баланса для электронов, ионов (Ar⁺ и Ar₂⁺) и атомов Ar в электронно-возбужденных состояниях записываются в следующем виде:

		(1)
		(2)
		(3)

Здесь Γ_e, Γⁱ_p, Γⁱ_n, n_e , nⁱ_p , nⁱ_n– потоки и плотности электронов (e), ионов и нейтральных частиц (n) i-ого типа; Sⁱ_e,p,n– суммарная скорость рождения и гибели соответствующих частиц i-ого типа в различных плазмохимических процессах; μⁱ_e,p , Dⁱ_e,p,n– коэффициенты подвижности и диффузии соответствующих частиц i-ого типа; E_c = -Ñj – локальное электрическое поле, обусловленное разделением зарядов, которые определяются из уравнения Пуассона для потенциала j:

(4)

где e это заряд электрона, ε₀ – диэлектрическая проницаемость вакуума.

Поскольку в изученных условиях и геометрии разрядной системы длина релаксации энергии электронов значительно превышает радиус разрядной трубки, для описания разряда используется самосогласованная модель в нелокальном приближении [28]. В этом случае локальная связь параметров электронной компоненты с СВЧ полем отсутствует, и заменяется уравнением баланса для плотности потока энергии электронов [29, 30]:

(5)

где Γ_ε- плотность потока энергии электронов с коэффициентами μ_ε = 5/3 μ_e, D_ε = 5/3 D_e , ε – плотность энергии электронов связанная со средней энергией электронов θ как ε = n_e·θ,

θ = 3/2 k_B·T_e, k_B– постоянная Больцмана, T_e – температура электронов. Выражение Q_in– определяет потерю энергии электронов в неупругих соударениях; Q_el– определяет потерю энергии электронов в упругих соударениях; σ – проводимость плазмы.

Электрическая компонента СВЧ поля E_m– вычисляется из динамического уравнения Максвелла. В случае стационарной структуры TM волн, установленных в резонаторе, уравнение Максвелла сводится к сингулярному комплексному уравнению для магнитной компоненты волны:

(6)

Здесь - относительная проницаемость и проводимость плазмы, где плотность электронов n_eнормализована по отношению к его критической величине n_c ≈ 7´10¹⁰ cm^-3 для данной частоты разряда f = 2.45 GHz. Относительная магнитная проницаемость равна 1, ν_col - частота столкновений электронов с нейтральными частицами.

Модель содержит предварительно вычисленные табличные файлы с константами скоростей реакций, которые включают электронный удар. Эти константы скоростей - функции локальных значений средней электронной энергии θ и концентрации электронов n_e. Функции распределения электронов по энергиям, которые необходимы для вычисления этих констант, получались при решении уравнения Больцмана для свободных электронов плазмы в двучленном приближении с самосогласованным набором сечений рассеяния для аргона.

Корректное моделирование требует учета большого количества электронно-возбужденных состояний атомов и молекул, колебательного распределения молекул, нескольких типов ионов. В Табл. 1 приведены процессы, включенные в кинетическую модель. Следующие электронно-возбужденные состояния атомов аргона учитывались:

· 4 нижних электронно-возбужденных состояния объединялись в два: метастабильное состояние Ar(M) ≡ (1s₅) + Ar(1s₃) и резонансное Ar(R) ≡ Ar(1s₂) + Ar(1s₄);

· для упрощения кинетической схемы, по аналогии с [27, 28], состояния с высоким порогом возбуждения объединялись в 3 смешанных уровня Ar(F, A and B) с уровнем Ar(F) (13.2 eV), являющимся суммой ³p⁵4p уровней, уровень Ar(A) (14.1 eV) – сумма ³p⁵5s и ³p⁵3d уровней, и Ar(B) (14.9 eV) – сумма уровней ³p⁵6s, ³p⁵5p, ³p⁵4d и ³p⁵4f .

Таблица 1. Процессы в аргоновой плазме, включенные в модель.

№	Процесс	k(сm³s^-1, сm⁶s^-1); A_i (s^-1);	Ссылки
Возбуждение из основного состояния
1	Ar + e ® Ar(M) + e	f(θ,n_e)	[13]
2	Ar + e ® Ar(R) + e	f(θ,n_e)	[13]
3	Ar + e ® Ar(F) + e	f(θ,n_e)	[13]
4	Ar + e ® Ar(A) + e	f(θ,n_e)	[13]
5	Ar + e ® Ar(B) + e	f(θ,n_e)	[13]
Ступенчатое возбуждение
6	Ar(M) + e ® Ar(F) + e	f(θ,n_e)	[14, 15]
7	Ar(R) + e ® Ar(F) + e	f(θ,n_e)	[16]
8	Ar(F) + e ® Ar(A) + e	f(θ,n_e)	[17]
9	Ar(F) + e ® Ar(B) + e	f(θ,n_e)	[17]
10	Ar(A) + e ® Ar(B) + e	f(θ,n_e)	[17]
Прямая, ступенчатая и химическая ионизация
11	Ar + e ® Ar⁺ + e + e	f(θ,n_e)	[18]
12	Ar(M) + e ® Ar⁺ + e + e	f(θ,n_e)	[19, 20]
13	Ar(R) + e ® Ar⁺ + e + e	f(θ,n_e)	[19, 20]
14	Ar(M) + Ar(M) ® Ar⁺ + Ar + e	a×1.2´10^-9	[21]
15	Ar(M) + Ar(M) ® Ar₂⁺ + e	(1-a)×1.2´10^-9	[21]
16	Ar(M) + Ar(R) ® Ar⁺ + Ar + e	a×2.1´10^-9	[21]
17	Ar(M) + Ar(R) ® Ar₂⁺ + e	(1-a)×2.1´10^-9	[21]
Перемешивание электронами
18	Ar(M) + e ® Ar(R) + e	2.35´10^-7	[21, 22]
19	Ar(R) + e ® Ar(M) + e	3.1´10^-7	[21, 22]
Диссоциативная рекомбинация
20	Ar₂⁺ + e ® Ar + Ar	1.1´10^-7×T_e^-0.5	[27]
Излучение
21	Ar(R) ® Ar + hn	t_eff^-1 = 1.19´10⁸× g_esc	[23-25]
22	Ar(F) ® Ar(M, R) + hn	t_eff^-1 = t_nat ^-1× g_esc	[23-25]
23	Ar(A) ® Ar(F) + hn	1.56´10⁷	[28]
24	Ar(B) ® Ar(A) + hn	8.6´10⁶	[28]
25	Ar(B) ® Ar(F) + hn	9.1´10⁵	[28]

4. Параметры расчета и визуализации

Геометрические параметры модели. Разряд зажигался в кварцевой трубке (4), см. рис. 2, 18 см в длину с внутренним диметром 5.2 мм и внешним - 6.8 мм, при давлении аргона - 0.5 Торр. Высота цилиндрической части резонатора (3) - 7.7 мм. Кварцевая трубка проходит через ось симметрии резонатора. Снаружи верхних и нижних металлических пластин резонатора кварцевая трубка окружена вертикальным цилиндром большего диаметра. Внешние части трубки вне резонатора равны по длине. Вертикальный коаксиальный волновод является частью СВЧ фидера. Источник волны TEM с частотой 2.45 ГГц расположен наверху волновода, так что нижнее сечение волновода (1) находится на верхней пластине цилиндрического резонатора. Центральный электрод (2) коаксиала введен в резонансную полость. Торец электрода находится посередине между верхней и нижней пластинами резонансной полости. Кварцевый стержень подстройки (5) лежит в горизонтальной плоскости и вводится в резонатор через боковую стенку.

Граничные условия и процедура вычислений. При решении системы уравнений (1)-(6) в модель закладывается геометрия системы и дополняется следующими граничными условиями. Нормальная составляющая магнитного поля полагалась равной нулю в бесконечно тонком слое металлической поверхности резонатора. Поскольку проток газа не влиял на кинетические процессы в плазме, предполагалось, что оба конца кварцевой разрядной трубки герметично запаяны. Принималось, что любая падающая волна рассеивается без отражения на стенках цилиндра. В верхней плоскости коаксиального сегмента со стержневой антенной находился идеальный безотражательный источник волны TEM с λ⁰= 12.45 см. Известно, что в резонаторах с низким Q-фактором электронная плотность микроволновой плазмы выше критического значения n_c[26]. Мы также знаем, что в плазме аргона при таких давлениях характерное значении средней энергии ~ 3-5 eV. Характерная плотность энергии для таких разрядов ε_c~3-5´10¹¹ eV·cm^-3. Мы предполагали, что около внутренней границы кварцевой трубки значения электронной плотности и плотности энергии должны быть намного меньшими, чем значения n_c и ε_c в объеме плазмы. Поэтому все дальнейшие вычисления были выполнены со следующими граничными значениями для электронной плотности и плотности энергии электронов: n_ew ≈ 5´10⁸ cm^-3, ε_w ≈ 5´10⁹ eV·cm^-3. Плотность Ar⁺ приравнивалась n_ew, концентрация Ar₂⁺ и всех возбужденных атомов аргона полагались равными нулю на стенке.

Используемые модули визуализации. В работе использовались штатные возможности визуализации системы Comsol Multiphysics. Особенности использования пакета состояли в том, что модуль постобработки и визуализации и вычислительный модуль прикладного пакета Comsol были разделены, и модуль визуализации мог в зависимости от поставленной задачи располагаться как удаленно на графической станции пользователя, так и на кластере визуализации с выводом изображения на видеостену высокого разрешения. При этом, был обеспечен удаленный полнофункциональный и интерактивный доступ с графической консоли пользователя для интерактивной визуализации результатов, за счет присоединения виртуальных дисплеев при инсталяции вычислительного модуля. При использовании модуля визуализации системы Comsol использовались режимы: Cross-Section Plot Parameters для исследования параметров модели методом поперечных сечений 3D объекта; Domain Plot Parameters для исследования переменных на границе области раздела объектов. Режим Arrow Plot использовался для визуализации векторного СВЧ-поля. Режим Slice – для отображения величин параметров задачи цветом в выбранной плоскости. Мы отказались в работе от классической схемы создания видеостены с использованием аппаратного контроллера и использовали модуль визуализации программного пакета SAGE для управления стеной. Использовалась обновленная версия SAGE2 [11], переписанная на платформе Java-script. Это дало возможность преобразования данных для отображения на стене в «сыром» виде в реальном времени непосредственно от программ, выполняющих расчеты. Кроме того, данный пакет позволяет подготовленные таким образом метаданные без каких-либо дополнительных преобразований передавать по сети в режиме реального времени на удаленные узлы визуализации под управлением SAGE, то есть осуществлять удаленный рендеринг данных высокого разрешения. Немаловажным фактором является и то, что данный программный пакет является свободно распространяемым.

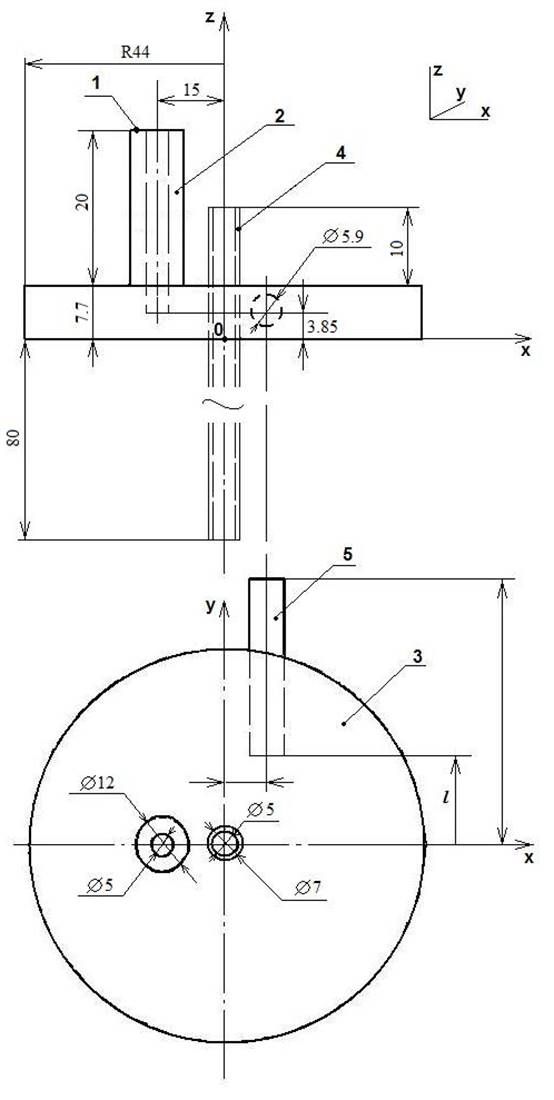
Рис. 2. Геометрия системы.

5. Результаты и обсуждение

Метод итеративной и интерактивной визуализации существенно упростил и ускорил процесс моделирования. Например, в процессе численного моделирования решался ряд проблем по сходимости, связанных с нелокальностью задачи. Для понимания таких параметров, как сходимость, выбиралась для первой итерации описания модель с разрядной трубкой ограниченной плоскостями резонатора, то есть, той областью, где ожидаются наиболее сильные градиенты электрического поля. На рис. 3 показан вариант расчета для пустого резонатора и усеченной трубки.

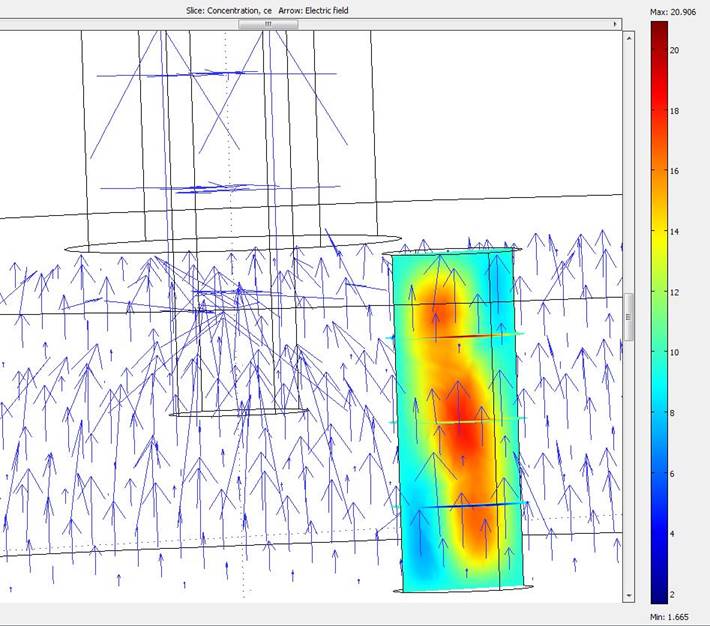
Рис. 3. Концентрация электронов и векторное поле напряженности электрического поля в разряде.

Здесь стрелками показана напряженность электрического поля, а цветовой градацией отражено изменение концентрации электронов в разрядной трубке.

После визуальной оценки полученных результатов, качественного сравнения по близости к экспериментальным данным, принималось решение о переходе к модели с реальной геометрией. Учет реальной геометрии разряда требует значительного большего числа точек сетки.

Выбор количества точек сетки определяется оптимальным соотношением времени затрачиваемого на проведение расчета и требуемой детализации описания исследуемых процессов. При расчетах в лаборатории с использованием персональных компьютерных систем не хватало оперативной памяти компьютера (4 Гб), максимальное число степеней свободы при счете достигало лишь 40000. Число точек сетки не превышало 6000. При таких параметрах моделирования вычисления останавливались в связи с нехваткой ресурсов. Возможности созданной специализированной среды позволили продолжить моделирование и увеличивать число точек сетки. На рис. 4 показан вариант первых итераций по выбору точек сетки.

Визуализация сетки позволяет наглядно оценить, насколько хорошо она удовлетворяет критериям точности расчета каждой области, и, если необходимо, внести в интерактивном режиме соответствующие коррективы в построение сетки. Количество точек сетки увеличивали пошагово (последовательными итерациями) в областях, где наблюдались наибольшие изменения напряженности электрического поля.

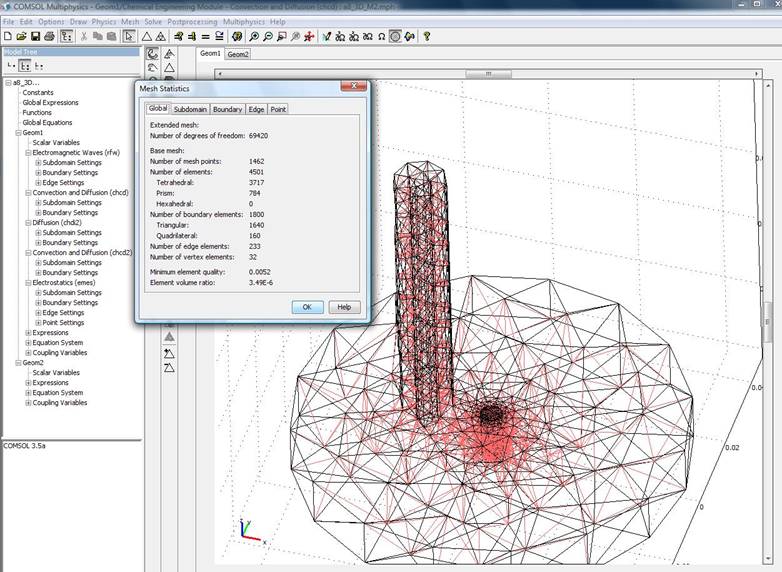
Рис. 4. Построение сетки области расчета.

В результате итераций, сходимость при детализации, учитывающей все изменения напряженности, обеспечивалась при следующих параметрах сетки (рис. 5): число степеней свободы было более 379000, а число точек сетки достигало 7233. Минимальный линейный размер ячейки составлял 1 мм.

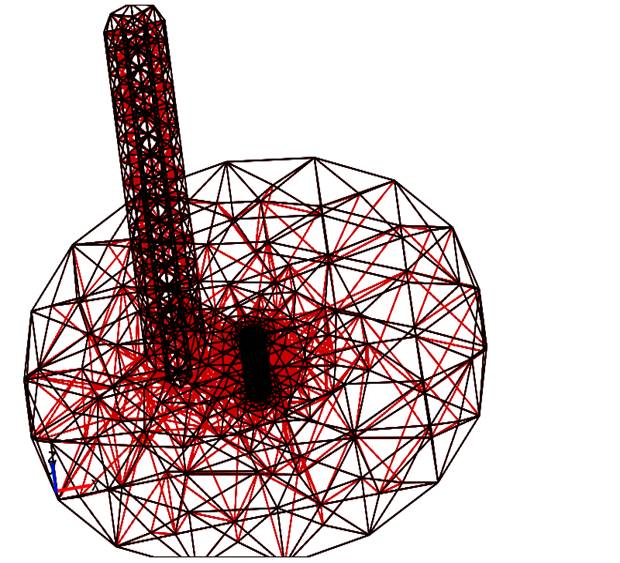
Рис. 5. Комбинированная сетка области расчета.

Для расчетов был выделен кластерный узел с двенадцатью CPU ядрами и памятью RAM – 24 GB. Наиболее активно в процессе счета участвовал центральный процессор, CPU. Нагрузка на ядра была близка к 100% в течение всего времени счета. Использование памяти в среднем не превышало 25 %. В процессе расчетов и визуализации, нагрузка на вычислительные ядра GPU‑ускорителей оказалась менее одного процента, использование GPU‑памяти соответствует использованию памяти графической оболочкой. С точки зрения процесса визуализации это означает, что в процессе рендеренга изображения не используются возможности GPU‑ускорителей. Исходя из этого, можно предположить, что текущая конфигурация и режим использования применимы на обычных вычислительных узлах, не имеющих графических карт, если они будут настроены с поддержкой виртуальных дисплеев.

В результате проведенных расчетов получены первые результаты 3D визуализации результатов численного моделирования СВЧ разряда в аргоне для 3-х мерной задачи с повышенными параметрами степени свободы и количеством точек для упрощенной геометрии СВЧ резонатора.

Визуализация результата расчета пространственного распределения электрического СВЧ поля показана на рис. 6. Визуальный анализ позволяет заключить, что плазма разделена на две области: центральное эллипсоидальное ядро, расположенное, главным образом, в резонаторе и немного вне его, и периферийный гомогенный столб, однородно заполняющий кварцевую трубку вне резонатора, то есть, поле концентрируется главным образом внутри резонатора с максимальными значениями на стенках кварцевой трубки. Вне резонатора волна спадает на расстоянии нескольких миллиметров.

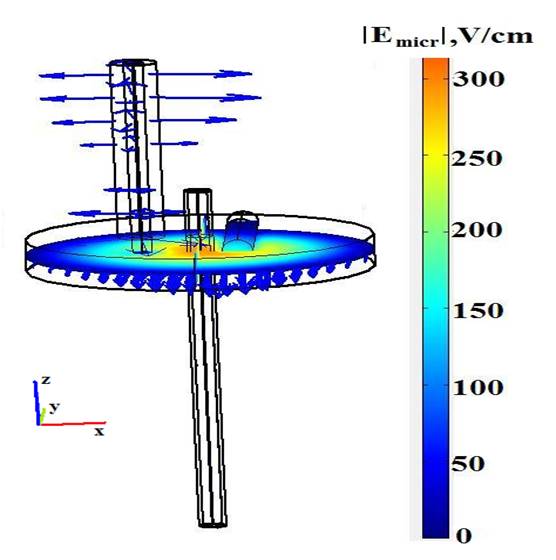
Рис. 6. Напряженность электрического поля в пустом резонаторе.

В отличие от микроволнового поля средняя электронная энергия не исчезает на выходе из полости резонатора, она остается постоянной и равной приблизительно 3 эВ.

Возможность использования локальных сечений внутри исследуемого объекта позволило выявить внутреннюю структуру и особенности параметров расчета в процессе трехмерной визуализации. Результат визуализации концентрации электронов в разряде представлен на рис. 7, где ce = N_e/n_c. Здесь N_e- концентрация электронов, n_c= 7 *10¹⁰cm^-3- критическая концентрация.

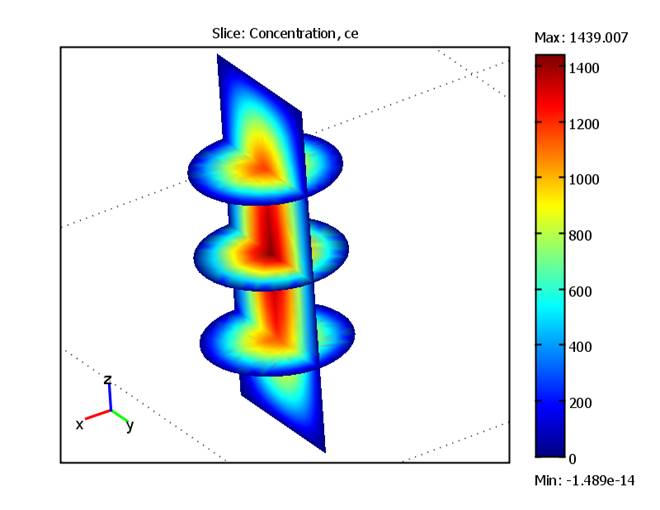
Рис. 7. Концентрация электронов в разряде.

Возможность использования консолидированных ресурсов, то есть, запуск модуля управления и постпроцессинга Comsol на кластере визуализации позволяет осуществлять доступ к модулю вычислений посредством тонкого клиента (vnc) и избавляет пользователя от необходимости иметь у себя клиентскую часть, настроенную для работы с кластером, а так же повышает безопасность кластера в целом, поскольку клиенту требуется доступ всего к одному узлу кластера с помощью клиент-серверного решения с открытым исходным кодом.

Используя модуль визуализации программного пакета SAGE, мы могли осуществлять вывод изображения в режиме высокого разрешения с кластера визуализации непосредственно на модульную видеостену, что позволяло проводить более детальные визуальные оценки и осуществлять сравнительный анализ всего комплекса полученных данных одновременно, рис. 8.

Рис. 8. Вывод изображений на модульную видеостену с кластера визуализации.

6. Заключение

Для проведения численного моделирования и 3D визуализации результатов была создана распределенная гетерогенная вычислительная среда, представляющая собой интегрированный набор программ и управляющих скриптов, связывающих процессы хранения, обработки и визуализации данных в общую систему вычислений с единой точкой входа.

Вычисления выполнялись на компьютерных ресурсах ЦКП «Комплекс моделирования и обработки данных исследовательских установок мега-класса» в НИЦ «Курчатовский институт».

Реализованная в этой среде архитектура вычислений позволила:

- методом итеративно-интерактивной визуализации анализировать результаты проводимого численного моделирования аргоновой плазмы Бинаккеровского СВЧ разряда;

- обеспечить полный защищенный доступ для внешних пользователей с предоставлением графической консоли непосредственно к узлам вычислений;

- осуществлять в единой технологической цепочке создание проекта, мониторинг и управление процессом счета, а также последующую визуализацию полученных данных в интерактивном режиме, в том числе, и в конфигурации с удаленным доступом.

Данная распределенная архитектура вычислений и визуализации поддерживает легкую миграцию вычислительной среды между инструментальными средствами визуализации (консолидированными и клиентскими), предоставляя пользователям, возможность масштабировать общий объем данных и разрешение их визуальных отображений.

Получены результаты визуализации пространственных распределений напряженности СВЧ поля в разряде, которые показали, что поле концентрируется главным образом внутри резонатора с максимальными значениями на стенках кварцевой трубки.

3D визуализация с использования локальных сечений помогла выявить внутреннюю структуру распределения концентрации электронов в разрядной трубке.

Литература

[1] Пилюгин В., Маликова Е., Пасько А., Аджиев В. Научная визуализация как метод анализа научных данных. Научная визуализация. 2012. т. 4. № 4. с. 56-70.

[2] Krinov P.S., Polyakov S.V., Iakobovski M.V. Visualisation in distributed computational systems of results of three dimensional computations. 4 International Conference of Mathematical Modeling: “Stankin”. 2001. v. 2, pp. 126–133

[3] Нестеров И.А. Интерактивная визуализация векторных полей на распределенных вычислительных системах. Матем. моделирование. 2008. т. 20. № 6, с. 3–14

[4] Bondarev A.E., Galaktionov V.A., Chechetkin V.M. Analysis of the Development Concepts and Methods of Visual Data Representation in Computational Physics. Computational Mathematics and Mathematical Physics. 2011. Vol. 51. No. 4. pp. 624–636.

[5] Jovovic J., Epstein I.L., Konjević N., YLebedev u.A., Šišović B., Tatarinov A.V. The Influence of Small Hydrogen Admixtures up to 5 % to a Low Pressure Nonuniform Microwave Discharge in Nitrogen. Plasma Chem. Plasma Process. 2012. 32. pp. 1093–1108.

[6] Lebedev Yu.A., Mavludov T.B., Epstein I.L., Chvyreva A.V., Tatarinov A.V. The effect of small additives of argon on the parameters of a non-uniform microwave discharge in nitrogen at reduced pressures. Plasma Sources Sci. Technol. 2012. 21. 015015.

[7] Лебедев Ю.А., Юсупова Е.В. Влияние постоянного поля на приповерхностную плазму сильно неоднородного СВЧ разряда. Физика плазмы. 2012. Т. 38. № 8. с. 677-693.

[8] Шахатов В.А., Лебедев Ю.А. Метод эмиссионной спектроскопии в исследовании влияния состава смеси гелия с азотом на характеристики тлеющего разряда постоянного тока и СВЧ разряда. Теплофизика высоких температур. 2012. Т. 50. № 5. с. 663–686.

[9] Энциклопедия низкотемпературной плазмы (т. 1-4). Под ред. В.Е. Фортова, М. Наука, 2000.

[10] Прикладная химия плазмы. Под ред. Ю.А. Лебедева, Н.А. Платэ, В.Е. Фортова, «Янус-К», Москва, 2006, 480 с.

[11] SAGE2, http://www.sagecommons.org/.

[12] COMSOL 3.5a http://www.comsol.com

[13] Yanguas-Gil, Cortrino J., Alves L.L. An update of argon inelastic cross sections for plasma discharges. J. Phys. D. Appl. Phys. 2005. pp. 1588-1598

[14] Boffard J.B., Piech G.A., Gehrke M.F. et all. Measurement of electron-impact excitation cross sections out of metastable levels of argon and comparison with ground-state excitation. Phys. Rev. 1999. A 59. 2749

[15] Bartschat K., Zeman V. Electron-impact excitation from the (3p⁵4s) metastable states of argon. Phys. Rev. 1999. A 59, R2552

[16] Gangwar R.K., Sharma L., Srivastava R., Stauffer A.D. Argon plasma modeling with detailed fine-structure cross sections. J. Appl. Phys. 2012. Vol. 111, Issue 5

[17] Drawin H.W., Emard F. Physica C85, 333, (1977)

[18] Rapp D., Englander-Golden P. Total Cross Sections for Ionization and Attachment in Gases by Electron Impact. I. Positive Ionization. J. Chem. Phys. 43, 1464,

[19] Hyman H.A. Electron-impact ionization cross sections for excited states of the rare gases (Ne, Ar, Kr, Xe), cadmium, and mercury. Phys. Rev. A. 1979. A20, 855.

[20] Dixon A.J., Harrison M.F., Smith A.C.H. in Abstracts of the VIII-th ISPEAC, Belgrad, 1973, p.405

[21] Karoulina E., Lebedev Yu. Computer simulation of microwave and DC plasmas: comparative characterisation of plasmas. J. Phys. D: Appl.Phys. 1992. Vol. 25. Pp. 401-412

[22] Ferreira C., Loureiro J., Ricard A. Populations in the metastable and the resonance levels of argon and stepwise ionization effects in a low‐pressure argon positive column. J. Appl. Phys. 1985. Vol. 57. Pp. 82-90

[23] H. van Tongeren. Positive column of the Cs–Ar low‐pressure discharge J. Appl. Phys. 1974. Vol. 45. 89

[24] Holstein T. Imprisonment of Resonance Radiation in Gases. Phys. Rev. 1947. vol. 72. Pp. 1212-1233

[25] Walsh P. Effect of Simultaneous Doppler and Collision Broadening and of Hyperfine Structure on the Imprisonment of Resonance Radiation. Phys. Rev. 1959. Vol. 116. Pp. 511-516

[26] Lebedev Yu.A., Polak L.S. High Energy Chem. HIECAP. 1980. Vol. 13. No. 5. pp. 331-348

[27] Biberman L.M., Vorob’ev V.S., Yakubov I.T. Kinetiks of Nonequilibrium Low-Temperature Plasmas. Moscow: Nauka, 1982; NY: Consultants Bureau, 1987.

[28] Dyatko N.A., Ionikh Y.Z., Kochetov I.V. et all. Experimental and theoretical study of the transition between diffuse and contracted forms of the glow discharge in argon. J. Phys. D: Appl.Phys. 2008. Vol. 41, 055204.

[29] Shkarofsky I.P., Johnston T.W., Bachynski M.P. The Particle Kinetics of Plasmas. Addison-Wesley PC. 1996.

[30] Hagelaar G.J.M., Pitchford L.C. Plasma Sources Sci. Technol. 2005. Vol. 14. Pp. 722-733.

SOLUTION OF PROBLEMS IN MODELING AND VISUALIZATION OF PROCESSES IN THE MICROWAVE DISCHARGE PLASMA

Yu.A. Lebedev, A.V. Tatarinov, I.L. Epstein, V.N. Timakin*, I.A. Tkachenko*

A.V.Topchiev Institute of Petrochemical Synthesis of the Russian Academy of Sciences

* National Research Centre “Kurchatov Institute”

lebedev@ips.ac.ru, atat@ips.ac.ru, epstein@ips.ac.ru, vtim@kiae.ru, tia@grid.kiae.ru

Abstract

In the article the relevance of development of specialized hardware-software complexes for visualization, the enhancement of algorithms of visual representation of data and the extension of opportunities of data display systems are discussed. Creation of a specialized distributed environment in order to solve 3D interactive visualization tasks of numerical simulation results of microwave discharge is described. Visualization of a computing mesh allowed to make visual estimates and to introduce necessary amendments in interactive mode. The realized distributed architecture of visualization supports easy migration of computing environment between instrumental visualization tools (consolidated or client's), providing an opportunity to scale the total amount of data and resolution of the images. Results of 3D visualization of the spatial distribution of the microwave field strength are shown on the example of a self-consistent simulation of argon plasma generated by means of the Beenakker cavity. The Spatial visualization by means of local cross sections of the computational domain let us discover an internal structure and features of the distribution of electron concentration in the discharge tube.

Keywords: simulation of the low-temperature plasma, data analysis, scientific visualization, scientific research, application software, visualization of data.

References

[1] Pilyugin V., Malikova E., Pasko A., Adzhiev V. Scientific visualization as method of scientific data analysis. Scientific visualization. 2012. vol. 4. no. 4, pp. 56-70. [In Russian]

[3] Nesterov I.A. Interaktivnaja vizualizacija vektornyh polej na raspredelennyh vychislitel'nyh sistemah [Interactive visualization of time-varying flow fields using high performance parallel systems]. Matem. Mod. 2008. Vol. 20. no. 6, pp. 3–14 [In Russian]

[4] Bondarev A.E., Galaktionov V.A., and Chechetkin V.M. Analysis of the Development Concepts and Methods of Visual Data Representation in Computational Physics. Computational Mathematics and Mathematical Physics. 2011. vol. 51. no. 4. pp. 624–636.

[5] Jovovic J., Epstein I.L., Konjević N., Lebedev Yu.A., Šišović B., Tatarinov A.V. The Influence of Small Hydrogen Admixtures up to 5 % to a Low Pressure Nonuniform Microwave Discharge in Nitrogen. Plasma Chem. Plasma Process. 2012. 32. pp. 1093–1108.

[7] Lebedev Yu.A., Yusupova E.V. Vlijanie postojannogo polja na pripoverhnostnuju plazmu sil'no neodnorodnogo SVCh razrjada [Effect of the dc Field on the Near Surface Plasma of a Highly Nonuniform Microwave Discharge]. Plasma Phys. Rep., 2012, 38, No. 8, pp. 677–683. [In Russian]

[8] Shakhatov V.A., Lebedev Yu.A. Metod jemissionnoj spektroskopii v issledovanii vlijanija sostava smesi gelija s azotom na harakteristiki tlejushhego razrjada postojannogo toka i SVCh razrjada [Radiation Spectroscopy in the Study of the Influence of a Helium–Nitrogen Mixture Composition on Parameters of DC Glow Discharge and Microwave Discharge]. High Temp. 2012. Vol. 50. No. 5. pp. 663–686. [In Russian]

[9] Encyclopedia of Low Temperature Plasma, ed. V. E. Fortov, 2000, v. 1-4. Moskow: Nauka, [In Russian].

[10] Chemistry of Low Temperature Plasma, ed. Yu. A. Lebedev, N.A. Plate, V. E. Fortov. Moskow: Yanus-K, 2006, 480 p. [In Russian].