ВИЗУАЛЬНЫЙ АНАЛИЗ КЛАСТЕРНЫХ СТРУКТУР В МНОГОМЕРНЫХ ОБЪЕМАХ ТЕКСТОВОЙ ИНФОРМАЦИИ

А.Е. Бондарев¹, А.В. Бондаренко², В.А. Галактионов¹, Э.С. Клышинский^1,3

¹Институт прикладной математики им. М.В.Келдыша РАН, Москва, Россия

²ФГУП ГосНИИАС, Москва, Россия

³НИУ ВШЭ, Москва, Россия

bond@keldysh.ru; vlgal@gin.keldysh.ru; klyshinsky@mail.ru

Содержание

1. Введение

2. Построение упругих карт

3. Алгоритм t-SNE

4. Подготовка и обработка массива текстовой информации

5. Визуальный анализ кластерных структур в тестовом многомерном объеме методом эластичных карт

6. Визуальный анализ кластерных структур в тестовом многомерном объеме методом t-SNE

7. Заключение

Благодарности

Литература

Аннотация

Работа рассматривает вопросы визуального анализа кластерных структур в многомерных объемах текстовой информации. Для анализа кластерных структур в многомерном объеме текстовых данных используются технологии построения упругих карт, представляющие собой методы отображения точек исходного многомерного пространства на вложенные в это пространство многообразия меньшей размерности. Варьируя поверхность упругой карты за счет последовательного уменьшения коэффициентов упругости, можно добиться лучшей аппроксимации картой многомерного облака данных. Применение технологий построения упругих карт для решения задач кластерного анализа не предполагает никакой априорной информации об изучаемых данных и не зависит от их природы, происхождения и т.п. Схожими свойствами обладает близкий по идеологии вероятностный подход к снижению размерности t-SNE. Данная работа содержит описание результатов построения упругих карт и применения подхода t-SNE для визуального анализа кластерных структур в многомерных объемах текстовой информации. Для упругих карт подробно описан и проиллюстрирован прием «квази-зум», позволяющий существенно улучшить результаты в области сгущения точек изучаемого многомерного пространства. Для обоих подходов (построение упругих карт и t-SNE) показана их работоспособность и применимость для решения задач кластеризации терминов естественного языка.

Ключевые слова: многомерные данные, визуальный анализ, упругие карты, смысловая близость слов, кластерные структуры.

1. Введение

В анализе многомерных данных особое место занимают задачи классификации. При классификации объема многомерных данных может решаться как задача разделения исследуемой совокупности явлений на классы, так и отнесения одного или нескольких явлений к уже существующим классам. Для решения подобных задач используются методы кластерного анализа. Методов и алгоритмов кластерного анализа на современном этапе существует очень много, они постоянно развиваются и отличаются большим разнообразием. Многообразие алгоритмов кластерного анализа обусловлено множеством различных критериев, выражающих те или иные аспекты качества автоматического группирования. Основные понятия кластерного анализа вместе с соответствующими численными методами и алгоритмами их реализации подробно описаны в работе [1].

Алгоритмы кластеризации многомерного облака данных обладают рядом общих недостатков. Если один и тот же многомерный объем исследовать разными методами кластеризации, получаются разные результаты. Если варьировать параметры настройки в одном и том же алгоритме, получаются также весьма разные результаты. И самое главное, при отыскании структур в многомерных объемах числовых данных, алгоритмы кластеризации зачастую сами привносят структуры в исследуемый объем. И еще одно важное замечание – алгоритмы кластеризации, как правило, «приспособлены» к данным определенного типа или происхождения, то есть они не являются полностью независимыми от природы происхождения самих многомерных данных. В некотором отвлеченном смысле, кластеризация используется для того, чтобы понять структуру исследуемых данных, но для своей корректной работы требует знания этой структуры.

Обойти эти проблемы отчасти можно с помощью применения подхода, относящегося к инструментам визуальной аналитики и являющегося синтезом нескольких алгоритмов понижения размерности и визуального представления многомерных данных во вложенных в исходный объем многообразиях меньшей размерности.

К таким алгоритмам можно отнести отображение исходного многомерного объема в главных компонентах (PCA), построение самоорганизующихся карт (SOM) [2], построение и отображение исходного многомерного объема в упругих картах (Elastic Maps) [3-6] с разными свойствами упругости или эластичности. Эти методы позволяют тем или иным образом выделить из исходного многомерного объема данных содержащуюся в нем кластерную структуру. Схожей идеологией построения обладает метод стохастического распределения соседей с использованием t-распределения Стьюдента – t-distributed stochastic neighbor embedding (t-SNE) [10].

Общей идеей реализации всех вышеперечисленных подходов является отображение многомерных данных в представимую человеком размерность, например, на плоскость, так, чтобы точки данных, близкие в исходном пространстве, были близки и на плоскости (на карте). С помощью визуализации мы можем получать большое количество информации о данных сразу, без какой-либо обработки. После подобного преобразования становятся более очевидными области группировки объектов и разреженные области.

Общий подход можно назвать «картографическим». Действительно, многие идеи и инструменты подхода имеют свои корни в теории построения географических информационных систем (ГИС). В работах [3-6] приведен ряд примеров применения подхода в целом к различным объемам многомерных данных.

Одним из основных достоинств данного «картографического» подхода к решению задач кластерного анализа в многомерном объеме данных является его полная независимость от самого исследуемого объема, природы его происхождения и т.п. Это позволяет применить данный подход к задачам анализа текстовой информации, где в качестве числовых характеристик выступают частоты употребления слов, в том числе для визуального анализа кластерных структур в многомерном объеме исходных данных при нечеткой смысловой группировке слов по их сочетаемости с другими словами.

В каждом из методов объекты, близко расположенные в исходном пространстве, сохраняют свое близкое расположение и в преобразованном пространстве. Однако снижение размерности позволяет сократить время на кластеризацию и упростить визуальный анализ имеющихся данных.

Достоинством метода t-SNE является сохранение общей структуры расположения точек при их переносе из многомерного пространства (вплоть до нескольких сотен тысяч измерений) в пространство с меньшей размерностью (два-три измерения). Подобный подход особенно важен при решении задачи автоматической кластеризации терминов естественного языка, где каждое слово описывается в пространстве признаков, составленном из всех слов словаря или его подмножества (например, всех существительных или прилагательных). Заметим, что для большой коллекции текстов размер словаря составляет порядка 200 000 слов, среди которых может встретиться около 30 000 глаголов, 60 000 существительных и 35 000 прилагательных (конкретные цифры зависят от выбранных текстов, их стиля, предметной области, авторства, объема коллекции и других параметров). Таким образом, анализ проводится в пространстве размерностью несколько десятков тысяч параметров. В подобных условиях применение методов снижения размерности становится актуальной задачей.

В данной работе основное внимание уделено изучению возможности применения методов упругих карт и t-SNE для анализа тематической близости слов русского языка.

Основой предлагаемого метода является анализ непосредственного окружения слов. Основная гипотеза состоит в том, что близкие по смыслу слова должны встречаться в примерно одинаковом контексте [14]. В связи с этим в пространстве признаков они будут находиться на относительно близком расстоянии друг от друга, тогда как отличающиеся слова будут находиться на более удаленном друг от друга расстоянии.

Снижение размерности пространства признаков и его последующая визуализация позволяет получать большое количество информации о данных без предварительной обработки. В этом случае становятся видимыми области группировки данных и разреженные области, количество кластеров, их форма, взаимное расположение и т.д. Также, как показывает практика, упрощается решение задач классификации. Обратим внимание, что это естественная классификация данных, не требующая каких-либо специальных действий над исходными данными.

Следует отметить, что подобная постановка задачи может оказаться весьма полезной при обработке, анализе и визуализации многомерных решений задач вычислительной газовой динамики, имеющих небольшую размерность [7-8].

2. Построение упругих карт

Суть «картографического» подхода заключается в построении вложенного в многомерное пространство данных двумерного многообразия (карты), которое определенным способом моделирует или аппроксимирует данные с последующей проекцией точек исследуемого облака данных на карту. Построение упругих карт (Elastic Map) полностью соответствует этому принципу. Идеология и алгоритмы реализации построения упругих карт подробно представлены в работах [3-6]. Подобная карта представляет собой систему упругих пружин, вложенную в многомерное пространство данных. Данный подход основывается на аналогии с задачами механики: главное многообразие, проходящее через «середину» данных, может быть представлено как упругая мембрана или пластинка. Метод упругих карт формулируется как оптимизационная задача, предполагающая оптимизацию заданного функционала от взаимного расположения карты и данных.

Согласно [5,6] основой для построения упругой карты является двумерная прямоугольная сетка G, вложенная в многомерное пространство, которая аппроксимирует данные и обладает регулируемыми свойствами упругости по отношению к растяжению и изгибу. Расположение узлов сетки ищется в результате решения оптимизационной задачи на нахождение минимума функционала:

где │X│- число точек в многомерном объеме данных X; m - число узлов сетки, λ, μ - коэффициенты упругости, отвечающие за растяжение и изогнутость сетки соответственно;

D₁, D₂, D₃ - слагаемые, отвечающие за свойства сетки:

D₁является мерой близости расположения узлов сетки к данным. Здесь K_ij подмножества точек из X, для которых узел сетки r^ij является ближайшим:

Слагаемое D₂ представляет меру растянутости сетки:

Слагаемое D₃ представляет меру изогнутости (кривизны) сетки:

Варьирование параметров упругости заключается в построении упругих карт с последовательным уменьшением коэффициентов упругости, в силу чего карта становится более мягкой и гибкой, наиболее оптимальным образом подстраиваясь к точкам исходного многомерного объема данных. После построения упругую карту можно развернуть в плоскость для наблюдения кластерной структуры в изучаемом объеме данных. Применение упругих карт позволяет более точно и четко определять кластерную структуру изучаемых многомерных объемов данных. Пример определения кластерной структуры в тестовом объеме многомерных данных с помощью построения упругих карт приведен в [9], где построение упругих карт и реализация последующей процедуры вариации коэффициентов упругости в сторону уменьшения позволили добиться четкого разделения данных на кластеры.

Следует отметить, что при построении упругих карт в многомерном облаке данных, состоящем из сгущений и отдельных отдаленных точек, возникает проблема масштабируемости. Упругая карта будет пытаться подстроиться под рассматриваемый объем в целом – как к отдаленным точкам, так и к областям сгущения, что, естественно, не может получиться одинаково хорошо. Для того чтобы решить эту проблему и обеспечить четкое представление о данных в области сгущений данная работа предлагает подход, названный «квази-зум» (quasi-Zoom), заключающийся в вырезании области сгущения из рассматриваемого облака многомерных данных и построения для вырезанной области упругой карты заново. Результаты применения этого подхода будут показаны ниже в соответствующем разделе.

3. Алгоритм t-SNE

Алгоритм t-SNE был предложен в статье [11], но на данный момент используется его модификация с заменой нормального распределения на распределение Стьюдента для данных низкой размерности [10]. В данном методе каждый объект описывается вектором в пространстве большой размерности. Для всех точек рассчитывается многомерное евклидово расстояние:

Эта формула показывает близость точек x_i и x_j при гауссовом распределении вокруг x_i с заданным отклонением σ, вычисляемым для каждой точки отдельно таким образом, чтобы точки в областях с большей плотностью имели меньшую дисперсию. Для этого используется оценка перплексии:

где H(p_i) – энтропия по Шеннону. На практике перплексия задается в качестве параметра метода.

Для двумерных или трехмерных соседей пары x_i и x_j, назовем их y_i и y_j, не представляет труда оценить условную вероятность, приняв стандартное отклонение равным :

Если точки отображения y_i и y_j корректно моделируют сходство между исходными точками высокой размерности x_i и x_j, то соответствующие условные вероятности p_j|i и q_j|i будут эквивалентны. В качестве оценки качества в классическом SNE используется расстояние Кульбака-Лейблера. SNE минимизирует сумму таких расстояний для всех точек отображения при помощи градиентного спуска. При реализации метода t-SNE в качестве альтернативы минимизации суммы дивергенций Кульбака-Лейблера между условными вероятностями p_i|j и q_i|j минимизируется одиночная дивергенцию между совместной вероятностью P в многомерном пространстве и совместной вероятностью Q в пространстве отображения:

где p_ii и q_ii = 0, p_ij = p_ji, q_ij = q_ji для любых i и j, а p_ij определяется по формуле:

где n — количество точек в наборе данных.

Для того, чтобы избежать скученности точек, в t-SNE используется t-распределение с одной степенью свободы. Совместная вероятность для пространства отображения в этом случае будет определяться следующей формулой:

4. Подготовка и обработка массива текстовой информации

Для проверки работоспособности вышеописанных методов были подготовлены наборы текстовых данных.

На первом этапе были получены текстовые корпуса из новостных источников. Общий объем текстовой коллекции составил примерно 1 млрд слов. Помимо этого, использовалась коллекция научных текстов (научные журналы, сборники трудов конференций, тексты диссертаций, авторефераты диссертаций) общим объемом около 150 млн. слов. В данной работе извлекались синтаксически связанные пары слов. Подобная информация извлекается следующим образом.

Шаг 1 – извлечение сочетаний из текста. На данном шаге проводится морфологическая разметка корпуса текстов. Далее по шаблонам отбираются глагольные сочетания. В формировании данной базы принимают участие существительные, однозначные по части речи, но, возможно, неоднозначные по падежу.

Шаг 2 – составление базы сочетаемости слов. Полученные на предыдущем шаге сочетания приводятся к нормальной форме, после чего рассчитывается их встречаемость. Из полученной базы отсеиваются сочетания, встретившиеся меньше заданного количества раз.

Шаг 3 – составление модели управления предлогов. Из сочетаний, полученных на Шаге 1, отбираются те, в которых существительное однозначно по падежу. Для них рассчитывается встречаемость пар вида «предлог+существительное в заданном падеже». Для удобства все пары с одним предлогом собираются в единую запись.

Шаг 4 – получение модели управления для глаголов. Из базы, полученной на шаге 1, строим базу сочетаний вида «глагол + предлог + падеж существительного», после чего отбрасываем все варианты, запрещенные моделью предлога или встречающиеся только один раз.

Шаг 5 – фильтрация базы сочетаемости. Из базы, полученной на шаге 1, отсеиваем все сочетания, не подходящие под полученную на шаге 4 модель управления. Одновременно может быть устранена падежная неоднозначность. В итоге мы получаем базу сочетаемости глаголов с существительными.

Для отсечения шумов отбрасываются все сочетания с частотой встречаемости ниже заданной. Кроме того, выбираются только те главные слова (и соответствующие им сочетания), у которых мощность множества зависимых слов превышает некоторое пороговое значение. Это необходимо, чтобы отсеять шум в извлекаемых из коллекции сочетаниях. Пороговое значение частоты встречаемости позволяет избавиться от случайно попавших в базу сочетаний, число различных сочетаний гарантирует нам достаточную статистику для сравнений.

Более подробно метод описывается в [12].

Всего при помощи регулярных выражений было извлечено около 7,5 млн уникальных сочетаний вида глагол+предлог+существительное и около 2,3 млн уникальных сочетаний существительное+прилагательное. Для первичных тестов из данного множества было отобрано около 100 глаголов со 155 наиболее связанными с ними существительными. Полученные таким образом данные далее рассматриваются как многомерный объем данных, представляющий собой 100 точек в 155-мерном пространстве. Числовые значения получающейся в результате матрицы определяются как частоты совместного употребления. Следует отметить, что среди отобранных глаголов содержался ряд пар, представляющих схожие глаголы совершенного и несовершенного вида. Это было сделано для дополнительного контроля в силу предположения, что точки, соответствующие подобным парам, должны находиться недалеко друг от друга на результирующем изображении.

5. Визуальный анализ кластерных структур в тестовом многомерном объеме методом эластичных карт

Универсальность технологии применения упругих карт к решению задач кластерного анализа позволяет нам применять эти технологии к данным любой природы, происхождения. В данном разделе рассматриваются результаты применения подхода построения упругих карт к задаче анализа текстовой информации. С точки зрения построения упругих карт исходный многомерный объем является совершенно стандартным. Рассмотрим ниже результаты построения упругих карт для тестового объема. Визуальное представление упругих карт, представленное ниже, получено с помощью открытого программного комплекса ViDaExpert, подробно описанного в [5].

Для начала представим изучаемый объем в пространстве, образованном первыми тремя главными компонентами. Результаты представлены на рисунке 1.

Рис. 1. Представление 155-мерного объема данных в пространстве главных компонент.

Из рисунка 1 видно, что большинство точек объема сосредоточено в одной области, а остальные имеют очень большой разброс. Заранее можно предположить, что при построении упругих карт возникнет проблема масштабируемости. Упругая карта будет пытаться подстроиться под рассматриваемый объем в целом – как к отдаленным точкам, так и к области сгущения, что, естественно, не может получиться одинаково хорошо.

Начнем построение упругих карт с самого простого варианта – так называемой «жесткой» карты, а затем будем ее постепенно смягчать, уменьшая коэффициенты изгиба и растяжения. Количество узлов карты задается как 12 х 12. Коэффициенты упругости, отвечающие за растяжение и изогнутость сетки, задаются как λ = 5, μ = 5.

На рисунках 2,3,4,5 представлены последовательно:

¾ построенная сетка упругой карты,

¾ упругая карта с раскраской по плотности данных,

¾ развертка упругой карты с раскраской по плотности данных,

¾ развертка упругой карты без раскраски для наглядности.

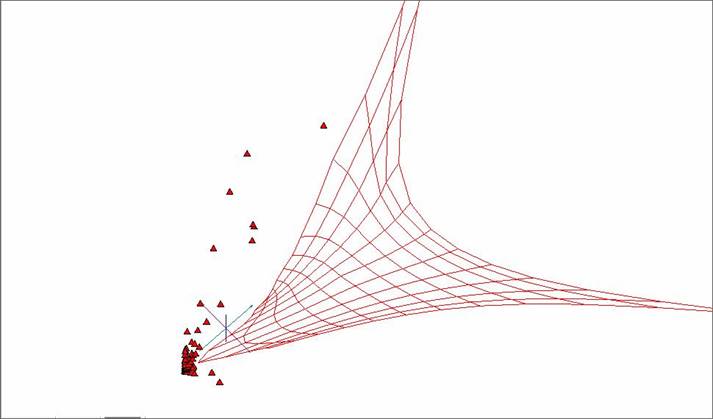
Рис. 2. Построенная сетка «жесткой» упругой карты.

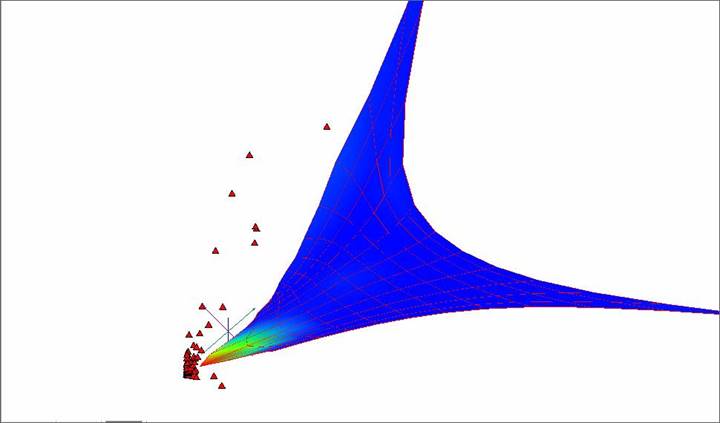
Рис. 3. «Жесткая» упругая карта с раскраской по плотности данных.

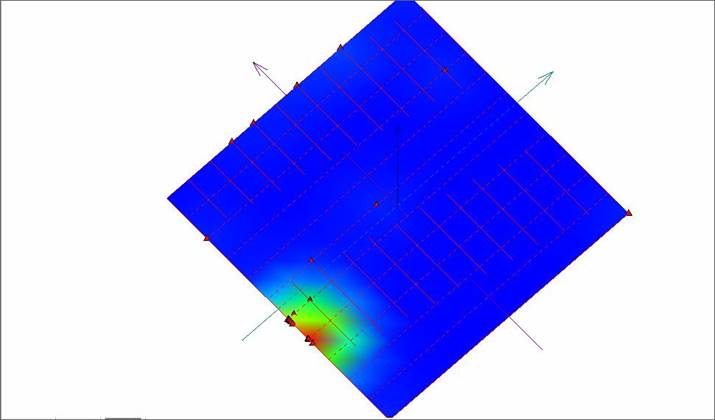
Рис. 4. Развертка «жесткой» упругой карты с раскраской по плотности данных.

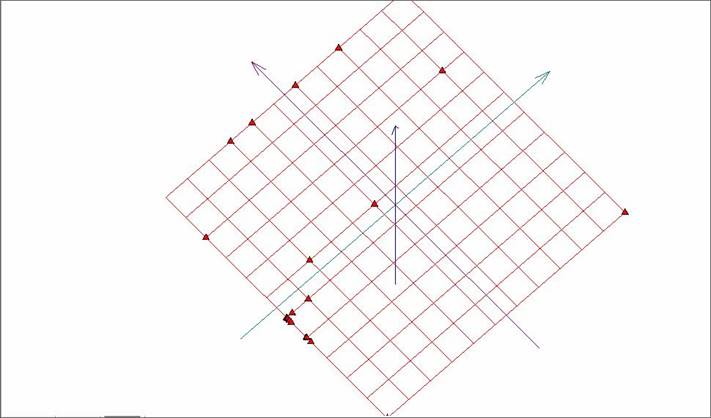
Рис. 5. Развертка «жесткой» упругой карты без раскраски.

На рисунках видно, что карта стремится отразить дальние разбросанные точки, почти не затрагивая область сгущения. Это связано с вышеупомянутой проблемой масштабируемости.

Реализуем процесс «смягчения» упругой карты за счет уменьшения коэффициентов изгиба и растяжения. Зададим коэффициенты упругости как λ = 0.01, μ = 0.01.

Для этого варианта задания коэффициентов упругости последовательность визуальных представлений для упругих карт показана на рисунках 6 - 9.

Рис. 6. Построенная сетка «мягкой» упругой карты при λ = 0.01, μ = 0.01.

Рис. 7. Построенная сетка «мягкой» упругой карты при λ = 0.01, μ = 0.01 с раскраской по плотности данных.

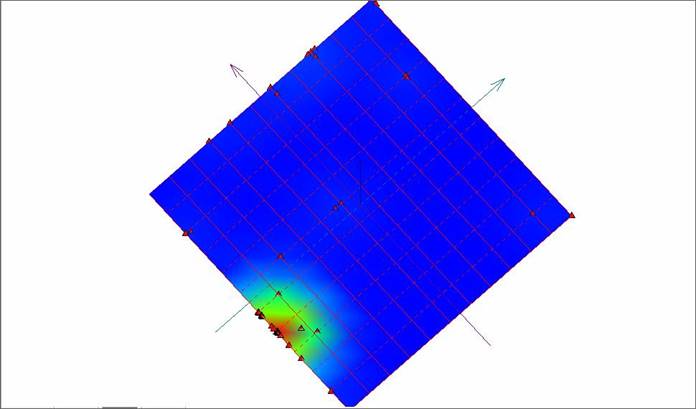
Рис. 8. Развертка «мягкой» упругой карты при λ = 0.01, μ = 0.01 с раскраской по плотности данных.

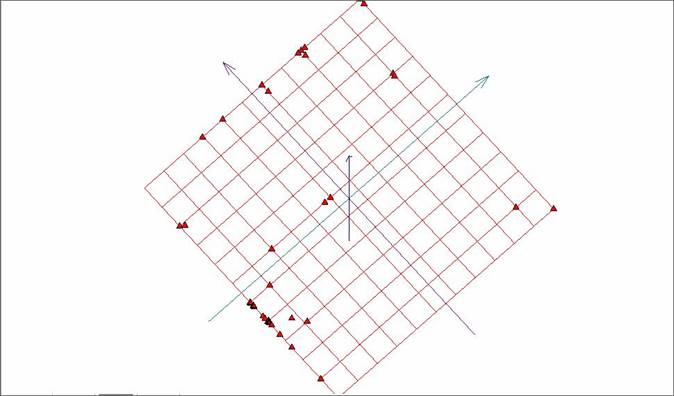
Рис. 9. Развертка «мягкой» упругой карты при λ = 0.01, μ = 0.01.

При этом варианте задания коэффициентов упругости карта пытается охватить изгибами поверхности, как удаленные точки, так и область сгущения. Тем не менее, количество разделившихся точек можно считать недостаточным.

Следующим шагом является задание более мелкого разбиения основной сетки упругой карты с целью сделать карту более подробной. В дальнейшем будем рассматривать только максимально «мягкие» варианты карт.

Зададим на каждое направление 25 узлов сетки. Результаты для этого построения представлены на рисунках 10 - 13.

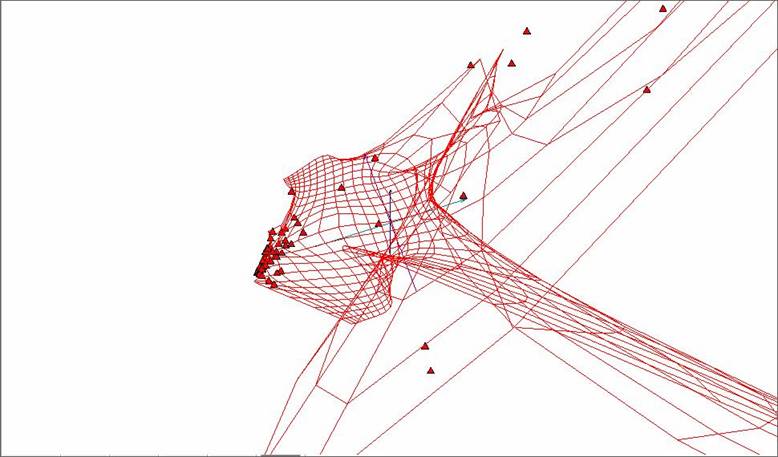
Рис. 10. Построенная сетка «мягкой» упругой карты при λ = 0.01, μ = 0.05 и количестве узлов 25х25.

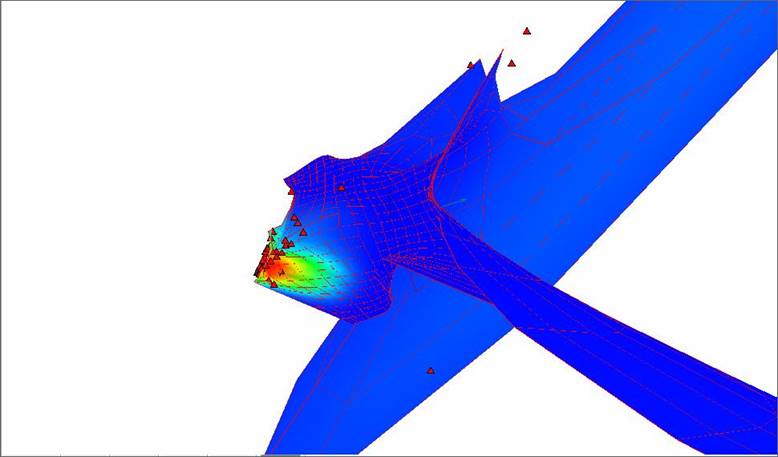
Рис. 11. Построенная сетка «мягкой» упругой карты при λ = 0.01, μ = 0.05 и количестве узлов 25х25 с раскраской по плотности данных.

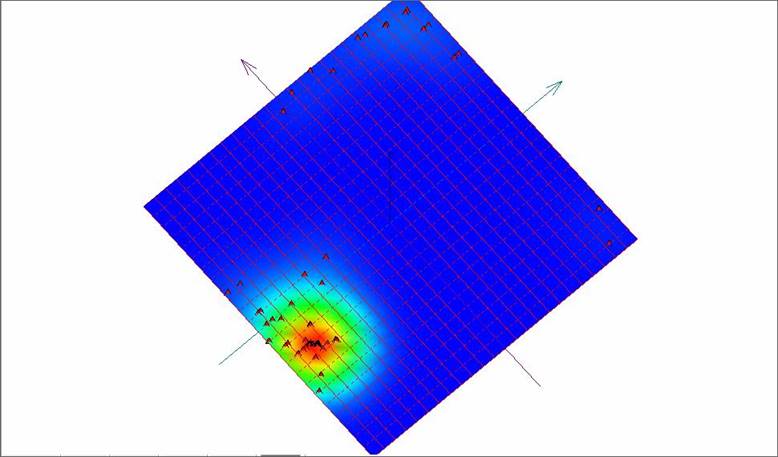
Рис. 12. Развертка «мягкой» упругой карты при λ = 0.01, μ = 0.049 и количестве узлов 25х25 с раскраской по плотности данных.

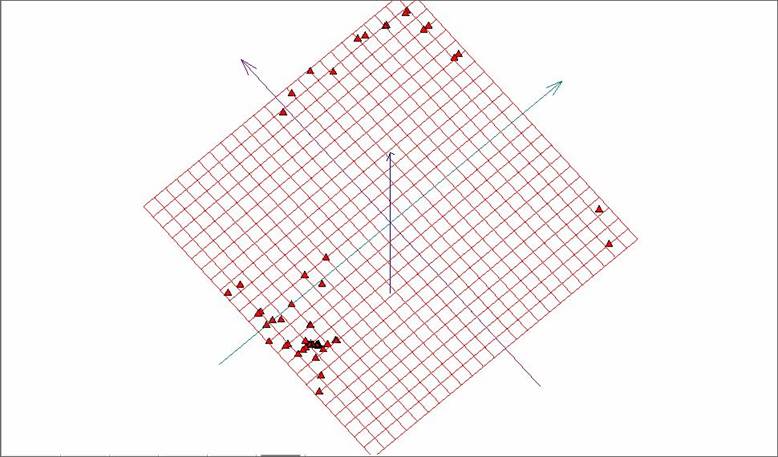
Рис. 13. Развертка «мягкой» упругой карты при λ = 0.01, μ = 0.05 и количестве узлов 25х25.

Этот вариант задания количества узлов сетки и коэффициентов упругости обеспечивает нам максимальное количество разделившихся точек. В нем больше раздельных точек на изображении. Однако некоторые точки на рисунке 13 — это несколько слипшихся исходных точек в многомерном пространстве, по сути кластер.

Таким образом, построение упругих карт с вариацией количества узлов исходной сетки упругой карты и вариацией значений коэффициентов упругости карты в сторону уменьшения позволяют добиться относительно лучшего разделения исходных точек на развертке карты.

Тем не менее этого недостаточно. Обратим внимание на темный треугольник на рисунке 13 – он представляет собой большое количество «слипшихся» точек. На рисунке 14 представлены те же результаты, что и на рисунке 13, но с аннотациями соответствующих глаголов для точек исследуемого объема.

Нашей целью является максимальное разделение точек в области сгущения. Для достижения этой цели предлагается применить подход, названный в данной работе «квази-зум» (Quasi-Zoom). Суть этого технологического приема заключается в том, что для более тонкой подстройки необходимо выделять большие кластеры в исследуемом объеме многомерных данных и проводить построение упругих карт для выделенных кластеров отдельно, организуя тем самым эффект подобный функции «zoom» в современной фототехнике. Это позволит избежать проблем с масштабируемостью, когда упругая карта должна описывать как области сгущения, так и сильно удаленные отдельные точки.

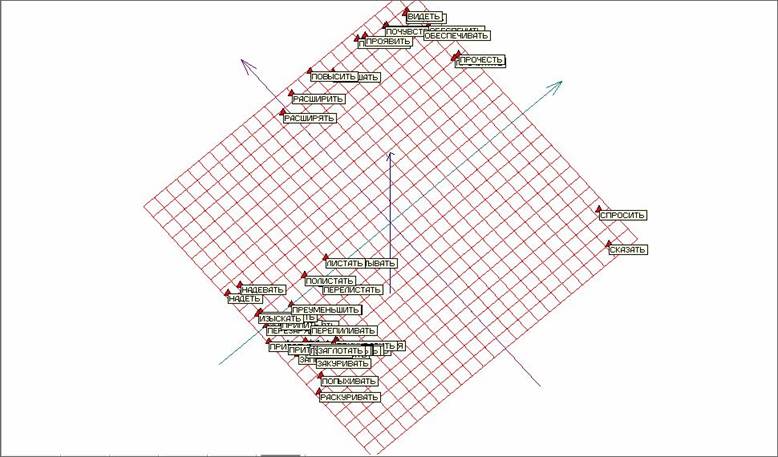
Рис. 14. Развертка «мягкой» упругой карты при λ = 0.01, μ = 0.05 и количестве узлов 25х25 с аннотациями.

На рисунке 15 представлена верхняя часть рисунка 14 крупным планом. Видно, что пары схожих глаголов несовершенной и совершенной формы лежат достаточно близко друг к другу, что дополнительно свидетельствует о применимости и работоспособности метода упругих карт применительно к задачам анализа текстовой информации. На рисунке 16 представлена крупным планом нижняя часть рисунка 14, где лежит основная область сгущения.

Для улучшения разделения в области сгущения применим подход «квази-зум». Из исходного многомерного объема данных вырежем отделившиеся точки верхней части развертки (рисунок 15). К получившемуся в результате этой процедуры новому объему многомерных данных заново применим построение упругой карты. При этом упругую карту будем строить сразу максимально мягкой с числом узлов сетки 25 х 25.

На рисунке 17 представлена получившаяся в результате сетка упругой карты после первого применения подхода «квази-зум». На рисунке 18 соответственно представлена развертка этой карты с раскраской по плотности данных. Рисунки показывают, что разделение точек удалось значительно улучшить. Однако под точкой, соответствующей наивысшей плотности данных скрываются еще 37 «слипшихся» слов – глаголов, приведенных на рисунке 19.

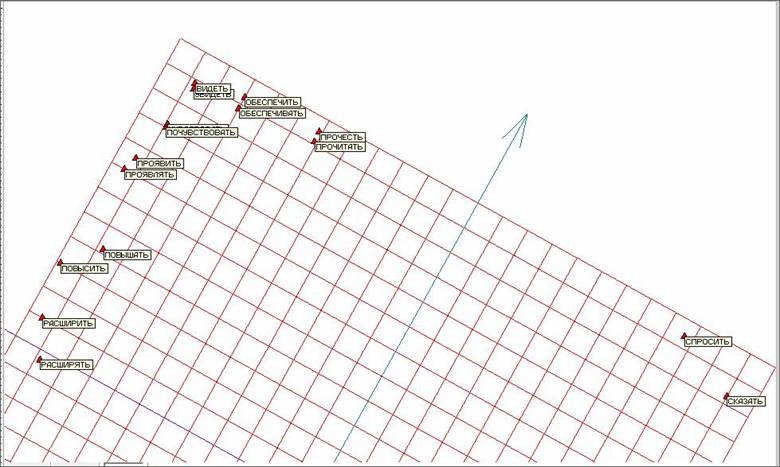
Рис. 15. Верхняя часть рисунка 14 с аннотациями.

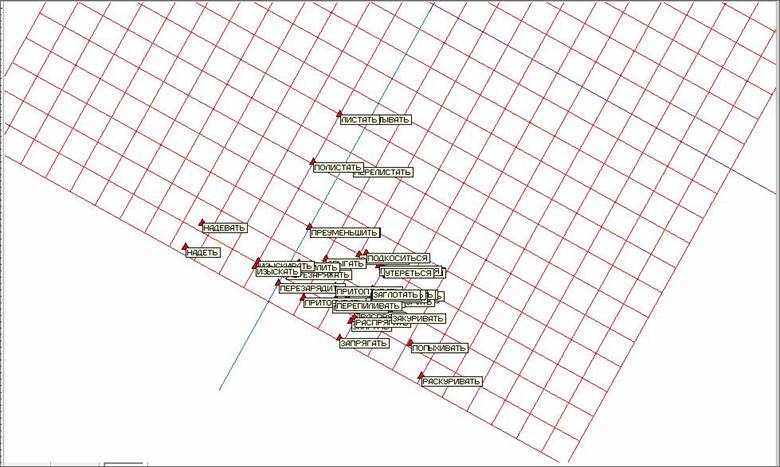
Рис. 16. Нижняя часть рисунка 14 с аннотациями.

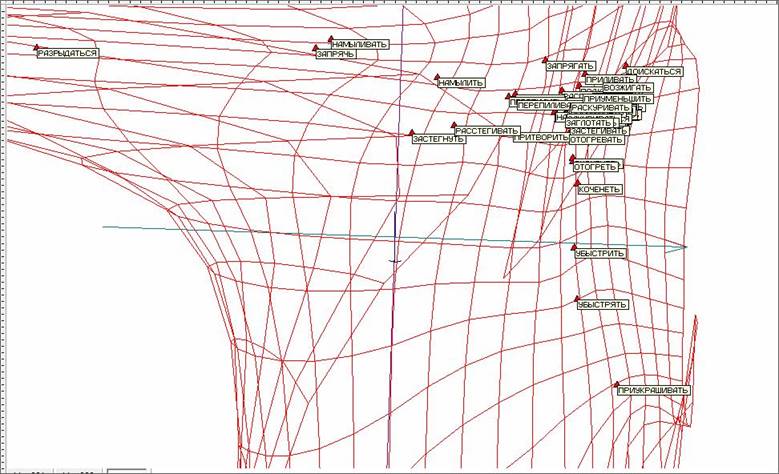
Рис. 17. Сетка упругой карты после первого применения подхода «квази-зум».

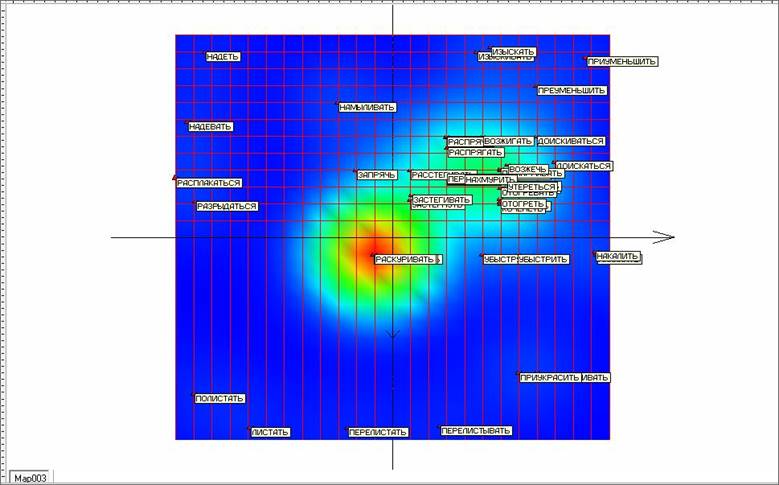
Рис. 18. Развертка упругой карты после первого применения подхода «квази-зум».

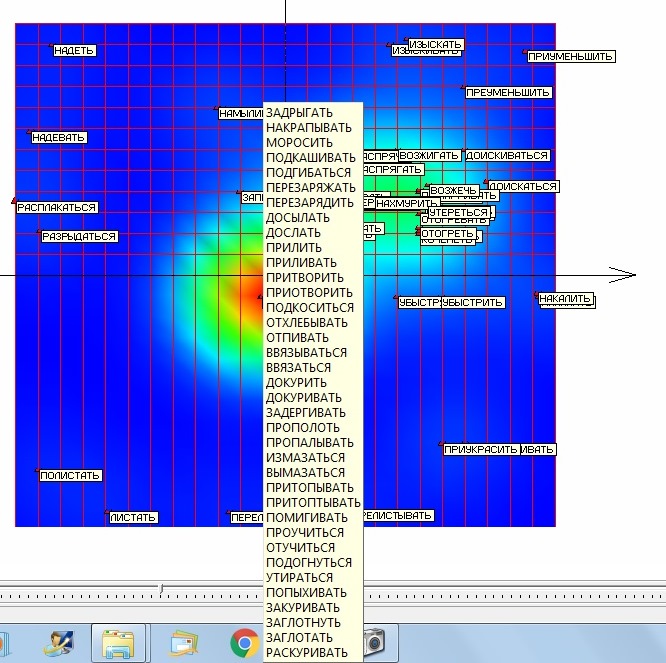
Рис. 19. Список «слипшихся глаголов в точке наивысшей плотности данных.

Для того, чтобы обеспечить разделение оставшихся 37 глаголов в точке наивысшей плотности данных, применим прием «квази-зум» еще раз. Снова вырезаются отделившиеся точки таким образом, чтобы в результирующем многомерном объеме данных остались только 37 «слипшихся точек».

Повторно проводим для получившегося нового многомерного объема данных из 37 точек построение максимально мягкой упругой карты из сетки с таким же количеством узлов, как и на предыдущем этапе. Результаты представлены на рисунке 20, где изображена развертка упругой карты с раскраской по плотности и списком «слипщихся» слов после вторичного применения приема «квази-зум». Большую часть точек удалось разделить, однако в зоне наивысшей плотности данных осталось еще 17 «слипшихся» точек.

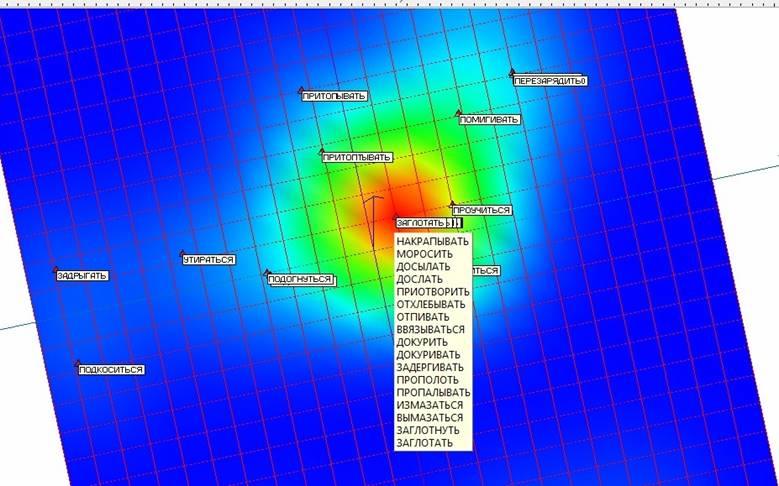
Рис. 20. Развертка упругой карты с раскраской по плотности и списком слипщихся» слов после вторичного применения приема «квази-зум».

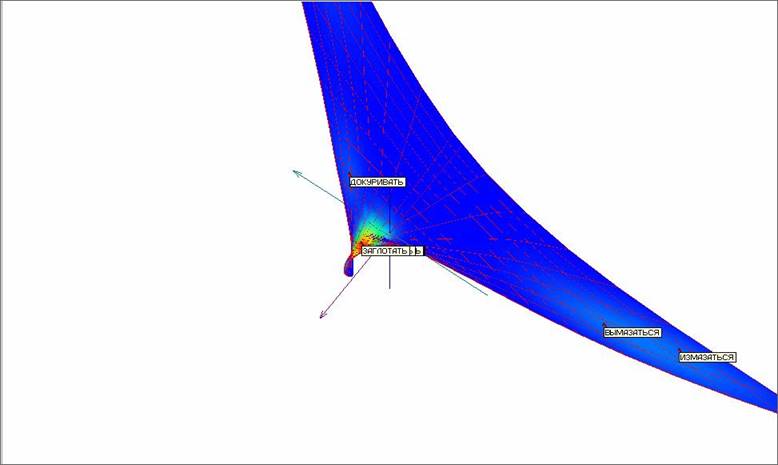
Рис. 21. Сетка упругой карты с раскраской по плотности после третьего применения процедуры «квази-зум».

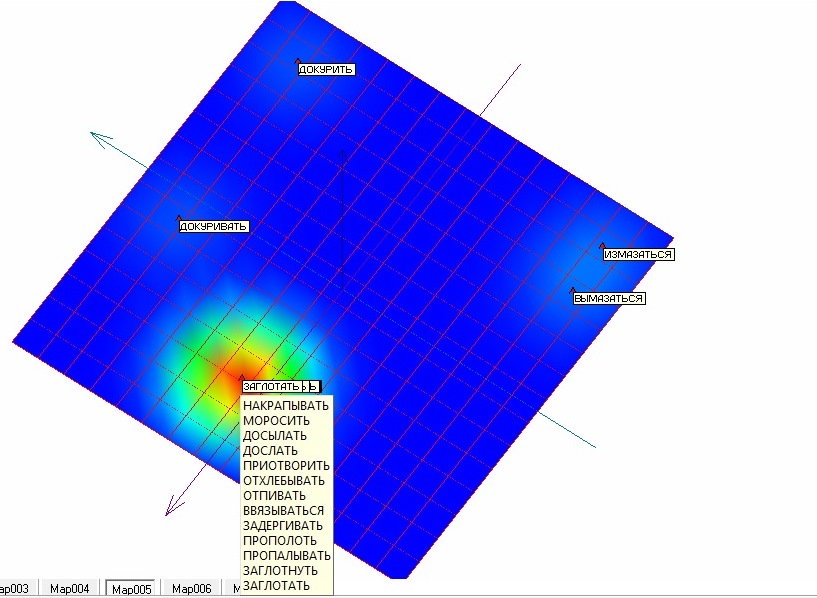
Рис. 22. Развертка упругой карты с раскраской по плотности после третьего применения процедуры «квази-зум».

Проводим процедуру «квази-зум» в третий раз для оставшихся 17 точек. Результаты представлены на рисунках 21 и 22 соответственно в виде упругой карты и ее развертки с раскраской по плотности. В результате третьего применения процедуры удалось отделить еще 4 точки. Непосредственный анализ частот встречаемости для оставшихся 13 точек показал, что все они имеют одинаковые координаты по всем измерениям равные нулю. Следовательно, их разделение невозможно в принципе.

Таким образом, процесс разделения точек в тестовом многомерном объеме данных с помощью построения упругих карт и применения процедуры «квази-зум» завершен полностью и успешно. Удалось разделить все точки многомерного объема данных, имеющие различные и отличающиеся от нуля координаты.

6. Визуальный анализ кластерных структур в тестовом многомерном объеме методом t-SNE

Аналогичная задача визуального анализа кластерных структур решалась с помощью применения метода t-SNE [10].

В связи с тем, что метод t-SNE изначально разрабатывался для наборов данных очень большой размерности, стандартная реализация метода на языке Python плохо работает с количеством точек меньше 200 в связи с резким увеличением значения перплексии, а найденные нестандартные не поддерживают заранее вычисленную косинусную меру сходства (речь о которой пойдет немного позднее). В связи с этим эксперименты с методом t-SNE проводились в два этапа. На первом этапе применялась реализация метода t-SNE с использованием метода Барнса-Хата, хорошо показавшая себя для малого числа точек. Расстояния измерялись в евклидовом пространстве.

Как видно из рис. 23, близкие по смыслу слова расположились близко друг от друга. Формы глаголов, отличающиеся совершенной и несовершенной степенью зачастую просто не различимы на рисунке без значительного увеличения масштаба. Между тем на рис. 24 показан центр распределения точек, в котором слова из одной смысловой группы находятся примерно на одинаковом расстоянии от слов из других групп.

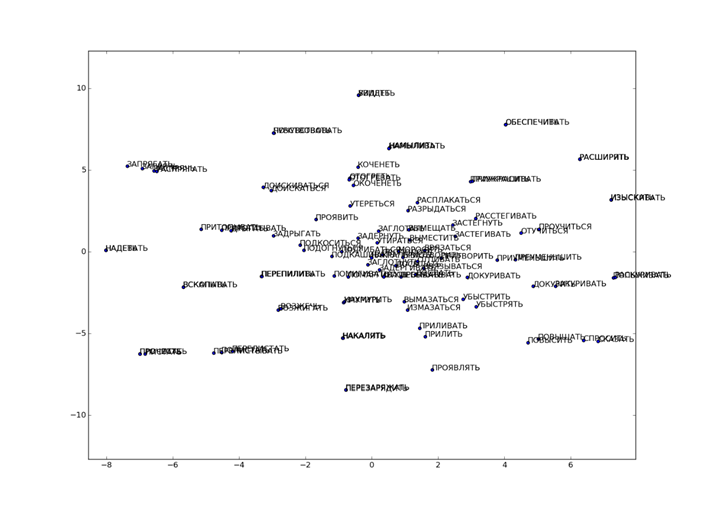
100points_bh_tsne

Рис. 23. Результаты применения t-SNE для выбранного набора данных.

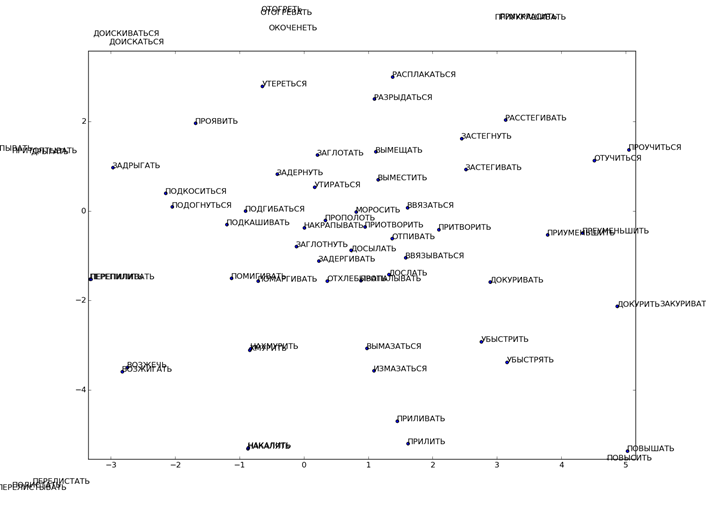
100points_bh_tsne_zoom

Рис. 24. Результаты применения t-SNE для выбранного набора данных (центральная часть).

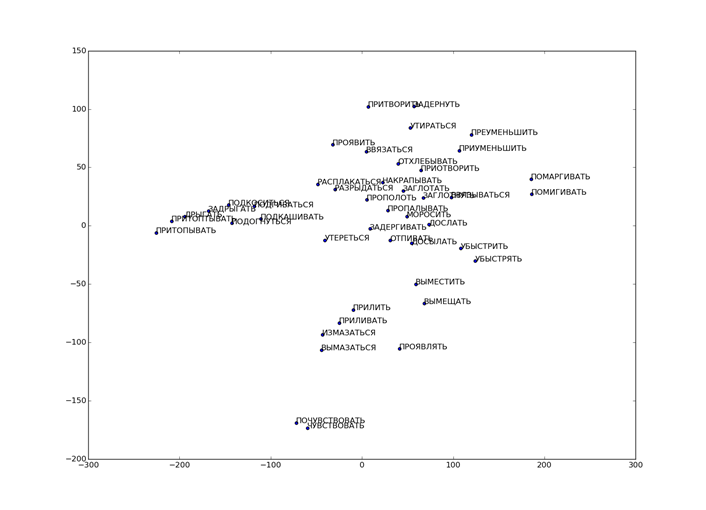
44points_bh_tsne

Рис. 25. Сокращенный набор данных, перплексия уменьшена до 10. На рисунке виден «рыхлый» кластер по центру, содержащий точки с одними и теми же координатами.

Мы также удалили часть слов, успешно объединенных методом и вынесенных на периферию. Одновременно значение перплексии было снижено с 30 до 5. Полученный результат показан на рис. 25. Как видно из рисунка, слова с одинаковыми координатами также сведены в одну группу, но при этом их координаты получились различными.

Обычно для обработки текстов на естественном языке используется косинусная мера сходства [13]. Но так как модифицированный вариант метода не имеет возможности рассчитывать ее или получать на вход, мы вынуждены были использовать модификацию из библиотеки sklearn, которая плохо работает с небольшими наборами данных. Для получения адекватных результатов были взяты 5000 пар глаголов (всего 4150 различных глаголов) для которых заранее были рассчитаны значения косинусной меры сходства (были взяты пары глаголов с максимальными значениями меры сходства). В итоге примерно 2000 глаголов были объединены в небольшие группы. Результаты кластеризации можно увидеть на рис. 26. Текстовые подписи к точкам убраны, так как при таком количестве объектов рисунок становится нечитаемым.

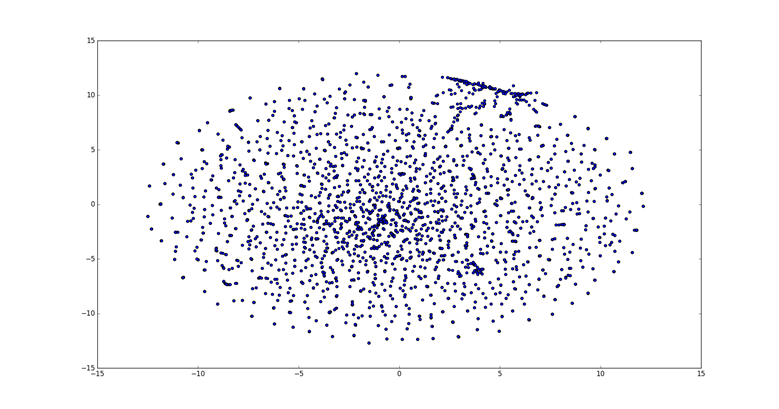
4150points_sk_tsne

Рис. 26. Результаты применения t-SNE для расширенного набора данных.

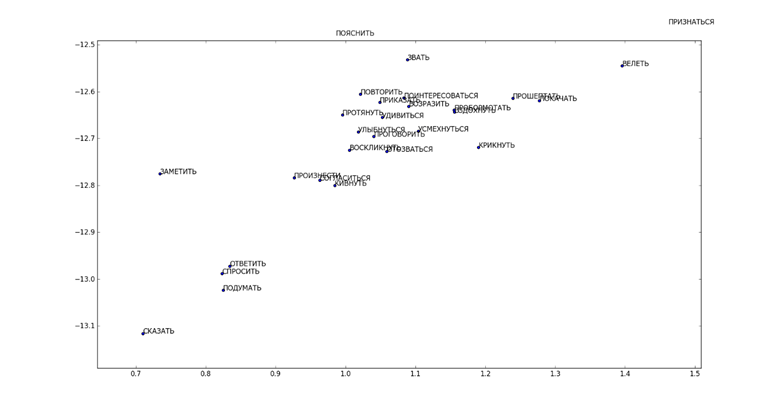
4150points_sk_tsne_zoom

Рис. 27. Результаты применения t-SNE для выбранного набора данных (фрагмент большого кластера в верхней части рис. 26).

Заметим, что качество объединения слов в группы падает, что является обычным явлением при увеличении числа слов. Пример одного из таких кластеров показан на рис. 27. При этом группы маленького размера продолжают сохранять точность объединения, но теряют полноту.

7. Заключение

Для анализа кластерных структур в многомерном объеме данных предлагается использовать технологии построения упругих карт, представляющие собой методы отображения точек исходного многомерного пространства на вложенные в это пространство многообразия меньшей размерности. Варьируя поверхность упругой карты за счет последовательного уменьшения коэффициентов упругости, можно добиться лучшего соответствия подстраивания карты под многомерное облако данных. После уменьшения коэффициентов изгиба и растянутости упругой карты, она становится более мягкой и гибкой, наиболее оптимальным образом подстраиваясь к точкам исходного многомерного объема данных. Применение технологий построения упругих карт для решения задач кластерного анализа не предполагает никакой априорной информации об изучаемых данных и не зависит от их природы, происхождения и т.п. Эти свойства позволяют применить технологии построения упругих карт для выявления кластерных структур при анализе текстовой информации. Схожими свойствами обладает близкий по идеологии вероятностный подход t-SNE.

Данная работа содержит описание результатов построения упругих карт и применения подхода t-SNE для визуального анализа кластерных структур в многомерных объемах текстовой информации. Для упругих карт подробно описан и проиллюстрирован прием «квази-зум», позволяющий существенно улучшить результаты. Для обоих подходов (построение упругих карт и t-SNE) показана их работоспособность и применимость для решения задач кластеризации терминов естественного языка.

Благодарности

Данная работа выполнена при поддержке грантов РФФИ (проекты 14-01-00769а и 16-01-00553а) в области научной визуализации и гранта РГНФ (проект 15-04-12019) в области обработки текстов на естественном языке.

Литература

1. Ким Дж., Мюллер Ч. и др. Факторный, дискриминантный и кластерный анализ. М.: Финансы и статистика, 1989. 216 с.

2. Kohonen T. Self-Organizing Maps. Springer: Berlin. Heidelberg. 1997.

3. Gorban A., Kegl B., Wunsch D., Zinovyev A. (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin. Heidelberg – New York, 2007.

4. Gorban A.N., Zinovyev A. Principal manifolds and graphs in practice: from molecular biology to dynamical systems International Journal of Neural Systems, Vol. 20, No. 3 (2010). Pp. 219–232.

5. Зиновьев А.Ю. Визуализация многомерных данных. Красноярск, Изд. КГТУ. 2000. 180 с.

6. Питенко А.А. Нейросетевой анализ в геоинформационных системах. Красноярск, Изд. КГТУ, 2000. 97 с.

7. Bondarev A.E., Galaktionov V.A., Chechetkin V.M. Analysis of the Development Concepts and Methods of Visual Data Representation in Computational Physics. Computational Mathematics and Mathematical Physics. 2011. Vol. 51. No. 4. pp. 624–636.

8. Bondarev A.E, Galaktionov V.A. Parametric Optimizing Analysis of Unsteady Structures and Visualization of Multidimensional Data. International Journal of Modeling, Simulation and Scientific Computing. 2013. Vol. 04. No. supp01. 13 p. DOI 10.1142/S1793962313410043.

9. Бондарев А.Е., Галактионов В.А. Построение методов визуального анализа кластерных структур в многомерных объемах данных. Научная визуализация. 2015. т.7. № 5. с. 87-101.

10. Van der Maaten L.J.P.; Hinton G.E. Visualizing High-Dimensional Data Using t-SNE. Journal of Machine Learning Research 9 (Nov 2008). Pp. 2579–2605

11. Hinton G.E., Roweis S.T. Stochastic Neighbor Embedding. In Advances in Neural Information. Processing Systems. Vol. 15. Pp. 833–840, Cambridge, MA, USA, 2002. The MIT Press.

12. Клышинский Э.С., Кочеткова Н.А. Метод автоматической генерации модели управления глаголов русского языка. Сб. трудов 12 национальной конференции по искусственному интеллекту КИИ-2012 (Белгород, 16-20 сентября 2012 г). том 1. Белгород: изд-во БГТУ, 2012. сс.227-235

13. Manning D. Automatic Acquisition of a Large Subcategorization Dictionary from Corpora. Proc. of the 31st Meeting of ACL. pp. 235–242.

14. Harris Z. Distributional structure. Word 1954. Vol. 10. No. (23). pp. 146–162.

VISUAL ANALYSIS OF CLUSTERS FOR A MULTIDIMENSIONAL TEXTUAL DATASET

A.E. Bondarev¹, A.V. Bondarenko², V.A. Galaktionov¹, E.S. Klyshinsky^{1, 3}

¹Keldysh Institute of Applied Mathematics RAS, Moscow, Russian Federation

²GOSNIIAS, Moscow, Russian Federation

³National Research University Higher School of Economics, Moscow, Russian Federation

bond@keldysh.ru; vlgal@gin.keldysh.ru; klyshinsky@mail.ru

Abstract

The paper considers the problems of visual analysis of clusters for multidimensional textual datasets. To analyze clusters in original data volume the elastic maps are used as the methods of original data points mapping to enclosed manifolds having less dimensionality. Diminishing the elasticity parameters one can design map surface which approximates the multidimensional textual dataset in question much better. This approach of elastic maps does not require any apriori information about data in question and does not depend on data nature, data origin, etc. Probabilistic algorithm t-SNE (t-distributed stochastic neighbor embedding) has similar properties and is quite close in ideology to elastic maps. The paper describes the results of both (elastic maps and t-SNE) approaches application to visual analysis of clusters in multidimensional textual datasets. For elastic maps a technology «Quasi-Zoom» is proposed. This technology allows to improve the results of cluster analysis in the fields of data points concentration. Presented results illustrate an efficiency and applicability of both approaches to cluster analysis of natural language terms.

Keywords: multidimensional data, visual analysis, elastic maps, distributional semantics, cluster structures.

References

1. Kim J., Mjuller Ch. and others. Faktornyj, diskriminantnyj i klasternyj analiz [Factor, discriminant and cluster analysis]. Moscow: Finance and statistics. 1989. 216 p. [In Russian]

2. Kohonen T. Self-Organizing Maps. Springer: Berlin. Heidelberg. 1997.

3. Gorban A., Kegl B., Wunsch D., Zinovyev A. (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin. Heidelberg – New York, 2007.

4. Gorban A.N., Zinovyev A. Principal manifolds and graphs in practice: from molecular biology to dynamical systems International Journal of Neural Systems, Vol. 20, No. 3 (2010). Pp. 219–232.

5. Zinov'ev A.Ju. Vizualizacija mnogomernyh dannyh [Visualization of multidimensional data]. Krasnoyarsk, publ. NGTU. 2000. 180 p. [In Russian]

6. Pitenko A.A. Nejrosetevoj analiz v geoinformacionnyh sistemah [Neural network analysis in information systems]. Krasnoyarsk, publ. NGTU. 2000. 97 p. [In Russian]

9. Bondarev A.E., Galaktionov V.A. Methods design for visual analysis of clusters in multidimensional data volumes. Scientific visualization. 2015. Vol.7. No. 5. pp. 87-101. [In Russian]

10. Van der Maaten L.J.P.; Hinton G.E. Visualizing High-Dimensional Data Using t-SNE. Journal of Machine Learning Research 9 (Nov 2008). Pp. 2579–2605

11. Hinton G.E., Roweis S.T. Stochastic Neighbor Embedding. In Advances in Neural Information. Processing Systems. Vol. 15. Pp. 833–840, Cambridge, MA, USA, 2002. The MIT Press.

12. Klyshinskij Je.S., Kochetkova N.A. Metod avtomaticheskoj generacii modeli upravlenija glagolov russkogo jazyka [Method of automatic generation control model of Russian verbs]. Coll. works 12 of a national conference on Artificial Intelligence KII 2012 (Belgorod, 16-20 September 2012). Volume 1. Belgorod: publ BSTU, 2012. pp. 227-235. [In Russian]

13. Manning D. Automatic Acquisition of a Large Subcategorization Dictionary from Corpora. Proc. of the 31st Meeting of ACL. pp. 235–242.

14. Harris Z. Distributional structure. Word 1954. Vol. 10. No. (23). pp. 146–162.