ВИЗУАЛИЗАЦИЯ УСТОЙЧИВОСТИ И РАСЧЕТА ФОРМЫ РАВНОВЕСНОЙ КАПИЛЛЯРНОЙ ПОВЕРХНОСТИ
А.А. Клячин, В.А. Клячин, Е.Г. Григорьева
klyachin-aa@yandex.ru, klchnv@mail.ru, e_grigoreva@mail.ru
Волгоградский государственный университет, Волгоград, Россия
Содержание
2. Алгоритм расчета равновесной капиллярной поверхности
3. Расчет поверхности, минимизирующей функционал типа площади
4. Устойчивость минимальных поверхностей.
Аннотация
Статья посвящена 3D моделированию равновесных капиллярных поверхностей и визуализации различных эффектов, связанных с их устойчивостью или неустойчивостью. Математически построение такой поверхности сводится к нахождению решения некоторого нелинейного уравнения с частными производными, удовлетворяющего определенному краевому условию (на границе задается угол контакта между жидкостью и смачиваемой твердой стенкой капиллярной трубки). Вопросы существования и единственности решения этой задачи достаточно подробно отражены, например, в книге Роберта Финна «Равновесные капиллярные поверхности. Математическая теория» (см., также приведенную там литературу). Для поиска приближенных решений мы используем вариационный метод конечных элементов, в котором в качестве базисных функций выбираются кусочно-линейные функции, заданные над триангуляцией расчетной области. Такой подход был использован нами при расчете форм поверхностей минимальной площади.
Нами получены следующие результаты
· Для указанного выше метода расчёта разработаны несколько программных процедур, позволяющих получать результаты расчёта в удобной для последующей обработки форме.
· Проведены тестовые расчеты для некоторых форм сечений капиллярных трубок: шестиугольника, восьмиугольника, квадрата. Смоделировано неустойчивое поведение капиллярной поверхности у граничной точки с достаточно малым углом между гранями капиллярной трубки, а также при критическом значении угла контакта. Приближенно также была вычислена высота поднятия жидкости, которая оказалась достаточно близкой с тем значениям, которое получается при вычислении по известным физическим формул. Это, в определенном смысле, подтверждает правильность используемого метода расчета.
· Получены формулы для производных функционалов типа площади кусочно-линейных аппроксимаций поверхностей произвольной топологии. Эти формулы необходимы для программной реализации процесса итераций градиентного спуска.
· Реализована система классов для конструирования приближенных решений вариационных задач типа капиллярных поверхностей. Кроме этого, данная система классов позволяет проводить численное исследование устойчивости экстремальных поверхностей для функционалов типа функционала площади.
Ключевые слова: поверхность минимальной площади, триангуляция, кусочно-линейная поверхность, аппроксимация функционала энергии, 3D моделирование
1. Введение
Статья посвящена 3D моделированию равновесных капиллярных поверхностей и визуализации различных эффектов, связанных с их устойчивостью или неустойчивостью. Математически построение такой поверхности сводится к нахождению решения некоторого нелинейного уравнения с частными производными, удовлетворяющего определенному краевому условию (на границе задается угол контакта между жидкостью и смачиваемой твердой стенкой капиллярной трубки). Вопросы существования и единственности решения этой задачи достаточно подробно отражены, например, в книге [1] (см., также приведенную там литературу). Для поиска приближенных решений мы используем вариационный метод конечных элементов, в котором в качестве базисных функций выбираются кусочно-линейные функции, заданные над триангуляцией расчетной области. Такой подход был использован нами при расчете форм поверхностей минимальной площади в работе [2], а обоснование этого метода для уравнения минимальной поверхности было дано в работе [3].
Визуализация и просмотр полученных поверхностей является следующим этапом геометрического моделирования. Визуализация подобного рода поверхностей, особенно с возможностью 3D обзора, позволяет провести качественный и количественный анализ построенных моделей, увидеть распределение физических и геометрических характеристик и величин вдоль рассматриваемой поверхности, произвести корректировку граничных, начальных и других исходных данных задачи на основе такого анализа.
В этом направлении нами получены следующие результаты
- Для указанного выше метода расчёта разработаны несколько программных процедур, позволяющих получать результаты расчёта в удобной для последующей обработки форме. Основной вычислительный модуль использует градиентный метод для минимизации интеграла энергии. Причем, нами реализована такая схема взаимодействия всех программных модулей, которая сводит к минимуму вносимые в эти программы изменения при переходе к различным энергетическим функционалам (в том числе интегралу энергии поверхностного натяжения жидкости), краевым условиям, триангуляциям и т. д. Этим мы достигаем универсальности разработанной системы программ.
- Проведены тестовые расчеты для некоторых форм сечений капиллярных трубок: шестиугольника, восьмиугольника, квадрата. Смоделировано неустойчивое поведение капиллярной поверхности у граничной точки с достаточно малым углом между гранями капиллярной трубки, а также при критическом значении угла контакта. Подтверждено, теоретически предсказанное в работе [1], такое поведение капиллярной поверхности при условии, что сумма угла контакта и угла между гранями меньше π. Визуально эта неустойчивость вблизи угловых граничных точках видна на представленных в работе рисунках. Помимо этого, случая, были проведены расчеты для сечений, которые имеют малый размер в каком-то одном направлении. Например, для прямоугольника, имеющего одну сторону фиксированной длины, а другую — достаточно малую. Приближенно также была вычислена высота поднятия жидкости, которая оказалась достаточно близкой с тем значениям, которое получается при вычислении по известным физическим формулам. Это, в определенном смысле, подтверждает правильность используемого метода расчета.
- Получены формулы для производных функционалов типа площади кусочно-линейных аппроксимаций поверхностей произвольной топологии. Эти формулы необходимы для программной реализации процесса итераций градиентного спуска.
- Реализована система классов для конструирования приближенных решений вариационных задач типа капиллярных поверхностей. Кроме этого, данная система классов позволяет проводить численное исследование устойчивости экстремальных поверхностей для функционалов типа функционала площади.
2. Алгоритм расчета равновесной капиллярной поверхности
Определение формы капиллярной поверхности в пространстве с
декартовыми координатами ![]() сводится
к решению нелинейного дифференциального уравнения
сводится
к решению нелинейного дифференциального уравнения
с краевыми условиями вида
![]()
где Ω – область с кусочно-гладкой
границей на плоскости и ![]() – угол контакта между поверхностью
жидкости и стенкой капиллярной трубки. Известно, что решение
– угол контакта между поверхностью
жидкости и стенкой капиллярной трубки. Известно, что решение ![]() описывает капиллярную
поверхность, находящуюся в равновесии, над областью Ω с заданным углом
контакта
описывает капиллярную
поверхность, находящуюся в равновесии, над областью Ω с заданным углом
контакта ![]() между этой поверхностью и стенкой
капиллярной трубки. Исследованию различных вопросов разрешимости данной краевой
задачи посвящено множество работ. Достаточно подробно изложены многие
результаты исследования вопроса существования, единственности и устойчивости в
монографии [1]. Известно, что данная краевая задача эквивалентна
нахождению гладкой функции
между этой поверхностью и стенкой
капиллярной трубки. Исследованию различных вопросов разрешимости данной краевой
задачи посвящено множество работ. Достаточно подробно изложены многие
результаты исследования вопроса существования, единственности и устойчивости в
монографии [1]. Известно, что данная краевая задача эквивалентна
нахождению гладкой функции ![]() , на которой достигает своего минимума
функционал энергии
, на которой достигает своего минимума
функционал энергии
![]()
За редким исключением найти точное решение данной краевой задачи невозможно. В этом случае прибегают к применению численных методов, что приводит к задаче разработки эффективных алгоритмов приближенного решения.
В своей работе мы используем следующий подход,
предусматривающий построение приближенных решений в виде кусочно-линейных
функций, заданных над произвольной областью и использующий триангуляцию этой
области. Под триангуляцией мы понимаем следующую конструкцию. Пусть задан
конечный набор точек ![]() на
плоскости. Триангуляцией набора точек называется совокупность треугольников
на
плоскости. Триангуляцией набора точек называется совокупность треугольников ![]() удовлетворяющих
условиям
удовлетворяющих
условиям
- любая точка
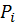 является
вершиной хотя бы одного треугольника;
является
вершиной хотя бы одного треугольника; - каждый треугольник содержит только три точки из данного набора, являющиеся вершинами этого треугольника.
Пусть Ω ограниченная плоская область. Триангуляцией
области Ω называется триангуляция произвольного конечного набора
точек, лежащего в замыкании области ![]() . Для
произвольного набора числовых значений
. Для
произвольного набора числовых значений ![]() определим
кусочно-линейную функцию
определим
кусочно-линейную функцию ![]() следующим образом. Построим функцию
следующим образом. Построим функцию ![]() на объединении всех треугольников
на объединении всех треугольников
![]() так,
что
так,
что ![]() и
функция
и
функция ![]() на
каждом треугольнике
на
каждом треугольнике ![]() .
Данная функция будет непрерывной и в каждом треугольнике определены её
частные производные
.
Данная функция будет непрерывной и в каждом треугольнике определены её
частные производные ![]() .
Поэтому значение функционала энергии функции
.
Поэтому значение функционала энергии функции ![]() вычисляется суммой
вычисляется суммой

Отметим, что график кусочно-линейной функции представляет собой набор треугольников в пространстве, примыкающих друг к другу по своим сторонам. На рисунках 1 и 2 приведены изображения графиков таких функций:

Рис. 1. Пример графика кусочно-линейной функции

Рис. 2. Пример кусочно-линейной поверхности
Для решения задачи (1)-(2) вариационным методом нами разработана основная процедура минимизации minimum_func_mix() и несколько вспомогательных, нужных для подготовки расчетов. Кратко опишем их работу. Отметим вначале, что точки и треугольники используемой триангуляции, а также значения граничной функции и результаты вычислений хранятся в четырех отдельных двоичных файлах. Структура этих файлов простая. Например, точки записаны в файле points.pnt, в котором первые 8 байт отводятся под количество этих точек, а дальше каждая точка занимает 20 байт - две координаты, соответствующие типу double и информация о принадлежности границе и типе граничного условия (int). Триангуляция этих точек хранится в другом файле triangles.trg, который имеет следующую структуру: вначале 8 байт отводится под общее число треугольников, затем идут номера точек, составляющих описываемый треугольник. Любые кусочно-линейные функции хранятся в файлах типа *.val, в которых записаны значения функции в узлах триангуляции. Одна из вспомогательных процедур формирует структуру, в который для каждого узла триангуляции заносится набор треугольников, содержащих эту точку в качестве вершины. Основная процедура minimum_func_mix() выполняет один шаг итерации минимизации функционала. Её входными аргументами являются два указателя на массивы исходных значений функции и пересчитанных значений, указатель на массив значений граничной функции, задающей нормальную производную функции, указатели на массивы вершин триангуляции, ее треугольников и указатель на структуру, содержащую информацию о примыкающих треугольниках.
Отметим, что были разработаны и вспомогательные классы SQAllPoints и SQAllTreug, в которых, в частности, имеются методы чтения из указанных выше файлов соответствующих данных (read_point() и read_treug()): по номеру вершины читаются ее координаты, по номеру треугольника читаются номера точек — вершин данного треугольника.
Класс SQIntegrand является базовым для задания минимизируемого функционала. Данный класс имеет виртуальные методы IntG(), Gu(), GradG(), которые в его производных классах содержат реализацию вычисления интегранда (подынтегральной функции) и его производных по функции и ее градиенту. Например, если требуется минимизировать указанный выше интеграл энергии, то создается класс, к примеру SQSurfCapillar, являющийся потомком класса SQIntegrand, с соответствующими методами:
double IntG(SQPoint point,SQPoint vect, double u)
{
double value;
value=sqrt(1+vect.x*vect.x+vect.y*vect.y)+(k/2)*u*u;
return value;
}
double Gu(SQPoint point,SQPoint vect, double u)
{
return k*u;
}
SQPoint gradG(SQPoint point, SQPoint vect, double u)
{
SQPoint grd(0.0,0.0);
grd.x=vect.x/sqrt(1+vect.x*vect.x+vect.y*vect.y);
grd.y=vect.y/sqrt(1+vect.x*vect.x+vect.y*vect.y);
return grd;
}
В случае, если необходимо будет рассчитывать поверхность,
которая минимизирует другой функционал, достаточно будет для него написать
похожий производный класс. При этом никаких исправлений в вычислительном
модуле, реализованном в классе SQComputer, вносить не нужно. Нами была
проверена данная возможность на примере интеграла Дирихле (класс SQDirich) и
расчета поверхностей, минимизирующих площадь поверхности при фиксированном
перекрываемом объеме (класс SQSurfArea). Третий интеграл в формуле (3) при
минимизации учитывается в функции minimum_func_mix(), так как его вид не
зависит от интегранда, а зависит только от контактного угла ![]() . Вообще
говоря, в правой части краевого условия (2) может находится и
функция граничной точки. Поэтому к вычислительному модулю подключается и файл
типа *.val, содержащий значения граничной функции в узлах триангуляции.
. Вообще
говоря, в правой части краевого условия (2) может находится и
функция граничной точки. Поэтому к вычислительному модулю подключается и файл
типа *.val, содержащий значения граничной функции в узлах триангуляции.
Результаты вычислений записываются в файл типа *.val. Отметим также, что в функции minimum_func_mix() реализована возможность задания как краевых условий Дирихле, т. е. значений искомого решения на границе области, так и смешанных краевых условий, содержащих условия на производные этого решения.
Нами написана также процедура окончательной обработки результатов вычисления, которая преобразует их в два типа файлов. Один из них текстовый файл типа *.tgs, каждая строка которого хранит трехмерные координаты одной точки модели. Три подряд идущие строки задают один треугольник в триангуляции поверхности. Другой файл является файлом стандартного формата 3D графики stl для хранения такой поверхности.
Для построения поверхностей и их изображения мы сохранили результаты вычислений в текстовом файле формата stl и воспользовались для просмотра программой Blender 2.74. Ниже приводим изображения некоторых из построенных поверхностей.

Рис. 3. Подъем жидкости в капиллярной трубке квадратного сечения со стороной 1 мм, 2 мм и 5 мм.

Рис. 4. Подъем жидкости в капиллярной трубке шестиугольного сечения с диаметром 1 мм, 2 мм и 5 мм.

Рис. 5. Подъем жидкости в капиллярной трубке восьмиугольного сечения со стороной 0,41 мм, 0,83 мм и 2,07 мм.
Дадим пояснения к приведенным рисункам. Рисунок 3 содержит
изображения свободной поверхности жидкости в капиллярной трубке, имеющей квадратное
сечение со стороной 5, 2 и 1 мм. На рисунках 4 и 5 показаны результаты расчета
для случая шестиугольного и восьмиугольного сечений трубки для различных
диаметров. Выбор такой формы сечения продиктован двумя обстоятельствами.
Во-первых, нас интересовал в первую очередь случай, когда область Ω имеет
негладкую границу, имеющую угловые точки, так как именно в этом случае мы можем
визуально представить неустойчивое поведение поверхности жидкости. Причем
раствор этих углов с внутренней стороны области должен иметь значение меньше
чем π. Во-вторых, мы остановились на симметричных сечениях, чтобы
была возможность оценить степень погрешности вычислений. Так как в случае
правильных многоугольников для такой оценки можно воспользоваться, к примеру,
асимптотической формулой вычисления подъема жидкости ![]() вдоль
оси симметрии капиллярной трубки (см. [1])
вдоль
оси симметрии капиллярной трубки (см. [1])
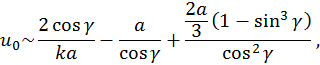
Где ![]() – радиус капиллярной трубки. Хотя нами и
доказана равномерная сходимость приближенных решений в работе [4], мы в
настоящей статье попытались визуально проиллюстрировать данный факт. При этом
взят такой угол контакта, при котором выполняются условия существования точного
решения (см. [1]). Стоит отметить, что результаты вычисления достаточно хорошо
согласуются с известными формулами вычисления высоты жидкости в капиллярной
трубке. Отличие составило около 2-5%.
– радиус капиллярной трубки. Хотя нами и
доказана равномерная сходимость приближенных решений в работе [4], мы в
настоящей статье попытались визуально проиллюстрировать данный факт. При этом
взят такой угол контакта, при котором выполняются условия существования точного
решения (см. [1]). Стоит отметить, что результаты вычисления достаточно хорошо
согласуются с известными формулами вычисления высоты жидкости в капиллярной
трубке. Отличие составило около 2-5%.
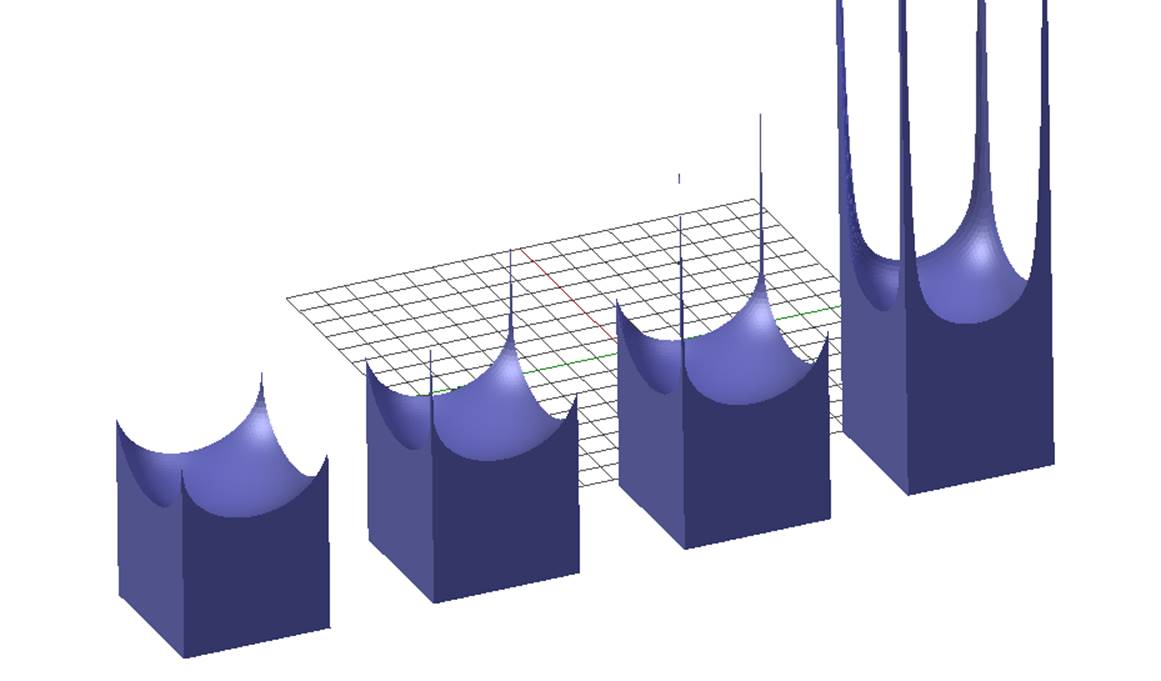
Рис. 6. Неустойчивое поведение жидкости при критическом значении угла контакта.
На рисунке 6 для квадратного сечения были проведены расчеты
в случае, когда угол контакта постепенно приближался к критическому значению, при
котором решение задачи (1)-(2) не существует. Для квадратного сечения таким
углом является угол ![]() . На
этом рисунке видно неустойчивое поведение поверхности жидкости около угловых
граничных точек: имеется резкий скачок, что соответствует теоретически
предсказанной ситуации в работе [1], в которой показано, что решение уравнения (1)
стремится в бесконечность в окрестности такой граничной точки.
. На
этом рисунке видно неустойчивое поведение поверхности жидкости около угловых
граничных точек: имеется резкий скачок, что соответствует теоретически
предсказанной ситуации в работе [1], в которой показано, что решение уравнения (1)
стремится в бесконечность в окрестности такой граничной точки.
Исходя из сказанного выше, можно сделать вывод о том, что разработанные программы позволяют
а) достаточно точно проводить вычисления формы поверхностей, на которых достигает своего минимума некоторый интеграл (площадь поверхности, энергия поверхностного натяжения, интеграл Дирихле и т. д.),
б) путем несложных и вполне естественных добавлений в код вспомогательных подпрограмм выполнять переход к различным минимизируемым функционалам.
3. Расчет поверхности, минимизирующей функционал типа площади
Частным случаем капиллярных поверхностей является класс
поверхностей, минимизирующих функционал площади -- класс минимальных
поверхностей. Для моделирования таких поверхностей произвольной топологии мы
обратимся к более общему случаю. Именно, пусть ![]() —
положительная однородная степени 1, выпуклая функция такая, что
—
положительная однородная степени 1, выпуклая функция такая, что ![]()
Для гладкой поверхности ![]() рассмотрим
величину
рассмотрим
величину
![]()
где ξ — вектор единичной нормали к поверхности M. Если M — кусочно-линейная аппроксимация поверхности M, то приближенное значение введенного функционала будет вычисляться согласно формуле
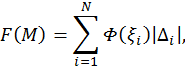
где M представляет собой объединение треугольников ![]() ,
, ![]() —
нормаль к плоскости этих треугольников, а
—
нормаль к плоскости этих треугольников, а ![]() —
площади треугольников. Поверхность M можно рассматривать как точку в
пространстве LM размерности 3n, где n -- число вершин на M.
Если задать в каждой точке-вершине поверхности вектор h, то этим
векторам будет соответствовать вектор в LM. Тогда оказывается, если
функционал F рассмотреть, как числовую функцию
—
площади треугольников. Поверхность M можно рассматривать как точку в
пространстве LM размерности 3n, где n -- число вершин на M.
Если задать в каждой точке-вершине поверхности вектор h, то этим
векторам будет соответствовать вектор в LM. Тогда оказывается, если
функционал F рассмотреть, как числовую функцию ![]() , то
имеет место формула
, то
имеет место формула
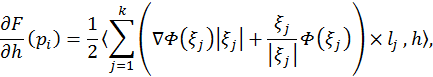
где сумма идет по всем треугольникам, имеющим вершину ![]() обозначает
нормаль к соответствующему треугольнику и
обозначает
нормаль к соответствующему треугольнику и ![]() вектор,
соединяющий вершины треугольника, не совпадающие с
вектор,
соединяющий вершины треугольника, не совпадающие с ![]() таким
образом, что эта вершина остается слева. Теоретическое обоснование
кусочно-линейной аппроксимации исследовалось, в частности, в работах [5]-[7].
таким
образом, что эта вершина остается слева. Теоретическое обоснование
кусочно-линейной аппроксимации исследовалось, в частности, в работах [5]-[7].
Пример 1. Рассмотрим случай ![]() . Тогда,
как нетрудно посчитать, получим
. Тогда,
как нетрудно посчитать, получим
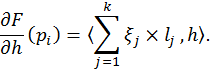
Если предположить, что поверхность M минимизирует
функционал ![]() , то
, то
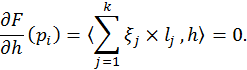
для любой вершины ![]() . Это
условие минимальности площади кусочно-линейной поверхности.
. Это
условие минимальности площади кусочно-линейной поверхности.
Для минимизации функционалов рассматриваемого вида применим
метод градиентного спуска. Рассмотрим некоторую кусочно-линейную поверхность ![]() .
Метод градиентного спуска предполагает на каждом шаге итерации получение
очередной поверхности
.
Метод градиентного спуска предполагает на каждом шаге итерации получение
очередной поверхности ![]() согласно
формуле
согласно
формуле
![]()
где равенство рассматривается как векторное соотношение в
пространстве LM, а числа ![]() будем
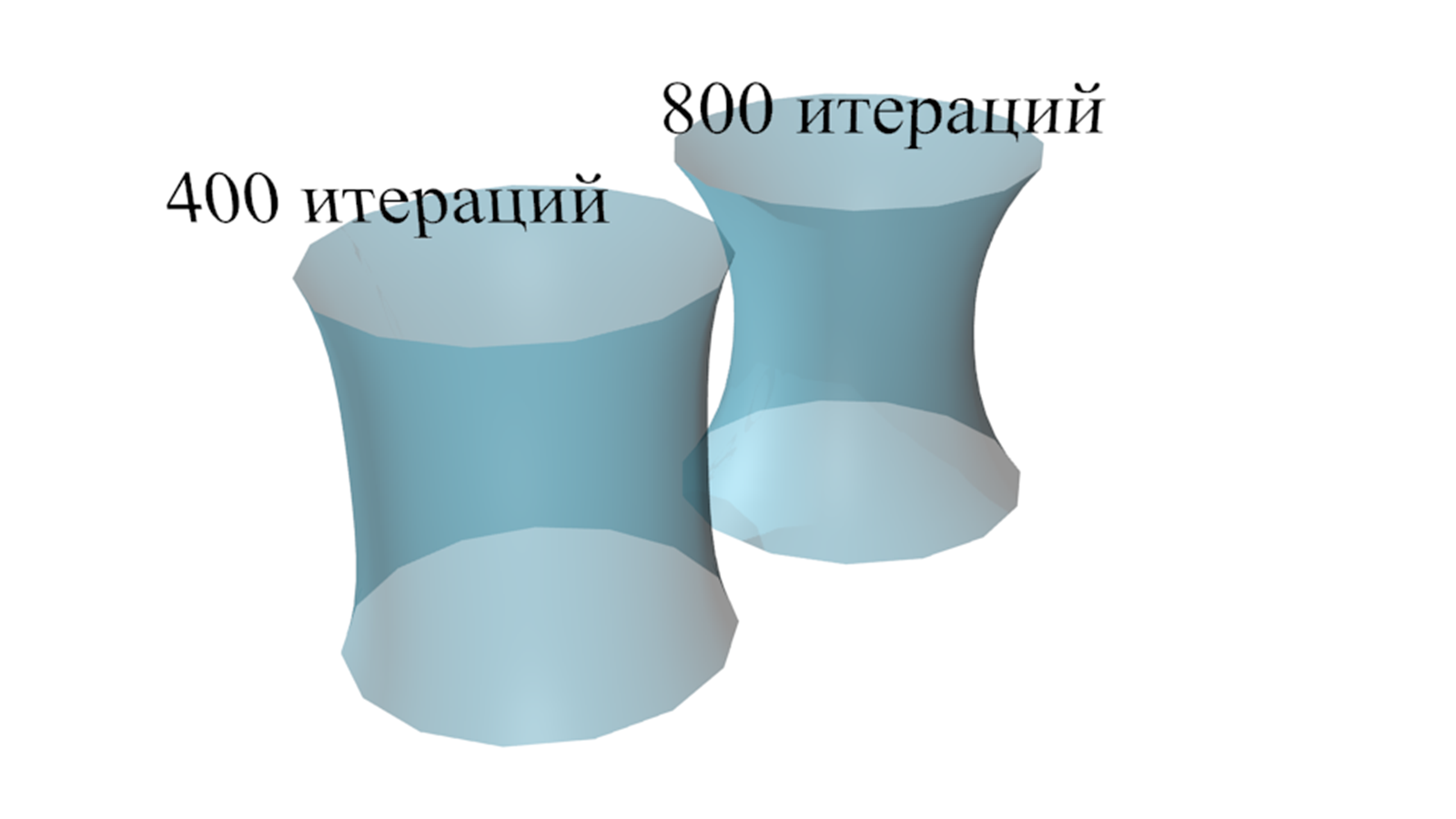
определять экспериментально. Ниже приведены результаты расчета поверхности
катеноида (минимальная поверхность вращения) для случая 400 и 800 итераций. В
обоих случаях
будем
определять экспериментально. Ниже приведены результаты расчета поверхности
катеноида (минимальная поверхность вращения) для случая 400 и 800 итераций. В
обоих случаях ![]() выбирается
равным 0,005. Вычисленная погрешность: в первом случае — 0,06, во втором случае
— 0,02.
выбирается
равным 0,005. Вычисленная погрешность: в первом случае — 0,06, во втором случае
— 0,02.
4. Устойчивость минимальных поверхностей.
Капиллярные поверхности представляют собой поверхности раздела различных сред, находящихся в равновесии. Физические аспекты устойчивости и неустойчивости равновесных поверхностей рассмотрены в книге [8]. С математической точки зрения устойчивость равновесной поверхности связана со значением величины вида
![]()
Где ![]() —
норма второй фундаментальной формы поверхности, а точная нижняя грань берется
по всем функциям
—
норма второй фундаментальной формы поверхности, а точная нижняя грань берется
по всем функциям ![]() ,
таким, что h=0 на границе поверхности M и с нулевым интегралом по
поверхности (следствие несжимаемости жидкой среды.)
,
таким, что h=0 на границе поверхности M и с нулевым интегралом по
поверхности (следствие несжимаемости жидкой среды.)
Для случая минимальных поверхностей объем занимаемый жидкостью считается равным нулю и последнее условие не требуется. Поверхность будет устойчивой, если только указанная выше величина больше 1.
В настоящей статье предлагается метод численного исследования
устойчивости равновесных поверхностей в ![]() ,
основанный на использовании пакета NumPy в виде расширения языка
программирования Python.
,
основанный на использовании пакета NumPy в виде расширения языка
программирования Python.
Пакет NumPy представляет собой расширение языка программирования Python, реализующее множество различных операций при работе с многомерными массивами данных. Несмотря на то, что этот пакет предназначен для использования его в контексте интерпретируемого языка, тем не менее массивы NumPy являются Си-подобными [9]. Так, что эти массивы могут управляться стандартными инструкциями языка Python. Удобство использования массивов NumPy, в частности, состоит в том, что для этих массивов перегружены арифметические операции и математические функции.
В настоящей статье мы покажем использование пакета для решения задачи численного анализа устойчивости экстремальных поверхностей. В качестве примера рассмотрим специальный класс минимальных поверхностей, имеющих параметрическое представление Эннепера – Вейерштрасса.
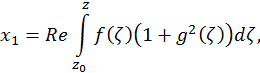
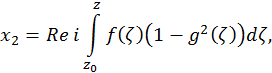
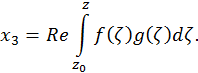
Ниже представлено изображение минимальной поверхности Каталана.

Здесь f,g — в общем случае некоторые мероморфные функции комплексного переменного, для которых интегралы в правых частях равны нулю по любому замкнутому контуру. Такие поверхности не являются, вообще говоря, графиками функций, и исследование их устойчивости представляет определенные сложности. Приведем пример такой поверхности, которая получила название триноид. Эта поверхность получается, если в приведенном выше представлении положить
![]()
Вид этой поверхности

Следует заметить, что функция f(z) для триноида имеет
три особые точки ![]() .
Исследуем поведение величины
.
Исследуем поведение величины ![]() при
изменении размера r области параметризации
при
изменении размера r области параметризации
![]()
С этой целью задачу вычисления величины ![]() сведем
к конечномерной задаче на минимум с помощью кусочно-линейной аппроксимации
рассматриваемой поверхности. После несложных преобразований получаем величину
сведем
к конечномерной задаче на минимум с помощью кусочно-линейной аппроксимации
рассматриваемой поверхности. После несложных преобразований получаем величину
![]()
Здесь A,B - симметричные положительно определенные
матрицы, ![]() -
вектор значений функции h(m) в узлах триангуляции поверхности M. Ниже
на графике показана зависимость величины
-
вектор значений функции h(m) в узлах триангуляции поверхности M. Ниже
на графике показана зависимость величины ![]() для
триноида от размера области определения параметризации поверхности.
для
триноида от размера области определения параметризации поверхности.
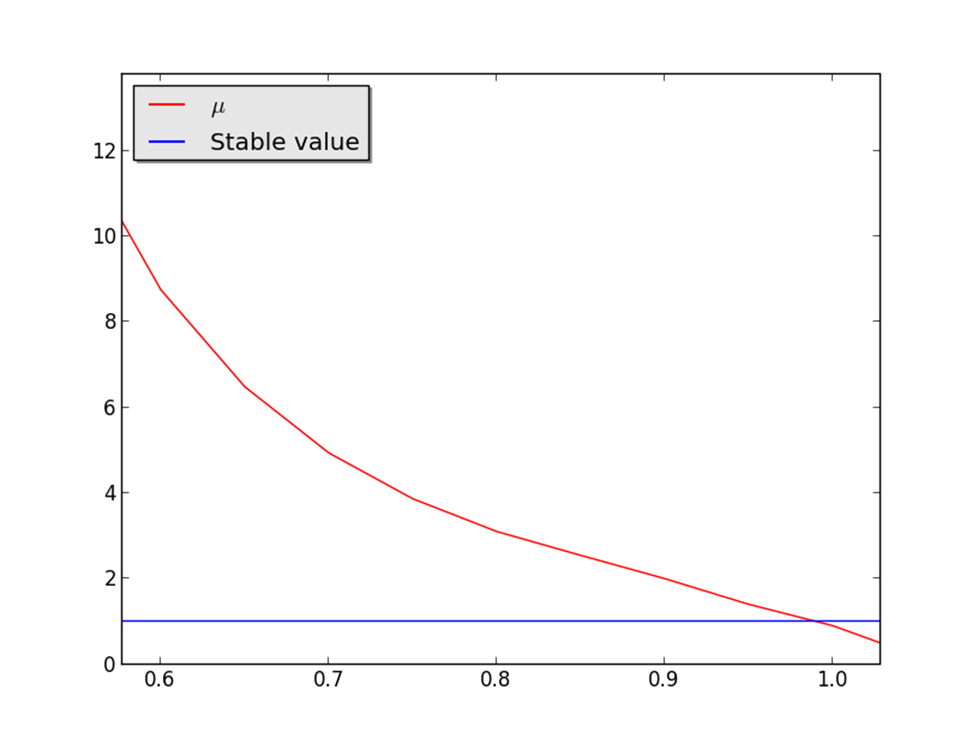
5. Заключение
В работе представлены результаты использования разработанных авторами программных модулей, решающих задачи:
- вычисление формы поверхности, моделирующей свободную поверхность жидкости в капиллярной трубке произвольного сечения. При этом, используя результаты численного эксперимента для различных диаметров капиллярной трубки и известную асимптотическую формулу расчета высоты поднятия жидкости, выполнена оценка степени погрешности вычислений;
- визуализация неустойчивого поведения такой поверхности при критическом значении угла контакта в угловых точках области, что отчасти подтверждает правильность выбранной вычислительной схемы и корректную работу разработанного программного обеспечения.
- расчет поверхностей произвольной топологии, минимизирующих функционал типа площади методом градиентного спуска. Реализация основана на применении модуля NumPy для языка программирования Python;
- расчет величины, характеризующей степень устойчивости экстремальной поверхности. Эта величина расчитывается как минимум функционала в виде отношения двух квадратичных форм. Реализация основана на применении модуля SciPy для языка программирования Python;
- визуализация минимальных поверхностей, заданных представлением Эннепера-Вейерштрасса. Визуализация выполнена средствами пакета Blender 2.74.
Работа выполнена при финансовой поддержке РФФИ (проект № 15-41-02517 р_поволжье_а).
Литература
[1] Финн Р. Равновесные капиллярные поверхности. Математическая теория. Пер. с англ. М.: Мир, 1989. 312 с.
[2] Клячин А.А., Клячин В.А., Григорьева Е.Г. Визуализация расчета формы поверхностей минимальной площади.Научная визуализация. 2014, Т.6, №2. с. 34-42.
[3] Гацунаев М.А., Клячин А.А. О равномерной сходимости кусочно-линейных решений уравнения минимальной поверхности. Уфимский математический журнал. Том 6, № 3 (2014), с. 3-16.
[4] Клячин А.А. О равномерной сходимости кусочно-линейных решений уравнения равновесной капиллярной поверхности. Сибирский журнал индустриальной математики, 2015. Том XVIII, № 2(62)
[5] Клячин В.А., Широкий А.А. Триангуляция Делоне многомерных поверхностей и ее аппроксимационные свойства. Изв. вузов. Матем., 2012, № 1, 31-39.
[6] Клячин В.А. О многомерном аналоге примера Шварца. Изв. РАН. Сер. матем., 2012, 76:4, 41-48.
[7] Клячин В.А., Пабат Е.А.C1-Аппроксимация поверхностей уровня функций, заданных на нерегулярных сетках. Сибирский журнал индустриальной математики. 2010. Т. XIII. № 2. С. 69-78.
[8] Саранин В.А. Равновесие жидкостей и его устойчивость. М.:Институт компьютерных исследований, 2002. 144 c.
[9] Олифант Т. Многомерные итераторы NumPy. В сборнике статей "Идеальный код" под ред. Э. Орама и Г. Уилсона, СПб.: Питер, 2011. с. 341-358.
VISUALIZATION OF STABILITY AND CALCULATION OF THE SHAPE OF THE EQUILIBRIUM CAPILLARY SURFACE
A.A. Klyachin, V.A. Klyachin, E.G. Grigorieva
Volgograd State University, Volgograd, Russia
klyachin-aa@yandex.ru, klchnv@mail.ru, e_grigoreva@mail.ru
Abstract
The article is devoted to the 3D modeling of equilibrium capillary surfaces and visualize various effects associated with the stable or unstable. The construction of such a surface is reduced to finding solutions of some nonlinear partial differential equations satisfying certain boundary condition (on the border is defined by the contact angle between the liquid and the wetted solid wall of the capillary tube). The existence and uniqueness of the solution of this problem in sufficient detail are reflected, for example, in Robert Finn "Equilibrium capillary surfaces. Mathematical Theory "(see., Also references therein). To find approximate solutions we use the variational finite element method, in which the basis functions are chosen piecewise linear functions defined on a triangulation of a calculation domain. This approach was used in the calculations of the surface shape of minimal area.
We obtained the following results
· For the above method of calculation, we developed several program procedures to get calculation results in a convenient form for subsequent processing.
· The test calculations for some forms of sections of capillary tubes: hexagon, octagon, a square. We modeled unstable behavior of the capillary surface at the boundary point with a sufficiently small angle between the faces of the capillary tube and the critical value of the angle of contact. Approximately also calculated the height of raising liquid which was quite close to the value that is obtained by calculating the known physical formulas. It is, in a sense, confirms the correctness of the used calculation method.
· The formulas for the derivatives of functional area type of piecewise linear approximations of surfaces of arbitrary topology are obtained. These formulas are needed for the software implementation process iterations gradient descent.
· Implemented a system of classes for constructing approximate solutions of variational problems such as capillary surfaces. In addition, this class system allows numerical study of the stability of the extreme types of functional surfaces for a functional area type.
Keywords: surface of minimal area, triangulation, piecewise linear surface, approximation of the energy functional, 3D modeling
References
[1] Finn R. Equilibrium capillary surface. Mathematical theory. Translate from English. Moscow: Mir, 1989. - 312.
[2] Klyachin A.A., Klyachin V.A., Grigorieva E.G. Visualization of calculation of minimal area surfaces. Scientific Visualization, 2014. Vol.6, №3, pp. 34-42.
[3] Gatsunaev M.A., Klyachin A.A. On uniform convergence of piecewise-linear solutions to minimal surface equation. Ufa Mathematical Journal. Volume 6, Number 3, pp. 3-16.
[4] Klyachin, A.A. On the uniform convergence of piecewise linear solutions of an equilibrium capillary surface equation. Journal of Applied and Industrial Mathematics, 2015, 9 (3), pp. 381-391.
[5] Klyaсhin VA., Shirokiy А.А. Triangulyatsiya Delone mnogomernykh poverkhnostey i ee approksimatsionnye svoystva [Delaunay triangulation of surfaces and approximations]. Izv. vuzov. Matematika [Russian Mathematics], 2012, vol. 56, no. 1, pp. 31-39.
[6] Klyaсhin V.A. О mnogomernom analoge primera Shvartsa [On a multidimensional analogue of the Schwarz example]. Izv. RAN. Seriya matematicheskaya [Izvestiya: Mathematics], 2012, vol. 76, no. 4, pp. 41-48.
[7] Klyaсhin VA., Pabat Е.А. C1 -approksimatsiya poverkhnostey urovnya funktsiy, zadannykh na neregulyarnykh setkakh [The CG-approximation of the level surfaces of functions defined on irregular meshes]. Sibirskiy zhurnal industrialnoy matematiki [Siberiam journal of industrial mathematics], 2010, vol. XIII, no. 2, pp. 69-78.
[8] Saranin VA. Ravnovesie zhidkostey i ego ustoychivost [Uquilibrium fluids and its stability]. Moscow, In-t kompyuter. issledovaniy Publ., 2002. 144 p.
[9] Olifant T. Mnogomernye iteratory NumPy [Multidimensional iterators NumPy]. Idealnyy kod : sb. st. / pod red. E. Orama i G. Uilsona [Beautiful Code, Edited by Andy Oram and Greg Wilson]. SPb., Piter Publ., 2011, pp. 341-358.