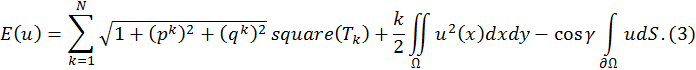VISUALIZATION OF STABILITY AND CALCULATION OF THE SHAPE OF THE EQUILIBRIUM CAPILLARY SURFACE
A.A. Klyachin, V.A. Klyachin, E.G. Grigorieva
Volgograd State University, Volgograd, Russia
klyachin-aa@yandex.ru, klchnv@mail.ru, e_grigoreva@mail.ru
Content
2. The algorithm forcalculating of the equilibrium capillary surface
3. The calculation of the surface, minimazing functional of square type
4. The stability of minimal surfaces
Abstract
The article is devoted to the 3D modeling of equilibrium capillary surfaces and visualize various effects associated with the stable or unstable. The construction of such a surface is reduced to finding solutions of some nonlinear partial differential equations satisfying certain boundary condition (on the border is defined by the contact angle between the liquid and the wetted solid wall of the capillary tube). The existence and uniqueness of the solution of this problem in sufficient detail are reflected, for example, in Robert Finn "Equilibrium capillary surfaces. Mathematical Theory" (see., Also references therein). To find approximate solutions we use the variational finite element method, in which the basis functions are chosen piecewise linear functions defined on a triangulation of a calculation domain. This approach was used in the calculations of the surface shape of minimal area.
We obtained the following results
· For the above method of calculation, we developed several program procedures to get calculation results in a convenient form for subsequent processing.
· The test calculations for some forms of sections of capillary tubes: hexagon, octagon, a square. We modeled unstable behavior of the capillary surface at the boundary point with a sufficiently small angle between the faces of the capillary tube and the critical value of the angle of contact. Approximately also calculated the height of raising liquid which was quite close to the value that is obtained by calculating the known physical formulas. It is, in a sense, confirms the correctness of the used calculation method.
· The formulas for the derivatives of functional area type of piecewise linear approximations of surfaces of arbitrary topology are obtained. These formulas are needed for the software implementation process iterations gradient descent.
· Implemented a system of classes for constructing approximate solutions of variational problems such as capillary surfaces. In addition, this class system allows numerical study of the stability of the extreme types of functional surfaces for a functional area type.
Keywords: surface of minimal area, triangulation, piecewise linear surface, approximation of the energy functional, 3D modeling
1. Intoduction
The article is devoted to 3D modeling of equilibrium capillary surfaces and visualization of various effects associated with their stability or instability. Mathematically, the construction of such a surface is reduced to finding solutions of some nonlinear partial differential equations satisfying certain boundary condition (on the border is defined by the contact angle between the liquid and solid wetted capillary wall). Questions of existence and uniqueness of solutions of this problem are reflected in detail, for example, in the book [1] (see., and references therein). To find approximate solutions we use the variational finite element method, in which the basis functions are chosen piecewise linear functions defined on a triangulation of the calculation domain. This approach has been used by us in calculating the shape of the surface of minimal area [2], and the study of this method for the minimal surface equation was given in [3].
Visualization and view the resulting surface is the next step of geometric modeling. Visualizing this kind of surfaces, especially with the possibility of 3D viewing, it allows for qualitative and quantitative analysis of the constructed models, see the distribution of physical and geometrical characteristics and values along the surface in question, an adjustment of the boundary, and other primary source of data on the basis of the analysis of the problem.
In this regard, we obtained the following results.
- For the above calculation method, it developed several software procedures which will permit the calculation results in a convenient form for subsequent processing. The main calculation module uses the gradient method for the minimization of the energy integral. Moreover, we have implemented such a scheme of interaction of all software modules, which minimizes insertion in the program changes during the transition to a different energy functionals (including the integral energy of the surface tension of the liquid), the boundary conditions, triangulations and so on. This we achieve universality of the developed software system.
- The test calculations for some forms of capillary cross-sections: a hexagon, octagon, square. Modeled erratic behavior of the equilibrium capillary surface at the boundary point with a sufficiently small angle between the faces of the capillary tube, as well as the critical value of the contact angle. It is confirmed theoretically predicted in [1], such behaviour of the equilibrium capillary surface under the condition that the sum of the contact angle and the angle between faces is less than π. Visually, this instability near the boundary corner points visible in the figures presented in the work. In addition to this case, the calculations were conducted for the sections that have a small size in a single direction. For example, a rectangle having one side of a fixed length, and the other - quite small. Approximately also it calculated the liquid lifting height, which was quite close to the value that is obtained by calculating the known physical formulas. It is, in a sense, confirms the correctness of the method of calculation used.
- We obtained formulas for functional derivatives of arbitrary topology surfaces piecewise linear approximation area type. These formulas are need to the program realisation of iteration process for the gradient method.
- System of classes for constructing of approximate solutions for variational problems of capillar surfaces type is implemented. Besides that, the given system of classes allows to carry out numerical researches of stability of extremal surfaces for the area type functionals.
2. The algorithm forcalculating of the equilibrium capillary surface
Determination of the shape of the equilibrium capillary surface
in space with Cartesian coordinates ![]() reduces to the solution of the nonlinear differential
equation
reduces to the solution of the nonlinear differential
equation
with boundary conditions of the form
where Ω is a domain with piecewise smooth boundary on the
plane ![]() and
and ![]() is the contact angle between
the liquid surface and the wall of the capillary tube. It is known that the solution
is the contact angle between
the liquid surface and the wall of the capillary tube. It is known that the solution
![]() describes
decision capillary surface, in equilibrium over a region Ω with a predetermined
contact angle
describes
decision capillary surface, in equilibrium over a region Ω with a predetermined
contact angle ![]() between the surface and the capillary tube
wall. There are many papers on various issues of the solvability of the boundary
value problem. Enough detail the many results of the study the question of the existence,
uniqueness and stability in the monograph [1]. It is known that the boundary value
problem is equivalent to finding a solution to a smooth function
between the surface and the capillary tube
wall. There are many papers on various issues of the solvability of the boundary
value problem. Enough detail the many results of the study the question of the existence,
uniqueness and stability in the monograph [1]. It is known that the boundary value
problem is equivalent to finding a solution to a smooth function ![]() , which reaches its minimum
energy functional
, which reaches its minimum
energy functional
![]()
With rare exception to find an exact solution to the boundary problem is impossible. In this case, resort to the use of numerical methods, which leads to the problem of the development of efficient algorithms for the approximate solutions.
In our work we use the following approach of constructing an
approximate solution in the form of piece-wise linear functions defined over an
arbitrary area and using triangulation in the area. By triangulation, we understand
the following construction. Let’s given a finite set of points ![]() on the
plane. Triangulation of a set of points is the set of triangles
on the
plane. Triangulation of a set of points is the set of triangles ![]() which
satisfies two conditions
which
satisfies two conditions
- any point
 is
a vertex of at least one of the triangle;
is
a vertex of at least one of the triangle; - each triangle comprises only three points from a given set, which are vertices of this triangle.
Let Ω be a bounded domain on the plain. Triangulation
of area Ω is called the triangulation of an arbitrary finite set of points
lying in the closure of ![]() . For an
arbitrary set of numeric values
. For an
arbitrary set of numeric values ![]() we define
a piecewise linear function
we define
a piecewise linear function ![]() by the following way. We construct a function
by the following way. We construct a function
![]() on
the union of all triangles
on
the union of all triangles ![]() so that
so that
![]() and function
and function
![]() for
each triangle
for
each triangle ![]() . This
function is continuous and in each triangle defined by its partial derivatives
. This
function is continuous and in each triangle defined by its partial derivatives ![]() . Therefore,
the energy value of the function
. Therefore,
the energy value of the function ![]() calculated sum
calculated sum
Note that the graph of a piecewise linear function is a set of triangles in a space adjacent to one another on their sides. Figures 1 and 2 are images of graphs of functions:

Fig. 1. Example graph piecewise-linear function

Fig. 2. Example graph piecewise-linear function
To solve the problem (1)-(2) using the variational method we have developed a basic procedure to minimize minimum_func_mix() and several auxiliary necessary for the preparation of calculations. Let us briefly describe their work. Firstly, we note that the points and triangles of used triangulation, as well as the values of the boundary function and the calculation results are stored in four separate binary files. The structure of these files is simple. For example, the points are recorded in a file points.pnt, in which the first 8 bytes are allocated to the number of these points, and each point within a 20-byte - two coordinates corresponding type and information on the type of boundary condition (int). Triangulation of these points is stored in another file triangles.trg, which has the following structure: first 8 bytes for the total number of triangles, followed by indexes of points that make up the described triangle. Any piecewise linear functions stored in the type of files *.val, in which the recorded value of the function at the nodes of triangulation. One of the auxiliary procedures forms a structure in which each node of the triangulation is stored a set of triangles having this point as a vertex. The basic procedure minimum_func_mix()performs one iteration step to minimize the functional. Its input arguments are two pointers to arrays of initial values of the function and the recalculated values, a pointer to an array boundary values of the function that defines the normal derivative function, pointers to arrays of vertices of the triangulation, its triangle and a pointer to a structure containing information about the adjacent triangles.
Note that have been developed and auxiliary classes SQAllPoints and SQAllTreug,in which, in particular, there are reading methods of the above respective data files (read_point() and read_treug()): by number vertices read its coordinates, by the index of the triangle is read numbers vertices of the triangle.
SQIntegrand class is the base for setting the minimizing functional. This class has virtual methods IntG(), Gu(), GradG(), which in its derived classes contain the implementation of the calculation of the integral (the integrand) and its derivatives with respect to function and its gradient. For example, if you want to minimize the energy integral above, the class is created, for example SQSurfCapillar, which is a descendant of the class SQIntegrand, with the appropriate methods:
double IntG(SQPoint point,SQPoint vect, double u)
{
double value;
value=sqrt(1+vect.x*vect.x+vect.y*vect.y)+(k/2)*u*u;
return value;
}
double Gu(SQPoint point,SQPoint vect, double u)
{
return k*u;
}
SQPoint gradG(SQPoint point, SQPoint vect, double u)
{
SQPoint grd(0.0,0.0);
grd.x=vect.x/sqrt(1+vect.x*vect.x+vect.y*vect.y);
grd.y=vect.y/sqrt(1+vect.x*vect.x+vect.y*vect.y);
return grd;
}
In case it will be necessary to calculate the surface that minimizes
other functional, enough for it to write the similar derived class. Thus any corrections
in a computing module, implemented in the class SQComputer, there is no need to
make. We've tested this possibility by the example of the Dirichlet integral (class
SQDirich) and calculating surfaces, minimizing the surface area of a fixed overlapping
scope (class SQSurfArea). The third integral in formula (3) taken into account when
minimizing in function minimum_func_mix(), as its form does not depend on the integrand,
but depends only on the contact angle ![]() . Generally,
the right side of the boundary condition (2) can be located function. Therefore,
the file of type *.val containing the values of the boundary function in nodes of
triangulation is connected in the computing unit.
. Generally,
the right side of the boundary condition (2) can be located function. Therefore,
the file of type *.val containing the values of the boundary function in nodes of
triangulation is connected in the computing unit.
The calculation results are written to the file of type *.val. Note also that in function minimum_func_mix() there is realized the possibility of a Dirichlet boundary conditions, that is, the values of the desired solution on the boundary and mixed boundary conditions containing derivatives of conditions on this decision.
We also have written procedure of finishing of calculation results, which transforms them into two types of files. One of this is type of text file *.tgs, each line of which stores three-dimensional coordinates of one-point model. Three successive rows define a triangle in the triangulation of the surface. The other file is a standard format stl of 3D graphics for storing such surface.
For the construction of surfaces and image we have retained the calculation results in a text file format stl and took advantage to show Blender 2.74 program. Here are images of some of the constructed surfaces.

Fig. 3. The rise of the liquid in the capillary tube of square cross section with a side of 1 mm, 2 mm and 5 mm.

Fig. 4. The rise of the liquid in the capillary tube of hexagonal cross section with a diameter of 1 mm, 2 mm and 5 mm.

Fig. 5. The rise of the liquid in the capillary tube of octagonal cross-section with a side of 0.41 mm, 0.83 mm and 2.07 mm.
Below we give an explanation to the figures. Figure 3 contains
images free liquid surface in the capillary tube having a square cross section with
a side of 5, 2 and 1 mm. Figures 4 and 5 show the results of the calculation in
the case of hexagonal and octagonal cross sections for different tube diameters.
Selecting a cross-sectional shape is dictated by two factors. First, we were interested
in the first case, when the area Ω has a smooth boundary having an angular
point, because in this case we can visualize the erratic behavior of the liquid
surface. Moreover, the solution of these angles with the inner side of the region
should have a value less than π. Secondly, we decided on symmetrical
sections that-be had the opportunity to assess the degree of error of calculations.
As in the case of regular polygons for such an assessment, you can use, for example,
the asymptotic formula of rise fluid ![]() along
the axis of symmetry of the capillary tube (see [1])
along
the axis of symmetry of the capillary tube (see [1])
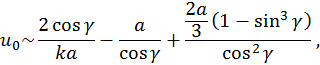
where ![]() – the radius of the capillary tube. Although
the uniform convergence of approximate solutions was proved in the [4], in this
article we have tried to visually illustrate this fact. At the same time, we take
such a contact angle at which the conditions of existence of exact solutions are
satisfied (see [1]). It should be noted that the calculation results are in good
agreement with the well-known formulas of calculating the height of the liquid in
the capillary tube. The difference amounted to about 2-5%.
– the radius of the capillary tube. Although
the uniform convergence of approximate solutions was proved in the [4], in this
article we have tried to visually illustrate this fact. At the same time, we take
such a contact angle at which the conditions of existence of exact solutions are
satisfied (see [1]). It should be noted that the calculation results are in good
agreement with the well-known formulas of calculating the height of the liquid in
the capillary tube. The difference amounted to about 2-5%.
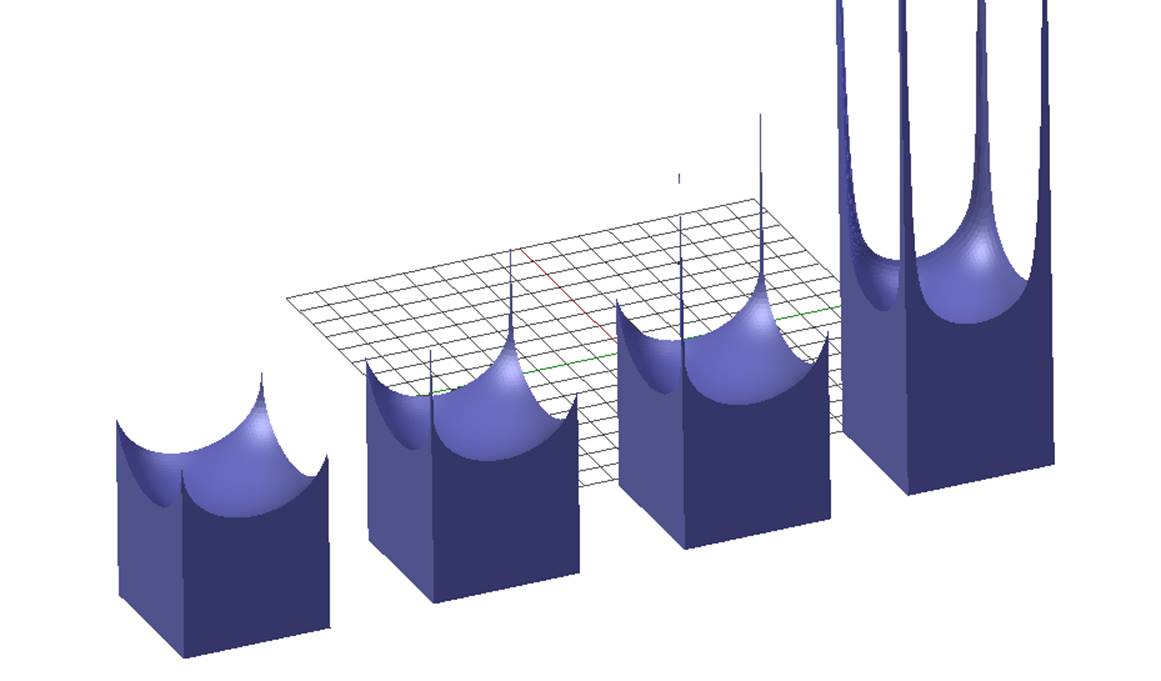
Fig. 6. Unstable liquid behavior at the critical value of the contact angle.
Figure 6 for square sections the calculations were carried out
in the case where the contact angle is gradually approaching the critical value
at which the solution of the problem (1)-(2) does not exist. For square section
this angle is ![]() . This figure
shows an unstable behavior of the liquid surface near the corner of the boundary
points: there is a sharp increase, which corresponds to the theoretically predicted
the situation in the [1], which indicates that a solution of equation (1) tends
to infinity in the vicinity of a boundary point.
. This figure
shows an unstable behavior of the liquid surface near the corner of the boundary
points: there is a sharp increase, which corresponds to the theoretically predicted
the situation in the [1], which indicates that a solution of equation (1) tends
to infinity in the vicinity of a boundary point.
Based on the foregoing, it can be concluded that the developed programs allow to:
a) accurately perform calculations of form surfaces on which reaches its minimum for a certain integral (surface area, the energy of the surface tension, the Dirichlet integral, and so on.);
b) by simple and quite natural additions to the code of auxiliary routines to perform at transition to a different minimized functional.
3. The calculation of the surface, minimazing functional of square type
The particular case of capillar surfaces is a class of surfaces
that minimaze area functional, so called minimal surfaces. For modellinf of such
surfaces of an arbitrary topology we reduce to more general case. Namely, let ![]() be a positive
homogeneous of degree 1 convex function such, that
be a positive
homogeneous of degree 1 convex function such, that ![]() .
.
For smooth surface ![]() we consider the quantity
we consider the quantity
![]()
where ξ is a unit normal vector of the surface M. If M is a piecewise linear approximation of the surface M, then approximate value of the described functional will be calculated by the formula
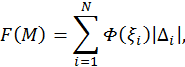
where ![]() is a union of triangles
is a union of triangles ![]() ,
, ![]() is a normal
of a plane of these triangles, and
is a normal
of a plane of these triangles, and ![]() are squares
of the triangles. The surface
are squares
of the triangles. The surface ![]() can be considered as a point in a space LM
of 3n-dimension, where n is a number of vertexes on
can be considered as a point in a space LM
of 3n-dimension, where n is a number of vertexes on ![]() . If we define a vector
h in each point, vertex of the surface, then a vector in LM will be
correspond to these vectors. Then it turns out, if the functional F consider
as a numerical function
. If we define a vector
h in each point, vertex of the surface, then a vector in LM will be
correspond to these vectors. Then it turns out, if the functional F consider
as a numerical function ![]() , so we
have a formula
, so we
have a formula
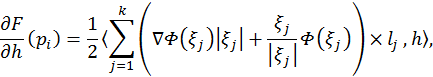
where the sum is taken by all triangles with vertex ![]() denotes
a normal to the corresponding triangle and
denotes
a normal to the corresponding triangle and ![]() is a vector,
connecting vertices of the triangle, not coinciding with
is a vector,
connecting vertices of the triangle, not coinciding with ![]() so, that
this vertex is on the left. The theoretical verfication of the piecewise linear
approximation was studied, in particular, in works [5]-[7].
so, that
this vertex is on the left. The theoretical verfication of the piecewise linear
approximation was studied, in particular, in works [5]-[7].
Example 1. Let consider a case, when ![]() . Then,we
obtain
. Then,we
obtain
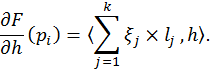
If we suppose, that the susface ![]() minimizes the functional
minimizes the functional
![]() ,
then
,
then
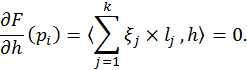
for each vertex ![]() . It is
a condition of minimal square for piecewise linear surface.
. It is
a condition of minimal square for piecewise linear surface.
For minimazing of funcionals of given type we use the gradient
method. Now we consider some piecewise linear surface ![]() . The gradient
method supposes obtaining surface
. The gradient
method supposes obtaining surface ![]() on each
iteration step by the formula
on each
iteration step by the formula
![]()
where the quantity is considered as a vector relation in the
space LM, and the numbers ![]() will be
calculated by experiment. Below we show results of calculation for catenoid surface
(minimal surface of rotarion) for cases 400 and 800 iterations. In both cases we
choose
will be
calculated by experiment. Below we show results of calculation for catenoid surface
(minimal surface of rotarion) for cases 400 and 800 iterations. In both cases we
choose ![]() is equal
to 0,005. The calculated error in the first case is equal to 0,06, in the second
case — 0,02.
is equal
to 0,005. The calculated error in the first case is equal to 0,06, in the second
case — 0,02.
4. The stability of minimal surfaces
Capillary surfaces are sufraces of different media in equilibruium. The physical aspects of stability and instability of equilibrium surfaces are considered in [8]. From mathematical point of view stability of the equilibrium surface is associated with the value of the type
![]()
where ![]() is a norm
of the second fundamental form for the surface, and the infimum takes over all functions
is a norm
of the second fundamental form for the surface, and the infimum takes over all functions
![]() such,
that h=0 on a boundary of the surface M and with zero integral by
the surface (as a corollary of incompressibilty for liquid mediums.)
such,
that h=0 on a boundary of the surface M and with zero integral by
the surface (as a corollary of incompressibilty for liquid mediums.)
For a case of minimal surfaces, the volume occupied by the liquid is equal to zero, and the last condition is not required. The surface will be stable if only the quantity determinated above be greater than 1.
In the present article a method of calculated investigation of
stability for equilibrium surfaces in ![]() , which
is founded on the using of NumPy packet is proposed.
, which
is founded on the using of NumPy packet is proposed.
The packet NumPy is an extension of programming language Python, which realizes a lot of different operations for a work with multi-dimensionall data arrays. In spite of the fact that this packet is destined for it's using in context of the interpretable language, nevertheless arrays of NumPy are C-similar [9]. Therefore, these arrays can be controlled by standart instructions of language Python. The convenience of using of NumPy arrays, in particular, is expressed in that for these arrays arithmetic operations and mathematical functions are overloaded.
In this article we describe the use of the packet for solving of the problem of analisys for stability of extremal surfaces calculation. As an example, we consider a specail class of minimal surfaces, which have Enneper-Weierstrass parametric representation
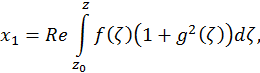
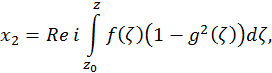
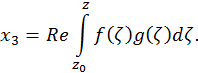
Below it’s introduced image of Catalan minimal surface.

Here f,g are some in general case meromorphic function of a complex variable, for which intergrals in the right hand are equal to zero over an every closed path. In general case, such surfaces are not graphs of functions, so research of its stability is enough difficult. We give an example of such surface, called trinoid. This surface can be obtained from the representation as before if we put
![]()
Form of this surface is

It should be noted, that for trinoid the function f(z)
have three singular points ![]() We study
the behaviour of the quantity
We study
the behaviour of the quantity ![]() under
change of size r of parametrisation domain
under
change of size r of parametrisation domain
![]()
To this end, the problem of calculating of ![]() is reduced
to the finite dimensional minimal problem by piecewise linear approximation of the
considered surface. After simple transformations we obtain the quanity
is reduced
to the finite dimensional minimal problem by piecewise linear approximation of the
considered surface. After simple transformations we obtain the quanity
![]()
Here A,B are symmetric positive defined matrices, ![]() is a vector
of values for the function h(m) in nodes of triangulation for the surface
M. Below on graph it is shown a dependence of
is a vector
of values for the function h(m) in nodes of triangulation for the surface
M. Below on graph it is shown a dependence of ![]() for the
trinoid from size of the domain of definition for the surface parametrization.
for the
trinoid from size of the domain of definition for the surface parametrization.
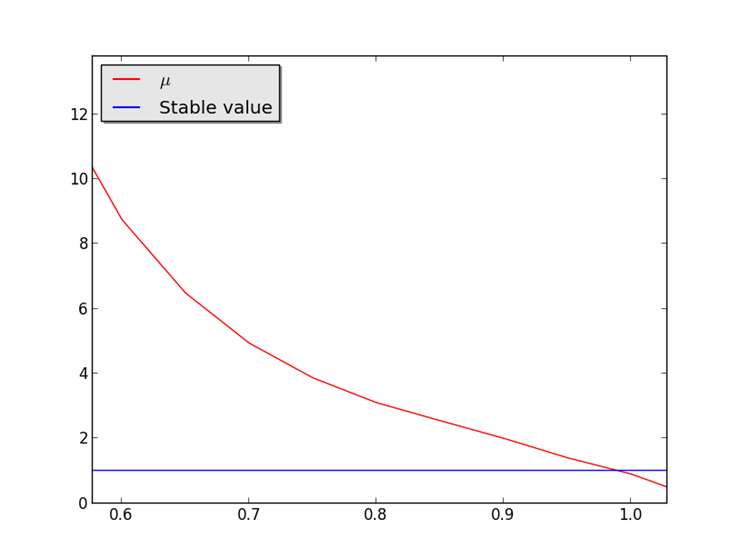
5. Conclusion
In this work we’ve shown results of using for program modules developed by authors and solving following problems:
- calculation of the form for the surface, modelling a free surface of the liquid in the cappilar tube of an arbitrary cut. Moreover, by using of results of calculated experiments for different diameters of the cappilar tube and by the known asymptotic formula for calculation of height of raising for liquid, we obtain the estimate of degree of calculation errors;
- visualization of the instable behavior such surface under critical value of contact angle in corner points of the domain, that is partially confirmed correctness of chosen calculating scheme and the correct work of developed program software.
- calculation of surfaces with an arbitrary topology, which minimize the area type functional by the gradient method. The realization is founded on use of NumPy module for programming language Python;
- calculation of the quantity, characterizing degree of stability for an extremal surface. This quantity can be obtained as a minimum of functional, which has a type of a ratio for two quadratic forms. The realization is founded on using of SciPy module for programming language Python;
- visualization of minimal surfaces, given by Enneper-Weierstrass representation. The visualization is made by Blender 2.74 packet.
Work is made under financial support of RFBR (project ? 15-41-02517 r_povoljie_a).
References
[1] Finn R. Equilibrium capillary surface. Mathematical theory. Translate from English. Moscow: Mir, 1989. - 312.
[2] Klyachin A.A., Klyachin V.A., Grigorieva E.G. Visualization of calculation of minimal area surfaces. Scientific Visualization, 2014. Vol.6, ?3, pp. 34-42.
[3] Gatsunaev M.A., Klyachin A.A. On uniform convergence of piecewise-linear solutions to minimal surface equation. Ufa Mathematical Journal. Volume 6, Number 3, pp. 3-16.
[4] Klyachin, A.A. On the uniform convergence of piecewise linear solutions of an equilibrium capillary surface equation. Journal of Applied and Industrial Mathematics, 2015, 9 (3), pp. 381-391.
[5] Klya?hin VA., Shirokiy ?.?. Triangulyatsiya Delone mnogomernykh poverkhnostey i ee approksimatsionnye svoystva [Delaunay triangulation of surfaces and approximations]. Izv. vuzov. Matematika [Russian Mathematics], 2012, vol. 56, no. 1, pp. 31-39.
[6] Klya?hin V.A. ? mnogomernom analoge primera Shvartsa [On a multidimensional analogue of the Schwarz example]. Izv. RAN. Seriya matematicheskaya [Izvestiya: Mathematics], 2012, vol. 76, no. 4, pp. 41-48.
[7] Klya?hin VA., Pabat ?.?. C1 -approksimatsiya poverkhnostey urovnya funktsiy, zadannykh na neregulyarnykh setkakh [The CG-approximation of the level surfaces of functions defined on irregular meshes]. Sibirskiy zhurnal industrialnoy matematiki [Siberiam journal of industrial mathematics], 2010, vol. XIII, no. 2, pp. 69-78.
[8] Saranin VA. Ravnovesie zhidkostey i ego ustoychivost [Uquilibrium fluids and its stability]. Moscow, In-t kompyuter. issledovaniy Publ., 2002. 144 p.
[9] Olifant T. Mnogomernye iteratory NumPy [Multidimensional iterators NumPy]. Idealnyy kod : sb. st. / pod red. E. Orama i G. Uilsona [Beautiful Code, Edited by Andy Oram and Greg Wilson]. SPb., Piter Publ., 2011, pp. 341-358.