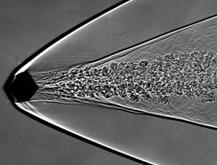
ВИЗУАЛИЗАЦИЯ СВЕРХЗВУКОВОГО ОБТЕКАНИЯ ФРАГМЕНТОВ КУБИЧЕСКОЙ ФОРМЫ

С.И. Герасимов^1,2,4, В.И. Ерофеев³,  В.А. Кикеев⁴,  Р.В. Герасимова¹, И.И. Каныгин^1,2, А.П. Фомкин²

¹ Саровский физико-технический институт НИЯУ МИФИ, 607186, Саров, Россия

² Российский федеральный ядерный центр - Всероссийский научно-исследовательский институт экспериментальной физики, 607190, Саров, Россия

³ Институт проблем машиностроения, Нижний Новгород, Россия

⁴ Нижегородский государственный технический университет им. Р.Е.Алексеева

s.i.gerasimov@mail.ru, erf04@sinn.ru, vkikeev@mail.ru, r.v.gerasimova@mail.ru

Содержание

1. Введение

2. Визуализация процессов при сверхзвуковом обтекании фрагментов кубической формы методом численного моделирования

3. Визуализация процесса сверхзвукового обтекания методом теневой фоторегистрации

4. Заключение

Литература

Аннотация

В статье представлены результаты расчетного и экспериментального исследования сверхзвукового обтекания потоком воздуха фрагментов кубической формы, различным образом ориентированных относительно направления набегающего потока, представлены результаты визуализации процесса сверхзвукового обтекания фрагментов кубической формы двумя методами: теоретическим  - на основе математической модели путем численного решения полных осредненных по Рейнольдсу уравнений Навье-Стокса с использованием инженерной программы SolidWorks, экспериментальным – с использованием метода теневого фотографирования.

Ключевые слова: сверхзвуковое обтекание, фрагмент кубической формы, метод численного решения, уравнения Навье-Стокса, модель турбулентности, теневая фоторегистрация.

1. Введение

Для наземной аэродинамической отработки широко применяется метод исследований в аэробаллистическом тире [1], при котором объект испытания выстреливается в свободный полет с заданными начальными условиями по скорости и углу атаки из пороховой или легкогазовой установки. В полете с помощью оптических средств внешнетраекторных измерений осуществляется многократная регистрация в фиксированные моменты времени положений объекта испытания и далее определяются его линейные и угловые координаты  центра масс в эти моменты времени. При испытаниях тел малых размеров, например, осколков, возникает ряд особенностей по сравнению со штатными испытаниями моделей. Недостоверность априорного знания характера движения таких элементов, их выход из зоны регистрации, обусловленный действием аэродинамических сил на гранях, ориентированных под углом к направлению полета, снижают количество регистрируемых положений и заставляют ограничиваться определением только линейных координат. Для получения рабочей сравнительной информации при таких исследованиях целесообразно иметь тестовые расчетно-экспериментальные данные по аэродинамическим характеристикам движения эталонных тел из того же материала и тех же размеров.

2. Визуализация процессов при сверхзвуковом обтекании фрагментов кубической формы методом численного моделирования

Ниже представлены результаты расчетного и экспериментального исследования сверхзвукового обтекания потоком воздуха фрагментов кубической формы, различным образом ориентированных относительно направления набегающего потока, представлены результаты визуализации процесса сверхзвукового обтекания тел кубической формы двумя методами: теоретическим  - на основе математической модели путем численного решения полных осредненных по Рейнольдсу уравнений Навье-Стокса с использованием инженерной программы SolidWorks (cерийный номер SolidWorks 2006 для учебных заведений - 9710 0044 1213 5426) [2] , экспериментальным – с использованием метода теневой фоторегистрации [3].

Моделируемым объектом являлся кубик с характерным размером грани 8 мм. Для определения влияния размеров расчетного домена на характер обтекания куба и коэффициент лобового сопротивления рассматривались несколько доменов различных размеров при одной начальной скорости обтекания (M = 7). Исходя из условий симметрии, была взята лишь четвертая часть полного, окружающего весь куб домена. Расчетный домен, используемый в дальнейших исследованиях влияния начальной скорости потока на коэффициент лобового сопротивления и на характер обтекания куба, имеет размеры 90×50×50 мм.

В качестве метода моделирования выбран метод численного решения осредненных по Рейнольдсу уравнений Навье-Стокса, дополненных k-ε - моделью турбулентности.

Этот метод реализован в современном инженерном программном пакете SolidWorks. Пакет представляет собой комбинацию полной версии системы как графической среды и гидрогазодинамического решателя (Flow Simulation), препроцессор которого позволяет реализовывать автоматизированный или ручной метод блочного построения расчетной сетки и ее последующей адаптации в зонах больших градиентов параметров потока. Данный пакет позволяет рассчитывать широкий круг различных течений: двумерные и трехмерные, ламинарные, турбулентные и переходные, несжимаемые, сжимаемые, с до-, транс- и сверхзвуковыми областями, стационарные и нестационарные течения многокомпонентных текучих сред в каналах и вокруг тел, с учетом гравитации, пограничного слоя, в том числе с учетом шероховатости стенок, с конвективным теплообменом между твердым телом и текучей средой. Твердое тело, в свою очередь, может состоять из нескольких материалов.

Наряду с описанными выше задачами, используемый при расчетах пакет имеет возможность моделировать течения с одновременным расчетом теплопередачи в твердых телах, т. е. с решением задачи сопряженного теплообмена, в том числе с учетом радиационного теплообмена между поверхностями; течения газовых смесей с равновесной конденсацией содержащегося в них водяного пара; течения воды с равновесной кавитацией или равновесным кипением; течения через пористые среды как через рассредоточенные сопротивления; ламинарные течения неньютоновских жидкостей; течения сжимаемых жидкостей; двухфазные течения как движение жидких или твердых частиц в потоке текучей среды.

В качестве граничных условий могут быть заданы условия непротекания и прилипания на стенке, тепловые условия на стенке, контактирующей с текучей средой, тепловые условия на внешней поверхности тела на границе расчетной области, параметры текучей среды на входных и выходных отверстиях модели во внутренних и внешних задачах или на границах расчетной области во внешних задачах. Помимо вышеперечисленного, могут быть заданы также вращательные и поступательные движения поверхности стенки, не меняющие геометрию стенки, или вращение тела в выделенной осесимметричной подобласти расчетной области. Возможно задание объемных источников тепла в текучей среде и в теле, если рассчитывается теплопередача в твердых телах, поверхностных источников тепла на поверхности твердого тела.

В результате решения определяются аэродинамические силы и моменты, действующие на обтекаемую поверхность объекта, так же вычисляются параметры обтекающего газа в расчетном объеме – поля распределения давлений, плотностей, температур, скоростей. Полученные результаты могут выводиться как в виде контурных распределений параметров течения в объеме, так и на поверхности тела, и в виде соответствующих графиков для любого выбранного сечения.

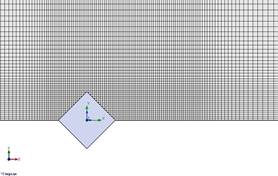
Рис. 1 - Фрагмент адаптированной сетки куба

На рисунке 1 приведена дважды адаптированная после 1000 и 2000 итераций, сетка для условий обтекания с начальной скоростью М = 10. Исходная сетка состояла из 317500 ячеек, а адаптированная сетка из 976340, 1754320 ячеек.

Трехмерный расчет процесса внешнего обтекания куба сверхзвуковым потоком сжимаемого газа проводился с учетом соответствующих граничных условий на поверхности куба и на стенках расчетного домена. Решались полные, осредненные по Рейнольдсу уравнения Навье-Стокса, дополненные двухпараметрической моделью турбулентности. Диапазон рассмотренных начальных скоростей обтекания составлял 2 – 10 M. Для воздуха использовалось уравнение состояния совершенного газа. В процессе расчета определялись полные в объеме домена поля для всех параметров обтекающего газа, определялось значение коэффициента лобового сопротивления куба. В процессе расчета определялись полные в объеме домена поля для всех параметров обтекающего газа, определялось значение коэффициента лобового сопротивления куба.

Коэффициент лобового сопротивления кубика определялся по формуле:

 ,

где - плотность среды, (кг/м³); - скорость набегающего потока, (м/с); - характерная площадь поперечного сечения куба перпендикулярно потоку, (м²);  - сила лобового сопротивления, определяемая в результате численного эксперимента. Необходимо отметить, что используемая в расчетах  модель турбулентности позволяет учитывать вязкое трение, соответствующие коэффициенты динамической и турбулентной вязкости выражаются через величины кинетической энергии  и диссипации кинетической энергии . Сила лобового сопротивления может определяться через нормальную (силу нормального давления) и касательную (силу трения) составляющие.

В результате численного решения определены аэродинамические силы, действующие на обтекаемую поверхность объекта, рассчитаны параметры обтекающего газа в расчетном объеме. На рис.2-5 представлены картины распределения давлений, плотностей, температур, скоростей вокруг обтекаемого кубика (М=9 (при начальной ориентации гранью и вершиной),10 (при начальной ориентации ребром)).

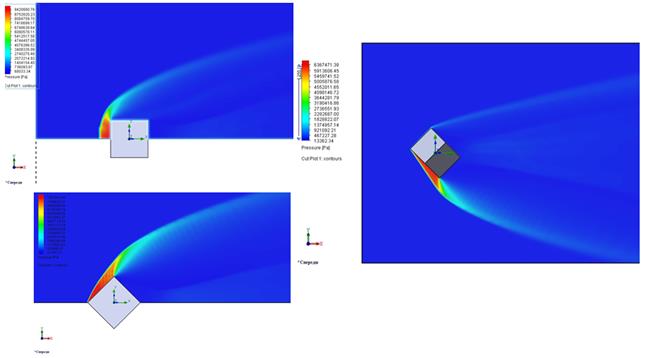
Рис.2 Поле распределения давления

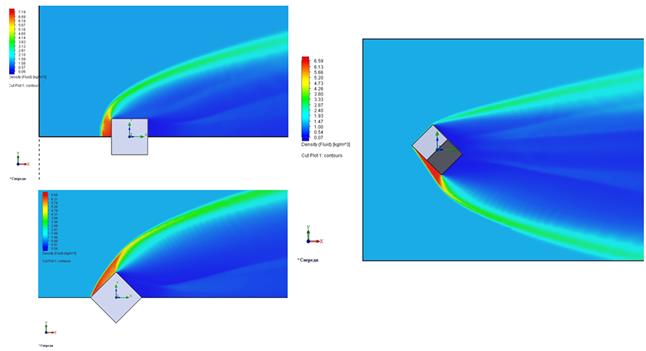
Рис.3 Поле распределения плотности

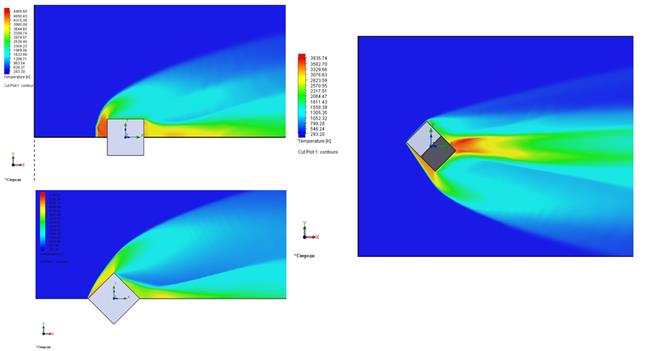
Рис.4 Поле распределения температур

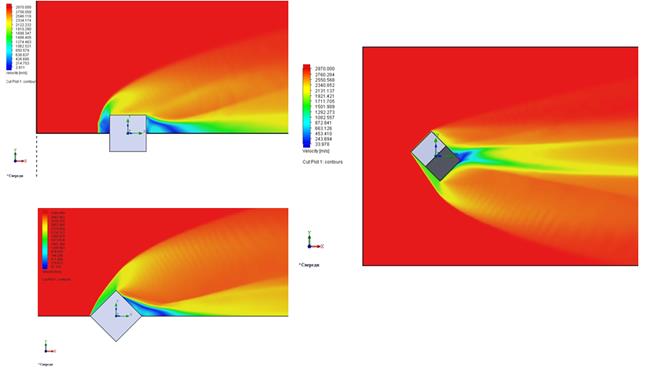
Рис.5 Поле распределения скорости

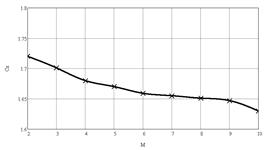
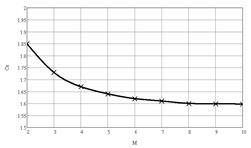
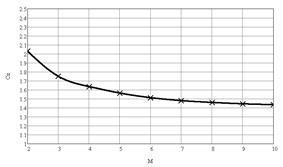
На рис.6 приведены результаты численного моделирования в виде зависимости коэффициента лобового сопротивления Сх от числа Маха при ориентациях обтекаемого кубика гранью, ребром и вершиной к набегающему потоку.

a	б
в

Рис.6 Зависимость коэффициента лобового сопротивления от числа Маха при различных ориентациях кубика к набегающему потоку: а - гранью, б – ребром, в - вершиной.

3. Визуализация процесса сверхзвукового обтекания методом теневой фоторегистрации

Исследовались тела из сплава ВНЖ («вольфрам – никель – железо») размером 8x8x8 мм (массой 8,7 г) при начальной ориентации к набегающему потоку гранью, ребром и вершиной. Регистрация внешнетраекторных линейных координат и полетного времени на траектории полета осуществлялась не менее чем в 12 точках на длине измерительного участка более 50 m в аэробаллистическом тире.

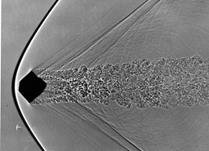
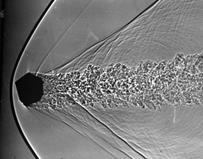
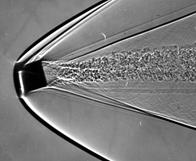
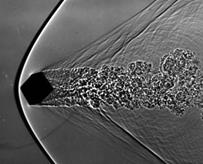
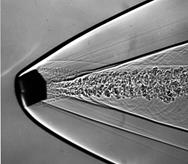
Испытания тел кубической формы при начальных скоростях метания V < 2 км/с проводились путем отстрела объекта испытаний из пороховой баллистической установки калибром 23 мм. В этих экспериментах, кроме внешнетраекторных параметров, получены широкоформатные теневые спектры обтекания (см. рис.7 a,б,в).

M=1,58	M=1,54 а)	M=3,4
М=1,54	М=3,11 б)	М=3,24
M=1,58	М=3,25 в)	М=3,33

Рис.7 Спектры обтекания кубика, первоначально ориентированных в канале ствола гранью (а), ребром (б), вершиной (в)

Полученные в каждом конкретном опыте данные внешнетраекторных измерений (ВТИ) положения центра масс использовались при определении коэффициента силы лобового сопротивления путем решения системы дифференциальных уравнений движения, которая в наибольшей мере (по минимуму взвешенной суммы квадратов невязок расчетных и измеренных значений координат) согласуется с данными измерений.

То есть по результатам внешнетраекторной регистрации положений объекта изучения (кубика) с помощью оптических средств осуществляется определение линейных координат его положения в пространстве в фиксированные моменты времени. Методика определения аэродинамических характеристик по результатам ВТИ построена на аппроксимации измерений элементов траектории объекта изучения численным решением системы дифференциальных уравнений движения. Аппроксимация осуществляется посредством итеративной (ввиду нелинейности задачи) минимизации целевой функции -  функционала, представляющего взвешенную сумму квадратов разностей между измеренными и расчетными значениями координат объекта изучения.

В качестве тестовых объектов при тех же режимах испытаний исследовались объекты формы шара из того же материала диаметром 10,4 мм.

На рис.8 приведена среднеопытная экспериментальная зависимость коэффициента силы лобового столкновения С_x от числа Маха M для тела кубической формы в диапазоне М_ср=(0,8-3,8)М с погрешностью 2σ ≤ 2%. С_x(М) для куба отнесен к площади миделя равновеликой по объему сферы.

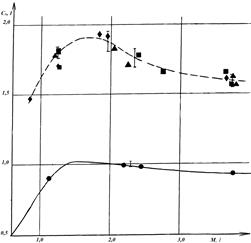
Рис. 8.  Экспериментальная зависимость коэффициента силы лобового сопротивления куба от числа Маха. Условные обозначения:

● – для шара диаметром 10,4 мм;

■, ▲, ♦  - для куба 8*8*8 мм, ориентированного гранью, ребром и вершиной соответственно.                   

4. Заключение

Проведено расчетно-экспериментальное исследование сверхзвукового движения фрагментов кубической формы, различным образом начально ориентированных относительно направления набегающего потока. Получены экспериментальные теневые спектры обтекания и расчетные картины распределения давлений, плотностей, температур, скоростей вокруг обтекаемого кубика. В результате экспериментальной отработки получены среднеопытные зависимости коэффициентов силы лобового сопротивления Сx(М) в диапазоне чисел Маха от 0,8 до 3,8 при отсутствии обгара и термомеханического разрушения. При этом экспериментальные данные для шариков хорошо согласуются с известными экспериментальными данными. Экспериментальная зависимость для кубиков получена с погрешностью 2σ ≤ 2% и не зависит от первоначальной ориентации объекта испытания в канале ствола баллистической установки. Кроме того, как показывают теневые картины на участке в 20 м от выходного сечения  канала ствола, из-за вращения может меняться начальная ориентация фрагмента в процессе полета, что приводит к сближению значений Сx(М).  В этой связи численные результаты имеют дополнительную ценность и позволяют сделать вывод о разумном переносе части решаемых задач с дорогостоящих опытов на математическое моделирование.

Полученные результаты относятся также к сверхзвуковым течениям в газовых каналах проточной части турбомашин и могут использоваться при изучении элементов конструкций, обтекаемых со сверхзвуковой скоростью. Настоящие исследования проводятся при финансовой поддержке Министерства образования и науки Российской Федерации в рамках Соглашения № 14.577.21.0104 с федеральным государственным бюджетным образовательным учреждением высшего профессионального образования «Нижегородский государственный технический университет им. Р.Е. Алексеева» (уникальный идентификатор проекта RFMEFI57714X0104).

Литература

1. С.И. Герасимов, Ю.И. Файков, С.А. Холин Кумулятивные источники света.-Саров:РФЯЦ-ВНИИЭФ, 2011.-327с.
2. http://www.solidworks.com/sw/purchase/product-demonstration.htm?mktid=2600

http://www.solidworks.ru/index.php?option=com_content&view=article&id=151&Itemid=66

http://www.solidworks.com/sw/products/simulation/flow-simulation.htm (доступно на 29.06.2015).

3. С.И. Герасимов, Ю.И. Файков Теневое фотографирование в расходящемся пучке света.- Саров:РФЯЦ-ВНИИЭФ, 2010.-344с.

---

VISUALIZATION OF SUPERSONIC FLOW AROUND A CUBE

S.I. Gerasimov^1,2,4, V.I. Erofeev³,  V.A. Kikeev ⁴,  R.V. Gerasimova¹, I.I. Kanygin^1,2, A.P. Fomkin²

¹ Sarov Physics and Technical Institute of National Research Nuclear University «MEPHI», Russia

² Russian Federal Nuclear Center - The All-Russian Research Institute of Experimental Physics, Sarov, Russia

³ Institute of Problems of Mechanical Engineering RAS, N.Novgorod, Russia

⁴ Nizhny Novgorod State Technical University n.a. R.E. Alekseev, N.Novgorod, Russia

E-mail: s.i.gerasimov@mail.ru, erf04@sinn.ru, vkikeev@mail.ru, r.v.gerasimova@mail.ru

Abstract

The article presents the results of computational and experimental studies of supersonic flow around a cube arbitrary oriented relative to the direction of the incoming flow. Supersonic flow visualization around the cubical objects was performed by two methods: computational - based on the complete Navier-Stokes equations averaged by Reynolds which are enabled  in the SolidWorks  engineering and  on the experimental – using the shadow photography.

Keywords: supersonic flow, cubical object, a method of numerical solution of the Navier-Stokes equations, turbulence model, shadow photography.

Literature

1. S.I. Gerasimov, Yu.I. Faykov, S.A. Kholin. Kumuljativnye istochniki sveta [Cumulative light sources]. Sarov, 2011, p.326. [in Russian].
2. http://www.solidworks.com/sw/purchase/product-demonstration.htm?mktid=2600

http://www.solidworks.ru/index.php?option=com_content&view=article&id=151&Itemid=66

http://www.solidworks.com/sw/products/simulation/flow-simulation.htm (accessed: 29.06.2015).

3. S.I. Gerasimov, Yu.I. Faykov. Tenevoe fotografirovanie v rashodjashhemsja puchke sveta [Shadow photography in divergent light beam].- Sarov: RFNC-VNIIEF, 2010, P.344. [in Russian].