VISUALIZATION AS A TOOL FOR URANIUM PROLIFERATION PROTECTION ASSESSMENT
A.N. Shmelev, E.G. Kulikov, N.I. Geraskin
National Research Nuclear University MEPhI (Moscow Engineering Physics Institute)
shmelan@mail.ru, EGKulikov@mephi.ru, NIGeraskin@mephi.ru
Contents
1. Schematic diagram of gun-type HNED
2. Calculation model for upper estimate of sub-critical masses assembling
3. Pre-detonation and fizzle yield
4. Isotope 232U as a powerful neutron source
5. Recommendations on uranium proliferation protection
Abstract
In the present paper calculation-theoretical model has been developed and visualized, which aims at quantitative assessment of uranium proliferation protection against creating gun-type hypothetical nuclear explosive device (HNED). The main nuclear, kinematic and thermal processes that occur in gun-type HNED are modeled. The model allows us to estimate the energy yield of gun-type HNED, assembled on the basis of uranium of a given isotopic composition, as well as to develop requirements that reduce energy yield down to a certain value.
Fundamentally new aspect is an approach that allows us to estimate the achievable time of subcritical masses assembling in gun-type HNED on the basis of uranium of a given isotopic composition. In this approach elements of interior ballistics and strength of materials theories are used, as well as neutron-physical properties of uranium of a given isotopic composition are taken into account.
The stochastic nature of the nuclear chain reaction is accounted for in accordance with the methodology of G.E. Hansen [1], which determines the probability of uninterrupted nuclear chain reaction. This allows us to link the necessary reduction of gun-type HNED energy yield with required neutron source.
In the present paper uranium is considered as fissionable material in gun-type HNED, namely, a mixture of (235U + 238U) with different enrichment on 235U. Proliferation protection of high-enriched uranium can be achieved by introducing a small amount of 232U, because [2, 3]:
1) 232U is a powerful source of α-particles capable of initiating (α,n)-reactions on light elements which are present in uranium as impurities. Thus, 232U creates large neutron source which leads to gun-type HNED pre-detonation
2) decay products of 232U (isotopes 208Tl and 212Bi) are a source of hard γ-radiation, which, among others, significantly improves the possibility of uranium detection (even at the level of 1 ppb 232U).
As uranium proliferation protection issues concern not only engineers, but also representatives of some of the humanities, visualization of these issues is essential. Moreover, the material presented in such a form is much easier for students to understand.
Key words: uranium proliferation protection, gun-type hypothetical nuclear explosive device.
1. Schematic diagram of gun-type HNED
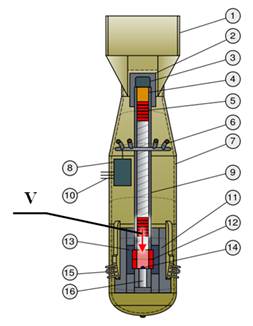
Principle of action of gun-type HNED is based on the fast assembling of two sub-critical masses into a single super-critical one (Fig. 1). Sub-critical masses assembling is carried out by chemical explosives blasting. This was the principle of action of “Little Boy” NED, dropped on Hiroshima (Japan) on August 6th, 1945 [4].
|
|
1 – vertical stabilizers 2 – steel breech 3 – detonator 4 – chemical explosives (cordite) 5 – “bullet” made from 235U: 6 “rings” (25.6 kg) 6 – barometric equipment 7 – plating 8 – control block 9 – barrel (steel, inner diameter 10 cm, length 2 m, weight 450 kg) 10 – connecting cables 11 – tamper (steel) 12 – target made from 235U: 2 “rings” (38.5 kg) 13 – tamper (tungsten carbide) 14 – neutron initiator 15 – radar antenna 16 – jack for boron absorber
|
Fig. 1. Schematic diagram of “Little Boy” NED
Fissionable material (90% 235U + 10% 238U) consists of two sub-critical masses: target and “bullet”. “Bullet” is shaped like a cylinder with a diameter of 10 cm and a height of 16 cm. Blasting of chemical explosives leads to “bullet” going fast into direction of target. Target is shaped like a hollow cylinder of an outer diameter and a height of 16 cm. At the moment of the maximum super-criticality when “bullet” is located entirely in the target, about three critical masses of uranium are formed [4].
The present article is based on the fundamental work performed in 1993 by J. Carson Mark [5], a distinguished scientist at Los Alamos National Laboratory and a former member of the Manhattan Project. Considering the device “Trinity” (the world’s first test of nuclear weapons technology that occurred on 16th of July, 1945, in the state of New Mexico, USA, as part of the Manhattan Project), J. Carson Mark demonstrated that the energy yield of the nuclear chain reaction is proportional to achieved super-criticality to the third power:
~ 
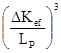, (1)
where: 
– achieved super-criticality;
– prompt neutrons life-time.
However, this estimate is only of a demonstrative nature of this effect, because it does not take into account the specific properties of fissile material and assembled gun-type HNED. In the present paper, an approach has been developed that allows us to get quantitative requirements to ensure proliferation protection of a given isotopic composition of uranium.
In this approach elements of interior ballistics and strength of materials theories are used, as well as neutron-physical properties of uranium of a given isotopic composition are taken into account (by means of neutron-physical calculations by Monte Carlo method).
So, from equation (1) it could be derived, that to get the maximum energy yield the state of high super-criticality should be achieved. Achieved super-criticality depends on the moment when nuclear chain reaction will lead to the beginning of the destruction of system integrity. Thus, system integrity destruction at the initial stage of subcritical masses assembling leads to low super-criticality (close to zero). Achieved super-criticality would be at its maximum level if system integrity destruction occurs when “bullet” is located entirely in the target. This requires high “bullet” velocity: indeed, in this case it can completely enter into the target before system integrity destruction.
High “bullet” velocity demands powerful chemical explosives, which means high pressure of powder gases in the barrel. Let us consider methodology that allows us to estimate the achievable “bullet” velocity, when the barrel withstands the resulting pressure of powder gases.
2. Calculation model for upper estimate of sub-critical masses assembling
Let us suppose that “bullet” moves under the constant pressure of powder gases. In this case its motion is uniformly accelerated, and based on Newton's second law one can find “bullet” velocity at the end of the barrel (i.e., at the moment of sub-critical masses assembling):
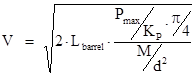, (2)
where: Lbarrel – barrel length;
Pmax – maximum pressure of powder gases withstood by the barrel;
KP – coefficient of uneven pressure of powder gases;
M – “bullet” mass;
d – “bullet” diameter.
Note, that in real guns coefficient of uneven pressure of powder gases KP ≈ 2.15 [6], the value which will be used in the further considerations.
“Bullet” mass and diameter are determined by neutron-physical properties of uranium. To determine Pmax let us use the equation of A.V. Gadolin (the barrel is a double-layer cylinder, technique used in practice) [7]:
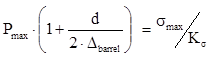, (3)
where: Δbarrel – barrel width;
σmax – the maximum stress in the barrel material;
Kσ – safety factor of the barrel material.
Now, substituting the value Pmax from the formula (3) into (2), one can estimate “bullet” velocity at the end of the barrel (which determines how fast the super-critical state is created, and, ultimately, gun-type HNED energy yield):
.
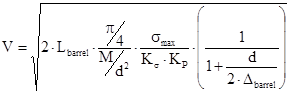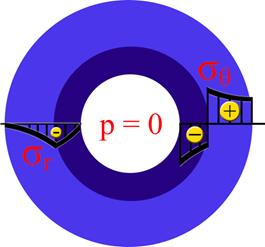
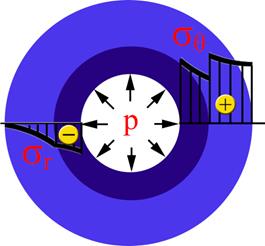
Note, that in the present paper the case is considered when the barrel is a two-layer cylinder. Visualization of normal (sr) and tangential (sθ) stresses in the material of the two-layer thick-walled cylindrical barrel, loaded with internal pressure is shown in Fig. 2. In practice, there are barrels consisting of more than two cylinders.
|
|
|
Fig. 2. The stress distributions in the barrel before and after the internal pressure load (left and right respectively)
Let us formulate the main points of the calculation model for upper estimate of “bullet” velocity at the end of the barrel:
1) “bullet” motion is uniformly accelerated;
2) Ks = 1.0: there is no reserve of strength;
3) σmax = 8 000 kG/cm2: if Ks = 1.0 then the maximum stress in the barrel material (σmax), which is used for real guns projects, is only 5 000 ÷ 6 000 kG/cm2;
4) KP = 2.15: that is typical for real guns [6];
5) the barrel has length of 10 meters and weight of 10 tons: larger dimensions and weight characteristics are too large for barrel handling and transportation.
Note, that some of the model’s points are real (KP = 2.15), while some are unachieved in practice (Ks = 1.0). As a result, this model will give us upper estimate of “bullet” velocity at the end of the barrel.
With the help of scientific visualization on the basis of the model formulated above the maximum “bullet” velocity at the end of the barrel should be estimated. This task, by fixed uranium enrichment, depends on two parameters (length and weight of the barrel) and, therefore, suggests using two-dimensional graphics as the most convenient option, as the range of achievable “bullet” velocity is limited by two curves: one curve corresponds to the barrel the length of which is 10 meters and the other curve corresponds to the barrel the weight of which is 10 tons. Having shaded the region of achievable “bullet” velocity one should find the maximum value, which is 665 m/s for the case when fissile material is (20% 235U + 80% 238U) and 1318 m/s for the case when fissile material is (90% 235U + 10% 238U) (Fig. 3).
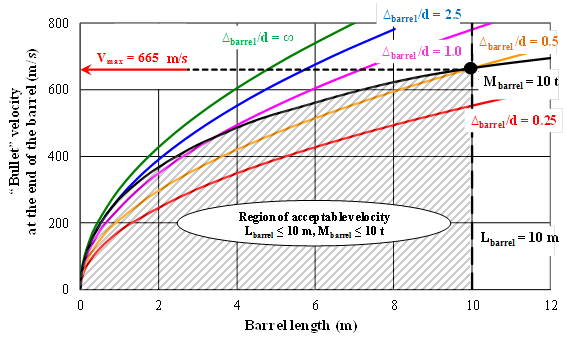
a) fissile material (20% 235U + 80% 238U)
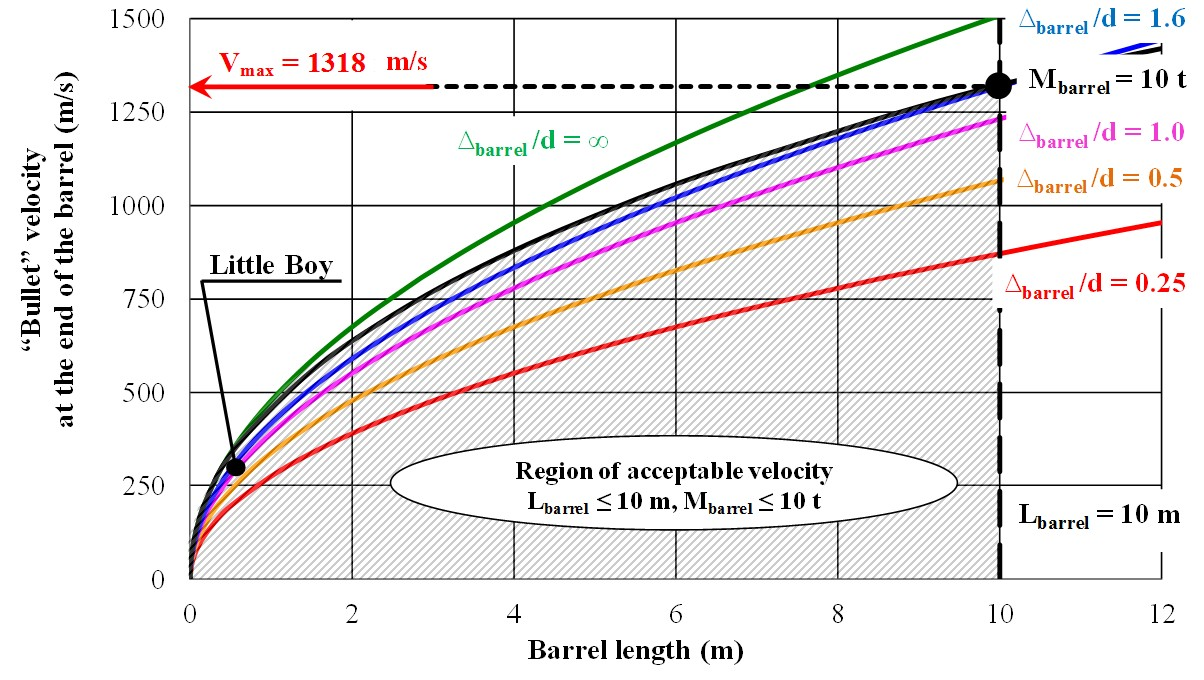
b) fissile material (90% 235U + 10% 238U)
Fig. 3. Estimating maximum “bullet” velocity at the end of the barrel Vmax
3. Pre-detonation and fizzle yield
To assess the evolution of neutron density in the fissionable material of gun-type HNED, the approach is used, which takes into account stochastic nature of nuclear chain reaction [8, 9].
Let us consider the linear input of reactivity as the mode of system transition from sub-critical state into super-critical one. In this case, effective neutron multiplication factor can be written as:
where: 
– change rate of 
;
t0 – time, that is required for the system to transit from critical state (Kef = 1) into the maximum super-critical state (Kef = (Kef)max).
It is assumed that t = 0 is the time moment when the system goes through a critical state, and initiated at time moment t1 an uninterrupted nuclear chain reaction continues until a time moment t2, when system loses its integrity. Note, that system loses its integrity after e45 acts of fission [5].
For assessing relative energy yield of gun-type HNED the approximation of “strong” neutron source is used, since this technique has no assumptions and takes into account the possibility of initiating uninterrupted nuclear chain reaction before the criticality is achieved [8].
Approximation of “strong” neutron source has the following equation for relative energy yield of gun-type HNED:
(4)
is defined as:
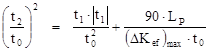, (5)
t1 is solution of the following equation:
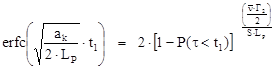, (6)
where: LP – prompt neutrons life-time;
– the maximum super-criticality value;
– cumulative probability of uninterrupted nuclear
chain reaction initiating at τ < t1 (pre-detonation
probability, considered at the level of 90%);
– average number of neutrons per fission;
– table parameter [10, 11].
On the basis of the maximum “bullet” velocity at the end of the barrel (Fig. 3) it is easy to estimate time t0, during which system super-criticality increases.
Fig. 4 shows the process of growth of the effective neutron multiplication factor Kef during subcritical masses assembling in gun-type HNED assembled on the basis of (20% 235U + 80% 238U). Let us consider the case when during sub-critical masses assembling the critical state (Kef = 1) is achieved at the time moment t = 0. After this moment the effective neutron multiplication factor Kef exceeds one and grows. Only in the case if sub-critical masses assembling process continues until the moment of the maximum super-criticality (i.e., t2 = t0), the maximum energy yield will be achieved (Xmax = 100%), as can be derived from equation (4). In fact, this is the normal mode of gun-type HNED operation.
For the normal mode of gun-type HNED operation (X = 100%, i.e. t2 = t0), on the basis of the equation (5) it is easy to determine moment of time t1 (uninterrupted nuclear chain reaction initiation), which is very close to moment of time t2 (system loses its integrity): the difference is a few hundredths of t0, i.e. e45 acts of fission occur very fast. Therefore, to ensure the maximum energy yield, t1 should be about 0.98 ¸ 0.99 t0.
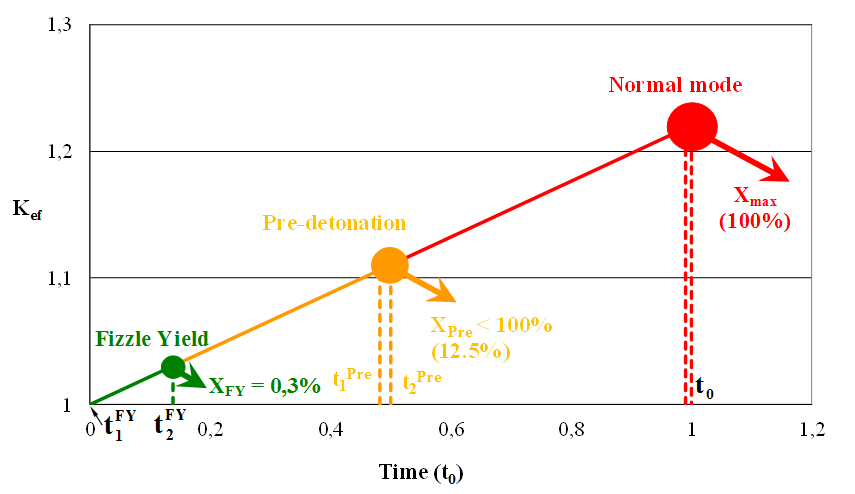
Fig. 4. Visualization of normal mode, pre-detonation and fizzle yield of gun-type HNED (20% 235U + 80% 238U)
A premature start of nuclear chain reaction (at time moment 
) is defined as
pre-detonation: in this case system loses its integrity at time moment 
. According to (4)
it means reduced energy yield XPre < 100% (Fig. 4). For
pre-detonation regime presented in Fig. 4 (t2 = 0.5∙t0)
relative energy yield XPre, which is proportional to (t2)3,
is 12.5%.
Among regimes of pre-detonation there is a special case when uninterrupted nuclear chain reaction initiates at the time moment of critical state (Kef = 1). This case is called fizzle yield (FY). It corresponds to the minimum energy yield 0.3% (in the approximation of “weak” neutron source) [5].
From Fig. 4 it can be concluded, that to ensure proliferation protection of uranium (reducing energy yield of HNED), one should introduce neutron source into uranium under consideration, strong enough to initiate uninterrupted nuclear chain reaction at the very moment of achieving critical state. This is the case when energy yield of gun-type HNED is the lowest.
Important point is that the method under consideration (reducing energy yield by introducing neutron source into fissionable material) has its limit: it is impossible to reduce energy yield down to zero (as applied to practically achievable neutron sources).
However, is it appropriate to try to achieve fizzle yield or is it reasonable to choose a smaller neutron source? What energy yield will be in this case? To answer this question, let us consider dependence of gun-type HNED relative energy yield X on neutron source S, introduced into uranium (Fig. 5). The consideration is made for uranium of two isotopic compositions: (20% 235U + 80% 238U) and (90% 235U + 10% 238U).
Fizzle yield regime is characterized by the following values:
XFY (20% 235U + 80% 238U) = 0.3%,
XFY (90% 235U + 10% 238U) = 0.7%.
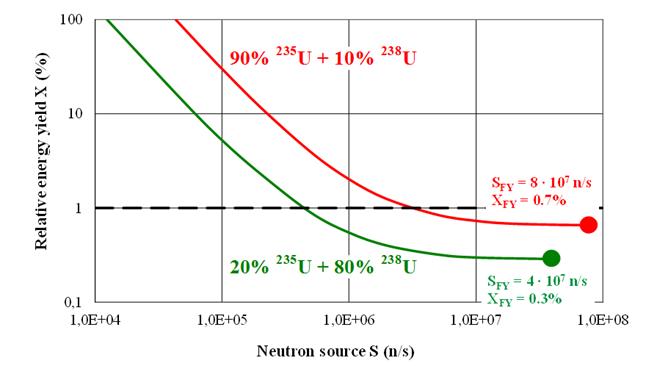
Fig. 5. Relative energy yield X on neutron source S (20% 235U + 80% 238U and 90% 235U + 10% 238U)
One can see that dependencies presented in Fig. 5 become flatter at high neutron sources. It is clear that the requirement for a neutron source providing fizzle yield regime is unnecessary and unfounded. Indeed, if the fissionable material is (20% 235U + 80% 238U), then at neutron source 106 n/s (i.e. 40 times smaller than SFY) relative energy yield X » 2×XFY (only 2 times larger than XFY). Therefore, as a requirement for a neutron source, apparently, it would be reasonable to choose S ~ 106 n/s, as its further increase does not lead to a noticeable decrease of energy yield.
Let us consider the requirement to reduce relative energy yield X down to 1% of the nominal value. This is achieved at the following neutron sources:
0.4×106 n/s for (20% 235U + 80% 238U);
3.1×106 n/s for (90% 235U + 10% 238U).
4. Isotope 232U as a powerful neutron source
How could one achieve mentioned above significant neutron source (S ~ 106 n/s, which reduces relative energy yield down to 1% of the nominal value)?
It is assumed to introduce isotope 232U into uranium. Isotope 232U is a powerful spontaneous fission neutron source: 1300 n/s×kg [12]. However, it is not enough to provide neutron source of about 106 n/s.
It is important to note that uranium contains admixture of light elements (such as lithium, beryllium, and so forth) as impurities. As a result of a-decay of heavy nuclei (mainly 232U, which has a relatively short half-life: 68.9 years [13]) emitted a-particles colliding with the nuclei of light elements, lead to neutron generation as a result of (a,n)-reaction. It was found out that the rate of neutron generation by means of (a,n)-reaction on nuclei of light elements is much larger than the rate of neutron generation by means of spontaneous fission reaction of 232U.
The required amount of 232U for creating a given neutron source depends on the exposure time of 232U. Indeed, over time (as a result of 232U decay) its decay products are accumulated, which are radioactive isotopes and emit α-particles: these α-particles will initiate additional (a,n)-reactions on nuclei of light elements admixture. The radioactive decay of 232U results in building-up 228Th, decay chain of which includes five fast α-decays, resulting in building-up stable isotope 208Pb [13].
As decay chain of 232U includes not only 228Th a-decay, but also several subsequent fast a-decays and due to the fact that the energy of a-particles emitted as a result of these decays is high enough to create a strong neutron source, it is reasonable to provide 232U exposure to accumulate 228Th.
The present consideration suggests that radioactive decays of daughter nuclides of 228Th (i.e. 224Ra and following nuclides) occur instantly along with the decay of 228Th. In practice, this is accomplished with a sufficiently good accuracy: while half-life of 228Th is equal to 1.91 years, the half-lives of its daughter nuclides are several orders of magnitude smaller [13].
Nuclear concentrations of 232U and 228Th depend on time as follows:
(7)
, (8)
where: 
, 
– nuclear concentrations of 232U and
228Th at time moment t;
, 
– decay constants of 232U and 228Th,
determined as follows:
, (9)
where 
– half-life: (232U) = 68.9 years, (228Th) = 1.91
years [13].
Then, on the basis of known concentrations of 232U and 228Th, determined by equations (7) and (8), one can estimate neutron source S (produced by 232U spontaneous fission and neutrons emitted as a result of (a,n)-reaction on nuclei of light elements) on 232U exposure time is presented in Fig. 6. Specific neutron source is considered (per unit of mass of 232U), and the content of impurities of light elements corresponds to the characteristics of uranium compounds, produced at Novosibirsk Chemical Concentrates Plant, which is one of the world’s leading manufacturers of the nuclear fuel for NPPs and for research reactors in Russia [14].
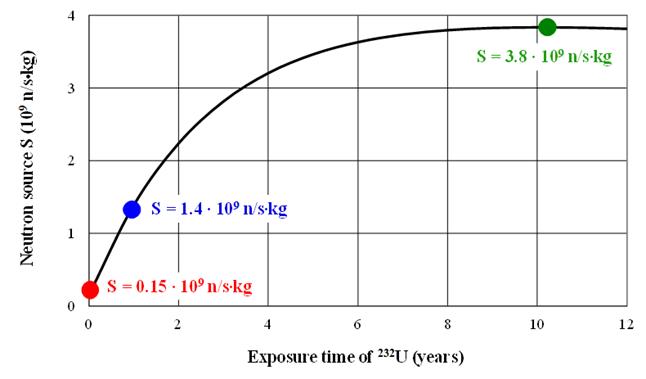
Fig. 6. Dependence of neutron source, created by 232U and light elements admixture, on exposure time of 232U
One can conclude that it is reasonable to organize the technological process in such a way that 232U would be exposed during some time before its introduction into uranium. Indeed, the specific neutron source, created by 232U and light elements admixture, increases significantly with increasing exposure time of 232U, especially at the first time periods (Fig. 6).
From Fig. 6 one can see that 232U exposure leads to an increase of specific neutron source from 0.15∙109 n/s∙kg (no exposure) to 3.8∙109 n/s∙kg when equilibrium concentration of 228Th is achieved (228Th accumulation rate is equal to 228Th decay rate). This state corresponds to 232U exposure time of about 10 years.
Let us consider using 232U of one year exposure time to create the required neutron source, which would provide the relative energy yield X at the level of 1% of the nominal value. In this case 232U is a neutron source of 1.4∙109 n/s∙kg (Fig. 6). Cases of no exposure, as well as exposure time equal to 10 years, will be presented for comparison as ultimate cases.
5. Recommendations on uranium proliferation protection
Let us estimate the amount of 232U, introduction of which into uranium could provide mentioned above neutron sources. Three exposure times of 232U were considered: no exposure; one year exposure; 10 years exposure (corresponds to 228Th equilibrium state). Three-dimensional visualization of the results is presented in Fig. 7.
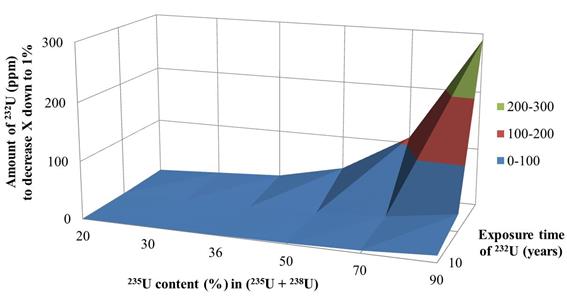
Fig. 7. Amount of 232U to decrease relative energy yield X down to 1% of the nominal value (various exposure times of 232U are considered)
From Fig. 7 one can conclude that exposure time of 232U is an important parameter: the larger it is the smaller amount of 232U is required for uranium proliferation protection. Assuming one year exposure time, one can see that the required amount of 232U for reducing X down to 1% of the nominal value is between 0.3 ppm (20% 235U + 80% 238U) and 30 ppm (90% 235U + 10% 238U) (Fig. 8).
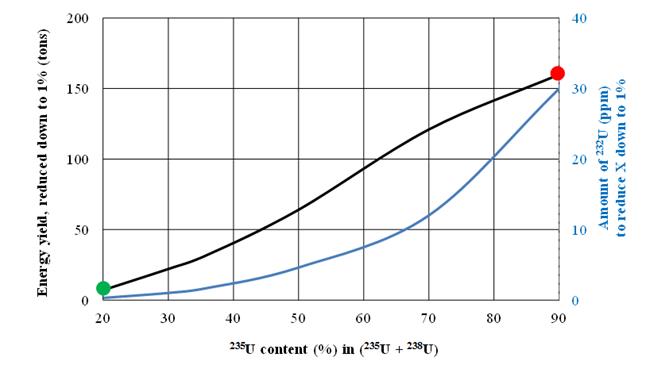
Fig. 8. Energy yield in pre-detonation regime and required amount of 232U
Fig. 8 shows a possible reduction of energy yield due to pre-detonation and required amount of 232U. Note, that for (20% 235U + 80% 238U) energy yield, decreased down to 1% of the nominal value, is equal to 7 tons. At the same time the weight of HNED, based on (20% 235U + 80% 238U), is at least 10 tons (barrel weight). Thus, such a HNED is not attractive in terms of its efficiency (marked by green color in Fig. 8).
On the other hand, in the case of (90% 235U + 10% 238U) energy yield, decreased down to 1% of the nominal value, is equal to 160 tons. Thus, the effectiveness of such a HNED should be recognized (marked by red color in Fig. 8). It is impossible to ensure proliferation protection of (90% 235U + 10% 238U) by introducing a neutron source into it: even an extremely strong neutron source could not reduce energy yield down to acceptable values.
6. Conclusion
On the basis of open literature data calculation-theoretical model has been developed and visualized, which allows us to estimate energy yield of gun-type HNED, based on uranium of a given isotopic composition, as well as to develop requirements that can reduce energy yield down to a certain value.
The novelty of gun-type HNED model is an approach that allows us to estimate the achievable time of super-criticality state creation in gun-type HNED, based on uranium of a given isotopic composition.
It was found out that in order to reduce the effectiveness of gun-type HNED it is reasonable to consider the introduction of neutron source, providing energy yield reduction down to ~ 1% of the nominal value with probability of 90%: further increase of neutron source does not lead to a significant reduction of energy yield.
Reduction of energy yield of gun-type HNED down to ~ 1% of the nominal value with probability of 90% requires the introduction of between 0.3 ppm 232U (fissionable material: 20% 235U + 80% 238U) and 30 ppm 232U (fissionable material: 90% 235U + 10% 238U).
Visualization of uranium proliferation protection issues is essential, as this subject concerns not only engineers, but also representatives of some of the humanities. Also, students tend to understand the material easier when it is presented in this way.
References
1. Hansen G.E. Assembly of Fissionable Material in the Presence of a Weak Neutron Source. Nuclear Science and Engineering, 1960, vol. 8. —709–719 p.
2. Kang J. and F. N. von Hippel. U-232 and the Proliferation-Resistance of U-233 in Spent Fuel. Science and Global Security, 2001, vol. 9. –1-32 p.
3. Gilfoyle G. P. and Parmentola J. A. Using Nuclear Materials To Prevent Nuclear Proliferation. Science and Global Security, 2001, vol. 9. –81-92 p.
4. Little Boy – Wikipedia, the free encyclopedia [Electronic resource]. URL: http://en.wikipedia.org/wiki/Little_Boy. (Available at 29.06.2015)
5. Mark J.C. Explosive Properties of Reactor-Grade Plutonium. Science and Global Security, 1993, Vol. 4. – 111-128 p.
6. Kofman V.L. Japonskie linkory Vtoroj mirovoj. “Jamato” i “Musasi” [Japanese battleships of the Second World War. “Yamato” and “Musasi”]. M.: Collection, Yauza, EKSMO, 2006.
7. Feodos’ev V.I. Soprotivlenie materialov [Strength of materials]. M.: Bauman Moscow State Technical University, 2001.
8. Hansen G.E. Assembly of Fissionable Material in the Presence of a Weak Neutron Source. Nuclear Science and Engineering, 1960, Vol. 8. –709–719 p.
9. Shabalin E.P. Impul'snye reaktory na bystryh nejtronah [Fast impulse reactors]. M.: Atomizdat, 1976.
10. Urig R. Statisticheskie metody v fizike jadernyh reaktorov [Statistical Methods in the Nuclear Reactor Physics]. M.: Atomizdat, 1974.
11. Seifritz W. Nukleare Sprengkörper – Bedrohung oder Energieversorgung für die Menschheit? – München: Karl Thiemig AG, 1984.
12. Reilly, Ensslin, Smith, and Kreiner. Passivnyj nerazrushajushhij analiz jadernyh materialov [Passive Nondestructive Assay of Nuclear Material]. M.: Binom, 2000.
13. Babichev A.P., Babushkina N.A., Bratkovsky A.M. et al. Fizicheskie velichiny: Spravochnik [Physical quantities: Reference book]. M.: Energoatomizdat, 1991.
14. Uranium compounds NCCP [Electronic resource]. URL: http://www.nccp.ru/en/products/uranium_compounds. (Available at 29.06.2015)