ВИЗУАЛИЗАЦИЯ ВИХРЕВЫХ СТРУКТУР МЕТОДОМ АНЕМОМЕТРИИ ПО ИЗОБРАЖЕНИЯМ ЧАСТИЦ
Н.М. Скорнякова1, Д.Г. Сычев1, А.Ю. Вараксин2, 3, М.Э. Ромаш2
1Национальный исследовательский университет «МЭИ», Россия, E-mail: nmskorn@mail.ru
2 Объединенный институт высоких температур РАН
3 Московский государственный технический университет им. Н.Э. Баумана, Россия
Содержание
2. Схема экспериментальной установки для визуализации
3. Визуализация путем прямой видеорегистрации
4. Визуализация векторного поля методом анемометрии по изображениям частиц
Аннотация
Представлены результаты прямой видеорегистрации свободных концентрированных воздушных вихрей и векторное поле скоростей в сечении вихря. Векторное поле скоростей визуализируется с помощью метода анемометрии по изображениям частиц.
Ключевые слова: визуализация, свободные концентрированные воздушные вихри, метод анемометрии по изображениям частиц, векторное поле скоростей.
1. Введение
Качественная и количественная визуализация физических процессов очень важна для их понимания. Не всякий процесс доступен для простейшего наблюдения человеческим глазом, а, как известно, информация, представленная в наглядной форме имеет больший вес, чем обычные формулы и гипотезы. Помимо прочего, текущее развитие технологий позволяет создавать все более и более качественные приборы регистрации изображений, что, соответственно, положительно сказывается на возможностях оптических методов визуализации. Одним из широко применяемых методов визуализации является метод анемометрии по изображениям частиц, при помощи которого и производились исследования в данной работе.
Метод анемометрии по изображениям частиц (в англоязычной литературе – PIV – Particle Image Veloсimetry) – метод цифровой визуализации потоков [1, 2]. В основе метода лежит рассеяние структурированного лазерного излучения на частицах, которыми засеян исследуемый поток. Лазерное излучение при помощи специальной оптики преобразуется в лазерный «нож», который подсвечивает движущиеся частицы в выбранном сечении потока. Процесс, как правило, записывается на скоростную видеокамеру. Далее выполняется кросс-корреляционная обработка полученных изображений, по результатам которой строится векторное поле скоростей.
Из необъятного множества различных физических процессов, исследование которых представляет тот или иной научный интерес, остановимся на аэродинамических процессах. Будет представлено физическое моделирование и визуализация свободных концентрированных воздушных вихрей (торнадо, смерч) [3, 4].
Смерч – это наименьшая по размерам, но характеризующаяся наибольшей скоростью вращения форма вихревого движения воздуха. Ширина смерча достигает от нескольких метров до двух-трёх километров, а высота от нескольких метров до одного-двух километров. Центральная часть узкая и высокая; стенки характеризуются очень высокими скоростями вращения.
Причины образования смерчей остаются не достаточно изученными и по сей день.
2. Схема экспериментальной установки для визуализации
Генерация вихревых структур осуществлялась путем создания неустойчивой стратификации воздуха над подстилающей поверхностью алюминиевого листа (диаметр – 1100 мм, толщина – 1,5 мм), нагреваемого снизу газовой горелкой (максимальная тепловая мощность – 3,5 кВт). Схема используемой экспериментальной установки и режимы нагрева подробно описаны в работах [5, 6]. Для визуализации образуемых вихревых структур применялись частицы магнезии (химическая формула – 4MgCO2Mg(OH)24H2O, физическая плотность – 3900 кг/м3), которые наносились тонким слоем на подстилающую поверхность перед проведением экспериментов. Фотография данной части экспериментальной установки представлена на рис. 1.

Рис. 1. Фотография экспериментальной установки для генерации вихревых структур
Система регистрации состоит из двух составляющих. Для прямой видеорегистрации применяется цифровая видеокамера (модель Sanyo VCC-6572P, Япония). Для визуализации по методу анемометрии по изображениям частиц генерируется лазерная плоскость, расположенная под углом 45° к подстилающей поверхности. Частицы магнезии, поднимающиеся вместе со сгенерированным свободным концентрированным воздушным вихрем, попадая в лазерную плоскость, рассеивают излучение, которое и регистрируется с помощью высокоскоростной цифровой видеокамеры Hispec1.
Приемная матрица видеокамеры изготовлена по технологии КМОП с размером пикселя 14 мкм, при котором обеспечивается высокая светочувствительность. В скоростном режиме при скорости съемки до 506 кадров/с разрешение получаемых с помощь камеры изображений будет максимально возможным для данной модели, равным 1280 пикселей × 1024 пикселей. Таким образом, данная камера оптимально подходит для регистрации быстро протекающих процессов. Глубина цвета при видеозаписи составляет 10 бит.
3. Визуализация путем прямой видеорегистрации
При прямой видеорегистрации для подсветки включается несколько светодиодных прожекторов, что позволяет визуально наблюдать свободный концентрированный воздушный вихрь. Основной проблемой проводимых исследований является непредсказуемость места и времени возникновения вихря. После образования вихрь также не находится на одном месте, а перемещается по случайной траектории. Структура вихря также претерпевает существенные изменения.

Видеоролик 1 – Прямая видеорегистрация свободного концентрированного воздушного вихря
В представленном видеоролике 1 периодически появляются частицы, подсвеченные зеленой лазерной плоскостью. Именно по этим частицам будет выполняться построение векторного поля по методу анемометрии по изображениям частиц.
4. Визуализация векторного поля методом анемометрии по изображениям частиц
В методе анемометрии по изображениям частиц (АИЧ) исходными данными являются ярко подсвеченных лазером частицы на темном фоне в два различных момента времени. Обработка данных изображений осуществляется с помощью кросскорреляционного метода. Кросскорреляция – это метод, позволяющий с помощью корреляционной функции рассчитать векторное поле смещения двух изображений (фото) относительно друг друга. Речь идет о двух кадрах (по одной экспозиции на каждый), на которых запечатлены движущиеся элементы – в противоположность методу автокорреляции, где используется всего один кадр с наложением двух экспозиций, т.е. обрабатываются два одинаковых изображения.
Сначала дадим определение корреляционной функции. Функция корреляции функций I1 и I2 в общем случае рассчитывается по формуле
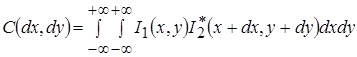 . (1)
. (1)
Покажем, как корреляционная функция позволяет найти смещение. Типичное изображение, используемое в кросскорреляционном методе, можно представить (в идеале) в виде множества одинаковых по размеру и высоте пиков на нулевом фоне. Пусть имеется два одномерных изображения (рис. 1) в виде нескольких одинаковых узких пиков. Зафиксируем второе изображение, а первое наложим на второе, и будем смещать относительно второго.
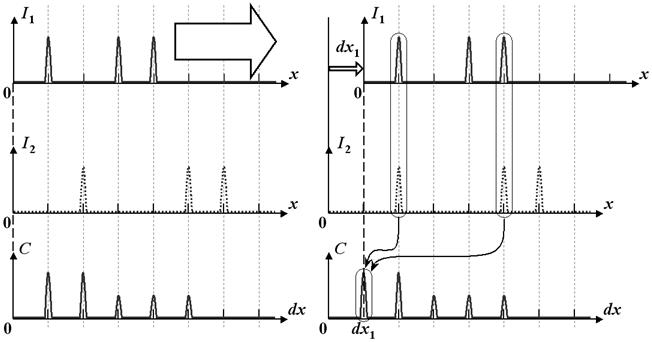
а б
а) – нулевое смещение; б) – пример смещения (dx1), при котором перекрываются две пары пиков на изображениях
Рис. 2 – Два одномерных изображения и соответствующая корреляционная функция
В данном случае по оси абсцисс откладывается смещение первого графика относительно второго. По оси ординат – значения, определяющиеся следующими условиями: при данном смещении графиков, если мысленно наложить первый, смещенный график на второй, в случае если пики первого и второго графиков вообще не совпадают, корреляционная функция равна нулю. Если же при данном смещении наблюдается совмещение пиков первого и второго графиков, корреляционная функция дает некоторый максимум, причем его величина пропорциональна количеству пар пересекшихся пиков.
Рассмотрим двухмерный случай. Пусть имеются два изображения, каждое из которых разбивается на равные квадраты, именуемые окнами опроса, на которых запечатлена группа движущихся элементов – частиц (рис. 2). Примем в качестве идеализации, что группа частиц движется, не меняя своей общей формы.
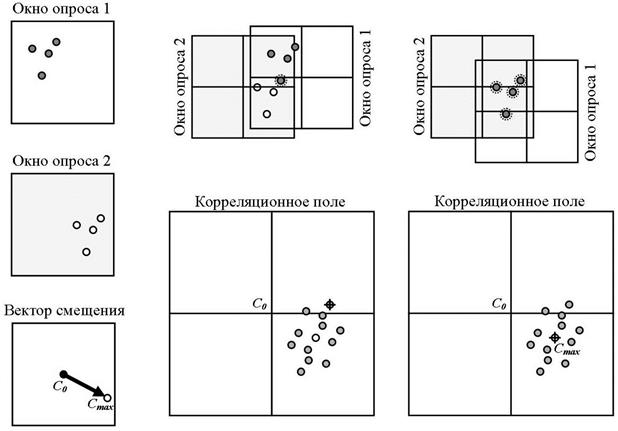
а б
C0 – центр корреляционного поля, Cmax – корреляционный максимум; перекрывающиеся пары пиков выделены пунктиром; крестом показано положение точки, в которой рассчитывается корреляционная функция; а) – случай, когда перекрывается одна пара пиков; б) – случай, когда перекрываются все пары пиков
Рис. 3 – Схема, поясняющая связь между корреляционной функцией и вектором смещения изображений
Как и в предыдущем случае, мысленно зафиксируем второе окно опроса, а первое будем смещать относительно второго. Так как окна опроса имеют конечные размеры, диапазон смещений, в котором рассчитывается корреляционная функция, имеет смысл, только если при соответствующем смещении окон опроса площадь их пересечения будет ненулевой (т.е. окна должны пересекаться). Отсюда нетрудно видеть, что данная область смещений, называемая корреляционным полем, имеет размер, в два раза превосходящий размер окна опроса. На рис. 3 у окон опроса для удобства показаны центры (при этом смещением являются координаты вектора, проведенного из центра второго окна к центру первого окна опроса). Представим, что оба окна опроса совмещены – это нулевое смещение, и оно соответствует центральной точке (началу координат) на корреляционном поле. Теперь будем смещать первое окно опроса в различных направлениях. При некоторых смещениях можно прийти к ситуации, когда при наложении окон опроса перекрывается по одному изображению частицы с каждого окна, и в соответствующей точке корреляционного поля получается небольшой максимум (речь идет конкретно о примере группы частиц на рис. 3, в произвольном случае может перекрыться и большее количество изображений частиц). Если же взять смещение окон, соответствующее реальному вектору смещения группы движущихся частиц, то, как нетрудно догадаться, произойдет совмещение всех изображений частиц. В соответствующей точке корреляционного поля будет максимум с большим по величине значением. Отсюда следует основной принцип метода кросскорреляции: для двух окон опроса с изображением движущихся мелких элементов рассчитывается корреляционная функция (корреляционное поле с началом координат в центре поля), затем в этом поле ищется максимальный пик, координаты которого будут координатами вектора смещения группы элементов. Естественно, что в реальных фотографиях присутствуют шумы (т.е. пики), участвующие в корреляции и приводящие к появлению шумов на корреляционном поле; также, в отличие от показанной выше модели, в реальности группа частиц при движении меняет свою форму, и перекрытия всех изображений элементов не получится. Но если фотографии имеют высокий контраст (что снижает влияние шумов), достаточное большое количество изображений элементов и правильно подобранный размер окна опроса, то бόльшая часть движущейся группы не поменяет форму. Благодаря этому, бόльшая часть изображений элементов перекроется и даст наибольший пик. Отсюда вытекает статистическая природа метода кросскорреляции – этот метод позволяет найти некий усредненный, среднестатический вектор смещения группы изображений элементов.
Рассмотрим простейший компьютерный алгоритм обработки изображений с помощью метода кросскорреляции. Примем, что нумерация элементов всех матриц начинается с нуля. Имеются два изображения одинакового размера, которые представляют собой матрицы (обозначим их как A и B). Каждый элемент матрицы – это пиксель фотографии, значение элемента – яркость этого пикселя. A и B разбиваются на квадратные зоны опроса, имеющие определенный размер, наиболее популярные – 32×32 и 64×64 пикселя (элемента). Программа с помощью счетчика последовательно меняет подвергающиеся обработке окна опроса, одинаково сканируя обе фотографии слева направо, сверху вниз (рис. 4).

Рис. 4. Пример: два изображения, каждое разбито на 30 окон опроса, выделена одна из пар окон опроса
В качестве конечного результата всей программы выступает матрица V, каждый элемент которой ставится в соответствие определенной паре окон опроса (O1 и O2) и представляет собой массив из двух чисел – координат вектора смещения для данной пары окон опроса. Количество строк и столбцов этой матрицы равно количеству окон опроса, умещающихся на изображении по вертикали и горизонтали соответственно (для рис. 4 матрица V будет состоять из 5 строк и 6 столбцов). По матрице V строится векторное поле. Для того чтобы рассчитать определенный элемент матрицы Vij, необходимо для соответствующей пары окон опроса O1 и O2 найти координаты максимума корреляционного поля. Корреляционное поле обозначим как матрицу С. На рис. 5 показано, как работает алгоритм расчета матрицы C на примере трех ее элементов.
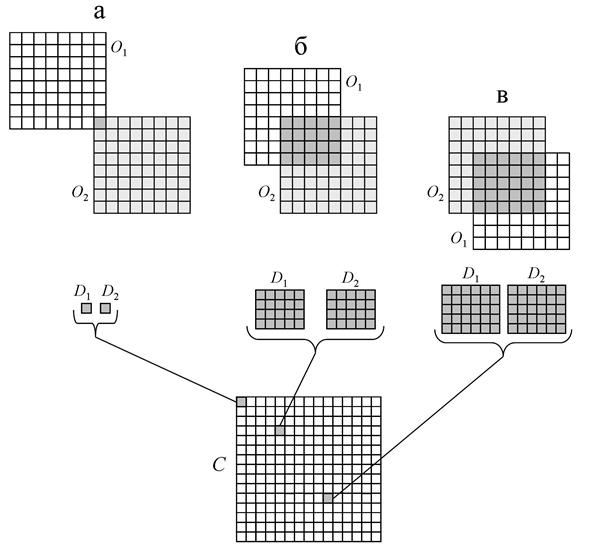
Создаются две матрицы окон опроса O1 и O2. Далее представим, что матрица O2 зафиксирована, а матрица O1 наложена на O2 и может смещаться.
а), б), в) – примеры различных случаев смещения окон опроса, также показано положение соответствующих элементов матрицы С
Рис. 5. Схема алгоритма расчета корреляционного поля, размер окна опроса 8×8 пикселей
С помощью счетчика по строкам и столбцам матрицей O1 как бы «сканируют» поверх матрицы O2, начиная с пересечения правого нижнего угла O1 и левого верхнего угла O2 (на рис. 5, а), и заканчивают «сканирование», когда пересекаются левый верхний угол O1 и правый нижний угол O2.Для каждого положения окна опроса O1 рассчитывается элемент матрицы корреляционного поля C. Если размер стороны окна опроса равен n пикселям, то размер матрицы C равен 2n-1 на 2n-1 элементов. Для произвольного элемента Cij величина соответсвующего реального смещения в пикселях p, q (по вертикали и горизонтали) определяется следующими выражениями: p = i – n + 1, q = j – n + 1 (это вытекает из того, что радиус-вектор смещения соединяет центры второго и первого окна). Для примера на рис. 5 матрица C имеет размер 15×15 элементов. В случае а) подразумевается смещение (-7; -7), в случае б) – (–4; –3), в случае в) – (3; 2). Рассмотрим, каким образом при заданном смещении вычисляется величина корреляционной функции. Создаются две одинаковые по размеру матрицы – D1 и D2, представляющие собой области пересечения обоих окон опроса, как фрагменты матриц O1 и O2 соответственно. Далее, значение корреляционной функции вычисляется как сумма произведений соответствующих элементов матриц D1 и D2, что следует из формулы (1), записанной в дискретном виде (т.к. программа оперирует матрицами):
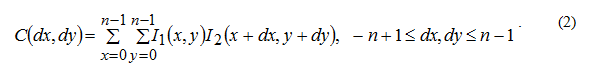
В данном случае для определенного смещения значение функции вычисляется по формуле
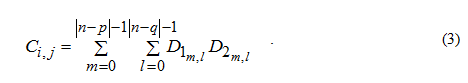
После того, как рассчитывается матрица C, в ней ищется элемент с максимальным значением. Вычисляются координаты смещения p и q по формулам p = i – n + 1, q = j – n + 1, где i и j – номер элемента с максимальным значением. Тогда значение (в виде массива из двух чисел) элемента матрицы V, соответствующего данной паре окон опроса, принимается равным (p; q). Далее берется следующая пара окон опроса, расчет корреляционного поля и поиск его максимума повторяется по приведенной выше схеме, и т.д., пока не будет полностью рассчитана матрица V. По матрице V строится векторное поле – результат расчета [7, 8].
В результате кросскорреляционной обработки видеоролика, представленного в предыдущем разделе, получится векторное поле скоростей свободного концентрированного вихря, представленного в видеоролике 2.

Видеоролик 2 – Векторное поле скоростей свободного концентрированного воздушного вихря
5. Заключение
В работе показана возможность визуализации методом прямой видеорегистрации, что позволяет представить структуру лабораторно сгенерированных свободных концентрированных воздушных вихрей, понять их характер движения.
Одновременно с этим была проведена регистрация методом анемометрии по изображениям частиц. В результате получены векторные поля скорости, которые позволят более подробно изучить характеристики образованных вихрей.
В дальнейшем планируется получить численные значения проекции скорости в различных сечениях вихря и в различные моменты времени.
Благодарности
Работа выполнена при поддержке Российского научного фонда (соглашение № 14-19-00453).
Список литературы
1. Raffel M., Willert C.E., Wereley S.T., Kompenhans J. Particle Image Velocimetry. Springer, 2007.
2. Скорнякова Н.М. Исследование микровихрей методом анемометрии изображения частиц. Труды 16-й Международной научной конференции «Лазерно-информационные технологии в медицине, биологии и геоэкологии», Новороссийск, 2008.
3. Varaksin A.Yu., Romash M.E., Kopeitsev V.N., Taekin S.I. The Possibility of Physical Simulation of Air Tornados under Laboratory Conditions. High Temperature, 2008, vol. 46, № 6, p. 888-891.
4. Varaksin A.Yu., Romash M.E., Kopeitsev V.N., Taekin S.I. The Parameters of Unstable Stratification of Air Leading to Generation of Free Vortexes. High Temperature, 2010, vol.48, № 2, p. 251-255.
5. Varaksin A.Y., Romash M.E., Kopeitsev V.N., Gorbachev M.A. Experimental Study of Wall-Free Non-Stationary Vortices Generation due to Air Unstable Stratification. Int. J. Heat Mass Transfer, 2012, vol. 55, p. 6567-6572.
6. Varaksin A.Y., RomashM.E., Kopeitsev V.N. Effect of Net Structures on Wall-Free Non-Stationary Air Heat Vortices. Int. J. Heat Mass Transfer, 2013, vol. 64, p. 817-828.
7. Skornyakova N.M., Sokolov M.M. and Tolkachev A.V. Cheap software for PIV image processing. CD proc. of 5 international symposium on Particle Image Velocimetry. Paper 3210. Pusan, Korea, 2003, 8 pp.
8. Poroikov A.Yu., Skornyakova N.M. An analysis of the image pattern correlation technique for measuring the bending of a metal surface. Measurement technique, vol. 53, №10, 2011, p. 1147-1151.
VIZUALIZATION OF VORTEX STRUCTURES BY PARTICLE IMAGE VELOCIMETRY
N.M. Skornyakova1, D.G. Sychev1, A.Yu. Varaksin2, 3, M.E. Romash2
1 National Research University (MPEI), Russia. E-mail: nmskorn@mail.ru
2 Joint Institute for High Temperatures of the Russian Academy of Sciences.
3 Bauman Moscow state technical university.
Abstract
The results of the direct video recording of free concentrated air vortices and the velocity vector field in the cross section of the vortex are presented. Velocity vector field is rendered by the method of the particle images velocimetry.
Keywords: vizualization, free concentrated air vortices, particle imafe velocimetry, vector field of velocity.
References
1. Raffel M., Willert C.E., Wereley S.T., Kompenhans J. Particle Image Velocimetry. Springer, 2007.
2. Skornjakova N.M. Issledovanie mikrovihrej metodom anemometrii izobrazhenija chastic [Research by microvortices anemometry particle images]. Proceedings of the 16th International Scientific Conference "Laser and Information technologies in medicine, biology and geo-ecology". Novorossiysk, 2008.
3. Varaksin A.Yu., Romash M.E., Kopeitsev V.N., Taekin S.I. The Possibility of Physical Simulation of Air Tornados under Laboratory Conditions. High Temperature, 2008, vol. 46, № 6, p. 888-891.
4. Varaksin A.Yu., Romash M.E., Kopeitsev V.N., Taekin S.I. The Parameters of Unstable Stratification of Air Leading to Generation of Free Vortexes. High Temperature, 2010, vol.48, № 2, p. 251-255.
5. Varaksin A.Y., Romash M.E., Kopeitsev V.N., Gorbachev M.A. Experimental Study of Wall-Free Non-Stationary Vortices Generation due to Air Unstable Stratification. Int. J. Heat Mass Transfer, 2012, vol. 55, p. 6567-6572.
6. Varaksin A.Y., RomashM.E., Kopeitsev V.N. Effect of Net Structures on Wall-Free Non-Stationary Air Heat Vortices. Int. J. Heat Mass Transfer, 2013, vol. 64, p. 817-828.
7. Skornyakova N.M., Sokolov M.M. and Tolkachev A.V. Cheap software for PIV image processing. CD proc. of 5 international symposium on Particle Image Velocimetry. Paper 3210. Pusan, Korea, 2003, 8 pp.
8. Poroikov A.Yu., Skornyakova N.M. An analysis of the image pattern correlation technique for measuring the bending of a metal surface. Measurement technique, vol. 53, №10, 2011, p. 1147-1151.