ПРИМЕНЕНИЕ МЕТОДА TIME-RESOLVED TOMOGRAPHIC PIV ДЛЯ ИССЛЕДОВАНИЯ ПРОЦЕССОВ ФОРМИРОВАНИЯ КОГЕРЕНТНЫХ ВИХРЕВЫХ СТРУКТУР В КВАЗИ-ДВУМЕРНОЙ ТУРБУЛЕНТНОЙ СТРУЕ

М.В. Шестаков ¹, М.П. Токарев ¹, Д.М. Маркович ^1,2

¹ Институт теплофизики СО РАН, Новосибирск, Россия, e-mail: mvsh@itp.nsc.ru

² Новосибирский государственный университет, Новосибирск, Россия, e-mail: dmark@itp.nsc.ru

Содержание

1. Введение

2. Описание метода

3. Описание эксперимента

4. Расположение и калибровка камер

5. Обработка данных

6. Результаты эксперимента

Аннотация

В докладе представлены результаты применения метода Tomographic PIV высокого временного разрешения для исследования процессов формирования и развития когерентных вихревых структур в квази-двумерной турбулентной струе. Получены трехкомпонентные трехмерные распределения скорости в объеме потока для ближнего и дальнего поля квази-двумерной турбулентной струи. На основании рассчитанных распределений Q критерия проанализированы процессы образования и развития вихревых структур в потоке. Показано, что в потоке квази-двумерной турбулентной струи формируются два типа когерентных вихревых структур: вторичные продольные вихревые структуры и квази-двумерные вихревые структуры, образующиеся вследствие развития сдвиговой неустойчивости Кельвина - Гельмгольца.

Ключевые слова: метод time-resolved tomographic piv, квази-двумерныя струя, динамика когерентных вихревых стркутур

1. Введение

Интерес к исследованию квази-двумерных турбулентных ограниченных струйных течений обусловлен широким распространением данного течения в технологических и природных процессах, в частности из-за наличия крупномасштабных когерентных квази-двумерных вихревых структур. Крупномасштабные когерентные структуры играют важную роль в процессах перемешивания и переноса массы (например, загрязняющих веществ и отложений), импульса и энергии в мелководных потоках, включая устья рек, озера, каналы и океаны. Квази-двумерное турбулентное течение является крайне сложным для численного и экспериментального моделирования. Сложность обусловлена наличием и взаимодействием двух сильно различных масштабов турбулентности: с одной стороны это трехмерные мелкомасштабные турбулентные движения масштаба h (толщина слоя жидкости), с другой стороны, крупномасштабные квази-двумерные турбулентные движения, обусловленные развитием сдвиговой неустойчивости в горизонтальном направлении.

Одной из первых работ, посвященных исследованию крупномасштабных квази-двумерных вихревых структур, является работа [5]. В работе исследовалась структура течения квази-двумерной струи, распространяющейся в узкий канал в широком диапазоне глубины канала h. Согласно работе [5] выделяют две области течения: ближнее поле струи (область трехмерного течения), в котором существенное влияние оказывают вторичные течения, и дальнее поле струи (область квази-двумерного течения), которое характеризуется наличием крупномасштабных квази-двумерных вихревых структур и проявлением эффекта меандрирования. В настоящее время исследования свойств крупномасштабных квази-двумерных вихревых структур и эффект меандрирования продолжаются, о чем свидетельствует ряд работ по численному и экспериментальному моделированию [4, 9, 10, 14].

Исторически сложилось, что исследования ближнего и дальнего поля квази-двумерной ограниченной струи проводились независимо и имели различные цели. Изначально интерес к исследованию ограниченных струйных течений был обусловлен развитием струйных логических элементов для военных и космических целей [6, 7, 11, 12, 13]. Эти работы касались исследования влияния ограничивающих стенок на структуру течения в ближнем поле струи и были направлены на развитие методов управления струйным потоком. В работах было показано, что в течении струи, ограниченной сверху и снизу двумя пластинами, в слое смешения образуются вторичные течения. В работе [6, 7] была предложена модель формирования вторичных течений на основе переориентации вихревых нитей. Турбулентные характеристики вторичных течений в ограниченных струях с различными соотношениями сопла были исследованы в работах [12, 13]. В работе [13] представлена пространственная вихревая структура, полученная с помощью визуализации. В работе [5] также частично исследовано ближнее поле квази-двумерной струи и качественно определена область существования вторичных течений. Для подтверждения гипотезы работ [6, 7], формирования вторичных течений в работе [2] с помощью TomoPIV метода были проведены измерения всех трех компонент скорости в объеме потока ближнего поля квази-двумерной струи. Анализируя реконструированные по 10 наиболее вероятным пространственным конфигурациям объемных мгновенных распределений трех компонент скорости, полученных с помощью POD разложения, удалось зафиксировать продольные вихревые структуры, которые являются ответственными за формирование вторичных течений. Оказалось, что существуют различия между структурой вторичных течений квази-двумерной струи и структурой вторичных течений ограниченных струй, исследованных в работах [6, 7]. Различие состоит в противоположных направлениях вращения вторичных течений, полученных в работе [7] и [2]. Низкое пространственное и временное разрешение в работе [2] не позволили объяснить эти различия и ответить на ряд вопросов, касающихся образования и развития когерентных вихревых структур в квази-двумерной турбулентной струе.

Наша работа является логическим продолжением работы [2] и направлена на исследование процессов формирования и развития вихревых структур, а также их взаимодействия между собой и стенкой.

2. Описание метода

Иллюстрация принципов работы алгоритма, используемого для получения поля скоростей в измерительном объеме потока, показана на рис. 1.

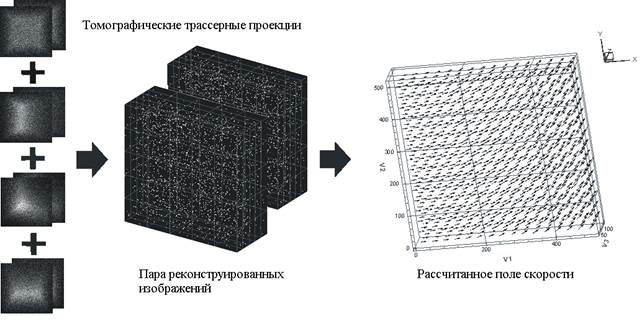
new_tomo_scheme

Рис. 1. Иллюстрация принципов работы алгоритма оценки поля скорости в методе Tomo PIV

Описание метода Tomo PIV приведено в работе [15], метод состоит из трех шагов: калибровка оптической системы, томографическая реконструкция и корреляционная обработка восстановленных объемных изображений частиц. Калибровка оптической системы состоит из геометрической калибровки всех камер, использующихся для регистрации области потока. Дополнительно для уточнения моделей камер применяется метод самокалибровки по зарегистрированным экспериментальным изображениям частиц [18]. Основным шагом получения поля скорости в методе Tomo PIV является восстановление трехмерного распределения интенсивности частиц алгоритмом итерационной алгебраической реконструкции. Для томографической реконструкции используются алгоритмы SMART и MENT [3]. Заключительным шагом Tomo PIV алгоритма является корреляционный анализ полученных пар объемных изображений частиц для оценки поля скорости (см. рис. 1). Принцип кросскорреляционного алгоритма, применяемого для томографических измерений, не отличается от алгоритма, используемого для плоскостных измерений, при этом добавляется оценка третьей компоненты скорости по глубине области измерения. Более подробное описание метода и его тестирование приведено в работе [1].

3. Описание эксперимента

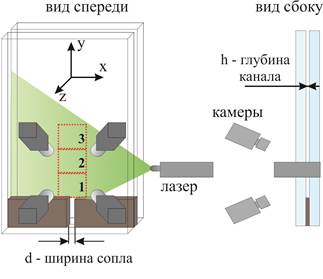
Фотография экспериментальной установки и схема измерительной системы представлена на рис. 2. Экспериментальная установка представляет собой гидродинамический контур с баком постоянного уровня, насосом, расходомером и рабочим участком. Рабочий участок представляет собой узкий прямоугольный канал размером 307x270 mm², образованный двумя плоскопараллельными пластинами из оргстекла, расположенными на расстоянии 4 мм друг от друга. Сопло формировалось двумя прямоугольными вставками, установленными в канал. Ширина сопла равнялась 10 мм. Число Рейнольдса рассчитывалось как Re = h_dU₀/ν = 20 000, где U₀ средне расходная скорость, а h_d гидравлический диаметр сопла.

Установка квази_струя_cr

Рис. 2. Экспериментальная установка и схема измерительной системы для высокоскоростных Tomo-PIV измерений в квази-двумерной турбулентной струе

Измерительная система состояла из высокоскоростного сдвоенного Nd: YAG лазера (Photonix DM-532-150 с энергией в импульсе 15 мДж при частоте работы 15 кГц), четырех высокоскоростных CMOS камер (Photron FASTCAM SA5 с разрешением 1024×1024 пикс, 12 бит с частотой съемки 7 кГц) и синхронизующего генератора импульсов Berkeley Nucleonics BNC 575. Лазерный нож толщиной 4 мм, который освещал весь измерительный объем между пластинами, формировался с помощью системы линз. В экспериментах мы использовали полиамидные частицы диаметром 50 мкм. В оптической системе камер использовались объективы SIGMA AF 105 мм f/2.8 EX DG MACRO. Объем измерительной области равнялся 50×50×4 мм³. Измерения проводились в трех последовательных областях, центры которых располагались на расстояниях 5h, 15h и 25h от края сопла. Измерения изображений частиц проводились с частотой съемки равной 10 кГц, что соответствовало задержке между кадрами в 100 мкс. Для первой измерительной области трехкомпонентное мгновенное распределение скорости рассчитывалась между соседними изображениями, что соответствовало частоте съемки 10 кГц, для второго и третьего измерительной области между каждым вторым изображением, что соответствовало частоте съемки 5 кГц.

4. Расположение и калибровка камер

Для обеспечения одинаковых параметров оптической системы каждой камеры, камеры были расположены в углах квадрата в плоскости параллельной центральной плоскости измерительного объема. Углы расположения камер в вертикальной и горизонтальной плоскости были равны 30 градусов. При такой конфигурации измерительной системы камеры располагались в четырех точках на сфере с центром, совпадающим с центром измерительного объема, в результате обеспечивались идентичные условия для каждой камеры, такие как углы поворота камер, углы коррекции Шаймпфлюга и расстояние от камер до центра измерительной области. Для выравнивания фокальной плоскости и плоскости матрицы были разработаны и изготовлены с помощью 3D печати адаптеры, позволяющие повернуть объектив относительно камеры в любой плоскости на угол от 0 до 12 градусов. Для калибровки оптической системы использовалась высокоточная калибровочная мишень Edmund Optics размерами 50×50 мм² с размером маркеров 1 мм, расположенных на декартовой сетке с шагом 1 мм. В результате малой глубины канала 4 мм перемещение калибровочной мишени было затруднительным. Поэтому для калибровки измерительного пространства перемещалась измерительная система в целом, а не мишень. Перемещение измерительной системы производилось с помощью высокоточной координатной системы и контролировалось с точностью 10 мкм. Перемещение измерительной системы пересчитывалось в перемещение мишени, учитывая разность между коэффициентами преломления жидкости и воздуха, при этом стенка канала рассматривалась как плоскопараллельная пластина, не изменяющая направления хода лучей. Измерения маркеров калибровочной мишени производились в пяти параллельных плоскостях по глубине измерительного объема.

5. Обработка данных

Для обработки данных использовалось программное обеспечение “ActualFlow”. Для уточнения параметров калибровки оптической модели производилась самокалибровка по 300 изображениям [18]. В результате самокалибровки конечное осредненное отклонение не превышало 0.05 пикселя. Перед реконструкцией объемов изображений частиц, проекции с каждой камеры предварительно обрабатывались, из них вычитался статистический минимум интенсивности (для каждого пикселя) по ансамблю исходных изображений. Восстановленный объем имел размеры 615×615×77 вокселей. Физический размер вокселя приблизительно равнялся 0.063×0.063×0.063 мм³. Объемная концентрация частиц была 8.5 частиц/мм³. Томографическая реконструкция производилась с помощью SMART алгоритма [3]. Распределение скорости рассчитывалось между соседними последовательными распределениями частиц. Корреляционный анализ проводился с использованием итерационного многосеточного алгоритма с непрерывным смещением измерительного окна. При расчете скорости было выполнено четыре итерации, две итерации с разрешением 64×64×32 вокселя и две итерации с разрешением 32×32×16 вокселя. Последняя итерация выполнялась с перекрытием 75%, в результате чего окончательный размер области для одного вектора скорости составил 0,5×0,5×0,25 мм³ с расстоянием половины размера между соседними векторами.

6. Результаты эксперимента

На рисунке 3 вверху показаны результаты высокоскоростной визуализации флуоресцентным красителем, визуализация проводилась на установке, описанной в работе [16]. На рисунке 3 вверху отражены характерные особенности квази-двумерной турбулентной струи; меандрирование струи и крупномасштабные квази-двумерные вихревые структуры, о которых сообщалась в работах других авторах [5, 9, 10]. Однако можно заметить еще одну особенность, связанную с областью вовлечения жидкости крупномасштабной квази-двумерной вихревой структурой. Во время вовлечения жидкости формируются области в виде продольных полос, в которых вовлеченная жидкость не перемешивается с подкрашенной жидкостью струи (области указаны стрелками).

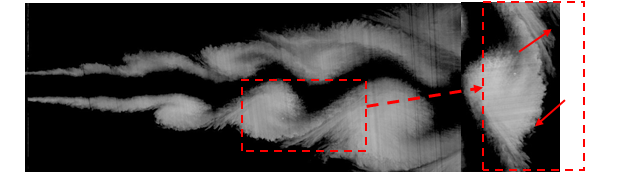
Рис. 3 Картина течения квази-двумерной турбулентной струи полученная с помощью высокоскоростной визуализации. Re=20 000, d/h = 10, h=2 мм, частота съемки 8400 кадров в секунду.

Процесс формирования этих продольных областей, обнаруженный нами впервые, послужил мотивацией для исследования трехмерной структуры течения и проведения экспериментов с применением высокоскоростного томаграфического PIV метода [17].

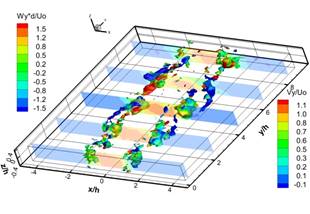
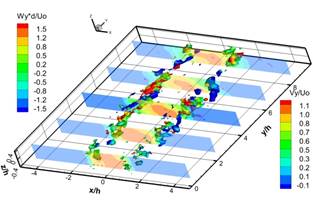
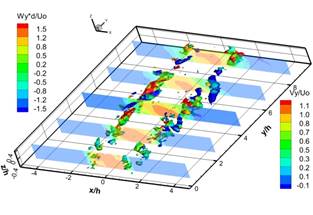
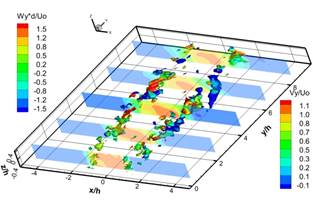
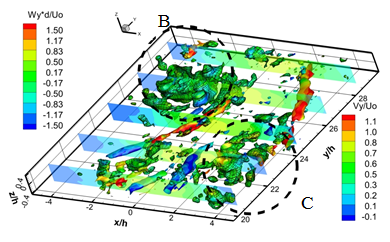
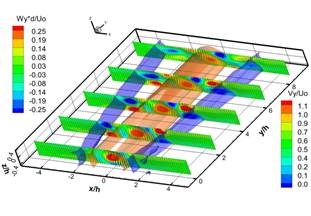
Для идентификации вихревых структур в потоке мы использовали распределения Q критерия, рассчитанного по мгновенным трехкомпонентным распределениям скорости [8]. На рисунке 4 показаны последовательные изоповерхности Q^3D критерия, цветом указано значение продольной компоненты завихренности. В пяти поперечных сечениях построена продольная компонента мгновенной скорости. Наличие в распределении Q^3D критерия ориентированных вдоль потока парных структур, окрашенных красным и синим цветом, указывает на наличие продольных вихревых структур, ориентированных по направлению потока и вращающихся в противоположные направления вокруг своей оси.

Re20k10d4h_z1_3DQ_inst_norm22

Re20k10d4h_z1_3DQ_inst_norm23

Re20k10d4h_z1_3DQ_inst_norm24

Re20k10d4h_z1_3DQ_inst_norm25

Re20k10d4h_z1_3DQ_inst_norm26

Re20k10d4h_z1_3DQ_inst_norm27

Рис. 4. Ближнее поле струи. Распределение Q³^D критерия для последовательных полей скорости с интервалом времени 100 мкс между ними.

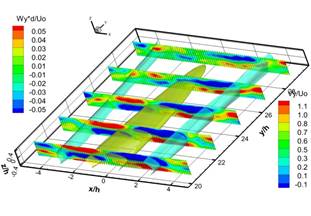
На рисунке 4 a-f представлена эволюция вторичных продольных вихревых структур в ближнем поле струи. Вторичные продольные вихревые структуры формируются парно в виде двух противоположно вращающихся вихревых структур. Формирование этих парных вихревых структур происходит в слое смешения струи вблизи ограничивающих поверхностей в результате вовлечения внешней жидкости вихревой структурой, образовавшейся вследствие сдвиговой неустойчивости Кельвина - Гельмгольца. Вниз по потоку линейный масштаб вторичных продольных вихревых структур увеличиваются, вследствие объединения сонаправленных продольных вихревых структур. Наличие вторичных продольных вихревых структур в ближнем поле струи приводит к образованию вторичных течений, которые впервые были обнаружены в работах [6, 7]. Согласно работе [5] вторичные течения в квази-двумерной струе исчезают на расстоянии 10h. Однако наши эксперименты показали наличие вторичных течений в дальнем поле струи, на расстоянии больше 20h.

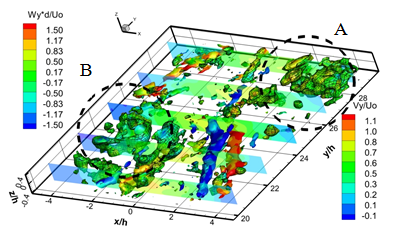
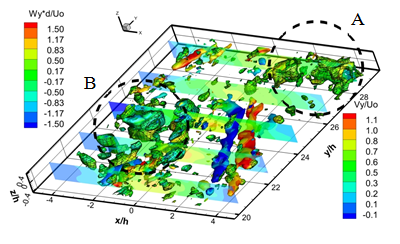
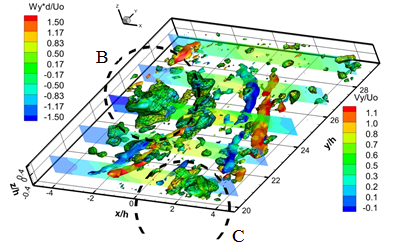
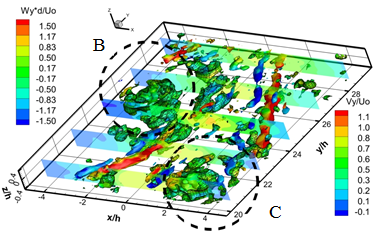
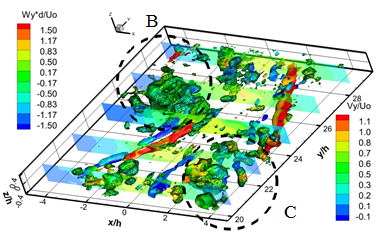
Рис. 5. Дальнее поле струи. Распределение Q³^Dи Q²^D критерия для каждого 14 -го последовательного поля скорости полученных с частотой съемки 5 000 кадров в секунду

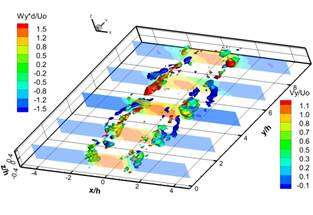
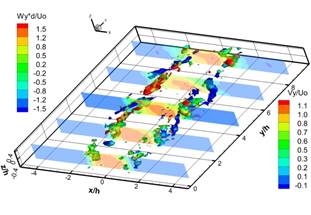
Рисунок 5 a-f показывает вихревые структуры в дальнем поле струи и динамику их взаимодействия. Динамика вторичных продольных вихревых структур в дальнем поле струи происходит следующем образом. В результате вращения вихревой структуры "A" происходит вовлечение противоположно вращающихся вторичных продольных вихревых структур в ядро струйного потока. В результате вторичные продольные вихревые структуры становятся ориентированными по направлению потока и попадают в область продольного растяжения. По мере движения вихревой структуры "A" вниз по потоку и развития вихревой структуры "B", вторичные структуры начинают смещаться от ядра на внешнюю границу струи. В результате смещения продольных вихревых структур к внешней границе струи, ближняя к ядру струи продольная вихревая структура исчезает, а дальняя усиливается и сносится на границу струи. Дальнейшее развитие вихревой структуры "B" вниз по потоку приводит к формированию пары противоположно вращающихся продольных вихревых структур с другой стороны струи. Взаимодействие структуры "B" и "С" приводит к усилению двух противоположно вращающихся вторичных продольных структур, аналогично случаю структур"A" и "B". В результате взаимодействия последовательных крупномасштабных вихревых структур и меандрирования струйного потока вторичные продольные вихревые структуры периодически вовлекаются в ядро струи, а затем периодически выносятся на границу струи.

Re20k10d4h_z1_stat_norm a)

Re20k10d4h_z3_stat_norm_vect b)

Рис. 6. Осредненное по времени трехмерное распределение скорости a) ближнего и b) дальнего поля струи для d/h = 2.5 и числа Re = 2×10⁴. Изоповерхности соответствуют двум значениям осредненной по времени продольной скорости. В поперечных сечениях показано распределение продольной компоненты завихренности рассчитанной по осредненному распределению скорости.

На рисунке 6 показаны изоповерхности продольной компоненты осредненной скорости и сечения продольной компоненты завихренности, рассчитанные по осредненному полю скорости для ближнего a) и дальнего b) поля струи. На рисунке 6 a) показано, что между ядром и границей струи существуют вторичные течения, которые представлены в сечениях положительным и отрицательным значением продольной компоненты завихренности (красный и синий цвет, соответственно). Вторичные течения являются следствием наличия в потоке вторичных продольных вихревых структур. На рисунке 6 b) показаны вторичные течения, формирующиеся в дальнем поле струи, которые являются менее интенсивными по сравнению с вторичными течениями ближнего поля струи. Их пространственная структура является более сложной, а область их влияния значительно шире. Вторичные течения в дальнем поле также являются следствием вторичных продольных вихревых структур (рис. 5), однако, как можно заметить, направление вращения вторичных течений в дальнем поле противоположное по сравнению с вторичными течениями в ближнем поле струи. Различие в противоположных направлениях вращения в дальнем и ближнем поле струи требует дальнейшего исследования.

7. Заключение

Применен метод Tomographic PIV высокого временного разрешения для исследования вихревой структуры в формирующемся течении турбулентной струи в узком канале. Выполнены 3D измерения всех компонент скорости в ближнем и дальнем поле квази-двумерной турбулентной струи. Последовательные распределения Q^3D критерия в ближнем поле струи показывают, что вторичные продольные вихревые структуры формируются в результате взаимодействия с вихревой структурой, образовавшейся вследствие сдвиговой неустойчивости Кельвина - Гельмгольца, с ограничивающей поверхностью. Впервые экспериментально показано наличие двух видов когерентных вихревых структур: крупномасштабных квази-двумерных вихревых структур и вторичных продольных вихревых структур в дальнем поле квази-двумерной турбулентной струи. Развитие вторичных продольных вихревых структур и их взаимодействие с крупномасштабными квази-двумерными вихревыми структурами носит сложный трехмерный характер и требует дальнейшего изучения.

Благодарности

Работа поддержана: грантом Российского научного фонда № 14-19-01685.

Список обозначений

Re – число Рейнольдса;

Q - критерий (1/с²);

U₀– средне расходная скорость (м/с);

h_d–– гидравлический диаметр (мм);

h – глубина канала (мм);

d – ширина сопла (мм).

Индексы:

3D – рассчитанный по трем компонентам скорости;

2D – рассчитанный по двум компонентам скорости.

Список литературы

1. Бильский А.В., Ложкин В.А., Маркович Д.М., Токарев М.П., Шестаков М.В. Оптимизация и тестирование томографического метода измерения скорости в объеме потока. Теплофизика и аэромеханика, Т. 18, № 4, 2011, с. 1-12.

2. Bilsky A.V., Markovich D.M., Shestakov M.V., Tokarev M.P. Tomographic PIV and planar Time-resolved PIV measurements in a turbulent slot jet. Proceeding of the 16th international symposium on applications of laser techniques to fluid mechanics, Lisbon, 2012.

3. Bilsky, A.V., Lozhkin, V.A., Markovich, D.M., and Tokarev, M.P. A maximum entropy reconstruction technique for tomographic particle image velocimetry. Measurement Science and Technology, vol. 24, 2013, 045301.

4. Daoyi, C., and Jirka, G.H. Linear stability analysis of turbulent mixing layers and jets in shallow water layers. Journal of Hydraulic Research, vol. 36, 1998, pp. 815-830.

5. Dracos, T, Giger, M, and Jirka, G (1992) Plane turbulent jets in a bounded fluid layer. Journal of Fluid Mechanics, vol. 241, pp. 587–614.

6. Foss, J. F. & Jones J. B, Secondary flow effects in a bounded rectangular jet. Journal of Fluids Engineering, vol. 90, 1968, pp. 241–248.

7. Holdeman J., and Foss J. The initiation, development, and decay of secondary flow in a bounded jet. Journal of Fluids Engineering, vol. 97, 1975, pp. 342-352.

8. Hunt, J.C.R., Wraya A.A., and Moin ,P. Eddies, stream, and convergence zones in turbulent flows. Center for Turbulence Research Report, CTR-S88, 1988p. 193.

9. Jirka, G. H. Large scale flow structures and mixing processes in shallow flows. Journal Hydraulic Research, vol. 39, 2001, pp. 567–573.

10. Landel J. R., Caulfield C. P. and Woods A. W. Meandering due to large eddies and the statistically self-similar dynamics of quasi-two-dimensional jets. Journal Fluids of Mechanics, vol. 692, 2012, pp. 347 368.

11. McCabe, A., An experimental investigation of a plane subsonic jet with an aspect ratio of three. Proceeding of the Proceedings of the Institution of Mechanical Engineers vol. 183, 1967 pp. 342-346.

12. Nozaki, T., et al., Study of a Bounded Jet Flow Considering the Initial Turbulence (Experiments with a Nozzle Having Aspect Ratio of 3). Bull. Jpn. Soc. Mech. Eng., vol.27, No.234, 1984, p.2730.

13. Nozaki, T., et al., Experimental Study of a Bounded Jet Flow (Mechanism of the Secondary Flow). Proceeding of the 4th International Symp. Flow Visualization, 1986, pp.495-499.

14. Peltier Y. Experimental and numerical investigation of meandering jets in shallow reservoir: potential impacts on deposit patterns. THESIS, Two-phase modeling for Sediment dynamics in Geophysical Flows, At Chatou, France 2013 http://hdl.handle.net/2268/155314.

15. Scarano, F. Tomographic PIV: principles and practice. Measurement Science and Technology, vol. 24, 2013, 012001.

16. Shestakov, M.V., Dulin, V.M., Tokarev, M.P., Sikovsky, D.P., and Markovich, D.M., PIV study of large-scale flow organisation in slot jets. International Journal of Heat and Fluid Flow, vol. 51, 2014, pp. 335-352.

17. Shestakov M.V., Dulin V.M., Tokarev M.P., Markovich D.M. Dynamics of primary and secondary vortices in a slot jet. Proceeding of the 9th international symposium on turbulence and shear flow phenomena, Melbourne, Australia, 2015.

18. Wieneke, B., Volume self-calibration for 3D particle image velocimetry. Experiments in Fluids, vol. 45, 2008 pp. 549-456.

APPLICATION OF TIME-RESOLVED TOMOGRAPHIC PIV TECHNIQUE FOR THE INVESTIGATION OF PROCESES FORMING OF VORTEX STRUCTURE IN QUASI TWO-DIMENSIONAL TURBULENT JET

M.V. Shestakov¹, M.P. Tokarev¹, D.M. Markovich ^1,2

¹Institute of Thermophysics SB RAS, Novosibirsk, Russia, e-mail: mvsh@itp.nsc.ru

² Novosibirsk State University, Novosibirsk, Russia, e-mail: dmark@itp.nsc.ru

Abstract

The work focuses on investigation of spatial-temporal 3D vortex structure of a quasi two-dimensional turbulent jet. Time-resolved tomographic PIV technique with repetition rate up to 10 kHz was used to measure 3D velocity distributions. It was shown that in quasi two-dimensional turbulent jet two types of coherent vortex structures exist. On the basis of instantaneous distributions of Q criterion 3D dynamics of vortex structure is studied. Longitudinal secondary vortex structures in far field of the quasi two-dimensional turbulent jet were detected for the first time.

Keywords: time-resolved tomographic PIV, quasi two-dimensional jet, dynamics of vortex structureshe

Reference

1. Bilsky A.V., Markovich D.M., Shestakov M.V., Tokarev M.P., ShestakovM.V. Optimizacija i testirovanie tomograficheskogo metoda izmerenija skorosti v ob`eme potoka [Optimization and testing the tomographic method of measuring the velocity in the flow volume]. Thermophysics and Aeromechanics, vo. 18, no. 4, 2011, pp. 1-12.