ОБЗОР ПОДХОДОВ К ГЕОМЕТРИЗАЦИИ ИСХОДНЫХ МНОГОМЕРНЫХ ДАННЫХ ПРИ ИХ АНАЛИЗЕ МЕТОДОМ КОМПЬЮТЕРНОЙ ВИЗУАЛИЗАЦИИ

В.В.Пилюгин¹, А.А.Пасько², И.Е.Мильман¹

¹Национальный исследовательский ядерный университет «МИФИ», Москва, Россия

²Британский национальный центр компьютерной анимации при университете Борнмута, Борнмут, Великобритания

VVPilyugin@mephi.ru, apasko@bournemouth.ac.uk, igalush@gmail.com

Содержание

1. Введение

2. Пространства многомерной аналитической геометрии.

3. Рациональный выбор класса пространств многомерной аналитической геометрии в задачах анализа исходных данных.

4. Заключение

Литература

Анотация

В процессе анализа различных данных методом компьютерной визуализации конвейер визуализации (visualization pipeline) исходных анализируемых данных часто включает геометризацию этих данных с использованием многомерных геометрических пространств. В данной статье рассматриваются вопросы рационального выбора класса таких пространств в задачах анализа исходных данных методом компьютерной визуализации.

Ключевые слова: геометризация, геометрическое пространство, многомерное пространство, компьютерная визуализация, многомерные данные, аффинное пространство, линейное пространство

1. Введение

Как было показано в работе [1], в процессе анализа научных данных методом компьютерной визуализации конвейер визуализации (visualization pipeline) исходных анализируемых научных данных часто включает геометризацию ( геометрическое моделирование ) этих данных с использованием многомерных геометрических пространств. Важно отметить, что это справедливо не только для случая анализа научных данных, но и анализа методом компьютерной визуализации данных произвольной природы, которые могут встречаться в других прикладных областях.

В качестве такого пространства в принципе может быть использовано любое из известных в математике многочисленных геометрических пространств. Каждое из этих пространств представляет собой множество некоторых объектов, которые принято называть точками [2]. Эти пространства отличаются друг от друга как природой входящих в них объектов, так и определенными в них геометрическими свойствами.

Рассмотрим вопросы рационального выбора такого пространства в задачах анализа исходных данных методом компьютерной визуализации.

2. Пространства многомерной аналитической геометрии.

Выбор того или иного многомерного геометрического пространства осуществляется пользователем в контексте решаемой им задачи анализа исходных данных. Однако в общем случае выбираемое геометрическое пространство должно удовлетворять следующим основным требованиям:

- простота и удобство при переходе от исходных данных к вводимым в рассмотрение геометрическим объектам;

- открытость геометрического пространства с точки зрения возможности варьирования его сложности и обладаемых им геометрических свойств;

- простота реализации (моделирования) на компьютере процедуры геометризации как шага алгоритма визуализации исходных данных.

Этим требованиям в целом отвечают пространства многомерной аналитической геометрии. Геометрические пространства многомерной аналитической геометрии определяются как множества точек, определенным образом сопоставленные с тем или иным линейным пространством [3].

Линейные пространства вводятся в рассмотрение в линейной алгебре и определяются как множества элементов той или иной природы, для которых задаются отношение равенства и операции сложения и умножения на число, отвечающие соответствующей аксиоматике. Элементы линейных пространств принято называть векторами. Примером линейных пространств могут служить пространство действительных чисел, пространство геометрических векторов, пространство матриц, пространство непрерывных функций. Простейшими пространствами многомерной аналитической геометрии являются аффинные пространства. Соответствие пространств многомерной аналитической геометрии и, в частности, аффинных пространств линейным пространствам определяется с помощью некоторого правила, которое задаёт отображение каждой пары точек на соответствующий вектор и отвечает так называемой точечно-векторной аксиоматике [3].

Пусть U – некоторое аффинное пространство, сопоставленное с линейным пространством L. Точки аффинного пространства будем, как это принято, обозначать заглавными буквами латинского алфавита, векторы линейного пространства – малыми буквами этого алфавита. Если паре точек А, В соответствует вектор х, то будем писать: . Здесь есть только новое обозначение вектора х, как это принято в многомерной аналитической геометрии. Первая из двух точек называется началом вектора , вторая – его концом.

Упомянутая выше точечно-векторная аксиоматика включает в себя две аксиомы:

1. для каждой точки А из U и каждого вектора х из L найдётся и притом единственная точка В из U такая, что ;

2. если , , , где – сумма векторов x и y.

Аффинное пространство U называется действительным или комплексным, конечномерным или бесконечномерным в зависимости от того, действительным или комплексным, конечномерным или бесконечномерным является соответствующее ему линейное пространство L. Важной характеристикой аффинного пространства U является его размерность, которой называют число, равное размерности линейного пространства L. Соответственно, под многомерным аффинным пространством U будем понимать такое аффинное пространство, размерность которого больше трёх.

Примером аффинного пространства, сопоставленного с линейным пространством, может служить трёхмерное аффинное пространство, которое сопоставлено так, как это делается в элементарной аналитической геометрии с множеством всех геометрических векторов, которое, как мы отмечали ранее, представляет собой линейное пространство.

В общем случае аффинное пространство U и соответствующее ему линейное пространство L представляют собой два различных множества. Однако отметим важный для нас факт, который заключается в том, что всякое линейное пространство L можно одновременно рассматривать, как аффинное пространство U [3]. Для этого достаточно векторы назвать точками и каждой паре векторов a, b, рассматриваемых как точки множества U, поставить в соответствие вектор , принадлежащий L. Если обозначить через факт рассмотрения вектора х в качестве точки Х, то данный способ задания аффинного пространства можно определить следующим образом:

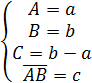(1)

Отсюда следует важный вывод о том, что при таком способе задания аффинного пространства простота и удобство его использования для целей геометрического моделирования определяется простотой и удобством использования исходного линейного пространства.

Важным для нас свойством аффинных пространств является известный способ и простота задания системы координат в этих пространствах. Система координат в аффинном пространстве U размерности n определяется следующим образом. В этом пространстве выбирается произвольная точка О, которую называют началом координат, а в соответствующем линейном пространстве L фиксируется какой-нибудь базис из векторов e₁,…,e_n. Пусть М – произвольная точка из U. Вместе с началом координат она определяет вектор , принадлежащий L, который называют радиус-вектором точки М. Раскладывая радиус-вектор по базису e₁,…,e_n, получают:

(2)

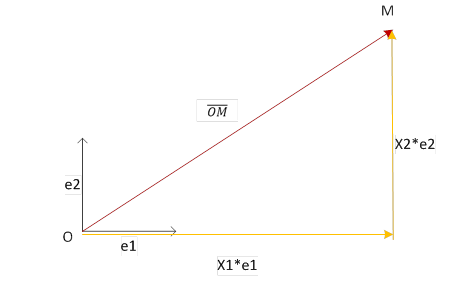
Рис. 1. Задание аффинных координат в базисе геометрических векторов e₁, e₂

Коэффициенты этого разложения x₁,…,x_n называются аффинными координатами точки M (относительно выбранной системы с началом О и базисом e₁,…,e_n) . Обратим внимание на то, что аффинная система координат задаётся в общем случае двумя разнородными объектами – точкой О из аффинного пространства и базисом e₁,…,e_n из линейного пространства. Естественное, в случае, когда линейное пространство одновременно рассматривается, как и аффинное, эти объекты становятся однородными, т. е. система координат определяется с помощью (n+1)-го вектора линейного пространства. Из теории линейных пространств известно, что разложение каждого вектора по некоторому фиксированному базису единственно, т. е. получается единственный набор координат. Следовательно, аффинные координаты каждой точки определяются однозначно ввиду единственности разложения вектора по базису e₁,…,e_n.

Отображение , ставящее в соответствие каждой паре точек А, В аффинного пространства U вектор х линейно пространства L, позволяет достаточно просто и естественно анализировать в аффинных пространствах взаимное расположение точек, а на базе этого осуществлять выделение геометрических фигур, т. е. некоторых подмножеств точек этого пространства, а также анализировать взаимное расположение геометрических фигур.

Так, например, плоскость той или иной размерности, которая является базовой фигурой в аффинных пространствах, определяется следующим образом. Пусть в n-мерном аффинном пространстве U зафиксирована произвольная точка А и в соответствующем пространстве L зафиксировано произвольное r-мерное подпространство L'.

Множество всех точек М аффинного пространства, для которых принадлежит L', называется r-мерной плоскостью, проходящей через точку А в направлении подпространства L'. Говорят также, что L' является направляющим подпространством этой плоскости. Точку М называют текущей точкой плоскости. В определении плоскости выделена точка А, однако можно показать, что все точки плоскости равноправны, т. е. роль точки А может играть любая точка, принадлежащая данной плоскости.

Важными частными случаями плоскости являются точка (нульмерная плоскость), прямая линия (одномерная плоскость), гиперплоскость ((n-1)-мерная плоскость), всё пространство (n-мерная плоскость). По отношению к плоскостям в аффинных пространствах вводятся такие понятия, как пересекающиеся, параллельные и скрещивающиеся плоскости. На базе плоскости весьма просто вводятся более сложные геометрические фигуры – полупространства, многогранники, параллелепипеды и др. [3].

Ещё одним важным свойством аффинных пространств, с точки зрения их использования для целей геометрического моделирования, является возможность ставить в соответствие, как геометрическим фигурам, так и выполняемым над ними операциям, аналитические описания, или, как принято говорить, аналитически описывать эти фигуры и преобразования.

В теории многомерных аффинных пространств доказывается, что упомянутым ранее плоскостям таких пространств можно ставить в соответствие аналитические описания с использованием аффинных координат точек, принадлежащих этим плоскостям. В частности известно, что в аффинном пространстве U размерности n и в любых аффинных координатах всякая плоскость S размерности m может быть задана системой линейных уравнений вида 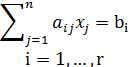[3]:

(3)

и ранга r=n-m, где x_j – координаты произвольной точки, принадлежащей плоскости. Данная система линейных уравнений является аналитическим описанием плоскости S в том смысле, что координаты любой точки, принадлежащий этой плоскости, являются решением этой системы, а наоборот, координаты любой точки, не принадлежащий этой плоскости, не являются решением этой системы. При переходе к новым аффинным координатам вид рассматриваемых линейных уравнений меняется. Кроме того, плоскость S в фиксированной системе аффинных координат может описываться различными системами уравнений. Геометрически это означает, что плоскость S можно определять, как пересечение различных наборов независимых гиперплоскостей в числе n-m. Независимость гиперплоскостей следует понимать в том смысле, что ранг совместной системы уравнений этих гиперплоскостей имеет максимально возможное значение, т. е. равен числу уравнений (r=n-m).

В многомерной аналитической геометрии также определены аналитические описания других, более сложных геометрических фигур – многогранников, параллелепипедов и т. д. Эти описания являются теми или иными производными приведённого выше аналитического описания плоскостей.

Следует также отметить, что аналитические описания геометрических фигур не обязательно должны быть координатными, т. е. построенными с использованием координат точек x_i, i=1,…, n, принадлежащих этим фигурам. Эти аналитические описания также могут быть векторными, т. е. построенными с использованием элементов линейного пространства, сопоставленного с аффинным пространством. Так, например, для гиперплоскости, координатным аналитическим описанием которой является линейное урав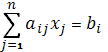нение вида , векторным аналитическим описанием будет векторное уравнение вида:

a(x)=c (4)

где:

а(х) – некоторая линейная форма, т. е. линейная числовая функция векторного аргумента,

х – радиус-вектор точки, принадлежащий гиперплоскости,

с – некоторое число.

Из теории многомерной аналитической геометрии известно, что и другим геометрическим фигурам аффинных пространств можно поставить в соответствие их векторные аналитические описания.

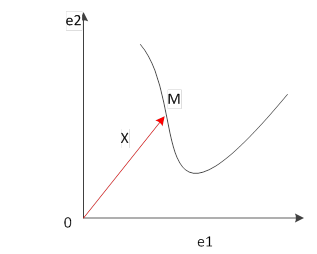
Рис. 2. Задание фигуры с помощью радиус вектора в пространстве геометрических векторов с базисом e₁, e₂

Аналитически можно также описывать операции над геометрическими фигурами в аффинных пространствах. Так, например, операциям, заданным в виде так называемых аффинных преобразований, отличительной чертой которых является то, что при аффинном преобразовании всякая плоскость размерности k переходит в плоскость той же размерности, можно поставить в соответствие в качестве аналитического описания следующие соотношения [3]:

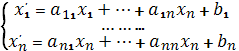(5)

Предполагается, что n×n-матрица не вырождена, т. е. Det A≠0. Эти соотношения являются аналитическим описанием операции аффинного преобразования в том смысле, что они связывают значения аффинных координат x_i и x_i’, i=1, 2,…, n, пар соответствующих друг другу точек исходной и результирующей геометрических фигур.

Используемые в многомерной аналитической геометрии понятия (как это, в частности, следует из приведённого выше материала) и, в том числе, аналитические описания геометрических фигур и выполняемых над ними операций во многом напоминают привычные для нас и наглядные понятия из курса элементарной аналитической геометрии. Однако понятия многомерной аналитической геометрии являются более сложными и разнообразными, имеют более абстрактный характер.

Если вводимая в рассмотрение пользователем процедура геометризации исходных данных предусматривает выполнение операций нахождения и использование различных метрических понятий, например таких, как расстояние между точками, длины линий, углы и т. д., то многомерные аффинные пространства, рассматриваемые нами до сих пор, уже не могут быть использованы для целей геометрического моделирования. Дело в том, что в отличие от пространства, изучаемого в элементарной геометрии, в этих пространствах не определены метрические понятия.

В этом случае необходимо использовать другие, более сложные пространства многомерной аналитической геометрии. Однако важно подчеркнуть, что эти пространства не противопоставляются аффинным, а могут быть получены путём доопределения в последних, причём известным и достаточно простым образом, необходимых метрических понятий. В этом проявляется одно из важных с точки зрения геометрического моделирования свойств пространств многомерной аналитической геометрии. С позиций моделирования эти пространства можно рассматривать, как некоторую единую геометрическую среду с изменяемыми функциональными возможностями.

Базовым метрическим понятием является понятие расстояния между точками. Это понятие, как и другие понятия пространств многомерной аналитической геометрии, определяется при помощи линейного пространства L, сопоставленного аффинному пространству U. Для этого в пространстве L вводят новую операцию – скалярное умножение векторов. Действие скалярного умножение ставит в соответствие каждой паре векторов x, y из L действительное число, которое обозначается (x, y) и называется скалярным произведением вектора x на вектор y. Правило, с помощью которого произвольной паре векторов ставится некоторое действительное число, может быть произвольным, однако оно должно обладать свойствами коммутативности, дистрибутивности, однородности и невырожденности, определяемыми соответствующими аксиомами.

На базе скалярного произведения в линейном пространстве L вводят понятия нормы вектора x, которым называется число , и квадратичной метрической формы данного пространства , или квадратичной метрики. Эта метрическая форма называется положительно определённой, если (x, x)>0 для всех х отличных от нулевого вектора. Линейное пространство L с заданным скалярным произведением называют также пространствами с квадратичной метрикой.

При помощи таким образом доопределённого линейного пространства L вводится понятие расстояния между точками аффинного пространства U, сопоставленного с данным линейным пространством. Для каждой пары точек A, B, из U расстояние между ними обозначается r(A, B) и определяется следующим образом:

(6)

В случае положительно определённой метрической формы (х, х) расстояние между точками равно нулю только тогда, когда эти точки совпадают, и , кроме того, для любых трёх точек А, В, С из U соблюдается неравенство треугольника . Если между точками аффинного пространства U определено таким образом расстояние, то говорят, что в аффинном пространстве U задана квадратичная метрика.

В аффинных координатах квадрат расстояния имеет выражение:

, (7)

где х₁¹, …, х₁ⁿ – аффинные координаты точки A, х₂¹, …, х₂ⁿ – аффинные координаты точки В. Правую часть этого выражения, квадратичную относительно разностей координат произвольных точек А и В, называют метрической формой пространства U.

Как мы видим, введённое понятие расстояния между точками многомерных аффинных пространств, как и рассмотренные выше другие геометрические понятия таких пространств, имеет координатное аналитическое описание.

Линейное пространство размерности n с квадратичной метрикой при условии, что его метрическая квадратичная форма положительно определена, называется n-мерным евклидовым линейным пространством. Аффинное пространство размерности n, если соответствующее ему линейное пространство является евклидовым, называется n-мерным евклидовым пространством [3].

Понятие расстояния между точками, как отмечалось выше, является базовым метрическим понятием. На его основе и наряду с ним можно вводить другие, интересующие человека с точки зрения геометрического моделирования метрические понятия, имеющие соответствующие аналитические описания. Таким образом, в целях геометрического моделирования аффинные пространства многомерной аналитической геометрии в случае необходимости могут служить базой для построения разнообразных многомерных метрических пространств.

Выше было отмечено, что в многомерных аффинных пространствах определён ряд топологических понятий, связанных с взаимным расположением геометрических фигур, которые соответственно могут быть использованы в процессе геометрического моделирования, если в этом есть необходимость. Однако в силу того, что на базе многомерных аффинных пространств в соответствии с описанным выше подходом можно строить многомерные метрические пространства, на основе последних можно вводить в рассмотрение многомерные топологические пространства. Причём делать это известным и простым способом, определяя понятие окрестности точек пространства через расстояние между точками. Так, для двух произвольных точек А и В можно полагать, что точка В принадлежит e-окрестности точки А, если

(8)

Следовательно, таким образом можно вводить в рассмотрение наряду с упомянутыми выше произвольные топологические понятия, заслуживающие внимание с точки зрения геометрического моделирования.

Так, например, в число операций над геометрическими фигурами, которые можно было бы использовать в процессе геометрического моделирования, можно включить гомеоморфные (топологически непрерывные) преобразования топологических пространств. Следует подчеркнуть, что вводимые таким образом топологические понятия будут иметь соответствующие координатные аналитические описания.

Нетрудно видеть, что природа пространств многомерной аналитической геометрии является удобной основой для определения в них произвольных геометрических понятий, интересующих человека.

Наконец, несомненным достоинством пространств многомерной аналитической геометрии является также то, что они во многом напоминают наглядное, привычное для человека и хорошо изученное трёхмерное пространство элементарной аналитической геометрии. Как мы знаем, это пространство определённым образом сопоставлено с линейным пространством геометрических векторов, что является основой для использования в нём привычной для нас декартовой системы координат – частного случая системы аффинных координат.

Необходимо также помнить о том, что пространства многомерной аналитической геометрии сами по себе в настоящее время хорошо изучены. Следовательно, известные их свойства могут служить прочной и плодотворной теоретической основой для разработки процедур геометрического моделирования.

3. Рациональный выбор класса пространств многомерной аналитической геометрии в задачах анализа исходных данных.

Проделанный выше анализ пространств многомерной аналитической геометрии с точки зрения их использования для целей геометрического моделирования в процессе анализа исходных данных показывает, что они полностью отвечают сформулированным в начале предъявляемым к ним требованиям.

Какие же из этих пространств в наибольшей степени отвечают таким требованиям? Для того чтобы попытаться ответить на этот вопрос, введём в рассмотрение один из классов этих пространств и проанализируем их свойства.

Введём сначала один класс линейных пространств, на базе которых попытаемся строить интересующие нас геометрические пространства. С этой целью рассмотрим множество, элементами которого служат все возможные упорядоченные наборы (кортежи) действительных чисел, по n чисел в каждом (n – некоторое фиксированное натуральное число). Назовём какой-нибудь набор из n чисел упорядоченным, будем считать, что составляющие его числа пронумерованы, при этом они не обязаны быть различными. Имея в виду, что элемент данного множества есть набор числе d₁,d₂, …, d_n, будем писать d={d₁, d₂,…, d_n}. Считая d произвольным, рассмотрим ещё один, также произвольный элемент d’={d₁’,d₂’, …, d_n’}. Элементы d и d’ полагаются равными в том и только в том случае, когда d₁=d₁’, d₂=d₂’, …, d_n=d_n’, Линейные операции над элементами данного множества (т. е. операции линейных пространств) определяются следующими соотношениями:

d+d’={d₁+d₁’,d₂+d₂’, …,d_n+d_n’}	(9)
ad={ad₁, ad₂, …, ad_n}

где a - произвольное действительное число.

В теории линейных пространств показано, что множество кортежей действительных числе d, рассматриваемое совместно с введёнными таким образом операциями сложения и умножения на действительное число, представляет собой действительное линейное пространство размерности n, т. к. данные операции удовлетворяют известным восьми аксиомам линейных пространств. Нулевым вектором в данном линейном пространстве является вектор t={0, 0, …0}. Противоположным для любого вектора v в данном линейном пространстве является вектор –v, а именно: -v={-v₁, -v₂, …, -v_n}. Заданное таким образом линейное пространство L обычно называют действительным координатным пространством и обозначают через K [3]. Здесь и далее кортежи действительных чисел, рассматриваемые в качестве векторов координатного пространства K, обозначаются через v={v₁, v₂, …, v_n}.

Размерность координатного пространства K, как сказано выше, равна n, т. е. существует набор векторов e₁, e₂, …, e_n из K (базис) такой, что для любого v из K можно записать:

v=x₁e₁+x₂e₂+…+x_ne_n , (10)

где x₁, x₂, …, x_n – координаты вектора v в данном базисе. В качестве такого базиса можно использовать тривиальный набор векторов из K:

e₁={1, 0, …, 0}	(11)
e₂={0, 1, …, 0}
………………..
e_n={0, 0, …, 1}

Действительно, согласно данному ранее определению линейных операций в K любой вектор из K линейно выражается через векторы e₁, e₂,…, e_n, а именно:

v={v₁, v₂, …, v_n}=v₁e₁+v₂e₂+…+v_ne_n. (12)

Отсюда ясно, что линейная комбинация векторов e₁, e₂,…, e_n равна нулевому вектору q={0, …, 0} только в случае, когда все её коэффициенты равны нулю. Значит, векторы e₁, e₂,…, e_n линейно независимы. Следовательно, с учётом того, что любой вектор из K линейно выражается через векторы e₁, e₂,…, e_n, а сами e₁, e₂,…, e_n линейно независимы, они составляют базис пространства K. Любое линейное пространство n-мерно тогда и только тогда, когда в нём есть базис, состоящий из n векторов. Следовательно, размерность рассматриваемого координатного пространства K действительно равна n. В дальнейшем координатное пространство K размерности n будем обозначать K_n.

Поставим в соответствие координатному пространству K_n аффинное пространство размерности n, которое в дальнейшем будем обозначать через W_n. В качестве точек аффинного пространства W_n будем использовать вектора координатного пространства K_n, т. е. для задания пространства W_n воспользуемся рассмотренным ранее простым способом построения аффинных пространств на базе линейных пространств. Суть этого способа, как отмечалось выше, заключается в том, что всякое линейное пространство можно одновременно рассматривать как аффинное пространство. Для этого достаточно векторы назвать точками и каждой паре векторов a, b, рассматриваемых как точки, поставить в соответствие вектор c=b-a. Если обозначать через X=x факт рассмотрения вектора х в качестве точки Х, то данный способ задания аффинного пространства можно определить следующим образом:

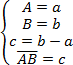(13)

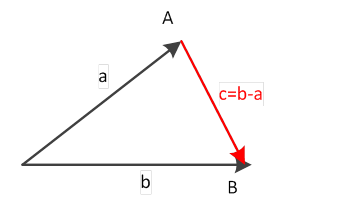
Рис. 3. Иллюстрация рассмотрения вектора как точки.

Обозначим точки пространства W_n через P={p₁, p₂, …, p_n}. Тогда в соответствии с данным способом аффинное пространство W_n будет определено следующим образом:

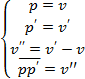(14)

Это можно переписать иначе:

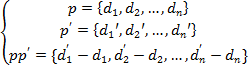(15)

В аффинном пространстве W_n можно выделить некоторую точку О={d₀₁, d₀₂, …, d_0n}. Тогда с произвольной точкой P сопоставляется её радиус-вектор . Используя понятие радиус-вектора можно ввести в пространстве W_n аффинную систему координат, состоящую из начала координат – точки О и некоторого базиса координатного пространства K_n. Аффинными координатами точки P будут являться коэффициенты разложения радиус-вектора по базису:

(16)

Важным свойством пространства W_n является то, что при выборе в качестве начала координат точки О={0, …, 0} и базиса e₁={1, 0, …, 0}, e₂={0, 1, …, 0}, …, e_n={0, 0, …, 1} компоненты любой точки (т. е. элементы соответствующего ей кортежа) и координаты этой точки совпадают, т. е. d₁=x₁, d₂=x₂, …, d_n=x_n. В случае выбора другой системы координат такое равенство уже выполняться не будет.

На базе данного аффинного пространства W_n, как и любого аффинного пространства многомерной аффинной геометрии, можно легко определять другие геометрические пространства, наделённые интересующими пользователя свойствами. Однако на базе пространства W_n это делается особо просто, если в качестве системы координат выбрать точку О={0, …, 0} и базис e₁={1, 0, …, 0}, e₂={0, 1, …, 0}, …, e_n={0, 0, …, 1}. Нетрудно видеть, что в этом случае соответствующие метрические и топологические понятия, о которых шла речь выше, тривиально просто выражаются через сами точки пространства W_n, а точнее сказать – через их компоненты.

В пространстве W_n, по аналогии с другими пространствами многомерной аналитической геометрии, геометрическим фигурам и выполняемым над ними операциям можно ставить в соответствие координатные и векторные аналитические описания. Однако данное пространство W_n позволяет наряду с координатными и векторными использовать также и нетрадиционные виды описаний. Так, например, геометрическим фигурам в пространстве W_n можно ставить в соответствие точечные описания. Суть точечного описания состоит в том, что все точки описываемой фигуры должны удовлетворять некоторому аналитическому соотношению. Для задания точечного описания выделяется некоторая точка P₀, а затем формулируется условие по отношению к P-P₀, где P – произвольная точка описываемой геометрической фигуры. Так, для описания отдельной точки пространства W_n можно использовать точечное уравнение:

P-P₀=0, (17)

где О – нулевой кортеж, т. е. О={0, 0, …, 0}.

Наряду с точечными описаниями в пространстве W_n можно также использовать компонентные описания. Суть компонентного описания геометрической фигуры заключается в том, что компоненты всех точек данной фигуры должны удовлетворять некоторым аналитическим соотношениям. Та же точка пространства W_n может быть описана системой компонентных уравнений:

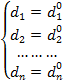(18)

где d_i и d_i⁰, i=1, 2,…, n – компоненты точек P и P₀ соответственно.

Как видно, точечные описания аналогичны традиционным векторным, а компонентные – координатным. Однако, использование компонентных описаний не требует, в отличие от координатных, введения базиса в пространстве W_n. Что касается точечных описаний, то они, в отличие от векторных, могут быть непосредственно использованы в качестве числовых моделей при компьютерной реализации алгоритмов визуализации исходных анализируемых данных.

Таким образом, проделанный анализ одного из классов пространств многомерной аналитической геометрии, а именно, совокупности пространств, включающей в себя сами пространства W_n различной размерности, а также пространства, которые могут быть определены на их основе, позволяет сделать вывод о том, что эти пространства выгодно отличаются своей простотой и удобством использования для целей геометрического моделирования. Следует особо подчеркнуть наглядность этих пространств, т. к. работа с множеством кортежей чисел является привычной и удобной для пользователя, прежде всего благодаря использованию естественной табличной интерпретации данного множества.

4. Заключение

Сформулированные и обоснованные выше общие положения рационального выбора многомерных геометрических пространств для целей геометрического моделирования были успешно использованы авторами при разработке ряда прикладных программных средств в Британском национальном центре компьютерной анимации при университете Борнмута и Национальном исследовательском ядерном университете. В настоящее время с использованием этих рекомендаций разрабатываются интерактивные программные средства, предназначенные для эффективного решения задач анализа различных многомерных данных методом компьютерной визуализации.

Литература

Pilyugin V., Malikova E., Adzhiev V., Pasko A., Some theoretical issues of scientific visualization as a method of data analysis, Transactions on Computational Science XIX, Lecture Notes in Computer Science, Vol. 7870, Springer-Verlag, 2013, pp. 131–142.
Мацуо Комацу, Многообразие геометрии: Пер. с япон. – М.:Знание, 1981.-208 c.
Ефимов Н.В.,Розендорн Э.Р., Линейная алгебра и многомерная геометрия:- М.: Наука, 1970.- 528 с.

SURVEY OF APPROACHES TO MULTIDIMENSIONAL DATA GEOMETRIZATION IN THE ANALYSIS USING COMPUTER VISUALIZATION

V.V. Pilyugin¹, A.A. Pasko², I.E. Milman¹

¹National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, Russian Federation

²National Centre for Computer Animation, Bournemouth University, Bournemouth, United Kingdom

VVPilyugin@mephi.ru, apasko@bournemouth.ac.uk, igalush@gmail.com

Abstract

During the analysis of various data using computer visualization, the visualization pipeline often contains the geometrization stage of this data using some multidimensional geometric space. In this article, we consider issues of a rational choice of a class of multidimensional spaces for the analysis of input data by the method of computer visualization.

Keywords: geometrization, geometric space, multidimensional space, computer visualization, multidimensional data, affine space, linear space

References

Pilyugin V., Malikova E., Adzhiev V., Pasko A., Some theoretical issues of scientific visualization as a method of data analysis, Transactions on Computational Science XIX, Lecture Notes in Computer Science, Vol. 7870, Springer-Verlag, 2013, pp. 131–142.
Matsuo Komatsu. Mnogoobrazie geometrii [The variety of geometry]. Translated from Japanese. Moscow: Science. 1981. 208 p. [In Russian]
Efimov N.V.,Rozendorn E.R.. Linejnaja algebra i mnogomernaja geometrija [Linear algebra and multidimensional geometry]. Moscow: Science. 1970. 528 p. [In Russian]