Разработка системы интерактивного визуального анализа многомерных данных
О.П. Масленников*, И.Е. Мильман*, А.Э. Сафиуллин*, А.Е. Бондарев**, Ш.У. Низаметдинов*, В.В. Пилюгин*
Национальный исследовательский ядерный университет "МИФИ", Россия*
Институт прикладной математики им. М.В.Келдыша РАН**
Москва, Россия
maslolpavl@gmail.com; igalush@gmail.com; amir147@rambler.ru; bond@keldysh.ru; sh_nizam@mail.ru; VVPilyugin@mephi.ru
Содержание
2. Функциональные возможности интерактивной системы визуального анализа
2.1. Решение задачи кластерного анализа 3D проекционным методом
2.2 Решение задачи дискриминантного анализа 2D и 3D проекционным методом
2.3. Решение задачи выделения кластеров 2D проекционным методом
Аннотация
Работа посвящена разработке интерактивной системы для решения задач анализа многомерных данных интерактивным визуальным методом. Визуальная аналитика предоставляет удобные средства для решения задач анализа многомерных данных и в данной работе показан инструментарий для решения задачи кластеризации, дискриминантного анализа и для анализа формы кластеров визуальным методом. Разрабатываемая система позволяет отобразить многомерное облако данных и проводить его анализ в пространствах меньшей размерности (2D и 3D), выдвигать и проверять различные гипотезы об исходных данных, с возможностью последующего построения предположений для проведения некоторых счетных методов, с помощью геометрических построений в интерактивном режиме.
Ключевые слова: визуальная аналитика, анализ многомерных данных, интерактивный интерфейс
1. Введение
Современные задачи обработки и анализа огромных разнородных объемов информации требуют интенсивного развития методов, принципов и программных средств, позволяющих осуществить их решение. В роли средства решения выступает сравнительно молодая междисциплинарная ветвь исследований – визуальная аналитика. Методы визуальной аналитики интенсивно внедряются во все значимые прикладные аспекты человеческой деятельности. Причиной этому служат, в первую очередь, заложенные в основу визуальной аналитики принципы универсализма, обеспечивающие успешную работу с разнотипными, конфликтующими между собой и динамически изменяющимися объемами информации.
Визуальная аналитика (Visual Analytics) представляет собой междисциплинарный раздел знаний, основанный на синтезе и дальнейшем совместном развитии методов и подходов из уже сложившихся областей научных исследований, таких как научная визуализация (Scientific Visualization), визуализация информации и информационных процессов (Information Visualization), анализ многомерных данных (Data Analysis).
Однако данный синтез является не просто суммированием методов и подходов из различных дисциплин. Он имеет своей целью анализ огромного объема информации, а целью этого анализа является обеспечение поддержки принятия оперативного и точного решения человеком. Поэтому визуальная аналитика включает в себя и компьютерную графику, и изучение законов человеческого восприятия, и построение интерфейсов, обеспечивающих наиболее быстрое и оптимальное восприятие. Визуальную аналитику часто называют «наукой аналитического обоснования, усиленной с помощью интерфейсов интерактивной визуализации» [1].
Визуальная аналитика объединяет различные методы и технологии во всех интегрируемых ею дисциплинах с целью максимально эффективного обеспечения взаимодействия «человек-компьютер». Схема, представляющая визуальную аналитику, как результат междисциплинарного синтеза, показана на рис.1. Общая цель применения методов визуальной аналитики к исследованию многомерного объема данных – получение максимально возможной информации об изучаемом облаке данных и обеспечение максимального понимания происходящих в нем процессов.
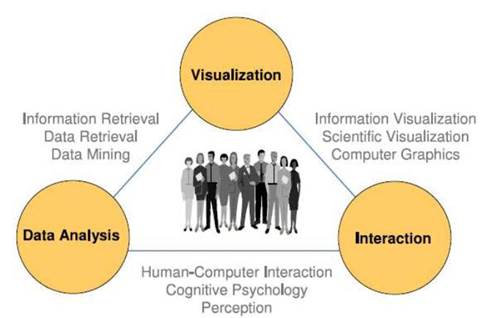
Рис.1. Визуальная аналитика как результат междисциплинарного синтеза [2].
Основные методы, подходы и алгоритмы визуальной аналитики описаны в работах [1,3–6]. В этих же работах приведен ряд примеров современного применения визуальной аналитики в различных сферах человеческой деятельности, а также приведены описания ряда программных продуктов, построенных на основе визуальной аналитики. Согласно [1,3–6], визуальная аналитика призвана организовать человеко-машинный интерфейс, усиливающий человеческие аналитические способности с помощью следующих методов:
- расширение оперативной памяти человека за счет использования визуализации;
- уменьшение области поиска путем представления большого объема данных в пространстве меньшей размерности;
- размещение информации в пространстве в соответствии с временными соотношениями;
- использование легких для восприятия представлений отношений между объектами;
- организация возможности восприятия большого числа потенциальных событий;
- организация управляемой среды для работы пользователя в пространстве параметрических значений;
- организация визуального представления и интерфейсов, обеспечивающих человеку возможность сразу видеть, исследовать и понимать огромные информационные объемы.
Реализация процедур визуальной аналитики применительно к большим информационным объемам подчиняется общей схеме, приведенной на рис.2. Первым этапом в данной последовательности процедур является подготовка данных. Обычно считается, что рассматриваемые данные являются сложными и гетерогенными, имеют смешанный тип и получены из разных источников. Также считается, что рассматриваемые данные обладают разным уровнем качества. На предварительном этапе проводится фильтрация данных, удаление шумов и преобразование данных с целью совместной обработки. Источники данных (например, хорошо организованные базы данных) выстраиваются таким образом, что бы обеспечить непрерывный входной поток данных. Далее данные обрабатываются и переводятся в абстрактный вид с помощью математических моделей, статистических моделей и методов Data Analysis. Далее проводится реализация визуального представления полученных абстракций с целью выявления характерных черт, включая общности и аномалии. Это дает возможность пользователю провести визуальную оценку полученных результатов. Организация визуальных представлений должна быть оптимизирована с учетом всех возможностей и ограничений человеческого зрения и восприятия. Интерактивный режим визуализации позволяет пользователю проводить обработку данных и получать необходимую информацию, обеспечивающую возможность трактовки рассматриваемого информационного объема.
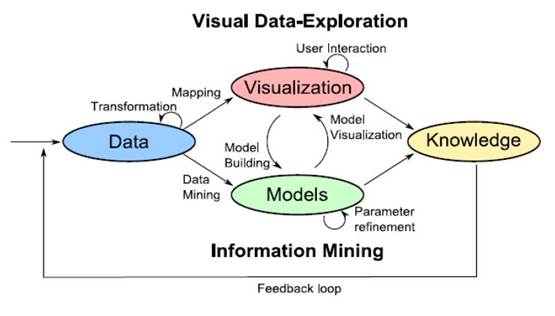
Рис.2. Общая схема процесса реализации визуальной аналитики многомерных данных [3].
При реализации этих процедур инструменты визуальной аналитики должны обеспечивать пользователю ряд возможностей, таких как:
- возможность визуализации данных с разных концептуальных точек зрения и на всех этапах: от «сырых» первичных данных до полученных абстракций;
- визуализация огромного количества информации в малом пространстве;
- извлечение из данных образов, отражающих общности, аномалии, соотношения между объектами и отдельные события;
- моделирование и верификация гипотез;
- оперативный обмен информацией.
Внимательное изучение литературы, посвященной описанию конкретных приложений в области визуальной аналитики, позволяет утверждать, что в реальности интерактивным системам работы с многомерными данными зачастую придается меньшее значение по сравнению с системами отображения результатов применения методов Data Analysis. В качестве примера можно привести такие системы, как система ситуационного оповещения AdAware [7], система визуальной аналитики в задачах самолетостроения [8], система визуальной аналитики текстовой информации VxInsight [9], программный комплекс SAS Visual Analytics [10], предназначенный для обработки и анализа больших объемов финансовой и экономической информации. Все указанные системы носят промышленный характер, являются коммерческими, предоставляют пользователю огромное количество интерфейсов и возможностей визуального представления данных. Однако в то же время все эти системы, по сути, настроены на внутреннюю обработку данных и представление их пользователю в удобном для него виде, не предоставляя возможности пользователю непосредственно работать с визуальными отображениями многомерного облака данных.
Данная работа представляет разрабатываемую интерактивную систему визуального анализа многомерных данных. В рамках разрабатываемой системы рассматриваются классические задачи анализа многомерных данных, такие как: построение кластеров и их оболочек в многомерном облаке данных, построение системы решающих правил для процедур классификации объектов, реализация отображения многомерного объема данных в двумерных проекциях на все возможные пары координат. Разрабатываемая система позволяет пользователю:
- непосредственно работать с отображениями данных в пространствах меньшей размерности – двумерных и трехмерных;
- выдвигать гипотезы о наличии кластеров и классов в облаке данных и проверять их непосредственно с помощью интерактивного геометрического моделирования;
- строить оболочки обнаруженных кластеров, максимально приближенные к данным, в системе координат главных компонент;
- принимать решения о возможности построения решающих правил для задач классификации новых объектов;
- проводить непосредственный поиск кластеров по множеству двумерных проекций и визуальный анализ значимости координатных направлений с точки зрения вклада в дисперсию.
Следует также отметить, что разрабатываемая интерактивная система, дает в перспективе возможность при дальнейшем применении математических методов анализа многомерных данных использовать полученные геометрические построения и гипотезы в качестве начальных приближений для более точных вычислений. При разработке интерактивной системы использовались материалы работ [11-14].
2. Функциональные возможности интерактивной системы визуального анализа
Разработанные на сегодняшний день функциональные возможности создаваемой системы интерактивного визуального анализа многомерных данных предоставляет пользователю возможность практического решения нескольких классических задач Data Analysis. Первой из них является задача кластеризации облака многомерных данных и построение оболочек для получаемых в процессе решения задачи кластеров. Вторая задача представляет собой классическую задачу дискриминантного анализа, пользователю предоставляется возможность решения задачи 2D и 3D проекционным методом. Третья задача предполагает обеспечение работы пользователя с матрицей двумерных проекций и возможности выделения кластеров 2D проекционным методом.
2.1. Решение задачи кластерного анализа 3D проекционным методом
В данную задачу входит анализ взаимного расположения многомерных точек интерактивным проекционным методом, который предусматривает построения проекций исходного n-мерного пространства на трехмерные подпространства и построение оболочки кластера для анализа формы и взаимного положения кластеров.
Проводится анализ взаимного расположения многомерных точек 
методом
проекций на 3-х мерные подпространства 
, где 
.
В исходном n-мерном пространстве строится отрезок между
точками, если расстояние между этими точками, меньше заданного порогового числа
.
При переходе от исходного n-мерного пространства к трехмерному, многомерные
точки отображаются в трехмерные точки, а отрезки, соединяющие эти точки, в
отрезки, соединяющие трехмерные точки. Далее, трехмерным точкам ставится в
соответствие сферы, цвет и радиус, которых задает пользователь. Отрезкам,
соединяющим трехмерные точки, ставятся в соответствие цилиндры, радиус которых
также задает пользователь. Цвет цилиндров задается в зависимости от расстояния.
Чем меньше отношение 
, тем
цилиндр будет краснее, а чем данное отношение ближе к единице, тем цилиндр
будет приобретать более синюю окраску.
Особым случаем проекции является проекция на трехмерное
пространство, при совпадении группы координат у нескольких точек исходного
пространства. Если в исходном пространстве у точек 
и 
, то
в проекции на подпространство 
,
точки трехмерного пространства совпадут. В этом случае, нельзя сделать суждение
о взаимном положении исходных точек, поэтому необходимо перейти к другому
подпространству 
, где 
.
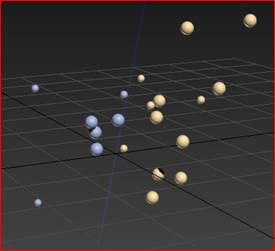
Рис. 3. Отображение множества точек при параметре 
На рисунке 3 изображено множество точек, для которых
сработал алгоритм для . на данном рисунке видно само множество
точек и связи между ними.
Такой вариант отображения данных позволяет проводить анализ взаимного расположения точек, выделять кластеры и делать суждения о расстояниях между исходными точками в n-мерном пространстве.
Предлагается алгоритм прохода и анализа процесса кластеризации для различных d, при этом предлагается подход изменения d таким образом, чтобы в начале все точки входили в один кластер, а завершать анализ разрывом последней связи. На каждом шаге параметр уменьшается, и пользователю системы предоставляется возможность делать суждения о количестве кластеров и, возможно, об их форме, мощности и составе, о расстояниях между кластерами.
Данный алгоритм был реализован в качестве скрипта к программе 3ds Max, на внутреннем языке maxscript.
Создано два режима перехода от одного минимального расстояния к другому. Первый — последовательное изменение d на такое значение, какое устраивает пользователя. И второй — анимация, с заданием начального и конечного параметра и количества кадров. Режимов просмотра анимации реализовано два — покадровый в 3ds Max или в качестве видео ряда в любом видео проигрывателе.
На рисунке 4 представлена анимация уменьшения 
от 5 до 0 за 600
кадров. Анимация представляется с частотой 30 кадров в секунду. В анимации
можно увидеть, как сначала отделяется кластер, состоящий из двух точек
(Справа). Затем, пропадают все синие циллиндры и можно выделить три кластера,
состоящие из двух, девятнадцати и двадцати одной точки.
Следующее наблюдаемое изменение — это разрыв связи внутри
кластера, состоящего из двух элементов. Далее, наблюдается стабильное состояние
системы, параметр приближается к максимальному расстоянию
между точками в кластерах. В анимации это отображено изменением цвета связей (с
красного на синий). Далее все связи внутри кластеров рвутся и в конце, при 
, все точки становятся
одиночными.
Рис. 4. Анимация уменьшения d от 5 до 0
После разбиения множества точек на кластеры пользователю предлагается возможность провести построение и анализ оболочки кластера. Оболочка кластера — это замкнутая поверхность такая, что все точки кластера лежат под одну сторону.
Построение оболочки проводится в трехмерном пространстве, однако, построение оболочки в трехмерном пространстве представляет собой определенный интерес с точки зрения анализа взаимного расположения точек в исходном n-мерном пространстве.
Простейшей оболочкой является прямоугольный параллелепипед. Для его построения вычисляются главные компоненты, основываясь на матрице ковариаций координат точек, входящих в кластер. Прямоугольный параллелепипед строится, принимая собственные вектора данной матрицы за каркас, центр параллелепипеда берется в центре кластера, рассчитанном по следующей формуле:
Длина, ширина и высота рассчитаны, как максимальный размах, по следующей формуле:
Где 
— i-я
координата точки в новом базисе.
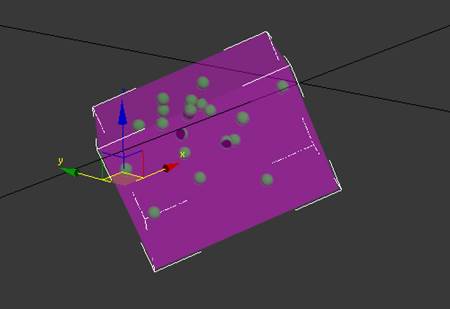
Рис. 5. Оболочка в виде прямоугольного параллелепипеда для кластера.
На рисунке 5 показан пример построения оболочки в виде
прямоугольного параллелепипеда, указаны направления исходных осей x, y, z.
Кластер представлен в виде зеленых сфер, оболочка — фиолетовый параллелепипед (прозрачность
30%). Собственные числа (
и
собственные вектора 
представлены
в таблице 1.
Таблица 1. Собственные значения и собственные вектора для оболочки в виде параллелепипеда.
|
Номер (Упорядочен по уменьшению λ) |
|
|
|
1 |
1.42611 |
[0.650317,-0.659275,0.377419] |
|
2 |
0.929802 |
[-0.296903,0.236731,0.925098] |
|
3 |
0.644084 |
[0.699233,0.713669,0.0418295] |
Второй способ построения оболочки реализован в виде
пересечения сфер. В трехмерном пространстве создаются сферы с центром в точках
(
— трехмерная
координата проекции точки исходного пространства на трехмерное
подпространство), относящихся к анализируемому кластеру, радиус сфер
вычисляется по следующей формуле:
Далее к множеству сфер 
применяется
теоретико-множественное пересечение, в результате которого получается сложная
поверхность, составленная из секторов сфер (Рис.6).
Рис. 6. Оболочка кластера, полученная пересечением сфер.
Данная оболочка часто охватывает меньший объем, а значит описывает оболочку более точно, чем это сделано в предыдущем методе.
К недостаткам данного метода следует отнести поведение на вытянутых кластерах, когда одно из собственных значений, полученных при вычислении главных компонент гораздо больше остальных собственных значений.
В качестве компромиссного варианта предлагается пересечение оболочек, полученных с помощью обоих вышеописанных методов (Рис.7).
Рис. 7. Оболочка, созданная пересечением двух оболочек.
Данная оболочка прилегает плотнее, чем оболочка в виде прямоугольного параллелепипеда и прилегает лучше, в случае вытянутого кластера.
Используя средства 3ds Max, пользователь может деформировать оболочку, чтобы сделать её ближе к кластеру. В таком случае, оболочка может являться невыпуклой (Рис.8).
Рис. 8. Деформированная оболочка
2.2 Решение задачи дискриминантного анализа 2D и 3D проекционным методом
Второй задачей, реализованной на сегодняшний день в разрабатываемой системе интерактивного визуального анализа многомерного облака данных, является классическая задача дискриминантного анализа. Задача решается с помощью проекционного метода, реализованного для 2D и 3D случаев.
В качестве исходных данных в данной задаче выступают 2 группы точек, заданных набором своих координат в исходном 4х мерном пространстве. Требуется получить решающее правило для данной задачи.
Основным предположением дискриминантного анализа является то, что существуют две или более группы, которые по некоторым переменным отличаются от других групп, причем такие переменные могут быть измерены по интервальной шкале либо по шкале отношений. Дискриминантный анализ помогает выявлять различия между группами и дает возможность классифицировать объекты по принципу максимального сходства. [11]
Основной целью является нахождение такой линейной комбинации
переменных, которая бы разделила рассматриваемые группы. 
Основным методом решения задачи дискриминантного анализа является метод нахождения коэффициентов гиперплоскости Фишера.
Для построения разделяющей гиперплоскости в данной работе предлагается использовать метод последовательных проекционных изображений.
Суть метода заключается в том, что если мы можем в проекции построить разделяющую плоскость, то при переходе к пространству с размерностью на единицу больше, данная плоскость будет являться так же разделяющей. В качестве алгоритма решения был предложен последовательный просмотр и анализ 2х и 3х-мерных проекций с целью нахождения разделяющей плоскости или системы таких плоскостей.
В качестве одного из алгоритмов работы с системой был предложен следующий алгоритм, как возможный сценарий работы пользователя в системе:
Шаг 0: Запуск программы, ввод размерности и файла данных с учебной выборкой.
Шаг 1: Проектирование исходного пространства на 3-х мерное пространство x1, x2, x3 и визуальная оценка полученной проекции, вращение полученной картинки путем работы со стандартными компонентами среды «Autodesk 3DS max». Поиск тривиального решения. (решения в проекции x1, x2, x3). Если удается найти и построить разделяющую плоскость, то переход к Шагу 8, если плоскость не подбирается, то переход к Шагу 4.
Шаг 2: Переход на 2-мерную проекцию x1, x2. Попытка построить разделяющую прямую. Если прямая построена, то Шаг 8, если не удается построить разделяющую прямую, переходим к следующей проекции и повторяем Шаг 2. Если были рассмотрены все 2х мерные проекции, то Шаг 3.
Шаг 3: Повторный просмотр проекции x1, x2, x3. Попытка построить разделяющую плоскость. Если плоскость построена, то Шаг 8, если не удается построить разделяющую плоскость, то переходим к следующей проекции. Если все 3-мерные проекции рассмотрены, то Шаг 4
Шаг 4: Переход на 2-мерную проекцию x1, x2. Попытка построить 2 разделяющих прямых. Если прямые построены, то Шаг 8, если не удается построить разделяющую прямую, то переход к следующей проекции, если все 2-мерные проекции рассмотрены, то Шаг 5
Шаг 5: Просмотр проекции x1, x2, x3. попытка построить 2 разделяющих плоскости. Если плоскость построена, то Шаг 8, если не удается построить разделяющую плоскость, то переход к следующей проекции, если все 3-мерные проекции рассмотрены, то Шаг 6.
Шаг 6: Переход на 2-мерную проекцию x1, x2. Попытка построить систему из 3-х и более разделяющих прямых. Если прямые построены, то Шаг 8, если не удается построить систему разделяющих прямых, то переход к следующей проекции, если все 2-мерные проекции рассмотрены, то Шаг 7
Шаг 7: В результате работы по данному алгоритму не было выявлено решающего правила, пользователю предоставлена возможность вернуться на Шаг2, либо сделать предположение о неразрешимости задачи дискриминантного анализа в данной постановки задачи для конкретного рассматриваемого набора многомерных данных.
Шаг 8: Получено решающее правило. Задача решена.
Шаг 9: Верификация полученного решающего правила на новых элементах, добавляемых пользователем.
Пример реализации разработанного метода представлен на рисунках 9-13 ниже.
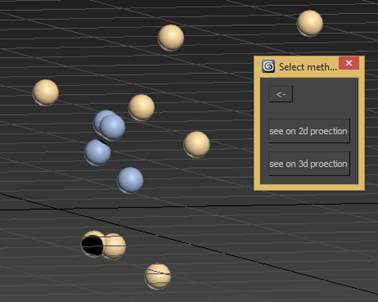
Рис. 9. Выбор режима работы.
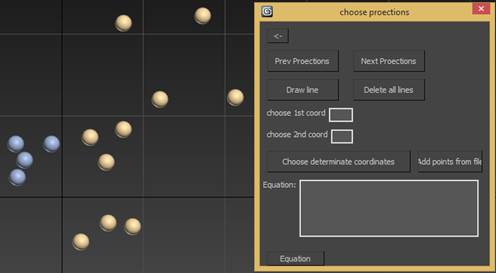
Рис. 10. Пользовательский интерфейс.
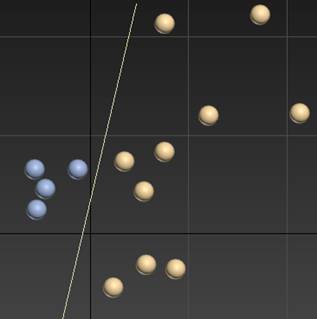
Рис. 11. Построение разделяющей прямой
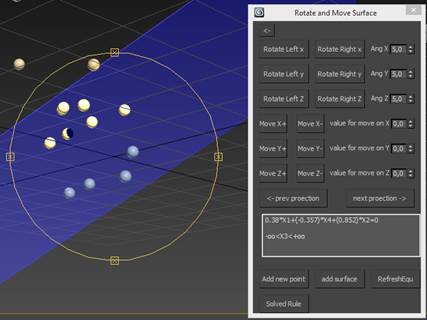
Рис. 12. Построение разделяющей плоскости.
После решения задачи дискриминантного анализа пользователю предоставляется возможность проведения верификации построенной формальной системы решающих правил. После проведения верификации пользователь может решать задачу классификации новых объектов, добавляемых к исходному многомерному объему данных (рис. 13).
|
|
|
|
Рис. 13. Решение задачи классификации новых объектов.(а- при построении системы разделяющих прямых, б- при построении разделяющей плоскости) |
|
Данный метод позволяет пользователю принимать решения о возможности построения решающих правил для задач классификации новых объектов.
2.3. Решение задачи выделения кластеров 2D проекционным методом
Третья задача, реализованная в данной интерактивной системе, предполагает обеспечение возможности работы пользователя с матрицей всевозможных двумерных проекций многомерного облака данных. На основе этой возможности решается задача выделения кластеров.
Данный метод базируется на гипотезе «компактности». Она заключается в том, что реализации одного и того же образа обычно отражаются в признаковом пространстве в геометрически близкие точки, образуя «компактные сгустки». Основываясь на этом, можем сделать суждение о том, что точки, близкие в n-мерном пространстве, близки в каждом двумерном подпространстве.
Алгоритм решения задачи:
Этап 1. Проецируем точки многомерного объема данных в двумерное пространство, получая таким образом матрицу проекций.
Этап 2. На одной из проекций выделяем характерные образования – кандидаты на сгустки.
Этап 3. Анализируем остальные проекции и в случае обнаружение точек, лежащих далеко от сгустка, исключаем их.
Этап 4. Помечаем оставшиеся выделенные точки как кластер. Исключаем данные точки из рассмотрения. Если у нас не осталось сгустков точек (одиночные точки, либо все точки помечены как кластер) то переходим к этапу 5, иначе к этапу 2.
Этап 5. Получены кластеры. Можно запустить алгоритм К-средних для улучшения разбиения.
Организация работы пользователя.
Пользователь начинает с того, что импортирует данные из файла Excel в программную систему и строит матрицу проекций (рис. 14).
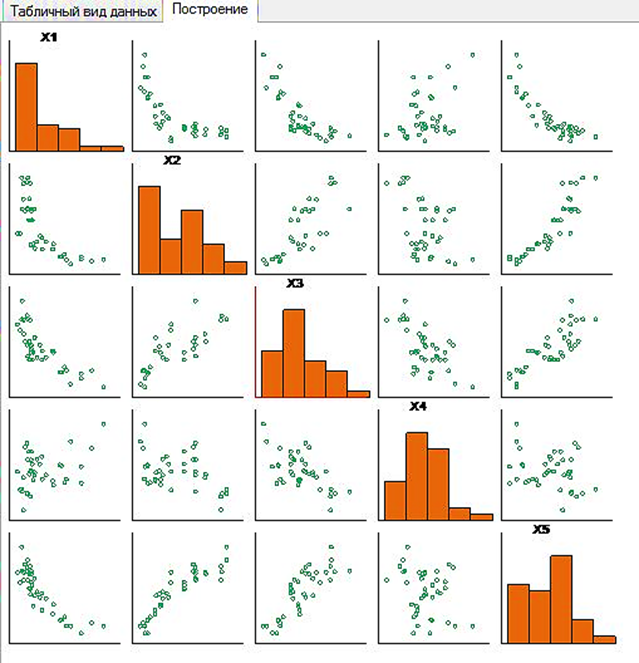
Рис.14. Матрица проекций.
Она представляет собой матрицу размера n*n, где по главной диагонали расположены гистограммы распределения исходных данных в проекции на данную ось, а в остальных клетках – проекции исходных данных на все возможные пары координат. При нажатии на элемент матрицы проекций, в правой половине окна программы мы видим увеличенную проекцию, с которой можем взаимодействовать.
Рассматривая элементы матрицы проекций, лежащих выше главной диагонали (т.к. элементы лежащие ниже главной диагонали отличаются только направлением осей координат), пользователь ищет наиболее плотное скопление точек, и выделяет их с помощью компьютерной мыши (рис.15).
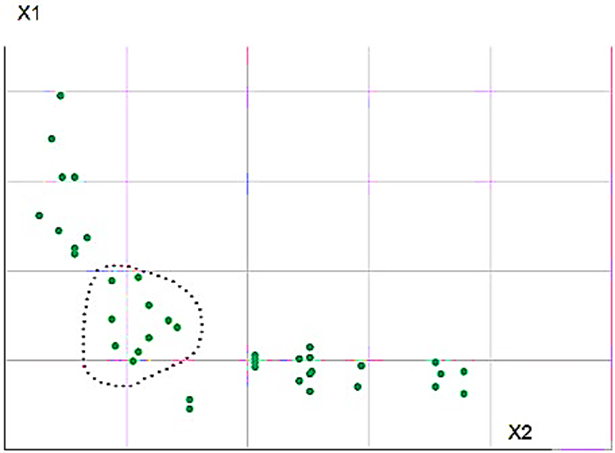
Рис. 15. Выделение точек с помощью компьютерной мыши в проекции х1 х2.
Невыделенные точки скрываются и далее работа продолжается только с оставшимися выделенными точками (рис. 16).
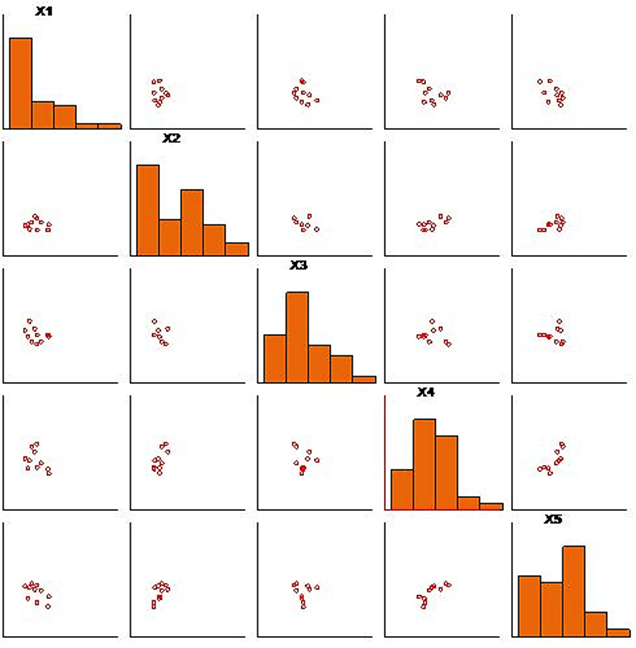
Рис 16. Матрица проекций. Показаны только выделенные точки.
Снова просматривается матрица проекций, ищутся точки, лежащие далеко от сгустка на одной из проекций; эти точки отбрасываются. Матрица проекций просматривается до тех пор, пока все точки не будут лежать плотно на всех проекциях (образуя компактный сгусток).
Получив компактный сгусток, его точки помечаются как принадлежащие одному кластеру (рис. 17). Для точек кластера пользователь может выбирать цвет, используя опцию «Характеристики кластера».
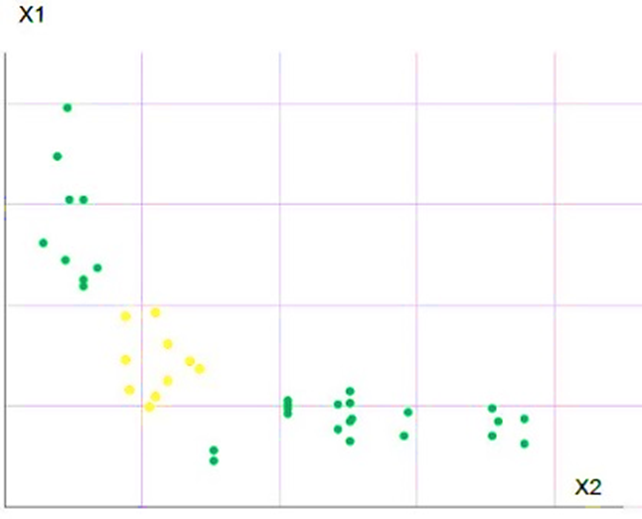
Рис. 17. Выделение кластера в проекции х1 х2.
Помеченные точки, принадлежащие одному кластеру, исключаются из дальнейшего рассмотрения. Снова идет поиск наиболее плотного скопления точек, и выделения их, после чего невыделенные точки опять скрываются. Матрица проекций просматривается заново до получения результата, удовлетворяющего пользователя.
Для улучшения результатов к полученным данным можно применить модифицированный алгоритм К-средних.
Реализация модифицированного алгоритма К средних:
На первом шаге в каждом кластере помечаются точка, которую можно принять за "центр" кластера. Затем все точки перераспределяются так, чтобы каждая точка включалась в тот кластер, расстояние до центра которого наименьшее.
Заново вычисляются центры кластеров, точки опять перераспределяются. Процесс продолжается, пока центры кластеров не стабилизируются либо число итераций не достигнет максимального.
Пользователю предоставляется возможность расчета T-статистики (доля межгруппового разброса) для оценки компактности разбиения исходного множества точек на кластеры.
Для наглядности представления результатов кластеризации строится профильная диаграмма, облегчающая интерпретацию полученных кластеров (рис 18).
На данной диаграмме для каждой переменной по вертикали откладываются точки, соответствующие средним значениям данной переменной в кластере. Точки одного кластера соединяются последовательно отрезками одного цвета, в результате чего получается ломаная, характеризующая кластер.
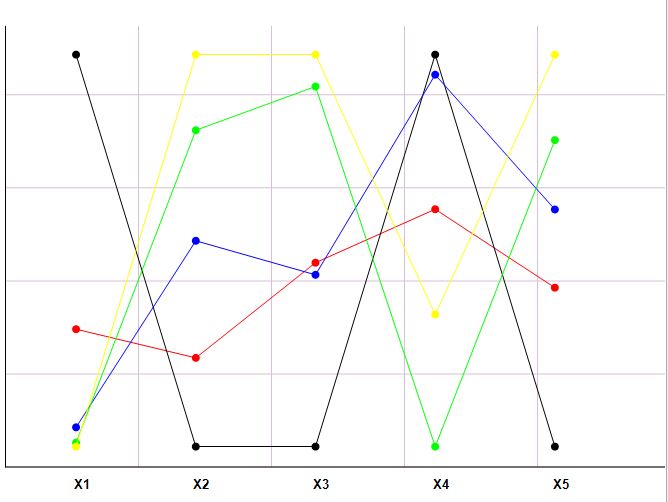
Рис 18. Профильная диаграмма.
Представив визуально полученные результаты, пользователь может определить, какие объекты являются спорными, т.е. могут принадлежать как одному, так и другому кластеру, какие группы вообще не имеют места быть в силу невозможности их содержательной интерпретации.
3. Заключение
Разрабатываемая система предоставляет ряд инструментов для проведения интерактивного визуального анализа многомерных данных различными способами.
На сегодняшний день в рамках системы реализованы три функциональных модуля, обеспечивающие интерактивное решение некоторых классических задач анализа многомерных данных. Основное отличие разрабатываемой системы от сушествующих, является то обстоятельство, что данная система предоставляет пользователю возможность непосредственной работы с многомерным облаком данных, построение различного рода проекций и решение задач анализа данных в этих проекциях в интерактивном режиме.
Следует также заметить, что набор инструментов предполагается значительно расширить, что даст возможность пользователю реализовать большее количество действий с многомерными данными. Построенные пользователем аналитические решения для исследуемого объема данных могут впоследствии использоваться как начальные приближения для более точных вычислений.
Литература
1. Thomas J., Cook K. Cook, Illuminating the Path: Research and Development Agenda for Visual Analytics. IEEE-Press, 2005.
2. http://www.visual-analytics.eu
3. Keim D. A, Mansmann F, Schneidewind J, Thomas J, Ziegler H: Visual analytics: Scope and challenges, Visual Data Mining: 2008, S. 82.
4. Keim D., Andrienko G., Fekete J.-D., Gorg C., Kohlhammer J., and Melancon G. “Visual Analytics: Definition, Process, and Challenges”, A. Kerren et al. (Eds.): Information Visualization, LNCS 4950, pp. 154–175, 2008. Springer-Verlag Berlin Heidelberg 2008.
5. Kielman, J. and Thomas, J. (Guest Eds.) (2009). Special Issue: Foundations and Frontiers of Visual Analytics, Information Visualization, Volume 8, Number 4, Winter 2009, p. 239-314.
6. Keim D., Kohlhammer J., Ellis G. and Mansmann F. (Eds.), Mastering the Information Age – Solving Problems with Visual Analytics, Eurographics Association, 2010.
7. Y. Livnat, J. Agutter, S. Moon, and S. Foresti, «Visual correlation for situational awareness» in IEEE Symposium on Information Visualization, 2005, pp. 95-102.
8. Dimitri N. Mavris, Olivia J. Pinon, David Fullmer Jr. «Systev design and modeling: a visual analytics approach», Proc. of 27-th International congress of the aeronautics ICAS-2101, 2010, 27 p.
9. http://www.cs.sandia.gov/projects/VxInsight/
10. http://www.sas.com/offices/europe/russia/hpa/index.html
11. Айвазян C.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Классификация и снижение размерности. М.: Финансы и статистика, 1989.
12. Пилюгин В.В., Маликова Е.Е., Пасько А.А., Аджиев В.Д. Научная визуализация как метод анализа научных данных / Научная визуализация. Т.4, № 4, с.8-25, 2012, URL: http://sv-journal.org/2012-4/062139.html
13. Бондарев А.Е., Галактионов В.А. Анализ многомерных данных в задачах многопараметрической оптимизации с применением методов визуализации / Научная визуализация. Т.4, № 2, с.1-13, 2012, URL: http://sv-journal.org/2012-2/012139.html
14. Основы научной визуализации [сайт]. URL: http://ifes.mephi.ru/unl/ (дата обращения: 10.05.2014)
Development of a system for analyzing of multidimensional data
O.P. Maslennikov*, I.E. Milman*, A.E. Safiulin*, A.E. Bondarev**, Sh.U. Nizametdinov*, V.V. Pilyugin*
National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Moscow, Russian Federation*
Keldysh Institute for Applied Mathematics RAS, Moscow, Russian Federation **
maslolpavl@gmail.com; igalush@gmail.com; amir147@rambler.ru; bond@keldysh.ru; sh_nizam@mail.ru; VVPilyugin@mephi.ru
Abstract
This paper is devoted to the development of a system for analyzing of multidimensional data using visualization method. Visual analytics provides convenient tools for solving problems of multidimensional data and this paper presents some tools for solving problems of clustering, discriminant analyzing and for analyzing the form of clusters using visual method. Developed system can display multidimensional cloud of data and allows the user to analyze it in a lower-dimensional space (2D and 3D), propose and test various hypotheses about the original data, with possibility of making assumptions for using calculating techniques, using geometric constructions in interactive mode.
Key words: visual analytics, multidimensional data analysis, interactive interface.
References
1) Thomas J., Cook K. Cook, Illuminating the Path: Research and Development Agenda for Visual Analytics. IEEE-Press, 2005.
2) http://www.visual-analytics.eu
3) Keim D. A, Mansmann F, Schneidewind J, Thomas J, Ziegler H: Visual analytics: Scope and challenges, Visual Data Mining: 2008, S. 82.
4) Keim D., Andrienko G., Fekete J.-D., Gorg C., Kohlhammer J., and Melancon G. “Visual Analytics: Definition, Process, and Challenges”, A. Kerren et al. (Eds.): Information Visualization, LNCS 4950, pp. 154–175, 2008. Springer-Verlag Berlin Heidelberg 2008.
5) Kielman, J. and Thomas, J. (Guest Eds.) (2009). Special Issue: Foundations and Frontiers of Visual Analytics, Information Visualization, Volume 8, Number 4, Winter 2009, p. 239-314.
6) Keim D., Kohlhammer J., Ellis G. and Mansmann F. (Eds.), Mastering the Information Age – Solving Problems with Visual Analytics, Eurographics Association, 2010.
7) Y. Livnat, J. Agutter, S. Moon, and S. Foresti, «Visual correlation for situational awareness» in IEEE Symposium on Information Visualization, 2005, pp. 95-102.
8) Dimitri N. Mavris, Olivia J. Pinon, David Fullmer Jr. «Systev design and modeling: a visual analytics approach», Proc. of 27-th International congress of the aeronautics ICAS-2101, 2010, 27 p.
9) http://www.cs.sandia.gov/projects/VxInsight/
10) http://www.sas.com/offices/europe/russia/hpa/index.html
11) Ai`vazian C.A., Eniukov I.S., Meshalkin L.D. Pricladnaia statistika. Classifikatciia i snizhenie razmernosti [Applied Statistics. Classification and dimensionality reduction]. M.: Finansy` i statistika, 1989.
12) Pilyugin V.V., Malikova E.E., Pasko A.A., Adzhiev V.D. Nauchnaia vizualizatciia kak metod analiza nauchny`kh danny`kh [Scientific visualization as method of scientific data analysis] / Scientific visualization. Volume 8, Number 4, pp.8-25, 2012, URL: http://sv-journal.org/2012-4/062139.html
13) Bondarev A.E., Galaktionov V.A. Analiz mnogomernyh dannyh v zadachah mnogoparametricheskoj optimizacii s primeneniem metodov vizualizacii [Multidimensional data analysis for multiparametric optimization problems using visualization methods] / Scientific visualization. Volume 4, Number 2, pp.1-13, 2012, URL: http://sv-journal.org/2012-2/012139.html
14) Osnovy nauchnoj vizualizacii [Basics of Scientific Visualization] [website]. URL: http://ifes.mephi.ru/unl/ (Date of circulation: 10.05.2014)