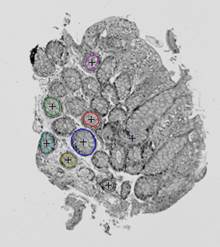
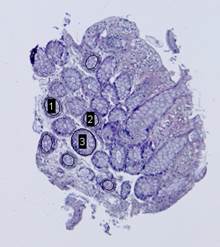
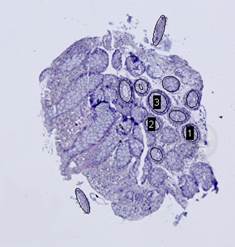
БЫСТРЫЕ АЛГОРИТМЫ СОВМЕЩЕНИЯ ГИСТОЛОГИЧЕСКИХ ИЗОБРАЖЕНИЙ
Д.И. Сунгатуллинаˡ, А.С. Крыловˡ, Д.Н. Фёдоров²
ˡ Лаборатория математических методов обработки изображений, факультет вычислительной математики и кибернетики, Московский государственный университет имени М. В. Ломоносова, Россия
² Российский научный центр хирургии имени академика Б.В. Петровского, Россия
diana.sungatullina@gmail.com, kryl@cs.msu.ru, dnfedorov@mail.med.ru
Содержание
2.1 Дескриптор контурных точек
2.2 Поиск соответствий между контурными точками
2.3 Вычисление параметров аффинного преобразования
2.4 Уточнение параметров аффинного преобразования
3. Результаты алгоритма совмещения по контурам
4. Метод, основанный на совмещении эллипсов
Аннотация
В данной работе предложены быстрые алгоритмы совмещения гистологических изображений. Первый метод, основанный на поиске соответствий между точками контуров шаблона и наблюдения, позволяет находить соответствия за время O(M log M), где M — число совмещаемых точек на контуре, практически не ухудшая качество совмещения по сравнению с обычно используемым венгерским алгоритмом, работающим за время O(M3). Высокая точность определения параметров преобразования достигается за счет итеративного процесса исключения точек контуров, совмещение которых прошло с максимальной ошибкой, и уточнения параметров для оставшихся точек. Второй метод, учитывая часто встречающуюся структуру гистологических изображений, содержащих эллипсовидные сечения желез, находит соответствия между эллипсами шаблона и наблюдения. Результирующее преобразование осуществляется по максимальному показателю перекрытия эллипсов. Первый алгоритм является универсальным для всех типов гистологических изображений, второй метод целесообразно применять в том случае, когда необходимо с высокой точностью совместить внутренние особенности тканей.
Ключевые слова: совмещение изображений, совмещение контуров, аффинные преобразования, детектирование эллипсов, обработка гистологических изображений, микроскопный анализ.
1. Введение
На современном этапе развития патоморфологии все большее значение приобретает проблема компьютерной обработки и анализа цифровых изображений. В ежедневной работе патоморфологов широко используются технологии виртуальной микроскопии, современные морфометрические исследования, автоматизированная оценка результатов иммуногистохимических исследований – все эти методы основаны на использовании цифровых изображений гистологических препаратов. В перспективе, методы математической обработки и анализа изображений гистологических образцов станут основой для создания алгоритмов, позволяющих оценивать их соответствие норме, выявлять те или иные отклонения, свойственные для каких-либо патологических процессов, то есть проводить морфологическую диагностику.
Одной из проблем обработки гистологических изображений является их стандартизация – все изображения в серии должны быть единообразно сориентированы, а ключевые морфологические структуры (железы, кровеносные сосуды, элементы стромы и т.д.) распознаны и сопоставлены. Решение этой проблемы возможно при помощи алгоритмов совмещения изображений. При совмещении изображений происходит пространственное выравнивание двух изображений сцены так, что для каждой точки первого изображения (наблюдение) ищется преобразование, которое ставит в соответствие точку на втором изображении (шаблон). Большинство существующих методов направлены на поиск параметров линейного преобразования [8], [3] (подобия, аффинного), однако некоторые приложения содержат и нелинейные преобразования [18] (проективное, полиномиальное, эластичное). В данной работе рассматриваются изотропные аффинные преобразования, что обусловлено особенностями микроскопической съемки срезов тканей.
Методы совмещения изображений можно разделить на две большие категории: методы, основанные на анализе интенсивности, и методы, основанные на анализе ключевых точек. Методы, основанные на анализе интенсивности, либо оценивают параметры преобразования непосредственно, используя интенсивности в совмещаемых областях [11], [2], либо определяют метрику и находят решение с помощью вычислительно трудоемкой нелинейной оптимизации [5]. Недостатками данных методов являются предположение о малости преобразований, а также проблемы локальных минимумов при оптимизации. Во втором случае на каждом изображении выделяются ключевые точки (замкнутые границы, контуры, пересечения линий, углы и так далее), характеризующие данное изображение [11], [4]. Параметры преобразования восстанавливаются на основе решения системы уравнений, которая была построена после извлечения ключевых точек и установления соответствий между ними. В качестве дескрипторов ключевых точек могут использоваться SIFT [10], SURF [1], функции Гаусса-Лагерра [12] и другие.
В данной работе представлено два метода совмещения гистологических изображений. Первый, основанный на совмещении контуров изображений, является универсальным для всех типов тканей, и описан в разделах 2-3. Второй метод учитывает внутренние особенности некоторых видов тканей и представлен в разделе 4.
2. Совмещение по контурам
Данный метод относится к классу методов, основанных на анализе ключевых точек, и является модификацией метода, описанного в [15].
Процесс совмещения контурных точек включает четыре этапа: вычисление дескриптора контурных точек, поиск соответствий между контурными точками, вычисление и уточнение параметров аффинного преобразования.
2.1 Дескриптор контурных точек
В первую очередь, для каждой точки ![]() замкнутого контура
замкнутого контура ![]() в плоскости
в плоскости ![]() устанавливается
ортогональная положительно определённая система координат
устанавливается
ортогональная положительно определённая система координат ![]() , где
, где ![]() — центр масс контура
фигуры,
— центр масс контура
фигуры, ![]() —
ось, коллинеарная вектору
—
ось, коллинеарная вектору ![]() ,
, ![]() — ось,
ортогональная оси
— ось,
ортогональная оси![]() , как
показано на Рис. 1.
, как
показано на Рис. 1.
После определения локальной системы координат ![]() все
точки контура
все
точки контура ![]() проецируются на ось
проецируются на ось ![]() .
Положим
.
Положим ![]() и
и ![]() минимальное
и максимальное значения проекций контура
минимальное
и максимальное значения проекций контура ![]() на
ось
на
ось ![]() .
Разделим отрезок
.
Разделим отрезок ![]() на
на ![]() часть:
часть:
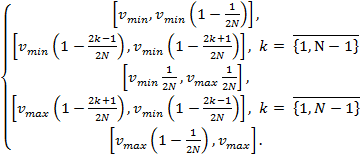 (1)
(1)
На каждом из этих отрезков найдем проекции двух точек контура
![]() и
и ![]() ,
расстояние между которыми максимально. В том случае, если пар точек несколько,
выбирается любая. Составим список точек, характеризующих точку
,
расстояние между которыми максимально. В том случае, если пар точек несколько,
выбирается любая. Составим список точек, характеризующих точку ![]() :
:
![]() (2)
(2)
Поскольку двум разным точкам контура может соответствовать
один и тот же список точек, в конец списка также добавим саму точку ![]() . Для каждой точки
. Для каждой точки ![]() контура
контура ![]() по списку точек (2)
вычисляется дескриптор DOPM [16]. Опишем его алгоритм.
по списку точек (2)
вычисляется дескриптор DOPM [16]. Опишем его алгоритм.
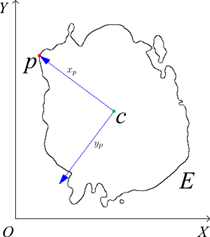
Рис. 1. Выбор локальной системы координат ![]() для
каждой точки
для
каждой точки ![]() контура
контура
![]() .
.
Далее будем полагать, что ![]() и
и ![]() содержат
центрированные координаты, то есть
содержат
центрированные координаты, то есть
![]() ,
,
![]() . (3)
. (3)
Для упрощения записи знак «^» будем опускать. Представим список точек (2) в виде матрицы:
![]() (4)
(4)
где каждая строка ![]() —
координаты i-ой точки в наборе точек (2). В предположении, что матрица
—
координаты i-ой точки в наборе точек (2). В предположении, что матрица ![]() полного ранга,
запишем ее в однородных координатах:
полного ранга,
запишем ее в однородных координатах:
![]() (5)
(5)
Тогда матрица аффинного преобразования ![]() в
однородной системе координат имеет вид:
в
однородной системе координат имеет вид:
![]()
![]() (6)
(6)
где ![]() —
вектор переноса,
—
вектор переноса, ![]() —
матрица линейного преобразования. Положим, что точки наблюдения
—
матрица линейного преобразования. Положим, что точки наблюдения ![]() получены из точек
шаблона
получены из точек
шаблона ![]() в результате аффинного преобразования
в результате аффинного преобразования
![]() и
перестановки
и
перестановки ![]() :
:
![]() (7)
(7)
где ![]() —
матрица перестановки, устанавливающая соответствия между точками шаблона и
наблюдения. Было показано [17], что если
—
матрица перестановки, устанавливающая соответствия между точками шаблона и
наблюдения. Было показано [17], что если ![]() ,
, ![]()
![]() —
матрицы ортогональных проекций на пространства столбцов матриц
—
матрицы ортогональных проекций на пространства столбцов матриц ![]() и
и ![]() соответственно,
то верно
соответственно,
то верно
![]() .(8)
.(8)
Данное равенство показывает, что матрицы ![]() и
и ![]() равны
с точностью до перестановки. Известно [6], что для матриц, равных с точностью
до перестановки, верно:
равны
с точностью до перестановки. Известно [6], что для матриц, равных с точностью
до перестановки, верно:
![]() (9)
(9)
где ![]() ,
, ![]() —
диагональные элементы
—
диагональные элементы ![]() и
и ![]() ,
соответственно. Таким образом, диагонали содержат одни и те же элементы, но в
разном порядке. Переупорядочив элементы, например, по убыванию, получим
дескриптор, инвариантный к аффинным преобразованиям.
,
соответственно. Таким образом, диагонали содержат одни и те же элементы, но в
разном порядке. Переупорядочив элементы, например, по убыванию, получим
дескриптор, инвариантный к аффинным преобразованиям.
Подробное доказательство аффинной инвариантности полученного дескриптора приведено в [15] и [16].
2.2 Поиск соответствий между контурными точками
Пусть ![]() —
точка на контуре шаблона,
—
точка на контуре шаблона, ![]() —
точка на контуре наблюдения. Стоимость соответствия двух точек,
—
точка на контуре наблюдения. Стоимость соответствия двух точек, ![]() ,
вычисляется через
,
вычисляется через ![]() -статистику
между дескрипторами:
-статистику
между дескрипторами:
![]() (10)
(10)
где ![]() и
и ![]() —
дескрипторы
—
дескрипторы ![]() и
и ![]() точек,
соответственно.
точек,
соответственно.
Для набора стоимостей ![]() для
всех пар точек
для
всех пар точек ![]() контуров
шаблона и наблюдения необходимо решить следующую задачу минимизации:
контуров
шаблона и наблюдения необходимо решить следующую задачу минимизации:
![]() (11)
(11)
Задача (11) является частным случаем задачи о назначениях,
классическим методом решения которой является венгерский алгоритм [9] с
вычислительной сложностью ![]() , где
, где ![]() — ранг матрицы
— ранг матрицы ![]() .
.
В данной работе вместо венгерского алгоритма предлагается
использовать более простой жадный алгоритм ближайшего соседа с вычислительной
сложностью ![]() [13]
и итеративно анализировать правильность совмещенных точек контура. Предлагаемый
ускоренный метод описан в разделе 2.4.
[13]
и итеративно анализировать правильность совмещенных точек контура. Предлагаемый
ускоренный метод описан в разделе 2.4.
2.3 Вычисление параметров аффинного преобразования
Внесем координаты сопоставленных точек шаблона и наблюдения
в столбцы матриц ![]() и Y
и Y ![]() ,
соответственно. Для поиска аффинного преобразования
,
соответственно. Для поиска аффинного преобразования ![]() с
матрицей A
с
матрицей A![]() и
вектором переноса
и
вектором переноса ![]() ограничимся
классом изотропных аффинных преобразований, для которых матрица
ограничимся
классом изотропных аффинных преобразований, для которых матрица ![]() представима в виде:
представима в виде:
![]() ,(12)
,(12)
где α — коэффициент масштабирования, ![]() — матрица поворота.
— матрица поворота.
Параметр ![]() находится из соотношения площадей фигур,
а вектор переноса
находится из соотношения площадей фигур,
а вектор переноса ![]() соединяет центры масс контуров шаблона и
наблюдения. Таким образом, необходимо найти лишь ортогональную матрицу поворота
соединяет центры масс контуров шаблона и
наблюдения. Таким образом, необходимо найти лишь ортогональную матрицу поворота
![]() .
Как и ранее,
.
Как и ранее, ![]() и
и ![]() содержат
центрированные координаты.
содержат
центрированные координаты.
Задача поиска оптимальной матрицы поворота в смысле среднеквадратичного отклонения между двумя системами координат по набору точек известна как задача Вахба [14]:
![]() (13)
(13)
Решение задачи (13) находится с помощью алгоритма Кабша [7], для чего вычисляется сингулярное разложение матрицы ковариации:
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() .(14)
.(14)
Тогда решение задачи (13) имеет вид:
![]() (15)
(15)
где ![]() —
искомая матрица поворота.
—
искомая матрица поворота.
2.4 Уточнение параметров аффинного преобразования
Ошибки сопоставления точек шаблона и наблюдения приводят к
решению ![]() ,
которое может сильно отличаться от точного решения
,
которое может сильно отличаться от точного решения ![]() задачи поиска матрицы
поворота. Основная идея предлагаемого метода состоит в следующем: итеративно
исключать половину точек, совмещение которых прошло с максимальной ошибкой,
повторять алгоритм (12)-(15) для оставшихся координат. Итеративный процесс
продолжается, пока точность совмещения шаблона и наблюдения растет, либо до тех
пор, пока не останется одна пара точек.
задачи поиска матрицы
поворота. Основная идея предлагаемого метода состоит в следующем: итеративно
исключать половину точек, совмещение которых прошло с максимальной ошибкой,
повторять алгоритм (12)-(15) для оставшихся координат. Итеративный процесс
продолжается, пока точность совмещения шаблона и наблюдения растет, либо до тех
пор, пока не останется одна пара точек.
Эффективность предложенного метода продемонстрируем на
примере. Рассмотрим ![]() произвольных равномерно распределённых
на единичной окружности точек, записанных в виде матрицы
произвольных равномерно распределённых
на единичной окружности точек, записанных в виде матрицы ![]() .
Повернем рассмотренные точки на произвольный угол ψ,
.
Повернем рассмотренные точки на произвольный угол ψ, ![]() точек перемешаем
произвольным образом,
точек перемешаем
произвольным образом, ![]() . Получим:
. Получим:
![]() ,(16)
,(16)
где ![]() —
матрица перестановки,
—
матрица перестановки, ![]() —
матрица поворота,
—
матрица поворота, ![]() —
наблюдение. С помощью алгоритма (12)-(15) вычислим угол поворота ψ,
используя 0, 1, 2 или 3 итерации исключения половины точек, совмещение которых
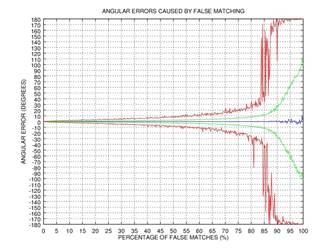
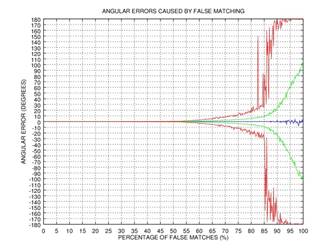
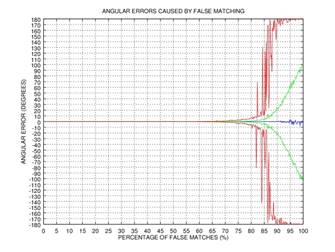
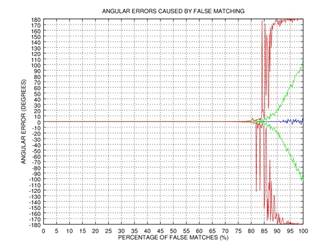
прошло с максимальной ошибкой. На Рис.2 представлены графики зависимостей
ошибки угла от количества неверно сопоставленных точек по результатам 1000
испытаний: синим цветом обозначено среднее значение ошибки, зеленым —
стандартное отклонение ошибки, красным — мода ошибки. Данный пример показывает,
что уже после 3-ей итерации даже при
—
наблюдение. С помощью алгоритма (12)-(15) вычислим угол поворота ψ,
используя 0, 1, 2 или 3 итерации исключения половины точек, совмещение которых
прошло с максимальной ошибкой. На Рис.2 представлены графики зависимостей
ошибки угла от количества неверно сопоставленных точек по результатам 1000
испытаний: синим цветом обозначено среднее значение ошибки, зеленым —
стандартное отклонение ошибки, красным — мода ошибки. Данный пример показывает,
что уже после 3-ей итерации даже при ![]() неверно сопоставленных точек ошибка в
определении угла близка к нулю.
неверно сопоставленных точек ошибка в
определении угла близка к нулю.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
Рис.2. Пример, демонстрирующий эффективность итерационного процесса удаления неверно сопоставленных точек: зависимость ошибки определения угла в зависимости от количества неверно сопоставленных точек; синим цветом обозначено среднее значение ошибки, зеленым — стандартное отклонение ошибки, красным — мода ошибки: 0 итераций (а), 1 итерация (б), 2 итерации (в), 3 итерации (г).
3. Результаты алгоритма совмещения по контурам
Для оценки точности совмещения двух сегментированных
изображений используется коэффициент Жаккара ![]() :
:
![]() (17)
(17)
где ![]() —
шаблон,
—
шаблон, ![]() —
наблюдение,
—
наблюдение, ![]() —
искомое преобразование, и пиковое отношение сигнала к шуму PSNR:
—
искомое преобразование, и пиковое отношение сигнала к шуму PSNR:
PSNR = 20 log (![]() ),(18)
),(18)
где MSE — среднеквадратичная ошибка для шаблона ![]() и преобразованного
наблюдения
и преобразованного
наблюдения![]() . Тестирование
метода производилось на 62 гистологических образцах, предоставленных РНЦХ им.
акад. Б.В. Петровского. Примеры работы предложенного метода совмещения
представлены на Рис.3-6. Характерные результаты сравнительного анализа
разработанного и существующих методов для гистологических изображений приведены
в Таблице 1.
. Тестирование
метода производилось на 62 гистологических образцах, предоставленных РНЦХ им.
акад. Б.В. Петровского. Примеры работы предложенного метода совмещения
представлены на Рис.3-6. Характерные результаты сравнительного анализа
разработанного и существующих методов для гистологических изображений приведены
в Таблице 1.
Таблица 1: Сравнение методов совмещения изображений.
|
Метод |
Сложность |
Точность |
|
DOPM + венгерский [15] |
|
0.9435 |
|
Метод моментов [2] |
|
0.8572 |
|
Предложенный |
|
0.9429 |
|
|
|
|
|
а) Шаблон |
б) Наблюдение |
в) |
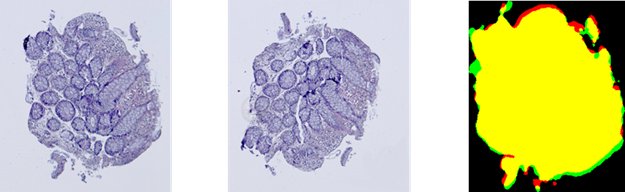
Рис. 3. Результаты работы программы по совмещению
гистологических изображений по контурам: красная фигура — шаблон ![]() , зеленая — наблюдение
, зеленая — наблюдение![]() , к которому применили
обратное преобразование
, к которому применили
обратное преобразование ![]() ,
желтая область — пересечение
,
желтая область — пересечение ![]() и
и ![]() .
.
|
|
||
|
а) Шаблон |
б) Наблюдение |
в) |
Рис. 4. Результаты алгоритма совмещения срезов тканей по
контурам: красным цветом обозначен шаблон ![]() ,
зеленым — наблюдение
,
зеленым — наблюдение ![]() , к которому применили обратное
преобразование
, к которому применили обратное
преобразование ![]() ,
желтая область — пересечение
,
желтая область — пересечение ![]() и
и ![]() .
.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
|
|
|
(д) |
(е) |
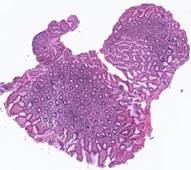
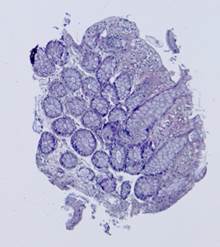
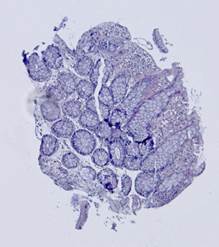
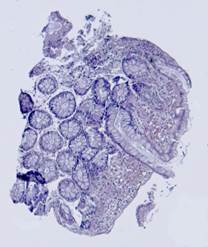
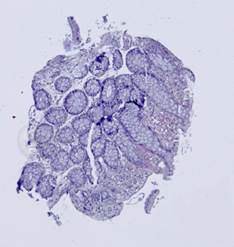
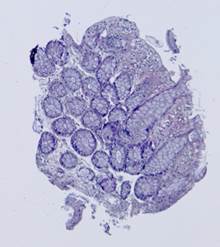
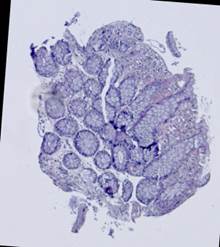
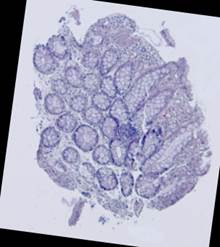
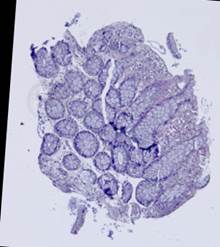
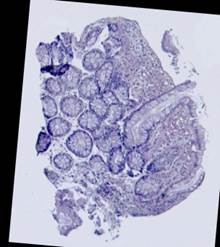
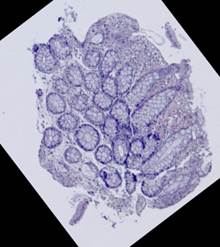
Рис. 5. Примеры гистологических изображений до выравнивания: шаблон (а), наблюдения (б)-(е).
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
|
|
|
(д) |
(е) |
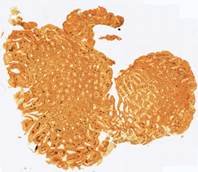
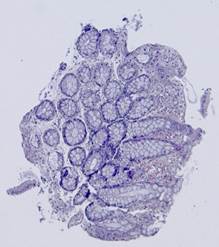
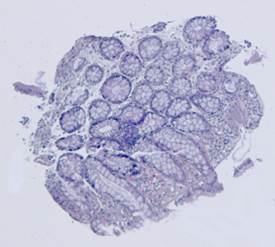
Рис. 6. Результаты алгоритма совмещения срезов тканей по контурам, представленных на Рис.5: шаблон (а), наблюдения (б)-(е).
4. Метод, основанный на совмещении эллипсов
Некоторые гистологические изображения, например, срезы слизистой оболочки толстой кишки, содержат эллипсовидные особенности, которые могут быть использованы для совмещения этих изображений.
Классическим методом обнаружения эллипсов является метод Хаффа [20], анализирующий пятимерное пространство параметров эллипса, что делает его практически неприменимым в силу крайне высокой вычислительной сложности при малых шагах квантования, и крайне низкой точности — при больших шагах. Неклассические методы, такие, как [21], позволяют находить эллипсы более эффективно за счет сокращения размерности пространства поиска, однако активно используют свойства эллипсов, что делает их крайне неустойчивыми. В связи с этим, было принято решение осуществлять поиск эллипсовидных областей путем выделения связных компонент на инвертированной карте контурных точек.
Применение детектора контуров Канни [22] непосредственно к исходному изображению приводит к разрыву контуров интересующих структур. Поэтому для замыкания этих контуров была использована нелинейная анизотропная диффузия [23], для чего искалось решение следующего уравнения в частных производных в некоторый момент времени:
![]() ,(19)
,(19)
где ![]() —
интенсивность изображения в точке
—
интенсивность изображения в точке ![]() и во
время
и во
время ![]() ,
, ![]() —
тензор диффузии для
—
тензор диффузии для ![]() в
точке
в
точке ![]() ,
использующий гессиан функции
,
использующий гессиан функции ![]() для
направления диффузии ортогонально градиенту. Результат такой предобработки
представлен на Рис.7(a). Затем с помощью детектора контуров Канни была получена
корректная карта контурных точек (Рис.7(б)).
для
направления диффузии ортогонально градиенту. Результат такой предобработки
представлен на Рис.7(a). Затем с помощью детектора контуров Канни была получена
корректная карта контурных точек (Рис.7(б)).
Далее инвертированная карта контуров разбивается на связные
компоненты, при этом из рассмотрения исключается компонента с наибольшей
площадью, соответствующая фону (Рис.7(в)). Также из рассмотрения исключаются
компоненты, отношение площади которых к площади их выпуклой оболочки не
превосходит ![]() ,
оставшиеся связные компоненты аппроксимируются эллипсами (Рис.7(г)).
,
оставшиеся связные компоненты аппроксимируются эллипсами (Рис.7(г)).
На заключительном этапе происходит сопоставление наборов
найденных эллипсов на изображениях шаблона и наблюдения. Предварительно эллипсы
наблюдения масштабируются в соответствии с отношением площадей фигур,
полученных в результате сегментации входных изображений. Затем для каждой пары
эллипсов на шаблоне и наблюдении производится попытка совмещения эллипсов при
помощи переноса и поворота, вычисленных по данной паре (проверяются оба
возможных варианта поворота), вычисляется показатель перекрытия ![]() :
:
![]() (20)
(20)
![]()
где ![]() и
и ![]() —
центроиды,
—
центроиды, ![]() и
и ![]() —
малые оси, а
—
малые оси, а ![]() и
и ![]() —
большие оси эллипсов шаблона и преобразованного наблюдения, соответственно. Для
вычисления результирующего аффинного преобразования используется пара эллипсов
с максимальным показателем перекрытия. На Рис.7(д)-(е), показана тройка пар
эллипсов с наилучшими показателями перекрытия.
—
большие оси эллипсов шаблона и преобразованного наблюдения, соответственно. Для
вычисления результирующего аффинного преобразования используется пара эллипсов
с максимальным показателем перекрытия. На Рис.7(д)-(е), показана тройка пар
эллипсов с наилучшими показателями перекрытия.
Данный метод, в отличие от метода совмещения по контурам, не зависит от формы среза, является устойчивым к разрывам ткани, а также позволяет отслеживать изменения внутренней структуры образцов. Результат работы метода совмещения по эллипсам представлен на Рис.8: по сравнению с методом совмещения по контурам (Рис.4), коэффициент Жаккара уменьшился на 0.01, однако пиковое отношение сигнала к шуму (PSNR) увеличилось на 0.9 дБ, что свидетельствует о более точном совмещении внутренних структур.
|
|
|
|
(а) |
(б) |
|
|
|
|
(в) |
(г) |
|
|
|
|
(д) |
(е) |
Рис.7. Этапы алгоритма совмещения срезов тканей по эллипсам: результат применения анизотропной диффузии (а), результат применения детектора Канни (б), выделенные связные области (в), выделенные эллипсы (г), совмещенные пары эллипсов шаблона (д) и наблюдения (е).
|
|
|
|
|
а) Шаблон |
б) Наблюдение |
в) |
Рис. 8. Результаты алгоритма совмещения срезов тканей по
эллипсам: красным цветом обозначен шаблон ![]() ,
зеленым — наблюдение
,
зеленым — наблюдение ![]() , к которому применили обратное
преобразование
, к которому применили обратное
преобразование ![]() ,
желтая область — пересечение
,
желтая область — пересечение ![]() и
и ![]() .
.
5. Заключение
Разработан быстрый алгоритм совмещения изображений
гистологических образцов, основанный на поиске соответствий между точками
контуров шаблона и наблюдения. Задача поиска соответствий известна как задача о
назначениях, классическим методом решения которой является венгерский алгоритм,
с вычислительной сложностью ![]() , где
, где ![]() — количество точек
контура шаблона или наблюдения. Предложенный метод позволяет находить
соответствия между точками шаблона и наблюдения за время
— количество точек
контура шаблона или наблюдения. Предложенный метод позволяет находить
соответствия между точками шаблона и наблюдения за время ![]() ,
практически не ухудшая качество совмещения, за счет итеративного процесса
исключения точек, совмещение которых прошло с максимальной ошибкой, и уточнения
параметров преобразования для оставшихся точек.
,
практически не ухудшая качество совмещения, за счет итеративного процесса
исключения точек, совмещение которых прошло с максимальной ошибкой, и уточнения
параметров преобразования для оставшихся точек.
Также разработан метод совмещения гистологических изображений с учетом внутренних особенностей ткани, когда отслеживание изменений внутренней структуры важнее, чем изменение формы. Предложенный алгоритм осуществляет совмещение эллипсовидных структур тканей. Проведенные эксперименты показали, что пиковое отношение сигнала к шуму при данном виде совмещения выше, чем при совмещении по контурам.
Благодарности
Работа выполнена при поддержке гранта Российского Научного Фонда 14-11-00308.
Список литературы
[1] H. Bay, A. Ess, T. Tuytelaars, L. Gool, “SURF: Speeded up robust features”, Computer Vision and Image Understanding, vol.110, no.3, pp.346-359, 2008.
[2] C. Domokos, J. Nemeth, and Z. Kato, “Nonlinear shape registration without correspondences”, IEEE Transactions on pattern analysis and machine intelligence, vol.34, no.5, pp.943-958, 2012.
[3] J. Feldmar and N. Ayache, “Rigit, affine and locally affine registration of free form surfaces”, International Journal of Computer Vision, vol.18, no.2, pp.99-119, 1996.
[4] H. Guo, A. Rangarajan, S. Joshi, and L. Younes, “Non-rigid registration of shapes via diffeomorphic point matching”, Proceedings of the IEEE International Symposium on Biomedical Imaging: From Nano to Macro, pp.924-927, 2004.
[5] M. S. Hansen, M. F. Hansen, and R. Larsen, “Diffeomorphic statistical deformation models”, Proceedings of the IEEE International Conference on Computer Vision, pp.1-8, 2007.
[6] R. Horn, C. Johnson, “Matrix analysis”, Cambridge, U. K.: Cambridge University Press, 1985.
[7] W. Kabsch, “A solution for the best rotation to relate two sets of vectors”, Acta Crystallographica Section A, vol.32, no.5, pp.922-923, 1976.
[8] A. Kadyrov and M. Petrou, “Affine parameter estimation for the trace transform”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.28, no.10, pp.1631-1645, 2006.
[9] H. Kuhn, “The Hungarian Method for the assignment problem”, Naval Research Logistics Quarterly, vol.2, no.1-2, pp.83-97, 1955.
[10] D. G. Low, “Distinctive image features from scale-invariant keypoints”, International Journal of Computer Vision, vol.60, pp.91-110, 2004.
[11] S. Mann, R. W. Picard, “Video orbits of the projective group a simple approach to featureless estimation of parameters”, IEEE Transactions on Image Processing, vol.6, no.9, pp.1281-1295, 1997.
[12] D. Sorokin, A. Krylov, “Gauss-Laguerre-Hermite methods of keypoint extraction”, Pattern Recognition and Image Analysis, vol.21, no.2, pp.332-334, 2011.
[13] P. Vaidya, “An O(n log n) algorithm for the all-nearest-neighbors problem”, Discrete and Computational Geometry journal, vol.4, no.1, pp.101-115, 1989.
[14] G. Wahba, “A Least Squares Estimate of Satellite Attitude”, SIAM Review, vol.7, no.3, pp.409-411, 1965.
[15] W. Wang, Y. Jiang, B. Xiong, and others, “Contour matching using the~affine-invariant support point set”, IET Computer Vision, vol.8, no.1, pp.35-44, 2014.
[16] Z. Wang, M. Liang, “Locally affine invariant descriptors for shape matching and retrieval”, IEEE Signal Processing Letters, vol.17, no.9, pp. 803-806, 2010.
[17] Z. Wang, H. Xia, “Dimension-free affine shape matching through subspace invariance”, IEEE Conf. Computer Vision and Pattern Recognition, pp.357-364. 2009.
[18] L. Zagorchev and A. Goshtasby, “A comparative study of transformation functions for nonrigit image registration”, IEEE Transactions on Image Processing, vol.15, no.3, pp.529-538, 2006.
[19] B. Zitova and J. Flusser, “Image registration methods: a survey”, Image and Vision Computing, vol.21, pp.977-1000, 2003.
[20] S. Tsuji, M. Matsumoto, “Detection of ellipses by a modified Hough transform”, IEEE Trans. Comput, vol. 27, pp.777–781, 1978.
[21] X.Yonghong and J. Qiang, “A New Efficient Ellipse Detection Method”, International Conference on Pattern Recognition, pp. 957–960, 2002.
[22] J. Canny, “A Computational Approach to Edge Detection”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.PAMI-8, No. 6, 679-698, November 1986.
[23] Joachim Weickert, “Anisotropic Diffusion in Image Processing”, B.G. Teubner Stuttgart, 1998.
FAST REGISTRATION ALGORITHMS FOR HISTOLOGICAL IMAGES
D.I. Sungatullina1, A.S. Krylov1, D.N. Fedorov2
1 Laboratory of Mathematical Methods of Image Processing of the Faculty of Computational Mathematics and Cybernetics of Lomonosov Moscow State University, Russia
2 Federal State Scientific Institution “B.V.Petrovsky National Research Center of Surgery”, Russia
diana.sungatullina@gmail.com, kryl@cs.msu.ru, dnfedorov@mail.med.ru
Abstract
In this paper, we propose two efficient registration algorithms for histological images. Our first algorithm is based on matching the contour points of an observation and a template, and performs in O(M log M) time, where M is the number of the contour points, with almost no loss in the quality of registration compared to the commonly used Hungarian algorithm, which has O(M3) time complexity. A high accuracy of the transform parameter estimation is achieved by an iterative exclusion of heavily mismatched contour points, followed by rectification of the parameters for the rest of the points. Our second algorithm takes advantage of a special structure of the histological images that contain elliptical gland slices, and finds corresponding ellipses on the observation and the template. The resulting transform is obtained from the pair of ellipses with maximum overlap index. The first method suits well for all types of histological images, while the second one is intended to be used for high-precision content-based alignment.
Keywords: image registration, contour-based registration, affine transformation, ellipse detection, histological images, microscopy analysis.
References
[1] H. Bay, A. Ess, T. Tuytelaars, L. Gool, “SURF: Speeded up robust features”, Computer Vision and Image Understanding, vol.110, no.3, pp.346-359, 2008.
[2] C. Domokos, J. Nemeth, and Z. Kato, “Nonlinear shape registration without correspondences”, IEEE Transactions on pattern analysis and machine intelligence, vol.34, no.5, pp.943-958, 2012.
[3] J. Feldmar and N. Ayache, “Rigit, affine and locally affine registration of free form surfaces”, International Journal of Computer Vision, vol.18, no.2, pp.99-119, 1996.
[4] H. Guo, A. Rangarajan, S. Joshi, and L. Younes, “Non-rigid registration of shapes via diffeomorphic point matching”, Proceedings of the IEEE International Symposium on Biomedical Imaging: From Nano to Macro, pp.924-927, 2004.
[5] M. S. Hansen, M. F. Hansen, and R. Larsen, “Diffeomorphic statistical deformation models”, Proceedings of the IEEE International Conference on Computer Vision, pp.1-8, 2007.
[6] R. Horn, C. Johnson, “Matrix analysis”, Cambridge, U. K.: Cambridge University Press, 1985.
[7] W. Kabsch, “A solution for the best rotation to relate two sets of vectors”, Acta Crystallographica Section A, vol.32, no.5, pp.922-923, 1976.
[8] A. Kadyrov and M. Petrou, “Affine parameter estimation for the trace transform”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.28, no.10, pp.1631-1645, 2006.
[9] H. Kuhn, “The Hungarian Method for the assignment problem”, Naval Research Logistics Quarterly, vol.2, no.1-2, pp.83-97, 1955.
[10] D. G. Low, “Distinctive image features from scale-invariant keypoints”, International Journal of Computer Vision, vol.60, pp.91-110, 2004.
[11] S. Mann, R. W. Picard, “Video orbits of the projective group a simple approach to featureless estimation of parameters”, IEEE Transactions on Image Processing, vol.6, no.9, pp.1281-1295, 1997.
[12] D. Sorokin, A. Krylov, “Gauss-Laguerre-Hermite methods of keypoint extraction”, Pattern Recognition and Image Analysis, vol.21, no.2, pp.332-334, 2011.
[13] P. Vaidya, “An O(n log n) algorithm for the all-nearest-neighbors problem”, Discrete and Computational Geometry journal, vol.4, no.1, pp.101-115, 1989.
[14] G. Wahba, “A Least Squares Estimate of Satellite Attitude”, SIAM Review, vol.7, no.3, pp.409-411, 1965.
[15] W. Wang, Y. Jiang, B. Xiong, and others, “Contour matching using the~affine-invariant support point set”, IET Computer Vision, vol.8, no.1, pp.35-44, 2014.
[16] Z. Wang, M. Liang, “Locally affine invariant descriptors for shape matching and retrieval”, IEEE Signal Processing Letters, vol.17, no.9, pp. 803-806, 2010.
[17] Z. Wang, H. Xia, “Dimension-free affine shape matching through subspace invariance”, IEEE Conf. Computer Vision and Pattern Recognition, pp.357-364. 2009.
[18] L. Zagorchev and A. Goshtasby, “A comparative study of transformation functions for nonrigit image registration”, IEEE Transactions on Image Processing, vol.15, no.3, pp.529-538, 2006.
[19] B. Zitova and J. Flusser, “Image registration methods: a survey”, Image and Vision Computing, vol.21, pp.977-1000, 2003.
[20] S. Tsuji, M. Matsumoto, “Detection of ellipses by a modified Hough transform”, IEEE Trans. Comput, vol. 27, pp.777–781, 1978.
[21] X.Yonghong and J. Qiang, “A New Efficient Ellipse Detection Method”, International Conference on Pattern Recognition, pp. 957–960, 2002.
[22] J. Canny, “A Computational Approach to Edge Detection”, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.PAMI-8, No. 6, 679-698, November 1986.
[23] Joachim Weickert, “Anisotropic Diffusion in Image Processing”, B.G. Teubner Stuttgart, 1998.