В рамках молекулярной динамики исследуется поведение тонкой жидкой пленки при ее быстром однородном нагреве со скоростью энерговклада 2-100 К/пс. Первоначальная толщина пленки вдоль оси Z составляет 48 нм. Общее количество частиц равнялось 96 000, а длина расчетной области в направлении Z задавалась равной 268 nm. В плоскости XxY использовались периодические граничные условия, а основные размеры пленки равнялись 8х8 нм. Результаты расчетов представлены в виде распределений температуры, плотности и скорости частиц в расчетной области, усредненных по плоскости пленки, а также в виде двумерных распределений плотности частиц в плоскости ZxX в диапазоне от времени нагрева от 0 до 800 пс. Визуализация и анализ полученных результатов указывают на существование четырех различных режимов поведения пленки в зависимости от скорости нагрева: квазистационарный режим с поверхностным испарением, взрывное (объемное) вскипание, спинодальный распад и разлет однофазного закритического флюида.

Ключевые слова: молекулярная динамика, тонкая пленка, объемный нагрев, поверхностное испарение, взрывное вскипание, спинодальный распад, визуализация

1. ВВЕДЕНИЕ

В уравнениях состояния различных веществ, которые продолжают активно исследоваться уже на протяжении многих лет [1], особое место занимает околокритическая область фазового перехода жидкость-пар. В равновесных условиях эта область характеризуется, в частности, возрастанием флуктуаций и расходимостью теплоемкости, что подтверждено многочисленными экспериментами для веществ с относительно небольшими значениями критических параметров [2-4]. Однако для многих веществ реализация исследований в стационарных равновесных условиях не представляется возможной из-за больших значений критических температур Т_с и давлений Р_с, которые по этой причине остаются плохо определенными. При использовании различных импульсных экспериментальных методов состояние исследуемого вещества оказывается, как правило, неравновесным, в частности, метастабильным в области двухфазных состояний [5]. В этой области имеется ряд нерешенных проблем, касающихся, поведения неравновесных состояний, в частности, особенностей поведения перегретой жидкой фазы при достижении температуры предельного перегрева. В таких условиях даже вопрос о том, как именно и в каких экспериментах могут проявляться околокритические особенности в нестационарных неравновесных условиях до самого последнего времени во многом остается открытым. Теоретический анализ подобных вопросов в настоящее время может быть выполнен с помощью математического моделирования в рамках молекулярно - динамического подхода, в котором поведение вещества описываются атомистическими моделями.

Атомистические модели позволяют проводить исследования в конденсированных, газовых и плазменных средах на уровне элементарных процессов и используются, в частности, для построения кинетических теорий гомогенного плавления и испарения. Основной сложностью атомистического подхода, наряду с проблемой выбора потенциала межчастичного взаимодействия, является огромная размерность моделей, количество уравнений в которых определяется количеством рассматриваемых частиц. Так при молекулярно - динамическом моделировании процессов в кубической области алюминия с ребром (постоянная гранецентрированной решетки a = 0,405 нм) возникает необходимость расчета траекторий огромного количества частиц, оценка которых составляет . Столь большое число уравнений с одной стороны служит основным ограничением пространственно – временного масштаба применения моделей молекулярной динамики (современный уровень исследований оперирует с числом уравнений порядка ), с другой - возникает острая проблема визуализации результатов моделирования.

Огромный объем информации и необходимость пространственно-временного отображения сильно неустойчивых режимов фазовых превращений типа фазового взрыва, спинодального распада перегретых метастабильных состояний и т. п., приводят к тому, что в задачах молекулярной динамики ценность получаемой информации в такой степени зависит от способа визуализации, что она начинает выполнять уже не функцию отображения (построения) образов, а трансформируется в полноценную компоненту научного исследования.

Молекулярно - динамический подход используется во многих работах, в частности, при анализе интенсивного лазерного воздействия на конденсированные среды [6-11]. Однако в этих работах роль поверхностного испарения для определенных режимов воздействия не была исследована с необходимой полнотой , которая может быть существенной уже в субнаносекундном диапазоне. Необходимо подчеркнуть, что быстрое фазовое превращение, как и всякий неравновесный процесс, существенно зависит от условий его реализации, в частности от скорости нагрева и динамики разлета, обусловленной инерционными или другими ограничениями.

В настоящей работе в рамках молекулярно - динамического подхода исследуется поведение тонкой жидкой пленки в течение ее быстрого однородного нагрева со скоростью 2-100 К/пс в субнаносекундной области с целью выяснения влияния поверхностного испарения на особенности процесса взрывной дезинтеграции сильно перегретой пленки. Визуализация результатов моделирования позволяет выполнить детальный анализ поведения неустойчивых метастабильных состояний в области их экстремальной неравновесности и последующей дезинтеграции.

2. ПОСТАНОВКА ЗАДАЧИ И МЕТОД ИССЛЕДОВАНИЯ

В качестве объекта исследования была выбрана жидкая диэлектрическая пленка начальной толщиной вдоль оси Z 48 нм, с общим размером счетной области по этой оси 268 нм. Частицы паровой фазы, достигшие границ этой области, удалялись из расчета (проницаемая безотражательная граница). Размеры счетной области по осям X, Y составляли 8 нм с периодическими граничными условиями. Общее число частиц в начальный момент составляло 96000. Масса частиц соответствовала массе атома алюминия. Наличие электронной подсистемы в явном виде не учитывается, и теплопроводность системы определяется взаимодействием тяжелых частиц. Критические параметры для такой системы составляли: T_c = 7600 К, P_c = 1.4 кбар, ρ_с = 0.48 г/см³.

2.1 Математическая модель

Математическая модель состоит из системы дифференциальных уравнений, их разностного аналога (разностной схемы), потенциала межатомного взаимодействия, специфически определяемых начальных и граничных условий.

В основе метода молекулярной динамики (МД) лежит модельное представление о многоатомной молекулярной системе, в которой все атомы представлены материальными точками, движение которых описывается в классическом случае уравнениями Ньютона. Таким образом, имеется 2N точечных частиц, каждая из которых имеет массу, радиус-вектор и скорость соответственно , где ; взаимодействует c остальными посредством сил , где – потенциальная энергия взаимодействия системы из N частиц; взаимодействует с внешними полями посредством силы .

Тогда эволюция данной модели будет описываться системой 2N обыкновенных дифференциальных уравнений движения:

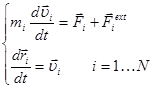(1)

2.2 Начальные условия

Для интегрирования системы уравнений (1) требуется знание координат и скоростей в начальный момент времени t = 0 всех N частиц. В начальный момент времени моделируемая среда представляет собой кристалл, поликристалл либо жидкость.

Для более точного задания начальных значений макроскопических параметров, а также для обеспечения устойчивого состояния системы, после установки координат и скоростей мы проводим релаксацию моделируемого объекта. Для имитации жидкости бывает трудно определить положения и скорости частиц точно сбалансированных по кинетической и потенциальной энергий. Это может приводить к нежелательной акустической вибрации. Для их эффективного подавления, в исходную систему уравнений (1) добавляется трение:

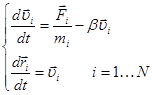. (2)

Совместное применение трения и термостата, возвращающего энергию в хаотическую составляющую движения частиц для удержания заданной температуры T, позволяет достаточно быстро вывести систему в стационарное состояние. После приведения системы в состояние покоя, несколько измененные значения постоянной решетки, учитывающие влияние границ объекта, будут получены автоматически. Кроме того, давление (напряжение) в системе во время релаксации может быть также установлено на желаемом уровне для дальнейшего моделирования с использованием баростата.

2.3 Граничные условия

Система (2) представляет собой систему обыкновенных дифференциальных уравнений. Для ее решения требуются только начальные условия. Граничные условия отсутствуют. Однако, при моделировании объектов сформированных системой частиц часто возникают дополнительные требования, которые могут быть удовлетворены наложением условий на границах объекта.

Таким образом, в области в виде тонкой пленки с толщиной H и бесконечной в направлениях X и Y, моделирование процессов выполняется в конечной расчетной области с размерами по осям , которая включает в себя часть пластины . Для имитации взаимодействия в той части, которая не входит в расчетную область, по осям X и Y используются периодические граничные условия с периодами ,, соответственно.

Периодические граничные условия по подразумевают, что частицы с координатой x в пределах , точно воспроизводят частицы для любых целых . То есть, частица, покидающая расчетную область через верхнюю границу , заменяется на частицу с таким же значением скорости, но вошедшую в расчетную область через нижнюю границу . Если штрихами пометить величины, относящиеся к новой частице, то

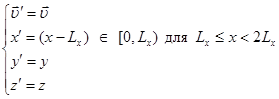
Аналогично для частицы, покидающей расчетную область через нижнюю границу :

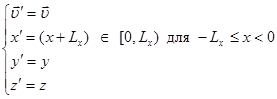
Второй важный аспект периодических граничных условий – сила и потенциальная энергия взаимодействия для частиц из приграничных областей: и , где r_cr – радиус обрезания потенциала (предполагается, что силами взаимодействия на расстояниях можно пренебречь).

Взаимодействие частицы i, координата x_i которой находится в интервале с частицами, находящимися за пределами расчетной области , моделируется с использованием частиц из расчетной области, радиус-векторы которых корректируются следующим образом при расчете силы взаимодействия :

где – единичный орт оси X.

Очевидно, все вышесказанное в равной степени относится и к периодическим граничным условиям вдоль координатной оси Y.

Вопрос о погрешности, вносимой периодическими граничными условиями, связан с искажением, вносимым в затухание фононных мод в кристалле. Очевидно, раздвигание границ уменьшает влияние на спектр фононных мод.

2.4 Потенциалы взаимодействия

В качестве потенциала взаимодействия мы использовали потенциал "ЕАМ" (Embedded Atom Model - EAM) [12,13], который хорошо зарекомендовал себя для материалов с металлической связью. Вклад в энергию хаотически расположенных ядер от взаимодействия с электронами, в соответствии с квантово- механической теорией функционала плотности, можно записать в виде уникального функционала полной электронной плотности (встроенный функционал). В этом случае, полная концентрация электронов в металле является линейной суперпозицией вкладов отдельных атомов, и сферически симметричной электронной плотности, создаваемой на отдельном атоме. Таким образом, полная энергия системы состоит из двух компонент - энергии парного взаимодействия атомов и энергии взаимодействия каждого атома с концентрацией электронов, производимых другими атомами:

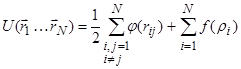где – парный потенциал, – функция “погружения” i-го атома, – суммарная электронная плотность для i-го атома, создаваемая сферически симметричными функциями одноэлектронной плотности других атомов.

В этой задаче, в качестве потенциала использовался один из полуэмпирических “embedded-atom” потенциалов, приведенных в [14]. В качестве парной части потенциала в [14] использовалась полиномиальная зависимость:

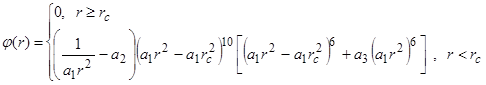
Для функций “погружения” и одноэлектронной плотности предложены следующие аналитические выражения:

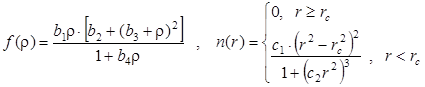
Здесь нм – радиус обрезания потенциала, - , - , - подгоночные константы.

Параметризация данного потенциала была выполнена на основе механических характеристик алюминия. Для оценки его применимости к решению теплофизических задач полезно сравнить с реальными тепловые характеристики, получающиеся с его помощью, такие как: температура плавления, удельная теплота плавления, теплоемкость, коэффициент теплового расширения [15].

3. ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ

3.1 Конечно-разностная аппроксимация

Как оптимальный компромисс между вычислительной эффективностью и требованиями точности, устойчивости широкое распространение в молекулярно-динамическом моделировании получил алгоритм Верле [16] в его наиболее удобной, так называемой, скоростной форме. Предлагаемая далее его модификация содержит в отличие от оригинала еще трение. Для системы уравнений (2) с вязкостью может быть записана следующая конечно разностная аппроксимация:

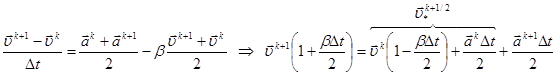
Здесь верхний индекс k – номер шага по времени, – ускорение, индекс i (номер частицы) опущен. Определение промежуточной скорости в полуцелый момент времени

эквивалентно разностной аппроксимации

В итоге, вычислительный алгоритм Верле в скоростной форме для системы (4) с вязкостью формулируется следующим образом. Предполагая, что все величины известны на момент времени , переход к следующему моменту времени производится по формулам

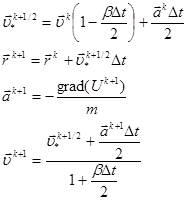(5)

Схема Верле не является консервативной в смысле точного выполнения закона сохранения энергии в разностном виде. Однако, статистически для системы частиц этот закон выполняется вполне удовлетворительно.

3.2 Вычисление макроскопических величин

В ходе молекулярно-динамического моделирования конденсированной среды достаточно быстро устанавливается локальное термодинамическое равновесие. Так характерное время установления локально-равновесного распределения в кристалле алюминия составляет единицы пикосекунд. Исходя из этого, могут быть определены основные термодинамические величины – давление (напряжения в кристалле) и температура.

Заметим, что подобная постановка задачи для исследования процесса испарения пленки диэлектрической жидкости (воды) использовалась в работе [17], однако при отсутствии объемного (взрывного) вскипания.

Использованные в настоящей работе методы расчета более подробно описаны в [15]. Начальное состояние пленки перед ее нагревом соответствовало равновесию с насыщенным паром при температуре 6400 К. Разлет пара ограничивался непроницаемыми отражающими стенками, которые находились на расстоянии 22 нм от правой и левой поверхностей пленки. При t ≥ 0 пленка подвергалась нагреву со скоростью 2-100 К/пс, который осуществлялся посредством соответствующего увеличения кинетической энергии частиц [18].

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

4.1 Медленный нагрев (стационарный режим)

Очевидно, что при достаточно медленном нагреве пленка может эволюционировать от своего начального состояния к режиму (квази)стационарного испарения с балансом между поглощаемой энергией и потерями на испарение, который зависит в частности, от толщины пленки.

Результаты вычислений для такого режима со скоростью нагрева 2 К/пс показаны на Рис. 1-8. На Рис.1а-1б представлены начальные распределения температуры, плотности и скорости частиц при t= 0, когда пленка находится в равновесии с ее насыщенным паром при температуре 6 400 К. Плотности пара и пленки при этом равны соответственно 0,04 и 1,3г/см³. Начальная толщина пленки составляет 48 нм, а размеры области, занимаемой насыщенным паром, составляют 22 нм с каждой стороны пленки.

После открытия границ и начала нагрева при t > 0 температура и плотность пара начинают уменьшаться и перестают быть однородными из-за процесса расширения (Рис 2, t = 1нс), а температура поверхности пленки также начинает уменьшаться из-за испарительного охлаждения (Рис.2, 5-6). Первоначально наблюдается также небольшое уменьшение температуры в объеме пленки, которое обусловлено, по-видимому, дополнительным расширением пленки из-за уменьшения внешнего давления , которое становится меньше давления насыщенного пара при данной температуре поверхности. Скорость направленного движения частиц пара у поверхности пленки первоначально относительно мала по сравнению с ее величиной на свободной границе паровой пленки, что соответствует этапу начального расширения слоя пара.(Рис. 2b).В дальнейшем скорость пара вблизи поверхности пленки существенно увеличивается, что характерно для процесса интенсивного испарения (Рис. 3b, 4b).

В результате этого процесса внутри пленки формируется выпуклый температурный профиль и соответствующий ему (согласно уравнению состояния) вогнутый профиль плотности (Рис. 5, 6).

Максимум температурного профили на временах t > 200 пс устанавливается на уровне ~ 6800 K ~ 0.9 T_c, где T_с~ 7600 K обозначает критическую температуру и практически не изменяется на протяжении последующих 500 пс как это видно из Рис. 5a - 6a.

Флуктуации плотности и температуры в конденсированной фазе относительно малы, следует отметить, что нагрев частиц реализуется только для тех частиц, плотность которых превышает уровень 0,3 от текущего максимума плотности.

Параметры такого квазистационарного режима испарения в простейшем приближении могут быть аналитически получены с использованием квадратичного распределения температуры по толщине пленки с максимумом в ее середине. Результаты таких аналитических оценок будут представлены отдельно.

Рассматриваемое квазистационарное состояние жидкости имеет ограниченное время жизни не только по причине конечной толщины испаряющейся пленки. Эта пленка находится в перегретом метастабильном состоянии, температура которого превышает температуру фазового равновесия (бинодали) для данного давления, а значение плотности меньше равновесной величины. В таком состоянии имеется конечная вероятность возникновения и развития гетерофазных флуктуаций вследствие спонтанной гомогенной нуклеации зародышей новой (паровой) фазы. Время ожидания таких флуктуаций быстро уменьшается по мере приближения T_m к температуре предельного перегрева (спинодали) ¹³.

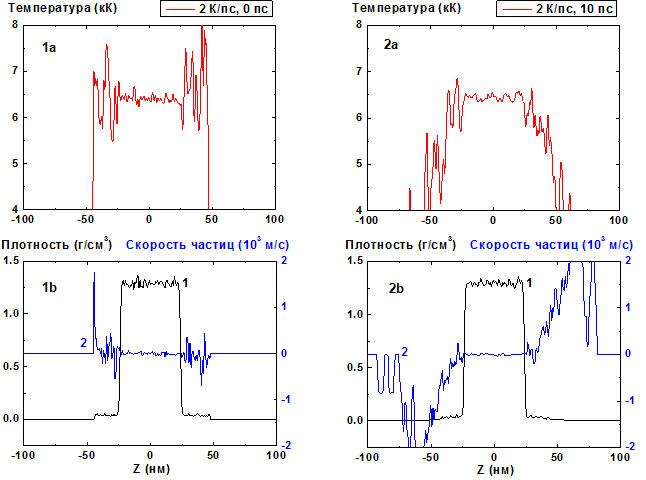
Рис. 1-2: Пространственные распределения температуры (1a-2a), плотности (1b-2b, кривая 1) и скорости частиц (1b-2b, кривая 2) в пленке в моменты времени 0, 10 пс при нагреве со скоростью 2 К/пс.

Рис. 3-4: Пространственные распределения частиц пленки в моменты времени 0, 10 пс при нагреве со скоростью 2 К/пс

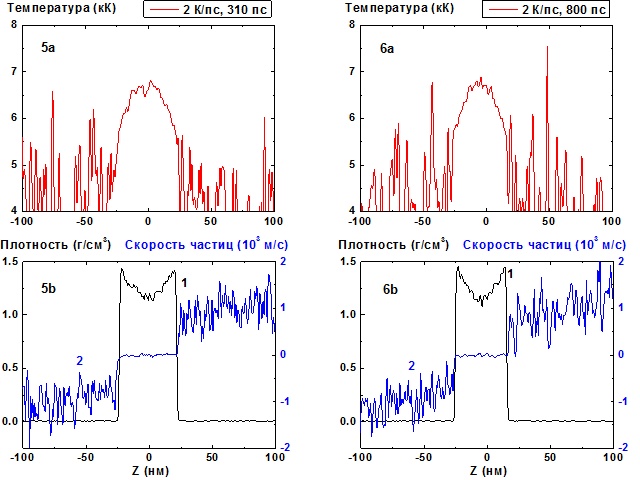
Рис. 5-6: Пространственные распределения температуры (5a-6a), плотности (5b-6b, кривая 1) и скорости частиц (5b-6b, кривая 2) в пленке в моменты времени 310, 800 пс при нагреве со скоростью 2 К/пс. 2 К/пс

Рис. 7-8: Пространственные распределения частиц пленки в моменты времени 310, 800 пс при нагреве со скоростью 2 К/пс.

4.2 Режим взрывного вскипания

При нагреве со скоростью 4 К/пс эволюция пленки из того же начального состояния вплоть до момента 240 пс (Рис. 9, 11) мало отличается от предыдущего случая и достигает максимальной температуры около 7000 K, что примерно на 200 К превышает значение при 2 К/пс.

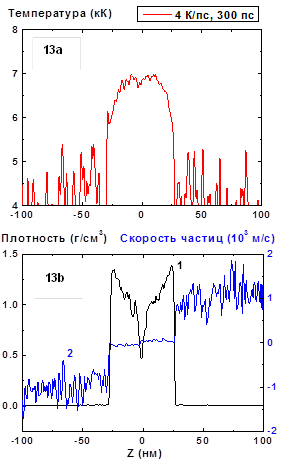
Затем, однако, вместо продолжения квазистационарного режима испарения начинается процесс взрывного вскипания, т.е. быстрого локального уменьшения плотности и формирования паровой полости внутри пленки вблизи максимума температурного профиля (Рис.10, 12, 13-16). Образование полости сопровождается локальным уменьшением температуры в области ее предшествующего максимума.

Максимальное значение температуры при которой начинается процесс взрывного вскипания превышает ее величину в квазистационарном режиме на малую величину T ~ 10^-2 T_c, что свидетельствует о достаточно резкой температурной границе начала взрывного вскипания в наносекундном режиме его ожидания¹³.

Резкая температурная зависимость времени ожидания взрывного вскипания известна ужа давно (В.П.Скрипов) ¹³. В рамках метода молекулярной динамики с использованием NPT ансамбля подобная зависимость исследовалась, например, в работе ¹⁴. Такой подход, однако, не позволяет наблюдать особенности взрывного распада, связанные с процессом поверхностного испарения

Возрастание флуктуаций плотности по сравнению с предыдущим режимом квазистационарного испарения видно уже на Рис. 9 (t = 240 пс), а при t = 300 пс (Рис. 13) минимальное значение плотности приближается к ее критическому значению 0.47 г/cм³. В то же самое время видно также уменьшение температуры в области температурного максимума вследствие начала испарительного процесса в образующуюся полость. Кроме того, необходимо отметить, что этот локальный минимум частично может быть связан и с относительным возрастанием теплоемкости конденсированной фазы C_pпо мере приближения температуры жидкости к границе предельного перегрева, если она достаточна близка к спинодали.

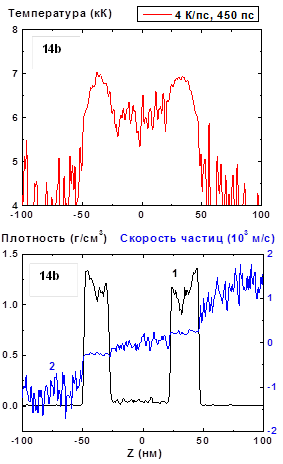
Дальнейший рост полости и движение образовавшихся фрагментов пленки определяется разностью давлений на внутренних и наружных сторонах фрагментов. Плотность пара внутри полости заметно превосходит ее значение снаружи фрагментов, как это видно по кривой распределения плотности на Рис.14b.

Зависимость от времени скорости фрагментов по небольшого различия их масс (или толщины h ). Более массивный правый фрагмент с толщиной h₂ = 25 ( при t = 450 пс) нм движется медленнее, чем левый с h₁ = 21нм (при t = 450 пс).В соответствии с законом сохранения импульса скорости и толщины фрагментов связаны соотношением v₁h₁ = v₂h₂в системе центра масс, которая совпадает с лабораторной системой.

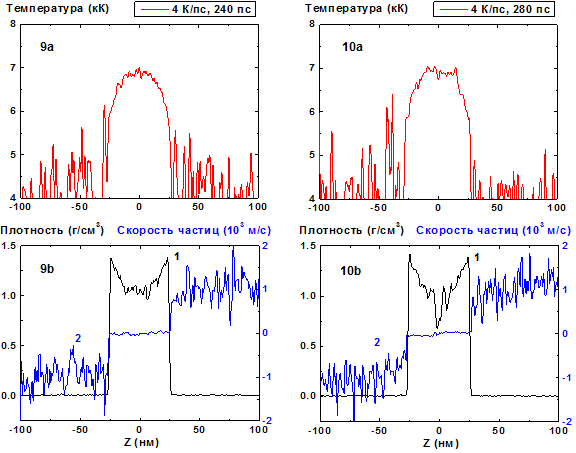
Рис. 9-10: Пространственные распределения температуры (9a-10a), плотности (9b-10b, кривая 1) и скорости частиц (9b-10b, кривая 2) в пленке в моменты времени 240, 280 пс при нагреве со скоростью 4 К/пс.

Рис. 11-12: Пространственные распределения частиц пленки в моменты времени 240, 280 пс при нагреве со скоростью 4 К/пс

Рис. 13-14: Пространственные распределения температуры (13a-14a), плотности (13b-14b, кривая 1) и скорости частиц (13b-14b, кривая 2) в пленке в моменты времени 300, 450 пс при нагреве со скоростью 4 К/пс. 4 К/пс

Рис. 15-16: Пространственные распределения частиц пленки в моменты времени 300, 450 пс при нагреве со скоростью 4 К/пс

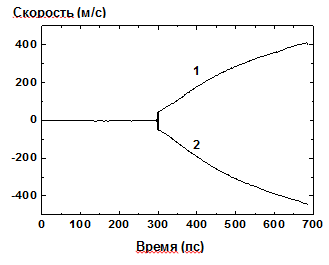
Рис. 17. Временная зависимость скорости разлета левого (1) и правого (2) фрагментов пленки при скорости нагрева 4 K/пс

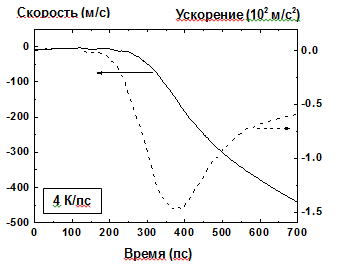
Рис. 18. Временная зависимость скорости (сплошная линия) и ускорения (пунктирная линия) левого (1) фрагмента при скорости нагрева 4 K/пс

Поведение скорости разлетающихся фрагментов от времени показано на Рис. 17. Скорость правого фрагмента по абсолютной величине оказывается несколько меньше левого из-за различия в их массах (центр масс системы покоится). Особый интерес представляет ускорение фрагментов в начальные моменты формирования паровой полости, поскольку это дает информацию о поведении давления во время взрывного вскипания. Однако из-за наличия больших флуктуаций точное количественное определение ускорения и соответствующего ему давления пока оказывается затруднительным.

На Рис.18 показано поведение смещения, скорости и ускорения внешней границы левого фрагмента. Максимальная величина ускорения a составляет примерно 1.5∙10¹²м/с² которому соответствует максимальное давление P_m = aρh + P₀ ~ 500 бар где ρ = 1.2 г/cм³, h = 23 нм и P₀ ~ 100 бар обозначает давление на внешней стороне фрагмента. Величина давления в молекулярно-динамических вычисления, которая подвержена значительным пространственно-временным флуктуациям, имеет усредненное значение 500 бар, что составляет примерно 0.35 P_c при величине критического давления P_c ~ 1420 бар. Это усредненное значение давления заметно меньше давления насыщения паров (690-840 бар) при температуре пленки T = 6800-7000 K, при приближении к которой начинает развиваться процесс взрывного вскипания.

Характерное время нарастания ускорения (~ 100 пс) определяется скоростью роста давления в полости, формирующейся при фазовом взрыве. Процесс формирования полости в данном временном интервале иллюстрируются на Рис.15-16 двумерными распределениями частиц. Следует отметить также, что время двойного пробега звука по толщине фрагмента не очень мало по сравнению со временем нарастания давления в полости, что может способствовать возбуждению гиперзвуковых колебаний в разлетающихся фрагментах.

Взрывное вскипание является существенно неравновесным процессом, который обусловлен быстрым ростом флуктуаций в метастабильном (неравновесном) состоянии перегретой жидкости. Этот процесс является стохастическим по своей природе и его развитие определяется не только средними значениями термодинамических параметров. В соответствии с этим обстоятельством при одной и той же скорости нагрева 4 К/пс из-за флуктуационного различия в начальных состояниях при взрывном вскипании может возникнуть не одна, а две полости разделенных по середине тонкой (5 нм) пленкой жидкой фазы, как это показано на Рис 19-20.

Рис 19-20 Двумерное распределение частиц пленки и пара в моменты времени 300 и 450 пс при нагреве со скоростью 4К/пс. (другие начальные условия – отличие во флуктуациях при тех же средних значениях)

4.3 Быстрый нагрев (околокритический режим абляции)

Увеличение скорости нагрева до 8 K/пс приводит к более сложному многосвязному распределению плотности распадающейся пленки (Рис.25-30) после первоначального квазиоднородного расширения (Рис.21-24). Момент начала распада пленки (180 пс) при T = 7000 K, когда ее флуктуирующая плотность приближается к значению 0.7 г/cм³, смещен к более ранним временам по сравнению с началом распада пленки (300 пс) на два фрагмента при 4 K/пс.

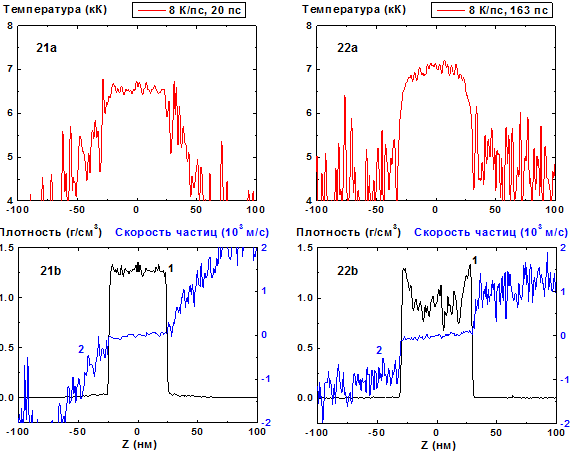
Рис. 21-22: Пространственные распределения температуры (21a-22a), плотности (21b-22b, кривая 1) и z-компоненты скорости части пленки и пара (21b-22b, кривая 2) в моменты времени 20 и 163 пс при нагреве со скоростью 8К/ пс. 8 К/пс

Рис 23-24 Двумерное распределение частиц пленки и пара в моменты времени 20 и 163 пс при нагреве со скоростью 8К/пс.

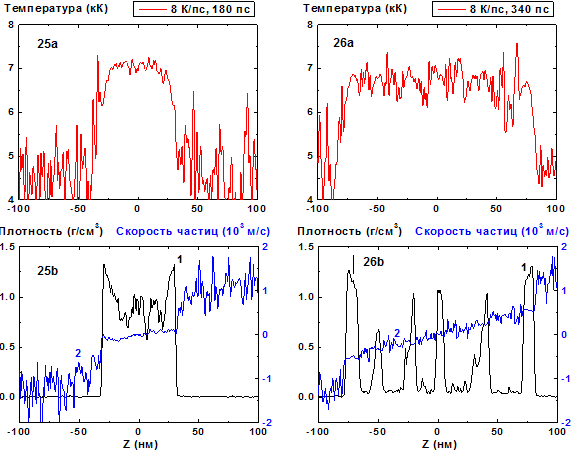
Рис. 25-26. Пространственные распределения температуры (25a-26a), плотности (25b-26b, кривая 1) и скорости частиц (25b-26b, кривая 2) в пленке в моменты времени 180, 340 пс при нагреве со скоростью 8 К/пс. 8 К/пс

Рис. 27-28: Пространственные распределения частиц пленки в моменты времени 180, 340 пс при нагреве со скоростью 8 К/пс

Начало взрывного распада пленки (180 пс) при T = 7000 К, когда флуктуирующая плотность достигает значения 0.7 г/см², смещается к более ранним временам в сравнении со случаем распада на два фрагмента (300 пс для 4 К/пс). При этом вогнутый профиль плотности пленки становится более широким вследствие увеличения количества больших флуктуаций, являющихся затравками для формирования фрагментов разлетающейся пленки.

Появление таких флуктуаций приводит к понижению средней плотности пленки и, несмотря на испарение материала, к относительному увеличению ее толщины, которое видно на Рис. 19-23, 25, пленки. Аналогичная эволюция наблюдается и при скорости нагрева 10 К/пс, однако количество фрагментов при этом увеличивается.

Отметим, что нагрев пленки касался только ее конденсированной части, в то время как источник нагрева не действовал в паровой фазе при всех ее плотностях не превышающих уровня 0.3 от максимального значения плотности конденсированной фазы в данной конфигурации.

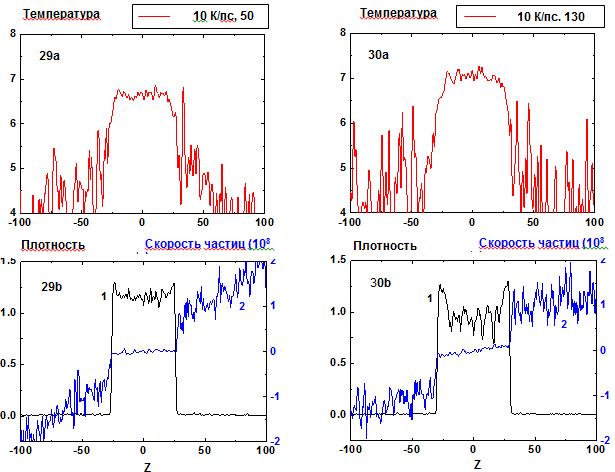
Рис 29-30: Пространственные распределения температуры (29a-30a), плотности (29b-30b, кривая 1) и z-компоненты скорости части пленки и пара (29b-30b, кривая 2) в моменты времени 50 и 130 пс при нагреве со скоростью10 К/ пс.

Рис. 31-32. Двумерное распределение частиц пленки и пара в моменты времени 50 и 130 пс при нагреве со скоростью10К/пс.

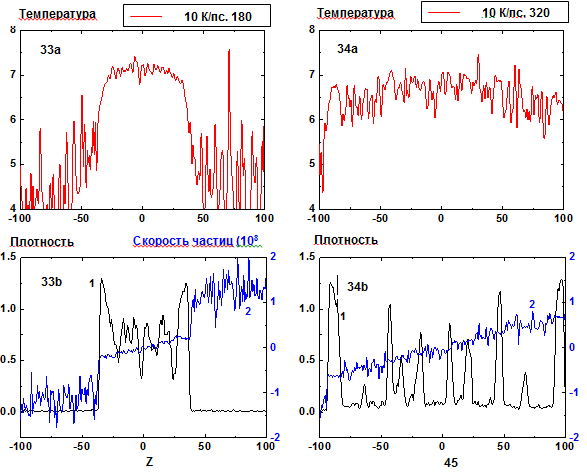
Рис. 33-34: Пространственные распределения температуры (33a-34a), плотности (33b-34b, кривая 1) и z-компоненты скорости части пленки и пара (33b-34b, кривая 2) в моменты времени 180 и 320 пс при нагреве со скоростью 10К/ пс. 10 К/пс

Рис. 35-36. Двумерное распределение частиц пленки и пара в моменты времени 180 и 320 пс при нагреве со скоростью10 К/пс.

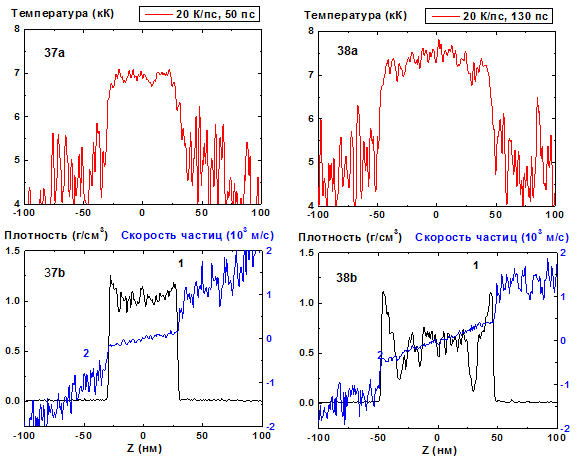
Рис. 37-38: Пространственные распределения температуры (37a-38a), плотности (37b-38b, кривая 1) и скорости частиц (37b-38b, кривая 2) в пленке в моменты времени 50, 130 пс при нагреве со скоростью 20 К/пс.

Рис. 39-40: Пространственные распределения частиц пленки в моменты времени 50, 130 пс при нагреве со скоростью 20 К/пс

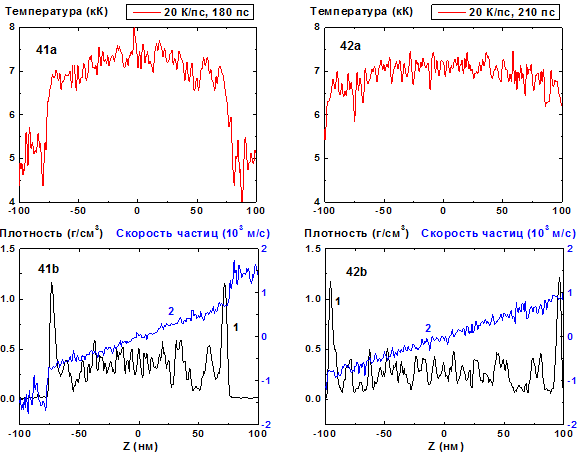
Рис. 41-42: Пространственные распределения температуры (41a-42a), плотности (41b-42b, кривая 1) и скорости частиц (41b-42b, кривая 2) в пленке в моменты времени 180, 210 пс при нагреве со скоростью 20 К/пс. 20 К/пс

Рис. 43-44: Пространственные распределения частиц пленки в моменты времени 180, 210 пс при нагреве со скоростью 20 К/пс

Следует отметить, что вогнутое распределение плотности пленки при увеличении скорости нагрева от 4 K/пс to 8 K/пс становится более широким из-за возрастания числа крупномасштабных флуктуаций. В результате развития такого флуктуационного уширения пленка распадается уже на шесть фрагментов (Рис. 21-28) , а не на два (или три) как это имело место при скорости нагрева 4 K/пс.

Уширение пленки перед началом распадом означает понижение ее средней плотности по сравнению с равновесным значением вследствие метастабильности (растянутости) перегретого жидкого состояния, в котором находится пленка. Уменьшение плотности становится более выраженным по мере приближения к критической точке. Такое изменение в характере эволюции параметров пленки в этой области иллюстрируется представленными на Рис 29-36 данными для скорости нагрева 10 K/пс.

Из сравнения Рис.25 и 36 , которые соответствуют одному и тому же моменту времени 180 пс от начала нагрева видно, что средняя толщина пленки во втором случае (~ 70 нм) заметно больше (более 30%), чем в первом. В результате эволюции такого перегретого состояния пленка при нагреве со скоростью10 K/пс распадается на большее число фрагментов, чем при 8 K/пс.

Для 20 K/пс число флуктуаций возрастает и вместо набора индивидуальных фрагментов конденсированной фазы с паровыми прослойками между ними, как это видно, например, из Рис. 14 или Рис. 34, образуется совокупность флуктуаций плотности с размытыми диффузионными границами между ее различающимися по плотности элементами, которая характерна для процесса спинодального распада.

Изменение режимов разрушения пленки от стадии взрывного вскипания до спинодального распада можно проследить также по двумерным распределениям частиц пленки и пара на Рис. 15-16, 27-28, 35-36, 39-40, 43-44, где скорость нагрева меняется от 4 K/пс до 20 K/пс. В этом диапазоне число различимых фрагментов растет, хотя их вертикальная (плоскостная) составляющая становится менее выраженной, за исключением двух граничных фрагментов, где влияние поверхностного испарения на процесс распада пленки оказывается наиболее заметным.

4.4 Быстрый нагрев – режим сверхкритического разлета

Очевидно, что дальнейшее увеличение скорости нагрева, начиная с некоторых его значений, будет приводить к уменьшению амплитуды флуктуаций плотности в процесса распада пленки вследствие увеличения их числа. Подобный режим фактически соответствует расширению плотного неидеального газового флюида, поскольку в процессе его нагрева описанные выше режимы взрывного вскипания и спинодального распада не успевают развиться при таких скоростях нагрева. Увеличение давления внутри пленки, которая не успевает полностью разгружаться, также вносит свой вклад в подавление развития взрывного вскипания и спинодального распада.

На Рис.45-52 показан процесс распада пленки при нагреве со скоростью 40 K/пс. Если в случае 10 K/пс стадия расширения становится выраженной на временах после 130 нс, то при 40 K/пс быстрое увеличение толщины пленки из-за падения ее плотности и увеличение скорости частиц пленки относительно ее центра (наклон кривой 2 на Рис.45) становятся значительными уже при t = 40 пс. В этом случае (t = 40 пс) толщина пленки увеличивается до 63 нм по сравнению с ее начальным значением 48 нм.

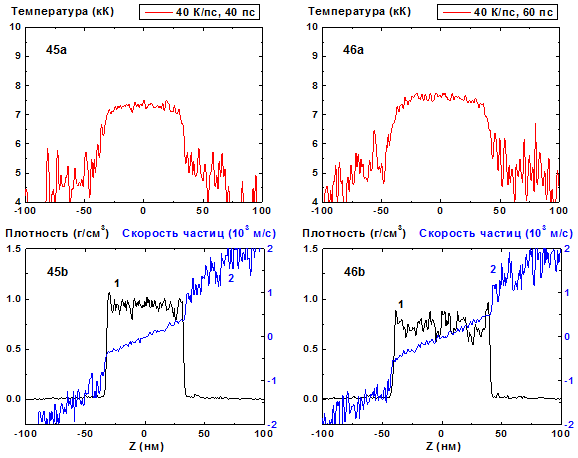
Рис. 45-46: Пространственные распределения температуры (45a-46a), плотности (45b-46b, кривая 1) и скорости частиц (45b-46b, кривая 2) в пленке в моменты времени 40, 60 пс при нагреве со скоростью 40 К/пс.

Рис. 47-48: Пространственные распределения частиц пленки в моменты времени 40, 60 пс при нагреве со скоростью 40 К/пс

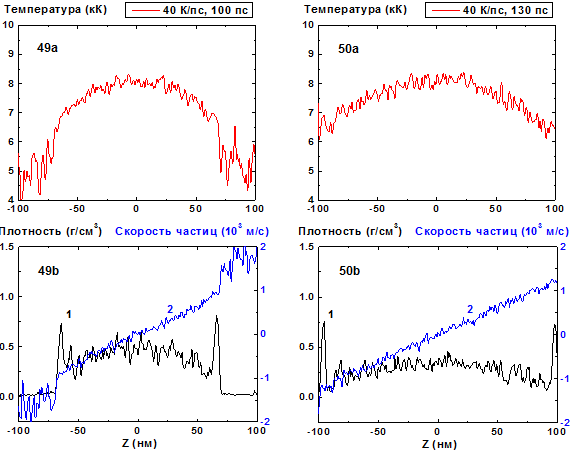
Рис. 49-50: Пространственные распределения температуры (49a-50a), плотности (49b-50b, кривая 1) и скорости частиц (49b-50b, кривая 2) в пленке в моменты времени 100, 130 пс при нагреве со скоростью 40 К/пс. 40 К/пс

Рис. 51-52: Пространственные распределения частиц пленки в моменты времени 100, 130 пс при нагреве со скоростью 40 К/пс

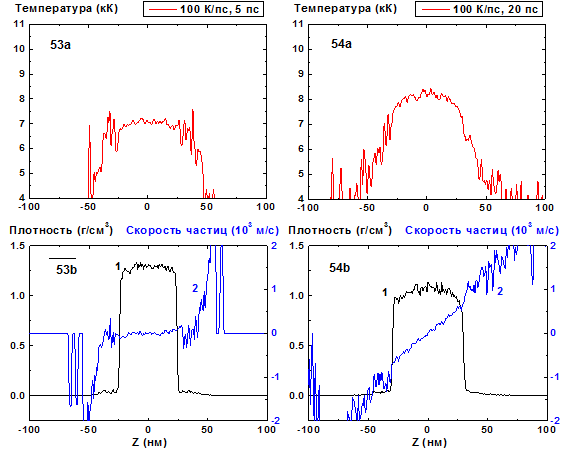
Рис. 53-54: Пространственные распределения температуры (53a-54a), плотности (53b-54b, кривая 1) и скорости частиц (53b-54b, кривая 2) в пленке в моменты времени 5, 20 пс при нагреве со скоростью 100 К/пс.

Рис. 55-56: Пространственные распределения частиц пленки в моменты времени 5, 20 пс при нагреве со скоростью 100 К/пс

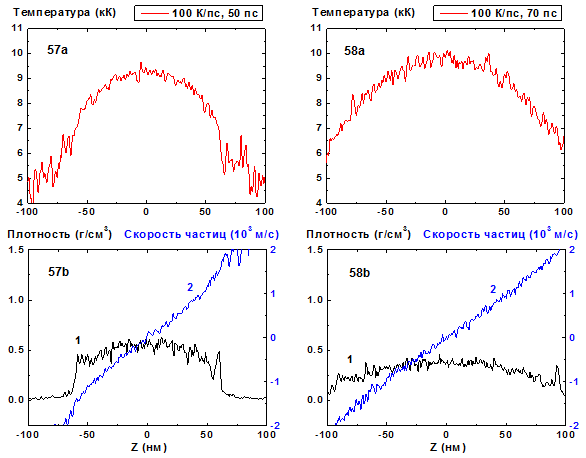
Рис. 57-58: Пространственные распределения температуры (57a-58a), плотности (57b-58b, кривая 1) и скорости частиц (57b-58b, кривая 2) в пленке в моменты времени 50, 70 пс при нагреве со скоростью 100 К/пс. 100 К/пс

Рис. 59-60: Пространственные распределения частиц пленки в моменты времени 50, 70 пс при нагреве со скоростью 100 К/пс

В сравнении со скоростями нагрева 8, 10 и 20 K/пс флуктуации плотности в пленке при больших скоростях нагрева оказываются сравнительно малыми, кроме приповерхностных скачков (пиков) плотности, обусловленных влиянием поверхностного испарения, Рис.49-50. Подобные пики наблюдаются также и при меньших скоростях нагрева (см. Рис. 5-6, 9-10, 25-26, 33-34, 41-42), поскольку влияние поверхностного испарения оказывается значительным для всех этих режимов, формируя, в частности, вогнутый профиль плотности в пленке. Эта роль поверхностного испарения была отмечена также в работе [19, 20]. При 100 K/пс эти приповерхностные пики плотности практически отсутствуют, как это видно из Рис. 53-60.

Для скоростей нагрева 40-100 K/пс за все время процесса не происходит формирование вогнутого распределения плотности пленки. Первоначально плоский профиль плотности становится затем выпуклым, а распределение частиц по скоростям приобретает наклонный вид, характерный для закритического однофазного разлета слоя флюида. Отметим, что при скорости нагрева 100 K/пс температура и давление в центре пленки превышают критические значения уже к моменту времени t = 5 пс, причем сам факт перехода через критическую область не сопровождается какими-либо заметными особенностями.

5. ЗАКЛЮЧЕНИЕ

Результаты настоящего исследования позволяют сделать вывод о существовании четырех различных режимов поведения тонкой пленки при ее интенсивном однородном нагреве.

При относительно малых скоростях нагрева 2 K/пс в диапазоне времен 0,8 нс наблюдается эволюция пленки от начального равновесного состояния с температурой 6 400 К к режиму квазистационарного поверхностного испарения, в котором затраты на испарение компенсируются поглощаемой энергией и максимальная температура в центре пленки стабилизируется примерно на уровне 6 800 К.

При увеличении скорости нагрева до 4 K/пс в момент времени t~280 нс после начала нагрева, когда максимальная температура в пленке достигает значений ~ 7000 K , начинается процесс взрывного вскипания, в ходе которого в центре пленки возникает паровая полость с резкими границами. В зависимости от флуктуаций в начальном состоянии пленки вместо одной полости может возникать структура из двух смежных полостей, разделенных тонкой (18 нм) прослойкой конденсированной фазы.

Следующий режим фазового превращения пленки приходится примерно на диапазон от 8 до 20 K/пс В этом диапазоне по мере увеличения скорости нагрева наблюдается рост амплитуды и числа флуктуаций плотности перед началом расслоения пленки на все возрастающее число областей паровой и конденсированной фазы, границы между которыми становятся все менее резкими, что характерно для режима спинодального распада. На верхней границе этого диапазона число крупномасштабных флуктуаций плотности уменьшается.

Диапазон 40-100 K/пс соответствует переходу к закритическому режиму расширения нагреваемой пленки, в ходе которого флуктуации плотности, характерные для двухфазной области состояний, фактически перестают наблюдаться. Если при 40 K/пс на исходных поверхностях пленки при ее расширении еще заметны уплотнения, связанные с влиянием поверхностного испарения, то при 100 K/пс это влияние уже не успевает проявляться.

Более детальное описание этих режимов возможно при анализе поведения средних значений и флуктуации параметров пленки в зависимости от времени, скорости нагрева и других условиях реализации процесса неравновесного фазового превращения.

Работа поддержана грантами РФФИ №13-02-01129а, № 15-07-05025.

ЛИТЕРАТУРА

1 В.Е.Фортов, И.В.Ломоносов. Я.Б.Зельдович и проблемы уравнений состояния вещества в экстремальных условиях. УФН, 2014, т.184, № 3, с.231 – 245.

2 М.А.Анисимов. Критические явления в жидкостях и жидких кристаллах. Москва, Наука, 1978, 271 с.

3 Ш. Ма. Современная теория критических явлений. М.: Мир, 1980. 298 с.

4 Г. Стенли. Фазовые переходы и критические явления. Мир, 1973, 425 с.

5 V.P.Skripov. Metastable liquids. Wiley, 1974.

6 L.V. Zhigilei, Z. Lin and D.S. Ivanov, “Atomistic modeling of short pulse laser ablation of metals: connections between melting, spallation, and phase explosion”, J. Phys. Chem. C, 2009, v.113, pp.11892-11906.

7 C.Wu, L.V. Zhigilei. Microscopic mechanisms of laser spallation and ablation of metal targets from large-scale molecular dynamics simulations Appl. Phys. A, 2014, v. 114, pp.11-32.

8 L. Zhang, X.Wang. Hybrid atomistic-macroscale modeling of long-time phase change in nanosecond laser–material interaction. Applied Surface Science, Vol. 255, Issue 5, Part 2, pp.3097–3103.

9 P.Lorazo, L.J.Lewis, M.Meunier, Thermodynamic pathways to melting, ablation, and solidification in absorbing solids under pulsed laser irradiation. Physical Review B, 2006, v.73, pp.134108.

10 S.I. Anisimov, V.V. Zhakhovskii, N.A. Inogamov, K. Nishihara, A.M. Oparin and Yu.V. Petrov, “Destruction of a solid film under the action of ultrashort laser pulse”. 2003, JETP Lett., v.77, pp.606-610.

11 G.E.Norman, S.V.Strarikov, V.V. Stegailov, Atomistic simulation of laser ablation of gold: effect of pressure relaxation. 2012, JETP, 114, pp.792-800.

12 M.S. Daw amd M.I. Baskes, “Embedded-atom method: Derivation and application to impurities and other defects in metals”, Phys. Rev. B, 29, 6443-6453 (1984).

13 S.M. Foiles, M.I. Baskes and M.S. Daw, “Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys”, Phys. Rev. B, 33, 7983-7991, (1986).

14 V.V. Zhakhovskii, N.A. Inogamov, Yu.V. Petrov, S.I. Ashitkov and K. Nishihara. “Two-temperature relaxation and melting after absorption of femtosecond laser pulse”, Appl. Surf. Sci., 255, 9592-9596 (2009).

15 В.И.Мажукин, А.В.Шапранов, В.Е.Пережигин. Математическое моделирование теплофизических свойств, процессов нагрева и плавления металлов методом молекулярной динамики. Mathematica Montisnigri, 2012, vol. XXIV, pp. 47 – 66.

16 L.Verlet, “Computer “experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules”, Phys. Rev., 159, 98-103, (1967).

17 T.H. Yang and C. Pan, “Molecular dynamics simulation of a thin water layer evaporation and evaporation coefficient”, Intern. Journ. of Heat and Mass Transfer, 2005, v.48, pp. 3516-3526.

18 V.I. Mazhukin, A.V. Shapranov, A.A. Samokhin, A.Yu. Ivochkin Mathematical modeling of non-equilibrium phase transition in rapidly heated thin liquid film. Mathematica Montesnigri, 2013, v. 27, pp. 65 - 90.

19 В.И. Мажукин, А.В. Шапранов, А.А. Самохин, А.Ю. Ивочкин. Моделирование взрывного вскипания тонкой пленки при однородном субнаносекундном нагреве. Математическое моделирование. 2014, т. 26, №3, с. 125-136.

20 V. I.Mazhukin, A.V.Shapranov, A.A.Samokhin, A.Yu.Ivochkin. Modeling the Thin Film Explosive Boiling Process in a Homogeneous Sub - Second Heating. Mathematical Models and Computer Simulations, 2014, Vol. 6, No. 5, pp. 542–550.

VISUALIZATION AND ANALYSIS OF THE RESULTS OF MOLECULAR-DYNAMIC MODELING OF INTENSIVE EVAPORATION OF LIQUID IN THE NEAR-CRITICAL REGION.

V.I. Mazhukin^1,2, A.V. Shapranov^1,2, A.A. Samokhin³, A.V. Mazhukin^1,2_,O.N. Koroleva^1,2

¹M.V. Keldysh Institute of Applied Mathematics, RAS, Moscow, Russia

²National Research Nuclear University MIPhI (Moscow Engineering Physics Institute)

³A.M. Prokhorov General Physics Institute, RAS, Moscow, Russia

vim@modhef.ru, asam40@mail.ru

Abstract

In the framework of molecular dynamics the behavior of thin liquid film during its rapid homogeneous heating with heat input rate 2-100 K/ps is studied. The initial film thickness through the z axis is 48 nm. The overall number of particles is 96 000 and the length of calculation area is 268 nm. In the film plane periodic boundary conditions were used with the main dimension 8x8 nm. The calculation results are presented in a form of distributions of temperature, density and particle velocity in the calculation area averaged over the film plane and also in the form of two-dimension particle density distributions in the zx plane in the range of heating time from 0 to 800 ps. Visualization and analysis of the obtained results suggest the existence of four different regimes of film behavior depending on the heating rate: quasi-stationary regime with surface evaporation, explosive (volume) boiling, spinodal decomposition and overcritical expansion.

Keywords: molecular dynamics, thin film, volume heating, surface evaporation, explosive (volume) boiling, spinodal decomposition, visualization.

REFERENCES

Fortov V E, Lomonosov I V “Ya.B. Zeldovich and equation of state problems for matter under extreme conditions” Phys. Usp., 2014, 57, pp. 219–233
A.Anisimov. Kriticheskie yavleniia v zhidkostiah i zhidkih kristalah[Critical phenomena in liquids and liquid crystals]. Moskva, Nauka [Science], 1978, 271 p.
Shang-Keng Ma. Modern Theory of Critical Phenomena. Benjamin, New York, 1976. Perseus, 2000, p. 561.
H.E.Stanley. Introduction to Phase Transitions and Critical Phenomena Oxford University Press, Oxford and New York 1971.
V.P.Skripov. Metastable liquids. Wiley, 1974
L.V. Zhigilei, Z. Lin and D.S. Ivanov, “Atomistic modeling of short pulse laser ablation of metals: connections between melting, spallation, and phase explosion”, J. Phys. Chem. C, 2009, v.113, pp.11892-11906.
C.Wu, L.V. Zhigilei. Microscopic mechanisms of laser spallation and ablation of metal targets from large-scale molecular dynamics simulations Appl. Phys. A, 2014, v. 114, pp.11-32.
L. Zhang, X.Wang. Hybrid atomistic-macroscale modeling of long-time phase change in nanosecond laser–material interaction. Applied Surface Science, vol. 255, Issue 5, Part 2, pp.3097–3103.
P.Lorazo, L.J.Lewis, M.Meunier, Thermodynamic pathways to melting, ablation, and solidification in absorbing solids under pulsed laser irradiation. Physical Review B, 2006, v.73, pp.134108.
S.I. Anisimov, V.V. Zhakhovskii, N.A. Inogamov, K. Nishihara, A.M. Oparin and Yu.V. Petrov, “Destruction of a solid film under the action of ultrashort laser pulse”. 2003, JETP Lett., v.77, pp.606-610.
G.E.Norman, S.V.Strarikov, V.V. Stegailov, Atomistic simulation of laser ablation of gold: effect of pressure relaxation. 2012, JETP, 114, pp.792-800.
M.S. Daw amd M.I. Baskes, Embedded-atom method: Derivation and application to impurities and other defects in metals, Phys. Rev. B, 29, 6443-6453 (1984).
S.M. Foiles, M.I. Baskes and M.S. Daw, Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Phys. Rev. B, 33, 7983-7991, (1986).
V.V. Zhakhovskii, N.A. Inogamov, Yu.V. Petrov, S.I. Ashitkov and K. Nishihara. Two-temperature relaxation and melting after absorption of femtosecond laser pulse. Appl. Surf. Sci., 2009, vol. 255, hh. 9592-9596.
V.I.Mazhukin, A.V.Shapranov, V.E.Perezhigin. Matematicheskoe modelirovanie teplofizicheskih svoystv, processov nagreva i plavleniia metallov metodom molekuliarnoy dinamiki. Mathematica Montisnigri, 2012, vol. 24, pp. 47 – 66.
L.Verlet. Computer “experiments on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules, Phys. Rev., 1967, vol. 159, pp. 98-103.
T.H. Yang and C. Pan. Molecular dynamics simulation of a thin water layer evaporation and evaporation coefficient. Int. Journ. of Heat and Mass Transfer, 2005, v. 48, pp. 3516-3526.
V.I. Mazhukin, A.V. Shapranov, A.A. Samokhin, A.Yu. Ivochkin Mathematical modeling of non-equilibrium phase transition in rapidly heated thin liquid film. Mathematica Montesnigri, 2013, v. 27, pp. 65 - 90.
V.I.Mazhukin, A.V.Shapranov, A.A.Samokhin, A.Yu.Ivochkin. Modelirovanie vzryvnogo vskipaniia tonkoy plenki pri odnorodnom subnanosekundnom nagpeve [MODELING OF THIN FILM EXPLOSIVE BOILING PROCESS DURING HOMOGENEOUS SUB-SECOND HEATING]. Matematicheskoe modelirovanie. 2014, vol. 26, №3, pp. 125-136.
V.I.Mazhukin, A.V.Shapranov, A.A.Samokhin, A.Yu.Ivochkin. Modeling the Thin Film Explosive Boiling Process in a Homogeneous Sub-Nanosecond Heating. Mathematical Models and Computer Simulations, 2014, Vol. 6, No. 5, pp. 542–550.