ВИЗУАЛИЗАЦИЯ РАСЧЕТА ФОРМЫ
ПОВЕРХНОСТЕЙ МИНИМАЛЬНОЙ ПЛОЩАДИ
А. Клячин, В. Клячин, Е. Григорьева
Волгоградский государственный университет, Волгоград, Россия
klyachin-aa@yandex.ru, klchnv@mail.ru, e_grigoreva@mail.ru
Содержание
2. Алгоритм расчета минимальной поверхности
3. Визуализация в среде Blender
4. Текстурирование минимальной поверхности с учетом значений гауссовой кривизны
Аннотация
Данная работа посвящена численному расчету и визуализации поверхностей, имеющих наименьшую площадь с фиксированным краем. Соответствующее дифференциальное уравнение является нелинейным, поэтому найти точное решение данной краевой задачи чаще всего не представляется возможным. Это приводит к задаче разработки эффективных методов приближенного решения соответствующего уравнения - уравнения минимальной поверхности. Важной задачей также является математическое обоснование найденных методов в плане устойчивости и сходимости приближенных решений. В рамках этой задачи, нами получены такие результаты:
- Исследованы некоторые математические аспекты применения расчётных формул и схем. Выполнены определённые шаги для обоснования применяемых методов приближённого решения уравнения минимальной поверхности.
- На основе разработанного метода аппроксимации дифференциальных уравнений, получена схема расчёта кусочно-линейной поверхности имеющей минимальную площадь среди таких же поверхностей с общим краем. Для данной схемы расчёта разработаны несколько программных модулей, позволяющих получать результаты расчёта в удобной для последующей обработки форме. Проведены тестовые расчёты минимальных поверхностей для различных пространственных контуров, состоящих из прямолинейных, параболических и круговых участков.
- Разработана программа на базе библиотеки OpenGL, позволяющая осуществить визуализацию трехмерных данных с возможностью задания способа закраски отдельных треугольников модели.
Разработан экспериментальный модуль MinSurf.py, который встраивается в среду Blender. В этом модуле реализуется система классов, предназначенных для хранения моделей минимальных поверхностей и осуществления таких действий как: деформация поверхности модели, автоматическое создание ключевых кадров для анимации деформации поверхности, окрашивания поверхностей моделей на основе технологии UV-текстурирования.
Ключевые слова: поверхность минимальной площади, триангуляция, кусочно-линейная поверхность, аппроксимация функционала площади, 3D моделирование, деформация поверхности, текстурирование поверхности.
При проектировании и конструировании современных форм архитектурных сооружений важное место занимает этап геометрического проектирования. Это достаточно подробно отражено, например, в книге [1] и отмечено в статье [2], где изучается проблема разработки тентовых тканевых конструкций. Визуализация и просмотр полученных поверхностей является следующим этапом геометрического проектирования. В практике проектирования покрытий сложной геометрической формы часто возникает задача определения координат дискретного множества точек. Это важно для расчета оболочек и для контроля при возведении оболочки в натуре. В приведенных выше работах подчеркивается, что наиболее предпочтительной формой поверхностей для тентовых тканевых конструкций, являются поверхности минимальной площади. Такие архитектурные сооружения имеют привлекательный внешний вид, они оптимальны в минимальном расходе материалов при строительстве и в уменьшении теплообмена с окружающей средой. Визуализация подобного рода поврхностей, особенно с возможностью 3D обзора, позволяет провести качественный и количественный анализ построенных моделей, увидеть распределение физических и геометрических характеристик и величин вдоль рассматриваемой поверхности, произвести корректировку граничных, начальных и других исходных данных задачи на основе такого анализа.
Минимальная поверхность имеет наименьшую площадь по сравнению со всеми другими поверхностями, проходящими через заданный в пространстве контур. Напряжённость в каждой точке минимальной поверхности постоянная. Это позволяет подбирать такой контур, который наилучшим образом воспринимал бы усилия с пролётной части покрытия [1]. Зачастую найти точное решение данной краевой задачи не представляется возможным. Поэтому приходится её решать численно, что приводит к задаче разработки эффективных методов приближенного решения соответствующего уравнения - уравнения минимальной поверхности. Важной задачей также является математическое обоснование найденных методов в плане устойчивости и сходимости приближенных решений.
В этом направлении нами получены следующие результаты:
- Исследованы некоторые математические аспекты применения расчётных формул и схем. Выполнены определённые шаги для обоснования применяемых методов приближённого решения уравнения минимальной поверхности [3], [4] (существование и единственность, сходимость и устойчивость).
- На основе разработанного метода аппроксимации дифференциальных уравнений, получена схема расчёта кусочно-линейной поверхности (т. е. поверхности, собранной в пространстве из примыкающих друг к другу треугольников) имеющей минимальную площадь среди таких же поверхностей с общим краем. Для данной схемы расчёта разработаны несколько программных модулей, позволяющих получать результаты расчёта в удобной для последующей обработки форме. Проведены тестовые расчёты минимальных поверхностей для различных пространственных контуров, состоящих из прямолинейных, параболических и круговых участков.
- Разработана программа, позволяющая осуществить визуализацию трехмерных данных с возможностью задания способа закраски отдельных треугольников модели. Предполагается, что расчетные данные для визуализации представлены в виде отдельного файла, соответственно в программе осуществлен разбор полученного файла данных и заполнение соответствующих массивов для хранения вершин, граней модели, описаны подходящие структуры данных. Визуализация осуществляется с помощью средств кросс-платформенной библиотеки OpenGL и позволяет организовать трехмерный обзор модели, задать параметры освещения и параметры для градиентного расчета цвета грани. Реализована возможность задания способа расчета цвета каждой грани с помощью некоторых формул. Частично реализован подход к вычислению параметров закраски отдельного треугольника с помощью аппроксимации гауссовой кривизны поверхности.
- Разработан
экспериментальный модуль MinSurf.py, который
встраивается в среду Blender. В этом модуле реализуется система
классов, предназначенных для хранения моделей поверхностей и
осуществления таких действий как: деформация поверхности модели,
автоматическое создание ключевых кадров для анимации деформации
поверхности, окрашивания поверхностей моделей на основе технологии
UV-текстурирования. При этом реализуются различные виды деформации. В
частности,
- деформация по заведомо известным функциям смещения вершин несущей сетки,
- деформация под воздействием фазового потока в общем случае неавтономной системы обыкновенных дифференциальных уравнений,
- деформация простого перемещения и вращения поверхности как твердого тела в пространстве,
Разработан также метод цепей хранения 3D модели, заданной в виде многогранной поверхности с треугольными гранями. Метод позволяет приблизительно в 3 раза уменьшить объем памяти, необходимой для хранения моделей. Данный метод основан на сокращении дублируемой информации о вершинах смежных треугольников.
2. Алгоритм расчета минимальной поверхности
Определение формы минимальной поверхности с заданным
контуром в пространстве с декартовыми координатами 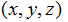 сводится к решению
нелинейного дифференциального уравнения
сводится к решению
нелинейного дифференциального уравнения
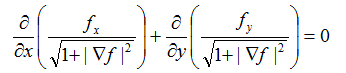 (1)
(1)
с краевыми условиями вида
где
–
область на
плоскости
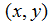 и
и
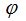 –
непрерывная функция, заданная на границе этой области. За
редким исключением найти точное решение данной краевой задачи
невозможно. В этом случае прибегают к применению численных методов, что
приводит к задаче разработки эффективных алгоритмов
приближенного
решения.
–
непрерывная функция, заданная на границе этой области. За
редким исключением найти точное решение данной краевой задачи
невозможно. В этом случае прибегают к применению численных методов, что
приводит к задаче разработки эффективных алгоритмов
приближенного
решения.
В
своей работе мы используем следующий подход, предусматривающий
построение минимальных поверхностей, заданных над произвольной областью
и использующий триангуляцию расчётной области. Под триангуляцией мы
понимаем следующую конструкцию. Пусть задан конечный набор
точек 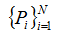 на плоскости. Триангуляцией набора точек называется набор
треугольников
на плоскости. Триангуляцией набора точек называется набор
треугольников 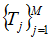 удовлетворяющих
условиям
удовлетворяющих
условиям
1.любая точка 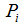 является вершиной хотя бы одного треугольника;
является вершиной хотя бы одного треугольника;
2.каждый треугольник содержит только три точки из данного набора, являющиеся вершинами этого треугольника.
Пусть ограниченная
плоская область. Триангуляцией
области
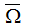
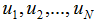
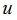
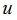
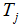
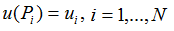
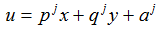
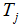 . Данная
функция будет непрерывной и
в каждом треугольнике определены её частные
производные
. Данная
функция будет непрерывной и
в каждом треугольнике определены её частные
производные 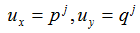
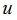
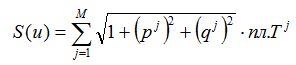
Отметим, что график кусочно-линейной функции представляет собой набор треугольников в пространстве, примыкающих друг к другу по своим сторонам. На рисунках 1 и 2 приведены изображения графиков таких функций:

Рис. 1. Пример кусочно-линейной функции

Рис. 2. Пример кусочно-линейной поверхности
Известно,
что решение краевой задачи для уравнения (1), при определенных
условиях, эквивалентно соответствующей вариационной задаче на минимум
площади. Следовательно, отыскивая минимум функции 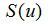 при фиксированных
значениях
при фиксированных
значениях  , отвечающих
граничным точкам, мы получим кусочно-линейную
поверхность, имеющую минимальную площадь среди всех кусочно-линейных
поверхностей с тем же краем. Построенная таким образом поверхность и
будет приближенным решением соответствующей краевой задачи уравнения
(1).
, отвечающих
граничным точкам, мы получим кусочно-линейную
поверхность, имеющую минимальную площадь среди всех кусочно-линейных
поверхностей с тем же краем. Построенная таким образом поверхность и
будет приближенным решением соответствующей краевой задачи уравнения
(1).
Для расчёта такой кусочно-линейной минимальной поверхности нами написана одна основная процедура minimum_func() и несколько вспомогательных процедур. Кратко опишем их работу. Отметим вначале, что точки и треугольники рассматриваемой триангуляции, а также значения граничной функции и результаты вычислений хранятся в четырех отдельных двоичных файлах. Структура этих файлов простая. Например, точки хранятся в файле points.pnt, в котором первые 8 байт отводятся под количество точек, а дальше каждая точка занимает 20 байт - две координаты, соответствующие типу double и информация о принадлежности границе (int):
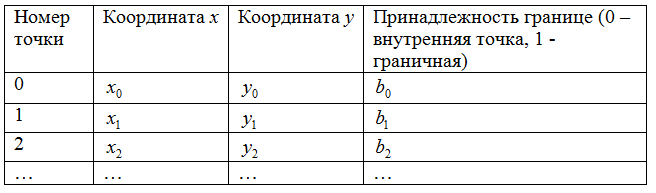
Триангуляция этих точек хранится в другом файле, который имеет следующую структуру: вначале 8 байт отводится под число треугольников, а следующие данные можно изобразить в виде таблицы
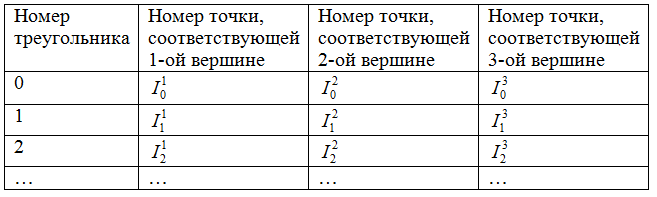
Одна из вспомогательных процедур формирует файл, в который для каждого узла триангуляции заносится набор треугольников, содержащих эту точку в качестве вершины. Структура этого файла выглядит следующим образом

Данный приём позволил существенно сократить время на вычисление
производных функции по переменным 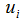 . Объясняется это вот чем. Поиск
минимума функции
. Объясняется это вот чем. Поиск
минимума функции 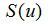 осуществляется
методом градиентного спуска, а его применение предполагает приближенное
вычисление ее производных. Однако, при
вычислении приращения этой функции по переменной
осуществляется
методом градиентного спуска, а его применение предполагает приближенное
вычисление ее производных. Однако, при
вычислении приращения этой функции по переменной 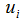 участвуют только те
треугольники, которые содержат вершину
участвуют только те
треугольники, которые содержат вершину 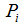 . Таким образом, обращаясь к
данным этого файла, мы можем не перебирать все треугольники
триангуляции, а соответствующие вычисления выполнить только для
считанных из этого файла треугольников.
. Таким образом, обращаясь к
данным этого файла, мы можем не перебирать все треугольники
триангуляции, а соответствующие вычисления выполнить только для
считанных из этого файла треугольников.
Далее, результаты всех вычислений сохраняются либо в двоичном файле, либо в текстовом, которые можно использовать для дальнейшей обработки. Например, вызов ещё одной вспомогательной функции позволяет сохранить результаты вычислений в текстовом файле формата STL. Тестирование разработанной программы осуществлялось на примере таких минимальных поверхностей, как поверхность Шерка, геликоид и катеноид. Погрешность вычислений составила около 0,007-0,01% даже для небольшого количества точек (от 121 до 441 точки). С помощью разработанных программ были рассчитаны поверхности минимальной площади для различных краевых пространственных контуров, состоящих из прямолинейных, параболических и круговых участков. Для построения поверхностей и их изображения мы сохранили результаты вычислений в текстовом файле формата stl и воспользовались для просмотра программой Blender 2.68a. Ниже приводим изображения некоторых из построенных минимальных поверхностей.
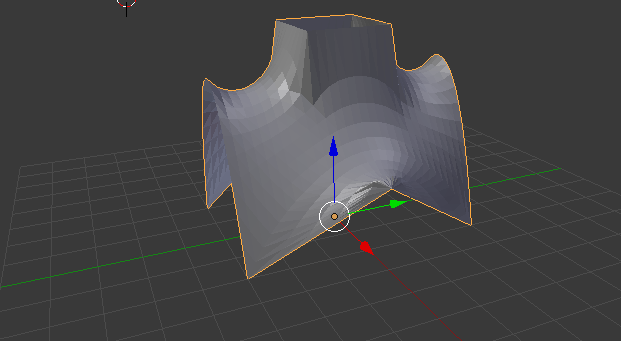
Рис. 3. Минимальная поверхность над шестиугольником с вырезанным квадратом
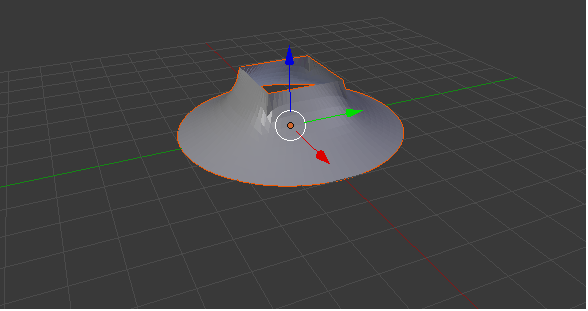
Рис. 4. Минимальная поверхность над кругом с вырезанным квадратом
Рис. 5. Минимальная
поверхность с краевым контуром, состоящем из
прямолинейных отрезков и круговых дуг
На рисунке 3 показана поверхность, построенная описанным выше алгоритмом, натянутая на два контура. Один из них состоит из двух параболических дуг и четырех прямолинейных отрезков, проектирующихся на шестиугольник. Второй контур представляет собой квадрат, проекция которого на горизонтальную плоскость лежит внутри шестиугольника. На рисунке 4 представлена минимальная поверхность, опирающаяся на окружность и на квадрат, расположенный на некоторой высоте над плоскостью (x,y). На рисунке 5 показана поверхность, построенная над квадратом и край которой состоит из двух отрезков и шести круговых дуг.
Отметим, что описанный выше подход позволяет находить приближённо минимальную поверхность над областью достаточно сложной формы. Например, как было отмечено выше, на рисунке 3 показана поверхность, построенная над шестиугольной областью с вырезанным из неё квадратом. Вообще, чтобы воспользоваться разработанной программой, достаточно наличия четырех входных файлов, которые содержат перечень точек, треугольников триангуляции, информацию о примыкающих к точкам треугольниках, а также значения граничной функции. Таким образом, достоинством разработанной программы является её универсальность и независимость от используемой расчётной сетки. Более того, программа позволяет минимизировать не только площадь. Если понадобится решать краевую задачу вариационным методом для другого дифференциального уравнения, отличного от уравнения минимальной поверхности, нам достаточно всего лишь задать соответствующий функционал. При этом остальные программные модули остаются без изменений.
3. Визуализация в среде Blender
Среда 3D моделирования Blender [6] позволяет расширять возможности посредством системы встраиваемых модулей, написанных на языке программирования Python. Встроенный модуль bpy [7] предоставляет программный интерфейс по полному управлению 3D моделями, их свойствами, анимацией и рендерингом. Поэтому предлагаемый средой Blender инструмент является весьма подходящей средой программирования и научной визуализации. На нижеприведенном рисунке показана среда Blender, расположенная внутри окна 3D обзора модель и размещенная в специальном окне текстового редактора программа, предназначенная для управления моделью и ее свойствами. Рассмотримзадачу конструирования деформированных поверхностей из некоторой начальной. Визуализация процесса последовательных приближений в задаче минимизации функционала площади может быть сведена к такого рода задаче. Но при решении данной задачи мы поставим дополнительное условие. Если поверхность представлена 3D моделью, то попытаемся представить в универсальном виде возможные модификации поверхности в зависимости от конкретной задачи. Например, деформация поверхности, ее текстурирование, масштабирование, построение сечений, проецирование и т.п. -- решения этих задач могут быть представлены единым программным интерфейсом и к тому же позволяющим комбинировать различиные модификации поверхности с целью получения требуемого результата визуализации.
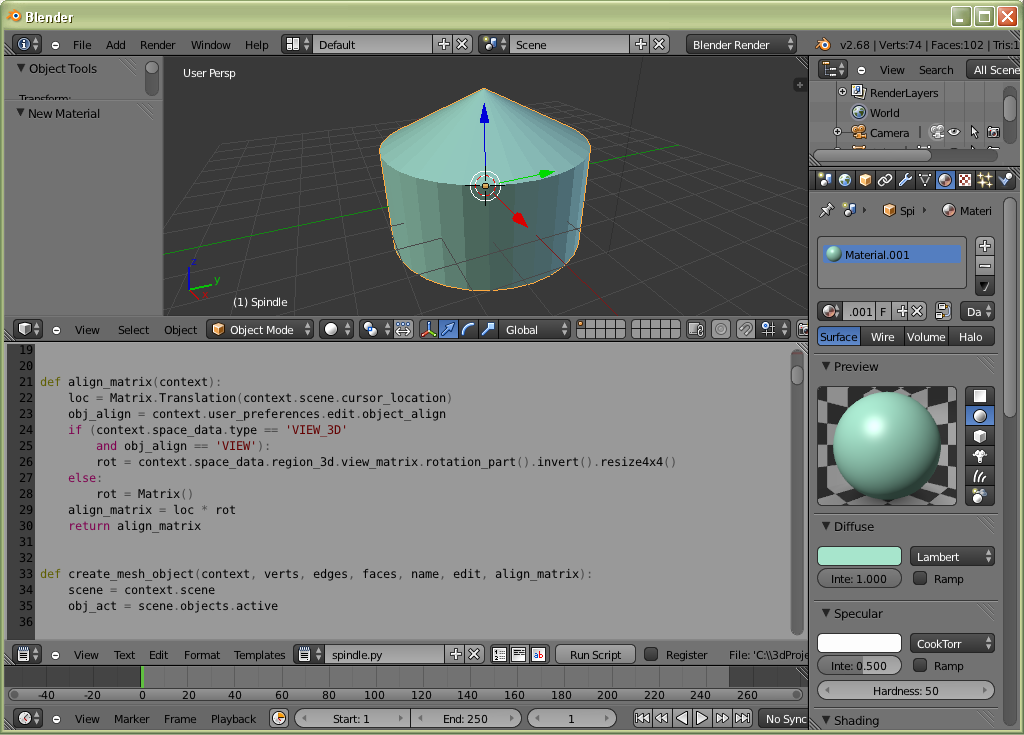
Рис. 6. Среда моделирования и программирования Blender 2.68a
С целью реализации упомянутого выше интерфейса приведем соответствующую диаграмму классов. При проектировании этой диаграммы мы пользовались идеями объектно-ориентированного проектирования представленными в книге [5]. Аннонсирована диаграмма классов в работе [8].
Рис. 7. Диаграмма классов модуля MinSurf.py
На этой диаграмме класс Extent -- базовый класс для реализации различных способов визуализации моделей и поверхностей. Для того, чтобы модификаторы и другие расширения могли преобразовывать 3D объекты нам понадобится специальный виртуальный метод в базовом классе Object, который мы назовем UpdateView(). Вызов этого метода приводит, например, к применению того или иного модификатора Blender к данному объекту, или к какому-либо другому преобразованию визуального представления модели или поверхности. Например, если мы хотим применить булевый модификатор B к объекту меша A, то в программе схематично это выглядит следующим образом:
A=Mesh.new()
C=Mesh.new()
B=Boolean.new(A)
B.SetOject(B,’UNION’)
B.UpdateView().
Еще одна возможность решаемая предыдущей схемой состоит в автоматизации процесса создания ключевых кадров анимации при деформации объектов. С этой целью создается дополнительный класс Deformator производный от класса Extent и класс ShapeKeys производный от Object предназначенный для хранения и управления информацией о ключевых формах объекта. Включение класса Deformator в иерархию расширений позволит применить ту же технологию, что и для модификаторов. Приведем соответствующую схему
Рис. 8. Класс Deformator является производным класса Extent
Применение указанной выше схемы позволяет комбинировать различные методы визуализации: можно только ограничиться деформацией, а можно добавить построение проекции поверхности на координатную плоскость. В коде это выглядит так.
A=Mesh.new() # Cоздается объект
B1=Deformator.new(A)# Создается объект, деформирующий А
B2=Projection.new(B1)# Создается объект осуществляющий построение проекции B1
B2.UpdateView() # Осуществляем итоговую визуализацию
Это достигается за счет вызова метода UpdateView() для декорируемых объектов. Пример работы подобных модификаторов можно посмотреть на нижеприведенных рисунках.
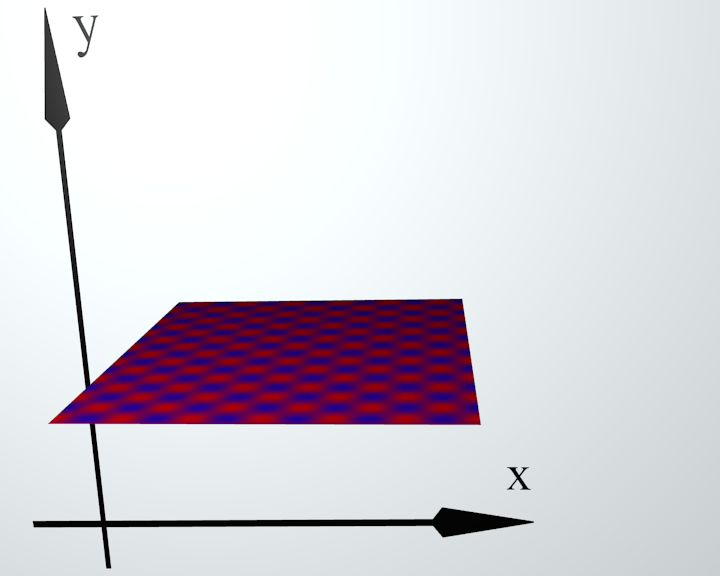
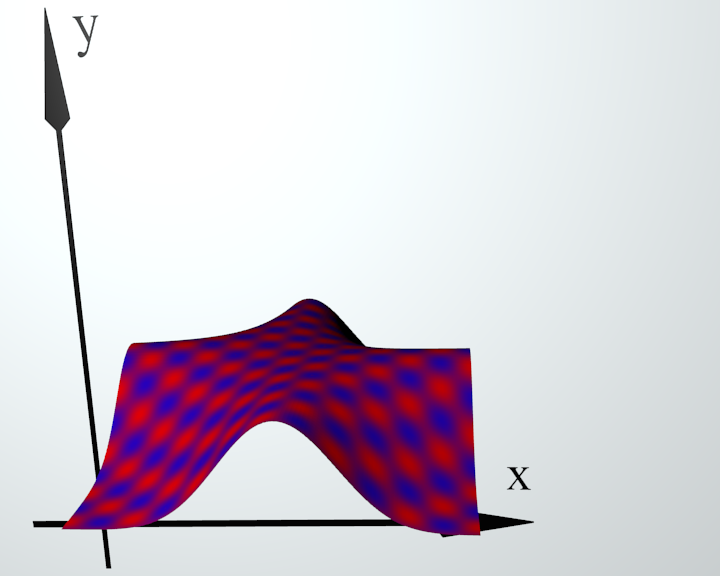
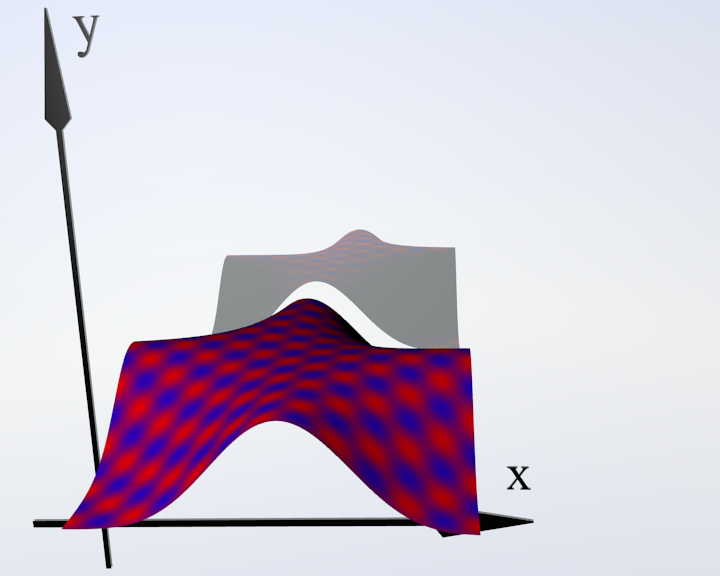
Рис. 9. Плоскость |
Рис. 10. Деформированная плоскость |
Рис. 11. Проекция на плоскость Oxy |
Класс Deformator может применяться для визуализации
- вариации поверхности под действием фазового потока в общем случае неавтономной системы обыкновенных дифференциальных уравнений;
- вариации геометрических характеристик поверхности при ее деформации с целью исследования устойчивости минимальной поверхности;
- динамики изменения формы моделей в процессах, описывающихся решениями дифференциальных уравнений с частными производными;
- процесса построения системы последовательных приближений при численном решении задач линейной алгебры, вычислительной геометрии, математической физики.
На нижеследующем анимационном рисунке показано изменение средней кривизны поверхности Шерка при локальной деформации самой поверхности. Синему оттенку соответствуют значения близкие к нулю, а красному оттенку -- близкие к максимуму средней кривизны.

Рис. 12. Вариация средней кривизны поверхности Шерка
На рисунке 12 иллюстрируется локальная деформация поверхности минимальной площади Шерка и визуализация изменения ее средней кривизны при такой деформации. Красными оттенками отмечаются области ненулевой средней кривизны, а синий цвет отвечает за участки нулевой средней кривизны поверхности. Такая визуализация позволяет увидеть неравномерное распределение напряжений упругих оболочек.
4. Текстурирование минимальной поверхности с учетом значений гауссовой кривизны
В этом разделе мы описываем разработанную программу для текстурирования поверхностей по значениям скалярной функции в узлах несущей сетки. Разработаная программа позволяет осуществить визуализацию трехмерных данных с возможностью задания способа закраски отдельных треугольников модели. При этом используется градиентный метод аппроксимации цвета внутри каждой треугольной грани. Предполагается, что расчетные данные для визуализации представлены в виде отдельного файла формата TGS, каждая строка которого хранит трехмерные координаты одной точки модели. Три подряд идущие строки задают один треугольник в триангуляции поверхности (см. таблицу).
| Номер строки файла | Координата x точки | Координата y точки | Координата z точки |
| 1. Первая вершина первого треугольника |
0.0 | 0.0 | 3.06614 |
| 2. Вторая вершина первого треугольника |
0.5 | 0.0 | 1.8811 |
| 3. Третья вершина первого треугольника |
0.5 | 0.5 | 1.41073 |
| 4. Первая вершина второго треугольника |
0.5 | 0.0 | 3.06614 |
| 5. и т.д. | 0.0 | 0.5 | 1.8811 |
В программе осуществлен разбор полученного файла данных и заполнение соответствующих массивов для хранения вершин, граней модели, описаны подходящие структуры данных. Визуализация осуществляется с помощью средств кросс-платформенной библиотеки OpenGL и позволяет организовать трехмерный обзор модели, задать параметры освещения и параметры для градиентного расчета цвета грани.
Реализована возможность задания способа расчета цвета каждой грани с помощью некоторых формул. Частично реализован подход к вычислению параметров закраски отдельного треугольника с помощью аппроксимации гауссовой кривизны поверхности. Напомним, что гауссова кривизна, наряду со средней кривизной поверхности, является одной из геометрических характеристик поверхности, возникающей в уравнениях безмоментной теории оболочек [9] Значения гауссовой кривизны в вершинах поверхности аппроксимируются согласно формуле
где
-- величина плоского угла i-й грани при данной вершине.
Сделаем некоторые пояснения. Известно, что в вершинах многогранной
поверхности гауссова кривизна определяется как площадь сферического
многоугольника, образованного нормалями тех граней, которым принадлежит
вершина. Это демонстрируется на нижеприведенном рисунке 13
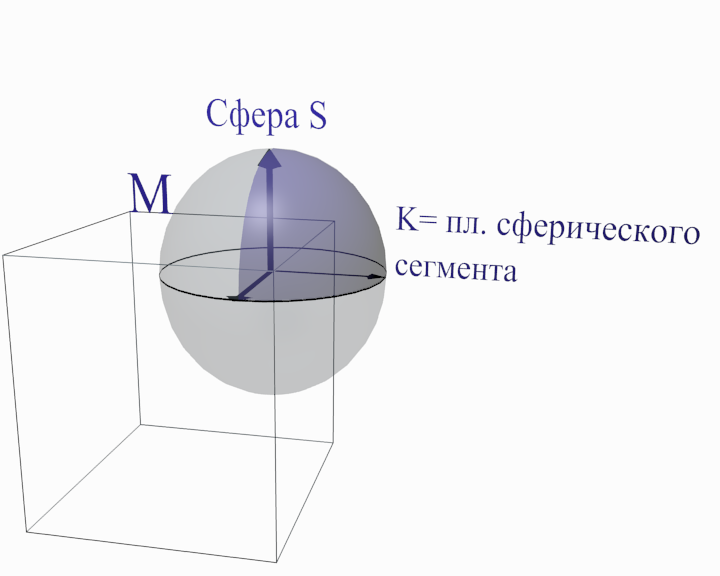
Рис. 13. Вычисление гауссовой кривизны в вершине многогранника
Согласно формулам сферической геометрии площадь сферического n-угольника равна
где -- внутренние углы
многоугольника. Из геометрических соображений будем иметь
Поэтому, окончательно получаем
С целью визуализации значений этой величины строится шкала пороговых значений кривизны вида
и для каждого промежутка разбиения назначается цвет из соответствующей цветовой шкалы
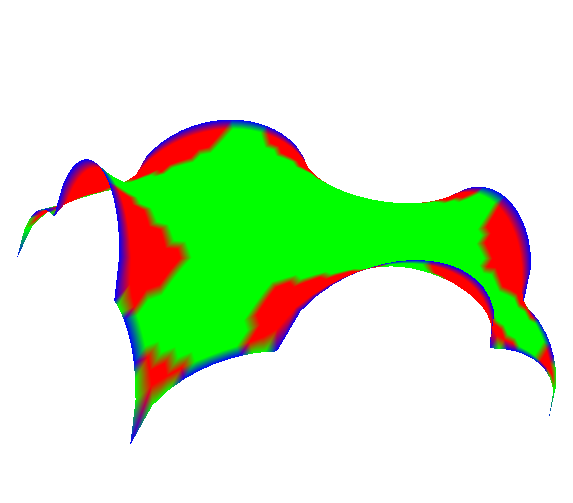

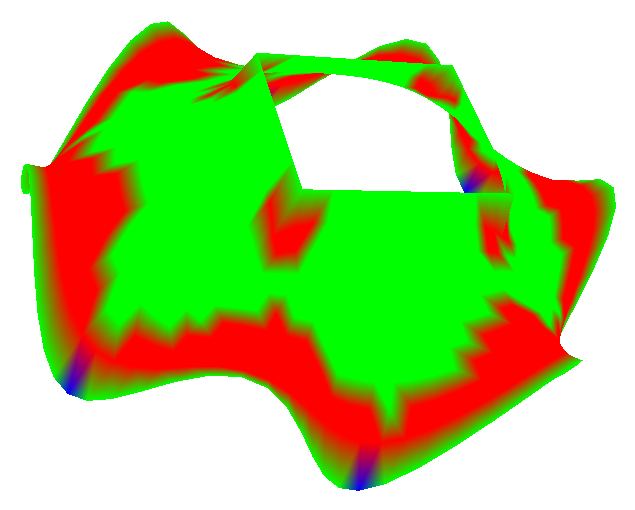
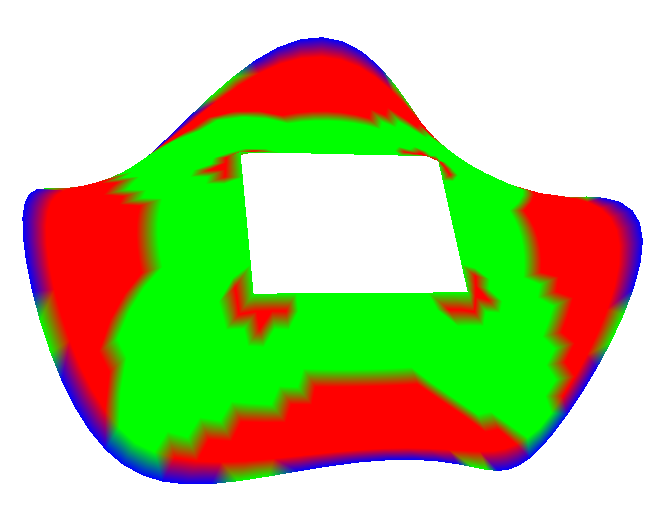
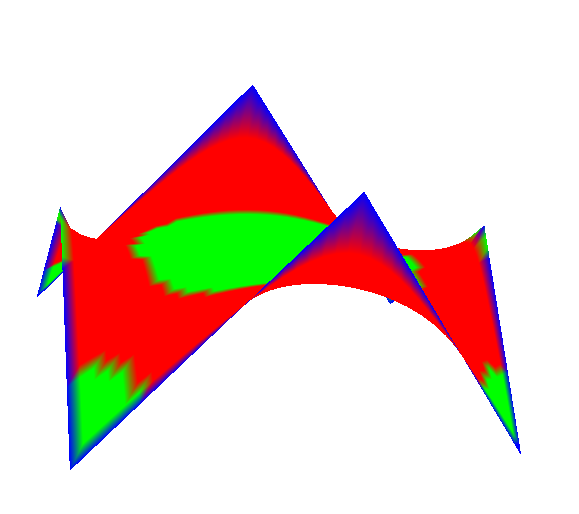
Рис. 14.
На рисунке 14 представлены примеры визуализации значений гауссовой кривизны минимальных поверхностей по четырем пороговым значениям (три цвета).
В работе применена разработанная авторами схема расчета кусочно-линейной поверхности, имеющей минимальную площадь среди таких же поверхностей с общим краем. По данной схеме расчёта разработаны несколько программных модулей, которые дают возможность получать результаты вычислений в удобной для последующей обработки форме. Проведены тестовые расчёты минимальных поверхностей для различных пространственных контуров, состоящих из прямолинейных, параболических и круговых участков. Выбранный подход для организации вычислений обладает определенной универсальностью, в том смысле, что код разработанных программ почти не потребует исправлений при изменении расчетной области и минимизируемого функционала. Это позволит без труда перейти к моделированию не только минимальной поверхности, но и поверхности раздела физических сред, на которой достигает минимума ее потенциальная энергия натяжения и смачивания (см. пп. 1.4-1.9 в [10]).
Работа выполнена при финансовой поддержке РФФИ (проект № 13-01-97034 р_поволжье_а).
[1]Михайленко В.Е., Ковалев С.Н., Конструирование форм современных архитектурных сооружений. Киев:Будiвельник, 1978. - 138 с.
[2]Абдюшев А.А., Мифтахутдинов И.Х., Осипов П.П. Проектирование непологих оболочек минимальной поверхности// Известия КазГАСУ, Строительные конструкции, здания и сооружения, 2009, № 2 (12).
[3]Клячин А.А. О скорости сходимости последовательности,
доставляющей минимум в вариационной задаче// Вестн. Волгогр. гос. ун-та.
Сер. 1, Мат. Физ. 2012. № 1 (16). С. 12-20.
[4]Клячин А.А. О кусочно-линейных почти-решениях эллиптических уравнений// Вестн. Волгогр. гос. ун-та. Сер. 1, Мат. Физ. 2013. №2(19). С. 19-26
[5]Э.Гамма, Р.Хелм, Р.Джонсон, Д.Влиссидес Приемы объектно-ориентированного проектирования. Паттерны проектирования. СПб. Изд-во Питер. 2007. 366 с.
[6]Официальный сайт Blender Foundation. URL: http://blender.org
[7] Официальная документация по функциям модуля bpy. URL: http://www.blender.org/documentation/blender_python_api_2_64_release/
[8]Клячин В.А. Объектно-ориентированная надстройка для модуля Python управления 3D моделями в среде Blender//Материалы VI Международной заочной научно-практической конференции "Научная дискуссия: вопросы физики, математики, информатики" Издательство Москва: Изд. «Международный центр науки и образования», 2013 г.
[9]Векуа И.Н. Обобщенные аналитические функции. М.: Наука. 1988. -- 512 с.
[10]Финн Р. Равновесные капиллярные поверхности. Математическая теория. Пер. с англ. -- М.: Мир, 1989. -- 312 с.
VISUALIZATION OF CALCULATION
OF MINIMAL AREA SURFACES
A. Klyachin, V. Klyachin, E. Grigorieva
Volgograd State University, Volgograd, Russian Federation
klyachin-aa@yandex.ru, klchnv@mail.ru, e_grigoreva@mail.ru
Abstract
This work is devoted to the numerical calculation and visualization of surfaces having the smallest area with a fixed boundary. The corresponding differential equation is nonlinear, so find an exact solution of the boundary value problem often is not possible. This leads to the problem of the development of effective methods for the approximate solution of the corresponding equation - the minimal surface equation. An important problem is to study mathematical methods found in terms of stability and convergence of approximate solutions. In this direction, we obtained the following results:
- We have studied some mathematical aspects of the calculation formulas and diagrams. Made some steps to justify the methods used an approximate solution of the minimal surface equation.
- On the basis of this method approximation of differential equations we obtain calculation scheme of piecewise linear surface having a minimum area of the same surfaces with a common boundary. For this calculation scheme we developed several software modules to obtain calculation results in a convenient form for subsequent processing. We done the test calculations of minimal surfaces for different spatial contours consisting of straight, parabolic and circular segments.
- The developed program is based on the library OpenGL and it allows the visualization of three-dimensional data with the ability to specify how to fill individual triangles model.
It was developed an experimental module MinSurf.py, which integrates into Blender. This module is implemented class system designed for storing models of minimal surfaces and implementation of such actions as: deformation of the surface model, automatically creating keyframes to animate the surface deformation, staining surfaces models based on technology UV-texturing.
Key words: surface of minimal area, triangulation, piecewise linear surface, approximation of the area functional, 3D modeling, deformation of surface, surface texturing.
References
[1]Mikhaylenko V.E., Kovalev S.N. Konstruirovanie form sovremennykh arkhitekturnykh sooruzheniy [Designing forms of modern architecture]. Kiev. Budivelnik, 1978, p. 138.
[2]Abdyushev A.A., Miftahutdinov I.H., Osipov, P.P. Proektirovanie nepologikh obolochek minimalnoy poverkhnosti [Design of shallow shells of minimal surface]. News KSUAE, Building construction, building, vol. 2009, no 2, 2009.
[3]Klyachin A.A. O skorosti skhodimosti posledovatelnosti, dostavlyayuschey minimum v variatsionnoy zadache [The rate of convergence of the sequence, which delivers minimum in the variational problem]. Vestn. Volgogr. Reg. Univ Ser. 1, Math. Ph., vol. 16, no 1, 2012, pp. 12-20.
[4]Klyachin A.A. On piecewise-linear almost-solutions of elliptic equations. Vestn. Volgogr. Reg. Univ Ser. 1, Math. Ph., vol. 19, no 21, 2013, pp. 19-26.
[5]E.Gamma, R.Helm, R.Johnson, D. Vlissides. Priemy obektno-orientirovannogo proektirovaniya [Priemy obektno-orientirovannogo proektirovaniya. Patterny proektirovaniya.]. Elements of reusable Object-Oriented software. St. Petersburg. Publisher Peter. 2007, p. 366.
[6]The official website for Blender Foundation. Available at: http://blender.org
[7]Official function module documentation bpy. Available at: http://www.blender.org/documentation/blender_python_api_2_64_release/
[8]V.A. Klyachin. Obektno-orientirovannaya nadstroyka dlya modulya Python upravleniya 3D modelyami v srede Blender [Object-oriented wrapper for Python module manipulate 3D models in the IDE Blender]. Materialy VI Mezhdunarodnoy zaochnoy nauchno-prakticheskoy konferentsii "Nauchnaya diskussiya: voprosy fiziki, matematiki, informatiki" [Proceedings of the VI International extramural scientific and practical conference "The scientific debate: questions of physics, mathematics, computer science"]. Moscow. "International Centre for Science and Education", 2013.
[9]I.N. Vekua. Obobschennye analiticheskie funktsii [Generalized analytic functions]. Nauka, 1988, p. 512.
[10]Finn R. Ravnovesnye kapillyarnye poverkhnosti [Equilibrium capillary surface]. Matematicheskaya teoriya [Mathematical theory]. Translate from English. Moscow. Mir, 1989, p. 312.