ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ РАСПАДА ВИХРЯ
ТЕЙЛОРА-ГРИНА В ЛАМИНАРНОМ И ТУРБУЛЕНТНОМ РЕЖИМАХ
И. Широков1, Т. Елизарова2
1 Московский государственный университет имени М.В. Ломоносова, Москва, Россия
2 Институт прикладной математики им. М.В. Келдыша РАН, Москва, Россия
ivanshirokov@inbox.ru, telizar@mail.ru
Оглавление
Математическая модель и метод численного решения
Результаты расчетов для Re=1600
Результаты расчетов для Re=280
Результаты расчетов для Re=100
Сравнение результатов для разных Re и энергетический спектр
Аннотация
Представлены результаты численного моделирования и компьютерной визуализации течения для классической задачи распада вихря Тейлора–Грина, полученные на основе сглаженной системы уравнений газодинамики, а именно квазигазодинамических (КГД) уравнений, описывающих течение вязкого сжимаемого газа. КГД-система может быть получена путем осреднения по времени системы Навье-Стокса (НС), и отличается от системы НС наличием существенно нелинейных членов с малым коэффициентом, имеющим размерность времени. КГД-система определяет эволюцию во времени плотности, скорости и давления газа, зависящих от эйлеровых координат и от времени. Температура, давление и плотность связаны уравнением состояния иде¬ального газа. На основе КГД-алгоритма решается задача о распаде вихря Тейлора–Грина в азоте при температуре, соответствующей нормальным условиям, при числе Маха, равном 0.1. Варьирование числа Рейнольдса обеспечивается рассмотрением течений при разных плотностях и давлениях.
Для численного решения КГД-системы использована явная по времени разностная схема. Все пространственные производные аппроксимируются центральными разностями со вторым порядком, а производные по времени с первым порядком. Расчет по явной схеме соответствует эволюции газодинамического течения по времени. Граничные условия являются периодическими по трем осям, что соответствует неограниченной области, заполненной идентичными вихрями. Для реализации периодических граничных условий использованы фиктивные ячейки.
Расчеты были проведены на многопроцессорном вычислительном комплексе К-100 Института прикладной математики им. М.В. Келдыша Российской академии наук. Использована технология распараллеливания вычислений, основанная на декомпозиции расчетной области плоскостями с применением стандарта передачи сообщений MPI. Программный комплекс обладает полной переносимостью между платформами, поддерживающими язык Си и стандарт MPI.
Показано, что КГД уравнения позволяют адекватно и единообразно моделировать как ламинарное, так и турбулентное развитие вихря без какой-либо подстройки параметров. Когда число Рейнольдса велико (Re=1600), результаты моделирования демонстрируют переход к турбулентному режиму с образованием мелкомасштабных структур. При этом энергетический спектр турбулентных пульсаций соответствует колмогоровскому закону убывания кинетической энергии с ростом частоты. При малых числах Рейнольдса (Re=280 и 100) вихрь затухает в ламинарном режиме.
Сравнение с эталонными данными показывает, что для моделирования турбулентных течений КГД–алгоритм требует существенно меньшее число расчетных точек по пространству для достижения такой же точности, как и методы прямого численного моделирования повышенных порядков аппроксимации. При использовании одинаковых пространственных сеток для Re=1600 точность КГД алгоритма превосходит точность LES метода с моделью подсеточной вязкости Смагоринского.
Эволюция течения, полученная посредством численного моделирования, визуально представлена изображением z-компоненты завихренности в трехмерной области. Приведенная визуализация позволяет наблюдать за развитием трехмерных структур в поле течения во времени и сравнивать эти структуры при различных режимах, включая ламинарно-турбулентный переход.
Ключевые слова: ламинарно-турбулентный переход, квазигазодинамические уравнения, конечно-разностные схемы, вихрь Тейлора–Грина
Эволюция вихревого течения, заданного в начальный момент в виде вихря Тейлора–Грина (Taylor–Green vortex, 1937), представляет собой наглядный пример распада первоначального одиночного стационарного вихря с последующим образованием каскада все более и более мелких вихревых образований, которые постепенно затухают за счет присущих течению диссипативных процессов. Данная задача хорошо изучена теоретически как для малых чисел Рейнольдса, при которых течение остается ламинарным, так и для больших чисел Рейнольдса, при которых начальное ламинарное течение трансформируется в турбулентный вихревой каскад. Поэтому задача об эволюции вихря Тейлора–Грина в ряде работ используется в качестве теста для проверки адекватности численных алгоритмов моделирования турбулентных течений, см., например, [1–5]. Детальная визуализация численных результатов, полученных для таких трехмерных нестационарных процессов, обеспечивает их понимание и адекватную трактовку.
Предлагаемая работа посвящена изучению возможностей квазигазодинамической (КГД) системы уравнений для расчета ламинарно-турбулентного перехода на примере указанного течения. Способы построения КГД системы уравнений и примеры ее использования изложены, например, в монографиях [6–8] и последующих публикациях. Некоторые результаты численного моделирования ламинарно-турбулентного перехода в рамках КГД уравнений представлены в работах [9–13]. Влияние КГД-диссипации на спектральные характеристики турбулентного течения, формирующегося при распаде трехмерного вихревого течения, приведены в [14]. Здесь же детально изложен алгоритм построения пространственного спектра кинетической энергии и прояснены вопросы точности численного моделирования этой задачи при сгущении пространственной сетки и варьировании параметра релаксации.
В данной работе на основе КГД-алгоритма решается задача о распаде вихря Тейлора–Грина в азоте при температуре, соответствующей нормальным условиям. Варьирование числа Рейнольдса обеспечивается рассмотрением течений при разных плотностях и давлениях. Результаты численного моделирования сопоставляются с известными результатами, полученными для ламинарных режимов распада (Re=100 и Re=280) и для турбулентного режима (Re=1600). Визуальный анализ численных результатов наглядно показывает процесс распада начального вихревого течения, сопровождающийся его усложнением с образованием разномасштабных вихревых структур и их нелинейным взаимодействием. Дальнейшая эволюция приводит к затуханию этих вихрей. При этом наглядно видны отличия вихревых структур для ламинарного и турбулентного режимов, а также сам момент формирования развитого турбулентного течения для Re=1600. Проведенные ниже расчеты выполнены на многопроцессорном вычислительном комплексе К-100 [15].
Известно, что численное исследование трехмерных нестационарных течений с использованием многопроцессорных вычислительных комплексов приводит к необходимости анализа больших объемов данных, что невозможно без использования программ визуализации [16]. В данном исследовании основной целью визуального представления является изображение вихревых структур в трехмерном поле течения, контроль их развития и трансформации по времени, а также сравнение структур при различных режимах течения. Последнее выполнено с помощью графической программы TecPlot. Аналогичный численный подход и близкие программные средства использовались ранее при расчетах колебаний в баке с жидкостью со свободной поверхностью, которые возникают при неравномерных движениях этой емкости [17].
В соответствии с [3] рассмотрим пространственную область кубической формы: ![]() в декартовых
координатах. В нашем случае
в декартовых
координатах. В нашем случае ![]() м. Область
заполнена газом (азотом). Состояние газа описывается следующими
параметрами:
м. Область
заполнена газом (азотом). Состояние газа описывается следующими
параметрами: ![]() –
плотностью,
–
плотностью, ![]() ,
, ![]() ,
, ![]() – макроскопической скоростью газа,
– макроскопической скоростью газа, ![]() – давлением. Совокупность компонент вектора
скорости будем также обозначать
– давлением. Совокупность компонент вектора
скорости будем также обозначать ![]() (аналогично для прочих векторов и
тензоров).
(аналогично для прочих векторов и
тензоров).
Используем традиционные начальные условия вихря Тейлора-Грина [1]:
![]() ,
, ![]() ,
, ![]() ,
,
![]() . (1)
. (1)
Начальное распределение
температуры является однородным по пространству: ![]() K.
Начальная плотность определяется уравнением состояния идеального газа:
K.
Начальная плотность определяется уравнением состояния идеального газа:
![]() .
(2)
.
(2)
Газовая постоянная азота ![]() Дж/(кг·К). Отметим, что постоянные параметры
Дж/(кг·К). Отметим, что постоянные параметры ![]() ,
, ![]() ,
, ![]() также
связаны уравнением состояния
также
связаны уравнением состояния ![]() . Введем
начальное число Маха как
. Введем
начальное число Маха как
![]() , (3)
, (3)
где скорость звука в азоте при начальных
условиях ![]() м/с, показатель адиабаты
м/с, показатель адиабаты ![]() [18]. В рассматриваемой задаче число Маха невелико, и
течение можно считать слабо сжимаемым [3].
[18]. В рассматриваемой задаче число Маха невелико, и
течение можно считать слабо сжимаемым [3].
Введем число Рейнольдса
![]() , (4)
, (4)
где ![]() кг/(м·с) – вязкость азота при температуре
кг/(м·с) – вязкость азота при температуре ![]() К [19]. В данной работе рассмотрены варианты Re=100, Re=280, Re=1600, которые сопоставляются с данными расчетов,
приведенными, соответственно, в [1], [4] и [3]. В [2] изложены результаты
решения аналогичной задачи затухания изотропной турбулентности для бесконечного
числа Рейнольдса, полученные с помощью пяти разностных алгоритмов высокого
порядка точности в приближении крупных вихрей (LES), а именно Jameson Multi-stage Scheme, Roe-TVD-MUSCL scheme, ENO.
К [19]. В данной работе рассмотрены варианты Re=100, Re=280, Re=1600, которые сопоставляются с данными расчетов,
приведенными, соответственно, в [1], [4] и [3]. В [2] изложены результаты
решения аналогичной задачи затухания изотропной турбулентности для бесконечного
числа Рейнольдса, полученные с помощью пяти разностных алгоритмов высокого
порядка точности в приближении крупных вихрей (LES), а именно Jameson Multi-stage Scheme, Roe-TVD-MUSCL scheme, ENO.
Порядок задания начальных
параметров следующий. Определяем характерную скорость ![]() через (3),
плотность
через (3),
плотность ![]() через (4), давление
через (4), давление ![]() , затем
задаем начальное распределение скорости и давления (1) и начальное
распределение плотности через (2).
, затем
задаем начальное распределение скорости и давления (1) и начальное
распределение плотности через (2).
Граничные условия являются периодическими, что физически означает неограниченную область, заполненную системой идентичных вихрей.
Математическая модель и метод численного решения
Течение газа будем описывать
макроскопической системой квазигазодинамических (КГД) уравнений [8]. Эта
система определяет эволюцию во времени плотности, скорости и давления газа,
зависящих от эйлеровых координат и от времени. Температура,
давление и плотность связаны
уравнением состояния идеального газа (2). Полная энергия единицы объема E и полная удельная энтальпия H вычисляются по формулам: ![]() ,
, ![]() ,
, ![]() – показатель адиабаты.
– показатель адиабаты.
Выпишем КГД систему в декартовых координатах [8, с. 94]:
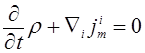 ,
(5)
,
(5)
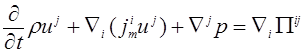 ,
(6)
,
(6)
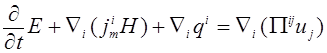 .
(7)
.
(7)
Вектор плотности
потока массы ![]() определяется следующим образом [8, с.
97]:
определяется следующим образом [8, с.
97]:
![]() ,
, 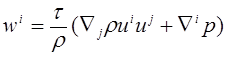 .
(8)
.
(8)
Выражения для тензора вязких напряжений ![]() и теплового потока
и теплового потока ![]() определяются так [8,
с. 83, 96].
определяются так [8,
с. 83, 96].
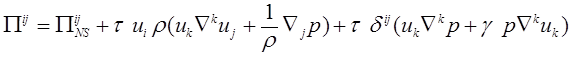 , (9)
, (9)
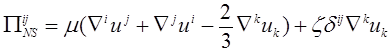 ,
(10)
,
(10)
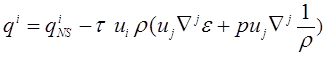 ,
, ![]() .
(11)
.
(11)
Здесь ![]() при
при ![]() и
и ![]() при
при ![]() – символ Кронекера,
– символ Кронекера, ![]() – внутренняя энергия на единицу массы
газа. Коэффициент теплопроводности выражается соотношением [8, с. 71]
– внутренняя энергия на единицу массы
газа. Коэффициент теплопроводности выражается соотношением [8, с. 71]
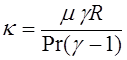 , (12)
, (12)
где Pr – число Прандтля. В рассматриваемой задаче Pr=0.71 [3].
Коэффициент динамической
вязкости ![]() в газе, входящий в выражения для тензора
вязких напряжений
в газе, входящий в выражения для тензора
вязких напряжений ![]() и теплового потока
и теплового потока ![]() (10)–(13), будем определять через температурную
зависимость [18]:
(10)–(13), будем определять через температурную
зависимость [18]:
![]() ,
(13)
,
(13)
где ![]() –
показатель, описывающий межмолекулярное взаимодействие в газе. В настоящей
работе
–
показатель, описывающий межмолекулярное взаимодействие в газе. В настоящей
работе ![]() [16]. Коэффициент второй (объемной) вязкости в рассматриваемой задаче в соответствии с
[3] предполагается равным нулю:
[16]. Коэффициент второй (объемной) вязкости в рассматриваемой задаче в соответствии с
[3] предполагается равным нулю: ![]() .
.
Определим значение
релаксационного параметра ![]() , входящего в (8)–(11):
, входящего в (8)–(11):
![]() , (14)
, (14)
где ![]() – локальная скорость звука, h – величина шага пространственной сетки. Слагаемые с коэффициентом
– локальная скорость звука, h – величина шага пространственной сетки. Слагаемые с коэффициентом ![]() представляют собой подсеточную диссипацию, которая сглаживает пульсации
газодинамических величин на масштабах порядка шага сетки. Коэффициент
представляют собой подсеточную диссипацию, которая сглаживает пульсации
газодинамических величин на масштабах порядка шага сетки. Коэффициент ![]() можно рассматривать как настроечный
параметр, определяющий уровень подсеточной диссипации.
можно рассматривать как настроечный
параметр, определяющий уровень подсеточной диссипации.
Для численного решения начально-краевой
задачи (5)–(14) с начальными условиями (1) методом конечных разностей введем в
области ![]() равномерную по пространству и по времени
сетку
равномерную по пространству и по времени
сетку ![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]() .
Отметим, что число шагов по времени
.
Отметим, что число шагов по времени ![]() заранее не определено.
Для всех газодинамических величин, зависящих от пространственных координат,
введем сеточные функции: для плотности
заранее не определено.
Для всех газодинамических величин, зависящих от пространственных координат,
введем сеточные функции: для плотности ![]() ,
аналогично для других величин. Размерности сеточных
функций такие же, как и размерности соответствующих физических величин.
,
аналогично для других величин. Размерности сеточных
функций такие же, как и размерности соответствующих физических величин.
Используем явную по времени разностную схему с аппроксимацией всех пространственных производных центральными разностями со вторым порядком, а производных по времени с первым порядком. Алгоритм построения разностной схемы такой же, как в работах [11–14]. Расчет по явной схеме соответствует эволюции газодинамического течения по времени. Для реализации периодических граничных условий используем фиктивные ячейки. Тогда, к примеру, сетку с N=130 будем обозначать как 1283 (т.е. без учета фиктивных ячеек).
Длину свободного пробега молекул газа для
начальных условий определим так: ![]() , где
, где ![]() [16]. Используемая математическая модель
требует выполнения условия
[16]. Используемая математическая модель
требует выполнения условия ![]() . Это условие справедливо
для всех расчетов настоящей работы.
. Это условие справедливо
для всех расчетов настоящей работы.
Шаг по времени определим из
условия Куранта [8, с. 140]: ![]() , где
, где ![]() – число Куранта. Отметим, что величина
– число Куранта. Отметим, что величина
![]() входит в выражение релаксационного
параметра
входит в выражение релаксационного
параметра ![]() (14).
(14).
Как и в работах [11–14], расчеты
проводятся в размерных переменных. Для сравнения с данными литературы авторы приводят результаты в безразмерном
виде. При этом в качестве определяющих параметров
используются ![]() ,
,
![]() и
и ![]() . Таким образом, безразмерное значение времени
. Таким образом, безразмерное значение времени ![]() , где
, где ![]() с, а
безразмерное значение удельной кинетической энергии
с, а
безразмерное значение удельной кинетической энергии![]() .
.
Эволюция вихревого течения, полученного в численном моделировании, показана с помощью визуального представления z-компоненты ротора скорости трехмерной области. Представление ротора скорости является общепринятым для исследования задачи течения Тейлора-Грина [1–3], обеспечивает наглядное и четкое отображение изучаемых структур в потоке и позволяет проводить сравнение данных расчетов с результатами других авторов.
Расчет по явной схеме проводится на многопроцессорном вычислительном комплексе К-100, при этом авторы используют технологию распараллеливания вычислений, основанную на декомпозиции расчетной области плоскостями x=const. Такая технология использует стандарт передачи сообщений MPI и с успехом применялась в работах [11–14]. Отметим, что программный комплекс обладает полной переносимостью между платформами, поддерживающими язык Си и стандарт MPI.
Результаты расчетов для Re=1600
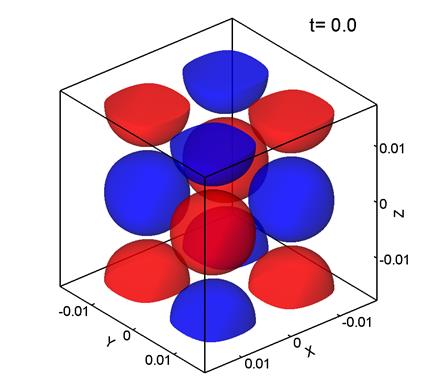
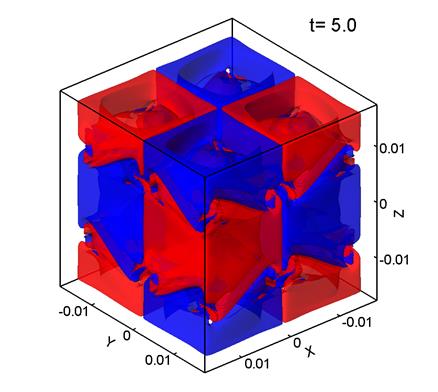
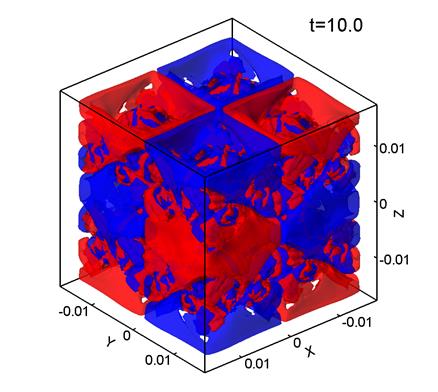
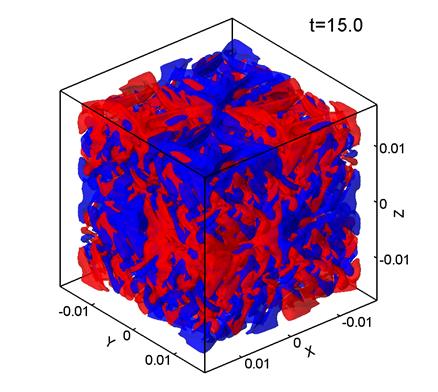
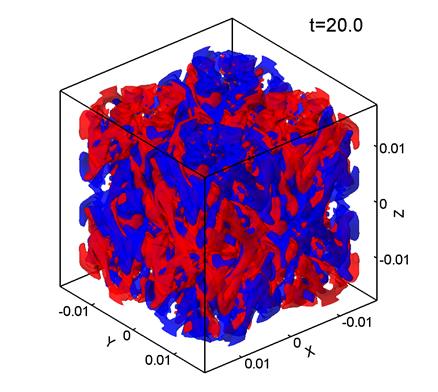
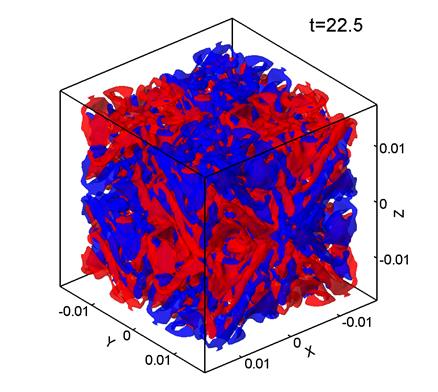
На рис. 1 представлены поверхности уровня ![]() –компоненты завихренности поля скорости, т. е. z–компоненты ротора скорости:
–компоненты завихренности поля скорости, т. е. z–компоненты ротора скорости:
![]()
Отметим, что величина ![]() вычисляется в безразмерном виде. Поверхности уровня
приведены для различных моментов безразмерного времени от
вычисляется в безразмерном виде. Поверхности уровня
приведены для различных моментов безразмерного времени от ![]() до
до ![]() .
Красный цвет соответствует Vz=0.7, синий Vz=-0.7. Параметры
расчета, представленного на рис. 1, следующие: размер сетки 1283, шаг сетки
.
Красный цвет соответствует Vz=0.7, синий Vz=-0.7. Параметры
расчета, представленного на рис. 1, следующие: размер сетки 1283, шаг сетки ![]() м,
м, ![]() .
.
(а)
(б)
(в) (г)
(д) (е)
Рис. 1.
Видно, что регулярное в начальный момент времени распределение скорости (1)
(рис. 1а) к моменту времени t=5 и 10 (рис. 1б, в) еще сохраняет «память» о
своем начальном распределении, но к моменту времени t=15 (рис. 1г) течение становится хаотическим, в котором почти
не наблюдается связь с первоначальным распределением скорости. Такое хаотическое распределение скоростей характерно для турбулентного течения. Наблюдаемые здесь особенности эволюции
течения хорошо согласуются с анализом эволюции вихря Тейлора–Грина, приведенным
в [1] для Re>500 и в [3, 5] для Re=1600. Заметим, что промежуток
безразмерного времени ![]() соответствует
характерному периоду вращения первоначального вихря (1).
соответствует
характерному периоду вращения первоначального вихря (1).
(а) (б)
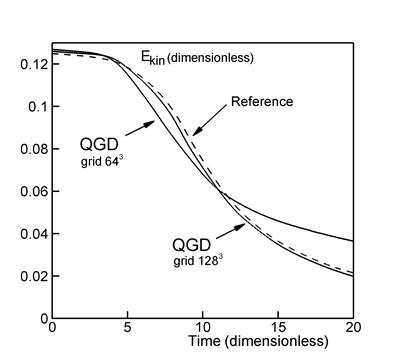
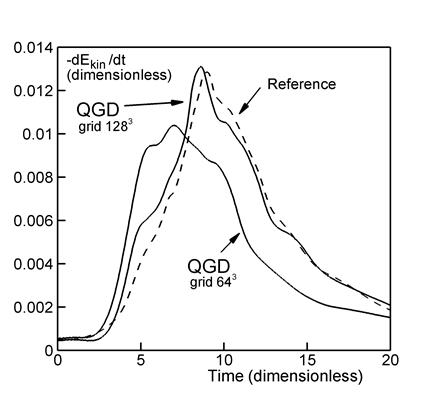
Рис. 2.
На рис. 2а представлены зависимости средней по рассматриваемому объему ![]() удельной кинетической энергии
газа
удельной кинетической энергии
газа ![]() от времени:
от времени:
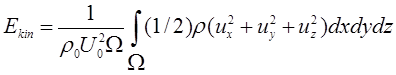
Кинетическая энергия и время представлены
в безразмерном виде. Сплошные кривые соответствуют расчетам, проведенным
авторами. При этом размерности разностных сеток 643 с шагом ![]() м
и 1283 с шагом
м
и 1283 с шагом
![]() м,
м, ![]() . Пунктирная кривая представляет эталонный результат из [3] с
использованием спектрального метода (dealiased pseudo-spectral code), а также различных вариантов разрывного
метода Галеркина.
. Пунктирная кривая представляет эталонный результат из [3] с
использованием спектрального метода (dealiased pseudo-spectral code), а также различных вариантов разрывного
метода Галеркина.
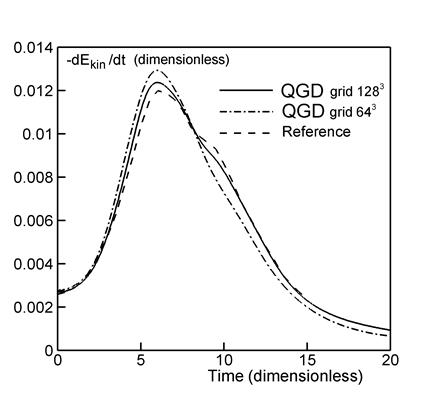
Рис. 2б демонстрирует зависимость скорости
диссипации кинетической энергии от времени, т. е. величины ![]() . Как и на рис. 2а, сплошные кривые получены авторами, а
пунктирная взята из [3]. Максимальное значение скорости диссипации кинетической
энергии определяет область перехода от ламинарного течения к турбулентному и
формирование спектра Колмогорова-Обухова (рис. 6). Из рис. 2 видно, что результаты
расчета на подробной пространственной сетке существенно ближе к эталонным
данным, чем результаты на грубой сетке.
. Как и на рис. 2а, сплошные кривые получены авторами, а
пунктирная взята из [3]. Максимальное значение скорости диссипации кинетической
энергии определяет область перехода от ламинарного течения к турбулентному и
формирование спектра Колмогорова-Обухова (рис. 6). Из рис. 2 видно, что результаты
расчета на подробной пространственной сетке существенно ближе к эталонным
данным, чем результаты на грубой сетке.
Результаты расчетов [14] для ![]() показывают, что увеличение коэффициента
показывают, что увеличение коэффициента ![]() от 0.1 до 0.9 приводит к сглаживанию графиков
от 0.1 до 0.9 приводит к сглаживанию графиков ![]() и смещению максимума распределения
и смещению максимума распределения ![]() в сторону меньших времен. Подобный эффект наблюдается и при
уменьшении числа точек пространственной сетки.
в сторону меньших времен. Подобный эффект наблюдается и при
уменьшении числа точек пространственной сетки.
Результаты моделирования течения Тейлора–Грина методом прямого численного моделирования (DNS) приведены в целом ряде работ, среди которых отметим [1,3,4] и [5]. В частности в [5] расчеты проведены на сетке с числом узлов 2563 с помощью методов высокого порядка точности по времени и пространству. Выбранное в этих расчетах число узлов оценивается как минимально допустимое для DNS подхода с точки зрения разрешения вихревых структур, соответствующих данному числу Рейнольдса. Полученные на основе КГД алгоритма графики (рис. 2) на сетке 1283 очень хорошо соответствуют данным [1] и [5], полученным на сетке 2563.
Использование приближения крупных вихрей (LES) позволяет сократить число расчетных точек в численном алгоритме. Результаты решения данной задачи LES-методом с использованием модели Смагоринского с числом точек 643 приведены в [5]. При этом максимальное значение скорости диссипации кинетической энергии оказывается заниженным и достигает значения порядка 0.006, в то время как эталонным значением является величина порядка 0.012. Таким образом, для данного течения LES модель Смагоринского оказывается слишком диссипативной. В указанном расчете используется динамический вариант модели Смагоринского, в котором величина подсеточной диссипации автоматически подстраивается в соответствии с разрешаемыми масштабами вихрей. Расчет по КГД алгоритму на сетке 643 дает величину максимума скорости диссипации ~ 0.01 (рис. 2б).
Результаты расчетов для Re=280
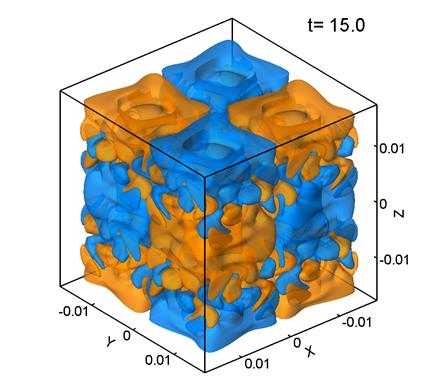
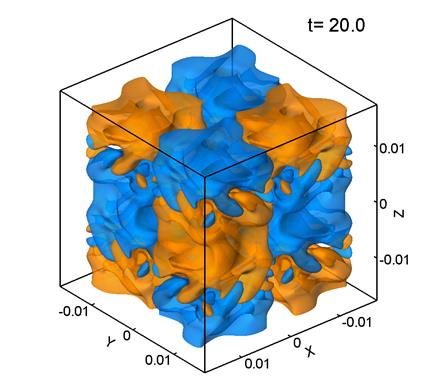
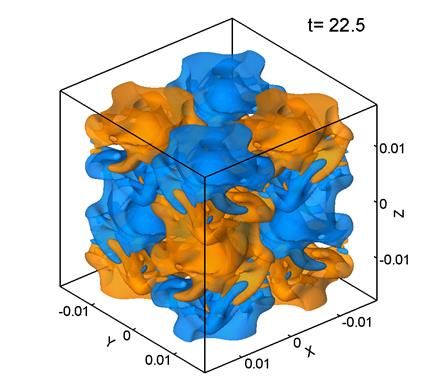
На рис. 3 представлены поверхности уровня ![]() –компоненты завихренности поля скорости. Желтый цвет
соответствует Vz=0.2, голубой Vz=-0.2. Параметры расчета,
представленного на рис. 3, следующие: размер
сетки 1283, шаг сетки
–компоненты завихренности поля скорости. Желтый цвет
соответствует Vz=0.2, голубой Vz=-0.2. Параметры расчета,
представленного на рис. 3, следующие: размер
сетки 1283, шаг сетки ![]() м,
м, ![]() .
.
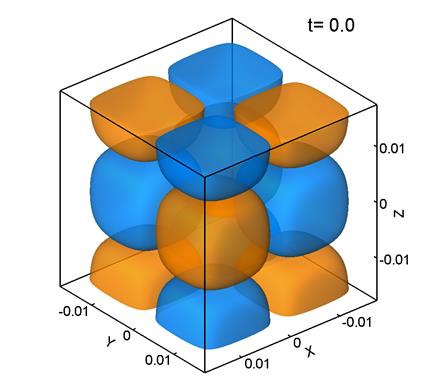
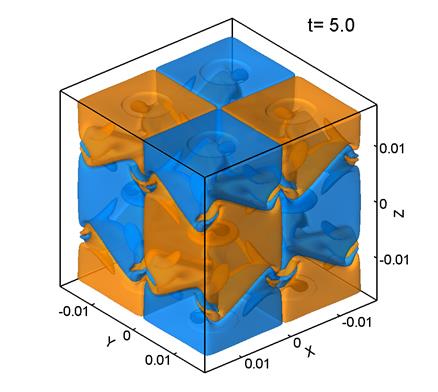
(а) (б)
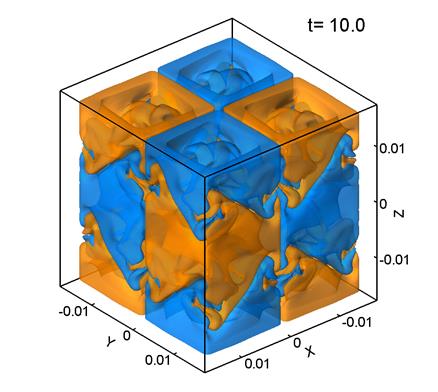
(в) (г)
(д) (е)
Рис. 3.
Из рис. 3 видно, что поле скорости в при Re=280 сохраняет общий характер начального регулярного распределения, хотя образуются и относительно мелкие структуры. В этом случает течение приобретает частично турбулентный характер.
(а) (б)
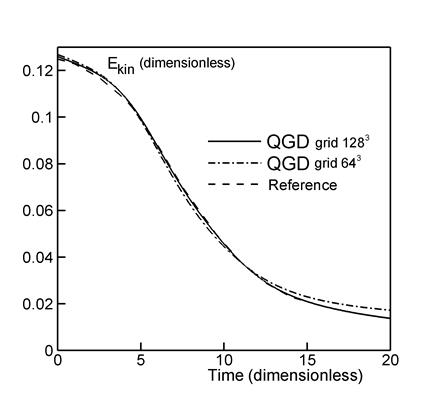
Рис. 4.
На рис. 4 представлены профили зависимости от времени удельной
кинетической энергии ![]() (а)
и скорости ее диссипации
(а)
и скорости ее диссипации ![]() (б)
для Re=280. Сплошные и штрих-пунктирные профили получены авторами, а
пунктирные – эталонные результаты из [4], полученные посредством спектрального
метода (Fergus
pseudo-spectral code) и
разрывного метода Галеркина с 963 степенями свободы. Размерности разностных сеток 643
(с шагом
(б)
для Re=280. Сплошные и штрих-пунктирные профили получены авторами, а
пунктирные – эталонные результаты из [4], полученные посредством спектрального
метода (Fergus
pseudo-spectral code) и
разрывного метода Галеркина с 963 степенями свободы. Размерности разностных сеток 643
(с шагом ![]() м,
штрих-пунктирная кривая) и 1283
(с шагом
м,
штрих-пунктирная кривая) и 1283
(с шагом ![]() м,
сплошная кривая),
м,
сплошная кривая),
![]() . Как и для случая Re=1600, результаты расчета на подробной пространственной сетке
ближе к эталонным данным, чем результаты на грубой сетке, хотя для Re=280 различие невелико.
. Как и для случая Re=1600, результаты расчета на подробной пространственной сетке
ближе к эталонным данным, чем результаты на грубой сетке, хотя для Re=280 различие невелико.
Результаты расчетов для Re=100
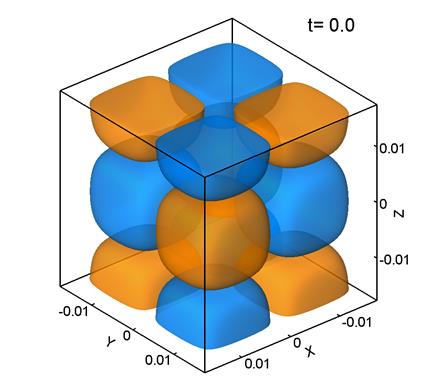
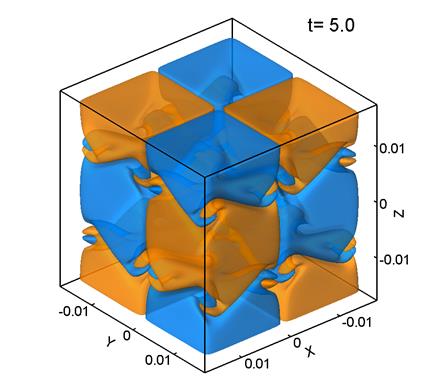
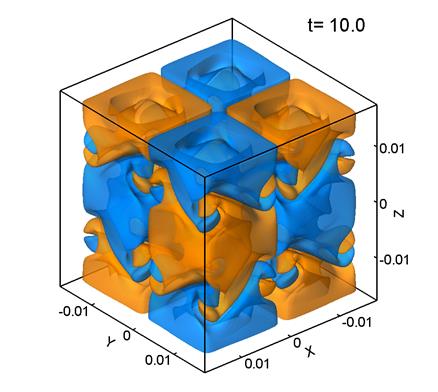
На рис.
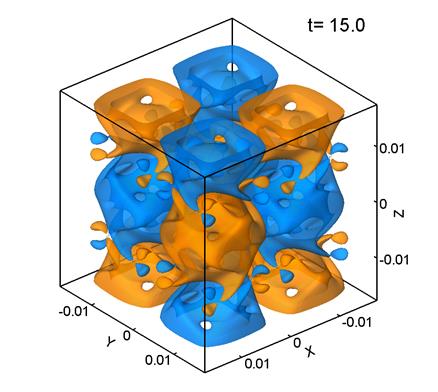
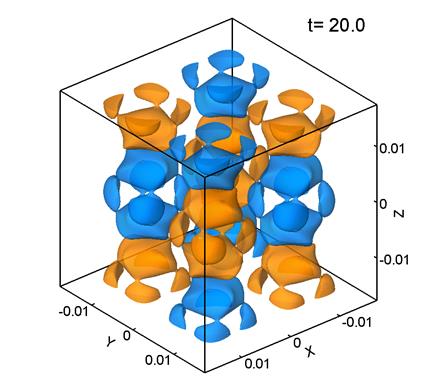
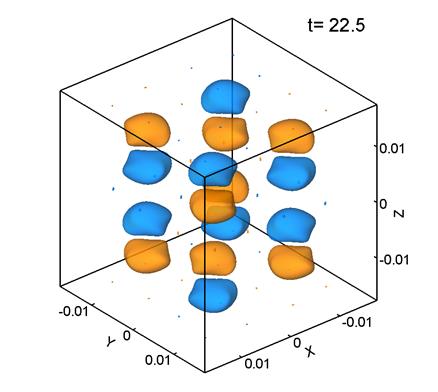
5 представлены поверхности уровня ![]() –компоненты завихренности поля скорости для расчета при Re=100. Параметры расчета следующие:: размер сетки 1283, шаг сетки
–компоненты завихренности поля скорости для расчета при Re=100. Параметры расчета следующие:: размер сетки 1283, шаг сетки ![]() м,
м, ![]() .
.
(а) (б)
(в) (г)
(д) (е)
Рис. 5.
(а) (б)
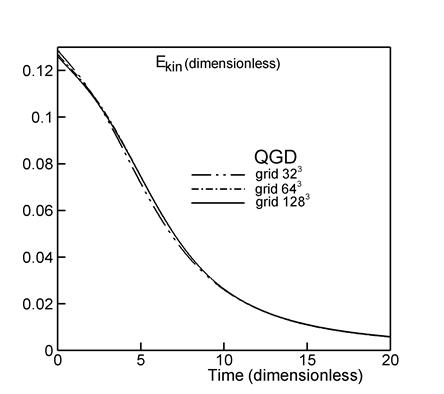
Рис. 6.
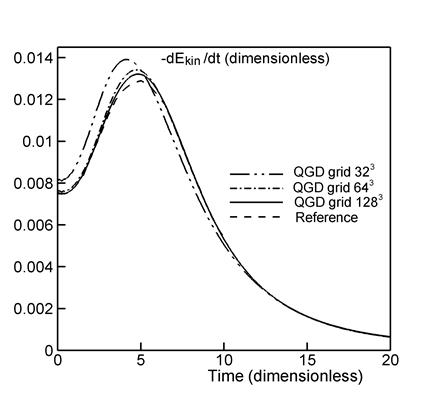
Профили зависимости кинетической энергии и
ее скорости диссипации ![]() от времени приведены
на рис. 6. При этом использованы три пространственные сетки: 323
(с шагом
от времени приведены
на рис. 6. При этом использованы три пространственные сетки: 323
(с шагом ![]() м),
643 (с шагом
м),
643 (с шагом
![]() м) и 1283 (с шагом
м) и 1283 (с шагом
![]() м),
м), ![]() . Как и для случая
Re=280, результаты расчета на подробной
пространственной сетке ближе к эталонным данным, чем результаты на грубых сетках.
Эталонный профиль (пунктирная кривая) приведен в [1]. Отметим, что даже очень
грубая сетка
. Как и для случая
Re=280, результаты расчета на подробной
пространственной сетке ближе к эталонным данным, чем результаты на грубых сетках.
Эталонный профиль (пунктирная кривая) приведен в [1]. Отметим, что даже очень
грубая сетка ![]() позволяет адекватно моделировать ламинарное течение Тейлора-Грина
при
позволяет адекватно моделировать ламинарное течение Тейлора-Грина
при ![]() .
.
Максимальное значение ![]() для Re=100 соответствует
времени t=4.5. К этому моменту времени течение еще
сохраняет «память» о начальном распределении
скорости и имеет анизотропный характер (рис. 5б). В дальнейшем картина течения также остается анизотропной. Таким образом, при распаде
одиночного вихря для Re=100 на
протяжении всего процесса эволюции течение носит ламинарный характер, при
котором не образуется хаотичное поле мелких вихрей, характерное для варианта Re=1600 (рис. 1г–е). Описанный характер
затухания вихря Тейлора–Грина соответствует данным, изложенным в [1] для
ламинарных течений, соответствующих Re<500.
для Re=100 соответствует
времени t=4.5. К этому моменту времени течение еще
сохраняет «память» о начальном распределении
скорости и имеет анизотропный характер (рис. 5б). В дальнейшем картина течения также остается анизотропной. Таким образом, при распаде
одиночного вихря для Re=100 на
протяжении всего процесса эволюции течение носит ламинарный характер, при
котором не образуется хаотичное поле мелких вихрей, характерное для варианта Re=1600 (рис. 1г–е). Описанный характер
затухания вихря Тейлора–Грина соответствует данным, изложенным в [1] для
ламинарных течений, соответствующих Re<500.
Сравнение результатов для разных Re и энергетический спектр
Рис. 7 показывает профили скорости
диссипации кинетической энергии ![]() в
зависимости от времени для трех значений числа Рейнольдса: 100, 280 и 1600. Также
на рис 7 приведены эталонные данные из [1], [4] и [3]. Положение максимума
скорости диссипации сдвигается вправо при увеличении числа Рейнольдса.
Результаты расчета для Re=100 и 1600
количественно совпадают с аналогичными профилями, приведенными на рис. 7 работы
[1]. В указанной работе расчет этих вариантов выполнен на сетке 2563 с использованием DNS
подхода.
в
зависимости от времени для трех значений числа Рейнольдса: 100, 280 и 1600. Также
на рис 7 приведены эталонные данные из [1], [4] и [3]. Положение максимума
скорости диссипации сдвигается вправо при увеличении числа Рейнольдса.
Результаты расчета для Re=100 и 1600
количественно совпадают с аналогичными профилями, приведенными на рис. 7 работы
[1]. В указанной работе расчет этих вариантов выполнен на сетке 2563 с использованием DNS
подхода.
Отметим, что используемая авторами КГД-модель не требует какой-либо модификации или подстройки параметров расчета при переходе от ламинарного случая к турбулентному. Расчет всех указанных вариантов проводится единообразно.
На рис. 8 изображен энергетический спектр
турбулентных пульсаций для Re=1600.
Методика вычисления спектра такая же, как в [14]. Также на рис. 6 изображена
прямая с колмогоровским угловым коэффициентом ![]() . Спектр вычислялся в момент времени t=8.5, когда профиль
. Спектр вычислялся в момент времени t=8.5, когда профиль ![]() достигает
максимума (рис. 2б). Профиль энергетического спектра аналогичен профилю для Re=1600 на рис. 4 работы [4], также профилю
для Re=1500 на рис. 8.3 работы [5]. При
вычислении спектра на рис. 6 использовались пространственные сетки 643 и 1283. Видно, что результаты на
различных сетках почти одинаковы, что говорит о
физически адекватном поведении турбулентного сглаживания. При сгущении пространственной сетки кривая спектральной плотности становится более гладкой и располагается
ближе к прямой с коэффициентом
достигает
максимума (рис. 2б). Профиль энергетического спектра аналогичен профилю для Re=1600 на рис. 4 работы [4], также профилю
для Re=1500 на рис. 8.3 работы [5]. При
вычислении спектра на рис. 6 использовались пространственные сетки 643 и 1283. Видно, что результаты на
различных сетках почти одинаковы, что говорит о
физически адекватном поведении турбулентного сглаживания. При сгущении пространственной сетки кривая спектральной плотности становится более гладкой и располагается
ближе к прямой с коэффициентом ![]() .
.
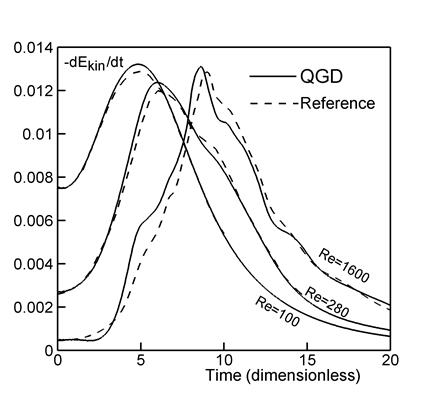
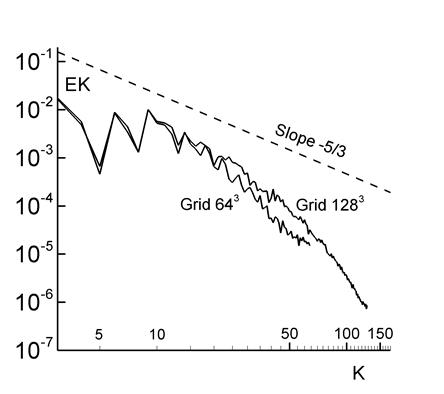
Рис. 7. Рис. 8.
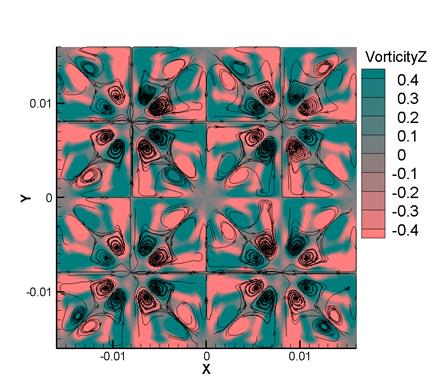
На рис. 9 изображены линии тока и контуры завихренности Vz в сечении z=0.008 м для Re=1600 (а) и Re=100 (б) при t=20. При Re=1600 наблюдается развитая вихревая структура течения. При Re=100 мелкие вихри отсутствуют. Кроме того, величина завихренности Vz для Re=1600 значительно выше, чем для Re=100. Таким образом, хорошо видна разница между турбулентным и ламинарным случаями. Рис. 9 демонстрирует такую же симметрию вычисленного решения, как и симметрия начальных условий (1), что говорит о корректности и устойчивости численного алгоритма.
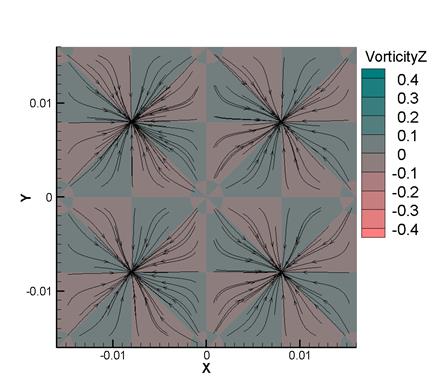
(а) (б)
Рис. 9.
Результаты прямого численного моделирования распада вихря Тейлора–Грина, проведенные авторами на основе КГД-алгоритма, показывают очень хорошее согласие с данными из различных работ, посвященных исследованию этого вихревого течения. При этом согласие имеет как качественный, так и количественный характер для всех рассмотренных чисел Рейнольдса, включая ламинарный и турбулентный режимы распада. Отметим, что в цитированных работах моделирование вихря Тейлора-Грина проводится с помощью разнообразных по своей структуре методов численного решения высоких порядков точности (конечно-разностных, спектральных, метода Галеркина) на более подробных сетках в рамках DNS подхода. При использовании одинаковых пространственных сеток для Re=1600 точность КГД алгоритма превосходит точность LES метода с моделью подсеточной вязкости Смагоринского.
КГД-алгоритм позволяет проводить прямое моделирование распада вихревого течения как в ламинарном, так и в турбулентном случае единообразно, без каких-либо изменений параметров численного алгоритма. Приведенные расчеты показывают перспективность применения КГД-алгоритма для численного моделирования ламинарно-турбулентного перехода и турбулентных газодинамических течений.
Подробная визуализация результатов численных расчетов, представленная в данной работе, позволяет наглядным образом отслеживать трансформации изучаемых гидродинамических режимов течения, включая ламинарно-турбулентный переход.
Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект РФФИ 13-01-00703-а.
[1] M. Brachet, D. Meiron, S. Orszag, B. Nickel, R. Morf, U. Frisch. Small-scale structure of the Taylor-Green vortex. J. Fluid Mech., 1983, vol. 130, pp. 411–452.
[2] E. Garnier, M. Mossi, P. Sagaut, P. Comte, M. Deville. On the use of shock-capturing schemes for large-eddy simulation. J. of Computational Physics, 1999, vol. 153, pp. 273–311.
[3] http://www.as.dlr.de (German Aerospace Center)
[4] JB Chapelier, M. De La Llave Plata, F. Renac, E. Martin. Final abstract for ONERA Taylor-Green DG participation. 1st International Workshop On High-Order CFD Methods. January 7-8, 2012 at the 50th AIAA Aerospace Sciences Meeting, Nashville, Tennessee
D. Fauconnier. Development of a Dynamic Finite Difference Method for Large-Eddy Simulation. PhD thesis. Ghent University. ISBN 978-90-8578-235-3. NUR 978,928. Wettelijk depot: D/2008/10.500/55
[6] Б.Н. Четверушкин. Кинетические схемы и квазигазодинамическая система уравнений. Москва: Макс Пресс. 2004.
[7] Ю.В. Шеретов. Динамика сплошных сред при пространственно-временном осреднении. Москва–Ижевск, НИЦ «Регулярная и хаотическая динамика». 2009.
[8] Т.Г. Елизарова. Квазигазодинамические уравнения и методы расчета вязких течений. Москва: Научный мир. 2007. – 352 с.
[9] Т.Г. Елизарова, П.Н. Никольский. Численное моделирование ламинарно-турбулентного перехода в течении за обратным уступом. Вестник Московского университета, серия 3. Физика. Астрономия. 2007. № 4, c. 14–17.
[10] T.G. Elizarova, V.V. Seregin. Filtered simulation method for turbulent heat and mass transfer in gas dynamic flows. Proceedings of the 6th International Symposium on turbulence, heat and mass transfer, Rome, Italy, 14–18, September 2009. Edited by K. Hanjalie, Y. Nagano, S. Jakirilic. Begell House Inc., p. 383–386.
[11] I. A. Shirokov, T.G. Elizarova, I. Fedioun, J.-C. Lengrand. Numerical simulation of the laminar-turbulent boundary-layer transition on a hypersonic forebody using the quasi-gas dynamic equations. 4th European Conference for Aerospace Sciences (EUCASS) 4–10 July 2011, St-Petersburg.
[12] И.А. Широков, Т.Г. Елизарова. Численное моделирование колебательного течения в окрестности гиперзвукового летательного аппарата. Математическое моделирование, 2012, т. 24, № 1, с. 21–32.
[13] Широков И.А., Елизарова Т.Г. Прямое численное моделирование ламинарно-турбулентного перехода в слое вязкого сжимаемого газа. Прикладная математика и информатика. № 42, М.: Изд-во факультета ВМК МГУ, 2013, 30–53.
[14] Т.Г. Елизарова, И.А. Широков. Тестирование КГД–алгоритма на примере задачи о распаде однородной изотропной турбулентности. Препринты ИПМ им. М.В. Келдыша. 2013. № 35. 19 с. URL: http://library.keldysh.ru/preprint.asp?id=2013-35
[15] http://www.kiam.ru
[16] Бондарев А.Е., Галактионов В.А., Чечеткин В.М. Научная визуализация в задачах вычислительной механики жидкости и газа. Журнал «Научная визуализация», 2010, т. 2, № 4, стр. 1-26.
[17] Елизарова Т.Г., Сабурин Д.С. Математическое моделирование и визуализация течений жидкости в грузовой емкости газовоза при его соударении с ледовым препятствием. Журнал «Научная визуализация», 2013, т. 5, № 4, стр. 118-139.
[18] Bird G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Clarendon press, Oxford, 1998.
[19] Таблица физических величин. Справочник под ред. акад. И.К. Кикоина. М.: Атомиздат, 1976, 1008 с.
NUMERICAL MODELING OF THE TAYLOR–GREEN
VORTEX
DECAY IN LAMINAR AND TURBULENT REGIMES
I. Shirokov1, T. Elizarova2
1 Moscow State University, Leninskie Gory, Moscow, Russian Federation
2 Keldysh Institute of Applied Mathematics RAS, Moscow, Russian Federation
ivanshirokov@inbox.ru, telizar@mail.ru
Abstract
We report the results of numerical modeling and visualization for the classical Taylor–Green vortex decay problem basing on smoothed gas dynamic equation system – namely quasi- gas dynamic (QGD) equations for viscous compressible gas flow. QGD system can be obtained by temporal averaging of Navier-Stokes system and differs form it by strongly non-linear terms with the small coefficient that has the dimension of time. The QGD system determines the temporal evolution of the gas density, velocity, and pressure as functions of Eulerian coordinates and time. The temperature, pressure, and density are related by the ideal gas state equation. The Taylor–Green vortex decay is examined for nitrogen at normal temperature with Mach number equal to 0.1. Variations in the Reynolds number are produced by varying the flow density and pressure.
The QGD system is approximated by an explicit time-differencing scheme. All spatial derivatives are approximated by central differences to second-order accuracy, and the time derivatives are approximated with the first-order accuracy. The computation based on the explicit scheme corresponds to the temporal evolution of the gas dynamic flow. The boundary conditions are periodic in three directions, which means that a system of identical Taylor–Green vortices is contained in an unbounded domain. The periodic boundary conditions are implemented by introducing shadow cells adjacent to the physical boundary.
The computations were carried out on the multiprocessor computer system K-100 at the Keldysh Institute of Applied Mathematics of the Russian Academy of Science. The numerical algorithm was parallelized as based on a decomposition of the computational domain by planes x=const with the use of the MPI standard. Our code is portable across different platforms supporting the C language and the MPI standard.
It is shown that QGD equations provide a uniform adequate numerical simulation of both laminar and turbulent evolution of the vortex in a unified manner without varying the parameters of the algorithm. For high Reynolds numbers (Re=1600) numerical results show the transition to turbulence, with the creation of small scale structures accomplished by special evolution of the kinetic energy decay with Kolmogorov scaling of kinetic energy spectrum. For small Reynolds numbers (Re=280 and 100) vortex decay remains laminar. Comparison with reference data show, that for turbulent flow QGD method requires less grid points to achieve the same accuracy compared with different variants of high-order DNS methods. On identical spatial grids at Re=1600, the QGD algorithm was found to be more accurate than the LES method with the Smagorinsky subgrid-scale eddy viscosity model.
The evolution of the vortex flow obtained in the numerical simulation is visualized by depicting the z-component of the vorticity in a 3D domain. Data visualization demonstrates a development of the 3D flow structures and gives opportunity to compare them for laminar and turbulent flow regimes, including a laminar-turbulent transition.
Key words: laminar-turbulent transition, quasi-gasdynamic equations, finite-different schemes, Taylor-Green flow
References
[1] M. Brachet, D. Meiron, S. Orszag, B. Nickel, R. Morf, U. Frisch. Small-scale structure of the Taylor-Green vortex. J. Fluid Mech., vol. 130, 1983, pp. 411–452.
[2] E. Garnier, M. Mossi, P. Sagaut, P. Comte, M. Deville. On the use of shock-capturing schemes for large-eddy simulation. J. of Computational Physics, vol. 153, 1999, pp. 273–311.
[3] Institute of Aerodynamics and Flow Technology. Available at: http://www.as.dlr.de (German Aerospace Center)
[4] JB Chapelier, M. De La Llave Plata, F. Renac, E. Martin. Final abstract for ONERA Taylor-Green DG participation. 1st International Workshop On High-Order CFD Methods. January 7-8, 2012 at the 50th AIAA Aerospace Sciences Meeting, Nashville, Tennessee.
[5] D. Fauconnier. Development of a Dynamic Finite Difference Method for Large-Eddy Simulation. PhD thesis. Ghent University. ISBN 978-90-8578-235-3. NUR 978, 928. Wettelijk depot: D/2008/10.500/55.
[6] B.N. Chetverushkin. Kinetic Schemes and Quasi-Gas Dynamic System of Equations. CIMNE, Barselona, 2008.
[7] Yu.V. Sheretov. Dinamika sploshnykh sred pri prostranstvenno-vremennom osrednenii [Continuum Dynamics under Spatiotemporal Averaging]. SPC Regular and 560 Chaotic Dynamics, Moscow-Izhevsk, 2009, in Russian.
[8] T.G. Elizarova, Quasi-Gas Dynamic Equations, Springer, Dordrecht, 2009. IBSN 978-3-642-0029-5.
[9] T. G. Elizarova and P. N. Nikol'skii. Chislennoe modelirovanie laminarno-turbulentnogo perekhoda v techenii za obratnym ustupom [Numerical simulation of the laminar–turbulent transition in the flow over a backward-facing step]. Vestnik Moskovskogo Universiteta, Ser. 3, Fiz. Astron., no 4, 2007, pp. 14–17.
[10] T.G. Elizarova, V.V. Seregin. Filtered simulation method for turbulent heat and mass transfer in gas dynamic flows. Proceedings of the 6th International Symposium on turbulence, heat and mass transfer, Rome, Italy, 14–18, September 2009. Edited by K. Hanjalie, Y. Nagano, S. Jakirilic. Begell House Inc., p. 383–386.
[11] I. A. Shirokov, T.G. Elizarova, I. Fedioun, J.-C. Lengrand. Numerical simulation of the laminar-turbulent boundary-layer transition on a hypersonic forebody using the quasi-gas dynamic equations. 4th European Conference for Aerospace Sciences (EUCASS) 4–10 July 2011, St-Petersburg.
[12] T. G. Elizarova, I. A. Shirokov. Chislennoe modelirovanie kolebatelnogo techeniya v okrestnosti giperzvukovogo letatelnogo apparata [Numerical simulation of a non-stationary flow in the vicinity 590 of a hypersonic vehicle]. Matematicheskoe modelirovanie [Math. Model Comput. Simul] vol. 4, no 4, 2012, pp. 410–418.
[13] I. A. Shirokov, T. G. Elizarova. Pryamoe chislennoe modelirovanie laminarno-turbulentnogo perekhoda v sloe vyazkogo szhimaemogo gaza [Direct simulation of laminar-turbulent transition in a viscous compressible gas layer]. Prikladnaya matematika i informatika [Comput. Math. Model], vol. 25, no 1, 2014, pp. 27–48.
[14] T.G. Elizarova, I.A. Shirokov. Testirovanie KGD–algoritma na primere zadachi o raspade odnorodnoy izotropnoy turbulentnosti [Testing of the QGD algorithm by a homogeneous isotropic gas-dynamic turbulence decay]. Preprint, Keldysh Institute of 615 Applied Mathematics of Russian Academy of Science, no 35, 2013, p. 19. Available at http://library.keldysh.ru/preprint.asp?id=2013-35.
[15] К-100. Available at: http://www.kiam.ru
[16] A.E. Bondarev, V.A. Galaktionov, V.M. Chechetkin. Scientific visualization in computational fluid dynamics. Scientific Visualization, vol. 2, no 4, 2010, pp. 1–26. Available at: http://sv-journal.com/2010-4/01.php
[17] T. Elizarova, D. Saburin. Mathematical modeling and visualization of the sloshing in the ice-breaker’s tank after impact interaction with ice barrier. Scientific Visualization, vol. 5, no 4, 2013, pp. 118–135. Available at: http://sv-journal.com/2013-4/07.php
[18] Bird G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Clarendon press, Oxford, 1998.
[19] Table of Physical Constants: Handbook, Ed. by I. K. Kikoin (Atomizdat, Moscow, 1976) [in Russian].