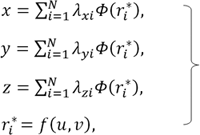ПРИМЕНЕНИЕ РАДИАЛЬНЫХ БАЗИСНЫХ ФУНКЦИЙ В НАУЧНОЙ ВИЗУАЛИЗАЦИИ

ПРИМЕНЕНИЕ РАДИАЛЬНЫХ БАЗИСНЫХ
ФУНКЦИЙ В НАУЧНОЙ ВИЗУАЛИЗАЦИИ

Ю. Косников

Пензенский государственный университетб Пенза, Россия

kosnikov@gmail.com

Оглавление

Введение

1. Особенности полигонального и сплайнового представления скалярного поля

2. Радиальные базисные функции в задачах визуализации

3. Визуализация скалярного поля с применением регуляризации расстановки опорных точек

4. Формирование полигональной сетки с применением табличных вычислений

Заключение

Список литературы

Аннотация

Предлагается последовательность действий по визуализации скалярного поля. Во многих приложениях экспериментальные данные представляются скалярным полем. Наглядной формой его визуализации является поверхность. Она должна быть гладкой, проходить через опорные точки скалярного поля и изменять ракурс обзора. Полигональная и сплайновая визуализация на нерегулярно расставленных опорных точках имеют недостатки. В статье описано представление скалярного поля на основе радиальных базисных функций. Поверхность строится из сегментов и описывается в параметрической системе координат. Предлагается от исходных опорных точек перейти к новым – регулярно расставленным в пространстве. На них строится полигональная сетка требуемой детальности. Для снижения затрат времени на визуализацию применяются табличные вычисления.

Предлагаемая статья является постановочной. Автор надеется на отзывы и критику коллег.

Ключевые слова: скалярное поле, опорная точка, радиальная базисная функция, регуляризация, составная поверхность, табличные вычисления.

Введение

Результаты вычислительного эксперимента, замеров физических величин, решения топологических задач, статистической обработки научных данных во многих случаях представляются скалярным полем. Его значения могут быть привязаны к некоторой пространственной поверхности. В качестве примера можно назвать распределение концентрации загрязнений в воздушном пространстве географического региона. В этом случае визуализация выполняется с привязкой к плоской карте региона. Для визуального анализа пространство загрязнений можно представить в виде набора изоповерхностей, проходящих через точки с одинаковой концентрацией. Та же задача может решаться путем использования цветового кодирования концентрации и привязки распределения цвета к пространственному рельефу региона. Тогда сам этот рельеф необходимо создать по топографическим замерам.

В каких-то случаях опорные точки могут быть расставлены в пространстве регулярно и находиться в узлах некоторой координатной сетки. Примером могут служить топографические замеры рельефа местности, привязанные к сетке геодезических координат. В других случаях это невозможно в принципе. Например, при решении задачи восстановления формы объекта в археологии этот объект может иметь утерянные фрагменты поверхности, которые не могут быть представлены опорными точками.

В любом из описанных примеров возникает необходимость изменения ракурса обзора поверхности в процессе визуального анализа, что требует пересчета изображения в режиме реального времени. Кроме того, для повышения наглядности пространственных конструкций при их отображении должно быть смоделировано освещение, для чего нужно вычислить нормали к поверхностям. Таким образом, задачи, которые приходится решать при визуализации научных данных, во многом сходны с задачами отображения трехмерных сцен. В общей постановке можно говорить о визуализации динамических пространственных объектов, форма которых задается набором характерных (опорных) точек. Критериями отображения таких объектов являются точное прохождение поверхностей через опорные точки, сохранение топологической тенденции пространственного рельефа, отсутствие на поверхностях разрывов, как минимум, первого и второго рода.

Современные средства отображения динамических объектов, например, графические библиотеки DirectX и OpenGL, требуют описать эти объекты в виде комбинации фрагментов простой формы – геометрических примитивов. Команды графических библиотек строят геометрические примитивы, используя их описания в форме набора характерных точек – вершин (vertex) [1]. Для наглядного представления скалярного поля в виде поверхности исходного набора опорных точек, как правило, недостаточно. Необходимо найти промежуточные точки, принадлежащие этой поверхности, и использовать их в качестве основы для описания геометрических примитивов. Такая задача решается с помощью интерполяции.

1. Особенности полигонального и сплайнового представления скалярного поля

Существует множество приемов визуализации скалярных полей, основанных на интерполяционных методах. В графических системах находят применение такие методы, как полиномиальная интерполяция и интерполяция на основе смешивающих функций. Полиномиальная интерполяция в рассматриваемом случае не всегда дает хорошие результаты. Так, полигональная сетка (ее описание – полиномы первой степени) дает ненаглядный – «граненый» – вид поверхности, так как ее представление имеет разрывы второго рода. Это особенно заметно на областях с редкой расстановкой опорных точек, а также при приближении поверхности к наблюдателю. Квадрики (полиномы второй степени) не годятся из-за сложности их гладкой стыковки. Полиномам высоких степеней свойственны осцилляции, что особенно проявляется при интерполяции на большом числе узлов (опорных точек).

Интерполяция, основанная на применении смешивающих функций (blending function) представляет описание координаты k текущей точки поверхности в виде взвешенной суммы некоторых геометрических параметров k_i, зависящих от координат опорных точек:

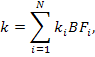
где BF_i – значение смешивающей функции i-ой опорной точки (весовой коэффициент);

N – количество опорных точек.

Из интерполяционных методов, использующих смешивающие функции, следует, прежде всего, назвать сплайн-интерполяцию. Сплайны различного вида, в частности, сплайны Безье и В-сплайны, широко применяются в геометрическом моделировании для описания кусочно-аналитических (составных) поверхностей [2,3]. Сплайн-функции не имеют разрывов первого и второго рода, при определенных условиях точно проходят через опорные точки, поддерживают топологическую тенденцию рельефа поверхности, то есть удовлетворяют сформулированным ранее критериям. Благодаря этим достоинствам сплайны широко применяются для графического представления поверхностей различной формы [4].

Но и сплайны не свободны от недостатков. Это, прежде всего, сложность выделения из «облака» исходных опорных точек тех точек, которые должны стать основой характеристических многогранников сплайновых отсеков. Как известно, форма многогранника (и форма привязанного к нему отсека) задается 16-ю вершинами. Для отсека Безье в качестве четырех угловых вершин могут быть использованы четыре соседние опорные точки скалярного поля, а остальные 12 вершин должны быть доопределены. Для описания отсека В-сплайна среди опорных точек скалярного поля также должны быть выбраны 16 вершин характеристического многогранника. При этом отсек строится вблизи четырех центральных вершин. Далее из прежних 16-ти вершин 12 оставляются, и к ним присоединяются 4 новых вершины. В результате образуется характеристический многогранник для следующего отсека В-сплайна. Построенные отсеки в общем случае не проходят точно через опорные точки. Чтобы обеспечить такое прохождение, нужно сначала найти новые опорные точки, такие, что описанный ими отсек точно пройдет через исходные опорные точки. Выполнять перечисленные операции в массиве неупорядоченных точек скалярного поля алгоритмически весьма затруднительно. Названные трудности дали право Цао Ену, автору еще одной формы геометрического моделирования поверхностей, назвать сплайновую интерполяцию «таинственным искусством» [5]. Кстати, поверхность Цао Ена также основана на применении смешивающих функций и позволяет описывать произвольные геометрические формы. Однако и она не свободна от недостатков, которые подробно описаны в [6].

2. Радиальные базисные функции в задачах визуализации

В последнее время для решения задач интерполяции часто применяются радиальные базисные функции (РБФ) [7,8,9]. В качестве РБФ Φ(r_i) используются различные функции, значения которых зависят от расстояния r_i между двумя точками пространства. Центры РБФ (ядра) совпадают с узлами интерполяции, например, с опорными точками. При вычислении координат промежуточной точки значения РБФ выступают в роли коэффициентов влияния опорных точек на текущую точку. Эти коэффициенты влияния определяются расстояниями от опорных точек до текущей точки.

В задачах интерполяции используют различные РБФ. По размеру области влияния они делятся на два класса. Представители первого из них имеют бесконечно большую область влияния, это, например, мультиквадрик

где с – константа.

Другой класс РБФ образуют функции, влияние которых локализовано в пространстве. Это, например,

инверсный квадрик ,

инверсный мультиквадрик ,

гауссиан ,

где ε – масштабный коэффициент.

Применение РБФ вполне удовлетворяет сформулированным критериям отображения скалярных полей. Применительно к задачам визуализации описания моделируемых с помощью РБФ поверхностей представляются в декартовом пространстве в общей форме [10]:

(1)

где N – количество опорных точек;

Φ(r_i) – РБФ i -ой опорной точки;

x_i, y_i, z_i – координаты i -ой опорной точки;

r_i – расстояние от i -ой опорной точки до текущей точки поверхности;

λ_i – коэффициент влияния РБФ i -ой опорной точки на текущую точку оверхности.

Общая форма описания позволяет находить координаты текущих точек поверхности без дополнительной информации о ее форме. Нахождение текущих координат основано на том или ином законе перебора точек пространства и подстановке координат этих точек в выражение (1). В случае F(x,y,z)=0 точка принадлежит поверхности. Таким путем можно получить промежуточные точки поверхности и принять их за вершины полигональной сетки.

Однако общая форма описания поверхности требует применения специальных приемов для определения коэффициентов λ_i. Действительно, для их нахождения нужно составить систему из N уравнений, неизвестными в которых будут эти коэффициенты. Уравнения составляются из условий прохождения выходной поверхности через N характерных точек с заранее известными координатами. Если в качестве таких характерных точек выбрать опорные точки поверхности, то возникнет система уравнений вида:

где r_i_j – расстояние между i-й и j-й опорными точками.

Условие прохождения выходной поверхности через опорные точки обращает правую часть каждого уравнения системы в ноль, что позволяет получить только тривиальное решение: Чтобы избежать тривиального решения, для описания выходной поверхности используют точки, не принадлежащие этой поверхности, а отстоящие от нее на известное расстояние (в них ). Например, выбирают точки, лежащие на нормалях к поверхности. Обычно восстановление поверхности проводится по неупорядоченному набору точек, тогда процессу построения нормалей должен предшествовать процесс их упорядочивания, например, при помощи триангуляции. После триангуляции нужно найти нормали к пространственным треугольникам и по ним вычислить нормали в опорных точках. Характерные точки на нормалях должны быть выбраны весьма умело, в противном случае выходная поверхность будет искажена [10]. Изложенное показывает, что нахождение характерных точек на нормалях к еще не существующей поверхности – довольно сложный процесс. Кроме того, такой подход не устраняет главного недостатка скалярного поля: нерегулярной расстановки опорных точек и, как следствие, сложности построения полигональной сетки, имеющей желаемую детальность. Участки с редкой расстановкой опорных точек после полигонизации по-прежнему будут иметь «граненый» вид.

3. Визуализация скалярного поля с применением регуляризации расстановки опорных точек

Для минимизации перечисленных трудностей можно предложить следующие приемы:

- перевод исходных опорных точек во вспомогательную параметрическую систему координат;

- регуляризация расстановки опорных точек;

- разбиение модели поверхности на сегменты;

- посегментное построение полигональной сетки в режиме реального времени с использованием табличных вычислений.

Построить полигональную сетку с заданной детальностью несложно, если исходные опорные точки (узлы) расставлены регулярно, то есть с постоянным шагом. Эта задача значительно облегчается при условии, что установлена последовательность расположения опорных точек. Их последовательность можно найти обычной сортировкой координат, если моделируемая поверхность описывается однозначной функцией. Для рассматриваемого случая (привязка значений физической величины к некоторой поверхности) это условие обычно выполняется или может быть выполнено путем перевода опорных точек во вспомогательную систему координат (СК). На рисунках 1,2 этот процесс показан для более наглядного плоского случая.

Опорные точки Р₁, Р₂,…, Р₈ задают линию, которая в исходной системе координат ху описывается многозначной функцией. Точки многозначности, выбранные в качестве примера, на кривых снабжены крестообразными отметками. Многозначность устраняется введением вспомогательной СК. Для незамкнутых поверхностей с небольшой крутизной сегментов в качестве вспомогательной может быть использована декартова СК, как это для плоского случая показано на рисунке 1,б. Теперь кривая на тех же опорных точках может быть описана в параметрической форме, а в качестве параметра принимается аргумент х^* вспомогательной СК. Результатом описания будет однозначная функция.

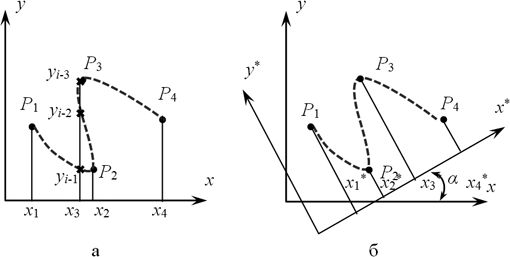
Рис. 1. Многозначная незамкнутая кривая на четырех опорных точках

(а) и устранение многозначности (б) этой кривой

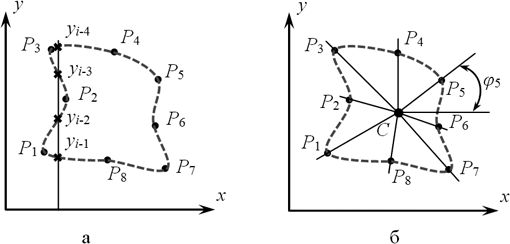
Рис. 2. Многозначная замкнутая кривая на восьми опорных точках

(а) и устранение многозначности (б) этой кривой

Для замкнутых поверхностей и поверхностей, имеющих участки с большой крутизной, в качестве вспомогательной больше подходит сферическая СК, а для плоского случая – полярная (рисунок 2,б). В ней аргументом является полярный угол φ. Параметрическое описание замкнутой поверхности можно представить однозначной функцией. Технология выбора вспомогательной СК и перевода в нее опорных точек будет показана в одной из следующих публикаций.

Теперь влияние опорных точек на текущую точку моделируемой поверхности определяется на поверхности аргументов, а алгоритм построения моделируемой поверхности принимает следующий вид:

- находятся проекции пространственных опорных точек на поверхность аргументов вспомогательной СК;

- на поверхности аргументов организуется обход точек по некоторому регулярному закону. Каждая такая точка принимается за проекцию пространственной текущей точки на поверхность аргументов;

- на поверхности аргументов определяются расстояния между проекциями опорных точек и проекцией текущей точки. Эти расстояния определяют влияние опорных точек поверхности на ее текущую точку;

- вычисляются пространственные координаты текущей точки поверхности по ее параметрическому описанию.

Параметрическое представление моделируемой поверхности с использованием аргументов вспомогательной СК в общем случае имеет вид

(2)

где – расстояние между проекциями i-ой опорной точки и текущей точки поверхности, определенное на поверхности аргументов вспомогательной СК;

λ_х_i, λ_yi, λ_zi, – коэффициенты влияния РБФ i-ой опорной точки на пространственные координаты текущей точки поверхности;

u, v – параметры (аргументы вспомогательной СК).

В описании (2) влияние опорной точки определяется на поверхности аргументов вспомогательной СК. В декартовом пространстве (u≡x^*, v≡y^*) его задает расстояние

, (3)

а в сферической СК (u≡φ, v≡θ) – угловое расстояние

(4)

где – декартовы координаты проекции i-ой опорной точки на плоскость аргументов вспомогательной СК;

– сферические координаты (азимутальный и полярный углы) i-ой опорной точки во вспомогательной СК;

– координаты текущей точки в декартовой и сферической вспомогательных СК.

Чтобы получить описание конкретной моделируемой поверхности, нужно найти N коэффициентов влияния опорных точек по каждой координате: (i=1,..,N), всего 3N коэффициентов. Они находятся из условия прохождения поверхности через опорные точки – раздельно по координатам x, y и z. Для этого на основе каждого из уравнений (2) составляется система из N уравнений, каждое из которых является условием прохождения поверхности через определенную (k-ю) опорную точку по своей координате:

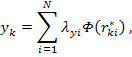
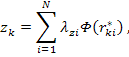
где – расстояние между i-ой и k-ой опорными точками на поверхности аргументов.

На примере первой системы уравнений покажем нахождение коэффициентов . В матричной форме система уравнений имеет вид

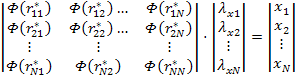или в свернутом виде с очевидными обозначениями – , откуда

Аналогично находятся остальные весовые коэффициенты.

Чтобы упростить алгоритм построения полигональной сетки с желаемой детальностью, нужно перейти к новому набору опорных точек, а именно, – к регулярно расставленным опорным точкам. Регулярная расстановка новых опорных точек достигается с использованием выражений (2),(3),(4) следующим образом. Организуется перебор значений параметров x^*, y^* или по некоторому регулярному закону с заданным шагом. Для каждой очередной пары значений по формуле (3) или (4) находятся и подставляются в систему (2) расстояния (i=1,..,N). Вычисленные по (2) значения дают очередную опорную точку поверхности в СК xyz.

Использование всего количества N опорных точек для описания поверхности выражениями (2) нерационально, так как затягивает вычисления. Это особенно значимо при визуализации протяженных поверхностей. Для сокращения времени вычислений нужно разбить моделируемую поверхность на сегменты, обрабатываемые последовательно, то есть представить поверхность как составную. В этом случае возникает задача гладкой стыковки сегментов. Она решается испытанным методом скользящего окна [6]. Его суть в том, что на множестве опорных точек организуется окно, включающее некоторое ограниченное количество опорных точек N_w, и производится расчет точек сегмента поверхности в центральной части этого окна. Размеры окна больше размеров сегмента, поэтому на текущую точку сегмента влияют не только опорные точки этого сегмента, но и соседние опорные точки. Другими словами, в расчете участвует N_w опорных точек, но сегмент строится на количестве опорных точек N_s<N_w. Далее окно сдвигается на величину сегмента, и строится следующий сегмент. Таким образом, одни и те же опорные точки участвуют в вычислении различных сегментов. Благодаря учету влияния соседних опорных точек составная поверхность оказывается достаточно близкой к желаемому («идеальному») виду. Возникающая при этом погрешность моделирования зависит от выбора РБФ и размеров сегментов и окна. На эту погрешность накладывается погрешность замены криволинейной поверхности полигональной сеткой, которая зависит от шага сетки. Количественные закономерности для названных погрешностей нуждаются в дополнительном исследовании. Следует также отметить, что при разбиении моделируемой поверхности на сегменты имеет смысл использовать РБФ, локализованные в пространстве, например, приведенные выше в качестве примера.

4. Формирование полигональной сетки с применением табличных вычислений

Для снижения затрат памяти графической системы на хранение модели поверхности можно строить полигональную сетку в режиме реального времени. Тогда в памяти будет храниться описание поверхности в виде ограниченного количества регулярно расставленных («новых») опорных точек, а реальная полигональная сетка будет возникать в процессе отображения. Применяемые на практике РБФ довольно сложны в вычислительном отношении, так как включают радикалы, степени, логарифмы [11]. Быстрый алгоритм их вычисления может быть основан на табличном нахождении значении РБФ. Построение полигональной сетки заключается в обходе поверхности аргументов u,v в выражениях (2) с некоторым шагом. Найденные промежуточные точки становятся вершинами полигональной сетки. При регулярной расстановке опорных точек промежуточные точки тоже будут расставлены регулярно (на поверхности аргументов).

Расстояния от опорных точек до промежуточных точек на этой поверхности принимают ограниченное число значений. Соответствующие им значения РБФ могут быть вычислены заранее и занесены в память графической системы. Адреса ячеек памяти будут соответствовать расстояниям Затраты памяти на хранение значений РБФ зависят от требуемой детальности полигональной сетки, то есть от числа промежуточных точек в пределах «клетки» опорных точек. Рисунок 3 иллюстрирует построение полигональной сетки в декартовой СК на плоскости аргументов x^*y^*. На нем клетка из четырех опорных точек разбивается на 32 треугольных полигона.

Рис. 3. Расстояния от опорных точек до вершин
полигональной сетки на плоскости аргументов

Для каждой опорной точки, влияющей на данный фрагмент полигональной сетки, должно быть заранее вычислено 25 расстояний до вершин полигонов. Но общие затраты памяти не связаны с количеством опорных точек прямой зависимостью. Дело в том, что расстояния до вершин, а следовательно, и значения РБФ для многих опорных точек совпадают по величине. Так, на рисунке 3 расстояния от трех опорных точек P_i, P_j, P_k до различных узлов полигональной сетки (на плоскости аргументов) одинаковы:

Для упрощения адресации памяти, хранящей значения РБФ, величины расстояний могут вычисляться в относительных единицах (шагах). Еще одним приемом упрощения адресации является использование вместо расстояний их квадратов, которые имеют в относительных единицах целочисленный формат.

Заключение

Перевод исходных опорных точек во вспомогательную параметрическую систему координат устраняет многозначность описывающей поверхность функции и позволяет простыми средствами установить последовательность расположения исходных опорных точек. Регуляризация расстановки опорных точек помогает регулярно расставить и узлы полигональной сетки, а также упрощает алгоритм ее формирования. Разбиение модели поверхности на сегменты повышает производительность вычислений за счет уменьшения числа слагаемых в выражениях (2). Использование табличных вычислений ускоряет нахождение значений РБФ. Сегментирование поверхности и табличные вычисления позволяют проводить визуализацию скалярного поля в режиме реального времени.

Список литературы

1. Блинова Т.А., Порев В.Н. Компьютерная графика / Под ред. В.Н.Порева. – К.: Издательство Юниор. – 2005. – 520 с.

2. Роджерс Д., Адамс Дж. Математические основы машинной графики. – М.: Мир. – 2001. – 604 с.

3. Голованов Н.Н. Геометрическое моделирование. – М.: Издательство физико-математической литературы. – 2002. – 472 с.

4. Шикин Е.В., Плис А.И. Кривые и поверхности на экране компьютера. Руководство по сплайнам для пользователей. – М.: ДИАЛОГ-МИФИ. – 1996. – 240 с.

5. Вайвил Д., Цао Ен, Тротмэн А. Поверхность Цао Ена: новый подход к геометрическим моделям произвольных форм // Программирование. – 1992. – №4. – С.4–16.

6. Косников Ю.Н. Геометрическое моделирование в графических системах реального времени: монография. – Пенза: Информац.-издат. центр Пенз. гос. ун-та. – 2006. – 218 с.

7. Duchon J. Splines Minimizing Rotation-invariant Semi-norms in Sobolev Spaces // Constructive Theory of Functions of Several Variables. — Berlin : Springer-Verlag, 1977. — № 571. — P. 85—100.

8. Savchenko V., Pasko A., Okunev O., Kunii T. Function representation of solids reconstructed from scattered surface points and contours // Computer Graphics Forum, vol.14, No.4, 1995. – Р.181-188.

9. Carr J. C . Surface interpolation with radial basis functions for medical imaging / J.C. Carr, W.R. Fright, R.K. Beatson // IEEE Trans. Medical Imaging. – 1997. – 16(1) – Р. 96–107.

10. Carr J.C. Reconstruction and Representation of 3D Objects with Radial Basis Function / J.C.Carr, R.K.Beatson, J.B.Cherrie, T.J.Mitchell, W.R.Fright, B.C.McCallum, T.R.Evans // ACM SIGGRAPH 2001. – 2001. – P.67–76.

11. Larsson E., Fornberg B. A Numerical Study of some Radial Basis Function based Solution Methods for Elliptic PDEs // Computers and Mathematics with Applications. – 2003. – №46. – Р.891–902.

APPLICATION OF RADIAL BASIS FUNCTIONS
IN SCIENTIFIC VIZUALIZATION

Y. Kosnikov

Penza state university, Penza, Russia

kosnikov@gmail.com

Annotation

The actions sequence on visualization of a scalar field is offered. Experimental data are presented in many applications by a scalar field. Visual form of its visualization is the surface. It has to be smooth, pass through reference points of a scalar field and to change a review foreshortening. Polygonal and spline visualization on irregularly placed reference points have shortcomings. In article a scalar field representation because of radial basis functions is described. The surface is formed from segments and is described in parametrical coordinates system. It is offered to pass from starting reference points to the new – regularly placed in space. On them the polygonal mesh of demanded detail is formed. Tabular calculations are applied to decrease in time expenses for visualization.

Keywords: scalar field, reference point, radial basis function, regularization, compound surface, tabular calculations.

References

1. Blinova T.A., Porev V.N. Kompyuternaya grafika [Computer Graphics]. – Kiev: publishing house «Junior». – 2005. – 520 p. (In Russian).

2. Rogers D.F., Adams J.A. Matematicheskie osnovy mashinnoy grafiki [Mathematical Elements for Computer Graphics (2nd Edition)]. – New York: McGraw-Hill. – 1990. – 611 р. (In Russian).

3. Golovanov N.N. Geometricheskoe modelirovanie [Geometrical Modeling]. – Moscow: publishing house of physical and mathematical literature. – 2002. – 472 p. (In Russian).

4. Shikin E.V., Plis A.I. Krivye i poverkhnosti na ekrane kompyutera. Rukovodstvo po splaynam dlya polzovateley [Curves and Surfaces on the Computer Screen. The guide to splines for users]. – Moscow: «DIALOG-MIFI». – 1996. – 240 p. (In Russian).

5. Wywill G., Сao En, Trotman A. Poverkhnost TSao Ena: novyy podkhod k geometricheskim modelyam proizvolnykh form [The Cao En Surface: A New Approach to Freeform Geometrical Models]. Programmirovanie [Programming & Computer Software]. – 1992. – vol. 18. – №4. – pp. 135-145. (In Russian).

6. Kosnikov Y.N. Geometricheskoe modelirovanie v graficheskikh sistemakh realnogo vremeni: monografiya [Geometrical Modeling in Real Time Graphic Systems]. Penza: Informats.-izdat. tsentr Penz. gos. un-ta. [Penza: publishing house of Penza State University]. – 2006. – 218 p. (In Russian).

7. Duchon J. Splines Minimizing Rotation-invariant Semi-norms in Sobolev Spaces. Constructive Theory of Functions of Several Variables. — Berlin: Springer-Verlag. – 1977. — № 571. — P. 85—100.

8. Savchenko V., Pasko A., Okunev O., Kunii T. Function Representation of Solids Reconstructed from Scattered Surface Points and Contours. Computer Graphics Forum. – 1995. – vol.14, №4. – Р.181-188.

9. Carr J. C. Surface Interpolation with Radial Basis Functions for Medical Imaging. J.C. Carr, W.R. Fright, R.K. Beatson . IEEE Trans. Medical Imaging. – 1997. – 16(1). – Р. 96–107.

10. Carr J.C. Reconstruction and Representation of 3D Objects with Radial Basis Function. J.C.Carr, R.K.Beatson, J.B.Cherrie, T.J.Mitchell, W.R.Fright, B.C.McCallum, T.R.Evans. ACM SIGGRAPH 2001. – 2001. – P.67–76.

11. Larsson E., Fornberg B. A Numerical Study of some Radial Basis Function based Solution Methods for Elliptic PDEs. Computers and Mathematics with Applications. – 2003. – №46. – Р.891–902.